第十章 (图与网络分析)要点
- 格式:doc
- 大小:3.76 MB
- 文档页数:54









8.1图与网络的基本知识8.1.1图与网络的基本概念8.1.1.1 图的定义自然界和人类社会中,大量的事物以及事物之间的关系,常可以用图形来描述。
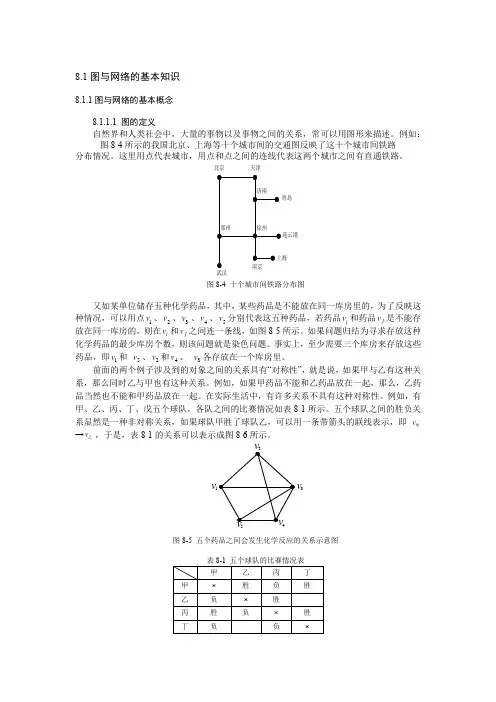
例如:图8-4所示的我国北京、上海等十个城市间的交通图反映了这十个城市间铁路 分布情况。
这里用点代表城市,用点和点之间的连线代表这两个城市之间有直通铁路。
图8-4 十个城市间铁路分布图又如某单位储存五种化学药品,其中,某些药品是不能放在同一库房里的,为了反映这种情况,可以用点、、、、分别代表这五种药品,若药品和药品是不能存放在同一库房的,则在和之间连一条线,如图8-5所示。
如果问题归结为寻求存放这种化学药品的最少库房个数,则该问题就是染色问题。
事实上,至少需要三个库房来存放这些药品,即和、和、各存放在一个库房里。
前面的两个例子涉及到的对象之间的关系具有“对称性”,就是说,如果甲与乙有这种关系,那么同时乙与甲也有这种关系。
例如,如果甲药品不能和乙药品放在一起,那么,乙药品当然也不能和甲药品放在一起。
在实际生活中,有许多关系不具有这种对称性。
例如,有甲、乙、丙、丁、戊五个球队,各队之间的比赛情况如表8-1所示。
五个球队之间的胜负关系显然是一种非对称关系,如果球队甲胜了球队乙,可以用一条带箭头的联线表示,即→,于是,表8-1的关系可以表示成图8-6所示。
图8-5 五个药品之间会发生化学反应的关系示意图北京武汉天津连云港1v 2v 3v 4v 5v i v j v i v j v 1v 5v 2v 4v 3v v 甲v 乙v 3v 145图8-6 五个球队比赛的胜负连线图从以上分析可以看出,我们常将所研究——对象看成一个点,用连线(带箭头或不带箭头)表示对象之间的某种特定的关系,这时连线的长短曲直无关紧要,重要的是两点之间有无线相连。
为了区别起见,把两点之间不带箭头的连线称为边,带箭头的连线称为弧。
由此,我们便抽象出图的概念。
图是描述对象之间某种特定关系的工具,用数字语言描述如下:定义8.1 一个图是由一个非空集合 V ,以及由V 中元素的无序(或有序)对组成的集合E (或A )所组成。
