下载文档原格式
势能函数与保守力的关系势能函数与保守力的关系势能函数和保守力是两个重要的物理概念，它们之间有着密切的关系。
势能函数描述了物体所处的位置的势能大小，而保守力则是指一类物理力，其做功与物体所经过的路径无关。
在本文中，我们将探讨势能函数与保守力之间的关系。
首先，我们需要了解什么是势能函数。
如果一个物体在场中的位置发生了变化，那么它的势能也会发生变化。
在一定条件下，物体的势能与位置之间存在一种确定的数学关系，这种关系就是势能函数。
在物理中，势能函数常常用U(x)来表示，其中X是物体的位置。
其次，我们需要明白什么是保守力。
保守力是指其做功与路径无关的力，也就是说，无论物体经历了怎样的路径，保守力所做的功都是相同的。
在物理中，保守力常常被描述为一类势力，它们的势能变化与位置之间存在确定的数学关系。
接着，我们来看一下势能函数与保守力之间的关系。
势能函数与保守力之间存在着一种紧密的联系，也就是说，如果一个力是保守力，那么它所描述的势能函数一定存在。
反之亦然，如果一个势能函数存在，那么它所描述的力一定是保守力。
这是因为在物理中，只有保守力才能描述为一类势力，保守力的存在必然导致势能函数的存在。
同样的，势能函数的存在也必然说明描述这种情形的力是保守力。
此外，我们还需要了解，保守力的势能函数在很多方面都是唯一的。
也就是说，对于一个特定的保守力，存在着唯一一个势能函数可以描述它，并且这个势能函数的形式是确定的。
这是由保守力的基本特性所决定的。
总结一下，势能函数与保守力之间存在着密切的关系。
保守力可以描述为一类势力，保守力的存在必然导致势能函数的存在。
同样的，势能函数的存在也必然说明所描述的力是保守力。
在大多数情况下，保守力的势能函数都是唯一的，这是由保守力的基本特性所决定的。
深入了解势能函数与保守力之间的关系有助于我们更好地理解物理学的基本概念，进一步提高我们的学术水平。
浅议物理学中的保守力和势能【摘要】保守力和势能在物理学中扮演着重要的角色。
保守力是指不依赖路径的力，其所做的功与路径无关。
势能则是对保守力的一种描述，是可用于确定力学系统状态的函数。
保守力和势能之间存在着密切的关系，一般通过势能函数来确定。
根据保守力和势能的关系，我们可以推导出机械能守恒定律，即在只受保守力的情况下，力学系统的机械能保持不变。
保守力和非保守力的区别在于是否可以用势能来描述。
保守力和势能的重要性体现在它们对力学系统的描述和分析中起到了关键作用，而在物理学中也有着广泛的应用。
为了更深入地理解和探索保守力和势能，未来的研究方向可能会集中在更复杂系统下的运用和拓展。
【关键词】保守力、势能、物理学、性质、关系、确定、守恒定律、区别、重要性、应用、未来研究方向。
1. 引言1.1 保守力的基本概念保守力是物理学中一个非常重要的概念，它在描述物体运动和相互作用过程中起着至关重要的作用。
保守力是一种在物体运动中所做的功与路径无关的力，即对于沿着任意闭合路径作功的保守力，总是零。
这意味着保守力对物体的位移所做的功只依赖于起点和终点，而与具体路径无关。
保守力的基本概念包括以下几个要点：1. 保守力与势能的关系：保守力可以用势能来描述和计算。
势能是对物体在某个力场中位置所储存的能量，而保守力则是通过势能的梯度来定义和推导的。
具体来说，对于一个保守力F，其对应的势能函数为U，满足F = -∇U。
这里的负号表示力是势能的负梯度方向，即力的方向指向势能减小的方向。
2. 势能的引入：为了便于描述和计算保守力对物体的作用，我们引入了势能这一概念。
势能可以是位置的函数，也可以是速度和其他物理量的函数。
通过引入势能，我们可以将关于保守力的问题转化为寻找势能函数和利用势能函数进行计算的问题。
保守力的基本概念包括了与势能的关系和势能的引入。
这些概念在物理学中有着广泛的应用和重要性，对于解决各种运动和相互作用问题都起着至关重要的作用。
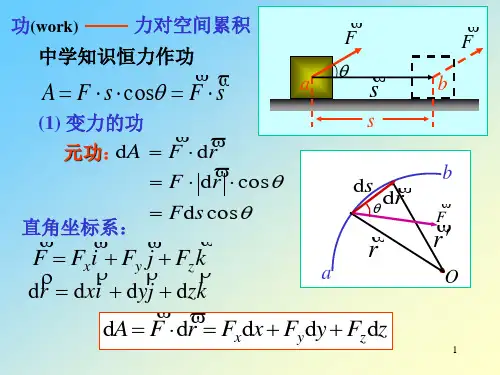
内容摘要详细介绍保守力的特定性质证明以及常见的保守力种类。
定义势能函数，论证了几种常见势能的计算方法。
保守力和势能是经典物理学中极其重要的内容，具有十分重要的研究意义。
为此，学者们在此领域研究十分深入，主要研究保守力和势能之间是怎样的关系，那么什么是保守力呢？保守力的本质是什么？势能又是怎么引入的，势能的定义是什么，以及引入势能后，保守力与势能的关系如何。
关键词：保守力势能势能零点平衡AbstractDetailed introduction of specific properties conservative force proof and common conservative force types. The nature of the potential energy of physical meaning of a deep elaborated, demonstrates the potential of common calculation methodsKey words:Conservative force Potential energy Potential energy zero Balance内容摘要引言 (1)1.保守力 (2)1.1保守力的定义 (2)1.2保守力的性质 (2)1.3保守力的证明 (2)2.势能 (3)2.1势能的定义 (3)2.2势能的性质 (4)2.3势能零点 (5)2.4物体在势能场中的平衡 (7)3.几种常见势能的计算 (7)3.1引力势能 (7)3.2重力势能 (8)3.3弹性势能 (9)3.4电势能 (9)3.5分子势能 (10)4.结束语 (12)5.参考文献 (13)6.致谢 (14)引言保守力和势能是经典物理学中极其重要的内容，具有十分重要的研究意义。
为此，学者们在此领域研究十分深入，主要研究保守力和势能之间是怎样的关系，那么什么是保守力呢？保守力的本质是什么？势能又是怎么引入的，势能的定义是什么，以及引入势能后，保守力与势能的关系如何。
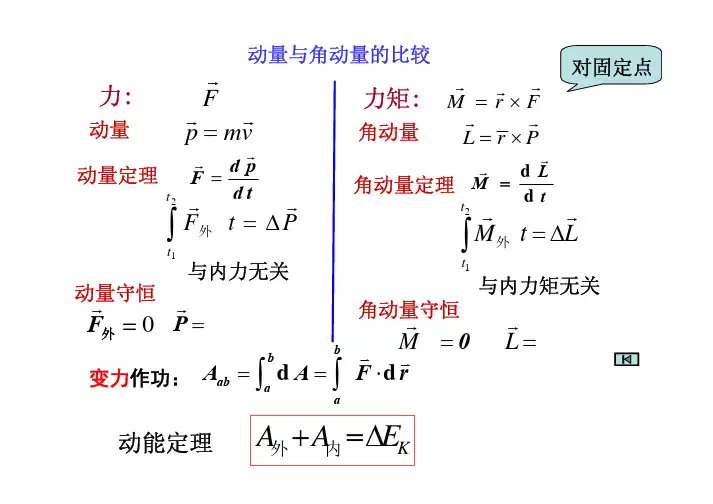
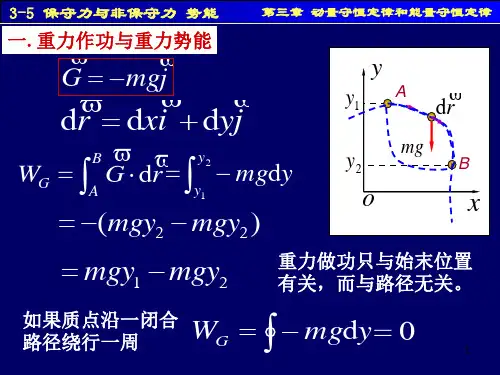
保守力做功和势能变化的关系
保守力做功和势能变化的关系是一个基本的物理原理，它描述了一个物体在受到保守力作用下，其势能的变化与所受的保守力所做的功之间的关系。
首先，我们来定义保守力。
保守力是一个与路径无关的力，它只与物体的位置有关。
这意味着，如果一个物体沿着一个闭合回路运动，受到的保守力所做的总功为零。
常见的保守力有重力和弹性力。
当一个物体受到保守力作用时，它的势能会发生变化。
势能是描述物体位置所具有的能量。
根据势能的定义，势能的变化可以通过将物体从一个位置移动到另一个位置时保守力所做的功来计算。
根据物体在保守力作用下的势能变化，我们可以得出以下关系：
势能变化 = -保守力所做的功
这个关系可以解释为，当保守力对物体做正功时，物体的势能减少；反之，当保守力对物体做负功时，物体的势能增加。
这个关系也可以用数学公式来表示。
假设物体在从位置A移动到位置B时，保守力所做的功为W_AB，物体在位置A的势能为U_A，位置B
的势能为U_B，则势能变化为：
ΔU = U_B - U_A = -W_AB
其中，ΔU表示势能变化。
需要注意的是，这个关系只适用于保守力。
非保守力所做的功不能简单地与势能变化相联系。
非保守力所做的功还需要考虑其他能量转化形式，比如热能、摩擦力等。
总结起来，保守力做功和势能变化之间存在着简单的关系。
势能变化等于保守力所做的功的负值。
这个关系对于理解物体在保守力作用下的运动和能量转化非常重要。
保守力 势能
一，力学中常见力的功
1， 万有引力的功
⎥⎦⎤
⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--==-=⋅=⋅=⎰⎰
⎰a b r r r r r r b
a
r Mm G r Mm G r Mm
G
dr r Mm G
d r r
Mm G -d A b
a b
a
b
a
2
2)(r
r r F
引力做功与路径无关。
2， 重力的功
)
())((a b h h h h y b
a
y x b
a m gh m gh m gdy dy F dy dx F F d A b
a b
a
--=-==
++=
⋅=⎰⎰
⎰⎰j i j i s F
重力做功与路径无关。
3， 弹性力的功
⎪
⎭
⎫ ⎝⎛--=-=⋅-=
⋅=⎰
⎰222
21212
1
a b x x x x b
a kx kx kx dx kx dr F A b
a
b
a
i i
弹性力做功与路径无关。
a b
【例】：试证明力做功与路径无关可表述为：⎰=⋅L
d 0r F
证：0=⋅-⋅=⋅+⋅=⋅⎰⎰⎰⎰⎰b
a
b a
a b
L
b a
d d d d d r F r F r F r F r F
二，保守力
由上可见，万有引力、重力、弹性力作功的特点都是与路径无关；
人们将做功的大小只与物体始末位置有关，而与所经历的路径无关的这类力叫做保守力。
所以万有引力、重力、弹性力均是常见的保守力。
它们都满足关系
0=⋅⎰L
d r F
保
三，势能
由保守力做功的表达式可以看出：
保守力做功＝某个只与质点位置有关的状态量的改变（负号表示“减少”）。
人们将这个只与位置有关的状态量叫“势能”。
通常用E P 表示。
所以 “保守力做功＝势能的减少”可表示为：
)(Pa Pb P E E E A --=∆-＝保
说明：（1）势能是质点系中相互作用的物体所共有的。
单个质点无势能可言。
（2）只有当保守力作为系统内力并做功时系统方可能有势能。
（3）势能差是绝对的，但势能却是相对的，它依赖于势能零点的选择。
()()[]C E C E E E A Pa Pb Pa Pb +-+-=--)(＝保
其中C 为任意常数，选择得当，可以使E P 的表达式获得最简形式。
一般⎪⎪⎩
⎪
⎪⎨⎧
====-=∞=2
21)()0)()0()()(kx x E x m gy y E y r Mm G r E r P P P 长处（弹性势能零点取弹簧原重力势能零点取地面处
处引力势能零点取无穷远
综上所述保守力场中任意一点的势能可表示为：
——物体在保守力场中任意一点的势能等于保守力将它从该点移到零势点所做的功。
四，势能曲线如下：
势能曲线的用途：
1，根据势能曲线可以讨论物体的运动，只有动能为正值时运动才可能发生； 2，利用势能曲线还可以求各个位置保守力
dx
dE F dx F dx F dA dE dA p x x p
-
===-=ϕcos
【例】 一质点在几个力的作用下，沿半径为R 的圆周运动，其中一个力是恒力F=F 0i ，如图所示。
当质点从A 点沿逆时针方向走过四分之三圆周到达B 点时恒力F 所做的功是多少？
解：
⎰⎰⎰-===⋅=-R F dx F Fds d A R
00
0cos θs F
思考：该力是否保守力？
【例】质量为m 的质点在外力作用下，其运动方程为r =Acos ωt i +Bsin ωt j (SI),式中A 、B 、ω都是正常数，试求：
（1）t=0时的速度； （2）t=π/2ω时的速度；
（3）力在t 1=0到t 2=π/2ω这段时间内所做的功。
（4）该力是保守力吗？ 解：
)
(2
1
2121)3(2/)2(0)1(cos sin 222202B A m m v m v A A t B t t B t A dt
d -=-=-====+-==ωωω
πωωωωωi
v j v j i r
v 0
（4）判断该力是否保守力，条件是考察质点运动一周该力做功是否为零。
)(2
121212
22202=-=-===B B m mv mv A B T t ωωj
v
B
【例】竖直悬挂的弹簧振子系由质量为m 、倔强系数为k 的轻弹簧构成。
试求以质点平衡位置为坐标原点和势能零点时，系统势能表达式。
解：取质点、弹簧和地球为系统， 质点平衡处（x=0）： mg kl = 任意位置处（x ） ，质点受合力 kx l x k mg F -=+-=)(
以平衡位置为势能零点，系统势能为
2002
1
)(kx kxdx Fdx x E x x =-==⎰⎰
20
2
02
1)()()()(21
)()(kx x E x E x E m gx
m gdx x E kx klx dx x l k x E G T x G x T =
+=-==+=+-=⎰⎰。
