第五讲——循环码.

智能信息技术导论 - 循环码一、概述循环码是一种在通信领域中广泛使用的编码方式。

它通过在数据中添加冗余位来实现错误检测和纠正的功能。

循环码在数字通信系统、计算机网络、存储系统等领域都有着重要的应用，是保障数据传输可靠性的重要技术手段之一。

二、循环码的原理循环码是一种线性块码，通过在数据位后面添加一系列的冗余位（也称为校验位）来构成编码后的数据。

冗余位的计算方式使循环码的编码、译码实现起来非常高效。

2.1 循环码的生成多项式循环码最重要的参数是生成多项式，它决定了编码和译码的方式。

生成多项式是一个不可分解的多项式，用于生成校验位。

在循环码中，校验位是通过数据位和生成多项式的模2乘法来计算得到的。

2.2 循环码的编码循环码的编码过程实际上就是将数据位和生成多项式进行一系列模2乘法的计算，并将结果作为校验位添加到数据位后面。

编码过程可以通过移位寄存器的方式实现，其中移位寄存器的初始状态为全0。

2.3 循环码的译码循环码的译码过程主要是通过计算接收到的编码数据位和生成多项式的模2除法来还原数据位。

译码过程中，接收到的编码数据位会与寄存器中的状态进行模2除法的计算，得到的结果会作为冗余位进行错误检测。

三、循环码的性质循环码具有许多重要性质，这些性质使得循环码在实际应用中具有较好的性能。

3.1 线性性质循环码满足线性性质，即两个编码字的异或结果仍然是一个有效的编码字。

这种性质使得循环码可以方便地进行编码和译码操作。

3.2 最小距离性质循环码的最小距离决定了它所能检测和纠正的错误的能力。

最小距离越大，循环码的纠错能力越强。

在设计循环码时，需要考虑到数据传输过程中可能出现的各种错误类型，以便选择合适的生成多项式和编码长度。

3.3 循环码的循环性循环码具有循环性，即将一个编码字进行循环移位后所得到的码字仍然是一个有效的编码字。

该性质使得循环码在传输过程中可以通过循环移位将错误传播到多个位上，从而提高错误的检测和纠正的能力。

8.5 循环码循环码是线性分组码中最重要的一个子类码，它的基本特点是编码电路及伴随式解码电路简单易行；循环码代数结构具有很多有用的特性，便于找到有效解码方法。

因此在实际差错控制系统中所使用的线性分组码，几乎都是循环码。

下面将介绍循环码的多项式表示及其性质，同时简介几种重要的循环码，CRC、BCH和R-S 码等。

8.5.1 循环码的描述1. 码多项式及其运算通式表示为：（8-69）于是称与为“同余”式，即[模]（8-70）如：则[模] 即能被整除利用这一运算原理，我们可对一个码字进行移位表示：如：的多项式表示为：使码组向左移2位（循环）则有对应多项式然后以去除得：这一结果表明，以作除法运算（称模）后，即与为同余因此，（模）应注意，利用这种同余式表示，必须加注（模），否则就不明确在什么条件下得到的这一同余关系式。

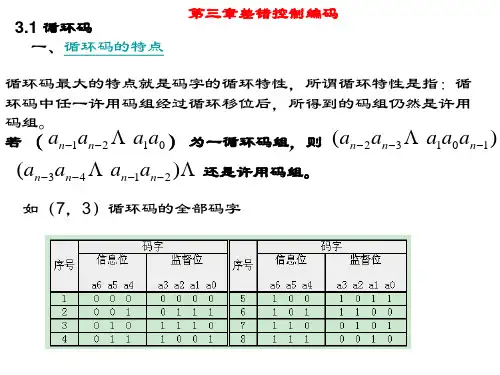
2.循环码的构成循环码的构成突出特点是只要是该码中的一个许用码组——码字，通过循环位其结果则可包括全部个非全0码字，如上面介绍的（7，3）分组码，从信码位0 0 1构成的码字（0011101）开始逐一向左（或者向右）移一位，可得其余6个码字：（0111010）、（1110100）、（1101001）、（1010011）、（0100111）、（1001110）。

若把这些码字写成码多项式，都具有同一个移位运算模式，并设（0011101）对应的码多项式，于是，有：（模)（8-71）这样，就构成了（7，3）循环码，如表8-4。

从表8-4看出，循环得到的（7，3）码，仍为系统码，信息码组均在表中码字的高位（左方）。

表8-4 （7，3）循环码移位（7，3）码码多项式（模）0 0 0 1 1 1 0 11 0 1 1 1 0 1 02 1 1 1 0 1 0 03 1 1 0 1 0 0 14 1 0 1 0 0 1 15 0 1 0 0 1 1 16 1 0 0 1 1 1 08.5.2 循环码生成多项式与生成矩阵1. 生成多项式由表8-4构成个非全0码字多项式的过程与结果看，我们从开始进行逐一循环，并以模运算，该码字正是信码组中最低位为1，对应码字多项式，在全部非全0码字中，它的最高位阶次也最低，并等于，即最高次项为，随后一系列码字都源于它的移位而形成，因此称其为生成多项式，即（8-72）然后再从的因式分解来进一步分析（8-73）我们可以将三个既约多项式因式任意组合成两个因式，可有（8-74）如：（8-75）（8-76）其中可以组合为二因式中包含最高次为4次的情况有两种，即展开式的第4及第5两组，都可以作为阶次最高为4的即（8-77）（8-78）在展开式中选用了其中一个（组合）因式为后，余下一个因式，则称其为循环码的监督多项式，如式（8-74）生成多项式与相应监督多项式乘积等于多项式。

循环码的原理及应用1. 背景介绍循环码是一种在计算机科学和信息通信领域应用广泛的编码技术。

它通过在数据中引入冗余信息，以便在传输过程中能够检测和纠正错误。

循环码不仅具有较强的错误检测和纠正能力，而且其编码和解码算法相对简单，可以在现有硬件平台上快速实现。

因此，它在诸如数据存储、通信协议、数字广播等领域得到了广泛的应用。

2. 循环码的原理循环码是一种纠错码，其基本原理是通过在待发送的数据中插入冗余位，使得发送方和接收方能够通过对数据进行简单的计算，检测和纠正传输过程中引入的错误。

循环码的核心概念是生成多项式和校验多项式。

生成多项式用于在发送方将数据进行编码，而校验多项式则用于在接收方检测和纠正传输中的错误。

具体来说，循环码将数据看作一个多项式，每个传输的数据位对应于多项式中的一个系数。

生成多项式是一个除法因子，它的阶数对应于冗余位的数量。

发送方将数据多项式与生成多项式相除，得到商多项式和余数多项式。

商多项式作为编码后的数据发送，余数多项式则添加到数据中作为冗余位。

接收方在接收到编码后的数据后，对接收到的多项式进行除法运算。

如果余数多项式为0，则表示没有错误；否则，余数多项式的系数对应于错误的位置，接收方可以根据这些错误位置进行纠正。

3. 循环码的应用3.1 数据存储循环码被广泛应用于数据存储系统中，例如硬盘驱动器和光盘。

在存储数据时，为了保证数据不被损坏，硬盘驱动器和光盘通常会采用循环码进行错误检测和纠正。

3.2 通信协议循环码也被广泛应用于各种通信协议中，例如以太网和蓝牙。

在大规模的数据通信中，循环码可以有效地检测和纠正传输过程中引入的比特错误。

3.3 数字广播在数字广播领域，循环码被用于对广播信号进行纠错。

通过在数字广播信号中引入循环码，接收方能够检测和纠正由于信号传输过程中引入的噪声和干扰导致的错误。

4. 总结循环码作为一种广泛应用的编码技术，具有较强的错误检测和纠正能力，以及简单的编码和解码算法。

10.4 循环码·循环码是线性分组码中最重要的一个子类。

·循环码除了具有线性分组码的封闭性外，还具有一个独特的特点：循环性。

所谓循环性是指：一个()k n ,循环码中每个码组经任意循环移位之后，仍然是一个码组。

表10.4.1给出了一种（7，3）循环码的全部码组。

其中，全零码组自身形成一个封闭的自我循环，其余码组形成一个周期为7=n 循环环。

可见，循环码是指它的任一码组循环移位后仍然是码组，而不是所有码组都可由一个码组循环而得。

·循环码的这一外在特点，给循环码的编译码实现带来了便利。

目前，实用差错控制系统中所使用的线性分组码几乎都是循环码或循环码的子类(如BCH 等)。

10.4.1 循环码的多项式描述1. 码多项式定义：码组A = ()011,,,a a a n Λ-的码多项式为()0111a x a x a x T n n +++=--Λ （10.4.1） 例如，码组A =（1100101）可以表示为()1256+++=x x x x T 。

在码多项式中，x 的幂次指示码元的位置，其系数代表码元的取值。

因此，我们并不关心x 本身的值。

2. 码多项式的按模运算在码多项式运算中也有类似的按模运算。

若一任意多项式()x F 被一n 次多项式()x N 除，得到商式()x Q 和一个次数小于n 的余式()x R ，即()()()()()x N x R x Q x N x F += （10.4.2） 或 ()()()()x R x Q x N x F += （10.4.3） 则在模()x N 运算下()()()[]x N x R x F m od ≡ （10.4.4）这里，码多项式系数仍按模2运算，即只取值0和1。

例10.4.1 124++x x 被13+x 除，求余式。

解 用长除法注意，由于在模2运算中，用加法代替了减法，故余式不是12+-x x 而是12++x x 。

111132324++++=+++x x x x x x x ()1mod 113224+++≡++x x x x x3. 循环码多项式的模运算把一个码组表示成码多项式的形式后，循环码的循环特性可按如下方式表示。

循环码的定义和特性定义循环码是一种具有循环特性的线性分组码。

它将k位信息位编码成n位码字，其中n-k为冗余位，用于检测和纠正错误。

特性循环码的两个重要特性是封闭性和循环性。

封闭性指的是两个循环码的和仍然是循环码；循环性指的是循环码的任意循环移位后的结果仍然是循环码。

循环码译码的原理工业控制在工业控制系统中，循环码的译码可用于数据传输的错误检测和纠正，确保控制系统的稳定性和安全性。

循环码译码的应用场景通信领域循环码在数字通信中应用广泛，如移动通信、卫星通信等。

在这些场景中，循环码的译码用于检测和纠正传输过程中的误码，提高通信质量。

存储领域在数据存储领域，如固态硬盘（SSD）、光盘等存储介质中，循环码的译码用于纠正存储数据的错误，提高数据的可靠性和完整性。

航空航天在航空航天领域，由于空间环境恶劣，通信链路容易受到干扰，循环码的译码对于确保航天器与地面站之间的可靠通信具有重要意义。

循环码的编码方法线性反馈移位寄存器法生成多项式法硬判决译码：硬判决译码方法是对接收到的信号进行量化，然后进行译码。

这种方法简单直接，但在低信噪比下性能较差。

循环码的译码方法软判决译码：与硬判决译码不同，软判决译码充分利用了接收信号的幅度信息，提高了译码性能。

但软判决译码实现复杂度相对较高。

迭代译码：迭代译码方法通过多次迭代，逐步逼近正确码字，以提高译码性能。

这种方法在长码长和高纠错能力下具有优势。

以上各种方法各有特点，在实际应用中，需根据具体场景和需求选择合适的方法。

循环码的纠错能力最小距离与纠错能力纠错算法纠错能力定义循环码的误码性能误码性能定义误码率与信噪比仿真与分析与其他码字的比较这是一种迭代算法，用于确定错误位置多项式并纠正错误。

BM算法是循环码译码中最常用的算法之一，具有高效和准确的特点。

BM（Berlekamp-Massey）算法该算法基于欧几里得算法求解最大公约数，能够找到错误图样，并用于纠正循环码中的错误。

相比于BM 算法，欧几里得算法在某些情况下更加简单。