拉普拉斯变换的基本性质、变换及反变换

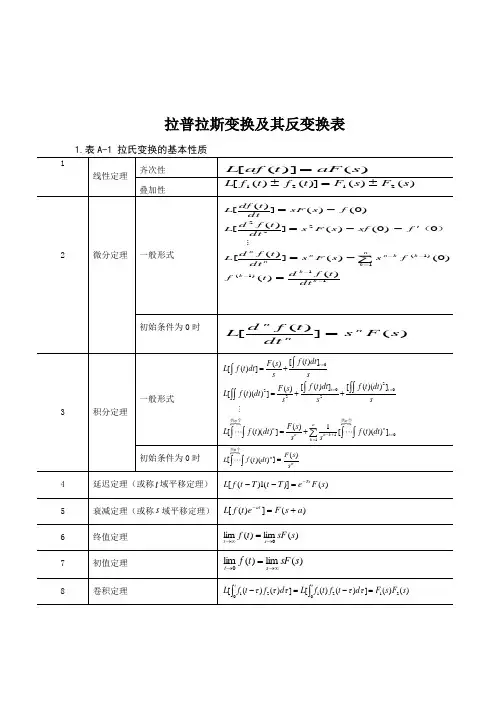
拉普拉斯变换及反变换1.拉氏变换的基本性质表-1 拉氏变换的基本性质1()([n n k f t dt s s-+=+∑⎰个2．常用函数的拉氏变换和z 变换表表-2 常用函数的拉氏变换和z 变换表3． 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

设)(s F 是s 的有理真分式，即1110111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==---- （m n >） 式中，系数n n a a a a ,,...,,110-和011,,,,m m b b b b -都是实常数；n m ,是正整数。

按代数定理可将)(s F 展开为部分分式。

分以下两种情况讨论。

（1）0)(=s A 无重根：这时，F(s)可展开为n 个简单的部分分式之和的形式，即∑=-=-++-++-+-=ni ii n n i i s s c s s c s s c s s c s s c s F 12211)( （1）式中，n s s s ,,,21 是特征方程A(s)＝0的根；i c 为待定常数，称为()F s 在i s 处的留数，可按下列两式计算：lim()()ii i s s c s s F s →=- （2）或iss i s A s B c ='=)()( （3）式中，)(s A '为)(s A 对s 的一阶导数。

根据拉氏变换的性质，从式（F-1）可求得原函数为[]⎥⎦⎤⎢⎣⎡-==∑=--n i i i s s c L s F L t f 111)()(＝1in s ti i c e =∑ (4)（2）0)(=s A 有重根：设0)(=s A 有r 重根1s ，F(s)可写为())()()()(11n r r s s s s s s s B s F ---=+=nn i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++-- 11111111)()()( 式中，1s 为F(s)的r 重根，1+r s ，…，n s 为F(s)的n r -个单根；其中，1+r c ，…，n c 仍按式(F-2)或式(F-3)计算，r c ，1-r c ，…，1c 则按下式计算：)()(lim 11s F s s c r s s r -=→11lim[()()]ir r s s dc s s F s ds-→=-)()(lim !11)()(1s F s s dsd j c r j j s s jr -=→- (5))()(lim )!1(11)1()1(11s F s s dsd r c r r r s s --=--→原函数)(t f 为 [])()(1s F Lt f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L 111111111)()()( t s nr i i t s r r r r ie c e c t c t r c t r c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-=1122111)!2()!1( （6）。

函数的拉普拉斯变换与逆变换定义函数f(t)的拉普拉斯变换定义为：F(s)=∫e−st∞f(t)dt其中s是一个复数变量。

性质拉普拉斯变换具有以下性质：1.线性性：对于任意常数a和b，以及函数f(t)和g(t)，有：L[af(t)+bg(t)]=aL[f(t)]+bL[g(t)]2.时移性：对于任意常数a，有：L[f(t−a)u(t−a)]=e−as F(s)其中u(t)是单位阶跃函数。

3.微分性：对于任意可导函数f(t)，有：L[f′(t)]=sF(s)−f(0)L[f″(t)]=s2F(s)−sf(0)−f′(0)4.积分性：对于任意可积函数f(t)，有：L[∫ft0(τ)dτ]=F(s)s5.卷积定理：对于任意两个函数f(t)和g(t)，有：L[f(t)∗g(t)]=F(s)G(s)其中∗表示卷积运算。

应用拉普拉斯变换在许多领域都有应用，包括：1.微分方程的求解：拉普拉斯变换可以将微分方程转化为代数方程，从而更容易求解。

2.信号处理：拉普拉斯变换可以用于分析和处理信号。

3. 控制理论：拉普拉斯变换可以用于分析和设计控制系统。

4. 电路分析：拉普拉斯变换可以用于分析和设计电路。

逆拉普拉斯变换拉普拉斯变换的逆变换定义为：f (t )=12πi ∫e st γ+i∞γ−i∞F (s )ds 其中 γ 是一个大于所有 F (s ) 的奇点实部的常数。

性质逆拉普拉斯变换具有以下性质：1. 线性性：对于任意常数 a 和 b ，以及函数 f (t ) 和 g (t )，有：L −1[aF (s )+bG (s )]=aL −1[F (s )]+bL −1[G (s )]2. 时移性：对于任意常数 a ，有：L −1[e as F (s )]=f (t −a )u (t −a )3. 微分性：对于任意可导函数 F (s )，有：L −1[sF (s )]=f′(t )L −1[s 2F (s )]=f″(t )4. 积分性：对于任意可积函数 F (s )，有：L −1[F (s )s ]=∫f t 0(τ)dτ 5. 卷积定理：对于任意两个函数 F (s ) 和 G (s )，有：L −1[F (s )G (s )]=f (t )∗g (t )应用逆拉普拉斯变换在许多领域都有应用，包括：1. 微分方程的求解：逆拉普拉斯变换可以将代数方程转化为微分方程，从而更容易求解。

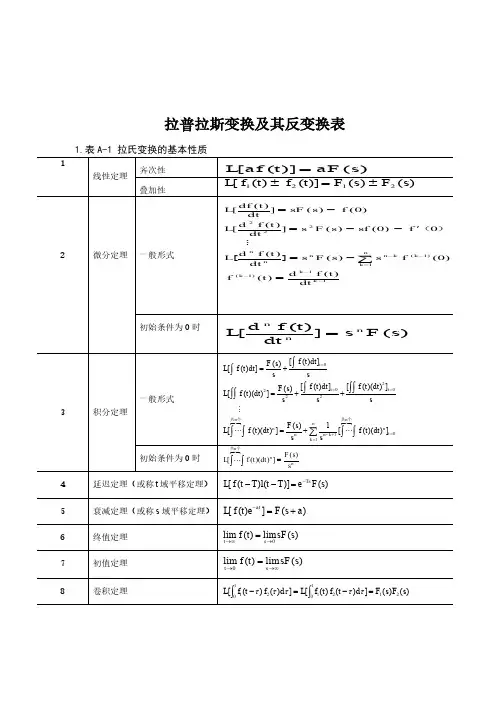
拉普拉斯变换及其反变换表3． 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

设)(s F 是s 的有理真分式11n 1n nn11m 1m mmas a s a s a b s b s b s b )s (A )s (B )s (F ++++++++==---- （m n >）式中系数n1n 1a ,a ,...,a ,a-，m1m 1b ,b ,b ,b - 都是实常数；n m ,是正整数。

按代数定理可将)(s F 展开为部分分式。

分以下两种情况讨论。

① 0)(=s A 无重根这时，F(s)可展开为n 个简单的部分分式之和的形式。

∑=-=-++-++-+-=n1i iinnii2211ss cs s c s s c s s c s s c )s (F 式中，Sn 2S 1S ，，， 是特征方程A(s)＝0的根。

i c 为待定常数，称为F(s)在i s 处的留数，可按下式计算： )s (F )s s (lim c is s i-=→或is s i)s (A )s (B c='=式中，)(s A '为)(s A 对s 的一阶导数。

根据拉氏变换的性质，从式（F-1）可求得原函数[]t s n 1i i n 1i i i 11i e c s s cL )s (F L )t (f -==--∑∑=⎥⎦⎤⎢⎣⎡-==② 0)(=s A 有重根设0)(=s A 有r 重根1s ，F(s)可写为())s s ()s s ()s s ()s (B s F n1r r 1---=+=nnii1r 1r 111r 11r r 1rss cs s c s s c )s s (c )s s (c )s s (c -++-++-+-++-+-++-- 式中，1s 为F(s)的r 重根，1+r s ，…, n s 为F(s)的n-r 个单根；其中，1+r c ，…, n c 仍按式(F-2)或(F-3)计算，r c ，1-r c ，…, 1c 则按下式计算：)s (F )s s (lim c r1s s r-=→)]s (F )s s ([dsdlim c -=)s (F )s s (dsd lim !j 1c -=)s (F )s s (dsdlim )!1r (1c --=原函数)(t f 为 [])()(1s F L t f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=s s cs s c s s c )s s (c )s s (c )s s (c L e c e c t c t )!2r (c t )!1r (c ∑+⎥⎦⎤⎢⎣⎡+++-+-= （F-6）。

附录A 拉普拉斯变换及反变换1.表A-1 拉氏变换的基本性质4198 卷积定理)()(])()([])()([21021021s F s F d t f t f L d f t f L tt =−=−∫∫τττττ2．表A-2 常用函数的拉氏变换和z 变换表4203． 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

设是的有理真分式)(s F s 01110111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==−−−−L L （） m n >式中系数，都是实常数；是正整数。

按代数定理可将展开为部分分式。

分以下两种情况讨论。

n n a a a a ,,...,,110−m m b b b b ,,,110−L n m ,)(s F ① 无重根0)(=s A 这时，F(s)可展开为n 个简单的部分分式之和的形式。

∑=−=−++−++−+−=ni ii n n i i s s c s s c s s c s s c s s c s F 12211)(L L （F-1）式中，是特征方程A(s)＝0的根。

为待定常数，称为F(s)在处的留数，可按下式计算： n s s s ,,,21L i c i s （F-2）)()(lim s F s s c i s s i i−=→或iss i s A s B c =′=)()( （F-3）式中，为对)(s A ′)(s A s 的一阶导数。

根据拉氏变换的性质，从式（F-1）可求得原函数[]⎥⎦⎤⎢⎣⎡−==∑=−−n i i i s s c L s F L t f 111)()(＝ (F-4)ts n i i ie c −=∑1②有重根 0)(=s A 设有r 重根，F(s)可写为0)(=s A 1s ())()()()(11n r rs s s s s s s B s F −−−=+L 421=nn i i r r r r r r s s c s s c s s c s s c s s c s s c −++−++−+−++−+−++−−L L L 11111111)()()( 式中，为F(s)的r 重根，，…, 为F(s)的n-r 个单根；1s 1+r s n s 其中，，…, 仍按式(F-2)或(F-3)计算，，，…, 则按下式计算： 1+r c n c r c 1−r c 1c)()(lim 11s F s s c r s s r −=→)]()([lim111s F s s dsdc r s s r −=→− M)()(lim !11)()(1s F s s dsd j c r j j s s jr −=→− (F-5) M)()(lim )!1(11)1()1(11s F s s dsd r c r r r s s −−=−−→原函数为 )(t f[])()(1s F Lt f −=⎥⎦⎤⎢⎣⎡−++−++−+−++−+−=++−−−n n i i r r r r r r s s c s s c s s c s s c s s c s s c L L L L 111111111)()()( t s nr i i t s r r r r ie c e c t c t r c t r c ∑+=−−−+⎥⎦⎤⎢⎣⎡+++−+−=1122111)!2()!1(L （F-6）4224.2.10 性质表及常用变换表为了便于查阅和应用，最后，将单边拉普拉斯变换的性质和常用单边拉普拉斯变换分别列于表4.1和4.2表中。

常用拉普拉斯变换及反变换拉普拉斯变换在工程和数学中是个非常实用的工具。

它不仅能帮助我们解决微分方程，还能简化许多复杂的问题。

今天我们就来聊聊常用的拉普拉斯变换和反变换，看看它们是如何发挥作用的。

一、拉普拉斯变换的基本概念1.1 定义拉普拉斯变换是一个积分变换，它将时间域的函数转换为复频域的函数。

简单来说，它把一个函数从“时间的世界”带到了“频率的世界”。

公式上，拉普拉斯变换可以表示为：\[ \mathcal{L}\{f(t)\} = F(s) = \int_0^{\infty} e^{-st} f(t) dt \]这里的 \( s \) 是复数变量，\( f(t) \) 是我们要变换的时间域函数，\( F(s) \) 则是变换后的结果。

1.2 性质拉普拉斯变换有几个重要的性质，比如线性性、时间延迟和微分等。

这些性质使得在实际应用中，可以灵活地对待不同类型的函数。

例如，线性性让我们可以把两个函数的变换简单相加，这对于解决复杂问题很有帮助。

二、常用的拉普拉斯变换2.1 单位阶跃函数单位阶跃函数 \( u(t) \) 是拉普拉斯变换中最常用的函数之一。

它的变换结果是：\[ \mathcal{L}\{u(t)\} = \frac{1}{s} \]这个简单的公式为很多工程应用奠定了基础，因为很多信号和系统可以用阶跃函数来描述。

2.2 指数函数另一个常见的函数是指数函数 \( e^{at} \)。

它的拉普拉斯变换结果为：\[ \mathcal{L}\{e^{at}\} = \frac{1}{s - a} \]这在处理自然衰减或增长的过程时特别有用，比如在电子电路中，我们经常会遇到这种情况。

2.3 正弦和余弦函数正弦和余弦函数的拉普拉斯变换也很重要。

它们分别为：\[ \mathcal{L}\{\sin(\omega t)\} = \frac{\omega}{s^2 + \omega^2} \] \[ \mathcal{L}\{\cos(\omega t)\} = \frac{s}{s^2 + \omega^2} \]这些变换结果在振动分析和控制系统中应用广泛，帮助我们理解系统的频率响应。

4194204213． 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

设)(s F 是s 的有理真分式1110111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==---- （m n >） 式中系数n n a a a a ,,...,,110-，m m b b b b ,,,110- 都是实常数；n m ,是正整数。

按代数定理可将)(s F 展开为部分分式。

分以下两种情况讨论。

① 0)(=s A 无重根这时，F(s)可展开为n 个简单的部分分式之和的形式。

∑=-=-++-++-+-=ni ii n n i i s s c s s c s s c s s c s s c s F 12211)( （F-1）式中，n s s s ,,,21 是特征方程A(s)＝0的根。

i c 为待定常数，称为F(s)在i s 处的留数，可按下式计算： )()(lim s F s s c i s s i i-=→ （F-2）或iss i s A s B c ='=)()( （F-3）式中，)(s A '为)(s A 对s 的一阶导数。

根据拉氏变换的性质，从式（F-1）可求得原函数422[]⎥⎦⎤⎢⎣⎡-==∑=--n i i i s s c L s F L t f 111)()(＝ts n i i ie c -=∑1(F-4) ② 0)(=s A 有重根设0)(=s A 有r 重根1s ，F(s)可写为())()()()(11n r rs s s s s s s B s F ---=+ =nn i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++-- 11111111)()()( 式中，1s 为F(s)的r 重根，1+r s ，…, n s 为F(s)的n-r 个单根；其中，1+r c ，…, n c 仍按式(F-2)或(F-3)计算，r c ，1-r c ，…, 1c 则按下式计算：)()(lim 11s F s s c r s s r -=→)]()([lim111s F s s dsdc r s s r -=→-)()(lim !11)()(1s F s s dsd j c r j j s s jr -=→- (F-5))()(lim )!1(11)1()1(11s F s s dsd r c r r r s s --=--→原函数)(t f 为 [])()(1s F Lt f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L 111111111)()()( t s nr i i t s r r r r ie c e c t c t r c t r c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-=1122111)!2()!1( （F-6）。

函数的拉普拉斯变换和反变换的性质函数的拉普拉斯变换和反变换是数学中的重要概念，它们被广泛应用于控制理论、信号处理、电路分析等领域。

在实际应用中，我们需要了解函数的拉普拉斯变换和反变换的性质，以便更好地理解这些概念。

下面我将从理论和实际应用两方面，分别探讨函数的拉普拉斯变换和反变换的性质。

函数的拉普拉斯变换的性质首先，我们来看函数的拉普拉斯变换的基本性质：1. 线性性：如果f(t)和g(t)的拉普拉斯变换分别为F(s)和G(s)，那么af(t)+bg(t)的拉普拉斯变换为aF(s)+bG(s)，其中a和b是实数或复数。

2. 移位性：如果f(t)的拉普拉斯变换为F(s)，那么f(t-a)的拉普拉斯变换为e^(-as)F(s)。

这意味着，在时间上移动f(t)相当于在频率域上乘以一个指数函数e^(-as)。

3. 导数性质：如果f(t)的导数为f'(t)，那么f(t)的拉普拉斯变换为F(s)，f'(t)的拉普拉斯变换为sF(s)-f(0)，其中f(0)是f(t)在t=0时的值。

4. 积分性质：如果f(t)的积分为F_0(t)，那么f(t)的拉普拉斯变换为F(s)/s，其中F(s)是f(t)的拉普拉斯变换。

5. 移位定理：如果f(t)的拉普拉斯变换为F(s)，那么f(t-a)的拉普拉斯变换为e^(-as)F(s)。

这意味着，在时间上移动f(t)相当于在频率域上乘以一个指数函数e^(-as)。

上述性质是函数的拉普拉斯变换的基本性质，可以帮助我们更好地理解函数的拉普拉斯变换。

函数的反变换的性质接下来，我们来看函数的反变换的性质。

函数的反变换实际上是将函数从频率域转换回时域，因此它的性质更加重要。

对于函数F(s)，记它的反变换为f(t)，即F(s)的反变换为f(t)=L^(-1){F(s)}。

则函数的反变换的性质如下：1. 线性性：如果F_1(s)和F_2(s)的反变换分别为f_1(t)和f_2(t)，那么aF_1(s)+bF_2(s)的反变换为af_1(t)+bf_2(t)。