当前位置：文档之家 › 运筹学-图论4

运筹学-图论4

  • 格式：ppt
  • 大小：340.50 KB
  • 文档页数：31

下载文档原格式

  / 31

合集下载

《运筹学》试题及答案大全

《运筹学》试题及答案大全

《运筹学》试题及参考答案一、填空题（每空2分，共10分）1、在线性规划问题中，称满足所有约束条件方程和非负限制的解为可行解。

2、在线性规划问题中，图解法适合用于处理变量为两个的线性规划问题。

3、求解不平衡的运输问题的基本思想是设立虚供地或虚需求点，化为供求平衡的标准形式。

4、在图论中，称无圈的连通图为树。

5、运输问题中求初始基本可行解的方法通常有最小费用法、西北角法两种方法。

二、（每小题5分，共10分）用图解法求解下列线性规划问题：1）max z =6x 1+4x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤+0781022122121x x x x x x x ，解：此题在“《运筹学》复习参考资料.doc ”中已有，不再重复。

2）min z =－3x 1+2x 2⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤-≤-≤+-≤+0,137210422422121212121x x x x x x x x x x 解：可行解域为abcda ，最优解为b 点。

⑴⑵⑶⑷⑸⑹、⑺由方程组⎩⎨⎧==+02242221x x x 解出x 1=11，x 2=0∴X *=⎪⎪⎭⎫⎝⎛21x x =（11，0）T∴min z =－3×11+2×0=－33三、（15分）某厂生产甲、乙两种产品，这两种产品均需要A 、B 、C 三种资源，每种产品的资源消耗量及单位产品销售后所能获得的利润值以及这三种资源的储备如下表所示：AB C 甲94370乙46101203602003001）建立使得该厂能获得最大利润的生产计划的线性规划模型；（5分）2）用单纯形法求该问题的最优解。

（10分）解：1）建立线性规划数学模型：设甲、乙产品的生产数量应为x 1、x 2，则x 1、x 2≥0，设z 是产品售后的总利润，则max z =70x 1+120x 2s.t.⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+0300103200643604921212121x x x x x x x x ，2）用单纯形法求最优解：加入松弛变量x 3，x 4，x 5，得到等效的标准模型：max z =70x 1+120x 2+0x 3+0x 4+0x 5s.t.⎪⎪⎩⎪⎪⎨⎧=≥=++=++=++5,...,2,1,03001032006436049521421321j x x x x x x x x x x j 列表计算如下：四、（10分）用大M 法或对偶单纯形法求解如下线性规划模型：min z =5x 1＋2x 2＋4x 3⎪⎩⎪⎨⎧≥≥++≥++0,,10536423321321321x x x x x x x x x 解：用大M 法，先化为等效的标准模型：max z /=－5x 1－2x 2－4x 3s.t.⎪⎩⎪⎨⎧=≥=-++=-++5,...,2,1,010********214321j y x x x x x x x x j增加人工变量x 6、x 7，得到：max z /=－5x 1－2x 2－4x 3－M x 6－M x 7s.t⎪⎩⎪⎨⎧=≥=+-++=+-++7,...,2,1,010*********2164321j x x x x x x x x x x x j大M 法单纯形表求解过程如下：五、（15分）给定下列运输问题：（表中数据为产地A i 到销地B j 的单位运费）B 1B 2B 3B 4s iA 1A 2A 312348765910119108015d j82212181）用最小费用法求初始运输方案，并写出相应的总运费；（5分）2）用1）得到的基本可行解，继续迭代求该问题的最优解。

运筹学(第四版)清华大学出版社《运筹学》教材编写组-第1章 绪论课件PPT

运筹学(第四版)清华大学出版社《运筹学》教材编写组-第1章 绪论课件PPT


❖ 在运筹学中除常用的数学方法以外，还引入 一些非数学方法和理论。
❖ 美国运筹学家沙旦(T.L.Saaty)，在20世纪70 年代末提出了层次分析法(AHP)。
❖ 切克兰特(P.B.Checkland)把传统的运筹学方 法称为硬系统思考，它适用于解决那种结构 明确的系统以及战术和技术性问题，而对于 结构不明确的，有人参与活动的系统就不太 胜任了。这就应采用软系统思考方法。
（例如投入产出方法）。在当时这些先遣者中，越民义先
生、刘源张院士、朱永津教授、桂湘云教授、陈锡康教授、
徐光煇教授、韩继业教授、李秉全教授、郭绍僖教授等。
2021/3/10
2
第2节 运筹学的性质和特点
❖ 运筹学是一门应用科学，至今还没有统一且 确切的定义。
❖ 莫斯(P.M.Morse)和金博尔(G.E.Kimball)曾对 运筹学下的定义是：“为决策机构在对其控 制下业务活动进行决策时，提供以数量化为 基础的科学方法。”
❖ 以上过程应反复进行。
2021/3/10
6
第4节 运筹学的模型
模型有三种基本形式： ❖ ①形象模型； ❖ ②模拟模型； ❖ ③符号或数学模型。
2021/3/10
7
构模的方法和思路有以下五种：
❖ (1) 直接分析法 ❖ (2) 类比法 ❖ (3) 数据分析法 ❖ (4) 试验分析法 ❖ (5) 想定(构想)法(scenario)
2021/3/10
12
近几年来出现一种新的批评
❖ 指出有些人只迷恋于数学模型的精巧、 复杂化，使用高深的数学工具，而不善 于处理面临大量新的不易解决的实际问 题。现代运筹学工作者面临的大量新问 题是经济、技术、社会、生态和政治等 因素交叉在一起的复杂系统。
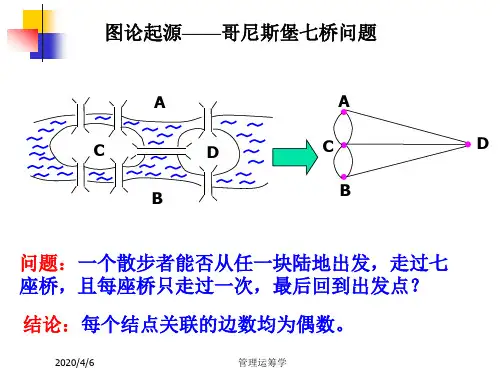
天津大学管理运筹学图论

天津大学管理运筹学图论


1
v2
2 [3, v1]
v1
3
v3 6
12
v4
10
[1, v1]
v5 2 v8
6 4 10 3
3
v9
v6 2
4
v7
2020/4/6
管理运筹学
[5, v3]
6 [0, v1]
1
v2
2 [3, v1]
v1
3
v3 6
12
v4
10
[1, v1]
[6, v2]
v5 2 v8
6 4 10 3
3
v9
v6 2
4
v7
二、图的支撑树
若一个图 G =（V , E）的支撑子图 T=（V , E´） 构成树，则称 T 为
G的支撑树，又称生成树、部分树。
例
(G)
2020/4/6
(G1)
(G2)
管理运(筹G学3)
(G4)
图的支撑树的应用举例
v1
[例] 某地新建5处居民点，拟修
5
道路连接5处，经勘测其道路可铺 v2
成如图所示。为使5处居民点都有
3K
B2
2 F 2 26 J
2020/4/6
D
H
管理运筹学
一、树的概念与性质
树 无圈连通图
例 判断下面图形哪个是树：
(A)
(B)
(C)
树的性质：
1、树中任两点中有且仅有一条链；
2、树任删去一边则不连通，故树是使图保持连通且具有最少边 数的一种图形。
3、边数 = 顶点数 – 1。
2020/4/6
管理运筹学
2020/4/6
管理运筹学
[5, v3]
运筹学理论：图论

运筹学理论：图论


5②
5
⑥4
3
③8
1 2
2 4
1 2
⑥4
0①
3
4
0①
3
7
4
6
⑤10
7
7
4
6
⑤10
3④ 7
3④
例
5②
5 2 3
题 ：
③6
5②
5 2
⑥4
3
③6
1 2
1 2
⑥4
0①
3
4
0①
3
4
7
4
7
6
⑤10
7
7
4
⑤9
6
3④
3④
例
5②
5 2 4 3
题 ：
③6
5②
5 2
⑥4
3
③6
1 2
1 2
⑥4
0①
3
0①
3
4
7
7
4
6
⑤7
7
例
①
题：
①
1
②
11
2 7 5
⑥
③ ② ④ ③ ⑤
3
6 9 ④ 10 4
⑥
8
⑤
破 圈 法（山东师院管梅谷75 Nhomakorabea）首先，把有权图的边按权的递减顺 序排列：a1, a2, …… , an。 再检查a1, 如果去掉a1, 图仍是连通 图, 则去掉a1, 否则令a1= e1,再用 同样方法检查a2 … 如此继续下去, 直到找出有n-1条边的连通图为止
A
D
例如：哥尼斯堡七桥图： d(A)=3 d(B)=3 C d(C)=5 d(D)=3
B
(四) 特殊点:
2024版清华大学出版《运筹学》第三版完整版课件

2024版清华大学出版《运筹学》第三版完整版课件


要点三
金融服务与投资管理
在金融服务和投资管理中，存储论可用 于优化资金配置和投资组合，降低风险 和提高收益。例如，通过定期订货模型 的运用，可以制定合理的投资策略和资 产配置方案，实现资产的保值增值和风 险控制。
2024/1/28
31
07
排队论
2024/1/28
32
排队论的基本概念
2024/1/28
清华大学出版《运筹 学》第三版完整版课
件
2024/1/28
1
目录
2024/1/28
• 绪论 • 线性规划 • 整数规划 • 动态规划 • 图与网络分析 • 存储论 • 排队论
2
01
绪论
2024/1/28
3
运筹学的定义与发展
运筹学的定义
运筹学是一门应用数学学科，主要研究如何在有限资源下做出最优决策，以最 大化效益或最小化成本。
目标函数
表示决策变量的线性函数，需要最大化或最 小化。
约束条件
表示决策变量需要满足的线性等式或不等式。
2024/1/28
决策变量
表示问题的未知数，需要在满足约束条件的 情况下求解目标函数的最优值。
8
线性规划问题的图解法
01
可行域
表示所有满足约束条件的决策变量构成的集合。
2024/1/28
02
目标函数等值线
2024/1/28
34
单服务台排队系统
M/M/1排队系统
到达间隔和服务时间均服从负指数分布的单服务台排队系 统。
M/D/1排பைடு நூலகம்系统
到达间隔服从负指数分布，服务时间服从确定型分布的单 服务台排队系统。
表格。
10
图论在运筹学中的名词解释

图论在运筹学中的名词解释

图论在运筹学中的名词解释一、引言运筹学是一门研究复杂问题的学科，它借助各种数学方法和技术，帮助我们做出最佳的决策。

图论作为运筹学的重要工具之一，被广泛应用于解决各类实际问题。

本文将就图论在运筹学中的几个重要名词进行解释和探讨。

二、图图是图论的核心概念之一。

它由一组顶点和连接这些顶点的边组成。

在运筹学中，图可以用来描述和分析各种现实场景。

比如，交通网络可以用图来表示，道路是边，路口是顶点；社交网络可以用图来表示，用户是顶点，社交关系是边。

通过构建和分析图，我们可以揭示事物之间的关联性和特征，并利用这些信息进行决策。

三、路径路径是图论中一个重要概念。

它指的是在图中顶点之间连接的一系列边的序列。

在运筹学中，路径常常被用来表示两个顶点之间的最佳路线或最优解。

比如，在物流配送中，我们需要找到从仓库到目的地的最短路径，以最大程度地降低运输成本和时间。

通过图论的路径算法，我们可以高效地找到这样的最短路径，为物流管理提供有效支持。

四、最小生成树最小生成树是一种特殊的图结构，它是原图的一个子图，包含了所有顶点，但只有足够的边连接这些顶点，并使得整个图的总权重最小。

在运筹学中，最小生成树常常被用于解决资源分配和网络设计等问题。

比如，在电力输送系统中，我们需要将发电站和各个消费点以最短的电网连接起来，以确保电能的高效分配和传输。

通过构建最小生成树，我们可以优化电网的布局，降低能源损耗，提高供电可靠性。

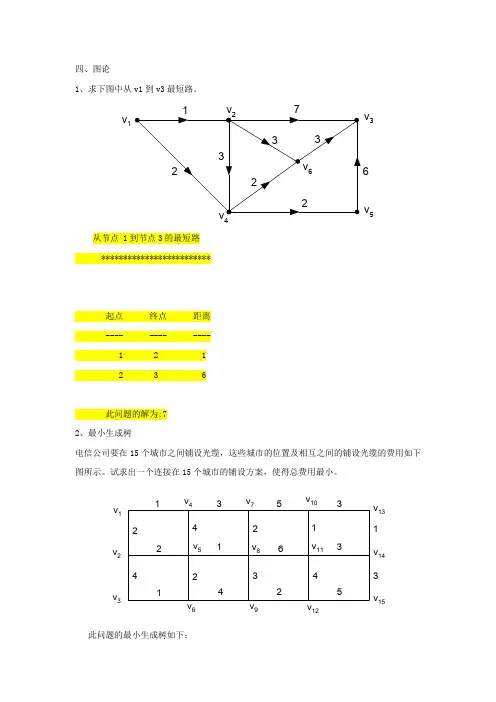
五、网络流网络流是图论中的一个重要概念，它用来描述在一个有向图中通过各个边所能承载的最大流量。

在运筹学中，网络流被广泛应用于流程设计和资源调度问题。

比如，在工厂生产调度中，我们需要在供应链上对原材料、组件和成品进行优化配送，以实现最佳生产效率和降低成本。

通过分析网络流，我们可以确定各个节点的产能和需求，从而优化生产计划和物流调度。

六、最短路径最短路径是图论中的一个重要问题，即在图中找到连接两个顶点的最短路径。

在运筹学中，最短路径经常被用于解决物流和通信等问题。

运筹学上机试题5-图论

运筹学上机试题5-图论

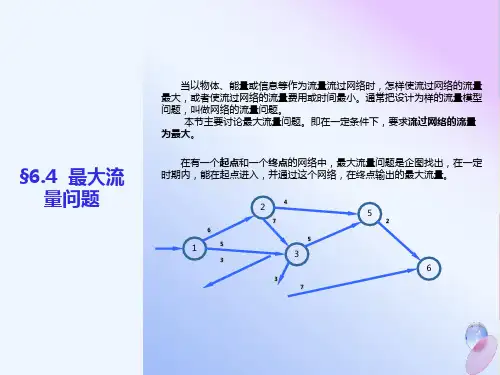
四、图论1、求下图中从v1到v3最短路。

v 1v 3v 546从节点 1到节点3的最短路 *************************起点 终点 距离 ---- ---- ---- 1 2 1 2 3 6此问题的解为:7 2、最小生成树电信公司要在15个城市之间铺设光缆，这些城市的位置及相互之间的铺设光缆的费用如下图所示。

试求出一个连接在15个城市的铺设方案，使得总费用最小。

v 1v 2v 3v 4v 5v 6v 7v 8v 9v 10v 11v 12v 13v 14v 152241131456422323135134此问题的最小生成树如下：*************************起点终点距离---- ---- ----1 4 11 2 22 5 25 8 15 6 26 3 18 7 28 9 39 12 212 11 411 10 110 13 313 14 114 15 3此问题的解为:283、最短路问题例. 求下图中从v1到各点的最短路，并指出有哪些点是不可达到的。

vv7v8v4从节点 1到节点2的最短路*************************起点终点距离---- ---- ---- 1 2 4此问题的解为:41到3没有路1到4没有路从节点 1到节点5的最短路*************************起点终点距离 ---- ---- ---- 1 5 1此问题的解为:1从节点 1到节点6的最短路*************************起点终点距离 ---- ---- ---- 1 5 1 5 6 6此问题的解为:7从节点 1到节点7的最短路*************************起点终点距离 ---- ---- ---- 1 7 3此问题的解为:3从节点 1到节点8的最短路*************************起点终点距离 ---- ---- ---- 1 5 1 5 6 66 8 3此问题的解为:104、最短路问题有6个村庄，各村庄的距离如下图所示。

运筹学-图论

运筹学-图论

初等链：链中所含的点均不相同, 也称通路；
圈：若 v0 ≠ vn 则称该链为开链，否则称为闭链或 回路或圈；
简单圈：如果在一个圈中所含的边均不相同 初等圈：除起点和终点外链中所含的点均不相
同的圈；
初等链: (v1 , v2 , v3 , v6 , v7 , v5 )
v1
初等圈： (v1 , v2 , v3 , v5 , v4 , v1 )
图的基本概念
图论中的图是由点、点与点之间的线所组成的。通常， 我们把点与点之间不带箭头的线叫做边，带箭头的线叫 做弧。
如果一个图是由点和边所构成的，那么称为无向图，
记作G=(V，E)，其中V表示图G 的点集合，E表示图G的
边集合。连接点vi , vj V 的边记作[vi , vj]，或者[vj , vi]。 如果一个图是由点和弧所构成的，那么称为它为有向
v2 （3） v3 （3）
（2）
v5
（4）
v1
v4（6）
多重图
以点v为端点的边的个数称为点v的度（次），记 作 d(v), 如 图 5.4 中 d(v1)=3 ， d(v2 )=4 ， d(v3 )=4 ， d(v4 )=3。
度为零的点称为弧立点，度为1的点称为悬挂点。 悬挂点的边称为悬挂边。度为奇数的点称为奇点， 度为偶数的点称为偶点。
郑州
济南 徐州
青岛 连云港
重庆
武汉 南京
上海
图5.3
例5.2 有六支球队进行足球比赛，我们分别用
点v1 ，…，v6表示这六支球队，它们之间的比赛情 况，也可以用图反映出来，已知v1队战胜v2 队，v2 队战胜v3 队，v3 队战胜v5队，如此等等。这个胜负
情况，可以用图5.3所示的有向图反映出来
交通分析习题课（运筹学）

交通分析习题课（运筹学）

习 题第二章 线性规划习题2－1 某桥梁工地需集合料3万立方米，集合料含量为：粘土含量不大于0.8％，细沙含量在5％～8％之间，粗沙含量在60％～70％之间，砾石含量在20％～30％之间，现有材料数量及单价如下表所示。

问如何配料才能使集合料的总成本费用最低？（试列出数学模型）。

2—2 将下列线性规划问题化成标准型：① 42154m ax x x x S ++=s.t.⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥+-≤-+≤+++=+0,,,843104480334304432143432432121x x x x x x x x x x x x x x x② 4321343m in x x x x S --+=s.t.⎪⎪⎪⎩⎪⎪⎪⎨⎧≤≥≤+-≥++=-+≤+0,0,8434040403213242132141x x x x x x x x x x x x x 2—3 用图解法求解下列线性规划问题：2152m ax x x S +=s.t.⎪⎪⎩⎪⎪⎨⎧≥≤+≤≤0,8234212121x x x x x x（答案：19=*S ，()T X 3,2=*。

）2—4 用单纯形法求解下列线性规划问题 ① 321834m in x x x S ++=s.t.⎪⎩⎪⎨⎧≥≥+≤+0,,5223213231x x x x x x x（答案：15=*S ，T X ),0,5,0(=*。

） ② 432132m ax x x x x S -++=s.t. ⎪⎪⎩⎪⎪⎨⎧≥=+++=++=++0,,,1022052153243214321321321x x x x x x x x x x x x x x （答案：15=*S ，T X )0,2/5,2/5,2/5(=*。

）第三章 特殊类型的线性规划习题3－1用表上作业法求解以下运输问题。

3－2某市区交通愿望图有三个始点和三个终点，始点发生的出行交通量a i ，终点吸引的交通量b j 及始终点之间的旅行费用如下所示。

运筹学基础-图论方法

运筹学基础-图论方法


间V的弧即为最小V截集，最小截集容量即为该网络最大流量；
最大流最小截 的标号法步骤
第二步：增广过程
1、对增广链中的前向弧，令 f=f +q (t)，q(t) 为节点 t 的标记 值
2、对增广链中的后向弧，令 f=fq (t) 3、非增广链上的所有支路流量保持不变
第三步：抹除图上所有标号，回到第一步
1
2
3
5
6 Θ=2
1
2
4
3 截止
截止，最大流量＝9+5＝14（或者最大流量＝7+5+2＝14
（六）利用 EXCEL求网 络最大流量
建立各结点间的流量矩阵
各结点间的流量矩阵
v1
v2
v3
v1
30
80
v2
v3
10
v4
v5
20 60
v6
2
20 30
1 80
10
100 3
v4
v5
60 100
10
4 70
10
5(34)
2(0)
6(01)
t
最大流量为5+9＝14
7(65)
2
4
(s+, 1) 9(9)
10(98)
第二条链：(s+,)→(s+,1) → (2-,1) → (1+,1)截止
又例：利用标 号法（确定最 小截集）求最
大流量
(3-,1)
(1+,1)
1
3(2)
4
5(5)
(s+,) s
3(3)
3(3(5) -,41()4)
1(0)
(s+,)
运筹学：动态规划、图与网络优化习题与答案

运筹学：动态规划、图与网络优化习题与答案

一、判断题1.动态规划分为线性动态规划和非线性动态规划。

（）正确答案：×2.对于一个动态规划问题，应用顺推法和逆推法可能会得到不同的最优解。

（）正确答案：×3.在用动态规划解题时，定义状态时应保证各个阶段中所做的决策的相互独立性。

（）正确答案：√4.动态规划计算中的“维数障碍”主要是由问题中阶段数的急剧增加而引起的。

（）正确答案：×二、选择题1.关于图论中图的概念，以下叙述（）正确。

A.图中的有向边表示研究对象，结点表示衔接关系。

B.图中的点表示研究对象，边表示点与点之间的关系。

C.图中任意两点之间必有边。

D.图的边数必定等于点数减1。

正确答案：B2. 关于树的概念，以下叙述（）正确。

A.树中的点数等于边数减1B.连通无圈的图必定是树C.含n个点的树是唯一的D.任一树中，去掉一条边仍为树。

正确答案：B3. 一个连通图中的最小树（）。

A.是唯一确定的B.可能不唯一C.可能不存在D.一定有多个。

正确答案：B4.关于最大流量问题，以下叙述（）正确。

A.一个容量网络的最大流是唯一确定的B.达到最大流的方案是唯一的C.当用标号法求最大流时，可能得到不同的最大流方案D.当最大流方案不唯一时，得到的最大流量应相同。

正确答案：D5. 图论中的图，以下叙述（）不正确。

A.图论中点表示研究对象，边或有向边表示研究对象之间的特定关系。

B.图论中的图，用点与点的相互位置，边的长短曲直来表示研究对象的相互关系。

C.图论中的边表示研究对象，点表示研究对象之间的特定关系。

D.图论中的图，可以改变点与点的相互位置。

只要不改变点与点的连接关系。

正确答案：C6. 关于最小树，以下叙述（）正确。

A.最小树是一个网络中连通所有点而边数最少的图B.最小树是一个网络中连通所有的点，而权数最少的图C.一个网络中的最大权边必不包含在其最小树内D.一个网络的最小树一般是不唯一的。

正确答案：B7.关于可行流，以下叙述（）不正确。

高高等教育运筹学课程--图论(3)


3、增广链
对可行流f={fij}：
非饱和弧：fij<Cij 非零流弧：fij>0
饱和弧：fij=Cij 零流弧：fij=0
链的方向：若µ是联结vs和vt的一条链，定义链的
方向是从vs到vt。 v2
5.2
v4
10.5
3.2
11.6
v1
4.1 5.1
8.3
v3
6.3
3.3
v6
17.2
v5
前向弧：弧的方向与链的方向一致，前向弧全体记为µ+。
（1）找增广链
如vt的第一个标号为k（或-k），则弧（vk，vt）∈µ （或弧（vt，vk) ∈µ)。检查vk的第一个标号，若为i（或i），则(vi,vk) ∈µ(或(vk,vi) ∈µ).再检查vi的第一个标号,依 此下去,直到vs。被找出的弧构成了增广链µ。 （2）流量调整
令调整量是 l(vt)，构造新的可行流f ’，
不难验证，
f ** ij
是一个可行流，且
V(f **) V(f *) V(f *)
这与f*是最大流的假设矛盾。 设D中不存在关于f *的增广链，证明f *是最大流。
定义V1 * ，令vs∈V1*，若vi∈V1*，且弧（vi，vj）上， fij*<Cij，则令vj∈ V1*，若vi∈V1*，且弧（vj，vi）上， fji*>0，则令vj∈ V1*。
后向弧：弧的方向与链的方向相反，后向弧全体记为µ-。
v2
10.5
v1 4.1
8.3
v3
5.2
3.2 5.1
6.3
v4
11.6
3.3
v5
v6
17.2
后向弧

运筹学PPT完整版

优化炼油程序及产品供应、配送和营销
每年节约成本600万美元 每年节约成本7000万
优化商业用户的电话销售中心选址
控制成本库存（制定最优再定购点和定购 量确保安全库存） 制定最优铁路时刻表并调整铁路日运营量
优化员工安排，以最低成本服务客户
每年节约成本4.06亿美元，销 售额大幅增加 每年节约成本380万美元
s.t

n j1
aij
xj
bi
(i 1,2,,m)
(2)
xj 0, j 1,2,,n (3)
求解线性规划问题，就是从满足约束条件(2)、(3)的方程组 中找出一个解，使目标函数(1)达到最大值。
线性规划问题的数学模型
Page 28
可行解：满足约束条件②、③的解为可行解。所有可行解 的集合为可行域。
(5) 目标函数是最小值，为了化为求最大值，令z′=-z,得到max z′=-z，即当z达到最小值时z′达到最大值，反之亦然;
线性规划问题的数学模型
标准形式如下：
maxZ 2x1 x2 3(x3 x3)0x4 0x5
5x1 x2 (x3 x3) x4 7
1 2
1 0
0 1
r(A)=2，2阶子矩阵有10个，其中基矩阵只有9个，即
5 1
1 1 5 0 1 1
B 1 106 B 2 6 2 B 3 101 B 4 6 0
5 1 1 0
1 1 1 0
1 0
B 5 100 B 6 2 1 B 7 2 0 B 8 6 1 B 9 0 1
线性规划问题的数学模型
Page 17
2. 线性规划的数学模型由三个要素构成 决策变量 Decision variables 目标函数 Objective function 约束条件 Constraints

运筹学图论


其中：
bi j

wi j 0
(vi , v j ) E (vi , v j ) E
24 2019/11/19
图的基本概念与模型
例6.3 下图所表示的图可以构造邻接矩阵M如下:
v1
v4
e9
v6
e1 v2
e2
e3
e5 e6
v3
e12
e10
v5
e11 v7
e4
e7
v8 v1
e8
v2
v3
2019/11/19
无向图
有向图 8
图与网络的基本知识
环, 多重边, 简单图
多重边
如果边e的两个端点相重，称该边为 环。如右图中边e1为环。如果两个点 之间多于一条，称为多重边，如右图 中的e4和e5，对无环、无多重边的图 称作简单图。含多重边的图称为多重 图。
e2 v2
e6
v4
e1 e4 v1 e3 e5 e7
定义6 在有向图中，以顶点v为始点的边数称为顶点v的 出次，记为d+(v)；以v为终点的边数称为v的入次，记为 d-(v)。顶点v的出次与入次的和称为点v的次。
定义7 图G=(V, E), 若E'是E的子集，若V'是V的子集，且 E'中的边仅与V'中的顶点相关联，则称G' = (V', E')为图 G的一个子图，特别地，若V' =V, 则称G'为G的一个生 成子图（支撑子图）。
1. 邻接矩阵 对于图G=（V，E），| V |=n， | E |=m，有nn阶方矩阵
A=(aij) nn，其中
aij

1, 0,
(vi , v j ) E 其他

运筹学图论概述


最短路线问题
一般针对赋权连通图(有向图或无向图皆可) ， 求两点之间所经路线权值之和为最小的路线
求解该问题可以采用上一章介绍的动态规划的 方法
该方法适用于无负初等回路(指所有边的权值之和 为负值的初等回路)的赋权连通图(有向图或无向图 皆可)；若有负初等回路，则不存在最短路线
该方法需要人工划分阶段，适合人工计算
在有向图中，由顶点指向外的弧的数目称为正度， 记为d+，指向该顶点的弧的数目称为负度，记为 d–
度数为0的点称为孤立点，度数为1的点称为悬挂点
图的基本概念(5)
与悬挂点连接的边称为悬挂边 若图中所有的点都是孤立点，则称为空图 定理6.1
所有顶点的度数之和，等于所有边数的两倍 原因：每条边关联两个顶点，计算顶点的度数时，每条
本章重点
图的基本概念 常见的四个问题的求解方法
图的含义
图是一种模型
如公路、铁路交通图，通讯网络图等
图是对现实的抽象
很多问题都可以用顶点和边来表示，一般顶点 表示实体，边(顶点与顶点之间的连线)表示实 体之间的关系，顶点和边的集合定义为图
图论的提出(1)
用图来描述事物及其联系，最早是由瑞士 数学家欧拉(Euler)于1736年解决哥尼斯堡七 桥问题时提出的
图的基本概念(7)
在有向图中，点边交错序列v0, e1, v1, e2, v2, …, vn-1, en, vn (其中ek=(vk-1, vk) )称为路
若v0≠vn，称为开路；反之，称为回路(注意和无向 图的回路区分开来)
若路中所含的边均不相同，称为简单路 若路中所含的顶点均不相同，称为初等路 除起点和终点外均不相同的回路，称为初等回路
因此，该算法一般应用于无负权值的赋权连 通有向图或无向图

运筹学_西安邮电大学中国大学mooc课后章节答案期末考试题库2023年

运筹学_西安邮电大学中国大学mooc课后章节答案期末考试题库2023年1.网络计划中有【图片】答案:正确2.一个线性规划问题若转化为动态规划方法求解时,应严格按变量的下标顺序来划分阶段,如将决定【图片】的值作为第一阶段,决定【图片】的值作为第二阶段等。

答案:错误3.避圈法(加边法)是：去掉图中所有边，从最短边开始添加，加边的过程中不能形成圈，直到有n条边(n为图的点数)。

答案:错误4.满足线性规划问题全部约束条件的解称为（）答案:可行解5.原问题与对偶问题的最优（）相同。

答案:目标函数值6.若一个链C除了第一个顶点和最后一个顶点相同外，没有相同的顶点和相同的边，则该链C称为（）答案:初等圈7.关于图论中的概念，以下的叙述正确。

答案:图中的点表示研究对象，边表示点与点之间的关系。

8.如线性规划问题存在最优解，则最优解一定对应可行域边界上的一个点。

（）答案:正确9.用分支定界法求解一个极大化的整数规划问题时，任何一个整数可行解的目标函数值是该问题目标函数值的初始下界。

（）答案:正确10.若线性规划问题的可行域可以伸展到无限，则该问题一定具有无界解。

答案:错误11.从一个树中去掉任意一条边，则余下的图是不连通的。

（）答案:正确12.任何线性规划一定有最优解。

答案:错误13.原问题变量的个数等于对偶问题约束条件的个数答案:正确14.含有孤立点的变量组不包含有闭回路答案:错误15.一对正负偏差变量至少一个大于零。

答案:错误16.线性规划求解可能出现无穷多最优解，目标规划也一样。

答案:正确17.任意可行流的流量不超过任意截集的截量。

（）答案:正确18.在动态规划中，定义状态时应保证各个阶段中所做的决策相互独立。

答案:正确19.整数规划模型不考虑变量的整数约束得到的相应的线性规划模型，如该模型有无穷多最优解，则整数规划模型也一定有无穷多最优解。

答案:错误20.下列变量组是一个闭回路的有（）答案:21.运输问题是一类特殊的线性规划问题，因而求解结果为（）答案:可能出现唯一最优解或无穷多最优解22.减少一个非基变量，目标值不变。

《管理运筹学》演示(图论)


v3 (v2 ,1)
检查 vs 相邻点 v1 和 v2 。 v2点，fs2 = cs2 =3，不满足标号条件；v1点，fs1 < cs1 , v1点标号为（ vs , l(v1) ）, l(v1) =min[ l(vs) ,( cs1 - fs1 )]= min[+ , 5-1] = 4； 检查 v1 相邻点 v3 和 v2 。 v3点，f13 = c13 =2，不满足标号条件； v2点，f21=1> 0 , v2点标号为（ -v1 , l(v2) ）, l(v2) =min[ l(v1) , f21]= min[4 , 1] = 1； 检查 v2 相邻点 v3 和 v4 。v3点，f32=1> 0 , v3点标号为（ -v2 , l(v3) ）, l(v3) =min[ l(v2) , f32]= min[1 , 1]=1 ； v4点，f24 < c24 =1，v4点标号为（ v2 , 1 ） ；
,
最大流量 v(f ) = 5
最小费用最大流问题
例：求下列网络最小费用最大流。弧旁数字为( bij , cij ) 步骤：
v1
(1,7)
vt
取 f ( 0 ) ＝0为初始可行流； 构造赋权有向图w( f ( 0 ))，
vs
解：
v1
0 0
v2
0
0
v3
vt
0
bij wij bij wij
v8
步 骤：
给 vs点以 P 标号，P(vs) = 0，其余各点给 T 标号，
T(vs) = ＋ ；
若 vs点为刚得到 P 标号的点，考虑这样的点 vj：
( vi , vj )属于A(或[vi , vj ] 属于E )，且vj 为 T 标号。对 vj 的T 标号进行如下的更改：
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
fs1<Cs1, 给v1标号(s, l(v1)), 其中
l(v1) min l(vs ), (Cs1 fs1) min ,5 1 4
在弧（vs，v2）上， fs2=Cs2=3, 不满足标号条件。
v2
(4，3) v4
(3，3)
(1，1)
(5，3)
（0，∞）vs
(1，1)
(5，1)
(3,0) vt
vi fij>0
vj (-i , l(vj))
l(vj)=min[l(vi),fji]
vj成为标号而未检查的点
重复上述步骤，一旦vt被标号，则得到一条vs到vt的 增广链。若所有标号都已检查过，而vt尚未标号，结束， 这时可行流，即最大流。
（二）调整过程 从vt开始，反向追踪，找出增广链µ，并在
µ上进行流量调整。 （1）找增广链
在弧（v2，v4）上，f24=3，C24=4，f24<C24, 给v4标号(2, l(v4)), 其中
l(v4 ) min l(v2 ), (C24 f24 ) min 1,1 1,
（-1，1）
v2
(4，3)
（2，1）
v4
(3，3)
(1，1)
(5，3)
（0，∞）vs
(1，1)
(5，1)
（s，v14） (2，2)
后向弧：弧的方向与链的方向相反，后向弧全体记为µ-。
v2
10.5
v1 4.1
8.3
v3
5.2
3.2 5.1
6.3
v4
11.6
3.3
v5
v6
17.2
后向弧
µ=(v1,v2,v3,v4,v5,v6)
µ+={(v1,v2) ,(v2,v3), (v3 , v4),(v5,v6)} µ- ={(v5,v4)}
(2，1)
（s，v14） (2，2) v3
（3）检查v1，在弧（v2，v1）上，f21>0， 给v2标号
(-1, l(v2)), 这里 l(v2 ) min l(v1), f 21 min 4,1 1,
在弧（v1，v3）上，f13=2， C13=2，不满足标号条件。
（-1，1）
v2
(4，3)
(3，3)
定义3 设f是一个可行流, µ是从vs到vt的一条链,若µ满 足下列条件,称之为(关于可行流f的)一条增广 链。
(vi,vj) ∈ µ+ (vi,vj) ∈ µ-
0≤fij<Cij 0 < fij ≤ Cij
前向弧是 非饱和弧， 后向弧 是非零流弧，
8.4 V1
5.0
3.3
V2
V3
5.4
V4
Cij.fij
(1，1)
（0，∞）vs
(1，1)
(5，1)
（s，v14） (2，2)
v4
(5，3)
(3,0) vt
(2，1)
v3
（4）检查v2，在弧（v3，v2）上，f32=1>0， 给v3标号
(-2, l(v3)), 这里 l(v3) min l(v2 ), f32 min 1,1 1,
（-1，1）
v2
(4，3)
流: 定义在弧集A上的一个函数f={f(vi,vj)}，并称 f(vi,vj)为弧(vi,vj)上的流量.(简记fij)
如(a)图是一个网络
v2
10
v1
4
弧旁数字：容量
8
v3
如(b)图是网络上的一个流v2
5
弧旁数字：流量 v1
1
3
v3
5
3
5 6
（a）
2
2
1
3
（b）
v4
11
3
v6
17
v5
v4
6
3
v6
2
v5
v2
10.5
vs 2.2
5.5
v1
4.3 v4
8.6 1.0
3.3
v5
5.4
8.7
v3
Cij.fij
Vi
Vj
2、可行流与最大流
定义2 满足下述条件的流f称为可行流: 1)容量限制条件: 对每一弧(vi,vj)∈A
0≤fij≤Cij 2)平衡条件: 对中间点vi(i≠s,t),有
fij
记V1*=V\ V1*，得截集（ V1*， V1*），显然有
f
* ij
C ij
0
(v i
,
v
j
)
(V1* ,
*
V1
)
(v i
,
v
j
)
*
(V1
,
V 1*
)
所以V(f*) = C（ V1*， V1*）。于是f*必是最大流
定理2 最大流最小截定理。任一个网络D中，从vs到 vt的最大流的流量等于分离vs，vt的最小截集 的容量。
(3,0) vt
(2，1)
v3
解：（一）标号过程
（1）给vs标上（0，∞）；
例 用标号法求下图网络的最大流。弧旁的数字是（Cij,fij)。
v2
(4，3)
(3，3)
(1，1)
（0，∞）vs
(1，1)
(5，1)
v1
(2，2)
v4
(5，3)
(3,0) vt
(2，1)
v3
解：（一）标号过程
（1）给vs标上（0，∞）； （2）检查vs，在弧（vs，v1）上，fs1=1，Cs1=5，
(1，1)
vs
(1，1)
(5，1)
v1
(2，2)
v4
(5，3)
(3,0) vt
(2，1)
v3
解：（一）标号过程
（1）给vs标上（0，∞）；
例 用标号法求下图网络的最大流。弧旁的数字是（Cij,fij)。
v2
(4，3)
(3，3)
(1，1)
v （0，） s
(1，1)
(5，1)
v1
(2，2)
v4
(5，3)
v2
(4，3)
（2，1）
v4
(3，3)
(1，1)
(5，3)
（0，∞）vs
(1，1)
(5，1)
（s，v14） (2，2)
(3,0) vt
(2，1)
v（3 -2，1）
（4）检查v2，在弧（v3，v2）上，f32=1>0， 给v3标号
(-2, l(v3)), 这里 l(v3) min l(v2 ), f32 min 1,1 1,
不难验证，
f ** ij
是一个可行流，且
V(f **) V(f *) V(f *)
这与f*是最大流的假设矛盾。 设D中不存在关于f *的增广链，证明f *是最大流。
定义V1 * ，令vs∈V1*，若vi∈V1*，且弧（vi，vj）上， fij*<Cij，则令vj∈ V1*，若vi∈V1*，且弧（vj，vi）上， fji*>0，则令vj∈ V1*。 因为不存在关于f*的增广链，故vt ∈V1*，
（-1，1）
v2
(4，3)
v（4 2，1）
(3，3)
(1，1)
(5，3)
（0，∞）vs
(1，1)
(5，1)
µ（vs,v1,v2,v3,vt） =1，
（s，v14）
在µ上进行流量
v2
(3，3)
(2，2) (4，3) (1，0)
(3,0) vt（3，1）
(2，1)
v3
（-2，1）
v4
(5，3)
=1的调整，得 可行流f ’如右
弧旁数字：运输数量。
问题：这个运输网络中，从v1到v6的最大输送量是多少？
一、基本概念与定理
1、网络与流
定义1 给定一个有向图D=（V，A），在V中指定 一点vs称为发点，指定另一点vt称为收点， 其余点称中间点。任意弧(vi，vj)∈A，有 Cij≥0，称为弧的容量。称D为一个容量网 络。记为D=（V，A，C）。
vs
(1，0)
(5，2)
(3,0) vt
(2，2)
图所示：
v1
(2，2) v3
去掉各点标号，从vs开始，重新标号。
v2
(4，3) v4
(3，3)
(1，0)
(5，3)
（0，∞） vs
(1，0)
(5，2)
(3,0) vt
(2，2)
（sv，1 3） (2，2) v3
点v1：标号过程无法进行，所以f ’即为最大流。
量），记为C （V1，V1）， 即
C(V1, V1)
Cij
(vi ,v j )(V1 ,V1 )
不难证明：任何一个可行流的流量V(f)都不会
超过任一截集的容量。即 V(f) C(V1, V1)
可行流f*，截集(V1*，V1*), 若V(f*)=C( V1*，V1*）， 则f*必是最大流， (V1*，V1*) 必是D的最小截集。
v4
(3，3)
((5，1)
(3,0) vt
(2，1)
（s，v14）
(2，2)
v3
（-2，1）
（4）检查v2，在弧（v3，v2）上，f32=1>0， 给v3标号
(-2, l(v3)), 这里 l(v3) min l(v2 ), f32 min 1,1 1,
（-1，1）
3、增广链
对可行流f={fij}：
非饱和弧：fij<Cij 非零流弧：fij>0
饱和弧：fij=Cij 零流弧：fij=0
链的方向：若µ是联结vs和vt的一条链，定义链的
方向是从vs到vt。 v2