09小学数学竞赛模拟题

09年春安海中心小学六年级数学竞赛测试卷(满分得120分,90分钟完卷)成绩一、计算。

（12分）1、 直接写出下列各式的结果：3.7+0.63= 5.1÷0.01= 500×3%= 2.5×6.7×4=75×99= 1322－199= 4.9×8.1= 0.32－0.22=74×5.6= ( ):7171= 431÷1.75= =⨯+⨯51)58(81 2、 下面各题怎样算简便就怎样算：（9分）200420032005⨯ 48×9.9＋48÷10 )85212(212+÷3、 解方程:(9分)53326=÷X 8(X －2)=2(X ＋7) 548384=+-X X二、填空。

（共28分，每题2分）1、六千零六十点零六万写作（ ），改写成用“一”作单位的数是（ ）省略亿后面的尾数写作（ ）。

2、我国成功举办2008年的第二十八届奥运会，按每4年举行1次，则第五十一届奥运会将在（ ）年举行。

这一年是平年还是闰年？（ ）。

３、832吨＝（ ）克 ３.１５时＝（ ）时（ ）分４、５÷７＝（ ）：２８＝)%(35)()(35≈= ５、把３米长的钢筋锯成一样长的小段，共锯了６次，每段占全长的)()(，每段长（ ）米。

６、钟面上６点１５分时，分针和时针所夹的角是（ ）度。

７、在一幅中国地图上，画有一条线段的比例尺：０ 5 10 15 20（千米）改成数值比例尺的形式是（ ）。

８、一长方体的长、宽、高分别为３、２、１厘米，一只小虫从A 点出发，沿棱爬行，如果要求不走重复路线，小虫回到出发点A 时，所走最长路程是（ ）厘米。

９、甲数是乙数的32，如果乙数增加２０，则乙数是甲数的４倍，甲数是（ ）。

10、在推导圆的面积公式时，将圆等分成若干份，拼成一个近似的长方形，已知拼成的长方形的周长比圆的周长多６厘米，圆的面积是（ ）平方厘米。

2009届小学数学奥林匹克竞赛预赛试题及答案2009届小学数学奥林匹克竞赛预赛试题及答案时间：2012-12-06 11:18 来源：世奥赛资讯站作者：世奥赛小编阅读：175次2009年小学数学奥林匹克预赛试卷及参考答案(本卷共12个题，每题10分，总分120分)1、23×( ＋)＋13×( －)－15×( ＋)=( )解：原式=69/11+11+13×15/23-39/11-30/11-15×13/23=112、(1－)(1－)…(1－)=( )解：原式=1/2×2/3×3/4×4/5×……×2007/2008×2008/2009=1/20093、两个整数相除，商数=4，余数=7。

已知被除数比除数大58，那么除数是( )。

解：设除数为x。

则x+58=4x+7 x=174、四位数- =5904，如果是偶数，那么=( 8892 )。

解：8892-2988=59045、右图中的三角形都是等腰直角三角形。

图中阴影部分的面积=( )。

解：5×5÷2÷2-2×2÷2=4.256、下面是一个乘法算式，它的得数是(69104 )。

１２□□×５□□□０４□□７０□□□□□解：1234×56=69014７、一个泉水池，每分钟涌出的泉水量不变。

如果用8台抽水机工作，10小时能把水抽干；如果用12台抽水机工作，6小时能把水抽干。

那么，用14台抽水机把水抽干，需要工作( )小时。

解：设1台抽水机1小时抽的水为1份。

则每小时涌出的泉水量为（8×10-12×6）÷（10-6）=2（份）原有的水量为8×10-10×2=60（份）用14台抽水机把水抽干，需要工作60÷（14-2）=5（小时）。

小升初数学模拟试题九（苏教版）一、选择题（共10小题）1．跳绳比赛上，小丽跳45个，小云跳的个数比小丽的2倍多一些，比小丽的3倍少一些，小云可能跳了（）个．A．90B．135C．110D．852．布袋里放了5个球：〇〇〇●●，任意摸一个再放回，小明连续摸了4次都是白球．如果再摸一次，认为下面说法正确的是（）A．可能摸到黑球B．一定能摸到黑球C．摸到黑球的可能性大D．不可能再摸到白球a3．北京的温度+5℃表示的是零上5℃，同时黑龙江的温度为﹣8℃，则﹣8℃表示的是（）A．零上8℃B．零下8℃C．8℃4．把一个长方体铁块熔铸成一个正方体后，体积（）A．变大B．变小C．不变D．无法比较5．口袋里有除颜色外都相同的10个球，其中5个红球，4个黄球，1个白球，从中任意摸出一个，有（）可能的结果．A．5种B．4种C．3种D．1种6．一块试验田，今年预计比去年增产10%，实际比预计降低了10%．实际产量与去年产量比（）A．实际产量高B．去年产量高C．产量相同7．学校体育室购进一批足球与篮球共360个，其中购进足球个数的25%比购进位篮球个数的 还多20个，学校体育室购进足球（）个．A．120B．160C．200D．2408．一个圆柱和一个圆锥等底等高，圆柱体积是1立方分米，圆锥体积是（）A．3立方分米B．1立方分米C． 立方分米D．5立方分米9．下面的几何体从侧面看，图形是的有（）。

A．（1）（2）（4）B．（2）（3）（4）C．（1）（3）（4）10．A、B、C、D四人一起完成一件工作，D做了一天就因病请假了，A结果做了6天，B做了5天，C做了4天，D作为休息的代价，拿出48元给A、B、C三人作为报酬，算劳务费，则这48元中A应分（）元．A．18B．19.2C．20D．32二、判断题（共5小题）11．a（a不为0）和它的倒数成正比例．（）12．因为 = ，所以 的分数单位是 ．（）13．甲数比乙数少 ，则甲数与乙数的比是4：3。

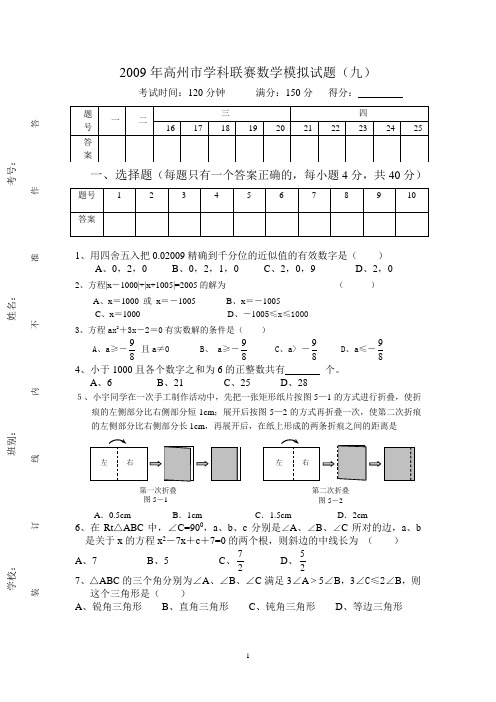
2009年高州市学科联赛数学模拟试题（九）考试时间：120分钟 满分：150分 得分：一、选择题（每题只有一个答案正确的，每小题4分，共40分）1、用四舍五入把0.02009精确到千分位的近似值的有效数字是（ ） A 、0，2，0 B 、0，2，1，0 C 、2，0，9 D 、2，02、方程|x －1000|+|x+1005|=2005的解为 （ ）A 、x ＝1000 或 x ＝－1005B 、x ＝－1005C 、x ＝1000D 、－1005≤x ≤1000 3、方程ax 2＋3x －2＝0有实数解的条件是（ ）A 、a ≥－89 且a ≠0 B 、 a ≥－89 C 、a> －89 D 、a ≤－89 4、小于1000且各个数字之和为6的正整数共有 个。

A 、6 B 、21 C 、25 D 、28５、小宇同学在一次手工制作活动中，先把一张矩形纸片按图5—1的方式进行折叠，使折痕的左侧部分比右侧部分短1cm ；展开后按图5—2的方式再折叠一次，使第二次折痕的左侧部分比右侧部分长1cm ，再展开后，在纸上形成的两条折痕之间的距离是A ．0.5cmB ．1cmC ．1.5cm D ．2cm6、在Rt △ABC 中，∠C=900，a 、b 、c 分别是∠A 、∠B 、∠C 所对的边，a 、b是关于x 的方程x 2－7x ＋c ＋7=0的两个根，则斜边的中线长为 （ ）A 、7B 、5C 、27D 、257、△ABC 的三个角分别为∠A 、∠B 、∠C 满足3∠A > 5∠B ，3∠C ≤2∠B ，则这个三角形是（ ）A 、锐角三角形B 、直角三角形C 、钝角三角形D 、等边三角形左 右 左 右 第二次折叠 第一次折叠 图5－1 图5－2------------------装--------------------订--------------------线--------------------内--------------------不--------------------准--------------------作--------------------答----------------------------学校：______________ 班别：______________ 姓名：______________ 考号：______________8、抛物线y=ax 2+2ax+a 2+2的一部分如图所示，那么该抛 物线在y 轴右侧与x 轴交点的坐标是……………( )A ．（12 ，0）；B ．（1， 0）；C ．（2， 0）；D ．（3， 0）9、如图，B 是线段AC 的中点，过点C 的直线l 与AC 成60的角，在直线l 上取一点P ，使得∠APB=300，则满足条件的点P 的个数是（ ） Ａ．3个 Ｂ．2个 Ｃ．1个Ｄ．不存在（第8题图）10、已知一列数：1，―2，3，―4，5，―6，7，… 将这列数排成下列形式：1行 1第2行 －2 3第3行 －4 5 －6第4行 7 －8 9 －10第5行 11 －12 13 －14 15 … …按照上述规律排下去，那么第10行从左边数第5个数等于 （ ） A ．50 B ．－50 C ．60 D ．－60二、耐心填一填：（每小题4分，共20分）12、已知直线Ｌ：y ＝px (p 是不等于０的实数)与直线 y ＝x ＋8的交点恰好是（横坐标和纵坐标都是整数），那么满足条件的直线Ｌ有 条。

2009年秋六年级上册数学竞赛试卷班级________ 姓名__________ 分数________题号 一 二 三 四 五 六 七 八 总分 得分取得好多成绩。

相信自己，聪明的你最棒！ 一．细心填一填，可别填错啦！（每空1分,共16分） 1．乙数与甲数的差是20，甲数是乙数的31。

甲、乙两数的和是（ ）。

2．三个数的平均数是40，它们的比是4：7：9。

这三个数中最大的数是（ ），最小的数是（ ）。

3．为了迎接元旦，六年级的同学买彩带装饰教室用去了33米，用去的比剩下的少41。

买回了（ ）米的彩带。

4．把一根7厘米长的铁丝剪成同样长的6段，每段是全长的 ，每段长 厘米。

5．一个分数，分子和分母都加上23后约分是1211；分子和分母都减去12后约分是54。

这个分数是（ ）。

6．一块正方形桌布平铺在圆形餐桌上，桌布的四角恰好刚刚接触地面，餐桌高1米，桌布对角线的长度是4米，餐桌桌面的面积是（ ）平方米。

7．一个数被256、307和1528除，所得的商都是非零自然数，这个数最小是（ ）。

8．有一种温度计上有两种刻度，摄氏度（℃）和华氏度（°F ），它们之间的换算关系式是：摄氏度×59＋32＝华氏度。

在摄氏（ ）度时，恰好是华氏86度。

9．景花园小区准备在广场前的一块正方形空地上修建一个最大的圆形花坛。

修建花坛的面积占正方形面积的（ ）。

10．3：7的前项加上21，要使比值不变，后项应该乘（ ）。

11．一个集邮爱好者买了1元和2元的邮票共100张，总值188元，这个集邮爱好者买了（ ）张1元和（ ）张2元的邮票。

12．把半径是5厘米的圆形纸片分成若干（偶数）等份，剪开拼成一个近似长方形，这个近似长方形的周长是（ ）厘米，面积是（ ）平方厘米。

二．选一选，把正确的答案填在括号里。

（5分）1．玲玲、明明和军军一起做摸球游戏，盒子中共有2个红球，15个黄球，6个蓝球，下面的说法正确的是（ ）。

分数应用题综合【知识讲述】分数应用题是研究数量之间份数关系的典型应用题，一方面它是在整数应用题上的延续和深化，另一方面，它有其自身的特点和解题规律．在解这类问题时，分析中数量之间的关系，准确找出“量”与“率”之间的对应是解题的关键． 关键：分数应用题经常要涉及到两个或两个以上的量，我们往往把其中的一个量看作是标准量．也称为：单位“1”，进行对比分析。

在几个量中，关键也是要找准单位“1”和对应的占比，以及对应量三者的关系 例如：（1）a 是b 的几分之几，就把数b 看作单位“1”． （2）甲比乙多18，乙比甲少几分之几？方法一：可设乙为单位“1”，则甲为19188+=，因此乙比甲少191889÷=. 方法二：可设乙为8份，则甲为9份，因此乙比甲少1199÷=. 怎样找准分数应用题中单位“1” （一）、部分数和总数在同一整体中，部分数和总数作比较关系时，部分数通常作为比较量，而总数则作为标准量，那么总数就是单位“1”。

例如：我国人口约占世界人口的几分之几？——世界人口是总数，我国人口是部分数，世界人口就是单位“1”。

解答题关键：只要找准总数和部分数，确定单位“1”就很容易了。

（二）、两种数量比较（比较量与标准量）分数应用题中，两种数量相比的关键句非常多。

有的是“比”字句，有的则没有“比”字，而是带有指向性特征的“占”、“是”、“相当于”。

在含有“比”字的关键句中，比后面的那个数量通常就作为标准量，也就是单位“1”。

例如：六（2）班男生比女生多——就是以女生人数为标准（单位“1”）， 解题关键：在另外一种没有比字的两种量相比的时候，我们通常找到分率，看“占”谁的，“相当于”谁的，“是”谁的几分之几。

这个“占”，“相当于”，“是”后面的数量——谁就是单位“！”。

（三）、原数量与现数量有的关键句中不是很明显地带有一些指向性特征的词语，也不是部分数和总数的关系。

这类分数应用题的单位“1”比较难找。

学习参考临川区第九小学2011-2012学年度第二学期六年级数学竞赛卷 一、填空题。

（21分）1. ( )÷( )= （ ）（ ）＝ ( )：( )= ( )%=0.252、从24的约数中，选出4个数，组成一个比例：( )。

3、地图上的线段比例尺是 0 30 60 90 120千米，那么图上的1厘米表示实际距离( )千米；如果实际距离是450千米，那么在图上要画( )厘米，把这个线段比例尺改成数值比例尺是( )。

4、一个圆柱的底面直径是4厘米，高是5厘米，这个圆柱的侧面积是( )，表面积是( )，和它等底等高的圆锥的体积是( )。

5、甲车3小时可从A 地到B 地，乙车4小时可从B 地到A 地，甲、乙两车速度的最简比是（ ）。

6、精密零件的长是5毫米，把它画在比例尺是12︰1的零件图上，长应画（ ）厘米。

7、一个圆柱的底面半径为2厘米，侧面展开后正好是一个正方形，这个圆柱的侧面积 是 （ ） 平方厘米8、已知A ×43=B ×31，A 与B 成（ ）比例，且A ∶B ＝（ ）∶（ ）。

9、用种子做发芽实验，45粒发芽，5粒没有发芽，发芽率（ ）。

10.把一个棱长是8厘米的正方体削成一个最大的圆柱体，这个圆柱体的体积是（ ）立方厘米，表面积是（ ）平方厘米。

11. 一个圆柱和一个圆锥等底等高，它们的体积和是24立方分米，那么圆锥的体积是( )立方分米，圆柱的体积是( )立方分米。

二、判断题（对的在括号里打“√”，错的打“×”）（5） (1)如果两个内项互为倒数，那么两个外项的乘积一定1。

……( )(2)圆的面积和半径成正比例 …………………………………( )(3)圆柱的底面半径和高各扩大3倍，体积就扩大9倍………… ( )(4)比例尺的前项一定是１。

…………( )(5)等底等高的长方体和圆柱体，它们的体积一定相等。

…( ) 三、选择题（10分）⑴ 15个圆锥可熔铸成（ ）个和圆锥等底等高的圆柱。

小学六年级数学奥林匹克竞赛题（含答案）某市举行小学数学竞赛.结果不低于80分的人数比80分以下的人数的4倍还多2人.及格的人数比不低于80分的人数多22人.恰是不及格人数的6倍.求参赛的总人数？解：设不低于80分的为A人.则80分以下的人数是（A-2）/4.及格的就是A+22.不及格的就是A+（A-2）/4-（A+22）=（A-90）/4.而6*（A-90）/4=A+22.则A=314.80分以下的人数是（A-2）/4.也即是78.参赛的总人数314+78=392电影票原价每张若干元,现在每张降低3元出售,观众增加一半,收入增加五分之一,一张电影票原价多少元？解：设一张电影票价x元(x-3)×（1+1/2）=(1+1/5)x(1+1/5)x这一步是什么意思.为什么这么做(x-3){现在电影票的单价}×（1+1/2){假如原来观众总数为整体1.则现在的观众人数为（1+2/1)}左边算式求出了总收入(1+1/5）x{其实这个算式应该是：1x*（1+5/1）把原观众人数看成整体1.则原来应收入1x元.而现在增加了原来的五分之一.就应该再*（1+5/1）.减缩后得到（1+1/5x）}如此计算后得到总收入.使方程左右相等甲乙在银行存款共9600元.如果两人分别取出自己存款的40%.再从甲存款中提120元给乙。

这时两人钱相等.求乙的存款答案取40％后.存款有9600×（1－40％）＝5760（元）这时.乙有：5760÷2＋120＝3000（元）乙原来有：3000÷（1－40％）＝5000（元）由奶糖和巧克力糖混合成一堆糖.如果增加10颗奶糖后.巧克力糖占总数的60%。

再增加30颗巧克力糖后.巧克力糖占总数的75%,那么原混合糖中有奶糖多少颗？巧克力糖多少颗？答案加10颗奶糖.巧克力占总数的60%.说明此时奶糖占40%.巧克力是奶糖的60/40=1。

5倍再增加30颗巧克力.巧克力占75%.奶糖占25%.巧克力是奶糖的3倍增加了3-1.5=1.5倍.说明30颗占1.5倍奶糖=30/1.5=20颗巧克力=1.5*20=30颗奶糖=20-10=10颗小明和小亮各有一些玻璃球.小明说：“你有球的个数比我少1/4！”小亮说：“你要是能给我你的1/6.我就比你多2个了。

分数应用题综合【知识讲述】分数应用题是研究数量之间份数关系的典型应用题，一方面它是在整数应用题上的延续和深化，另一方面，它有其自身的特点和解题规律．在解这类问题时，分析中数量之间的关系，准确找出“量”与“率”之间的对应是解题的关键． 关键：分数应用题经常要涉及到两个或两个以上的量，我们往往把其中的一个量看作是标准量．也称为：单位“1”，进行对比分析。

在几个量中，关键也是要找准单位“1”和对应的占比，以及对应量三者的关系 例如：（1）a 是b 的几分之几，就把数b 看作单位“1”． （2）甲比乙多18，乙比甲少几分之几？方法一：可设乙为单位“1”，则甲为19188+=，因此乙比甲少191889÷=. 方法二：可设乙为8份，则甲为9份，因此乙比甲少1199÷=.怎样找准分数应用题中单位“1” （一）、部分数和总数在同一整体中，部分数和总数作比较关系时，部分数通常作为比较量，而总数则作为标准量，那么总数就是单位“1”。

例如：我国人口约占世界人口的几分之几？——世界人口是总数，我国人口是部分数，世界人口就是单位“1”。

解答题关键：只要找准总数和部分数，确定单位“1”就很容易了。

（二）、两种数量比较（比较量与标准量）分数应用题中，两种数量相比的关键句非常多。

有的是“比”字句，有的则没有“比”字，而是带有指向性特征的“占”、“是”、“相当于”。

在含有“比”字的关键句中，比后面的那个数量通常就作为标准量，也就是单位“1”。

例如：六（2）班男生比女生多——就是以女生人数为标准（单位“1”）， 解题关键：在另外一种没有比字的两种量相比的时候，我们通常找到分率，看“占”谁的，“相当于”谁的，“是”谁的几分之几。

这个“占”，“相当于”，“是”后面的数量——谁就是单位“！”。

（三）、原数量与现数量有的关键句中不是很明显地带有一些指向性特征的词语，也不是部分数和总数的关系。

这类分数应用题的单位“1”比较难找。