小学六年级数学竞赛练习题及答案

六年级数学第三单元竞赛练习题3一填空1、（ ）的51是最小的四位数。

2、最大的两位数是（ ）的31。

3、甲数的51与乙数的61相等，甲数是90，乙数是（ ）。

4、一台拖拉机，53小时耕地85公顷，1小时耕地多少公顷？正确列式是（ ） ；耕地1公顷要多少小时？正确列式是（ ）。

5、一个数分别与32、74相乘，乘得的两个积的和是1413，原来这个数是（ ）。

6、一根木头截去全长的31，正好截去31米，这根木头还有（ ）米。

7、8米的43和30米的（ ）同样长。

8、甲、乙两数相差0.4，甲的43和乙的65相等，甲、乙两数之和是（ ）。

9、甲、乙两数相差45，甲数的75等于乙数的65，甲数是（ ）。

10、一本书共160页，小时第一天读81，第二天读15页，还剩下全书的（ ）。

11、一根彩带的长度等于它本身长度的43加上43米，这根彩带长（ ）米。

12、两个数相除，商是60，余数是商的121，被除数是545，除数是（ ）。

13、实验小学六年级有男生55人，比女生多15人，要使妇生人数占全年级人数的209，需转入（ ）名学生。

14、一个最简分数，把它的分子扩大3倍，分母缩小2倍后得2134，原分数是（ ）。

15、学校有彩色粉笔48盒，比白粉笔的83少3盒，学校有白粉笔（ ）。

16、一捆绳子，用去它的52还多7米，还剩20米，这捆绳子长（ ）米。

17、梁昕和吴飞从甲地到乙地，梁昕的速度经吴飞的速度快51，已知吴飞行这段路用30分钟，梁昕行这段路用（ ）分钟。

18、一条路，已修的经没修的少41，这时修了这条路的（ ）。

19、甲、乙两个数的和是18，如果把甲数的101给乙数，这时甲、乙两数恰好相等，原来乙数比甲数少（ ）。

20、大伟看一本故事书，第一天看了30页，第二天看的是第一天的32还多5页，两天看了全书页数的175，全书共有（ ）页。

21、回民小学五年二班，女生人数比全班的53多2人，男生有22人，五年二班一共有（ ）。

北师大版小学数学六年级上册比赛场次练习卷（带解析）1．4个人两两握手一次，共需握手( )次。

2．学校武术队为了联络方便，设计一种联络方式．一旦有事，先由教练同时通知两位队长，这两位队长再分别同时通知两名同学，依此类推，每人再同时通知两个人．如果每同时通知两人共需1分钟，4分钟可以通知到（）名同学．3．用4、1、3这三个数字可以组成（）个不同的三位数，它们别是（）。

其中最大的是（），最小的是（）。

4．3个好朋友见面握手问好，每两人握一次，共握了（）次。

5．少年军校共有510名学生，为联络方便，设计了一种联络方式．一旦有事，先由校长通知两名班长，这两名班长再分别通知两名同学，以此类推，每名学生再通知两名学生．如果每同时通知两名学生共需1分钟，通知到所有学生至少需要（）分钟。

6．胜利小学四（2）班和四（3）班进行羽毛球对抗赛，约定三局两胜，现在四（3）班估计到了四（2）班的出场次序，四（3）班要想获胜应怎样安排自己队员的出场次序呢？7．江惠从家到江堤—共有（）条路可走。

8．4顶不同的帽子，小军和小刚两人各戴一顶，一共有（）种不同的搭配方法。

9．小红有2顶不同的帽子，3件不同的上衣，她一共有（）种搭配方法．10．小明想买一本英语读物和一本数学读物，一共有（）种不同的买法。

11．下面两个盒子里分别装着写有1，2，3，4，5的卡片，从每个盒子里各摸出一张卡片，摸出的两张卡片的数字之和可能是（）。

12．有面值分别是1角、2角、5角、1元的钱币，每两种钱币组合，能组合出（）种不同的钱数。

分别是：（）。

13．去猴山有（）条路。

设计三条能参观很多景点的线路：（线路不要重复）14．4个班的同学举行拔河比赛，每2个班必须赛一场，共要进行（）场比赛。

15．学校合唱队为联络方便，设计了一种联络方式，一旦有事，先由领队老师通知队长，接着领队老师、队长通知2名同学，每次接到通知的人都加入到通知的行列……若每通一个电话需1分钟，那么至少经过( )分钟就可通知完合唱队的45人？（包括队长在内）16．笑笑从家到图书馆有（）条路可以走？17．贝贝领着小弟弟在公园玩耍，小弟弟走到贝贝处有（）条路可走？（涂色部分为供游人行走的路）18．下图中的线段表示贝贝从家到学校所能经过的街道。

小学数学六年级竞赛试题解决问题练习440道学校名称：班级：学号：姓名：1.一种VCD影碟机的售价是600元，比原来降价415。

原来的价钱是多少元？2.小明读一本书，第一天读了这本书的13多5页，第二天读了这本书的12少一页，第三天读完剩下的21页。

这本书共多少页？3.某工程队要铺设一条公路，前20天已铺设了2。

8千米，照这样计算，剩下的4。

2千米，还要多少天才能铺完？（用比例解）4.一项工程，甲独做要10小时，乙独做要15小时。

现在甲乙合做，多少小时可以完成？5. 一张课桌比一把椅子贵10元，如果椅子的单价是课桌单价的35，课桌和椅子的单价各是多少元？6. 有一袋大米，第一周吃了40%，第二周吃了12千克，还剩6千克。

这袋大米原来有多少千克 ？7. 将一个体积是753.6立方米的圆柱体钢材熔铸成一个底面半径是4厘米的圆锥体模型，这个圆珠笔锥体模型的高是多少厘米？8.某化工厂采用新技术后，每天用原料18吨，这样原来6天用的原料，现在可以用10天，这个厂现在比过去每天节约多少吨原料？9.加工一批零件，师傅独做8小时完成，徒弟独做10小时完成，师徒二人合作2.5小时后，还没有加工的零件占这批零件的几分之几？10.用边长15厘米的方砖给教室铺地，需要2000块；如果用边长25厘米的方砖铺地需要多少块？11.一根圆柱形钢材，截下2米，量得它得横截面得直径是4厘米，如果每立方厘米的钢重7.8克，截下的这段钢材重多少千克？（得数保留整千克数）12. 一列火车从甲地开往乙地，已经行了35，离乙地还有450千米，甲乙两地之间的路程是多少千米？13. 小红看一本故事书，第一天看了45页，第二天看了全书的 14，第二天看的页数恰好比第一天多20%，这本书一共有多少页？14. 把一个棱长6分米的正方体木块，削成一个最大的圆锥体，需要削去多少立方分米的木块？15. 服装厂接到生产1200件衬衫的任务，前3天完成了40%，照这样计算，完成生产任务还要多少天？16. 甲乙两港相距140千米，一艘轮船从甲港驶向乙港用了4。

小学六年级奥数练习及答案解析十讲小学六年级奥数题及答案1.某市举行小学数学竞赛，结果不低于80分的人数比80分以下的人数的4倍还多2人，及格的人数比不低于80分的人数多22人，恰是不及格人数的6倍，求参赛的总人数？解：设不低于80分的为A人，则80分以下的人数是（A-2）/4，及格的就是A+22，不及格的就是A+（A-2）/4-（A+22）=（A-90）/4，而6*（A-90）/4=A+22，则A=314，80分以下的人数是（A-2）/4，也即是78，参赛的总人数314+78=3922.电影票原价每张若干元,现在每张降低3元出售,观众增加一半,收入增加五分之一,一张电影票原价多少元？解：设一张电影票价x元(x-3)×（1+1/2）=(1+1/5)x(1+1/5)x这一步是什么意思，为什么这么做(x-3){现在电影票的单价}×（1+1/2){假如原来观众总数为整体1，则现在的观众人数为（1+2/1)}左边算式求出了总收入(1+1/5）x{其实这个算式应该是：1x*（1+5/1）把原观众人数看成整体1，则原来应收入1x 元，而现在增加了原来的五分之一，就应该再*（1+5/1），减缩后得到（1+1/5x）}如此计算后得到总收入，使方程左右相等3.甲乙在银行存款共9600元，如果两人分别取出自己存款的40%，再从甲存款中提120元给乙。

这时两人钱相等，求乙的存款答案取40％后，存款有9600×（1－40％）＝5760（元）这时，乙有：5760÷2＋120＝3000（元）乙原来有：3000÷（1－40％）＝5000（元）4.由奶糖和巧克力糖混合成一堆糖，如果增加10颗奶糖后，巧克力糖占总数的60%。

再增加30颗巧克力糖后，巧克力糖占总数的75%,那么原混合糖中有奶糖多少颗？巧克力糖多少颗？答案加10颗奶糖，巧克力占总数的60%，说明此时奶糖占40%，巧克力是奶糖的60/40=1。

百分数应用题【题目1】甲数比乙数少20%，那么乙数比甲数多百分之几？【题目2】有一堆糖果，其中奶糖占45%，再放入16块水果糖后，奶糖就只占25%，这堆糖中有奶糖多少块？【题目3】一个正方体的棱长增加原长的1/2，他的表面积比原表面积增加百分之几？【题目4】商店有篮球和排球共45个，其中篮球占60%，当卖出一批篮球后，篮球占现在总数的25%，卖出的篮球是多少个？【题目5】把一个正方形的一边减少20%，另一边增加2公尺，得到一个长方形，他与原来的正方形面积相等，那么正方形的面积是多少平方公尺？【题目6】已知甲校学生数是乙校学生数的40%，甲校女生数是甲校学生数的30%，乙校男生数是乙校学生数的42%，那么，两校女生数占两校学生总数的百分之几？【题目7】把25公克盐放进100公克水里制成盐水，制成的这种盐水，含盐量是百分之几？【题目8】某次会议，昨天参加会议的男代表比女代表多700人，今天男代表减少10%，女代表增加5%，今天共1995人出席会议，昨天参加会议的有多少人？【题目9】有甲、乙两家商店，如甲店的利润增加20%，乙店的利润减少10%，那么，这两店的利润就相同，问原来甲店的利润是原来乙店的利润的百分之几？【题目10】有浓度为3.2%的盐水500公克，为把他变成浓度是8%的盐水，需要使他蒸发掉多少公克的水？【参考答案】1．【解答】20%÷（1－20%）=25%。

2．【解答】16÷【（1－25%）÷25%―（1―45%）÷45%】=9（块）。

3．【解答】【（1＋1/2）×（1＋1/2）×6】÷（1×1×6）－1 = 125%。

4．【解答】45×60%－18×【25%÷（1－25%）】= 6（个）。

5．【解答】【2×（1－20%）÷20%】2 = 64（平方公尺）。

小学数学六年级奥数《分数的巧算（一）》练习题（含答案）一、填空题1.计算:=÷-⨯+⨯2582.432.02588.6 . 2.=⨯÷⎪⎭⎫ ⎝⎛++1919989898199800980019001900980980190190989898191919 . 3.1000减去它的一半,再减去余下的三分之一,再减去余下的四分之一,依此下去,直到余下的五百分之一,最后剩下 .4.计算:=⨯+⋅⋅⋅+⨯+⨯+⨯100991431321211 . 5.计算:=+++++++496124811241621311814121 . 6.计算:=+--+3121131211 . 7.计算:=⨯+⨯+⨯655161544151433141 . 8.计算:=++⋅⋅⋅+++++⋅⋅⋅+++199719953991199619943989537425313199719961995199619951994543432321 . 9.计算:=⎪⎭⎫ ⎝⎛-⨯-⎪⎭⎫ ⎝⎛+⨯+⎪⎭⎫ ⎝⎛-⨯761231537615312353123176 . 10.计算:⎪⎭⎫ ⎝⎛+++-⎪⎭⎫ ⎝⎛++++⎪⎭⎫ ⎝⎛+++-⎪⎭⎫ ⎝⎛+++20115110151161121814112191613181614121 = .二、解答题11.尽可能化简427863887116690151. 12.计算:⎪⎭⎫ ⎝⎛+⋅⋅⋅+-+-+⋅⋅⋅+⎪⎭⎫ ⎝⎛-+-+⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛-+914637281941322314312213211211.13.计算:1999321132112111+⋅⋅⋅++++⋅⋅⋅++++++. 14.计算: ⎪⎭⎫ ⎝⎛⨯-⨯⎪⎭⎫ ⎝⎛⨯-⨯⋅⋅⋅⨯⎪⎭⎫ ⎝⎛⨯-⨯⎪⎭⎫ ⎝⎛⨯-⨯⎪⎭⎫ ⎝⎛⨯-⨯⎪⎭⎫ ⎝⎛⨯-9997319896317531643153314231.———————————————答 案—————————————————————— 1. 513. 原式()12.48.62582582.42582588.6-+=-⨯+⨯= 51351610258==⨯=. 2. 19915. 原式101191019898191000198001000119001001980100119010101981010119⨯⨯⨯÷⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯= 19981998981998199819⨯⨯⎪⎭⎫ ⎝⎛++= 19915192941998199898193==⨯⨯⨯=.3. 2 1000减去它的一半,余下⎪⎭⎫ ⎝⎛-⨯2111000,再减去余下的31, 余下⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯3112111000,再减去余下的41, 余下⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯4113112111000,…, 直到减去余下的五百分之一,最后剩下:⎪⎭⎫ ⎝⎛-⨯⋅⋅⋅⨯⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯500114113112111000 5004994332211000⨯⋅⋅⋅⨯⨯⨯⨯= 2=4. 10099. 原式⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⋅⋅⋅+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=100199199198141313121211 1009910011=-=. 5. 1615. 原式⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=124162162131131181414121211 ⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+4961248124811241 4961311311811-++-= 163131187161231187⨯+=⎪⎭⎫ ⎝⎛-⨯+=161516187=+=. 6. 542. 原式5425144758745873153116311631==⨯==-+=+--+=.7. 123. 原式655660544550433440⨯⎪⎭⎫ ⎝⎛++⨯⎪⎭⎫ ⎝⎛++⨯⎪⎭⎫ ⎝⎛+= 123150140130=+++++=.8. 21. 原式⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⋅⋅⋅+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⋅⋅⋅+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=19972399219962399052842632419971199619961199551441331221=.9. 1原式=()()()532376123765315376231+⨯+-⨯--⨯ 1111=+-=. 10. 14465. 原式⎪⎭⎫ ⎝⎛+++⨯-⎪⎭⎫ ⎝⎛+++⨯+⎪⎭⎫ ⎝⎛+++⨯-⎪⎭⎫ ⎝⎛+++⨯=413121151413121141413121131413121121 ⎪⎭⎫ ⎝⎛-+-⨯⎪⎭⎫ ⎝⎛+++=514131214131211 1446560131225201611234612=⨯=⎪⎭⎫ ⎝⎛+⨯+++=.11. 分子数字之和等于30,故它可以被3整除,分母奇位上数字之和与偶位上数字之和的差为32-21=11,所以它可以被11整除,把这此因数提出,得:1131138896717338896717=⨯⨯.12.原式=⎪⎭⎫ ⎝⎛+⋅⋅⋅++-⎪⎭⎫ ⎝⎛+⋅⋅⋅+++⎪⎭⎫ ⎝⎛+⋅⋅⋅++-⎪⎭⎫ ⎝⎛+⋅⋅⋅++++4642413732312822211914131211 91828173727164636261555251+⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+++⎪⎭⎫ ⎝⎛+++-⎪⎭⎫ ⎝⎛+⋅⋅⋅+++ 9183761061265512764128731298212109+-+⨯-⨯⨯+⨯⨯-⨯⨯+⨯⨯-⨯=9183763534213281845+-+-+-+-= 91837641532730+-+-+=504533=. 13.因为2)1(21+=+⋅⋅⋅++n n n ,所以 原式=200019992432322212⨯+⋅⋅⋅+⨯+⨯+⨯ ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+⋅⋅⋅+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=2000119991413131212112 100099912000112=⎥⎦⎤⎢⎣⎡-=.14.因为()()()()()()()()()11311131111312+---=+--+-=+--K K K K K K K K K ()()()()()()112211222+-+-=+--=K K K K K K K ,所以 原式()()()()()()()()()()()()()()()()()()()()198198298298197197297297151525251414242413132323+-+-⨯+-+-⨯⋅⋅⋅⨯+-+-⨯+-+-⨯+-+-= 99971009698969995647353624251⨯⨯⨯⨯⨯⋅⋅⋅⨯⨯⨯⨯⨯⨯⨯⨯⨯=97259710041=⨯=.。

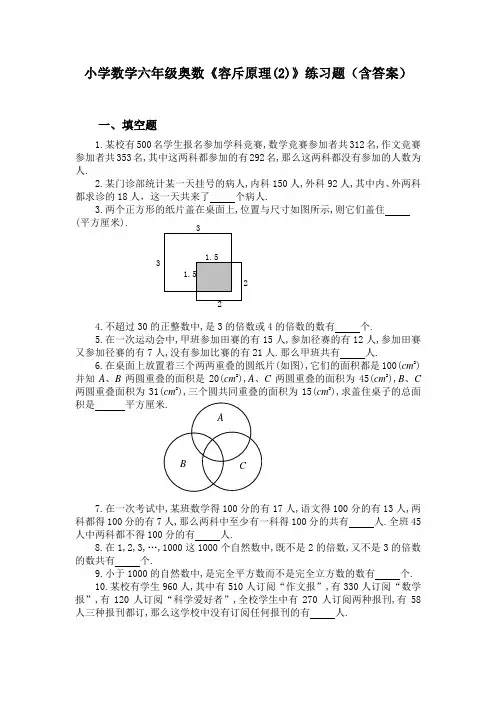
小学数学六年级奥数《容斥原理(2)》练习题（含答案）一、填空题1.某校有500名学生报名参加学科竞赛,数学竞赛参加者共312名,作文竞赛参加者共353名,其中这两科都参加的有292名,那么这两科都没有参加的人数为 人.2.某门诊部统计某一天挂号的病人,内科150人,外科92人,其中内、外两科都求诊的18人，这一天共来了 个病人.3.两个正方形的纸片盖在桌面上,位置与尺寸如图所示,则它们盖住 (平方厘米).4.不超过30的正整数中,是3的倍数或4的倍数的数有 个.5.在一次运动会中,甲班参加田赛的有15人,参加径赛的有12人,参加田赛又参加径赛的有7人,没有参加比赛的有21人.那么甲班共有 人.6.在桌面上放置着三个两两重叠的圆纸片(如图),它们的面积都是100(cm 2)并知A 、B 两圆重叠的面积是20(cm 2),A 、C 两圆重叠的面积为45(cm 2),B 、C 两圆重叠面积为31(cm 2),三个圆共同重叠的面积为15(cm 2),求盖住桌子的总面积是平方厘米.7.在一次考试中,某班数学得100分的有17人,语文得100分的有13人,两科都得100分的有7人,那么两科中至少有一科得100分的共有 人.全班45人中两科都不得100分的有 人.8.在1,2,3,…,1000这1000个自然数中,既不是2的倍数,又不是3的倍数的数共有 个.9.小于1000的自然数中,是完全平方数而不是完全立方数的数有 个.10.某校有学生960人,其中有510人订阅“作文报”,有330人订阅“数学报”,有120人订阅“科学爱好者”,全校学生中有270人订阅两种报刊,有58人三种报刊都订,那么这学校中没有订阅任何报刊的有 人.2 AB C二、解答题11.70名学生参加体育比赛,短跑得奖的31人,投掷得奖的36人,弹跳得奖的29人,短跑与投掷二项均得奖的12人,跑、跳、投三项均得奖的有5人,只得弹跳奖的有7人,只得投掷奖的有15人.求(1)只得短跑奖的人数;(2)得二项奖的总人数;(3)一项奖均未得的人数.12.64人订A 、B 、C 三种杂志.订A 种杂志的28人,订B 种杂志的有41人,订C 种杂志的有20人, 订A 、B 两种杂志的有10人,订B 、C 两种杂志的有12人,订A 、C 两种杂志的有12人,问三种杂志都订的有多少人?13.求从1到1994中不能被5整除,也不能被6或7整除的自然数的个数.14.夏日的一天,有十个同学去吃冷饮.向服务员交出需要冷饮的统计,数字如下,有6个人要可可,有5个人要咖啡,有5个人要果汁,有3个人既要可可又要果汁,有一个人既要可可、咖啡又要了果汁.求证其中一定有一个人什么冷饮也没有要.———————————————答 案——————————————————————1. 127从图中可以看出:参加数学、作文竞赛的总人数为312+353-292=373(人) 从而可知这两科都没有参加的人数为500-373=127(人).2. 224从图可以看出,来诊病人总数为150+92-18=224(人).3. 10.75把两个正方形面积加起来得22+32=13,但其中多算了一块阴影部分的面积,这部分面积为 1.52=2.25(平方厘米),故两个正方形盖住的总面积是22+32-1.52=13-2.25=10.75(cm 2)4. 15内科 150人 外科92人18 人不超过30的3的倍数有10330=⎥⎦⎤⎢⎣⎡(个),不超过30的4的倍数有7430=⎥⎦⎤⎢⎣⎡-(个);不超过30的3⨯4=12的倍数有24330=⎥⎦⎤⎢⎣⎡⨯(个),因此不超过30的正整数中是3的倍数,或是4的倍数的数共有10+7-2=15(个).5. 41如图所示,易知总人数为(15+12-7)+21=41(人).6. 219由容斥原理知,盖住桌面的总面积为100+100+100-(20+45+31)+15=219(平方厘米).7. 23;22至少一科得100分的有17+13-7=23(人),两科都不得100分的有45-23=22(人).8. 333在1~1000的自然数中,2的倍数有50021000=⎥⎦⎤⎢⎣⎡(个),3的倍数有33331000=⎥⎦⎤⎢⎣⎡(个),2⨯3=6的倍数共有166321000=⎥⎦⎤⎢⎣⎡⨯(个),故是2或是3的倍数共有500+333-166=667(个),从而既不是2的倍数,又不是3的倍数的数共有1000-667=333(个).9. 28小于1000的自然数中,是完全平方数的有12、22、…,312共31个.其中12=13,82=43,272=93.又是完全立方数,故符合条件的数有31-3=28(个)10. 121由容斥原理知,或订“作文报”或订“数学报”或订“科学爱好者”的总人数为510+330+120-270+58=748(人)故三种报刊都没有订的人数为960-748=212(人).11. (1)如图,用矩形表示参赛的70个学生,而用三个圆表示分别在跑、 跳、投中得奖的人.数学 语文 7 17 13设x 为只得短跑奖的人数,y 为只在短跑和弹跳两项得奖的人数,z 为只在弹跑与投掷两项得奖的人数,u 为只在投掷和短跑两项得奖的人数.则有u =12-5=7(人),z =36-15-12=9(人),y =29-5-7=8(人),x =31-12-8=11(人).即只得短跑奖的有11人.(2)得二次奖的人数为y +z +u =8+9+7=24(人).(3)因至少得一次奖的人数为x +y +z +u +5+7+15=62(人),故一项奖均未得的人数为70-62=8(人).12. 设三种杂志均订的人数为x ,则有28+41+20-10-12-12+x =64,解得x =9,即三种杂志都订的有9人.13. 在1~1994中,能被5整除的个数为39851994=⎥⎦⎤⎢⎣⎡;能被6整除的个数为33261994=⎥⎦⎤⎢⎣⎡;能被7整除的个数为28471994=⎥⎦⎤⎢⎣⎡;能被5⨯6=30整除的个数为66301994=⎥⎦⎤⎢⎣⎡;能被5⨯7=35整除的数为56351994=⎥⎦⎤⎢⎣⎡;能被6⨯7=42整除的个数为47421994=⎥⎦⎤⎢⎣⎡;能被5⨯6⨯7=210整除的个数为92101994=⎥⎦⎤⎢⎣⎡. 根据容斥原理,1~1994中或能被5,或能被6,或能被7整除的数的个数为:(398+332+284)-(66+54+47)+9=854,从而不能被5整除,也不能被6或7整除的自然数的个数为1994-854=1140(个).14. 要了冷饮的总人数为6+5+5-3-2-3+1=9(人),但总人数为10人,故一定有一个人什么冷饮也没有要.AB C x。

小学六年级奥数试题（8篇）小学六年级奥数试题(8篇)在学习和工作的日常里，我们都经常看到试题的身影，试题可以帮助参考者清楚地认识自己的知识掌握程度。

你知道什么样的试题才算得上好试题吗？以下是小编整理的小学六年级奥数试题，仅供参考，欢迎大家阅读。

小学六年级奥数试题11、(鸡兔同笼问题)小丽买回0.8元一本和0.4元一本的练习本共50本，付出人民币32元。

0.8元一本的练习本有多少本?2、(年龄问题)5年前父亲的年龄是儿子的7倍。

15年后父亲的年龄是儿子的二倍，父亲和儿子今年各是多少岁?3、(盈亏问题)王老师发笔记本给学生们，每人6本则剩下41本，每人8本则差29本。

求有多少个学生?有多少个笔记本?4、(还原问题)便民水果店卖芒果，第一次卖掉总数的一半多2个，第二次卖掉剩下的一半多1个，第三次卖掉第二次卖后剩下的一半少1个，这时只剩下11个芒果。

求水果店里原来一共有多少个芒果?5、(置换问题)学校买回6张桌子和6把椅子共用去192元。

已知3张桌子的价钱和5把椅子的价钱相等，每张桌子和每把椅子各是多少元?6、(安排)烤面包的架子上一次最多只能烤两个面包，烤一个面包每面需要2分钟，那么烤三个面包最少需要多少分钟?7、(油和桶问题)一桶油连桶共重18千克，用去油的一半后，连桶还重9.75千克，原有油多少千克?桶重多少千克?8、(和倍)青青农场一共养鸡、鸭、鹅共12100只，鸭的只数是鸡的2倍，鹅的只数是鸭的4倍，问鸡、鸭、鹅各有多少只?9、(鸡兔同笼)实验小学举行数学竞赛，每做对一题得9分，做错一题倒扣3分，共有12道题，小旺得了84分，小旺做错了几道题?10、(相遇问题)甲、乙两人同时从相距20xx米的两地相向而行，甲每分钟行55米，乙每分钟行45米，如果一只狗与甲同时同向而行，每分钟行120米，遇到乙后，立即回头向甲跑去，遇到甲再向乙跑去。

这样不断来回，直到甲和乙相遇为止，狗共行了多少米?小学六年级奥数试题2标有A、B、C、D、E、F、G记号的七盏灯顺次排成一行，每盏灯安装着一个开关，现在A、C、D、G四盏灯亮着，其余三盏灯是灭的。

小学六年级奥林匹克数学竞赛题及答案1.已知一张桌子的价钱是一把椅子的10倍，又知一张桌子比一把椅子多288元，一张桌子和一把椅子各多少元？解题思路：由已知条件可知，一张桌子比一把椅子多的288元，正好是一把椅子价钱的（10-1）倍，由此可求得一把椅子的价钱。

再根据椅子的价钱，就可求得一张桌子的价钱。

答题：解：一把椅子的价钱：288÷（10-1）=32（元）一张桌子的价钱：32×10=320（元）答：一张桌子320元，一把椅子32元。

2. 3箱苹果重45千克。

一箱梨比一箱苹果多5千克，3箱梨重多少千克？解题思路：可先求出3箱梨比3箱苹果多的重量，再加上3箱苹果的重量，就是3箱梨的重量。

答题：解：45+5×3=45+15=60（千克）答：3箱梨重60千克。

3. 甲乙二人从两地同时相对而行，经过4小时，在距离中点4千米处相遇。

甲比乙速度快，甲每小时比乙快多少千米？解题思路：根据在距离中点4千米处相遇和甲比乙速度快，可知甲比乙多走4×2千米，又知经过4小时相遇。

即可求甲比乙每小时快多少千米。

答题：解：4×2÷4=8÷4=2（千米）答：甲每小时比乙快2千米。

4. 李军和张强付同样多的钱买了同一种铅笔，李军要了13支，张强要了7支，李军又给张强0.6元钱。

每支铅笔多少钱？解题思路：根据两人付同样多的钱买同一种铅笔和李军要了13支，张强要了7支，可知每人应该得（13+7）÷2支，而李军要了13支比应得的多了3支，因此又给张强0.6元钱，即可求每支铅笔的价钱。

答题：解：0.6÷[13-（13+7）÷2]=0.6÷[13—20÷2]=0.6÷3=0.2（元）答：每支铅笔0.2元。

5.甲乙两辆客车上午8时同时从两个车站出发，相向而行，经过一段时间，两车同时到达一条河的两岸。

由于河上的桥正在维修，车辆禁止通行，两车需交换乘客，然后按原路返回各自出发的车站，到站时已是下午2点。

小学数学奥数竞赛列方程解应用题专项练习试卷及答案解析（50道）1、某班原分成两个小组活动，第一组26人，第二组22人，根据学校活动器材的数量，要将一组人数调整为二组人数的一半，应从一组调多少人到二组去？【答案】10【解析】如果从第一组调人到第二组去，那么第一组还有人，第二组有人，现在第一组人数是第二组的一半，根据这个等量关系可以列出方程．设应从第一组调人到第二组去，由题意得：两边同乘以得：2、有三个连续的整数，已知最小的数加上中间的数的两倍再加上最大的数的三倍的和是68，求这三个连续整数.【答案】10、11、12【解析】设最小的那个数为，那么中间的数和最大的数分别为和．则．所以这三个连续整数依次为10、11、12．3、兄弟二人共养鸭550只，当哥哥卖掉自己养鸭总数的一半，弟弟卖出70只时，两人余下的鸭只数相等，求兄弟两人原来各养鸭多少只？【答案】兄原来养鸭320只，弟原来养鸭230只【解析】解：设兄原来养鸭x只，则弟原来养鸭只．（只）4、小军原有故事书的本数是小力的3倍，小军又买来7本书，小力买来6本书后，小军所有的书是小力的2倍，两人原来各有多少本书？【答案】小力原有故事书5本，小军原有故事书15本【解析】解：设小力原有故事书x本，则小军原有故事书3x本（本）5、六年级学生去秋游，要分成15个组，一部分由8人组成一个小组，另一部分由5个人组成一个小组，8人组成小组的总人数比5人组成小组的总人数多3人，求六年级共有多少名同学参加秋游？【答案】93【解析】设8人小组有x组，则5人小组有组（名）6、五年级一班同学参加学校植树活动，派男、女生共12人去取树苗，男同学每人拿3棵，女同学每人拿2棵，正好全部取完；如果男、女生人数调换一下，则还差2棵不能取回．问：原来男、女生人数各是多少？【答案】原来男生有7人，女生有5人【解析】设原来男生有人，女生有人，依题意列方程：．所以原来男生有7人，女生有5人．7、苹果和梨共80斤，价值200元，已知苹果2元一斤，梨元一斤，那么苹果和梨各多少斤？【答案】苹果有30斤，梨有50斤【解析】设苹果斤，梨斤，则有，解得．所以苹果有30斤，梨有50斤．8、甲、乙、丙三人同乘汽车到外地旅行，三人所带行李的重量都超过了可免费携带行李的重量，需另付行李费，三人共付4元，而三人行李共重150千克．如果一个人带150千克的行李，除免费部分外，应另付行李费8元．求每人可免费携带的行李重量.【答案】30千克【解析】设每人可免费携带千克行李．一方面，三人可免费携带千克行李，三人携带150千克行李超重千克，超重行李共付4元行李费；另一方面，一人携带150千克行李超重千克，超重行李需付行李费8元．根据超重行李每千克应付的钱数相同，可列方程：．所以每人可免费携带的行李重量为30千克．9、汽车以每小时千米的速度笔直地开向寂静的山谷，驾驶员按一声喇叭，秒后听到回音，听到回音时汽车离山谷多远？(声音的速度以米/秒计算)【答案】676米【解析】通过画线段图可以看出，声音秒经过的距离等于汽车秒经过的距离与汽车与山谷距离的倍之和．千米/小时米/秒米/秒，设听到回音时汽车离山谷米，根据题意可得：，答：听到回音时汽车离山谷米远．10、平行四边形的周长是80厘米，以边为底时，高为12厘米；以边为底时，高为20厘米，求平行四边形的面积．【答案】300平方厘米【解析】平行四边形的周长是两条邻边之和的2倍，所以厘米，设的长为厘米，的长为厘米，则，解得．所以平行四边形的面积是平方厘米．11、小龙、小虎、小方和小圆四个孩子共有45个球，但不知道每个人各有几个球，如果变动一下，小龙的球减少2个，小虎的球增加2个，小方的球增加一倍，小圆的球减少一半，那么四个人球的个数就一样多了．求原来每个人各有几个球？【答案】分别有球12、8、5、20个【解析】设变动后四个孩子都有球个，则变动前这四个孩子拥有的球数分别为、、、；则可列方程得，化简为，解得；因此，原来这四个孩子分别有球12、8、5、20个．12、甲、乙、丙共有100本课外书．甲的本数除以乙的本数，丙的本数除以甲的本数，商都是5，而且余数也都是1．乙有书多少本？【答案】3【解析】方法一：设乙有课外书x本，则甲有课外书本，丙有课外书（本），于是有，即，解得．方法二：丙的本数超过乙的25倍，所以乙至多有3本书．显然乙的书至少2本，如果乙有2本书，那么甲有（本），丙有（本），三人共有的书不到100本，所以乙有书3本．13、有甲、乙、丙三堆石子，从甲堆中取出8个给乙堆后，甲、乙两堆的石子数就相等了；再从乙堆中取出6个给丙堆，乙、丙两堆的石子数也相等；此时又从丙堆中取2个给甲堆，使甲堆石子数是丙堆石子数的2倍，问：原来甲堆有多少个石子？【答案】26【解析】解：设甲堆原来有x个石子，那么甲堆取出8个给乙堆后，甲乙两堆都是个石子；再从乙堆中取出6个给丙堆，乙、丙两堆的石子数都变成（）个石子；此时又从丙堆中取2个给甲堆，那么甲堆石子数变成（）个，丙堆石子数变成（）个，有，解得．题目中的变化过程比较多，在设立未知数后，一步步跟上分析，把每一步的变化结果都用x的式子表示出来，最后建立等量关系．14、某旅游点有儿童票、成人票两种规格的门票卖，儿童票的价格为30元，成人票的价格为40元，如果是团体还可以买平均32元一位的团体票，一个由8个家庭组成的旅游团(每个家庭由两位大人，或两个大人、一个小孩组成)来景点旅游，如果他们买团体票那么可以比他们各自买票少花120元，问这个旅游团一共有多少人？【答案】20【解析】设八个家庭中有个是三口之家，是个两口之家，则：，所以旅游团一共有人。

小学六年级数学工程问题竞赛练习题1．甲乙两个水管单独开，注满一池水，分别需要20小时，16小时.丙水管单独开，排一池水要10小时，若水池没水，同时打开甲乙两水管，5小时后，再打开排水管丙，问水池注满还是要多少小时？解：1/20+1/16＝9/80表示甲乙的工作效率9/80×5＝45/80表示5小时后进水量1-45/80＝35/80表示还要的进水量35/80÷（9/80-1/10）＝35表示还要35小时注满答：5小时后还要35小时就能将水池注满。

2．修一条水渠，单独修，甲队需要20天完成，乙队需要30天完成。

如果两队合作，由于彼此施工有影响，他们的工作效率就要降低，甲队的工作效率是原来的五分之四，乙队工作效率只有原来的十分之九。

现在计划16天修完这条水渠，且要求两队合作的天数尽可能少，那么两队要合作几天？解：由题意得，甲的工效为1/20，乙的工效为1/30，甲乙的合作工效为1/20*4/5+1/30*9/10＝7/100，可知甲乙合作工效>甲的工效>乙的工效。

又因为，要求“两队合作的天数尽可能少”，所以应该让做的快的甲多做，16天内实在来不及的才应该让甲乙合作完成。

只有这样才能“两队合作的天数尽可能少”。

设合作时间为x天，则甲独做时间为（16-x）天1/20*（16-x）+7/100*x＝1x＝10答：甲乙最短合作10天3．一件工作，甲、乙合做需4小时完成，乙、丙合做需5小时完成。

现在先请甲、丙合做2小时后，余下的乙还需做6小时完成。

乙单独做完这件工作要多少小时？解：由题意知，1/4表示甲乙合作1小时的工作量，1/5表示乙丙合作1小时的工作量（1/4+1/5）×2＝9/10表示甲做了2小时、乙做了4小时、丙做了2小时的工作量。

根据“甲、丙合做2小时后，余下的乙还需做6小时完成”可知甲做2小时、乙做6小时、丙做2小时一共的工作量为1。

所以1－9/10＝1/10表示乙做6-4＝2小时的工作量。

1.小学六年级奥数练习题及答案解析甲、乙、丙三人在A、B两块地植树，A地要植900棵，B地要植1250棵。

已知甲、乙、丙每天分别能植树24，30，32棵，甲在A地植树，丙在B地植树，乙先在A地植树，然后转到B地植树。

两块地同时开始同时结束，乙应在开始后第几天从A地转到B地？【解析】总棵数是900＋1250＝2150棵，每天可以植树24＋30＋32＝86棵需要种的天数是2150÷86＝25天甲25天完成24×25＝600棵那么乙就要完成900-600=300棵之后，才去帮丙即做了300÷30＝10天之后即第11天从A地转到B地。

2.小学六年级奥数练习题及答案解析有三块草地，面积分别是5，15，24亩。

草地上的草一样厚，而且长得一样快。

第一块草地可供10头牛吃30天，第二块草地可供28头牛吃45天，问第三块地可供多少头牛吃80天？【解析】这是一道牛吃草问题，是比较复杂的牛吃草问题。

把每头牛每天吃的草看作1份。

因为第一块草地5亩面积原有草量＋5亩面积30天长的草＝10×30＝300份所以每亩面积原有草量和每亩面积30天长的草是300÷5＝60份因为第二块草地15亩面积原有草量＋15亩面积45天长的草＝28×45＝1260份所以每亩面积原有草量和每亩面积45天长的草是1260÷15＝84份所以45－30＝15天，每亩面积长84－60＝24份所以，每亩面积每天长24÷15＝1.6份所以，每亩原有草量60－30×1.6＝12份第三块地面积是24亩，所以每天要长1.6×24＝38.4份，原有草就有24×12＝288份新生长的每天就要用38.4头牛去吃，其余的牛每天去吃原有的草，那么原有的草就要够吃80天，因此288÷80＝3.6头牛所以，一共需要38.4＋3.6＝42头牛来吃。

两种解法：解法一：设每头牛每天的吃草量为1，则每亩30天的总草量为：10*30/5=60；每亩45天的总草量为：28*45/15=84那么每亩每天的新生长草量为(84-60)/(45-30)=1.6每亩原有草量为60-1.6*30=12，那么24亩原有草量为12*24=288，24亩80天新长草量为24*1.6*80=3072，24亩80天共有草量3072+288=3360，所有3360/80=42(头)。

北师大版小学数学六年级上册比赛场次练习卷（带解析）1．4个人两两握手一次，共需握手( )次。

2．学校武术队为了联络方便，设计一种联络方式．一旦有事，先由教练同时通知两位队长，这两位队长再分别同时通知两名同学，依此类推，每人再同时通知两个人．如果每同时通知两人共需1分钟，4分钟可以通知到（）名同学．3．用4、1、3这三个数字可以组成（）个不同的三位数，它们别是（）。

其中最大的是（），最小的是（）。

4．3个好朋友见面握手问好，每两人握一次，共握了（）次。

5．少年军校共有510名学生，为联络方便，设计了一种联络方式．一旦有事，先由校长通知两名班长，这两名班长再分别通知两名同学，以此类推，每名学生再通知两名学生．如果每同时通知两名学生共需1分钟，通知到所有学生至少需要（）分钟。

6．胜利小学四（2）班和四（3）班进行羽毛球对抗赛，约定三局两胜，现在四（3）班估计到了四（2）班的出场次序，四（3）班要想获胜应怎样安排自己队员的出场次序呢？7．江惠从家到江堤—共有（）条路可走。

8．4顶不同的帽子，小军和小刚两人各戴一顶，一共有（）种不同的搭配方法。

9．小红有2顶不同的帽子，3件不同的上衣，她一共有（）种搭配方法．10．小明想买一本英语读物和一本数学读物，一共有（）种不同的买法。

11．下面两个盒子里分别装着写有1，2，3，4，5的卡片，从每个盒子里各摸出一张卡片，摸出的两张卡片的数字之和可能是（）。

12．有面值分别是1角、2角、5角、1元的钱币，每两种钱币组合，能组合出（）种不同的钱数。

分别是：（）。

13．去猴山有（）条路。

设计三条能参观很多景点的线路：（线路不要重复）14．4个班的同学举行拔河比赛，每2个班必须赛一场，共要进行（）场比赛。

15．学校合唱队为联络方便，设计了一种联络方式，一旦有事，先由领队老师通知队长，接着领队老师、队长通知2名同学，每次接到通知的人都加入到通知的行列……若每通一个电话需1分钟，那么至少经过( )分钟就可通知完合唱队的45人？（包括队长在内）16．笑笑从家到图书馆有（）条路可以走？17．贝贝领着小弟弟在公园玩耍，小弟弟走到贝贝处有（）条路可走？（涂色部分为供游人行走的路）18．下图中的线段表示贝贝从家到学校所能经过的街道。

⼩学数学六年级奥数《最值问题（1）》练习题（含答案）⼩学数学六年级奥数《最值问题(1)》练习题（含答案）⼀、填空题1.⼀把钥匙只能开⼀把锁.现在有4把钥匙4把锁,但不知哪把钥匙开哪把锁,最多要试次才能配好全部的钥匙和锁.2.⽤长和宽分别是4厘⽶和3厘⽶的长⽅形⼩⽊块,拼成⼀个正⽅形,最少要⽤这样的⽊块块.3.⼀个⼀位⼩数⽤四舍五⼊法取近似值精确到万位,记作50000.在取近似值以前,这个数的最⼤值是 .4.100个⾃然数,它们的总和是10000,在这些数⾥,奇数的个数⽐偶数的个数多,那么这些数⾥⾄多有个偶数.5.975?935?972?( ),要使这个连乘积的最后四个数字都是零.在括号内最⼩应填 .6.有三个连续⾃然数,它们依次是12、13、14的倍数,这三个连续⾃然数中(除13外)是13倍数的那个数最⼩是 .7.下图九个数中取出三个数来,这三个数都不在同⼀横⾏,也不在同⼀纵⾏.问:怎样取才能使这三个数之和最⼤,最⼤数是 .8.农民叔叔阿根想⽤20块长2⽶,宽1.2⽶的⾦属⽹建⼀个靠墙的长⽅形鸡窝.为了防⽌鸡飞出,所建鸡窝的⾼度不得低于2⽶,要使鸡窝⾯积最⼤,长⽅形的长和宽分别应是 .9.⼀个三⾓形的三条边长是三个两位的连续偶数,它们的末位数字和能被7整除,这个三⾓形的最⼤周长等于 .10.农场计划挖⼀个⾯积为432m 2的长⽅形养鱼池,鱼池周围两侧分别有3m 和4m 的堤堰如图所⽰,要想占地总⾯积最⼩,⽔池的长和宽应为 .⼆、解答题11.下图中,已知a 、b 、c 、d 、e、f 是不同的⾃然数,且前⾯标有两个箭头的每⼀个数恰等于箭头起点的两数的和(如b =a +d ),那么图中c 最⼩应为多少?a b cd ef12.唐⽼鸭与⽶⽼⿏进⾏⼀万⽶赛跑,⽶⽼⿏的速度是每分钟125⽶,唐⽼鸭的速度是每分钟100⽶.唐⽼鸭⼿中掌握着⼀种迫使⽶⽼⿏倒退的电⼦遥控器,通过这种遥控器发出第n 次指令,⽶⽼⿏就以原速度的n ?10%倒退⼀分钟,然后再按原来的速度继续前进,如果唐⽼鸭想在⽐赛中获胜,那么它通过遥控器发出指令的次数⾄少应是多少次?13.某游泳馆出售冬季学⽣游泳卡,每张240元,使⽤规定:不记名,每卡每次只限⼀⼈,每⼈只限⼀次.某班有48名学⽣,⽼师打算组织学⽣集体去游泳,除需购买若⼲张游泳卡,每次游泳还需包⼀辆汽车,⽆论乘坐多少名学⽣,每次的包车费均为40元.若要使每个同学游8次,每⼈最少交多少钱?14.某商店需要制作如图所⽰的⼯字形架100个,每个由铝合⾦型材长为2.3⽶,1.7⽶,1.3⽶各⼀根组装⽽成.市场上可购得该铝合⾦型材的原料长为 6.3⽶.问:⾄少要买回多少根原材料,才能满⾜要求(不计损耗)?———————————————答案——————————————————————1. 6第⼀把钥匙最坏的情况要试3次,第⼆把要试2次,第三把要试1次,共计6次.2. 12因4和3的最⼩公倍数为12,故最少需这样的⽊块12块.3. 50000.44. 48⼀共有100个⾃然数,其中奇数应多于50个,因为这100个⾃然数的总和是偶数,所以奇数的个数是偶数,⾄少有52个,因⽽⾄多有48个.5. 20因975=39?52,935=187?5,972=243?22,要使其积为1000的倍数,⾄少应乘以5?22=20.6. 1105因为12、13、14的公倍数分别加上12、13、14后才依次是12、13、14倍数的连续⾃然数,故要求是13的倍数的最⼩⾃然数,只须先求12、13、14的最⼩公倍数为1092,再加上13得1105.7. 20第⼀横⾏取6,第⼆横⾏取7,第三横⾏取7.8. 12⽶,6⽶.⾦属⽹应竖着放,才能使鸡窝⾼度不低于2⽶.如图,设长⽅形的长和宽分别是x ⽶和y ⽶,则有x +2y =1.2?20=24.长⽅形的⾯积为S =xy =()y x 221?.因为x 与2y 的和等于24是⼀个定值,故它们的乘积当它们相等时最⼤,此时长⽅形的⾯积S 也最⼤,于是有:x =12,y =6.9. 264依题意,末位数字和能被7整除的只有7、14、21等三种.但三个两位的连续偶数相加其和也⼀定是偶数,故符合题意的只有14.这样三个最⼤的两位连续偶数.它们的末位数字⼜能被7整除的,便是90、88、86，它们的和即三⾓形最⼤周长为90+88+86=264.10. 24m ,18m如图,设⽔池边长为xm ,宽为ym ,则有xy =432,占地总⾯积S =(x +8)(y +6)m 2 于是S =xy +6x +8y +48=6x +8y +480.因6x +8y=48?432为定值,故当6x =8y 时,S 最⼩,此时x =24,y =18.11. 依题意,d 应当取最⼩值1,那么a 和f 只能⼀个为2,另⼀个为4.这样,根据b =a +d ,e =d +f ,b 和e 便只能⼀个为3,另⼀个为5,⽽c =b +e .所以c 最⼩应为3+5=8.12. ⽶⽼⿏跑完全程⽤的时间为10000÷125=80(分),唐⽼鸭跑完全程的时间为10000÷100=100(分).唐⽼鸭第n 次发出指令浪费⽶⽼⿏的时间为n n 1.01125%101251+=??+. 当n 次取数为1、2、3、4…13时,⽶⽼⿏浪费时间为1.1+1.2+1.3+1.4+…+2.3=22.1(分)⼤于20分.因为⽶⽼⿏早到100-80=20分,唐⽼鸭要想获胜,必须使⽶⽼⿏浪费的时间超过20分钟,因此唐⽼鸭通过遥控器⾄少要发13次指令才能在⽐赛中获胜.13.设⼀共买了x 张卡,⼀共游泳y 次,则共有xy =48?8=384(⼈次),总运费为:(240x +40y )元.因240x ?40y =240?40?384是⼀定值,故当240x =40y ,即y =6x 时和最⼩,此时可求得x =8,y =48.总⽤费为240?8+40?48=3840(元),平均每⼈最少要交3840÷48=80(元).显然④⑤⑥三种⽅案损耗较⼩. ④⑤⑥⑦⽅案依次切割原材料42根、14根、29根和1根共⽤原材料42+14+29+1=86(根).。

小学六年级数学竞赛奥数综合练习题1、五年级三班学生参加课外兴趣小组，每人至少参加一项。

其中有25人参加自然兴趣小组，35人参加美术兴趣小组，27人参加语文兴趣小组，参加语文同时又参加美术兴趣小组的有12人，参加自然同时又参加美术兴趣小组的有8人，参加自然同时又参加语文兴趣小组的有9人，语文、美术、自然3科兴趣小组都参加的有4人。

求这个班的学生人数。

2、如图8-1，已知甲、乙、丙3个圆的面积均为30，甲与乙、乙与丙、甲与丙重合部分的面积分别为6，8，5，而3个圆覆盖的总面积为73。

求阴影部分的面积。

3、四年级一班有46名学生参加3项课外活动。

其中有24人参加了数学小组，20人参加了语文小组，参加文艺小组的人数是既参加数学小组又参加文艺小组人数的3.5倍，又是3项活动都参加人数的7倍，既参加文艺小组也参加语文小组的人数相当于3项都参加的人数的2倍，既参加数学小组又参加语文小组的有10人。

求参加文艺小组的人数。

4、图书室有100本书，借阅图书者需要在图书上签名。

已知在100本书中有甲、乙、丙签名的分别有33，44和55本，其中同时有甲、乙签名的图书为29本，同时有甲、丙签名的图书有25本，同时有乙、丙签名的图书有36本。

问这批图书中最少有多少本没有被甲、乙、丙中的任何一人借阅过？5、5条同样长的线段拼成了一个五角星。

如果每条线段上恰有1994个点被染成红色，那么在这个五角星上红色点最少有多少个？6、甲、乙、丙同时给100盆花浇水。

已知甲浇了78盆，乙浇了68盆，丙浇了58盆，那么3人都浇过的花最少有多少盆？7、甲、乙、丙都在读同一本故事书，书中有100个故事。

每个人都从某一个故事开始，按顺序往后读。

已知甲读了75个故事，乙读了60个故事，丙读了52个故事。

那么甲、乙、丙3人共同读过的故事最少有多少个？8、已知4205和2813都是29的倍数，1392和7018是不是29的倍数？9、如果两个数的和是64，这两个数的积可以整除4875，那么这两个数的差是多少？10、用0～9这十个数码组成五个两位数，每个数字只用一次，要求它们的和是奇数，那么这五个两位数的和最大是多少？。

⑸ ⑹在 ABCD 长方形中， O 是长方形的中心， BC 长20 厘米， AB 长12 厘米， DE = 4AE ，CF = 3DF ，那么阴影部分的面积是多少平方厘米？格点与割补练习题3. 一． 夯实基础：E1. A如图，计算这个格点多边形的面积．D IFIIIBIIC(a )(b )(c )O2.如图，计算各个格点多边形的面积．⑴⑵⑶ ⑷5. 如图是一个漂亮礼盒的平面图，已知相邻两个格点距离为 1，请求出礼盒平面图的面积。

C 二． 拓展提高：6. 右图是一个8 12 面积单位的图形．求矩形内的箭形 ABCDEFGH 的面积．HFADB7. 求格点中“乡村小屋”的面积是多少？分别计算图中两个格点多边形的面积．（1） （2）GE4.9. 图中有21 个点，其中相邻三点所形成的等边三角形的面积为1 ，试计算四边形的面积。

三. 超常挑战10. 如图，一个面积为 2009 平方厘米的长方形，被分割成了一个长方形、两个等腰直角三角形、三个梯形．已知除了阴影长方形外，其它的五块面积都相等，且 B 是 AC 的中点； 那么阴影长方形的面积是多少厘米．BCA11. 如图，三角形 ABC 和 DEF 是两个完全相同的等腰直角三角形，其中 DF 长9 厘米，CF长3 厘米，那么阴影部分的面积是多少平方厘米？ADECBFB8. 如图，每相邻三个点所形成的三角形都是面积为1 的等边三角形，计算 ABC 的面积．ACO12. 如图涂阴影部分的小正六角星形面积是 16 平方厘米，问：大正六角星形面积是多少平方厘米？13. 如图，六边形 ABCDEF 为正六边形，P 为对角线CF 上一点，若 PBC 、PEF 的面积为3与4 ，则正六边形 ABCDEF 的面积多少？14. 如图，ABCD 是边长为8 厘米的正方形，梯形 AEBD 的对角线相交于O ，三角形 AOE 的面积比三角形 BOD 的面积小16 平方厘米，则梯形 AEBD 的面积是多少平方厘米？ADEB C四．杯赛演练：15. (“新加坡小学数学奥林匹克”竞赛试题)下图是一个方格网，计算阴影部分的面积．1 cm1 cm2利用“扩展法”或者“割补法”我们都可以简单的得到⑴、⑵的面积分别为9 和10 5. 对两个三角形进行拓展计算：左边三角形的面积= 4⨯ 4 -1⨯ 2 ÷ 2 - 4⨯ 3 ÷ 2 - 4⨯ 2 ÷ 2 = 54. 答案：1. 方法一(扩展法)：这是个三角形，虽然有三角形面积公式可用，但判断它的底和高却十分困难，只能另想别的办法。