2020中考数学复习方案基础小卷速测(十)等边(腰)三角形相关计算与证明

三角形满分：100分一、选择题(本大题共10小题，每小题3分，共30分)1．若一个角为65°，则它的补角的度数为()A．25°B．35°C．115°D．125°2．如图，△ABC是锐角三角形，过点C作CD⊥AB，垂足为D，则点C到直线AB的距离是() A．线段CA的长B．线段CD的长C．线段AD的长D．线段AB的长3．如图，有一块含有30°角的直角三角板的两个顶点放在直尺的对边上．如果∠2＝44°，那么∠1的度数是()A．14°B．15°C．16°D．17°4．已知三角形的两边长分别为4和6，则第三边可能是()A．2B．7C．10D．125．如图，在△ABC中，∠A＝60°，∠B＝40°，则∠C等于()A．100°B．80°C．60°D．40°6．如图，∠ACD是△ABC的外角，CE平分∠ACD，若∠A＝60°，∠B＝40°，则∠ECD等于() A．40°B．45°C．50°D．55°7．如图，已知BG是∠ABC的平分线，DE⊥AB于点E，DF⊥BC于点F，DE＝6，则DF的长度是()A．2B．3C．4D．68．如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB＝AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD()A．∠B＝∠CB．AD＝AEC．BD＝CED．BE＝CD9．如图，在Rt△ABC中，∠ACB＝90°，CD为AB边上的高，CE为AB边上的中线，AD＝2，CE ＝5，则CD等于()A．2B．3C．4D．2 310．如图，在平行四边形ABCD中，点E在边DC上，DE∶EC＝3∶1，连接AE交BD于点F，则△DEF的面积与△BAF的面积之比为()A．3∶4B．9∶16C．9∶1D．3∶1二、填空题(本大题共6小题，每小题4分，共24分)11．如图，平面上直线a，b分别经过线段OK两端点(数据如图)，则a，b相交所成的锐角是.11题12题13题15题16题12．如图，∠AOB＝40°，OP平分∠AOB，点C为射线OP上一点，作CD⊥OA于点D，在∠POB 的内部作CE∥OB，则∠DCE＝度．13．如图，在△ABC中，AC＝10，BC＝6，AB的垂直平分线交AB于点D，交AC于点E，则△BCE 的周长是.14．已知等腰三角形的一个外角为130°，则它的顶角的度数为.15．如图，在△ABC中，BO，CO分别平分∠ABC，∠ACB.若∠BOC＝110°，则∠A＝. 16．如图，在Rt△ABC中，CD是斜边AB上的中线，已知CD＝2，AC＝3，则sin B的值是.三、解答题(一)(本大题共3小题，每小题6分，共18分)17．计算：2cos 60°＋4sin 60°·tan 30°－cos245°.18．如图，AB∥CD，∠1＝∠2.求证：AM∥CN.19．如图，已知：∠AOB及边OB上一点C.求作：∠OCD，使得∠OCD＝∠AOB.要求：(1)尺规作图，保留作图痕迹，不写作法(说明：作出一个即可)；(2)请你写出作图的依据．四、解答题(二)(本大题共4小题，共28分)20．如图，在△ABC中，AB＝AC，CD是∠ACB的平分线，DE∥BC，交AC于点E.(1)求证：DE＝CE；(2)若∠CDE＝35°，求∠A的度数．21．如图，在△ABC中，AB＝AC，点D，E，F分别在边AB，BC，AC上，且BD＝CE，BE＝CF.(1)求证：ED＝EF；(2)当点G是DF的中点时，请判断EG和DF的位置关系，并说明理由．22．在数学实践活动课上，老师带领同学们到附近的湿地公园测量园内雕塑的高度．如图，他们用测角仪在A处测得雕塑顶端点C的仰角为30°，再往雕塑方向前进4米至B处，测得仰角为45°.问：该雕塑有多高？(测角仪高度忽略不计，结果不取近似值)23．如图，在四边形ABCD中，∠ABC＝90°，AC＝AD，M，N分别为AC，CD的中点，连接BM，MN，BN.（1）求证：BM＝MN；（2）∠BAD＝60°，AC平分∠BAD，AC＝2，求BN的长．参考答案：1~10：CBCBB CDDCB 11. 30° 12. 130 13. 16 14. 50°或80 15. 40° 16. 3417. 解：原式＝2×12＋4×32×33－⎝⎛⎭⎫222＝1＋2－12＝52.18. 证明：∵AB ∥CD ，∴∠EAB ＝∠ECD ， ∵∠1＝∠2，∴∠EAM ＝∠ECN ，∴AM ∥CN. 19. 解：(1)如图，∠OCD 即为所求．(2) 作图的依据为SSS.20.(1)证明：∵CD 是∠ACB 的平分线， ∴∠BCD ＝∠ECD.∵DE ∥BC ，∴∠EDC ＝∠BCD ， ∴∠EDC ＝∠ECD ，∴DE ＝CE. (2)解：∵∠ECD ＝∠EDC ＝35°， ∴∠ACB ＝2∠ECD ＝70°.∵AB ＝AC ，∴∠ABC ＝∠ACB ＝70°，∴∠A ＝180°－∠ABC －∠ACB ＝180°－70°－70°＝40°. 21.(1)证明：∵AB ＝AC ，∴∠B ＝∠C ， 在△BDE 和△CEF 中，⎩⎪⎨⎪⎧BD ＝CE ，∠B ＝∠C ，BE ＝CF ，∴△BDE ≌△CEF (SAS )，∴ED ＝EF . (2)解：∵点G 是DF 的中点，又ED ＝EF ， ∴EG 垂直平分DF .理由：等腰三角形底边上的高线与中线重合． 22.设CD ＝x 米，∵∠CBD ＝45°，∠BDC ＝90°，∴BD ＝CD ＝x 米， ∵∠A ＝30°，AD ＝AB ＋BD ＝4＋x ， ∴tan A ＝CD AD ，即33＝x 4＋x ，解得x ＝2＋23.答：该雕塑的高度为(2＋23)米．23.(1)证明：在△CAD 中，∵M ，N 分别是AC ，CD 的中点， ∴MN ∥AD ，MN ＝12AD ，在Rt △ABC 中，∵M 是AC 中点，∴BM ＝12AC ，∵AC ＝AD ，∴MN ＝BM.(2)解：∵∠BAD ＝60°，AC 平分∠BAD ， ∴∠BAC ＝∠DAC ＝30°，由(1)可知，BM ＝12AC ＝AM ＝MC ，∴∠BMC ＝∠BAM ＋∠ABM ＝2∠BAM ＝60°， ∵MN ∥AD ，∴∠NMC ＝∠DAC ＝30°，∴∠BMN ＝∠BMC ＋∠NMC ＝90°，∴BN 2＝BM 2＋MN 2， 由(1)可知MN ＝BM ＝12AC ＝1，∴BN ＝2.。

06三角形2一、选择题:1．（江苏省镇江市丹徒区江心实验学校2019届九年级3月份调研考试数学试题）如图，在五边形ABCDE 中，∠A+∠B+∠E=300°，DP,CP分别平分∠EDC、∠BCD，则∠P的度数是A．60°B．65°C．55°D．50°【答案】A【解析】∵五边形的内角和等于540°，∠A+∠B+∠E=300°，∴∠BCD+∠CDE=540°﹣300°=240°，∵∠BCD、∠CDE的平分线在五边形内相交于点O，∴∠PDC+∠PCD=（∠BCD+∠CDE）=120°，∴∠P=180°﹣120°=60°．故选A．2．（江苏省镇江市丹阳市2019年中考一模数学试题）如图，在长方形纸片ABC D中，AD= 4cm，把纸片沿直线AC折叠，点B落在E处，AE交DC于点O，若OC=5cm，则CD的长为A．6cm B．7cmC．8cm D．10cm【答案】C【解析】根据折叠前后角相等可知∠BAC=∠EAC，∵四边形ABCD是矩形，∴AB∥CD，∴∠BAC =∠ACD ， ∴∠EAC =∠ACD ， ∴AO =CO =5cm ，在直角三角形ADO 中，DO ，CD = AB =DO +CO =3+5=8cm ． 故选C ．【点睛】本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．3．（江苏省如皋市2019届九年级第一次模拟考试数学试题）如图，点D 在△ABC 的边AB 的延长线上，DE ∥BC ，若∠A ＝35°,∠C ＝24°,则∠D 的度数是A ．24°B ．59°C ．60°D ．69°【答案】B【解析】∵∠A =35°，∠C =24°， ∴∠DBC =∠A +∠C =35°+24°=59°， 又∵DE ∥BC ， ∴∠D =∠DBC =59°， 故选B.【点睛】本题考查了平行线的性质，三角形外角的性质，熟练掌握相关的性质是解题的关键.4．（江苏省2019年苏州市常熟市中考数学模拟试题）如图，ABC △是一块直角三角板，90,30C A ∠=︒∠=︒，现将三角板叠放在一把直尺上，AC 与直尺的两边分别交于点D ，E ，AB 与直尺的两边分别交于点F ，G ，若∠1=40°，则∠2的度数为A．40ºB．50ºC．60ºD．70º【答案】D【解析】∵DF∥EG，∴∠1＝∠DFG＝40°，又∵∠A＝30°，∴∠2＝∠A+∠DFG＝30°+40°＝70°，故选D．【点睛】本题主要考查了平行线的性质以及三角形外角性质的运用，解题时注意：两直线平行，内错角相等．5．（江苏省盐城市阜宁县实验初级中学2019-2020学年九年级上学期12月月考数学试题）如图，M（0，﹣3）、N（0，﹣9），半径为5的⊙A经过M、N，则A点坐标为A．（-5，-6）B．（4，-6）C．（-6，-4）D．（-4，-6）【答案】D【解析】过A作AB⊥NM交y轴于B，连接AM，∵点M （0，−3）、N （0，−9）， ∴MN ＝6， ∴BM ＝BN ＝3， ∴OB ＝3＋3＝6，∴()06B -，， ∵=5AM ，由勾股定理得：4AB ==， ∴点A 的坐标为（−4，−6）， 故答案为：（−4，−6）．【点睛】本题考查了勾股定理和垂径定理，能根据垂径定理求出BM 和BN 是解此题的关键． 6．（江苏省无锡市2019届九年级中考适应性考试数学试题（三））如图，字母B 所代表的正方形的面积是A ．12B ．144C ．13D ．194【答案】B【解析】如图，根据勾股定理我们可以得出： a 2+b 2＝c 2a 2＝25，c 2＝169，b 2＝169﹣25＝144， 因此B 的面积是144． 故选B ．【点睛】本题主要考查了正方形的面积公式和勾股定理的应用．只要搞清楚直角三角形的斜边和直角边本题就容易多了．7．（江苏省无锡市江阴市青阳片2019-2020学年九年级上学期期中数学试题）根据圆规作图的痕迹，可用直尺成功找到三角形外心的是A ．B ．C ．D ．【答案】C【解析】三角形外心为三边的垂直平分线的交点，由基本作图得到C 选项作了两边的垂直平分线，从而可用直尺成功找到三角形外心． 故选C ．【点睛】本题考查了作图﹣基本作图：熟练掌握基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）．也考查了三角形的外心．8．（江苏省苏州市2019届九年级中考数学模拟试题（一））如图，已知60AOB ∠=︒，点P 在OA 上，12OP =.点M 、N 在OB 边上，PM PN =.若2MN =，则OM =A ．3B ．4C．5D．6【答案】C【解析】过P作PQ⊥MN，∵PM=PN，∴MQ=NQ=1，在Rt△OPQ中，OP=12，∠AOB=60°，∴∠OPQ=30°，∴OQ=6，则OM=OQ-QM=6-1=5．故选：C．【点睛】本题考查等腰三角形的性质，以及含30度直角三角形的性质，熟练掌握等腰三角形以及含30°直角三角形的性质是解题的关键．9．（江苏省南通市海安市十校联考2019-2020学年九年级上学期期中数学试题）如图，△ABD是等边三角形，以AD为边向外作△ADE，使∠AED＝30°，且AE＝3，DE＝2，连接BE，则BE的长为A．4 BC．5 D【答案】B【解析】作EF⊥AE，且EF=DE，连接AF、DF，因为∠AEF=90°，所以∠DEF=90°-30°=60°，DE=EF，所以△DEF是等边三角形，所以∠EDF=60°，∠ADF=∠BDE，因为AD=BD，DE=EF，∠ADF=∠BDE，所以△BDE≌△ADF，所以BE=AF=B．【点睛】本题主要考查的就是三角形全等证明的应用以及直角三角形勾股定理的应用，解决这个问题的关键就是要能够作出辅助线，将所求的线段转化到直角三角形中，利用勾股定理进行求解．对于这种无法直接计算的题目，我们可以通过旋转，作直角三角形等将所求的线段放到特殊的三角形中，然后来进行求解，特别需要注意的就是题目中出现30°、45°、135°等特殊角的时候．10．（江苏省南京市联合体（秦淮下关浦口沿江)2019年中考三模数学试题）如图，在一张长方形纸条上画一条截线AB，将纸条沿截线AB折叠，则△ABC一定是A．等腰三角形B．直角三角形C．等边三角形D．等腰直角三角形【答案】A【解析】如图：∵所给图形是长方形，∴∠1＝∠2，∵∠2＝∠ABC，∴∠1＝∠ABC，∴AC＝BC，即△ABC为等腰三角形．故选：A．【点睛】本题考查了翻折变换的问题，综合性较强，注意熟练掌握翻折不变性、平行线的性质、等腰三角形的性质．二、填空题11．（2019年江苏省连云港市海州区新海实验中学九年级（下）第一次月考数学试题）如图，在△AB C中，AC＝8，BC＝5，AB的垂直平分线DE交AB于点D，交边AC于点E，则△BCE的周长为_______．【答案】13【解析】已知DE是AB的垂直平分线，根据线段的垂直平分线的性质得到EA=EB，所以△BCE的周长=BC+EC+EB=BC+EC+EA=BC+AC=13，12．（江苏省南通市海安市十校2019-2020学年九年级上学期10月月考数学试题）平面直角坐标系中，C（0，4），A为x轴上一动点，连接AC，将AC绕A点顺时针旋转90°得到AB，当点A在x轴上运动时，OB+BC 的最小值为_____．【答案】【解析】过点B作BE⊥x轴，∴∠AEB=∠COA=90°，∵将AC绕A点顺时针旋转90°得到AB，∴∠CAB=90°，AC=AB，∴∠OCA+∠CAO=∠CAO+∠BAE=90°，∴∠OCA=∠BAE，∴△ACO≌△BAE，∴CO=AE=4，OA=BE，如图，作点O关于BE的对称点D，则BE垂直平分OD，∴OB =DB ，∴当点C 、B 、D 三点共线时OB +BC =BD +BC =CD ，OB +BC 的最小值为CD ； 设点A 坐标为（x ，0），则OA =x （0x ≥）， ∴点E 为（x +4，0），则点D 为（2x +8，0）， ∴OD =2x +8，在直角三角形OCD 中，由勾股定理，得：222CD OC OD =+，∴CD ==， ∵0x ≥，∴当0x =时，CD 有最小值，CD 的最小值为：min CD ==，∴OB +BC 的最小值为：【点睛】本题考查了旋转的性质，全等三角形的判定和性质，二次函数的性质，轴对称求最短距离问题，以及勾股定理，解题的关键是正确理解题意，找到使OB +BC 得到最小值的情况，然后进行分析解答.13．（江苏省徐州市2019届中考模拟考试数学试题）如图，在△AB C 中，AB =5cm ，AC =3cm ，BC 的垂直平分线分别交AB 、BC 于D 、E ，则△ACD 的周长为__________cm ． 【答案】8【解析】∵DE 是BC 的垂直平分线， ∴BD =CD ，∴AB =AD +BD =AD +CD ，∴△ACD 的周长=AD +CD +AC =AB +AC =8cm ； 故答案为8【点睛】本题主要考查了线段垂直平分线的性质和三角形的周长，掌握线段的垂直平分线上的点到线段两端点的距离相等.14．（江苏省东台市第四联盟2019届九年级下学期学情调查一数学试题）等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为__________．【答案】60°或120°【解析】如图（1），∵AB=AC，BD⊥AC，∴∠ADB=90°，∵∠ABD=30°，∴∠A=60°；如图（2），∵AB=AC，BD⊥AC，∴∠BDC=90°，∵∠ABD=30°，∴∠BAD=60°，∴∠BAC=120°；综上所述，它的顶角度数为：60°或120°．【点睛】此题考查了等腰三角形的性质．此题难度适中，注意掌握分类讨论思想的应用是解此题的关键．15．（江苏省常州市新北区外国语学校2019届九年级下学期一模数学试题）在Rt△AB C中，∠ACB=90°，AC=8，BC=6，点D、E分别在AC、AB上，且△ADE是直角三角形，△BDE是等腰三角形，则BE=_________.【答案】307或154．【解析】①如图1中，当∠AED=90°，DE=BE时，设DE=BE=x．在Rt△AB C中，∵AC=8，BC=6，∴AB，∵∠A=∠A，∠AED=∠C=90°，∴△AED∽△ACB，∴AE DE AC BC=，∴1086x x-=，解得x=307．②如图2中，当∠ADE=90°，DE=EB时，设DE=BE=x，∵△ADE∽△ACB，∴DE AE BC AB=，∴10610x x-=，解得x=154，综上所述，BE的值为307或154．【点睛】本题考查等腰三角形的性质，相似三角形的判定和性质等知识，解题的关键是学会利用参数构建方程解决问题.16．（江苏省盐城市建湖县2019-2020学年九年级上学期期中数学试题）如图，BC＝cm，点D是线段BC上的一点，分别以BD、CD为边在BC的同侧作等边三角形ABD和等边三角形CDE，AC、BE相交于点P，则点D从点B运动到点C时，点P的运动路径长（含与点B、C重合）为_________.【答案】16π3【解析】作△BCP的外接圆⊙O，过点O作OF⊥BC于F，延长OF交⊙O于G，连接BG，CG，OB，OC，∵△ABD和△CDE是等边三角形，∴∠ABD=∠EDC=60°，∴AB//DE，∠ABD+∠ADE=∠EDC+∠ADE，∴∠ABE=∠BED，∠BDE=∠ADC，在△BDE和△AD C中，BD ADBDE ADC DE DC=⎧⎪∠=∠⎨⎪=⎩，∴△BDE≌△ADC，∴∠BED=∠ACD，∴∠ACD=∠ABE，∴∠ACD+∠EBC=∠ABE+∠EBC=∠ABD=60°，∴∠BPC=180°-（∠ACD+∠EBC）=120°，∴点D从点B运动到点C时，点P的运动路径长（含与点B、C重合）为»BC的长，∵OG⊥BC，∠BGC=∠BPC=120°，∴BF=12BC=12×，∠OGB=12∠BGC=60°，∵OB=OG，∴△OBG是等边三角形，∴∠BOG=60°，∴∠BOC=2∠BOG=120°，∠OBF=30°，∴OF=12 OB，∴OB 2=OF 2+BF 2，即OB 2=(12OB )22, 解得OB =8，（负值舍去），∴»BC=120π8180⨯=16π3，故答案为：16π3【点睛】本题考查等边三角形的性质、全等三角形的判定与性质、圆周角定理及垂径定理，根据圆周角定理确定点P 的运动轨迹是解题关键.17．（江苏省东台市第四联盟2019届九年级下学期学情调查一数学试题）如图，在等边△AB C 中，AB =4，点P 是BC 边上的动点，点P 关于直线AB ，AC 的对称点分别为M ，N ，则线段MN 长的取值范围是.【答案】6MN ≤≤.【解析】如图１，当点P 为BC 的中点时，MN 最短．此时E 、F 分别为AB 、AC 的中点， ∴PE =12AC ，PF =12AB ，EF =12BC ， ∴MN =ME +EF +FN =PE +EF +PF =6；如图2，当点P 和点B （或点C ）重合时，此时BN （或CM ）最长．此时G （H ）为AB （AC ）的中点，∴CG （BH ，CM （BN ．故线段MN 长的取值范围是6≤MN18．（江苏省徐州市2019届九年级第二次模拟考试数学试题）如图，△AB C 中，AB =AC ，∠A =40º，点P 是△ABC 内一点，连结PB 、PC ，∠1=∠2，则∠BPC 的度数是_________．【答案】110°【解析】∵△ABC 中，AB =AC ，∠A =40°， ∴∠ABC =12(180°−40°)＝70°， ∴∠1+∠PBC =70°， ∵∠1=∠2， ∴∠2+∠PBC =70°，∴∠BPC =180°-（∠2+∠PBC ）=180°-70°=110°， 故答案为：1100．【点睛】此题考查等腰三角形的性质，关键是根据等腰三角形的性质和三角形内角和解答．19．（江苏省盐城市中学2019-2020学年九年级上学期第一次月考数学试题）已知：在ABC △中，AB AC =．(1)求作：ABC △的外接圆．(要求：尺规作图，保留作图痕迹，不写作法) (2)若ABC △的外接圆的圆心O 到BC 边的距离为4，6BC =，则O S =e ．【答案】（1）见解析；（2）25π 【解析】（1）如图O e 即为所求．（2）设线段BC 的垂直平分线交BC 于点E ． 由题意4,3OE BE EC ===，在Rt OBE △中，5OB ==，∴2π·525πO S ==圆． 故答案为25π．【点睛】本题考查作图-复杂作图，等腰三角形的性质，三角形的外接圆与外心等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．三、解答题20．（江苏省镇江市丹徒区江心实验学校2019-2020学年九年级12月份月考数学试题）三角形的两边长分别为3和4，第三边的长是方程x 2﹣8x +15=0的解，求此三角形的面积【答案】6或【解析】x 2﹣8x +15=0，解得123,5x x ==，根据三角形三边关系可知，此三角形第三边大于1且小于7， ∴当三边长为3，4，5时，三角形是直角三角形，其面积S =134=62⨯⨯； 当三边长为3，3，4时，三角形为等腰三角形，∴面积为S =142⨯∴三角形面积为：6或【点睛】本题考查了解一元二次方程-因式分解法：因式分解法就是利用因式分解求出方程的解的方法，这种方法简便易用，是解一元二次方程最常用的方法．也考查了三角形三边的关系、勾股定理及三角形面积的求法．21．（江苏省扬州市江都区邵樊片2019-2020学年九年级上学期第一次质量检测数学试题）已知关于x 的方程22(21)0x m x m m -+++=. (1)用含m 的代数式表示这个方程的实数根.(2)若Rt ABC ∆的两边a b 、恰好是这个方程的两根，另一边长5c =，求m 的值. 【答案】(1)11x m =+，2x m =；(2)3m =或12m =.【解析】(1)22(21)0x m x m m -+++=()2224[(21)]4b ac m m m -=-+-+ 2244144m m m m =++--1=∴2112m x +±=∴11x m =+，2x m =(2)当5c =为斜边时，22(1)25m m ++=13m =，24m =-(舍去)当边长为1m +斜边时2225(1)m m +=+12m =综上：3m =或12m =【点睛】本题考查的是求根公式与勾股定理，解题的关键是根据求根公式和根据勾股定理列出关于m 的方程，注意把不合题意的解舍去．22．（江苏省镇江市丹徒区江心实验学校2019届九年级3月份调研考试数学试题）如图，点A 、D 、C 、F 在同一条直线上，AD =CF ，AB =DE ，BC =EF . (1)求证：ΔABC ≌△DEF ；(2)若∠A =55°，∠B =88°，求∠F 的度数.【答案】（1）证明见解析；（2）37°【解析】（1）∵AC =AD +DC ，DF =DC +CF ，且AD =CF ∴AC =DF在△ABC 和△DEF 中，AB DEBC EF AC DF =⎧⎪=⎨⎪=⎩∴△ABC≌△DEF（SSS）（2）由（1）可知，∠F=∠ACB，∵∠A=55°，∠B=88°，∴∠ACB=180°－（∠A+∠B）=180°－（55°+88°）=37°，∴∠F=∠ACB=37°.【点睛】本题考查三角形全等的判定方法和全等三角形的性质，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．23．（江苏省如皋市2019届九年级第一次模拟考试数学试题）如图，A、B、C是直线l上的三个点，∠DAB ＝∠DBE＝∠ECB＝a，且BD＝BE．（1）求证：AC＝AD+CE；（2）若a＝120°，点F在直线l的上方，△BEF为等边三角形，补全图形，请判断△ACF的形状，并说明理由．【答案】（1）详见解析；（2）△ACF为等边三角形．【解析】（1）∵∠DAB＝∠DBE＝α，∴∠ADB+∠ABD＝∠CBE+∠ABD＝180°﹣α．∴∠ADB＝∠CBE在△ADB和△CBE中，∵ADB CBEDAB BCEDB BE∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADB≌△CBE（AAS）∴AD＝CB，AB＝CE．∴AC＝AB+BC＝AD+CE （2）补全图形．△ACF为等边三角形．理由如下：∵△BEF为等边三角形，∴BF＝EF，∠BFE＝∠FBE＝∠FEB＝60°．∵∠DBE＝120°，∴∠DBF＝60°．∵∠ABD＝∠CEB（已证），∴∠ABD+∠DBF＝∠CEB+∠FEB，即∠ABF＝∠CEF．∵AB＝CE（已证），∴△AFB≌△CFE（SAS），∴AF＝CF，∠AFB＝∠CFE．∴∠AFC＝∠AFB+∠BFC＝∠CFE+∠BFC＝60°．∴△ACF为等边三角形．【点睛】本题考查了全等三角形的判定和性质，等边三角形的判定和性质，熟练运用全等三角形的判定和性质是本题关键．24．（2019年江苏省无锡市中考数学试题）如图，在△AB C中，AB=AC,点D、E分别在AB、AC上，BD=CE，BE、CD相交于点0；△≌△；求证：（1）DBC ECB.（2）OB OC【答案】（1）见解析；（2）见解析. 【解析】(1)∵AB =AC ， ∴∠ECB =∠DBC ， 在DBC ECB ∆∆与中BD CE DBC ECB BC CB =⎧⎪∠=∠⎨⎪=⎩， ∴DBC ECB △≌△；（2）由（1）DBC ECB △≌△， ∴∠DCB =∠EBC ， ∴OB =O C.【点睛】本题考查了全等三角形的判定与性质，等腰三角形的性质与判定，熟练掌握全等三角形的判定定理与性质定理是解题的关键.25．（江苏省南通市海安市八校联考2019-2020学年九年级上学期第一次阶段性测试数学试题）如图，等腰Rt △AB C 中，BA =BC ，∠ABC =90°，点D 在AC 上，将△ABD 绕点B 沿顺时针方向旋转90°后，得到△CBE ． （1）求∠DCE 的度数；（2）若AB =4，CD =3AD ，求DE 的长．【答案】（1）90°；（2）【解析】（1）∵△ABCD 为等腰直角三角形， ∴∠BAD =∠BCD =45°．由旋转的性质可知∠BAD =∠BCE =45°． ∴∠DCE =∠BCE +∠BCA =45°+45°=90°． （2）∵BA =BC ，∠ABC =90°， ∴AC=．∵CD=3AD，∴AD，DC．由旋转的性质可知：AD=EC．∴DE=21。

2020中考数学复习基础测试卷专练：等边三角形（含答案）一、选择题1.等腰三角形的两边长分别为5cm和7cm，则它的周长为（）A．17cm B．19cm C．21cm D．17cm或19cm2.若等腰三角形的顶角为40°，则它的底角度数为( )A．40°B．50°C．60°D．70°3．如图，△ABC中，∠B=55°，∠C=30°，分别以点A和C为圆心，以大于12AC的长为半径画弧，两弧相交于M，N,作直线MN，交BC于D，连接AD，则∠BAD的度数为（）A.65° B.60° C.55° D.45°4．如图，△ABC中，AB=5，AC=6，BC=4，边AB的垂直平分线交AC于点D，则△BDC的周长是（）A．8 B．9 C．10 D．115．如图，△ABC是等边三角形，BD是中线，延长BC到E，使CE=CD，连接DE．下面给出的四个结论，①BD⊥AC；②BD平分∠ABC；③BD=DE；④∠BDE=120°．其中正确的个数是（）A．1个B．2个C．3个D．4个6．如图，在△PAB中，PA=PB，M，N，K分别是边PA，PB，AB上的点，且AM=BK，BN=AK，若∠MKN=44°，则∠P的度数为( ).A.44°B.66°C.88°D.92°二、填空题7．如图，在△ABC中，AB=AC，D为BC中点，∠BAD=35°，则∠C的度数为______．8.如图，△ABC中，AB=AC，∠A=36°，BD是AC边上的高，则∠DBC的度数是______．1．如图，已知点B、C、D、E在同一直线上，△ABC是等边三角形，且CG=CD，DF=DE，则∠E=______．10.如图，在△ABC中，∠ABC=∠ACB=72°，BD、CE分别是∠ABC和∠ACB的平分线，它们的交点为F，则图中等腰三角形有 ______个．三、解答题11.如图，已知AB=AC=AD，且AD∥BC，求证：∠C=2∠D．12.如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE=DF，∠A=∠D．（1）求证：AB=CD．（2）若AB=CF，∠B=30°，求∠D的度数．13.如图，△ABC的边AB的延长线上有一个点D，过点D作DF⊥AC于F，交BC于E，且BD=BE，求证：△ABC为等腰三角形．14．如图，在△ABC中，BP平分∠ABC，CP平分∠ACB，且PD∥AB，PE∥AC，BC=5，求△PDE的周长．15．如图，△ABC、△ADE是等边三角形，B、C、D在同一直线上．求证：（1）CE=AC+DC；（2）∠ECD=60°．参考答案1. D2.D 3．A4．C 【解析】∵ED是AB的垂直平分线，∴AD=BD，∵△BDC的周长=DB+BC+CD，∴△BDC的周长=AD+BC+CD=AC+BC=6+4=10．5．D 【解析】∵△ABC是等边三角形，BD是AC上的中线，∴∠ADB=∠CDB=90°，BD平分∠ABC，∴BD⊥AC，∵∠ACB=∠CDE+∠DEC=60°，CD=CE，∴∠CDE=∠DEC=30°，∴∠CBD=∠DEC，∴DB=DE．∠BDE=∠CDB+∠CDE=120°.所以这四项都是正确的．6．D【解析】∵PA=PB，∴∠A=∠B，在△AMK和△BKN中，∴△AMK≌△BKN，∴∠AMK=∠BKN，∵∠MKB=∠MKN+∠NKB=∠A+∠AMK，∴∠A=∠MKN=44°，∴∠P=180°-∠A-∠B=92°。

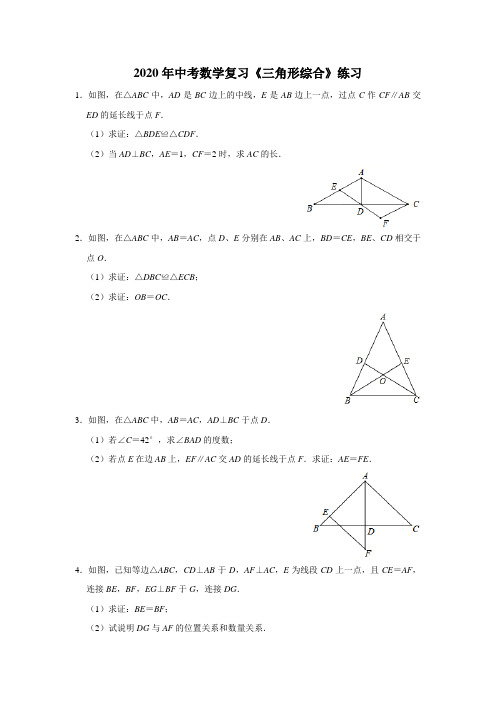
2020年中考数学复习《三角形综合》练习1．如图，在△ABC中，AD是BC边上的中线，E是AB边上一点，过点C作CF∥AB交ED的延长线于点F．（1）求证：△BDE≌△CDF．（2）当AD⊥BC，AE＝1，CF＝2时，求AC的长．2．如图，在△ABC中，AB＝AC，点D、E分别在AB、AC上，BD＝CE，BE、CD相交于点O．（1）求证：△DBC≌△ECB；（2）求证：OB＝OC．3．如图，在△ABC中，AB＝AC，AD⊥BC于点D．（1）若∠C＝42°，求∠BAD的度数；（2）若点E在边AB上，EF∥AC交AD的延长线于点F．求证：AE＝FE．4．如图，已知等边△ABC，CD⊥AB于D，AF⊥AC，E为线段CD上一点，且CE＝AF，连接BE，BF，EG⊥BF于G，连接DG．（1）求证：BE＝BF；（2）试说明DG与AF的位置关系和数量关系．5．例2 如图，在△ABC中，D，E分别是边BC，AB的中点，AD，CE相交于点G，求证：＝＝证明：连结ED．请根据教材提示，结合图①，写出完整的证明过程．结论应用：在▱ABCD中，对角线AC、BD交于点O，E为边BC的中点，AE、BD交于点F．（1）如图②，若▱ABCD为正方形，且AB＝6，则OF的长为．（2）如图③，连结DE交AC于点G，若四边形OFEG的面积为，则▱ABCD的面积为．6．如图，在△ABC中，内角A、B、C所对的边分别为a、b、c．（1）若a＝6，b＝8，c＝12，请直接写出∠A与∠B的和与∠C的大小关系；（2）求证：△ABC的内角和等于180°；（3）若＝，求证：△ABC是直角三角形．7．如图，在△ABC中，AB＝AC，D是BC边上的中点，连结AD，BE平分∠ABC交AC于点E，过点E作EF∥BC交AB于点F．（1）若∠C＝36°，求∠BAD的度数；（2）求证：FB＝FE．8．已知，在Rt△ABC中，∠ACB＝90°，D是BC边上一点，连接AD，分别以CD和AD 为直角边作Rt△CDE和Rt△ADF，使∠DCE＝∠ADF＝90°，点E，F在BC下方，连接EF．（1）如图1，当BC＝AC，CE＝CD，DF＝AD时，求证：①∠CAD＝∠CDF，②BD＝EF；（2）如图2，当BC＝2AC，CE＝2CD，DF＝2AD时，猜想BD和EF之间的数量关系？并说明理由．9．如图，△ABC和△ADE中，AB＝AD＝6，BC＝DE，∠B＝∠D＝30°，边AD与边BC 交于点P（不与点B，C重合），点B，E在AD异侧，I为△APC的内心．（1）求证：∠BAD＝∠CAE；（2）设AP＝x，请用含x的式子表示PD，并求PD的最大值；（3）当AB⊥AC时，∠AIC的取值范围为m°＜∠AIC＜n°，分别直接写出m，n的值．10．在△ABC中，∠BAC＝90°，AB＝AC，AD⊥BC于点D．（1）如图1，点M，N分别在AD，AB上，且∠BMN＝90°，当∠AMN＝30°，AB＝2时，求线段AM的长；（2）如图2，点E，F分别在AB，AC上，且∠EDF＝90°，求证：BE＝AF；（3）如图3，点M在AD的延长线上，点N在AC上，且∠BMN＝90°，求证：AB+AN ＝AM．11．如图，是具有公共边AB的两个直角三角形，其中，AC＝BC，∠ACB＝∠ADB＝90°．（1）如图1，若延长DA到点E，使AE＝BD，连接CD，CE．①求证：CD＝CE，CD⊥CE；②求证：AD+BD＝CD；（2）若△ABC与△ABD位置如图2所示，请直接写出线段AD，BD，CD的数量关系．12．如图，△ABC是等腰直角三角形，∠ACB＝90°，D是射线CB上一点（点D不与点B 重合），以AD为斜边作等腰直角三角形ADE（点E和点C在AB的同侧），连接CE．（1）如图①，当点D与点C重合时，直接写出CE与AB的位置关系；（2）如图②，当点D与点C不重合时，（1）的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；（3）当∠EAC＝15°时，请直接写出的值．13．如图，等边△ABC中，AB＝6，点D在BC上，BD＝4，点E为边AC上一动点（不与点C重合），△CDE关于DE的轴对称图形为△FDE．（1）当点F在AC上时，求证：DF∥AB；（2）设△ACD的面积为S1，△ABF的面积为S2，记S＝S1﹣S2，S是否存在最大值？若存在，求出S的最大值；若不存在，请说明理由；（3）当B，F，E三点共线时．求AE的长．14．如图，△ABC中，AB＝AC，∠BAC＝90°，点D，E分别在AB，BC上，∠EAD＝∠EDA，点F为DE的延长线与AC的延长线的交点．（1）求证：DE＝EF；（2）判断BD和CF的数量关系，并说明理由；（3）若AB＝3，AE＝，求BD的长．15．如图，△ABC中，AB＝AC，DE垂直平分AB，交线段BC于点E（点E与点C不重合），点F为AC上一点，点G为AB上一点（点G与点A不重合），且∠GEF+∠BAC＝180°．（1）如图1，当∠B＝45°时，线段AG和CF的数量关系是．（2）如图2，当∠B＝30°时，猜想线段AG和CF的数量关系，并加以证明．（3）若AB＝6，DG＝1，cos B＝，请直接写出CF的长．16．如图，在△ABC中，AB＝7.5，AC＝9，S△ABC＝．动点P从A点出发，沿AB方向以每秒5个单位长度的速度向B点匀速运动，动点Q从C点同时出发，以相同的速度沿CA方向向A点匀速运动，当点P运动到B点时，P、Q两点同时停止运动，以PQ为边作正△PQM（P、Q、M按逆时针排序），以QC为边在AC上方作正△QCN，设点P运动时间为t秒．（1）求cos A的值；（2）当△PQM与△QCN的面积满足S△PQM＝S△QCN时，求t的值；（3）当t为何值时，△PQM的某个顶点（Q点除外）落在△QCN的边上．17．（1）问题发现如图1，在△OAB和△OCD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝40°，连接AC，BD交于点M．填空：①的值为；②∠AMB的度数为．（2）类比探究如图2，在△OAB和△OCD中，∠AOB＝∠COD＝90°，∠OAB＝∠OCD＝30°，连接AC交BD的延长线于点M．请判断的值及∠AMB的度数，并说明理由；（3）拓展延伸在（2）的条件下，将△OCD绕点O在平面内旋转，AC，BD所在直线交于点M，若OD ＝1，OB＝，请直接写出当点C与点M重合时AC的长．18．（1）操作发现：如图①，小明画了一个等腰三角形ABC，其中AB＝AC，在△ABC的外侧分别以AB，AC为腰作了两个等腰直角三角形ABD，ACE，分别取BD，CE，BC的中点M，N，G，连接GM，GN．小明发现了：线段GM与GN的数量关系是；位置关系是．（2）类比思考：如图②，小明在此基础上进行了深入思考．把等腰三角形ABC换为一般的锐角三角形，其中AB＞AC，其它条件不变，小明发现的上述结论还成立吗？请说明理由．（3）深入研究：如图③，小明在（2）的基础上，又作了进一步的探究．向△ABC的内侧分别作等腰直角三角形ABD，ACE，其它条件不变，试判断△GMN的形状，并给与证明．19．如图1，Rt△ABC中，∠ACB＝90°，点D为边AC上一点，DE⊥AB于点E．点M为BD中点，CM的延长线交AB于点F．（1）求证：CM＝EM；（2）若∠BAC＝50°，求∠EMF的大小；（3）如图2，若△DAE≌△CEM，点N为CM的中点，求证：AN∥EM．20．如图，在Rt△ABC中，AC＝BC，∠ACB＝90°，点D，E分别在AC，BC上，且CD ＝CE．（1）如图1，求证：∠CAE＝∠CBD；（2）如图2，F是BD的中点，求证：AE⊥CF；（3）如图3，F，G分别是BD，AE的中点，若AC＝2，CE＝1，求△CGF的面积．答案与解析一．解答题（共20小题）1．如图，在△ABC中，AD是BC边上的中线，E是AB边上一点，过点C作CF∥AB交ED的延长线于点F．（1）求证：△BDE≌△CDF．（2）当AD⊥BC，AE＝1，CF＝2时，求AC的长．【分析】（1）根据平行线的性质得到∠B＝∠FCD，∠BED＝∠F，由AD是BC边上的中线，得到BD＝CD，于是得到结论；（2）根据全等三角形的性质得到BE＝CF＝2，求得AB＝AE+BE＝1+2＝3，于是得到结论．【解答】（1）证明：∵CF∥AB，∴∠B＝∠FCD，∠BED＝∠F，∵AD是BC边上的中线，∴BD＝CD，∴△BDE≌△CDF（AAS）；（2）解：∵△BDE≌△CDF，∴BE＝CF＝2，∴AB＝AE+BE＝1+2＝3，∵AD⊥BC，BD＝CD，∴AC＝AB＝3．2．如图，在△ABC中，AB＝AC，点D、E分别在AB、AC上，BD＝CE，BE、CD相交于点O．（1）求证：△DBC≌△ECB；（2）求证：OB＝OC．【分析】（1）根据等腰三角形的性质得到∠ECB＝∠DBC根据全等三角形的判定定理即可得到结论；（2）根据全等三角形的性质得到∠DCB＝∠EBC根据等腰三角形的判定定理即可得到OB＝OC【解答】（1）证明：∵AB＝AC，∴∠ECB＝∠DBC，在△DBC与△ECB中，∴△DBC≌△ECB（SAS）；（2）证明：由（1）知△DBC≌△ECB，∴∠DCB＝∠EBC，∴OB＝OC．3．如图，在△ABC中，AB＝AC，AD⊥BC于点D．（1）若∠C＝42°，求∠BAD的度数；（2）若点E在边AB上，EF∥AC交AD的延长线于点F．求证：AE＝FE．【分析】（1）根据等腰三角形的性质得到∠BAD＝∠CAD，根据三角形的内角和即可得到∠BAD＝∠CAD＝90°﹣42°＝48°；（2）根据等腰三角形的性质得到∠BAD＝∠CAD根据平行线的性质得到∠F＝∠CAD，等量代换得到∠BAD＝∠F，于是得到结论．【解答】解：（1）∵AB＝AC，AD⊥BC于点D，∴∠BAD＝∠CAD，∠ADC＝90°，又∠C＝42°，∴∠BAD＝∠CAD＝90°﹣42°＝48°；（2）∵AB＝AC，AD⊥BC于点D，∴∠BAD＝∠CAD，∵EF∥AC，∴∠F＝∠CAD，∴∠BAD＝∠F，∴AE＝FE．4．如图，已知等边△ABC，CD⊥AB于D，AF⊥AC，E为线段CD上一点，且CE＝AF，连接BE，BF，EG⊥BF于G，连接DG．（1）求证：BE＝BF；（2）试说明DG与AF的位置关系和数量关系．【分析】（1）由等边三角形的性质可得AB＝AC＝BC，∠BAC＝∠ACB＝∠ABC＝60°，BD＝AD，∠BCD＝30°，由“SAS”可证△ABF≌△CBE，可得BF＝BE；（2）通过证明△BEF是等边三角形，可得BG＝GF，由三角形中位线定理可得AF＝2GD，AF∥DG．【解答】证明：（1）∵△ABC是等边三角形∴AB＝AC＝BC，∠BAC＝∠ACB＝∠ABC＝60°∵CD⊥AB，AC＝BC∴BD＝AD，∠BCD＝30°，∵AF⊥AC∴∠F AC＝90°∴∠F AB＝∠F AC﹣∠BAC＝30°∴∠F AB＝∠ECB，且AB＝BC，AF＝CE∴△ABF≌△CBE（SAS）∴BF＝BE（2）AF＝2GD，AF∥DG理由如下：连接EF，∵△ABF≌△CBE∴∠ABF＝∠CBE，∵∠ABE+∠EBC＝60°∴∠ABE+∠ABF＝60°，且BE＝BF∴△BEF是等边三角形，且GE⊥BF∴BG＝FG，且BD＝AD∴AF＝2GD，AF∥DG5．教材呈现：如图是华师版九年级上册数学教材第78页的部分内容．例2 如图，在△ABC中，D，E分别是边BC，AB的中点，AD，CE相交于点G，求证：＝＝证明：连结ED．请根据教材提示，结合图①，写出完整的证明过程．结论应用：在▱ABCD中，对角线AC、BD交于点O，E为边BC的中点，AE、BD交于点F．（1）如图②，若▱ABCD为正方形，且AB＝6，则OF的长为．（2）如图③，连结DE交AC于点G，若四边形OFEG的面积为，则▱ABCD的面积为6．【分析】教材呈现：如图①，连结ED．根据三角形中位线定理可得DE∥AC，DE＝AC，那么△DEG∽△ACG，由相似三角形对应边成比例以及比例的性质即可证明＝＝；结论应用：（1）如图②．先证明△BEF∽△DAF，得出BF＝DF，那么BF＝BD，又BO＝BD，可得OF＝OB﹣BF＝BD，由正方形的性质求出BD＝6，即可求出OF ＝；（2）如图③，连接OE．由（1）易证＝2．根据同高的两个三角形面积之比等于底边之比得出△BEF与△OEF的面积比＝＝2，同理，△CEG与△OEG的面积比＝2，那么△CEG的面积+△BEF的面积＝2（△OEG的面积+△OEF的面积）＝2×＝1，所以△BOC的面积＝，进而求出▱ABCD的面积＝4×＝6．【解答】教材呈现：证明：如图①，连结ED．∵在△ABC中，D，E分别是边BC，AB的中点，∴DE∥AC，DE＝AC，∴△DEG∽△ACG，∴＝＝＝2，∴＝＝；结论应用：（1）解：如图②．∵四边形ABCD为正方形，E为边BC的中点，对角线AC、BD交于点O，∴AD∥BC，BE＝BC＝AD，BO＝BD，∴△BEF∽△DAF，∴＝＝，∴BF＝DF，∴BF＝BD，∵BO＝BD，∴OF＝OB﹣BF＝BD﹣BD＝BD，∵正方形ABCD中，AB＝6，∴BD＝6，∴OF＝．故答案为；（2）解：如图③，连接OE．由（1）知，BF＝BD，OF＝BD，∴＝2．∵△BEF与△OEF的高相同，∴△BEF与△OEF的面积比＝＝2，同理，△CEG与△OEG的面积比＝2，∴△CEG的面积+△BEF的面积＝2（△OEG的面积+△OEF的面积）＝2×＝1，∴▱ABCD的面积＝4×＝6．故答案为6．6．如图，在△ABC中，内角A、B、C所对的边分别为a、b、c．（1）若a＝6，b＝8，c＝12，请直接写出∠A与∠B的和与∠C的大小关系；（2）求证：△ABC的内角和等于180°；（3）若＝，求证：△ABC是直角三角形．【分析】（1）根据三角形中大角对大边，即可得到结论；（2）画出图形，写出已知，求证；过点A作直线MN∥BC，根据平行线性质得出∠MAB ＝∠B，∠NAC＝∠C，代入∠MAB+∠BAC+∠NAC＝180°即可求出答案；（3）化简等式即可得到a2+c2＝b2，根据勾股定理的逆定理即可得到结论．【解答】解：（1）∵在△ABC中，a＝6，b＝8，c＝12，∴∠A+∠B＜∠C；（2）如图，过点B作MN∥AC，∵MN∥AC，∴∠MBA＝∠A，∠NBC＝∠C（两直线平行，内错角相等），∵∠MBA+∠ABC+∠NBC＝180°（平角的定义），∴∠A+∠ABC+∠C＝180°（等量代换），即：三角形三个内角的和等于180°；（3）∵＝，∴ac＝（a+b+c）（a﹣b+c）＝[（a2+2ac+c2）﹣b2]，∴2ac＝a2+2ac+c2﹣b2，∴a2+c2＝b2，∴△ABC是直角三角形．7．如图，在△ABC中，AB＝AC，D是BC边上的中点，连结AD，BE平分∠ABC交AC于点E，过点E作EF∥BC交AB于点F．（1）若∠C＝36°，求∠BAD的度数；（2）求证：FB＝FE．【分析】（1）利用等腰三角形的三线合一的性质证明∠ADB＝90°，再利用等腰三角形的性质求出∠ABC即可解决问题．（2）只要证明∠FBE＝∠FEB即可解决问题．【解答】（1）解：∵AB＝AC，∴∠C＝∠ABC，∵∠C＝36°，∴∠ABC＝36°，∵BD＝CD，AB＝AC，∴AD⊥BC，∴∠ADB＝90°，∴∠BAD＝90°﹣36°＝54°．（2）证明：∵BE平分∠ABC，∴∠ABE＝∠CBE＝∠ABC，∵EF∥BC，∴∠FEB＝∠CBE，∴∠FBE＝∠FEB，∴FB＝FE．8．已知，在Rt△ABC中，∠ACB＝90°，D是BC边上一点，连接AD，分别以CD和AD 为直角边作Rt△CDE和Rt△ADF，使∠DCE＝∠ADF＝90°，点E，F在BC下方，连接EF．（1）如图1，当BC＝AC，CE＝CD，DF＝AD时，求证：①∠CAD＝∠CDF，②BD＝EF；（2）如图2，当BC＝2AC，CE＝2CD，DF＝2AD时，猜想BD和EF之间的数量关系？并说明理由．【分析】（1）①根据同角的余角相等证明；②作FH⊥BC交BC的延长线于H，证明△ACD≌△DHF，根据全等三角形的性质得到DH＝AC，结合图形证明即可；（2）作FG⊥BC交BC的延长线于G，证明△ACD∽△DGF，根据相似三角形的性质得到DG＝2AC，证明结论．【解答】（1）证明：①∵∠ACB＝90°，∴∠CAD+∠ADC＝90°，∵∠CDF+∠ADC＝90°，∴∠CAD＝∠CDF；②作FH⊥BC交BC的延长线于H，则四边形FECH为矩形，∴CH＝EF，在△ACD和△DHF中，，∴△ACD≌△DHF（AAS）∴DH＝AC，∵AC＝CB，∴DH＝CB，∴DH﹣CD＝CB﹣CD，即HG＝BD，∴BD＝EF；（2）BD＝EF，理由如下：作FG⊥BC交BC的延长线于G，∵∠CAD＝∠GDF，∠ACD＝∠DGF＝90°，∴△ACD∽△DGF，∴＝＝＝2，即DG＝2AC，GF＝2CD，∵BC＝2AC，CE＝2CD，∴BC＝DG，GF＝CE，∴BD＝CG，∵GF∥CE，GF＝CE，∠G＝90°，∴四边形FECG为矩形，∴CG＝EF，∴BD＝EF．9．如图，△ABC和△ADE中，AB＝AD＝6，BC＝DE，∠B＝∠D＝30°，边AD与边BC 交于点P（不与点B，C重合），点B，E在AD异侧，I为△APC的内心．（1）求证：∠BAD＝∠CAE；（2）设AP＝x，请用含x的式子表示PD，并求PD的最大值；（3）当AB⊥AC时，∠AIC的取值范围为m°＜∠AIC＜n°，分别直接写出m，n的值．【分析】（1）由条件易证△ABC≌△ADE，得∠BAC＝∠DAE，∴∠BAD＝∠CAE．（2）PD＝AD﹣AP＝6﹣x，∵点P在线段BC上且不与B、C重合，∴AP的最小值即AP⊥BC时AP的长度，此时PD可得最大值．（3）I为△APC的内心，即I为△APC角平分线的交点，应用“三角形内角和等于180°“及角平分线定义即可表示出∠AIC，从而得到m，n的值．【解答】解：（1）在△ABC和△ADE中，（如图1）∴△ABC≌△ADE（SAS）∴∠BAC＝∠DAE即∠BAD+∠DAC＝∠DAC+∠CAE∴∠BAD＝∠CAE．（2）∵AD＝6，AP＝x，∴PD＝6﹣x当AD⊥BC时，AP＝AB＝3最小，即PD＝6﹣3＝3为PD的最大值．（3）如图2，设∠BAP＝α，则∠APC＝α+30°，∵AB⊥AC∴∠BAC＝90°，∠PCA＝60°，∠P AC＝90°﹣α，∵I为△APC的内心∴AI、CI分别平分∠P AC，∠PCA，∴∠IAC＝∠P AC，∠ICA＝∠PCA∴∠AIC＝180°﹣（∠IAC+∠ICA）＝180°﹣（∠P AC+∠PCA）＝180°﹣（90°﹣α+60°）＝α+105°∵0＜α＜90°，∴105°＜α+105°＜150°，即105°＜∠AIC＜150°，∴m＝105，n＝150．10．在△ABC中，∠BAC＝90°，AB＝AC，AD⊥BC于点D．（1）如图1，点M，N分别在AD，AB上，且∠BMN＝90°，当∠AMN＝30°，AB＝2时，求线段AM的长；（2）如图2，点E，F分别在AB，AC上，且∠EDF＝90°，求证：BE＝AF；（3）如图3，点M在AD的延长线上，点N在AC上，且∠BMN＝90°，求证：AB+AN ＝AM．【分析】（1）根据等腰三角形的性质、直角三角形的性质得到AD＝BD＝DC＝，求出∠MBD＝30°，根据勾股定理计算即可；（2）证明△BDE≌△ADF，根据全等三角形的性质证明；（3）过点M作ME∥BC交AB的延长线于E，证明△BME≌△AMN，根据全等三角形的性质得到BE＝AN，根据等腰直角三角形的性质、勾股定理证明结论．【解答】（1）解：∵∠BAC＝90°，AB＝AC，AD⊥BC，∴AD＝BD＝DC，∠ABC＝∠ACB＝45°，∠BAD＝∠CAD＝45°，∵AB＝2，∴AD＝BD＝DC＝，∵∠AMN＝30°，∴∠BMD＝180°﹣90°﹣30°＝60°，∴∠MBD＝30°，∴BM＝2DM，由勾股定理得，BM2﹣DM2＝BD2，即（2DM）2﹣DM2＝（）2，解得，DM＝，∴AM＝AD﹣DM＝﹣；（2）证明：∵AD⊥BC，∠EDF＝90°，∴∠BDE＝∠ADF，在△BDE和△ADF中，，∴△BDE≌△ADF（ASA）∴BE＝AF；（3）证明：过点M作ME∥BC交AB的延长线于E，∴∠AME＝90°，则AE＝AM，∠E＝45°，∴ME＝MA，∵∠AME＝90°，∠BMN＝90°，∴∠BME＝∠AMN，在△BME和△NMA中，，∴△BME≌△NMA（ASA），∴BE＝AN，∴AB+AN＝AB+BE＝AE＝AM．11．如图，是具有公共边AB的两个直角三角形，其中，AC＝BC，∠ACB＝∠ADB＝90°．（1）如图1，若延长DA到点E，使AE＝BD，连接CD，CE．①求证：CD＝CE，CD⊥CE；②求证：AD+BD＝CD；（2）若△ABC与△ABD位置如图2所示，请直接写出线段AD，BD，CD的数量关系．【分析】（1）①根据四边形的内角和得到∠DAC+∠DBC＝180°，推出∠DBC＝∠EAC，根据全等三角形的性质得到CD＝CE，∠BCD＝∠ACE，求得∠DCE＝90°，根据垂直的定义得到结论；②由已知条件得到△CDE是等腰直角三角形，求得DE＝CD，根据线段的和差即可得到结论；（2）如图2，在AD上截取AE＝BD，连接CE，根据等腰直角三角形的性质得到∠BAC ＝∠ABC＝45°，求得∠CBD＝∠CAE，根据全等三角形的性质得到CD＝CE，∠BCD ＝∠ACE，求得∠DCE＝90°，根据线段的和差即可得到结论．【解答】（1）证明：①在四边形ADBC中，∠DAC+∠DBC+∠ADB+∠ACB＝360°，∵∠ADB+∠ACB＝180°，∴∠DAC+∠DBC＝180°，∵∠EAC+∠DAC＝180°，∴∠DBC＝∠EAC，∵BD＝AE，BC＝AC，∴△BCD≌△ACE（SAS），∴CD＝CE，∠BCD＝∠ACE，∵∠BCD+∠DCA＝90°，∴∠ACE+∠DCA＝90°，∴∠DCE＝90°，∴CD⊥CE；②∵CD＝CE，CD⊥CE，∴△CDE是等腰直角三角形，∴DE＝CD，∵DE＝AD+AE，AE＝BD，∴DE＝AD+BD，∴AD+BD＝CD；（2）解：AD﹣BD＝CD；理由：如图2，在AD上截取AE＝BD，连接CE，∵AC＝BC，∠ACB＝90°，∴∠BAC＝∠ABC＝45°，∵∠ADB＝90°，∴∠CBD＝90°﹣∠BAD﹣∠ABC＝90°﹣∠BAD﹣45°＝45°﹣∠BAD，∵∠CAE＝∠BAC﹣∠BAD＝45°﹣∠BAD，∴∠CBD＝∠CAE，∵BD＝AE，BC＝AC，∴△CBD≌△CAE（SAS），∴CD＝CE，∠BCD＝∠ACE，∵∠ACE+∠BCE＝∠ACB＝90°，∴∠BCD+∠BCE＝90°，即∠DCE＝90°，∴DE＝＝＝CD，∵DE＝AD﹣AE＝AD﹣BD，∴AD﹣BD＝CD．12．如图，△ABC是等腰直角三角形，∠ACB＝90°，D是射线CB上一点（点D不与点B 重合），以AD为斜边作等腰直角三角形ADE（点E和点C在AB的同侧），连接CE．（1）如图①，当点D与点C重合时，直接写出CE与AB的位置关系；（2）如图②，当点D与点C不重合时，（1）的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；（3）当∠EAC＝15°时，请直接写出的值．【分析】（1）根据等腰直角三角形的性质、平行线的判定定理解答；（2）在AF上截取AF＝CD，连接EF，证明△EAF≌△EDC，根据全等三角形的性质得到EF＝EC，∠AEF＝∠DEC，根据平行线的判定定理证明；（3）分图②、图③两种情况，根据全等三角形的性质、等腰直角三角形的性质计算，得到答案．【解答】解：（1）当点D与点C重合时，CE∥AB，理由如下：∵△ABC是等腰直角三角形，∴∠CAB＝45°，∵△ADE是等腰直角三角形，∴∠ADE＝45°，∴∠CAB＝∠ADE，∴CE∥AB；（2）当点D与点C不重合时，（1）的结论仍然成立，理由如下：在AC上截取AF＝CD，连接EF，∵∠AED＝∠ACB＝90°，∴∠EAF＝∠EDC，在△EAF和△EDC中，，∴△EAF≌△EDC（SAS），∴EF＝EC，∠AEF＝∠DEC，∵∠AED＝90°，∴∠FEC＝90°，∴∠ECA＝45°，∴∠ECA＝∠CAB，∴CE∥AB；（3）如图②，∠EAC＝15°，∴∠CAD＝30°，∴AD＝2CD，AC＝CD，∴FC＝（﹣1）CD，∵△CEF为等腰直角三角形，∴EC＝FC＝CD，∵△ABC是等腰直角三角形，∴AB＝AC＝CD，∴＝＝，如图③，∠EAC＝15°，由（2）得，∠EDC＝∠EAC＝15°，∴∠ADC＝30°，∴CD＝AC，AB＝AC，延长AC至G，使AG＝CD，∴CG＝AG﹣AC＝DC﹣AC＝AC﹣AC，在△EAG和△EDC中，，∴△EAG≌△EDC（SAS），∴EG＝EC，∠AEG＝∠DEC，∴∠CEG＝90°，∴△CEG为等腰直角三角形，∴EC＝CG＝AC，∴＝，综上所述，当∠EAC＝15°时，的值为或．13．如图，等边△ABC中，AB＝6，点D在BC上，BD＝4，点E为边AC上一动点（不与点C重合），△CDE关于DE的轴对称图形为△FDE．（1）当点F在AC上时，求证：DF∥AB；（2）设△ACD的面积为S1，△ABF的面积为S2，记S＝S1﹣S2，S是否存在最大值？若存在，求出S的最大值；若不存在，请说明理由；（3）当B，F，E三点共线时．求AE的长．【分析】（1）由折叠的性质和等边三角形的性质可得∠DFC＝∠A，可证DF∥AB；（2）过点D作DM⊥AB交AB于点M，由题意可得点F在以D为圆心，DF为半径的圆上，由△ACD的面积为S1的值是定值，则当点F在DM上时，S△ABF最小时，S最大；（3）过点D作DG⊥EF于点G，过点E作EH⊥CD于点H，由勾股定理可求BG的长，通过证明△BGD∽△BHE，可求EC的长，即可求AE的长．【解答】解：（1）∵△ABC是等边三角形∴∠A＝∠B＝∠C＝60°由折叠可知：DF＝DC，且点F在AC上∴∠DFC＝∠C＝60°∴∠DFC＝∠A（2）存在，过点D作DM⊥AB交AB于点M，∵AB＝BC＝6，BD＝4，∴CD＝2∴DF＝2，∴点F在以D为圆心，DF为半径的圆上，∴当点F在DM上时，S△ABF最小，∵BD＝4，DM⊥AB，∠ABC＝60°∴MD＝2∴S△ABF的最小值＝×6×（2﹣2）＝6﹣6∴S最大值＝×2×3﹣（6﹣6）＝﹣3+6（3）如图，过点D作DG⊥EF于点G，过点E作EH⊥CD于点H，∵△CDE关于DE的轴对称图形为△FDE∴DF＝DC＝2，∠EFD＝∠C＝60°∵GD⊥EF，∠EFD＝60°∴FG＝1，DG＝FG＝∵BD2＝BG2+DG2，∴16＝3+（BF+1）2，∴BF＝﹣1∵EH⊥BC，∠C＝60°∴CH＝，EH＝HC＝EC∵∠GBD＝∠EBH，∠BGD＝∠BHE＝90°∴△BGD∽△BHE∴∴∴EC＝﹣1∴AE＝AC﹣EC＝7﹣14．如图，△ABC中，AB＝AC，∠BAC＝90°，点D，E分别在AB，BC上，∠EAD＝∠EDA，点F为DE的延长线与AC的延长线的交点．（1）求证：DE＝EF；（2）判断BD和CF的数量关系，并说明理由；（3）若AB＝3，AE＝，求BD的长．【分析】（1）只要证明EA＝ED，EA＝EF即可解决问题；（2）结论：BD＝CF．如图2中，在BE上取一点M，使得ME＝CE，连接DM．想办法证明DM＝CF，DM＝BD即可；（3）如图3中，过点E作EN⊥AD交AD于点N．设BD＝x，则DN＝，DE＝AE ＝，由∠B＝45°，EN⊥BN．推出EN＝BN＝x+＝，在Rt△DEN中，根据DN2+NE2＝DE2，构建方程即可解决问题；【解答】（1）证明：如图1中，∵∠BAC＝90°，∴∠EAD+∠CAE＝90°，∠EDA+∠F＝90°，∵∠EAD＝∠EDA，∴∠EAC＝∠F，∴EA＝ED，EA＝EF，∴DE＝EF．（2）解：结论：BD＝CF．理由：如图2中，在BE上取一点M，使得ME＝CE，连接DM．∵DE＝EF．∠DEM＝∠CEF，EM＝EC．∴△DEM≌△FEC，∴DM＝CF，∠MDE＝∠F，∴DM∥CF，∴∠BDM＝∠BAC＝90°，∵AB＝AC，∴∠DBM＝45°，∴BD＝DM，∴BD＝CF．（3）如图3中，过点E作EN⊥AD交AD于点N．∵EA＝ED，EN⊥AD，∴AN＝ND，设BD＝x，则DN＝，DE＝AE＝，∵∠B＝45°，EN⊥BN．∴EN＝BN＝x+＝，在Rt△DEN中，∵DN2+NE2＝DE2，∴（）2+（）2＝（）2解得x＝1或﹣1（舍弃）∴BD＝1．15．如图，△ABC中，AB＝AC，DE垂直平分AB，交线段BC于点E（点E与点C不重合），点F为AC上一点，点G为AB上一点（点G与点A不重合），且∠GEF+∠BAC＝180°．（1）如图1，当∠B＝45°时，线段AG和CF的数量关系是AG＝CF．（2）如图2，当∠B＝30°时，猜想线段AG和CF的数量关系，并加以证明．（3）若AB＝6，DG＝1，cos B＝，请直接写出CF的长．【分析】（1）如图1，连接AE，根据线段垂直平分线的性质得到AE＝BE，根据等腰直角三角形的性质得到∠BAE＝∠B＝45°，BE＝EC＝AE，∠BAE＝∠EAC＝∠C＝45°，根据全等三角形的性质即可得到结论；（2）如图2，连接AE，根据等腰三角形的性质和三角形的内角和得到∠BAC＝120°，根据线段垂直平分线的性质得到AE＝BE，求得∠BAE＝∠B＝30°，根据相似三角形的性质得到，解直角三角形即可得到AG＝CF；（3）①当G在DA上时，如图3，连接AE，根据线段垂直平分线的性质得到AD＝BD ＝3，AE＝BE，由三角函数的定义得到BE＝＝＝4，根据相似三角形的性质得到＝，过A作AH⊥BC于点H由三角函数的定义即可得到结论．②当点G在BD 上，如图4，方法同（1）．【解答】解：（1）相等，理由：如图1，连接AE，∵DE垂直平分AB，∴AE＝BE，∴∠BAE＝∠B＝45°，∴AE⊥BC，∵AB＝AC，∴BE＝EC＝AE，∠BAE＝∠EAC＝∠C＝45°，∵∠GEF+∠BAC＝180°，∴∠AGE+∠AFE＝360°﹣180°＝180°，∵∠AFE+∠CFE＝180°，∴∠AGE＝∠CFE，∵∠GAE＝∠C＝45°，∴△AEG≌△CEF（AAS），∴AG＝CF；故答案为：AG＝CF；（2）AG＝CF，理由：如图2，连接AE，∵AB＝AC，∴∠B＝∠C＝30°，∴∠BAC＝120°，∵DE垂直平分AB，∴AE＝BE，∴∠BAE＝∠B＝30°，∴∠CAE＝90°，∠BAE＝∠C，∵∠GEF+∠BAC＝180°，∴∠AGE+∠AFE＝180°，∵∠CFE+∠AFE＝180°，∴∠AGE＝∠CFE，∴△AGE∽△CFE，∴，在Rt△ACE中，∵∠C＝30°，∴＝sin C＝，∴＝，∴AG＝CF；（3）①当G在DA上时，如图3，连接AE，∵DE垂直平分AB，∴AD＝BD＝3，AE＝BE，∵cos B＝，∴BE＝＝＝4，∴AE＝BE＝4，∴∠BAE＝∠B，∵AB＝AC，∴∠B＝∠C，∴∠C＝∠BAE，∵∠GEF+∠BAC＝180°，∴∠AGE+∠AFE＝360°﹣180°＝180°，∵∠AFE+∠CFE＝180°，∴∠CFE＝∠AGE，∴△CFE∽△AGE，∴＝，过A作AH⊥BC于点H，∵cos B＝，cos45°＝，∵＞，∴∠B＜45°，∴E在H的左侧，∵cos B＝，∴BH＝AB＝×6＝，∵AB＝AC，∴BC＝2BH＝9，∵BE＝4，∴CE＝9﹣4＝5，∵AG＝AD﹣DG＝3﹣1＝2，∴＝，∴CF＝2.5；②当点G在BD上，如图4，同（1）可得，△CFE∽△AGE，∴＝，∵AG＝AD+DG＝3+1＝4，∴＝，∴CF＝5，综上所述，CF的长为2.5或5．16．如图，在△ABC中，AB＝7.5，AC＝9，S△ABC＝．动点P从A点出发，沿AB方向以每秒5个单位长度的速度向B点匀速运动，动点Q从C点同时出发，以相同的速度沿CA方向向A点匀速运动，当点P运动到B点时，P、Q两点同时停止运动，以PQ为边作正△PQM（P、Q、M按逆时针排序），以QC为边在AC上方作正△QCN，设点P运动时间为t秒．（1）求cos A的值；（2）当△PQM与△QCN的面积满足S△PQM＝S△QCN时，求t的值；（3）当t为何值时，△PQM的某个顶点（Q点除外）落在△QCN的边上．【分析】（1）如图1中，作BE⊥AC于E．利用三角形的面积公式求出BE，利用勾股定理求出AE即可解决问题；（2）如图2中，作PH⊥AC于H．利用S△PQM＝S△QCN构建方程即可解决问题；（3）分两种情形：①如图3中，当点M落在QN上时，作PH⊥AC于H．②如图4中，当点M在CQ上时，作PH⊥AC于H．分别构建方程求解即可；【解答】解：（1）如图1中，作BE⊥AC于E．∵S△ABC＝•AC•BE＝，∴BE＝，在Rt△ABE中，AE＝＝6，∴coaA＝＝＝．（2）如图2中，作PH⊥AC于H．∵P A＝5t，PH＝3t，AH＝4t，HQ＝AC﹣AH﹣CQ＝9﹣9t，∴PQ2＝PH2+HQ2＝9t2+（9﹣9t）2，∵S△PQM＝S△QCN，∴•PQ2＝וCQ2，∴9t2+（9﹣9t）2＝×（5t）2，整理得：5t2﹣18t+9＝0，解得t＝3（舍弃）或．∴当t＝时，满足S△PQM＝S△QCN．（3）①如图3中，当点M落在QN上时，作PH⊥AC于H．易知：PM∥AC，∴∠MPQ＝∠PQH＝60°，∴PH＝HQ，∴3t＝（9﹣9t），∴t＝．②如图4中，当点M在CQ上时，作PH⊥AC于H．同法可得PH＝QH，∴3t＝（9t﹣9），∴t＝，综上所述，当t＝s或s时，△PQM的某个顶点（Q点除外）落在△QCN 的边上．17．（1）问题发现如图1，在△OAB和△OCD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝40°，连接AC，BD交于点M．填空：①的值为1；②∠AMB的度数为40°．（2）类比探究如图2，在△OAB和△OCD中，∠AOB＝∠COD＝90°，∠OAB＝∠OCD＝30°，连接AC交BD的延长线于点M．请判断的值及∠AMB的度数，并说明理由；（3）拓展延伸在（2）的条件下，将△OCD绕点O在平面内旋转，AC，BD所在直线交于点M，若OD ＝1，OB＝，请直接写出当点C与点M重合时AC的长．【分析】（1）①证明△COA≌△DOB（SAS），得AC＝BD，比值为1；②由△COA≌△DOB，得∠CAO＝∠DBO，根据三角形的内角和定理得：∠AMB＝180°﹣（∠DBO+∠OAB+∠ABD）＝40°；（2）根据两边的比相等且夹角相等可得△AOC∽△BOD，则＝，由全等三角形的性质得∠AMB的度数；（3）正确画图形，当点C与点M重合时，有两种情况：如图3和4，同理可得：△AOC ∽△BOD，则∠AMB＝90°，，可得AC的长．【解答】解：（1）问题发现①如图1，∵∠AOB＝∠COD＝40°，∴∠COA＝∠DOB，∵OC＝OD，OA＝OB，∴△COA≌△DOB（SAS），∴AC＝BD，∴＝1，②∵△COA≌△DOB，∴∠CAO＝∠DBO，∵∠AOB＝40°，∴∠OAB+∠ABO＝140°，在△AMB中，∠AMB＝180°﹣（∠CAO+∠OAB+∠ABD）＝180°﹣（∠DBO+∠OAB+∠ABD）＝180°﹣140°＝40°，故答案为：①1；②40°；（2）类比探究如图2，＝，∠AMB＝90°，理由是：Rt△COD中，∠DCO＝30°，∠DOC＝90°，∴，同理得：，∴，∵∠AOB＝∠COD＝90°，∴∠AOC＝∠BOD，∴△AOC∽△BOD，∴＝，∠CAO＝∠DBO，在△AMB中，∠AMB＝180°﹣（∠MAB+∠ABM）＝180°﹣（∠OAB+∠ABM+∠DBO）＝90°；（3）拓展延伸①点C与点M重合时，如图3，同理得：△AOC∽△BOD，∴∠AMB＝90°，，设BD＝x，则AC＝x，Rt△COD中，∠OCD＝30°，OD＝1，∴CD＝2，BC＝x﹣2，Rt△AOB中，∠OAB＝30°，OB＝，∴AB＝2OB＝2，在Rt△AMB中，由勾股定理得：AC2+BC2＝AB2，，x2﹣x﹣6＝0，（x﹣3）（x+2）＝0，x1＝3，x2＝﹣2，∴AC＝3；②点C与点M重合时，如图4，同理得：∠AMB＝90°，，设BD＝x，则AC＝x，在Rt△AMB中，由勾股定理得：AC2+BC2＝AB2，+（x+2）2＝x2+x﹣6＝0，（x+3）（x﹣2）＝0，x1＝﹣3，x2＝2，∴AC＝2；综上所述，AC的长为3或2．18．（1）操作发现：如图①，小明画了一个等腰三角形ABC，其中AB＝AC，在△ABC的外侧分别以AB，AC为腰作了两个等腰直角三角形ABD，ACE，分别取BD，CE，BC的中点M，N，G，连接GM，GN．小明发现了：线段GM与GN的数量关系是MG＝NG；位置关系是MG⊥NG．（2）类比思考：如图②，小明在此基础上进行了深入思考．把等腰三角形ABC换为一般的锐角三角形，其中AB＞AC，其它条件不变，小明发现的上述结论还成立吗？请说明理由．（3）深入研究：如图③，小明在（2）的基础上，又作了进一步的探究．向△ABC的内侧分别作等腰直角三角形ABD，ACE，其它条件不变，试判断△GMN的形状，并给与证明．【分析】（1）利用SAS判断出△ACD≌△AEB，得出CD＝BE，∠ADC＝∠ABE，进而判断出∠BDC+∠DBH＝90°，即：∠BHD＝90°，最后用三角形中位线定理即可得出结论；（2）同（1）的方法即可得出结论；（3）同（1）的方法得出MG＝NG，最后利用三角形中位线定理和等量代换即可得出结论．【解答】解：（1）连接BE，CD相交于H，∵△ABD和△ACE都是等腰直角三角形，∴AB＝AD，AC＝AE，∠BAD＝∠CAE＝90°∴∠CAD＝∠BAE，∴△ACD≌△AEB（SAS），∴CD＝BE，∠ADC＝∠ABE，∴∠BDC+∠DBH＝∠BDC+∠ABD+∠ABE＝∠BDC+∠ABD+∠ADC＝∠ADB+∠ABD＝90°，∴∠BHD＝90°，∴CD⊥BE，∵点M，G分别是BD，BC的中点，∴MG CD，同理：NG BE，∴MG＝NG，MG⊥NG，故答案为：MG＝NG，MG⊥NG；（2）连接CD，BE相交于点H，同（1）的方法得，MG＝NG，MG⊥NG；（3）连接EB，DC，延长线相交于H，同（1）的方法得，MG＝NG，同（1）的方法得，△ABE≌△ADC，∴∠AEB＝∠ACD，∴∠CEH+∠ECH＝∠AEH﹣∠AEC+180°﹣∠ACD﹣∠ACE＝∠ACD﹣45°+180°﹣∠ACD﹣45°＝90°，∴∠DHE＝90°，同（1）的方法得，MG⊥NG，∴△MGN是等腰直角三角形．19．如图1，Rt△ABC中，∠ACB＝90°，点D为边AC上一点，DE⊥AB于点E．点M为BD中点，CM的延长线交AB于点F．（1）求证：CM＝EM；（2）若∠BAC＝50°，求∠EMF的大小；（3）如图2，若△DAE≌△CEM，点N为CM的中点，求证：AN∥EM．【分析】（1）利用直角三角形斜边中线的性质定理即可证明；（2）利用四边形内角和定理求出∠CME即可解决问题；（3）首先证明△ADE是等腰直角三角形，△DEM是等边三角形，设FM＝a，则AE＝CM＝EM＝a，EF＝2a，推出＝，＝，由此即可解决问题；【解答】（1）证明：如图1中，∵DE⊥AB，∴∠DEB＝∠DCB＝90°，∵DM＝MB，∴CM＝DB，EM＝DB，∴CM＝EM．（2）解：∵∠AED＝90°，∠A＝50°，∴∠ADE＝40°，∠CDE＝140°，∵CM＝DM＝ME，∴∠MCD＝∠MDC，∠MDE＝∠MED，∴∠CME＝360°﹣2×140°＝80°，∴∠EMF＝180°﹣∠CME＝100°．（3）证明：如图2中，设FM＝a．∵△DAE≌△CEM，CM＝EM，∴AE＝ED＝EM＝CM＝DM，∠AED＝∠CME＝90°∴△ADE是等腰直角三角形，△DEM是等边三角形，∴∠DEM＝60°，∠MEF＝30°，∴AE＝CM＝EM＝a，EF＝2a，∵CN＝NM，∴MN＝a，∴＝，＝，∴＝，∴EM∥AN．（也可以连接AM利用等腰三角形的三线合一的性质证明）20．如图，在Rt△ABC中，AC＝BC，∠ACB＝90°，点D，E分别在AC，BC上，且CD ＝CE．（1）如图1，求证：∠CAE＝∠CBD；（2）如图2，F是BD的中点，求证：AE⊥CF；（3）如图3，F，G分别是BD，AE的中点，若AC＝2，CE＝1，求△CGF的面积．【分析】（1）直接判断出△ACE≌△BCD即可得出结论；（2）先判断出∠BCF＝∠CBF，进而得出∠BCF＝∠CAE，即可得出结论；（3）先求出BD＝3，进而求出CF＝，同理：EG＝，再利用等面积法求出ME，进而求出GM，最后用面积公式即可得出结论．【解答】解：（1）在△ACE和△BCD中，，∴△ACE≌△BCD，∴∠CAE＝∠CBD；（2）如图2，记AE与CF的交点为M，在Rt△BCD中，点F是BD的中点，∴CF＝BF，∴∠BCF＝∠CBF，由（1）知，∠CAE＝∠CBD，∴∠BCF＝∠CAE，∴∠CAE+∠ACF＝∠BCF+∠ACF＝∠ACB＝90°，∴∠AMC＝90°，∴AE⊥CF；（3）如图3，记AE与CF的交点为M，∵AC＝2，∴BC＝AC＝2，∵CE＝1，∴CD＝CE＝1，在Rt△BCD中，根据勾股定理得，BD＝＝3，∵点F是BD中点，∴CF＝DF＝BD＝，同理：EG＝AE＝，连接EF，过点F作FH⊥BC，∵∠ACB＝90°，点F是BD的中点，∴FH＝CD＝，∴S△CEF＝CE•FH＝×1×＝，由（2）知，AE⊥CF，∴S△CEF＝CF•ME＝×ME＝ME，∴ME＝，∴ME＝，∴GM＝EG﹣ME＝﹣＝，∴S△CFG＝CF•GM＝××＝．。

2020届中考数学复习专题：三角形1．定义：如果一个三角形一边上的中线与这条边上的高线之比为，那么称这个三角形为“神奇三角形”．（1）已知：Rt△ABC中，∠ACB＝90°．①当AC＝BC时，求证：△ABC是“神奇三角形”；②当AC≠BC时，且△ABC是“神奇三角形”，求tan A的值；（2）如图，在△ABC中，AB＝AC，CD是AB边上的中线，若∠DCB＝45°，求证：△ABC 是“神奇三角形”．2．如图，在等边三角形ABC中，BC＝8，过BC边上一点P，作∠DPE＝60°，分别与边AB，AC相交于点D与点E．（1）在图中找出与∠EPC始终相等的角，并说明理由；（2）若△PDE为正三角形时，求BD+CE的值；（3）当DE∥BC时，请用BP表示BD，并求出BD的最大值．3．在等腰直角△ABC中，AB＝AC，∠BAC＝90°，以CA为边在∠ACB的另一侧作∠ACM＝∠ACB，点D为射线BC上任意一点，在射线CM上截取CE＝BD，连接AD、DE、AE．（1）如图1，当点D落在线段BC的延长线上时，直接写出∠ADE的度数；（2）如图2，当点D落在线段BC（不含边界）上时，AC与DE交于点F，请问（1）中的结论是否仍成立？如果成立，请给出证明；如果不成立，请说明理由；（3）如图2，作AH⊥BC，垂足为H，作AG⊥EC，垂足为G，连接HG，判断△GHC的形状，并说明理由．4．（1）发现如图1，△ABC和△ADE均为等边三角形，点D在BC边上，连接CE．填空：①∠DCE的度数是；②线段CA、CE、CD之间的数量关系是．（2）探究如图2，△ABC和△ADE均为等腰直角三角形，∠BAC＝∠DAE＝90°，点D在BC边上，连接CE．请判断∠DCE的度数及线段CA、CE、CD之间的数量关系，并说明理由．（3）应用如图3，在Rt△ABC中，∠A＝90°，AC＝4，AB＝6．若点D满足DB＝DC，且∠BDC＝90°，请直接写出DA的长．5．如图1，在平面直角坐标系中，已知点A （a ，0），B （b ，0），C （2，7），连接AC ，交y 轴于D ，且a ＝，（）2＝5．（1）求点D 的坐标．（2）如图2，y 轴上是否存在一点P ，使得△ACP 的面积与△ABC 的面积相等？若存在，求点P 的坐标，若不存在，说明理由．（3）如图3，若Q （m ，n ）是x 轴上方一点，且△QBC 的面积为20，试说明：7m +3n 是否为定值，若为定值，请求出其值，若不是，请说明理由．6．如图，以直角三角形AOC 的直角顶点O 为原点，以OC 、OA 所在直线为x 轴和y 轴建立平面直角坐标系，点A （0，a ），C （b ，0）满足．D 为线段AC 的中点．在平面直角坐标系中，以任意两点P （x 1，y 1）、Q （x 2，y 2）为端点的线段中点坐标为，．（1）则A点的坐标为；点C的坐标为．D点的坐标为．（2）已知坐标轴上有两动点P、Q同时出发，P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动，Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动，点Q到达A点整个运动随之结束．设运动时间为t（t＞0）秒．问：是否存在这样的t，使S△ODP ＝S△ODQ，若存在，请求出t的值；若不存在，请说明理由．（3）点F是线段AC上一点，满足∠FOC＝∠FCO，点G是第二象限中一点，连OG，使得∠AOG＝∠AOF．点E是线段OA上一动点，连CE交OF于点H，当点E在线段OA上运动的过程中，的值是否会发生变化？若不变，请求出它的值；若变化，请说明理由．7．已知：如图，在平面直角坐标系中，点A（a，0）、B（0，b）、且|a+2|+（b+2a）2＝0，点P为x轴上一动点，连接BP；（1）求点A、B的坐标；（2）如图，在第一象限内作BC⊥AB且BC＝AB，连接CP，当CP⊥BC时，作CD⊥BP于点D，求线段CD的长度；（3）在第一象限内作BQ⊥BP且BQ＝BP，连接PQ，设P（p，0），直接写出S△PCQ＝（用含p的式子表示）．8．在△ABC和△DBE中，CA＝CB，EB＝ED，点D在AC上．（1）如图1，若∠ABC＝∠DBE＝60°，求证：∠ECB＝∠A；（2）如图2，设BC与DE交于点F．当∠ABC＝∠DBE＝45°时，求证：CE∥AB；（3）在（2）的条件下，若tan∠DEC＝时，求的值．9．如图，在△ABC中，BC＝7cm，AC＝24cm，AB＝25cm，P点在BC上，从B点到C点运动（不包括C点），点P运动的速度为2cm/s；Q点在AC上从C点运动到A点（不包括A点），速度为5cm/s．若点P、Q分别从B、C同时运动，请解答下面的问题，并写出探索主要过程：（1）经过多少时间后，P、Q两点的距离为5cm？的面积为15cm2？（2）经过多少时间后，S△PCQ（3）用含t的代数式表示△PCQ的面积，并用配方法说明t为何值时△PCQ的面积最大，最大面积是多少？10．我们规定，三角形任意两边的“广益值”等于第三边上的中线和这边一半的平方差．如图1，在△ABC中，AO是BC边上的中线，AB与AC的“广益值”就等于AO2﹣BO2的值，可记为AB∇AC＝OA2﹣BO2．（1）在△ABC中，若∠ACB＝90°，AB∇AC＝81，求AC的值．（2）如图2，在△ABC中，AB＝AC＝12，∠BAC＝120°，求AB∇AC，BA∇BC的值．＝24，AC＝8，AB∇AC＝﹣64，求（3）如图3，在△ABC中，AO是BC边上的中线，S△ABCBC和AB的长．11．已知：等边△ABC中．（1）如图1，点M是BC的中点，点N在AB边上，满足∠AMN＝60°，求的值；（2）如图2，点M在AB边上（M为非中点，不与A、B重合），点N在CB的延长线上且∠MNB＝∠MCB，求证：AM＝BN．（3）如图3，点P为AC边的中点，点E在AB的延长线上，点F在BC的延长线上，满足∠AEP＝∠PFC，求的值．12．如图，等边△ABC的边长为15cm，现有两点M，N分别从点A，点B同时出发，沿三角形的边顺时针运动，已知点M的速度为1cm/s，点N的速度为2cm/s．当点N第一次到达B点时，M，N同时停止运动（1）点M、N运动几秒后，M，N两点重合？（2）点M、N运动几秒后，△AMN为等边三角形？（3）当点M，N在BC边上运动时，能否得到以MN为底边的等腰三角形AMN？如存在，请求出此时M，N运动的时间．13．通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比例相互唯一确定，因此，边长与角的大小之间可以相互转化．类似地，可以在等腰三角形中建立边角之间的关系．我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图①，在△ABC中，AB＝AC，顶角A的正对记作sadA，这时sadA＝＝．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．根据上述角的正对定义，解下列问题：（1）sad60°＝．（2）对于0°＜A＜180°，∠A的正对值sadA的取值范围是．（3）如图②，已知∠C＝90°，sin A＝，其中∠A为锐角，试求sadA的值．14．如图，在Rt△ABC中，∠ACB＝90°，BC＝4，sin∠ABC＝，点D为射线BC上一点，联结AD，过点B作BE⊥AD分别交射线AD、AC于点E、F，联结DF，过点A作AG∥BD，交直线BE于点G．（1）当点D在BC的延长线上时，如果CD＝2，求tan∠FBC；（2）当点D在BC的延长线上时，设AG＝x，S＝y，求y关于x的函数关系式（不需△DAF要写函数的定义域）；（3）如果AG＝8，求DE的长．15．如图，点O为平面直角坐标系的原点，三角形ABC中，∠BAC＝90°，AB＝m．顶点A，C的坐标分别为（1，0），（n，0），且|m﹣3|+（n﹣5）2＝0．（1）求三角形ABC的面积；（2）动点P从点C出发沿射线CA方向以每秒1个单位长度的速度运动，设点P的运动时间为t秒，连接PB，请用含t的式子表示三角形ABP的面积；（3）在（2）的条件下，当三角形ABP的面积为时，直线BP与y轴相交于点D，求点D的坐标．16．已知△ABC和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°．（1）若D为AB上一动点时（如图1），①求证：△ACD≌△BCE．②试求线段AD，BD，DE间满足的数量关系．（2）当点D在△ABC内部时（如图2），延长AD交BE于点F．①求证：AF⊥BE．②连结BD，当△BDE为等边三角形时，直接写出△DCE与△ABC的边长之比．17．如图，直角坐标系中，点A，B分别在x，y轴上，点B的坐标为（0，2），∠BAO＝30°．以AB为边在第一象限作等边△ABC，MN垂直平分OA，MA⊥AB．（1）求AB的长．（2）求证：MB＝OC．（3）如图2，连接MC交AB于点P．点P是否为MC的中点？请说明理由．18．在△ABC中，AB＝BC，∠A＝40°，BD⊥AC垂足为D．（1）填空：∠ABC＝°；（2）E是线段BD上的动点，连结EC，将线段EC绕点E按顺时针方向旋转80°，点C 的对应点是点F，连接CF，得到△CEF．①如图1，若点F在直线BD上，AB＝a，AC＝b，求EB+EC的值．②连结AF，直线AF与直线BC是否平行，为什么？19．如图，在平面直角坐标系中，点A（0，a），B（b，0），且a，b满足2a2+2ab+b2﹣8a+16＝0，点P为AB上一个动点（不与A，B）重合），连接OP．（1）直接写出a＝，b＝；（2）如图1，过点P作OP的垂线交过点A平行于x轴的直线于点C，若点，求点C的坐标；（3）如图2，以OP为斜边在OP右侧作等腰Rt△OPD，PD＝OD．连接BD，当点P从B向A运动过程中，△BOD的面积是否发生变化，请判断并说明理由．20．（1）如图①，小明同学作出△ABC两条角平分线AD，BE得到交点I，就指出若连接CI，则CI平分∠ACB，你觉得有道理吗？为什么？（2）如图②，Rt△ABC中，AC＝5，AC＝12，AB＝13，△ABC的角平分线CD上有一点I，设点I到边AB的距离为d．（d为正实数）小季、小何同学经过探究，有以下发现：小季发现：d的最大值为．小何发现：当d＝2时，连接AI，则AI平分∠BAC．请分别判断小季、小何的发现是否正确？并说明理由．参考答案1．解：（1）①证明：如图，作AC边上的中线BM，设CM＝AM＝a，则BC＝AC＝2a，∵∠ACB＝90°，∴BM＝＝＝a，∴，∴△ABC是“神奇三角形”；②当AC边上的中线与AC边上的高的比为时，设BM＝a，BC＝2a，∵∠ACB＝90°，∴CM＝＝a，∴AC＝2a，∴AC＝BC，不合题意，舍去；同理，当BC边上的中线与BC边上的高的比为时，也不符合题意，舍去；当AB边上的中线与AB边上的高的比为时，当BC＞AC时，如图，作AB边上的中线CM，作AB边上的高线CD，设CM＝a，CD＝2a，则DM＝a，∵∠ACB＝90°，∴CM＝AB＝AM，∴AD＝（﹣1）a，∴tan A＝＝，当BC＜AC时，如图，作AB边上的中线CM，作AB边上的高线CD，同理可得，tan A＝．综合可得tan A的值为或．（2）证明：如图，作CH⊥AB于点H，AE⊥BC于点E，AE交CD于K，连接BK，∵AB＝AC，∴E是BC的中点，∵CD是AB边上的中线，∴点K是△ABC的重心，∴KC＝2DK，∵AE是BC的垂直平分线，∴KC＝KB，∴∠KBC＝∠KCB＝45°，∴∠CKB＝90°，即BK⊥CD，∴＝tan∠CDH＝＝2，∴，∴△ABC是“神奇三角形”．2．解：（1）∠BDP＝∠EPC，理由如下：∵△ABC为等边三角形，∴∠B＝60°，∵∠DPE＝60°，∴∠DPE＝∠B，∵∠DPC是△BDP的外角，∴∠DPE+∠EPC＝∠B+∠BDP，∴∠EPC＝∠BDP；（2）∵△PDE为正三角形，∴PD＝PE，在△BDP和△CPE中，，∴△BDP≌△CPE（AAS），∴BD＝CP，BP＝CE，∴BD+CE＝CP+BP＝BC＝8；（3）∵DE∥BC，△ABC为等边三角形，∴△ADE为等边三角形，∴AD＝AE，∴BD＝CE，∵∠B＝∠C，∠EPC＝∠BDP，∴△BDP∽△CPE，∴＝，即＝，整理得，BD＝，﹣BP2+8BP＝﹣（BP﹣4）2+16，∴BD的最大值为4．3．（1）解：∠ADE＝45°．∵AB＝AC，∠BAC＝90°，∴∠ABC＝∠ACB＝45°，∵∠ACM＝∠ACB，∴∠ACM＝∠ABC，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS），∴AD＝AE，∠CAE＝∠BAD，∴∠DAE＝∠BAC＝90°，∴∠ADE＝45°；（2）（1）中的结论成立证明：∵∠BAC＝90°，AB＝AC，∴∠B＝∠ACB＝45°．∵∠ACM＝∠ACB，∴∠B＝∠ACM＝45°．在△ABD和△ACE中，，∴△ABD≌△ACE（SAS）．∴AD＝AE，∠BAD＝∠CAE．∴∠CAE+∠DAC＝∠BAD+∠DAC＝∠BAC＝90°．即∠DAE＝90°．∵AD＝AE，∴∠ADE＝∠AED＝45°．（3）△CGH为等腰直角三角形．理由如下：∵∠BCA＝∠ACE＝45°，∴∠GCH＝90°，又∵AH⊥BC，AG⊥CE，∴AG＝AH，∵∠ACG＝∠AGC＝45°，∴AG＝CG，∵AB＝AC，AH⊥BC，∴∠HCA＝∠HAC＝45°，∴AH＝HC，∴CH＝CG，∴△CGH为等腰直角三角形．4．（1）发现解：①∵在△ABC中，AB＝AC，∠BAC＝60°，∴∠BAC＝∠DAE＝60°，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，即∠BAD＝∠CAE，在△BAD和△CAE中，，∴△BAD≌△CAE（SAS），∴∠ACE＝∠B＝60°，∴∠DCE＝∠ACE+∠ACB＝60°+60°＝120°；故答案为：120°，②∵△BAD≌△CAE，∴BD＝CE，∴BC＝BD+CD＝EC+CD，∴CA＝BC＝CE+CD；故答案为：CA＝CE+CD．（2）探究∠DCE＝90°；CA＝CD+CE．理由：∵△ABC和△ADE均为等腰直角三角形，∠BAC＝∠DAE＝90°，∴AB＝AC，AD＝AE，∠BAC﹣∠DAC＝∠DAE﹣∠DAC，即∠BAD＝∠CAE．∴△BAD≌△CAE（SAS）．∴BD＝CE，∠B＝∠ACE＝45°．∴∠DCE＝∠ACB+∠ACE＝90°．在等腰直角三角形ABC中，CB＝CA，∵CB＝CD+DB＝CD+CE，∴CA＝CD+CE．（3）应用DA＝5或．作DE⊥AB于E，连接AD，∵在Rt△ABC中，AB＝6，AC＝4，∠BAC＝90°，∴BC＝＝＝2，∵∠BDC＝90°，DB＝DC，∴DB＝DC＝，∠BCD＝∠CBD＝45°，∵∠BDC＝∠BAC＝90°，∴点B，C，A，D四点共圆，∴∠DAE＝45°，∴△ADE是等腰直角三角形，∴AE＝DE，∴BE＝6﹣DE，∵BE2+DE2＝BD2，∴DE2+（6﹣DE）2＝26，∴DE＝1，DE＝5，∴AD＝或AD＝5．5．解：（1）∵a＝，（）2＝5，∴a＝﹣5，b＝5，∵A（a，0），B（b，0），∴A（﹣5，0），B（5，0），∴OA＝OB＝5．如图1，连接OC，设OD＝x，∵C（2，7），∴S△AOC＝×5×7＝17.5，∵S△AOC ＝S△AOD+S△COD，∴5x•＝17.5，∴x＝5，∴点D的坐标为（0，5）；（2）如图2，∵A（﹣5，0），B（5，0），C（2，7），∴S△ABC＝×（5+5）×7＝35，∵点P在y轴上，∴设点P的坐标为（0，y），∵S△ACP ＝S△ADP+S△CDP，D（0，5），∴5×|5﹣y|×+2×|5﹣y|×＝35，解得：y＝﹣5或15，∴点P的坐标为（0，﹣5）或（0，15）；（3）7m+3n是定值．∵点Q在x轴的上方，∴分两种情况考虑，如图3，当点Q在直线BC的左侧时，过点Q作QH⊥x轴，垂足为H，连接CH，∵S△QBC ＝S△QHC+S△HBC﹣S△QHB，且S△QBC＝20，∴，∴7m+3n＝﹣5．如图4，当点Q在直线BC的右侧时，过点Q作QH⊥x轴，垂足为H，连接CH，∵S△QBC ＝S△QHC+S△HBC﹣S△QHB，且S△QBC＝20，∴＝20，∴7m+3n＝75，综上所述，7m+3n的值为﹣5或75．6．解：（1）∵．∴a﹣2b＝0，b﹣2＝0，解得a＝4，b＝2，∴A（0，4），C（2，0）；∴x＝＝1，y＝＝2，∴D（1，2）．故答案为（0，4），（2，0），（1，2）．（2）如图1中，由条件可知：P点从C点运动到O点时间为2秒，Q点从O点运动到A点时间为2秒，∴0＜t≤2时，点Q在线段AO上，即CP＝t，OP＝2﹣t，OQ＝2t，AQ＝4﹣2t，∴S△DOP ＝OP•y D＝（2﹣t）×2＝2﹣t，S△DOQ＝OQ•x D＝×2t×1＝t，∵S△ODP ＝S△ODQ，∴2﹣t＝t，∴t＝1；（3）的值不变，其值为2．理由如下：如图2中，∵∠2+∠3＝90°，又∵∠1＝∠2，∠3＝∠FCO，∴∠GOC+∠ACO＝180°，∴OG∥AC，∴∠1＝∠CAO，∴∠OEC＝∠CAO+∠4＝∠1+∠4，如图，过H点作AC的平行线，交x轴于P，则∠4＝∠PHC，PH∥OG，∴∠PHO＝∠GOF＝∠1+∠2，∴∠OHC＝∠OHP+∠PHC＝∠GOF+∠4＝∠1+∠2+∠4，∴＝，＝，＝2．7．解：（1）∵|a+2|+（b+2a）2＝0，∴a+2＝0，b+2a＝0，解得a＝﹣2，b＝4，∴A（﹣2，0），B（0，4）；（2）如图1所示，过C作CE⊥OB于E，与PB交于F，∵BC⊥AB，∴∠ABO+∠EBC＝90°，在Rt△BCE中，∠EBC+∠BCE＝90°，∴∠ABO＝∠BCE，在△AOB和△BEC中，，∴△AOB≌△BEC（AAS），∴BE＝AO＝2，又∵OB＝4，∴E为OB的中点，∵EC∥OP，∴EF为△BOP的中位线，则F为BP的中点，在Rt△BCP中，CF为斜边上的中线，∴CF＝PB＝BF，∴∠BCE＝∠CBD＝∠ABO，在△AOB和△CDB中，∴△AOB≌△CDB（AAS），∴CD＝AO＝2；（3）如图2所示，过B作BG⊥CQ于点G，延长QC与x轴交于H，∵∠ABP+∠PBC＝90°，∠PBC+CBQ＝90°，∴∠ABP＝∠CBQ，在△ABP与△CBQ中，，∴△ABP≌△CBQ（SAS），∴∠BPO＝∠BQG，CQ＝AP＝2+p，在△BOP和△BGQ中，，∴△BOP≌△BGQ（AAS），∴∠OBP＝∠GBQ，BG＝BO＝4，又∵∠GBQ+∠PBG＝90°，∴∠OBP+∠PBG＝90°，即∠OBG＝90°，在四边形OBGH中，∠OBG＝∠BOG＝∠BGH＝90°，∴∠OHG＝90°，∴PH是△PCQ中CQ边上的高，PH＝OH﹣OP＝4﹣p，＝•（2+p）（4﹣p）＝﹣+p+4．∴S△PCQ故答案为：．8．（1）证明：∵CA＝CB，EB＝ED，∠ABC＝∠DBE＝60°，∴△ABC和△DBE都是等边三角形，∴AB＝BC，DB＝BE，∠A＝60°．∵∠ABC＝∠DBE＝60°，∴∠ABD＝∠CBE，∴△ABD≌△CBE（SAS）．∴∠A＝∠ECB；（2）证明：∵∠ABC＝∠DBE＝45°，CA＝CB，EB＝ED，∴△ABC和△DBE都是等腰直角三角形，∴∠CAB＝45°，∴，∴，∵∠ABC＝∠DBE，∴∠ABD＝∠CBE，∴△ABD∽△CBE，∴∠BAD＝∠BCE＝45°，∵∠ABC＝45°，∴∠ABC＝∠BCE，∴CE∥AB；（3）解：过点D作DM⊥CE于点M，过点D作DN∥AB交CB于点N，∵∠ACB＝90°，∠BCE＝45°，∴∠DCM＝45°，∴∠MDC＝∠DCM＝45°，∴DM＝MC，设DM＝MC＝a，∴a，∵DN∥AB，∴△DCN为等腰直角三角形，∴DN＝DC＝2a，∵tan∠DEC＝，∴ME＝2DM，∴CE＝a，∴，∵CE∥DN，∴△CEF∽△DNF，∴．9．解：（1）连接PQ ，设经过ts 后，P 、Q 两点的距离为5cm ，ts 后，PC ＝7﹣2tcm ，CQ ＝5tcm ，根据勾股定理可知PC 2+CQ 2＝PQ 2， 代入数据（7﹣2t ）2+（5t ）2＝（5）2；解得t ＝1或t ＝﹣（不合题意舍去）；（2）设经过ts 后，S △PCQ 的面积为15cm 2ts 后，PC ＝7﹣2tcm ，CQ ＝5tcm ，S △PCQ ＝×PC ×CQ ＝×（7﹣2t ）×5t ＝15解得t 1＝2，t 2＝1.5，经过2或1.5s 后，S △PCQ 的面积为15cm 2．（3）设经过ts 后，△PCQ 的面积最大，ts 后，PC ＝7﹣2tcm ，CQ ＝5tcm ，S △PCQ ＝×PC ×CQ ＝×（7﹣2t ）×5t ＝×（﹣2t 2+7t ）．＝﹣5．∴当t ＝s 时，△PCQ 的面积最大，最大值为cm 2．10．解：（1）如图1，AO 是BC 边上的中线，∵∠ACB＝90°，∴AO2﹣OC2＝AC2，∵AB∇AC＝81，∴AO2﹣OC2＝81，∴AC2＝81，∴AC＝9；（2）①如图2，取BC的中点O，连接AO，∵AB＝AC，∴AO⊥BC，∵∠BAC＝120°，∴∠ABC＝30°，在Rt△AOB中，∴＝＝6，∴AB∇AC＝AO2﹣BO2＝36﹣108＝﹣72；②如图3，取AC的中点D，连接BD，∴AC＝6，过点B作BE⊥AC交CA的延长线于点E，∴∠BAE＝180°﹣∠BAC＝60°，∴∠ABE＝30°，∵AB＝12，∴AE＝6，∴BE＝＝＝6．∴DE＝AD+AE＝12，∴＝＝6，∴BA∇BC＝BD2﹣CD2＝＝216；（3）作BD⊥CD，如图4，＝24，AC＝8，∵S△ABC∴＝6，∵AB∇AC＝﹣64，AO是BC边上的中线，∴AO2﹣OC2＝﹣64，∴OC2﹣AO2＝64，又∵AC2＝82＝64，∴OC2﹣AO2＝AC2，∴∠AOC＝90°，∴OA＝2×＝3，∴＝＝．∴，在Rt△BCD中，＝＝16，∴AD＝CD﹣AC＝16﹣8，∴＝＝10．11．解：（1）∵△ABC为等边三角形，∴∠B＝∠BAC＝60°，AB＝AC，∵点M是BC的中点，∴∠MAN＝30°，∠AMB＝90°，∵∠AMN＝60°，∴∠BMN＝30°，∴BM＝2BN，AB＝2BM，设BN＝x，则BM＝2x，AB＝4x，∴AN＝3x，∴；（2）证明：如图2，过点M作MG∥NC交AC于点G，∴∠A＝∠AMG＝∠AGM＝60°，∴△AMG为等边三角形，∴AM＝AG，∴BM＝CG，∵∠AGM＝∠ABC＝60°，∴∠MGC＝∠NBM＝120°，∵MG∥BC，∴∠GMC＝∠MCB，∵∠MNB＝∠MCB，∴∠GMC＝∠MNB，∴△MGC≌△NBM（AAS），∴MG＝BN，∵△AMG为等边三角形，∴AM＝MG，∴AM＝BN；（3）如图3，过点P作PM∥BC交AB于点M，∴△AMP为等边三角形，∴AP＝MP，∠AMP＝60°，∵P为AC的中点，∴AP＝PC，∴MP＝PC，∵∠ACB＝60°，∴∠EMP＝∠PCF＝120°，∵∠AEP＝∠PFC，∴△PCF≌△PME（AAS），∴CF＝ME，∴BF﹣BE＝BC+CF﹣ME+MB，又∵P为AC的中点，MP∥BC，∴MB＝，∴BF﹣BE＝BC+BC＝，∴．12．解：（1）设运动t秒，M、N两点重合，根据题意得：2t﹣t＝15，∴t＝15，答：点M，N运动15秒后，M、N两点重合；（2）如图1，设点M、N运动x秒后，△AMN为等边三角形，∴AN＝AM，由运动知，AN＝15﹣2x，AM＝x，∴15﹣2x＝x，解得：x＝5，∴点M、N运动5秒后，△AMN是等边三角形；（3）假设存在，如图2，设M、N运动y秒后，得到以MN为底边的等腰三角形AMN，∴AM＝AN，∴∠AMN＝∠ANM，∵△ABC是等边三角形，∴AB＝AC，∠C＝∠B＝60°，∴△ACN≌△ABM（AAS），∴CN＝BM，∴CM＝BN，由运动知，CM＝y﹣15，BN＝15×3﹣2y，∴y﹣15＝15×3﹣2y，∴y＝20，故点M，N在BC边上运动时，能得到以MN为底边的等腰三角形AMN，此时M，N运动的时间为20秒．13．解：（1）根据正对定义，当顶角为60°时，等腰三角形底角为60°，则三角形为等边三角形，则sad60°＝＝1．故答案为：1．（2）当∠A接近0°时，sadA接近0，当∠A接近180°时，等腰三角形的底接近于腰的二倍，故sadA接近2．于是sadA的取值范围是0＜sadA＜2．故答案为：0＜sadA＜2．（3）在AB上取点D，使AD＝AC，过点D作DE⊥AC于E，连接CD，如图．∵在Rt△ADE中，＝sin A＝，设AD＝AC＝5x，则DE＝3x，AE＝4x．∴CE＝x．∴在Rt△CDE中，CD＝＝x．∴sad A＝＝＝．14．解：（1）∵∠ACB＝90°，BC＝4，sin∠ABC＝，∴设AC＝3x，AB＝5x，∴（3x）2+16＝（5x）2，∴x＝1，即AC＝3，∵BE⊥AD，∴∠AEF＝90°，∵∠AFE＝∠CFB，∴∠DAC＝∠FBC，∴tan∠FBC＝tan∠DAC＝＝；（2）∵AG∥BD，∴∠AGF＝∠CBF，∴tan∠AGF＝tan∠CBF，∴，，∴，∴．∴＝．∵∠EAF＝∠CBF，∴，∴，∴S＝＝；△DAF（3）①当点D在BC的延长线上时，如图1，∵AG＝8，BC＝4，AG∥BD，∴，∴AF＝2CF，∵AC＝3，∴AF＝2，CF＝1，∴，∴，设AE＝x，GE＝4x，∴x2+16x2＝82，解得x＝，即AE＝．同理tan∠DAC＝tan∠CBF，∴，∴DC＝，∴AD＝＝＝．∴＝．②当点D在BC的边上时，如图2，∵AG∥BD，AG＝8，BC＝4，∴．∴AF＝6，∵∠EAF＝∠CBF＝∠ABC，∴cos∠EAF＝cos∠ABC，∴，∴，同理，∴，∴．∴DE＝AE﹣AD＝．综合以上可得DE的长为或．15．解：（1）∵|m﹣3|+（n﹣5）2＝0．∴|m﹣3|＝0，（n﹣5）2＝0．∴m＝3，n＝5，∴B（1，3），C（5，0），∴AB＝3，AC＝4，∴三角形ABC的面积＝；（2）①如图1，当点P在线段AC上时，PC＝t，AP＝4﹣t，三角形ABP的面积为＝＝6﹣．②如图2，当点P在线段AC的延长线上时，PC＝t，AP＝t﹣4，三角形ABP的面积为3＝．（3）①当点P在线段AC上时，6﹣．解得t＝﹣1（舍去）．②如图3，当点P在线段AC的延长线上时，．解得t＝9．∴OP＝4，PA＝5，∵∠BAC＝90°＝∠DOA，∴OD∥AB，∴．解得OD＝．∵点D在y轴上且在原点O的上方，∴点D的坐标为（0，）．16．（1）①证明：如图1，∵△ABC和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°．∴AC＝BC，CD＝CE，∠A＝∠ABC＝45°，∠ACB﹣∠DCB＝∠ECD﹣∠DCB，∴∠ACD＝∠BCE，∴△ACD≌△BCE（SAS）．②解：∵△ACD≌△BCE．∴AD＝BE，∠CBE＝∠A＝45°，∴∠DBE＝90°，∴BD2+BE2＝DE2，即BD2+AD2＝DE2，（2）①证明：如图2，∵△ABC和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°．∴由（1）易知△ACD≌△BCE．∴∠DAC＝∠CBE，∴∠ABF+∠BAF＝∠ABC+∠CBE+∠BAF＝∠ABC+∠BAF+∠DAC＝∠ABC+∠BAC＝90°．∴∠AFB＝90°，即AF⊥BE．②如图3，∵△BDE为等边三角形，DF⊥BE，∴∠DEF＝60°，设EF＝BF＝a，则DE＝2a，∴a，∵BD＝BE，DC＝CE，∴BC是DE的垂直平分线，∴NE＝a，BN＝a，∴BC＝．∴．即△DCE与△ABC的边长之比为．17．（1）解：∵B（0，2），∴OB＝2，在Rt△AOB中，∠BAO＝30°，∴AB＝2OB＝4；（2）证明：，∵AM⊥AB，∴∠BAM＝90°，∴∠MAN＝90°﹣∠BAO＝60°，∵MN垂直平分OA，∴∠ANM＝90°，∴∠AMN＝30°，∴MA＝2AN＝OA，∵△ABC是等边三角形，∴AC＝AB，∠BAC＝60°，∴∠OAC＝90°＝∠MAB，∴△MAB≌△OAC（SAS），∴MB＝OC；（3）解：P是MC的中点．理由如下：如图2，过点C作CH⊥AB于H，∴∠AHC＝90°＝∠HAM，∵△ABC是等边三角形，∴BC＝AB，∠BCH＝∠ACH＝30°＝∠BAO，∴△BCH≌△BAO（AAS），∴OA＝CH，由（2）知，AM＝OA，∴AM＝CH，∵∠CPH＝∠MPA，∴△CHP≌△MAP（AAS），∴CP＝MP，即点P为MC的中点．18．解：（1）∵AB＝BC，∴∠A＝∠BCA＝40°，∴∠ABC＝180°﹣∠A﹣∠BCA＝180°﹣40°﹣40°＝100°故答案为：100．（2）①在△ABC中，AB＝BC，BD⊥AC，∴AD＝DC，∠ABF＝50°，∵EC＝EF，∠CEF＝80°，点F在BD上，∴∠DFC＝50°，又∠ADB＝∠CDF＝90°，∴△ABD≌△CFD（AAS），∴BD＝DF，∴BE+EC＝BE+EF＝2BD＝2＝2＝2．②连结AE并延长交BC于M．若点F在直线BD上，BF是AC的垂直平分线，∵∠AFD＝∠DFC＝50°，又∠ABF＝50°，∴AF∥BC，若点F在直线BD的左侧，如图2，∵EC＝EF＝AE，∴∠MEF＝2∠EAF，∵∠MEC＝2∠EAD，∴2∠DAF＝∠CEF，∴∠DAF＝40°，∠BCA＝40°．∴AF∥BC．若点F在直线BD的右侧，如图3．∵EC＝EF＝AE，∴∠MEF＝2∠EAF，∵∠MEC＝2∠EAD，∴2∠DAF＝∠CEF，∴∠DAF＝40°，∠BCA＝40°．∴AF∥BC．19．解：（1）∵2a2+2ab+b2﹣8a+16＝0，∴（a+b）2+（a﹣4）2＝0，∴a+b＝0，a﹣4＝0，即a＝4，b＝﹣4，故答案为：4，﹣4；（2）过点P作PM⊥AP交y轴于点M，过P作PN⊥y轴于点N，∵∠OPC＝∠MPA＝∠OAC＝90°，∴∠OPM＝∠APC，∠POM＝∠C，∵∠PAM＝45°，∴PA＝PM，∴△ACP≌△MOP（AAS），∴AC＝MO，又∵，∴，∴AC＝MO＝1，∴C（1，4）；（3）△BOD的面积不发生变化，理由，∵点A（0，4），B（﹣4，0），∴直线AB的解析式为y＝x+4，①当点P的横坐标大于等于﹣2而小于0时，设D（m，n）如图2，过点D作DF⊥x轴于F，过点P作PE⊥DF，交FD的延长线于E，∴∠PED＝∠DFO＝90°，OF＝m，DF＝n，∴∠DPE+∠PDE＝90°，∵∠ODP＝90°，∴∠PDE+∠ODF＝90°，∴∠DPE＝∠ODE，∵DP＝OD，∴△PDE≌△DOF（AAS），∴DE＝OF＝m，PE＝DF＝n，∴EF＝DE+DF＝m+n，PE﹣OF＝n﹣m，∴P（m﹣n，m+n），而点P在线段AB上，∴m+n＝m﹣n+4，∴n＝2，∴点D的纵坐标为2，②当点P的横坐标小于﹣2而大于﹣4时，如图3，同①的方法得出点D的纵坐标为2，即：点P从点B向点A运动的过程中，点D的纵坐标始终为2，∴S＝OB•|y D|＝×4×2＝4，△BOD即：点P从点B向点A运动的过程中，△BOD的面积始终不变，是4．20．解：如图1，过I点分别作IM，IN，IK垂直于AB，BC，AC于点M，N，K，连接IC，∵AI平分∠BAC，IM⊥AB，IK⊥AC，∴IM＝IK，同理IM＝IN，∴IK＝IN，又∵IK⊥AC，IN⊥BC，∴CI平分∠BCA；（2）如图2，过C点作CE⊥AB于点E，则d的最大值为CE长，∵AC＝5，BC＝12，∴＝，又∵＝30，∴CE＝，∴d的最大值为．∴小季正确；假设此时AI平分∠BAC，如图3，连接BI，过I点作IG，IH，IF分别垂直于AC，BC，AB 于点G，H，F，∵AI平分∠BAC，CD平分∠ACB，∴BI平分∠CBA，∵IG⊥AC，IH⊥BC，ID⊥AB，∴IG＝IH＝IF＝d，∵S△ACB ＝S△AIC+S△BIC+S△ABI，∴，∴＝，∴d＝2，∴假设成立，当d＝2时，连接AI，则AI平分∠BAC，∴小何正确．。

2020年中考数学复习专题练：《三角形综合》1．如图：在四边形ABCD中，AB∥CD，∠BCD＝90°，且AB＝2，DC＝BC＝4．（1）求sin∠ADC的值．（2）E是四边形内一点，F是四边形外一点，且∠EDC＝∠FBC，DE＝BF，试判断△ECF 的形状．（等腰直角三角形）（3）在（2）的条件下，当BE：CE＝1：2，∠BEC＝135°时，求sin∠BFE的值．2．如图1，在△ABC中，∠B＝60°，点M从点B出发沿射线BC方向，在射线BC上运动．在点M运动的过程中，连结AM，并以AM为边在射线BC上方，作等边△AMN，连结CN．（1）当∠BAM＝°时，AB＝2BM；（2）请添加一个条件：，使得△ABC为等边三角形；①如图1，当△ABC为等边三角形时，求证：CN+CM＝AC；②如图2，当点M运动到线段BC之外（即点M在线段BC的延长线上时），其它条件不变（△ABC仍为等边三角形），请写出此时线段CN、CM、AC满足的数量关系，并证明．3．综合与实践：操作发现：如图，已知△ABC和△ADE均为等腰三角形，AB＝AC，AD＝AE，将这两个三角形放置在一起，使点B，D，E在同一直线上，连接CE．（1）如图1，若∠ABC＝∠ACB＝∠ADE＝∠AED＝55°，求证：△BAD≌△CAE；（2）在（1）的条件下，求∠BEC的度数；拓广探索：（3）如图2，若∠CAB＝∠EAD＝120°，BD＝4，CF为△BCE中BE边上的高，请直接写出EF的长度．4．如图，在△ABC中，AB＝AC＝5，BC＝6，点D是边AB上的动点（点D不与点AB重合），点G在边AB的延长线上，∠CDE＝∠A，∠GBE＝∠ABC，DE与边BC交于点F．（1）求cos A的值；（2）当∠A＝2∠ACD时，求AD的长；（3）点D在边AB上运动的过程中，AD：BE的值是否会发生变化？如果不变化，请求AD：BE的值；如果变化，请说明理由．5．如图1，OA＝2，OB＝4，以点A为顶点，AB为腰在第三象限作等腰直角△ABC．（Ⅰ）求C点的坐标；（Ⅱ）如图2，OA＝2，P为y轴负半轴上的一个动点，若以P为直角顶点，PA为腰等腰直角△APD，过D作DE⊥x轴于E点，求OP﹣DE的值；（Ⅲ）如图3，点F坐标为（﹣4，﹣4），点G（0，m）在y轴负半轴，点H（n，0）x 轴的正半轴，且FH⊥FG，求m+n的值．6．如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，动点P从点A出发沿线段AB以每秒3个单位长的速度运动至点B，过点P作PQ⊥AB射线AC于点Q．设点P的运动时间为t秒（t＞0）．（1）线段CQ的长为（用含t的代数式表示）（2）当△APQ与△ABC的周长的比为1：4时，求t的值．（3）设△APQ与△ABC重叠部分图形的面积为S，求S与t之间的函数关系式．（4）当直线PQ把△ABC分成的两部分图形中有一个是轴对称图形时，直接写出t的值．7．如图，在平面内给定△ABC，AB＝AC，点O到△ABC的三个顶点的距离均等于c（c为常数），到点O的距离等于c的所有点组成图形G，过点A作AB的垂线交BC于点E，交图形G于点D，延长DA，在DA的延长线上存在一点F，使得∠ABF＝∠ABC．（1）依题意补全图形；（2）判断直线BF与图形G交点的个数并证明；（3）若AD＝4，cos∠ABF＝，求DE的长．8．如图，△ABC是等边三角形，AB＝8，AH⊥BC，垂足为H点，点D是射线AH上的动点，连接CD，以CD为边在CD的下方作等边△CDE，连接BE．（1）当点D在线段AH上时，设AD＝x，△CDE的面积为y，求y关于x的函数解析式，并求出自变量x的取值范围；（2）当△CDE的面积等于△ABC的面积的时，判断线段CE与△ABC的边是否存在特殊的位置关系？若存在，说出是什么关系并证明；若不存在，请说明理由．9．如图，已知A、B是线段MN上的两点，MN＝4，MA＝1，MB＞1．以A为圆心以AM为半径作圆弧，以B为圆心以BN为半径作圆弧，两圆弧相交于点C构成△ABC，设AB＝x．（1）求x的取值范围；（2）若△ABC为直角三角形，求x的值；（3）当∠CAB是锐角时，求△ABC的最大面积？10．如图，在Rt△ABC中，∠C＝90°，AC＝4cm，BC＝3cm，D是边AC上一点，且CD＝1cm．动点P从点D出发，以1cm/s的速度沿D→A向终点A匀速运动；同时动点Q从点B出发，以1m/s的速度沿B→C向终点C匀速运动，连结PQ，设点P的运动时间为ts，△CPQ的面积为Scm2（1）当PQ＝3时，求t的值；（2）求S与t之间的函数关系式，并写出自变量t的取值范围；（3）连结DQ，当直线DQ将△CPQ分成面积比为1：2两部分时，直接写出t的值，并写出此时S的值．11．如图，△ABC是边长为2的等边三角形，点D与点B分别位于直线AC的两侧，且AD＝AC，联结BD、CD，BD交直线AC于点E．（1）当∠CAD＝90°时，求线段AE的长．（2）过点A作AH⊥CD，垂足为点H，直线AH交BD于点F，①当∠CAD＜120°时，设AE＝x，y＝（其中S△BCE 表示△BCE的面积，S△AEF表示△AEF的面积），求y关于x的函数关系式，并写出x的取值范围；②当＝7时，请直接写出线段AE的长．12．如图，平面直角坐标系中有点A（﹣1，0）和y轴上一动点B（0，a），其中a＞0，以B点为直角顶点在第二象限内作等腰直角△ABC，设点C的坐标为（c，d）（1）当a＝2时，则C点的坐标为（，）；（2）动点B在运动的过程中，试判断c+d的值是否发生变化？若不变，请求出其值；若发生变化，请说明理由；（3）当a＝2时，在第一象限内是否存在一点P，使△PAB与△ABC全等？若存在，直接写出P点坐标；若不存在，请说明理由13．平面直角坐标系中，若点A（a，b），且+＝0，点B（m，m），其中m＞1，R点在x轴正半轴上，RA⊥RB（1）求a、b的值；（2）连接AB交y轴于E，连接ER，若∠ARO＝15°，求的值；（3）点D（﹣1，0）、C（0，1），射线DC分别交线段AR、AB于点S、T，若SC＝n，CT ＝k，试用含n的式子表示k．14．在平面直角坐标系中，A（﹣3，﹣2），B（2，4）．（1）如图1，求△AOB的面积；（2）如图2，求AB与两坐标轴的交点C，D坐标；（3）在坐标轴上求作点P，使△ABP的面积为6，求P点坐标，利用图3解答．15．如图，在平面直角坐标系中，点O为坐标原点，点A的坐标为（0，4），点B在x的负半轴上，△AOB的面积为8，作△AOB关于y轴的对称图形，点B的对应点为C．（1）求线段OC的长；（2）点D从A点出发，沿线段AO向终点O运动，同时点E从点C出发，沿x轴的正方向运动，且CE＝AD，连接DE交AC于点G，判断DG和EG的数量关系，并说明理由．（3）在（2）的条件下，当∠CEG＝∠ABD时，求点G点坐标．16．在Rt△ABC中，AC＝BC，∠ACB＝90°，点D是BC上一点．（1）如图1，AD平分∠BAC，求证：AB＝AC+CD；（2）如图2，点E在线段AD上，且∠CED＝45°，∠BED＝30°，求证：BE＝2AE；（3）如图3，CD＝BD，过B点作BM⊥AD交AD的延长线于点M，连接CM，过C点作CN⊥CM交AD于N，求证：DN＝3DM．17．如图，在Rt△ABC中，＝nM为BC上的一点，连接BM．（1）如图1，若n＝1，①当M为AC的中点，当BM⊥CD于H，连接AH，求∠AHD的度数；②如图2，当H为CD的中点，∠AHD＝45°，求的值和∠CAH的度数；（2）如图3，CH⊥AM于H，连接CH并延长交AC于Q，M为AC中点，直接写出tan∠BHQ 的值（用含n的式子表示）．18．如图1，在等边△ABC中，E、D两点分别在边AB、BC上，BE＝CD，AD、CE相交于点F．（1）求∠AFE的度数；（2）过点A作AH⊥CE于H，求证：2FH+FD＝CE；（3）如图2，延长CE至点P，连接BP，∠BPC＝30°，且CF＝CP，求的值．（提示：可以过点A作∠KAF＝60°，AK交PC于点K，连接KB）19．在等边△ABC中，点E，F分别在边AB，BC上．（1）如图1，若AE＝BF，以AC为边作等边△ACD，AF交CE于点O，连接OD．求证：①AF＝CE；②OD平分∠AOC；（2）如图2，若AE＝2CF，作∠BCP＝∠AEC，CP交AF的延长线于点P，求证：CE＝CP．20．已知等边△ABC和等腰△CDE，CD＝DE，∠CDE＝120°．（1）如图1，点D在BC上，点E在AB上，P是BE的中点，连接AD，PD，则线段AD与PD之间的数量关系为；（2）如图2，点D在△ABC内部，点E在△ABC外部，P是BE的中点，连接AD，PD，则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；（3）如图3，若点D在△ABC内部，点E和点B重合，点P在BC下方，且PB+PC为定值，当PD最大时，∠BPC的度数为．参考答案1．解：（1）如图1，过点A作AM⊥DC于M，∵∠BCD＝90°，AM⊥CD，∴AM∥BC，AB∥CD，∴四边形ABCM是平行四边形，且∠BCD＝90°，∴四边形ABCM是矩形，∴AM＝CB＝4，AB＝CM＝2，∴DM＝2，∴AD＝＝＝2，∴sin∠ADC＝＝＝；（2）△DEF是等腰直角三角形，理由如下：∵∠EDC＝∠FBC，DE＝BF，BC＝CD，∴△CDE≌△CBF（SAS）∴∠DCE＝∠BCF，CE＝CF，∴∠DCE+∠ECB＝∠BCF+∠BCE，∴∠DCB＝∠ECF＝90°，且CE＝CF，∴△DEF是等腰直角三角形；（3）设BE＝k，则CE＝CF＝2k，∴EF＝2k，∵∠BEC＝135°，又∠CEF＝45°，∴∠BEF＝90°，∴BF＝＝＝3k，∴sin∠BFE＝．2．解：（1）当∠BAM＝30°时，∴∠AMB＝180°﹣60°﹣30°＝90°，∴AB＝2BM；故答案为：30；（2）添加一个条件AB＝AC，可得△ABC为等边三角形；故答案为：AB＝AC；①如图1中，∵△ABC与△AMN是等边三角形，∴AB＝AC，AM＝AN，∠BAC＝∠MAN＝60°，∴∠BAC﹣∠MAC＝∠MAN﹣∠MAC，即∠BAM＝∠CAN，在△BAM与△CAN中，，∴△BAM≌△CAN（SAS），∴BM＝CN；②成立，理由：如图2中，∵△ABC与△AMN是等边三角形，∴AB＝AC，AM＝AN，∠BAC＝∠MAN＝60°，∴∠BAC+∠MAC＝∠MAN+∠MAC，即∠BAM＝∠CAN，在△BAM与△CAN中，，∴△BAM≌△CAN（SAS），∴BM＝CN．3．（1）证明：如图1中，∵∠ABC＝∠ACB＝∠ADE＝∠AED，∴∠EAD＝∠CAB，∴∠EAC＝∠DAB，∵AE＝AD，AC＝AB，∴△BAD≌△CAE（SAS）．（2）解：如图1中，设AC交BE于O．∵∠ABC＝∠ACB＝55°，∴∠BAC＝180°﹣110°＝70°，∵△BAD≌△CAE，∴∠ABO＝∠ECO，∵∠EOC＝∠AOB，∴∠CEO＝∠BAO＝70°，即∠BEC＝70°．（3）解：如图2中，∵∠CAB＝∠EAD＝120°，∴∠BAD＝∠CAE，∵AB＝AC，AD＝AE，∴△BAD≌△CAE（SAS），∴∠BAD＝∠ACE，BD＝EC＝4，同法可证∠BEC＝∠BAC＝120°，∴∠FEC＝60°，∵CF⊥EF，∴∠F＝90°，∴∠FCE＝30°，∴EF＝EC＝2．4．解：（1）作AH⊥BC于H，BM⊥AC于M．∵AB＝AC，AH⊥BC，∴BH＝CH＝3，∴AH＝＝＝4，＝•BC•AH＝•AC•BM，∵S△ABC∴BM＝＝，∴AM＝＝＝，∴cos A＝＝．（2）设AH交CD于K．∵∠BAC＝2∠ACD，∠BAH＝∠CAH，∴∠CAK＝∠ACK，∴CK＝AK，设CK＝AK＝x，在Rt△CKH中，则有x2＝（4﹣x）2+32，解得x＝，∴AK＝CK＝，∵∠ADK＝∠ADC，∠DAK＝∠ACD，∴△ADK∽△CDA，∴＝＝＝＝，设AD＝m，DK＝n，则有，解得m＝，n＝．∴AD＝．（3）结论：AD：BE＝5：6值不变．理由：∵∠GBE＝∠ABC，∠BAC+2∠ABC＝180°，∠GBE+∠EBC+∠ABC＝180°，∴∠EBC＝∠BAC，∵∠EDC＝∠BAC，∴∠EBC＝∠EDC，∴D，B，E，C四点共圆，∴∠EDB＝∠ECB，∵∠EDB+∠EDC＝∠ACD+∠DAC，∠EDC＝∠DAC，∴∠EDB＝∠ACD，∴∠ECB＝∠ACD，∴△ACD∽△BCE，∴＝＝．5．解：（Ⅰ）如图1，过C作CM⊥x轴于M点，如图1所示：∵CM⊥OA，AC⊥AB，∴∠MAC+∠OAB＝90°，∠OAB+∠OBA＝90°，∴∠MAC＝∠OBA，在△MAC和△OBA中，，∴△MAC≌△OBA（AAS），∴CM＝OA＝2，MA＝OB＝4，∴OM＝6，∴点C的坐标为（﹣6，﹣2），故答案为（﹣6，﹣2）；（Ⅱ）如图2，过D作DQ⊥OP于Q点，则四边形OEDQ是矩形，∴DE＝OQ，∵∠APO+∠QPD＝90°，∠APO+∠OAP＝90°，∴∠QPD＝∠OAP，在△AOP和△PDQ中，，∴△AOP≌△PDQ（AAS），∴AO＝PQ＝2，∴OP﹣DE＝OP﹣OQ＝PQ＝OA＝2；（Ⅲ）如图3，过点F分别作FS⊥x轴于S点，FT⊥y轴于T点，则∠HSF＝∠GTF＝90°＝∠SOT，∴四边形OSFT是正方形，∴FS＝FT＝4，∠EFT＝90°＝∠HFG，∴∠HFS＝∠GFT，在△FSH和△FTG中，，∴△FSH≌△FTG（AAS），∴GT＝HS，又∵G（0，m），H（n，0），点F坐标为（﹣4，﹣4），∴OT═OS＝4，∴GT＝﹣4﹣m，HS＝n﹣（﹣4）＝n+4，∴﹣4﹣m＝n+4，∴m+n＝﹣8．6．解：（1）在Rt△ABC中，tan A＝＝＝，由题意得，AP＝3t，在Rt△APQ中，tan A＝＝，∴PQ＝AP＝4t，根据勾股定理得，AQ＝＝＝5t．当0＜t≤时，如图1所示：CQ＝AC﹣AQ＝6﹣5t；当＜t≤时，如图2所示：CQ＝AQ﹣AC＝5t﹣6；故答案为：6﹣5t或5t﹣6；（2）∵PQ⊥AB，∴∠APQ＝90°＝∠ACB，∵∠A＝∠A，∴△APQ∽△ACB，∴＝＝，即＝，解得：t＝，即当△APQ与△ABC的周长的比为1：4时，t为秒．（3）分两种情况：①当0＜t≤时，如图1所示：△APQ与△ABC重叠部分图形的面积为S＝△APQ的面积＝×3t×4t＝6t2；即S＝6t2（0＜t≤）；②当＜t≤时，如图2所示：由（1）得：PQ＝3t，PQ＝4t，AQ＝5t，同（2）得：△CDQ∽△PAQ，∴＝＝，即＝＝，解得：CD＝（5t﹣6），∴△APQ与△ABC重叠部分图形的面积为S＝△APQ的面积﹣△CDQ的面积＝×3t×4t ﹣×（5t﹣6）×（5t﹣6）＝﹣t2+t﹣；即S＝﹣t2+t﹣（＜t≤）；（4）由（1）知，AQ＝5t，PQ＝4t，CQ＝6﹣5t或CQ＝5t﹣6，当CQ＝PQ时，四边形BCQP是轴对称图形，则4t＝6﹣5t，∴t＝；当＜t≤时，设PQ和BC相交于D，当AC＝AP时，四边形ACDP是轴对称图形，则6＝3t，∴t＝2．综上所述，当直线PQ把△ABC分成的两部分图形中有一个是轴对称图形时，t的值为秒或2秒．7．解：（1）如图，作AB，AC的垂直平分线交于点O，以O为圆心，OB长为半径作圆，⊙O 为图形G；（2）直线BF与图形G交点只有一个，理由如下：∵AD⊥AB，∴∠BAD＝90°，∴BD是直径，∠ADB+∠ABD＝90°，∵AB＝AC，∴∠ACB＝∠ABC，∵∠ACB＝∠ADB，∠ABF＝∠ABC，∴∠ABF＝∠ADB，∴∠ABF+∠ABD＝90°，∴∠DBF＝90°，∴BD⊥BF，且OB是半径，∴BF是圆O的切线，∴直线BF与图形G交点的只有一个；（3）∵cos∠ABF＝cos∠ADB＝＝，∴BD＝5，∴AB＝＝＝3，∵∠ABE＝∠ADB，∠BAE＝∠BAD＝90°，∴△ABE∽△ADB，∴，∴∴AE＝，∴DE＝AD﹣AE＝．8．解：（1）∵△ABC是等边三角形，AB＝8，AH⊥BC，∴BC＝AC＝AB＝8，BH＝HC＝4，∠HAC＝30°，∴AH＝HC＝4，∴DH＝4﹣x，∴DC2＝DH2+CH2＝（4﹣x）2+16∵△CDE是等边三角形，＝CD2＝[（4﹣x）2+16]＝x2﹣6x+16（0≤x≤4）∴y＝S△CDE（2）∵当△CDE的面积等于△ABC的面积的，∴x2﹣6x+16＝××64，∴x＝或，当x＝时，即AD＝，如图1，∴DH＝AH﹣AD＝，∵tan∠DCH＝＝＝，∴∠DCH＝30°，∴∠ACD＝∠ACB﹣∠DCH＝30°，∴∠ACE＝∠DCE+∠ACD＝90°，∴CE⊥AC；当x＝时，即AD＝，如图2，∴DH＝AD﹣AH＝，∵tan∠DCH＝＝＝，∴∠DCH＝30°，∴∠BCE＝∠DCH+∠DCE＝90°，∴CE⊥BC．9．解：（1）∵在△ABC中，AC＝1，AB＝x，BC＝3﹣x．，解得1＜x＜2；（2）①若AC为斜边，则1＝x2+（3﹣x）2，即x2﹣3x+4＝0，无解，②若AB为斜边，则x2＝（3﹣x）2+1，解得x＝，满足1＜x＜2，③若BC为斜边，则（3﹣x）2＝1+x2，解得x＝，满足1＜x＜2，综上，x＝或；（3）在△ABC中，作CD⊥AB于D，设CD＝h，△ABC的面积为S，则S＝xh，①若点D在线段AB上，则+＝x，∴（3﹣x）2﹣h2＝x2﹣2x+1﹣h2，即x＝3x﹣4，∴x2（1﹣h2）＝9x2﹣24x+16，即x2h2＝﹣8x2+24x﹣16．∴S2＝x2h2＝﹣2x2+6x﹣4＝﹣2（x﹣）2+（≤x＜2），当x＝时（满足≤x＜2），S2取最大值，从而S取最大值；②若点D在线段MA上，则﹣＝x，同理可，得S2＝x2h2＝﹣2x2+6x﹣4＝﹣2（x﹣）2+（1＜x≤），易知此时S＜，综合①②得，△ABC的最大面积为．10．解：（1）由题意PC＝1+t，CQ＝3﹣t，在Rt△PQC中，∵∠C＝90°，PQ＝3，PC＝1+t，CQ＝3﹣t，∴32＝（1+t）2+（3﹣t）2，解得t＝．∴PQ＝3时，t的值为．（2）S＝•PC•CQ＝•（1+t）（3﹣t）＝﹣t2+t+（0≤t≤3）．（3）∵直线DQ将△CPQ分成面积比为1：2两部分，∴CD＝2PD或PD＝2CD，∴1＝2t或t＝2，解得t＝或2，当t＝时，S＝﹣×++＝，当t＝2时，S＝﹣×4+2+＝，∴t＝s或2s时，直线DQ将△CPQ分成面积比为1：2两部分．11．解：（1）∵△ABC是等边三角形，∴AB＝BC﹣AC＝2，∠BAC＝∠ABC＝∠ACB＝60°．∵AD＝AC，∴AD＝AB，∴∠ABD＝∠ADB，∵∠ABD+∠ADB+∠BAC+∠CAD＝180°，∠CAD＝90°，∠ABD＝15°，∴∠EBC＝45°．过点E作EG⊥BC，垂足为点G．设AE＝x，则EC＝2﹣x．在Rt△CGE中，∠ACB＝60°，∴，，∴BG＝2﹣CG＝1+x，在Rt△BGE中，∠EBC＝45°，∴，解得．所以线段AE的长是．（2）①设∠ABD＝α，则∠BDA＝α，∠DAC＝∠BAD﹣∠BAC＝120°﹣2α．∵AD＝AC，AH⊥CD，∴，又∵∠AEF＝60°+α，∴∠AFE＝60°，∴∠AFE＝∠ACB，又∵∠AEF＝∠BEC，∴△AEF∽△BEC，∴，由（1）得在Rt△CGE中，，，∴BE2＝BG2+EG2＝x2﹣2x+4，∴（0＜x＜2）．②当∠CAD＜120°时，y＝7，则有7＝，整理得3x2+x﹣2＝0，解得x＝或﹣1（舍弃），．当120°＜∠CAD＜180°时，同法可得y＝当y＝7时，7＝，整理得3x2﹣x﹣2＝0，解得x＝﹣（舍弃）或1，∴AE＝1．12．解：（1）如图1中，过点C作CE⊥y轴于E，则∠CEB＝∠AOB．∵△ABC是等腰直角三角形，∴BC＝BA，∠ABC＝90°，∴∠BCE+∠CBE＝90°＝∠BAO+∠CBE，∴∠BCE＝∠ABO，在△BCE和△BAO中，，∴△CBE≌△BAO（AAS），∵A（﹣1，0），B（0，2），∴AO＝BE＝1，OB＝CE＝2，∴OE＝1+2＝3，∴C（﹣2，3），故答案为：﹣2，3；（2）动点A在运动的过程中，c+d的值不变．过点C作CE⊥y轴于E，则∠CEA＝∠AOB，∵△ABC是等腰直角三角形，∴BC＝BA，∠ABC＝90°，∴∠BCE+∠CBE＝90°＝∠ABO+∠CBE，∴∠BCE＝∠ABO，在△BCE和△BAO中，，∴△CBE≌△BAO（AAS），∵B（﹣1，0），A（0，a），∴BO＝AE＝1，AO＝CE＝a，∴OE＝1+a，∴C（﹣a，1+a），又∵点C的坐标为（c，d），∴c+d＝﹣a+1+a＝1，即c+d的值不变；（3）存在，使△PAB与△ABC全等，如图2中，过C作CM⊥x轴于M，过P作PE⊥x轴于E则∠CMB＝∠PEB＝90°，∵△CAB≌△PAB，∴∠PBA＝∠CBA＝45°，BC＝BP，∴∠CBP＝90°，∴∠MCB+∠CBM＝90°，∠CBM+∠PBE＝90°，∴∠MCB＝∠PBE，在△CMB和△BEP中，，∴△CMB≌△BEP（AAS），∴PE＝BM，CM＝BE，∵C（﹣2，3），B（﹣1，0），∴PE＝1，OE＝BE﹣BO＝3﹣1＝2，即P的坐标是（2，1）．13．解：（1）∵+＝0，又∵≥0，≥0，∴a＝﹣1，b＝1．（2）如图1中，作AM⊥x轴于M，AH⊥y轴于H，在RM上取一点K，使得AK＝KR，连接AK，AO．∵A（﹣1，1），∴AM＝AH＝1，∵AK＝KR，∴∠KRA＝∠KAR＝15°，∴∠AKM＝∠KAR+∠KRA＝30°，∴AK＝KR＝2AM＝2，MK＝，∴MR＝2+，∴AR＝＝＝+，∵B（m，m），∴OB平分∠EOB，∵OA平分∠EOM，∴OA⊥OB，∴∠AOB＝∠ARB＝90°，∴A，O，R，B四点共圆，∴∠BAR＝∠BOR＝45°，∴△ABR是等腰直角三角形，∴AB＝AR＝2+2，∵AH∥MR，∴∠HAR＝∠ARM＝15°，∴∠EA＝30°，∴AE＝＝，∴＝＝．（3）如图，作SH⊥AD于H．由题意四边形ADOC是正方形，∴∠ACD＝45°＝∠CAT+∠ATC，∵∠CAT+∠SAC＝45°，∴∠SAC＝∠ATC，∵∠ASC＝∠TSA，∴△SAC∽△STA，∴＝，∴SA2＝SC•ST，∵CS＝n，CT＝k，CD＝，∴SH＝DH＝（﹣n），AH＝n，∴AS2＝AH2+HS2＝n2+（﹣n）2＝n（n+k），∴k＝（0＜n＜）．14．解：（1）如图1，过A作AC∥x轴，过B作BC⊥AC于C，BC交x轴于E，AC交y轴于D，∵A （﹣3，﹣2），B （2，4），∴△AOB 的面积＝S △ACB ﹣S △AOD ﹣S △BOE ﹣S 长方形ODCE ， ＝﹣﹣﹣2×2，＝15﹣3﹣4﹣4，＝4；（2）设直线AB 的解析式为：y ＝kx +b （k ≠0）， 则，解得：，∴直线AB 的解析式为：y ＝x +，当x ＝0时，y ＝，∴C （0，），当y ＝0时，x +＝0，解得：x ＝﹣，∴D （，0）；（3）①当点P 在x 轴上时，∵△ABP 的面积为6， ∴＝6，∴PD ＝2，如图3，点P 在x 轴的正半轴上，P （，0）；同理得当点P在x轴的负半轴上，P（﹣，0）；②当点P在y轴上时，＝6，∴CP＝，∴P（0，4）或（0，﹣）；综上，点P的坐标是（，0）或（，0）或（0，4）或（0，）．15．解：（1）如图1中，∵A（0，4），∴OA＝4，＝×OB×OA＝8，∵S△AOB∴OB＝4，∵△AOB与△AOC关于y轴对称，∴OC＝OB＝4．（2）如图2中，结论：DG＝GE．理由：作DH∥EC交AC于H．∵OA＝OC，∠AOC＝90°，∴∠DAH＝∠ACO＝45°，∵DH∥OC，∴∠AHD＝∠ACO＝45°，∴∠DAH＝∠AHD，∴AD＝DH，∵AD＝EC，∴DH＝EC，∵∠DHG＝∠GCE，∠DGH＝∠CGE，∴△DGH≌△EGC（AAS），∴DG＝EG．（3）如图3中，连接DB，DC，作DH∥EC交AC于H．设AD＝DH＝x，则AH＝x，HC＝4﹣x，∵HG＝CG，∴HG＝HC＝2﹣x，∵OA⊥BC，OB＝OC，∴AB＝AC，DB＝DC，∴∠ABC＝∠ACB，∠DBO＝∠DCO，∴∠ABD＝∠ACD，∵∠CEG＝∠ABD，∴∠ACD＝∠CEG，∵DH∥CE，∴∠HDG＝∠CEG＝∠DCH，∵∠DHG＝∠DHC，∴△DHG∽△CHD，∴＝，∴＝，解得x＝2，∴AH＝CH＝2，∴H（2，2），∵GH＝GC，∴G（3，1）．16．证明：（1）如图1中，作DH⊥AB于H．∵∠ACD＝∠AHD＝90°，AD＝AD，∠DAC＝∠DAH，∴△ADC≌△ADH（ASA），∴AC＝AH，DC＝DH，∵CA＝CB，∠C＝90°，∴∠B＝45°，∵∠DHB＝90°，∴∠HDB＝∠B＝45°，∴HD＝HB，∴BH＝CD，（2）如图2中，作BM⊥AD交AD的延长线于M，连接CM．∵∠ACB＝∠AMB＝90°，∴C，A，B，M四点共圆，∴∠AMC＝∠ABC＝45°，∵∠CEM＝45°，∴∠CEM＝∠CME，∴CE＝CM，∴∠ECM＝∠ACB＝90°，∴∠ACE＝∠BCM，∵CA＝CB，CE＝CM，∴△ACE≌△BCM（SAS），∴AE＝BM，∵在Rt∠EMB中，∠MEB＝30°，∵BE＝2BM＝2AE．（3）如图3中，作CH⊥MN于H．∵∠ACB＝∠AMB＝90°，∴C，A，B，M四点共圆，∵CN⊥CM，∴∠NCM＝90°∴∠CNM＝∠CMN，∴CN＝CM，∵CH⊥MN，∴HN＝HM．∵CD＝DB，∠CHD＝∠BMD＝90°，∠ADH＝∠BDM，∴△CHD≌△BMD（AAS），∴DH＝DM，∵HN＝HM，∴DN＝3DM．17．解：（1）①如图1中，作AK⊥CD交CD的延长线于K．∵CD⊥BM，AK⊥CK，∠ACB＝90°，∴∠CHB＝∠K＝90°，∠CBH+∠BCH＝90°，∠BCH+∠ACK＝90°，∴∠CBH＝∠ACK，∵CB＝CA，∴△CHB≌△AKC（AAS），∴AK＝CH，∵∠CHM＝∠K＝90°，∴MH∥AK，∵AM＝BM，∴CH＝KH，∴AK＝KH，∵∠K＝90°，∴∠AHD＝45°．②如图2中，作AK⊥CD交CD的延长线于K，作CM⊥AB于M．设DH＝CH＝a．∵CA＝CB，∠ACB＝90°，∴∠CAB＝45°，∵∠AHD＝45°，∠AHD＝∠ACH+∠CAH，∴∠ACH+∠CAH＝∠CAH+∠DAH，∴∠DAH＝∠ACD，∵∠ADH＝∠CAD，∴△ADH∽△CDA，∴＝，∴＝，∴AD＝a，∵CA＝CB，∠ACB＝90°，CM⊥AB，∴AM＝BM，∴CM＝AM＝BM，设AM＝CM＝BM＝x，在Rt△CMD中，∵CM2＝DM2+CD2，∴x2+（x﹣a）2＝4a2，解得x＝a（负根已经舍弃）．∴BD＝AB﹣AD＝（+）a﹣a＝a，∴＝＝．∵△ADH∽△CDA，∴＝＝，设AH＝m，则AC＝m，AK＝KH＝m，∴tan∠ACK＝＝，∴∠ACH＝30°，∴∠CAH＝∠AHD﹣∠ACH＝45°﹣30°＝15°．（2）作AJ⊥BM交BM的延长线于J．设AM＝CM＝y，则BC＝2yn．∵CH⊥BM，BM＝＝＝•y，∴CH＝＝＝•y，∴HM＝＝•y，∵AJ⊥BJ，CH⊥BJ，∴∠J＝∠CHM＝90°，∵∠AMJ＝∠CMH，AM＝CM，∴△AMJ≌△CMH（AAS），∴AJ＝CH＝•y，HM＝JM＝•y，∵∠BHQ＝∠AHJ，∴tan∠BHQ＝tan∠AHJ＝＝＝n．18．（1）解：如图1中．∵△ABC为等边三角形，∴AC＝BC，∠BAC＝∠ABC＝∠ACB＝60°，在△EBC和△DCA中，，∴△EBC≌△DCA（SAS），∴∠BCE＝∠DAC，∵∠BCE+∠ACE＝60°，∴∠DAC+∠ACE＝60°，∴∠AFE＝60°．（2）证明：如图1中，∵AH⊥EC，∴∠AHF＝90°，在Rt△AFH中，∵∠AFH＝60°，∴∠FAH＝30°，∴AF＝2FH，∵△EBC≌△DCA，∴EC＝AD，∵AD＝AF+DF＝2FH+DF，∴2FH+DF＝EC．（3）解：在PF上取一点K使得KF＝AF，连接AK、BK，∵∠AFK＝60°，AF＝KF，∴△AFK为等边三角形，∴∠KAF＝60°，∴∠KAB＝∠FAC，在△ABK和△AFC中，，∴△ABK≌△AFC（SAS），∴∠AKB＝∠AFC＝120°，∴∠BKE＝120°﹣60°＝60°，∵∠BPC＝30°，∴∠PBK＝30°，∴FP＝CK，∴PK＝CK，∵FP＝FK+PK∴FP＝AF+CF，∵CF＝CP，设CP＝9a，∵CF＝2a，∴FP＝7a，∴AF＝5a，∴＝＝．19．（1）证明：①如图1中，∵△ABC是等边三角形，∴AB＝BC，∠B＝∠BAC＝60°，∵AE＝BF，∴△ABF≌△CAE（SAS），∴AF＝EC．②如图1中，∵△ABF≌△CAE，∴∠BAF＝∠ACE，∵∠AOE＝∠OAC+∠ACO＝∠OCA+∠BAF＝∠BAC＝60°，又∵△ACD是等边三角形，∴∠ADC＝∠DAC＝∠DCA＝60°，∴∠AOE＝∠ADC，∵∠AOE+∠AOC＝180°，∴∠ADC+∠AOC＝180°，∴A，D，C，O四点共圆，∴∠AOD＝∠ACD＝60°，∠COD＝∠CAD＝60°，∴∠AOD＝∠COD，∴OD平分∠AOC．（2）证明：如图2中，取AE的中点M，连接CM．∵AE＝2CF，AM＝ME，∴AM＝CF，∵∠CAM＝∠ACF＝60°，AC＝CA，∴△ACM≌△CAF（SAS），∴∠ACM＝∠CAF，∵∠CME＝∠CAM+∠ACM＝60°+∠ACM，∠CFP＝∠ACF+∠CAF＝60°+∠CAF，∴∠CME＝∠CFP，∵EM＝CF，∠PCF＝∠CEM，∴△CME≌△PFC（ASA），∴CE＝PC．20．解：（1）结论：AD＝2PD．理由：如图1中，∵△ABC是等边三角形，∴∠B＝60°，∵∠EDC＝120°，∴∠EDB＝180°﹣120°＝60°，∴∠B＝∠EDB＝∠BED＝60°，∴△BDE是等边三角形，∵BP＝PE，∴DP⊥AB，∴∠APD＝90°，∵DE＝DC，DE＝DB，∴BD＝CD，∵AB＝AC，∠BAC＝60°，∴∠PAD＝∠BAC＝30°，∴AD＝2PD．（2）结论成立．理由：延长DP到N，使得PN＝PD，连接BN，EN，延长ED到M，使得DM＝DE，连接BD，BM，CM．∵DE＝DC＝DM，∠MDC＝180°﹣∠EDC＝60°，∴△DCM是等边三角形，∵CA＝CB，CM＝CD，∠DCM＝∠ACB＝60°，∴∠BCM＝∠ACD，∴△BCM≌△ACD（SAS），∴AD＝BM，∵PB＝PE，PD＝PN，∴四边形BNED是平行四边形，∴BN∥DE，BN＝DE，∵DE＝DM，∴BN＝DM，BN∥DM，∴四边形BNDM是平行四边形，∴BM＝DN＝2PD，∴AD＝2PD．（3）如图3中，作∠PDK＝∠BDC＝120°，且PD＝PK，连接PK，CK．∵DB＝DC，DP＝DK，∠BDC＝∠PDK，∴∠BDP＝∠CDK，∴△PDB≌△KDC（SAS），∴PB＝CK，∵PB+PC＝PC+CK＝定值，∴P，C，K共线时，PK定值最大，此时PD的值最大，此时，∠DPB＝∠DKP＝∠DPK＝30°，∠BPC＝∠DPB+∠DPK＝60°．故答案为60°．。

2020年中考数学三角形专题复习(名师精选全国真题，值得下载练习)一、选择题1.若一个等腰三角形的两边长分别为2，4，则第三边的长为（）A. 2B. 3C. 4D. 2或42.如图，在ΔABC中，AC=BC , ∠A=40°，观察图中尺规作图的痕迹，可知∠BCG的度数为（）A. 40°B. 45°C. 50°D. 60°3.若长度分别为a，3，5的三条线段能组成一个三角形，则a的值可以是（）A. 1B. 2C. 3D. 84.“三等分角”大约是在公元前五世纪由古希腊人提出来的。

借助如图所示的“三等分角仪”能三等分任一角。

这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC=CD=DE，点D，E可在槽中滑动，若∠BDE=75°，则∠CDE的度数是（）A. 60°B. 65°C. 75°D. 80°5.如图，在ΔABC中AC=BC，点D和E分别在AB和AC上，且AD=AE.连接DE，过点A的直线GH与DE平行，若∠C=40∘，则∠GAD的度数为（）A. 40∘B. 45∘C. 55∘D. 70∘6.一个等腰三角形的底边长是6，腰长是一元二次方程x2−8x+15=0的一根，则此三角形的周长是（）A. 16B. 12C. 14D. 12或167.如图，已知∠AOB．按照以下步骤作图：①以点O为圆心，以适当的长为半径作弧，分别交∠AOB的两边于C，D两点，连接CD．②分别以点C，D为圆心，以大于线段OC的长为半径作弧，两弧在∠AOB内交于点E，连接CE，DE．③连接OE交CD于点M．下列结论中错误的是（）A. ∠CEO=∠DEOB. CM=MDC. ∠OCD=∠ECDD. S四边形OCED=12CD⋅OE8.如图，D是AB上一点，DF交AC于点E，DE=FE，FC//AB，若AB=4，CF=3，则BD的长是( )A. 0.5B. 1C. 1.5D. 29.如图，在等腰直角三角形ABC中，∠BAC＝90°，一个三角尺的直角顶点与BC边的中点O重合，且两条直角边分别经过点A和点B，将三角尺绕点O按顺时针方向旋转任意一个锐角，当三角尺的两直角边与AB，AC分别交于点E，F时，下列结论中错误的是（）A. AE ＋AF =ACB. ∠BEO ＋∠OFC =180°C. OE +OF =√22BC D. S 四边形AEOF =12S ΔABC 10.如图，在 Rt △ABC 中， ∠BAC =90° ， ∠B =36° ，AD 是斜边BC 上的中线，将△ACD 沿AD 对折，使点C 落在点F 处，线段DF 与AB 相交于点E ，则∠BED 等于（ ）A. 120°B. 108°C. 72°D. 36°11.如图，在 Rt △ABC 中， ∠ACB ＝90° ，分别以点 B 和点 C 为圆心，大于 12BC 的长为半径作弧，两弧相交于 D,E 两点，作直线 DE 交 AB 于点 F ，交 BC 于点 G ，连结 CF ．若 AC ＝3,CG ＝2 ，则 CF 的长为（ ）A. 52B. 3C. 2D. 72 12.如图，在直角三角形 ABC 中， ∠C =90°,AC =BC ， E 是 AB 的中点，过点 E 作 AC 和 BC 的垂线，垂足分别为点 D 和点 F ，四边形 CDEF 沿着 CA 方向匀速运动，点 C 与点 A 重合时停止运动，设运动时间为 t ，运动过程中四边形 CDEF 与 ΔABC 的重叠部分面积为 S ．则 S 关于 t 的函数图象大致为（ ）A. B. C. D.13.如图，在ΔABC中，D在AC边上，AD：DC＝1：2，O是BD的中点，连接AO并延长交BC于E，则BE：EC＝（）A. 1：2B. 1：3C. 1：4D. 2：314.如图所示的网格由边长相同的小正方形组成，点A、B、C、D、E、F、G在小正方形的顶点上，则ΔABC的重心是（）A. 点DB. 点EC. 点FD. 点G15.如图，正方形ABCD的对角线AC，BD相交于点O，点E在BD上由点B向点D运动（点E不与点B 重合），连接AE，将线段AE绕点A逆时针旋转90得到线段AF，连接BF交AO于点G.设BE的长为x，OG的长为y，下列图象中大致反映y与x之间的函数关系的是（）A. B. C. D.二、填空题16.若实数m、n满足|m﹣3|+√n−4＝0，且m、n恰好是直角三角形的两条边，则该直角三角形的斜边长为________.17.如图，在Rt△ABC的纸片中，∠C＝90°，AC＝5，AB＝13.点D在边BC上，以AD为折痕将△ADB折叠得到△ADB′，AB′与边BC交于点E.若△DEB′为直角三角形，则BD的长是________.18.如图，在△ABC中，AC=BC，将△ABC绕点A逆时针旋转60°，得到△ADE.若AB=2，∠ACB=30°，则线段CD的长度为________.19.如图，在△ABC中，∠C＝90°，DE是AB的垂直平分线，AD恰好平分∠BAC.若DE＝1，则BC的长是________.AB2，则tanC=________。

中考数学复习基础测试卷专练：等边三角形（含答案）中考数学复习基础测试卷专练：等边三角形（含答案）中考数学复习基础测试卷专练：等边三角形（含答案）一、选择题1.等腰三角形的两边长分别为5cm和7cm，则它的周长为（）3．如图，△ABC中，∠B=55°，∠C=30°，分别以点A和C为圆心，以大于AC 的长为半径画弧，两弧相交于M，N,作直线MN，交BC于D，连接AD，则∠BAD 的度数为（）A.65°B.60°C.55°D.45°4．如图，△ABC中，AB=5，AC=6，BC=4，边AB的垂直平分线交AC于点D，则△BDC的周长是（）5．如图，△ABC是等边三角形，BD是中线，延长BC到E，使CE=CD，连接中正确的个数是（）6．如图，在△PAB中，PA=PB，M，N，K分别是边PA，PB，AB上的点，且AM=BK，BN=AK，若∠MKN=44°，则∠P的度数为( ).A.44°B.66°C.88°D.92°二、填空题7．如图，在△ABC中，AB=AC，D为BC中点，∠BAD=35°，则∠C的度数为______．8.如图，△ABC中，AB=AC，∠A=36°，BD是AC边上的高，则∠DBC的度数是______．!--[if !supportLists]-- 1．!--[endif]-- 如图，已知点B、C、D、E在同一直线上，△ABC是等边三角形，且CG=CD，DF=DE，则∠E=______．10.如图，在△ABC中，∠ABC=∠ACB=72°，BD、CE分别是∠ABC和∠ACB的平分线，它们的交点为F，三、解答题11.如图，已知AB=AC=AD，且AD∥BC，求证：∠C=2∠D．12.如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE=DF，∠A=∠D．（1）求证：AB=CD．（2）若AB=CF，∠B=30°，求∠D的度数．13.如图，△ABC的边AB的延长线上有一个点D，过点D作DF⊥AC于F，交BC于E，且BD=BE，求证：△ABC为等腰三角形．14．如图，在△ABC中，BP平分∠ABC，CP平分∠ACB，且PD∥AB，PE∥AC，BC=5，求△PDE的周长．15．如图，△ABC、△ADE是等边三角形，B、C、D在同一直线上．求证：（1）CE=AC+DC；（2）∠ECD=60°．参考答案1. D2.D 3．A4．C [解析]∵ED是AB的垂直平分线，∴AD=BD，∵△BDC的周长=DB+BC+CD，∴△BDC的周长=AD+BC+CD=AC+BC=6+4=10．5．D [解析]∵△ABC是等边三角形，BD是AC上的中线，∴∠ADB=∠CDB=90°，BD平分∠ABC，∴BD⊥AC，∵∠ACB=∠CDE+∠DEC=60°，CD=CE，∴∠CBD=∠DEC，∴DB=DE．∠BDE=∠CDB+∠CDE=120°.所以这四项都是正确的．6．D[解析]∵PA=PB，∴∠A=∠B，在△AMK和△BKN中，∴△AMK≌△BKN，∴∠AMK=∠BKN，∵∠MKB=∠MKN+∠NKB=∠A+∠AMK，∴∠A=∠MKN=44°，∴∠P=180°-∠A-∠B=92°。

第19讲:全等三角形一、复习目标1、理解全等形、全等三角形的定义，掌握全等三角形的性质与判定方法。

2、能正确、恰当选用三角形全等的条件推证三角形全等、角相等、线段相等的问题。

3、理解角平线的性质定理和判定定理。

二、课时安排1课时三、复习重难点1、全等三角形的性质与判定全套资料联系QQ/微信：14032256582、综合运用全等三角形的性质与判定证题四、教学过程（一）知识梳理全等图形及全等三角形能够完全重合的两个图形就是______全等图形全等图形的形状和_______完全相同全等三角形能够完全重合的两个三角形就是全等三角形完全重合有两层含义：说明(1)图形的形状相同；(2)图形的大小相等全等三角形的性质性质1 全等三角形的对应边________性质2 全等三角形的对应角________性质3 全等三角形的对应边上的高________性质4 全等三角形的对应边上的中线________性质5 全等三角形的对应角平分线________全等三角形的判定基本判定方法1.三条边对应相等的两个三角形全等(简记为SSS)2.两个角和它们的夹边对应相等的两个三角形全等(简记为____ )3.两个角和其中一个角的对边对应相等的两个三角形全等(简记为____ )4.两条边和它们的夹角对应相等的两个三角形全等(简记为____ )5.斜边和一条直角边对应相等的两个直角三角形全等(简记为____ )拓展延伸满足下列条件的三角形是全等三角形：(1)有两边和其中一边上的中线对应相等的两个三角形全等；(2)有两边和第三边上的中线对应相等的两个三角形全等；(3)有两角和其中一角的平分线对应相等的两个三角形全等；(4)有两角和第三个角的平分线对应相等的两个三角形全等；(5)有两边和其中一边上的高对应相等的锐角(或钝角)三角形全等；(6)有两边和第三边上的高对应相等的锐角(或钝角)三角形全等总结判定三角形全等，无论哪种方法，都要有三组元素对应相等，且其中最少要有一组对应边相等利用“尺规”作三角形的类型1 已知三角形的三边，求作三角形2 已知三角形的两边及其夹角，求作三角形3 已知三角形的两角及其夹边，求作三角形4 已知三角形的两角及其其中一角的对边，求作三角形5 已知直角三角形一条直角边和斜边，求作三角形角平分线的性质与判定性质角平分线上的点到角两边的______相等判定角的内部到角两边的距离相等的点在这个角的______上（二）题型、技巧归纳考点1全等三角形性质与判定的综合应用 技巧归纳：1．解决全等三角形问题的一般思路：①先用全等三角形的性质及其他知识，寻求判定一对三角形全等的条件；②再用已判定的全等三角形的性质去解决其他问题．即由已知条件(包含全等三角形)判定新三角形全等、相应的线段或角的关系；全套资料联系QQ/微信：14032256582．轴对称、平移、旋转前后的两个图形全等；3．利用全等三角形性质求角的度数时注意挖掘条件，例如对顶角相等、互余、互补等． 考点2全等三角形开放性问题 技巧归纳：由于判定全等三角形的方法很多，所以题目中常给出(有些是推出)两个条件，让同学们再添加一个条件，得出全等，再去解决其他问题．这种题型可充分考查学生对全等三角形的掌握的牢固与灵活程度．（三）典例精讲例1 已知：AB ＝AE ，∠1＝∠2，∠B ＝∠E ，求证：BC ＝ED.[解析] 由∠1＝∠2可得：∠EAD ＝∠BAC ，再有条件AB ＝AE ，∠B ＝∠E 可利用ASA 证明△ABC ≌△AED ，再根据全等三角形对应边相等可得BC ＝ED .证明：∵∠1＝∠2，∴∠1＋∠BAD ＝∠2＋∠BAD ，即∠BAC ＝∠EAD. ∴在△BAC 与△EAD 中， ⎩⎪⎨⎪⎧∠B ＝∠E ，AB ＝AE ，∠BAC ＝∠EAD.∴△BAC ≌△EAD ，∴BC ＝ED.全套资料联系QQ/微信：1403225658例2 如图在△ABC 中，点D 是BC 的中点，作射线AD ，在线段AD 及其延长线上分别取点E 、F ，连接CE 、BF.添加一个条件，使得△BDF ≌△CDE ，并加以证明．你添加的条件是________．(不添加辅助线)[解析] 由已知可证∠EDC ＝∠BDF ，又DC ＝DB ，因为三角形全等条件中必须是三个元素，并且一定有一组对应边相等．故添加的条件是：DE ＝DF 或(CE ∥BF 或∠ECD ＝∠DBF 或∠DEC ＝∠DFB )；解：(1)添加的条件是：DE ＝DF(或CE ∥BF 或∠ECD ＝∠DBF 或∠DEC ＝∠DFB 等)． (2)证明：在△BDF 和△CDE 中， ∵⎩⎪⎨⎪⎧BD ＝CD ，∠EDC ＝∠FDB ，DE ＝DF ， ∴△BDF ≌△CDE （四）归纳小结本部分内容要求熟练掌握全等形、全等三角形的定义，掌握全等三角形的性质与判定方法。

2019-2020学年中考数学深度复习讲义（教案+中考真题+模拟试题+单元测试）等腰三角形◆考点聚焦1．等腰三角形的判定与性质．2．等边三角形的判定与性质．3．运用等腰三角形、等边三角形的判定与性质解决有关计算与证明问题．◆备考后法1．运用三角形不等关系，•结合等腰三角形的判定与性质解决等腰三角形中高、边、角的计算问题，并要注意分类讨论．2．要正确辨析等腰三角形的判定与性质．3．能熟练运用等腰三角形、方程（组）、函数等知识综合解决实际问题．◆识记巩固1．等腰三角形的性质定理及推论：____________________________．2．等腰三角形的判定定理及推论：____________________________．识记巩固参考答案:1．等腰三角形的两个底角相等（等边对等角）；•等腰三角形的顶角平分线平分底边并且垂直于底边（三线合一）；等边三角形的各有都相等，且每个角都等于60°.2．如果一个三角形的两角相等，那么这两个角所对的边也相等（等角对等边）．•三个角都相等的三角形是等边三角形；有一个角是60°的等腰三角形是等边三角形．在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.◆典例解析例1 （2011浙江衢州，23,10分），.ABC∠=∠==C AC BC∆是一张等腰直角三角形纸板，Rt2要在这张纸板中剪出一个尽可能大的正方形，有甲、乙两种剪法（如图1），比较甲、乙两种剪法，哪种剪法所得的正方形面积更大？请说明理由.图1中甲种剪法称为第1次剪取，记所得的正方形面积为1S ；按照甲种剪法，在余下的ADE BDF ∆∆和中，分别剪取正方形，得到两个相同的正方形，称为第2次剪取，并记这两个正方形面积和为2S (如图2)，则2=S ；再在余下的四个三角形中，用同样的方法分别剪取正方形，得到四个相同的正方形，称为第3次剪取，并记这四个正方形的面积和为3S (如图3)；继续操作下去…则第10次剪取时，10S = .求第10次剪取后，余下的所有小三角形的面积和.【答案】(1)解法1：如图甲，由题意得,1,1CFDE AE DE EC EC S ====正方形即.如图乙，设MN x =，则由题意，得,AM MQ PN NB MN x =====23389PNMQx x S ∴==∴==正方形解得 又819> ∴甲种剪法所得的正方形的面积更大说明：图甲可另解为：由题意得点D 、E 、F 分别为AB AC BC 、、的中点，112ABC CFDE S S ==正方形解法2：如图甲，由题意得AE DE EC ==，即EC=1如图乙，设,MN x AM MQ QP PN NB MN x =======则由题意得33221x x EC MN∴==>>解得又即 ∴甲种剪法所得的正方形的面积更大F E BQ(2)212S =(3)10912S = (3)解法1：探索规律可知：112n n S -=‘ 剩余三角形的面积和为：()12109911112212422S S S ⎛⎫-+++=-++++= ⎪⎝⎭ 解法2：由题意可知， 第一次剪取后剩余三角形面积和为112=1=S S -第二次剪取后剩余三角形面积和为12211122S S S -=-== 第三次剪取后剩余三角形面积和为233111244S S S -=-==第十次剪取后剩余三角形面积和为9101091=2S S S -= 例2 如图，△ABC 中，E ，F 分别是AB ，AC 上的点．①AD 平分∠BAC ；②DE ⊥AB ，•DF•⊥AC ；③AD ⊥EF ．以此三个中的两个为条件，另一个为结论，可构成三个命题，即：①②③；①③②；②③①．（1）试判断上述三个命题是否正确（直接作答）；（2）请证明你认为正确的命题．解析 （1）①②⇒③正确；①③⇒②错误；②③⇒①正确．（2）先证①②⇒③，如图1．∵AD 平分∠BAC ，DE ⊥AB ，DF ⊥AC ，∴DE=DF ，∠AED=∠AFD=90°．在Rt △AED 和Rt △AFD 中，,,DE DF AD AD =⎧⎨=⎩∴△AED ≌△AFD （HL ）．∴AE=AF ．∴△AEF 是等腰三角形，∴AD ⊥EF ．再证②③⇒①．图1 图2 图3方法一：如图2，DE ⊥AB ，EF ⊥AD ，DF ⊥AC ．易证△DEH ∽△DAE ，△DFH ∽△DAF ．∴,DE DH DH DF AD DE DF AD==， ∴DE 2=AD·DH，DF 2=DH·AD． ∴DE 2=DF 2，∴DE=DF，∴AD 平分∠BAC．方法二：如图3，取AD 的中点O ，连结EO ，FO ．∵DE ⊥AB ，DF ⊥AC ，∴OE ，OF 分别是Rt △ADE ，Rt △ADF 斜边上的中线．∴OE=12AD ，OF=12AD ． 即O 点到A ，E ，D ，F 的距离相等． ∴A ，E ，D ，F 四点在以O 为圆心，12AD 为半径的圆上，AD 是直径，EF 是⊙O 的弦，而EF•⊥AD ，∴AD 平分EDF ，即ED DF =．∴∠DAE=∠DAF ，即AD 平分∠BAC ．点评 本题是义务教育课程标准实验教科书数学（人教版）八年级上第111•页拓广探索题的变式与拓展，该例在教材中多次以不同形式出现，八年级（上）（人教版）第150页第13题，第158页第11题．因此，•在九年级的学习过程中一定要重视教材中的典型例题，习题，想一想这些题还可以进行怎样的变式，•与前后的知识与方法有什么联系，还可以得到什么结论等．这样可以不断提高自己的综合解题能力．2011年真题一、选择题1. （2011浙江省舟山，7，3分）如图，边长为4的等边△ABC 中，DE 为中位线，则四边形BCED 的面积为（ ）（A ）32 （B ）33 （C ）34 （D ）36【答案】B2. （2011四川南充市，10，3分）如图，⊿ABC 和⊿CDE 均为等腰直角三角形，点B,C,D 在一条直线上，点M 是AE 的中点，下列结论：①tan∠AEC=CDBC ;②S ⊿ABC +S ⊿CDE ≧S ⊿ACE ;③BM⊥DM;④BM=DM.正确结论的个数是（ ） （A ）1个 （B ）2个 （C ）3个 （D ）4个MEC A【答案】D3. （2011浙江义乌，10，3分）如图，△ABC 和△ADE 都是等腰直角三角形，∠BAC =∠DAE =90°，四边形ACDE 是平行四边形，连结CE 交AD 于点F ，连结BD 交CE 于点G ，连结BE . 下列结论中：① CE =BD ； ② △ADC 是等腰直角三角形；③ ∠ADB =∠AEB ； ④ CD ·AE =EF ·CG ；一定正确的结论有A ．1个B ．2个C ．3个D ．4个 【答案】D4. （2011台湾全区，30）如图(十三)，ΔABC 中，以B 为圆心，长为半径画弧，分别交、ABC E FG（第7题） ABC DEAB于D 、E 两点，并连接BD 、DE ．若∠A =30∘，AB ＝AC ，则∠BDE 的度数为何？A ． 45B ． 52．5C ． 67．5D ． 75【答案】Ｃ5. （2011台湾全区，34）如图(十六)，有两全等的正三角形ABC 、DEF ，且D 、A 分别为△ABC 、△DEF的重心．固定D 点，将△DEF 逆时针旋转，使得A 落在DE 上，如图(十七)所示．求图(十六)与图(十七)中，两个三角形重迭区域的面积比为何？A ．2：1B ． 3：2C ． 4：3D ． 5：4【答案】Ｃ6. （2011山东济宁，3，3分）如果一个等腰三角形的两边长分别是5cm 和6cm ，那么此三角形的周长是A ．15cmB ．16cmC ．17cmD ．16cm 或17cm【答案】D7. （2011四川凉山州，8，4分）如图，在ABC △中，13AB AC ==，10BC =，点D 为BC 的中点，DE DE AB ⊥，垂足为点E ，则DE 等于（ ）A ．1013B ．1513C ．6013D ．7513【答案】C8.二、填空题1. （2011山东滨州，15，4分）边长为6cm 的等边三角形中，其一边上高的长度为________.【答案】2. （2011山东烟台，14,4分）等腰三角形的周长为14，其一边长为4，那么，它的底边为 .【答案】4或63. （2011浙江杭州，16，4）在等腰Rt △ABC 中，∠C =90°，AC ＝1，过点C 作直线l ∥AB ，F 是l 上的一点，且AB ＝AF ，则点F 到直线BC 的距离为 ．4. （2011浙江台州，14,5分）已知等边△ABC 中，点D,E 分别在边AB,BC 上，把△BDE 沿直线DE 翻折，使点B 落在点B ˊ处，DB ˊ,EB ˊ分别交边AC 于点F ，G ，若∠ADF=80º ，则∠EGC 的度数为【答案】80º5. （2011浙江省嘉兴，14，5分）如图，在△ABC 中，AB =AC ，︒=∠40A ，则△ABC 的外角∠BCD ＝ °．【答案】1106. （2011湖南邵阳，11，3分）如图（四）所示，在△ABC 中，AB=AC ，∠B=50°，则∠A=_______。