沪教版数学七年级上册 4.5 角的比较与补(余)角

4.5课题：角的比较与补（余）角一、学习目标：1、会比较两个角的大小，能够结合图形实际将一个角写成两个角和差的形式。

2、了解角平分线的意义，并能够用符号语言表示。

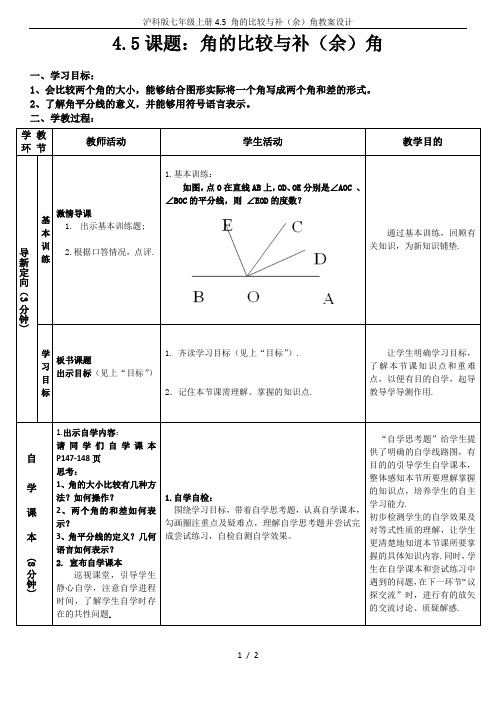
二、学教过程：学教环节教师活动学生活动教学目的导新定向（3分钟) 基本训练激情导课1.出示基本训练题;2.根据口答情况，点评.1.基本训练：如图，点O在直线AB上，OD、OE分别是∠AOC 、∠BOC的平分线，则∠EOD的度数？通过基本训练，回顾有关知识，为新知识铺垫.学习目标板书课题出示目标（见上“目标”）1. 齐读学习目标（见上“目标”）.2．记住本节课需理解、掌握的知识点.让学生明确学习目标，了解本节课知识点和重难点，以便有目的自学，起导教导学导测作用.自学课本 (8分钟)1.出示自学内容：请同学们自学课本P147-148页思考：1、角的大小比较有几种方法？如何操作？2、两个角的和差如何表示？3、角平分线的定义？几何语言如何表示？2. 宣布自学课本巡视课堂，引导学生静心自学，注意自学进程时间，了解学生自学时存在的共性问题.1.自学自检：围绕学习目标，带着自学思考题，认真自学课本，勾画圈注重点及疑难点，理解自学思考题并尝试完成尝试练习，自检自测自学效果。

“自学思考题”给学生提供了明确的自学线路图，有目的的引导学生自学课本，整体感知本节所要理解掌握的知识点，培养学生的自主学习能力.初步检测学生的自学效果及对等式性质的理解，让学生更清楚地知道本节课所要掌握的具体知识内容.同时，学生在自学课本和尝试练习中遇到的问题，在下一环节“议探交流”时，进行有的放矢的交流讨论、质疑解惑.教后反思：议 探 交 流(8 分 钟)宣布议探交流开始 1.对议：出示对议交流内容，对议开始. 2.组议：出示自学思考题（见PPT ），宣布组议开始，质疑解惑.3.巡堂：观察了解学生的讨论情况，了解存在共性问题，引导学困小组解决问题.师友对议：全体学生起立，针对自学提纲同组师友对议，师问友答，你讲我听，对于师友不理解的问题，互帮互学，不理解的做好记录，以备组议. 组议解惑：对议交流后，由组长组织讨论自学思考题和对议中没有解决的问题. 安排展示：由组长直接安排一对展示师友，准备展示.1.起立对议，以促使每位学生参与交流讨论;2.组议意在解惑，帮助自学自检和对议中没有解决的问题，促使每个同学理解掌握自学知识内容，促进互帮互学和团队合作学习的意识;3.以保证每组都有展示人.展 示 评 讲(10 分 钟)1.指名展示：要求学友展示自学提纲中的问题和尝试练习. 2.后进展示：指名后进生文字叙述.3.教师点评：对学友和后进生的回答作适当纠正和鼓励. 4.归纳小结：师生归纳数轴的画法.师友展示：针对自学思考题，师友同时起立，老师点名，学友回答，师傅点评补充.质疑补充：师友展示，其他小组注意倾听，发现问题和不足大胆质疑、纠错补充.做好笔记：在教师点评和归纳小结中，学生要快速做好重要知识点的记录.1.学生展示其自学成果，巩固本节知识内容，锻炼表达能力，培养独立学习的习惯，进而提高其学习能力.2.鼓励师友展示点评、他组质疑补充，培养促进学生质疑问难.3.教师点评讲解，强调知识点重难点，使学生对本节知识有更深刻的认识和把握.当 堂 检测（8 分钟）当堂检测： （见右栏） 教师巡视：教师巡视解题情况，个别辅导. 公布答案：对于没有达到要求的学生，可以通过师友互助解决，并加以订正. 点评小结：针对学生做题情况，简而精的进行点评、小结、强调.当堂检测:如图：OC 、OD 分别是∠AOB 、∠BOE 的平分线，（1）如果∠AOB=700， ∠BOE=600，那么∠1+ ∠2= --------（2） 如果∠1+ ∠2 =550，则∠AOE= --------自我订正，或组内师友互帮订正.当堂检测是为了让学生进一步落实本堂教学目标，更好的了解和掌握重难点，提高学理解能力.通过当堂检测，教师点评，进一步检查新课教学效果，同时也能够培优。

4.5角的比较与补（余）角
【教学目标】
1•在现实情境中，进一步丰富锐角、钝角、直角及大小的认识.
2. 学会比较角的大小，能估计一个角的大小.
3. 在操作活动中认识角平分线，能画出一个角的平分线.
4. 在具体情境中了解余角与补角，懂得等角的余角相等，等角的补角相等，并能运用这些性质解决一些简单的实际问题.
【重点难点】
重点：角的大小的比较方法，从图形中观察角的和、差关系.
难点：余角与补角的性质.
【教学过程设计】
【教学小结】
【板书设计】
4.5角的比较与补（余）角
1•比较方法：叠合法、度量法 2.角的平分线：在角的内部，以角的顶点为端点
的一条射线把这
个角分成两个相等的角，这条射线叫做角的平分线
互补：两个角的和是180
互余：两个角的和是90° 4.性质：同角 （或等角 ）的补（余）角相等 .
3.角的关系
【教学反思】
本节课主要采用“复习导入——学生自主探索与小组合作交流——概括明晰”的教学思路，把探索知识的主动权完全交给学生.合作学习的方式，使得全体学生都能在横向交流中各尽所能，取长补短，各有所获，共同发展.。

《4.5 角的比较与补（余）角》◆教材剖析上一节我们学习了角和角的有关观点，掌握了角的胸怀单位以及单位之间的换算 .本节就是进一步研究有关角的知识，经过指引学生察看比较角的大小，加深学生对角的关系的认识，使学生掌握角的比较方法 .帮助学生理解角的和差，掌握角的均分线的定义，以及余角、补角的观点及性质，为进一步学习角的画法确立基础.◆ 教课目的【知识与能力目标】1.会比较两个角的大小，理解角的和差；2.认识角均分线的意义及观点；3.理解余角、补角的观点，掌握余角和补角的性质 .【过程与方法目标】经过实质察看、操作，领会角的大小，掌握比较角的大小的比较方法，培育学生的察看思想能力及合情推理能力 .【感情态度价值观目标】在操作、察看、思虑、发现的过程中，领会学习几何知识的思想方法，培育学生剖析问题、解决问题的能力以及合作学习和独立思虑的优秀学习习惯 .◆教课重难点【教课要点】1.角的大小比较方法以及角均分线的观点；2.两角互补、互余的观点及性质 .【教课难点】从图形中察看角的数目关系.◆ 课前准备多媒体课件 .◆ 教课过程一、情境引入问题：怎样比较两条线段的长短的？①胸怀法：分别量出两条线段的长度，而后再比较大小.②叠合法：把两条线段叠合在一同比较大小.问题：要怎样比较角的大小呢？【设计企图】经过学过的比较线段的方法，运用类比的思想，引出比较角的大小的方法 .二、研究新知1．角的比较 .角的大小的比较方法：(1)胸怀法：①将量角器的中心点与角的极点重合；②量角器的零度刻度线与角的一边重叠；③角的另一边落在量角器的什么刻度线上.(2)叠合法：叠合∠DEF 与∠ABC ，把∠DEF 挪动，使它的极点E 移到和∠ABC 的极点 B 重合，一边 ED 和 BA 重合，另一边 EF 和 BC 落在 BA 的同旁 .如图①，假如 EF 和 BC 重合，那么∠ DEF＝∠ ABC ；如图②，假如 EF 落在∠ ABC 的内部，那么∠ DEF＜∠ ABC ；如图③，假如 EF 落在∠ ABC 的外面，那么∠ DEF＞∠ ABC.【设计企图】运用类比的思想，经过研究，使学生掌握角的大小的比较方法，为进一步学习角的和差等知识做铺垫 .2.角均分线的定义及性质 .(1)认识角的和差 .问题：你能将∠ AOC 写成两个角的和与两个角的差的形式吗？∠AOC 是∠ AOB 与∠ BOC 的和，记作∠ AOC＝∠ AOB ＋∠ BOC，∠AOB 是∠ AOC 与∠ COB 的差，记作∠ AOB ＝∠ AOC－∠ COB.近似地，∠ AOC －∠AOB ＝∠ COB.例 1如图④，求解以下问题：(1)比较∠AOC 与∠ BOC，∠ BOD 与∠ COD 的大小；(2)将∠ AOC 写成两个角的和与两个角的差的形式.解： (1)由图④能够看出：∠AOC＞∠ BOC(OB 在∠ AOC 内)∠BOD＞∠ COD(OC 在∠ BOD 内)(2)∠AOC＝∠ AOB ＋∠ BOC，∠AOC＝∠ AOD —∠ DOC.(2)认识角的均分线 .定义：在角的内部，以角的极点为端点的一条射线把这个角分红两个相等的角，这条射线叫做这个角的均分线 .如图⑤， OC 是∠ AOB 的均分线，这时有：∠AOC＝∠ COB＝1∠AOB，2∠AOB ＝2∠ AOC＝2∠COB.【设计企图】经过研究，使学生认识角的和差，掌握角均分线的定义及性质，为进一步学习余角、补角等知识做铺垫 .3.余角和补角的观点及性质 .问题：已知∠ α、∠ β、∠ γ的，比较它们的大小，并思虑∠ α与∠β、∠ β与∠ γ之间有什么特别关系？互为余角定义：假如两个角的和等于一个直角，就说这两个角互为余角，简称互余，此中一个角是另一个角的余角．若∠α＋∠ β＝90°，那么∠ α与∠ β互余 . 反之若∠α与∠ β互余，那么∠α＋∠ β＝90°.∠ α是∠ β的余角，相同∠ β也是∠ α的余角 .互为补角定义：假如两个角的和等于一个平角，就说这两个角互为补角，简称互补，此中一个角是另一个角的补角 .若∠β＋∠ γ＝90°，那么∠ β与∠ γ互补 . 反之若∠β与∠ γ互补，那么∠β＋∠ γ＝180°.∠ β是∠γ的补角，相同∠ γ也是∠ β的余补 .例 2 如图⑥，∠ 1＝∠ 3，∠1 与∠ 2 互补，∠ 3 与∠ 4 互补，那么∠ 2 与∠ 4 有什么关系？图⑥解：由于∠ 1 与∠ 2 互补，因此∠ 2＝180°－∠ 1.由于∠ 3 与∠ 4 互补，因此∠ 4＝180°－∠ 3.又由于∠ 1＝∠ 3，因此∠ 2＝∠ 4.能够获得补角的性质：同角(或等角 )的补角相等 .问题：余角有无上边补角近似的性质？假如有，你能说明道理吗？余角的性质：同角的余角相等，即：若∠A＋∠ B＝ 90°，∠ A＋∠ C＝90°，则∠ B＝∠ C；等角的余角相等，即：若∠ A＋∠ B＝90°，∠ D＋∠C ＝90°，∠ A＝∠ D，则∠ B＝∠ C.【设计企图】经过详细的例子，使学生认识余角、补角的观点，并掌握余角、补角的性质 .三、稳固练习1.依据图⑦，回答以下问题：(1)比较∠ FOD 与∠ FOE 的大小；(2)借助三角尺比较∠ DOE 与∠ DOF 的大小．图⑦2.一个角的补角比它的余角的 4 倍少 30°，求这个角的度数．四、讲堂总结问题：经过这节课的学习，你有哪些收获？1.角的大小的比较方法：(1)胸怀法； (2)叠合法 .2.角均分线的定义及性质：在角的内部，以角的极点为端点的一条射线把这个角分红两个相等的角，这条射线叫做这个角的均分线 .若 OC 是∠ AOB 的均分线，则∠ AOC＝∠ COB＝1∠AOB ，∠2AOB ＝2∠AOC ＝2∠COB.3.余角和补角的观点及性质：余角的定义：假如两个角的和等于一个直角，就说这两个角互为余角，简称互余，此中一个角是另一个角的余角．余角的性质：同角 (或等角 )的余角相等 .补角的定义：假如两个角的和等于一个平角，就说这两个角互为补角，简称互补，此中一个角是另一个角的补角 .补角的性质：同角 (或等角 )的补角相等 .◆ 教课反省略 .。