【配套K12】[学习](全国通用版)2019版高考化学大一轮复习 第七章 化学反应速率和化学平衡 增

考点一：氧化还原反应及相关概念氧化还原反应判断依据：反应前后有元素的化合价发生变化。

本质：电子转移(得失或偏移)。

相关概念概括为“升失氧、降得还，剂性一致、其他相反”。

氧化性是指得电子的性质(或能力)；还原性是指失电子的性质(或能力)。

氧化性、还原性的强弱取决于得、失电子的难易程度，与得、失电子数目的多少无关。

如：Na －e －===Na－3e －===Al 3＋，但根据金属活动性顺序可知，Na 比Al 活泼，更易失去电子，所以Na 的还原性比氧化还原反应电子转移的表示方法双线桥法：①标变价，②画箭头(反应物指向生成物)，③算数目，④说变化。

用双线桥法标出MnO 2与浓盐酸加热反应的电子转移的方向和数目：。

第07讲 氧化还原反应的概念和规律01了解氧化还原反应的概念。

掌握氧化性、还原性强弱的比较及价态规律的应用。

重点·夯基易错归纳　(2)单线桥法：箭头由失电子原子指向得电子原子，线桥上只标电子转移的数目，不标“得”“失”字样。

用单线桥法标出铜和浓硝酸反应的电子转移的方向和数目：(浓)===Cu(NO 3)2＋2NO 2↑＋2H 2O 。

归纳　。

4．常见的氧化剂和还原剂(1)常见的氧化剂常见的氧化剂包括某些非金属单质、含有高价态元素的化合物、过氧化物等。

如：(2)常见的还原剂常见的还原剂包括活泼的金属单质、非金属阴离子及含低价态元素的化合物、低价金属阳离子、某些非金属单质及其氢化物等。

如：金属氢化物(如NaH 等)、NaBH 4也是重要还原剂。

5．氧化还原反应与四种基本反应类型的关系分析下列四个化学反应：A ．2Na ＋2H 2O===2NaOH ＋H 2↑B ．2HClO =====光照2HCl ＋O 2↑C ．4NH 3＋5O 2=====催化剂△4NO ＋6H 2O1．在氧化还原反应中，非金属单质不一定是氧化剂( )2．某元素从游离态变为化合态，则该元素一定被还原( )3．有单质参加或生成的化学反应不一定是氧化还原反应( )4．氧化还原反应中的反应物不是氧化剂就是还原剂( )5．氧化还原反应中有一种元素被氧化时，一定有另一种元素被还原( )答案　1.√　2.×　3.√　4.×　5.×元素化合价处于中间价态的物质既有氧化性，又有还原性。

高考化学第一轮复习全套资料第一部分：知识篇策略1化学基本概念的分析与判断金点子：化学基本概念较多，许多相近相似的概念容易混淆，且考查时试题的灵活性较大。

如何把握其实质，认识其规律及应用？主要在于要抓住问题的实质，掌握其分类方法及金属、非金属、酸、碱、盐、氧化物的相互关系和转化规律，是解决这类问题的基础。

经典题：例题1 ：（2001年全国高考）下列过程中，不涉及．．．化学变化的是（）A．甘油加水作护肤剂B．用明矾净化水C．烹鱼时加入少量的料酒和食醋可减少腥味，增加香味D．烧菜用过的铁锅，经放置常出现红棕色斑迹方法：从有无新物质生成，对题中选项分别进行分析。

捷径：充分利用物质的物理性质和化学性质，对四种物质的应用及现象进行剖析知：甘油用作护肤剂是利用了甘油的吸水性，不涉及化学变化。

明矾净化水，是利用了Al3+水解产生的Al(OH)3胶体的吸附作用；烹鱼时加入少量的料酒和食醋可减少腥味，增加香味，是两者部分发生了酯化反应之故；烧菜用过的铁锅，经放置出现红棕色斑迹，属铁的吸氧腐蚀。

此三者均为化学变化。

故选A。

总结：对物质性质进行分析，从而找出有无新物质生成，是解答此类试题的关键。

例题2 ：（1996年上海高考）下列电子式书写错误的是( ).方法：从化合物(离子化合物、共价化合物)—→原子的电子式—→得失电子—→化合物或原子团电子式，对题中选项逐一分析的。

捷径：根据上述方法，分析CO2分子中电子总数少于原子中的电子总数，故A选项错。

B项中N与N 之间为三键，且等于原子的电子总数，故B正确。

C有一个负电荷，为从外界得到一个电子，正确。

D为离子化合物，存在一个非极性共价键，正确。

以此得正确选项为A。

总结：电子式的书写是中学化学用语中的重点内容。

此类试题要求考生从原子的电子式及形成化合物时电子的得失与偏移进行分析而获解。

例题3 ：（1996年上海高考）下列物质有固定元素组成的是( )A．空气B．石蜡C．氨水D．二氧化氮气体方法：从纯净物与混合物进行分析。

题型六有机化学基础(选考) 1.(2018·大连市高三一模)聚对苯二甲酸乙二醇酯(PET俗称涤纶树脂，是一种重要的有机高分子材料。

其结构为。

利用有机物A合成PET的路线如下图所示：已知：根据题意回答下列问题：(1)B的化学名称是________________，C所含官能团的名称是________。

(2)由1,3­丁二烯可制备顺式聚1,3­丁二烯，写出顺式聚1,3­丁二烯的结构简式：________________________________________________________________________。

(3)A→D、B→C的反应类型分别为______________、____________。

(4)写出C＋F―→PET的化学反应方程式：__________________________________________ ________________________________________________________________________。

(5)G是F的同系物，其相对分子质量比F多28，G的核磁共振氢谱有三组峰，峰面积比为3∶1∶1，则符合该条件的G的同分异构体共有________种，写出其中一种结构简式________________________________________________________________________________________________________________________________________________。

(6)参照上述合成路线，以1,3­丁二烯为原料(无机试剂任选)，设计制备丁苯橡胶()答案(1) 1,2­二溴乙烷羟基(2)(3)加成反应取代反应催化剂(4)(5)4、、、(任写其中一种即可)(6)解析根据PET()的结构简式可知，由单体对苯二甲酸和乙二醇发生缩聚反应而得，根据结构流程中结构可知，C为乙二醇，F为对苯二甲酸；A为乙烯，乙烯与溴发生加成反应生成B为1,2­二溴乙烷；1,2­二溴乙烷在氢氧化钠的水溶液中加热发生取代反应生成乙二醇；乙烯与加热反应生成D为，催化得到二甲苯，二甲苯被酸性高锰酸钾氧化生成对苯二甲酸。

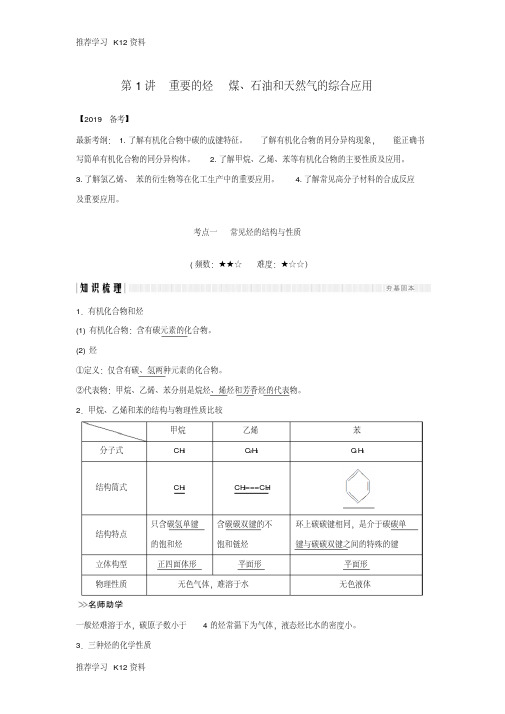
第1讲重要的烃煤、石油和天然气的综合应用【2019·备考】最新考纲：1.了解有机化合物中碳的成键特征。

了解有机化合物的同分异构现象，能正确书写简单有机化合物的同分异构体。

2.了解甲烷、乙烯、苯等有机化合物的主要性质及应用。

3.了解氯乙烯、苯的衍生物等在化工生产中的重要应用。

4.了解常见高分子材料的合成反应及重要应用。

考点一常见烃的结构与性质(频数：★★☆难度：★☆☆）1．有机化合物和烃(1)有机化合物：含有碳元素的化合物。

(2)烃①定义：仅含有碳、氢两种元素的化合物。

②代表物：甲烷、乙烯、苯分别是烷烃、烯烃和芳香烃的代表物。

2．甲烷、乙烯和苯的结构与物理性质比较甲烷乙烯苯分子式CH4C2H4C6H6结构简式CH4CH2===CH2结构特点只含碳氢单键的饱和烃含碳碳双键的不饱和链烃环上碳碳键相同，是介于碳碳单键与碳碳双键之间的特殊的键立体构型正四面体形平面形平面形物理性质无色气体，难溶于水无色液体一般烃难溶于水，碳原子数小于4的烃常温下为气体，液态烃比水的密度小。

3．三种烃的化学性质(1)甲烷(CH 4)①稳定性：与强酸、强碱和强氧化剂等一般不发生化学反应。

②燃烧反应：化学方程式为CH 4＋2O 2――→点燃CO 2＋2H 2O(产生淡蓝色火焰)。

③取代反应：在光照条件下与Cl 2发生取代反应，第一步反应的方程式为CH 4＋Cl 2――→光照CH3Cl ＋HCl ，继续反应依次又生成了CH 2Cl 2、CHCl 3、CCl 4。

(2)乙烯(CH 2===CH 2) 完成下列方程式：①燃烧反应：CH 2===CH 2＋3O 2――→点燃2CO 2＋2H 2O 。

(火焰明亮且伴有黑烟)(3)苯(C 6H 6)完成下列方程式：。

考点二铁盐和亚铁盐李仕才1．亚铁盐含有Fe2＋的溶液呈浅绿色，既有氧化性，又有还原性。

(1)氧化性：Fe2＋与Zn反应的离子方程式：Zn＋Fe2＋===Fe＋Zn2＋。

(2)还原性：Fe2＋与Cl2反应的离子方程式：2Fe2＋＋Cl2===2Fe3＋＋2Cl－。

(3)特性：含有Fe2＋的盐溶液遇K3[Fe(CN)6]溶液生成蓝色沉淀。

2．铁盐含Fe3＋的溶液呈黄色，Fe3＋具有较强的氧化性。

(1)氧化性：①Fe3＋与Cu反应的离子方程式：2Fe3＋＋Cu===Cu2＋＋2Fe2＋。

②Fe3＋与I－反应的离子方程式：2Fe3＋＋2I－===2Fe2＋＋I2。

(2)特性：含有Fe3＋的盐溶液遇KSCN溶液变成红色。

(3)Fe2＋与Fe3＋的相互转化用离子方程式实现下列转化：①Cl2、②NO－3、H＋、③H2O2、H＋、④MnO－4、H＋Fe3＋Fe2＋⑤Fe、⑥Cu、⑦H2S①2Fe2＋＋Cl2===2Fe3＋＋2Cl－；②3Fe2＋＋4H＋＋NO－3===3Fe3＋＋2H2O＋NO↑；③2Fe2＋＋H2O2＋2H＋===2Fe3＋＋2H2O；④5Fe2＋＋MnO－4＋8H＋===5Fe3＋＋Mn2＋＋4H2O；⑤2Fe3＋＋Fe===3Fe2＋；⑥Cu＋2Fe3＋===Cu2＋＋2Fe2＋；⑦2Fe 3＋＋H 2S===2Fe 2＋＋S↓＋2H ＋。

3．Fe 3＋、Fe 2＋的检验 (1)Fe 3＋的检验方法一：取出少量被检验的溶液于试管中，滴加KSCN 溶液，溶液变红色，证明有Fe 3＋存在。

方法二：取出少量被检验的溶液于试管中，加入NaOH 溶液，产生红褐色沉淀，证明有Fe 3＋存在。

(2)Fe 2＋的检验方法一：取出少量被检验的溶液于试管中，滴加KSCN 溶液，无现象，再滴加氯水，若变成红色(或血红色)溶液，说明有Fe 2＋存在(鉴别时不能先滴加氯水)。

2Fe 2＋＋Cl 2===2Fe 3＋＋2Cl －， Fe 3＋＋3SCN－3(红色或血红色)。

2019年高考第化学一轮复习同步训练（含答案）化学是自然科学的一种，以下是2019年高考第化学一轮复习同步训练，请考生刚好练习。

一、选择题(本题包括10小题,每小题6分,共60分)1.(2019成都模拟)下列说法正确的是 ()①试验室保存FeCl3溶液应加少量稀盐酸,并且放入少量的铁粉②氢氧化钠溶液保存在配有橡胶塞的细口瓶中③向溶液中滴入氯化钡溶液,再加稀硝酸能检验溶液中是否含有S④用丁达尔效应可以区分食盐水和淀粉溶液⑤工业上可用金属铝与V2O5在高温下冶炼矾,铝作还原剂A.②④⑤B.①②⑤C.①②④D.②③④2.化学试验中常将某些溶液或试剂进行酸化或碱化。

下列处理中正确的是A.检验KClO3中的氯元素,可加入AgNO3和稀硝酸B.为提高KMnO4溶液的氧化实力,用浓盐酸将KMnO4溶液酸化C.检验蔗糖在稀硫酸中水解产生的葡萄糖,应先用NaOH溶液碱化后才能进一步检验D.检验溶液中是否含有S时,先加氯化钡溶液,再加稀盐酸酸化3.(2019太原模拟)下列试验可行的是 ()A.加入适量铜粉除去Cu(NO3)2溶液中的AgNO3杂质B.用NaOH溶液除去CO2中混有的HCl气体C.用浓硫酸与蛋白质的颜色反应鉴别部分蛋白质D.用乙醇从碘水中萃取碘4.如图表示从固体混合物中分别X的两种方案,请依据方案1和方案2指出下列说法合理的是 ()方案1方案2A.可以选用方案1分别碳酸氢钠中含有的氯化铵B.方案1中残留物应当具有的性质是受热易挥发C.方案2中加入的试剂确定能够与除X外的物质发生化学反应D.方案2中加入NaOH溶液可以分别出SiO2和Fe2O3混合物中的Fe2O35.某同学想用试验证明高锰酸钾的紫红色是Mn的颜色,而不是K+的颜色,他设计了以下试验方案。

请你推断下列方案与本试验目的无关的是 ()A.视察氯化钾溶液没有颜色,表明溶液中的K+无色B.在氯化钾溶液中加入适量锌粉振荡,静置后未见明显变更,表明锌与K+不反应C.在高锰酸钾溶液中加入适量锌粉、振荡、静置后紫红色褪去,表明Mn为紫红色D.将高锰酸钾晶体加热分解,所得的固体质量减轻6.大胆、科学的假设与猜想是科学探究的先导和价值所在。

课时2 物质的量浓度及其溶液的配制一、选择题1．用已准确称量过的氢氧化钠固体配制0.20 mol·L－1的氢氧化钠溶液250 mL，要用到的仪器是()①250 mL容量瓶②托盘天平③烧瓶④胶头滴管⑤烧杯⑥玻璃棒⑦试管⑧药匙A．①④⑤⑥B．①②④⑤C．①②④⑤⑥⑧D．全部解析由于只需要进行溶解、转移、洗涤和定容操作，故需用的仪器只是①④⑤⑥。

答案 A2．(2017·洛阳模拟)下列溶液中Cl－的物质的量浓度最大的是() A．200 mL 2.5 mol·L－1MgCl2溶液B．1 000 mL 2.5 mol·L－1NaCl溶液C．250 mL 1 mol·L－1AlCl3溶液D．300 mL 5 mol·L－1KClO3溶液答案 A3．下列溶液中，溶质的物质的量浓度不是1 mol·L－1的是() A．10 g NaOH固体溶解在水中配成250 mL溶液B．将80 g SO3溶于水并配成1 L的溶液C．将0.5 mol·L－1的NaNO3溶液100 mL加热蒸发掉50 g水的溶液D．标况下，将22.4 L氯化氢气体溶于水配成1 L溶液解析A项，c(NaOH)＝10 g40 g·mol－10.25 L＝1 mol·L－1；B项，c(H2SO4)＝80 g80 g·mol－11 L＝1 mol·L－1；C项，蒸发掉50 g水后，溶液的体积并不是50 mL，NaNO3的浓度也不是1 mol·L－1；D项，c(HCl)＝22.4 L22.4 L·mol－11 L＝1 mol·L－1。

答案 C4．下列叙述正确的是()A．将5.85 g NaCl晶体溶入100 mL水中，制得1 mol·L－1NaCl溶液B．将1体积c mol·L－1硫酸用水稀释为5体积，得到0.2c mol·L－1硫酸C．将25 g无水CuSO4溶于水配制成100 mL溶液，其浓度为1 mol·L－1D．将w g a% NaCl溶液蒸发掉w/2 g水，得到4a% NaCl溶液解析A项，NaCl溶于水后，溶液的体积大于100 mL，所得溶液中c(NaCl)小于1 mol·L－1；C项，CuSO4的物质的量大于0.1 mol，则c(CuSO4)大于1 mol·L －1；D项，若不析出晶体，得到的是2a%的NaCl溶液。

届步步高大一轮复习讲义_化学人教版第1 讲物质的组成、性质和分类【考纲要求】1.了解分类法在化学科学研究和化学学习中的重要作用，能根据物质的组成和性质对物质进行分类。

2.了解分散系的概念、分类方法，掌握胶体的概念、重要性质及应用，掌握Fe(OH)3胶体的制备方法。

3.理解混合物和纯净物、单质和化合物的概念，理解酸、碱、盐、氧化物的概念及其相互关系。

重难点：物质的分类和胶体的性质。

知识梳理探究高考练出高分知识梳理题型构建考点一物质的组成考点二物质的分类物质的组成、性质和分类考点三物质的性质与变化考点四分散系、胶体知识梳理探究高考练出高分知识梳理题型构建I考点一物质的组成不同单质叫同素异形体。

同种元素形成的_________由几种不同的单质或化合物组成的物质混合物和纯净物探究高考由同种单质或化合物组成的物质。

知识梳理练出高分知识梳理题型构建【递进题组】题组一1 2题组二345知识梳理探究高考练出高分知识梳理题型构建题组一12题组二345在化学变化中复合离子+ 如NH 4等可以再分题组一组成物质的微粒1.判断下列说法是否正确？若不正确,说出理由。

①元素在自然界中的存在形式有原子、分子或离子。

②在化学变化中，分子可以再分，离子和原子不可以再分。

③同一种元素可能有多种不同原子，同一种原子也可能形成不同的离子。

④原子与该原子形成的离子相对质量几乎相等。

⑤由同一种元素组成的物质一定是同一种物质。

⑥物质的化学性质一定是由分子保持的。

⑦质子数、中子数和电子数都相同的粒子一定是同一种粒子。

金刚石、石墨均是由C 元素组成,但不是同一种物质，互为同素异形体如Fe是由原子构成的；化学性质由铁原子保持如N2和CO知识梳理探究高考练出高分知识梳理题型构建题组一12题组二3452.下列各组物质能真实表示物质分子组成的是 A . NO、C2H5OH、HNO3、I2 B . CaO、N2、HCl、H2O C. NH3、H2S、Si、CO ( A )CaO是离子化合物，不存在分子D. CO2、SiO2、__、H2SO4Si和SiO2都是由原子直接构成。

【大高考】2017版高考数学一轮总复习第7章不等式、推理与证明第五节推理与证明AB卷文新人教A版1.(2016·新课标全国Ⅲ，4)某旅游城市为向游客介绍本地的气温情况，绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15 ℃，B点表示四月的平均最低气温约为5 ℃.下面叙述不正确的是( )A.各月的平均最低气温都在0 ℃以上B.七月的平均温差比一月的平均温差大C.三月和十一月的平均最高气温基本相同D.平均最高气温高于20 ℃的月份有5个解析由题意知，平均最高气温高于20 ℃的六月，七月，八月，故选D.答案 D2.(2016·新课标全国Ⅱ，16)有三张卡片，分别写有1和2，1和3，2和3.甲，乙，丙三人各取走一张卡片，甲看了乙的卡片后说：“我与乙的卡片上相同的数字不是2”，乙看了丙的卡片后说：“我与丙的卡片上相同的数字不是1”，丙说：“我的卡片上的数字之和不是5”，则甲的卡片上的数字是________.解析由丙说：“我的卡片上的数字之和不是5”可知，丙为“1和2”或“1和3”，又乙说“我与丙的卡片上相同的数字不是1”，所以乙只可能为“2和3”，所以由甲说“我与乙的卡片上相同的数字不是2”，所以甲只能为“1和3”.答案1和33.(2014·课标Ⅰ，14)甲、乙、丙三位同学被问到是否去过A，B，C三个城市时，甲说：我去过的城市比乙多，但没去过B城市；乙说：我没去过C城市；丙说：我们三人去过同一城市.由此可判断乙去过的城市为________.解析根据甲和丙的回答推测乙没去过B城市，又知乙没去过C城市，故乙去过A城市. 答案A1.(2016·浙江，8)如图，点列{A n }，{B n }分别在某锐角的两边上，且|A n A n ＋1|＝|A n ＋1A n ＋2|，A n ≠A n ＋2，n ∈N *，|B n B n ＋1|＝|B n ＋1B n ＋2|，B n ≠B n＋2，n ∈N *(P ≠Q 表示点P 与Q 不重合).若d n ＝|A n B n |，S n 为△A n B n B n ＋1的面积，则( ) A.{S n }是等差数列 B.{S 2n }是等差数列C.{d n }是等差数列D.{d 2n }是等差数列解析 S n 表示点A n 到对面直线的距离(设为h n )乘以|B n B n －1|长度一半，即S n ＝12h n |B n B n －1|，由题目中条件可知|B n B n －1|的长度为定值，过A 1作垂直得到初始距离h 1，那么A 1，A n 和两个垂足构成等腰梯形，则h n ＝h 1＋|A 1A n |tan θ(其中θ为两条线所成的锐角，为定值)， 从而S n ＝12(h 1＋|A 1A n |tan θ)|B n B n ＋1|，S n ＋1＝12(h 1＋|A 1A n ＋1|)|B n B n ＋1|，则S n ＋1－S n ＝12|A n A n ＋1||B n B n ＋1|tan θ，都为定值，所以S n ＋1－S n 为定值，故选A. 答案 A2.(2016·山东，12)观察下列等式：⎝ ⎛⎭⎪⎫sin π3－2＋⎝⎛⎭⎪⎫sin 2π3－2＝43×1×2；⎝ ⎛⎭⎪⎫sin π5－2＋⎝ ⎛⎭⎪⎫sin 2π5－2＋⎝ ⎛⎭⎪⎫sin 3π5－2＋⎝ ⎛⎭⎪⎫sin 4π5－2＝43×2×3； ⎝ ⎛⎭⎪⎫sin π7－2＋⎝ ⎛⎭⎪⎫sin 2π7－2＋⎝ ⎛⎭⎪⎫sin 3π7－2＋…＋⎝ ⎛⎭⎪⎫sin 6π7－2＝43×3×4； ⎝ ⎛⎭⎪⎫sin π9－2＋⎝ ⎛⎭⎪⎫sin 2π9－2＋⎝ ⎛⎭⎪⎫sin 3π9－2＋…＋⎝⎛⎭⎪⎫sin 8π9－2＝43×4×5； ……照此规律，⎝ ⎛⎭⎪⎫sinπ2n ＋1－2＋⎝ ⎛⎭⎪⎫sin 2π2n ＋1－2＋⎝ ⎛⎭⎪⎫sin 3π2n ＋1－2＋…＋⎝ ⎛⎭⎪⎫sin 2n π2n ＋1－2＝________.解析 观察等式右边的规律：第1个数都是43，第2个数对应行数n ，第3个数为n ＋1.答案 43×n ×(n ＋1)3.(2015·陕西，16)观察下列等式 1－12＝121－12＋13－14＝13＋141－12＋13－14＋15－16＝14＋15＋16 ……据此规律，第n 个等式可为________.解析 等式左边的特征：第1个等式有2项，第2个有4项，第3个有6项，且正负交错，故第n 个等式左边有2n 项且正负交错，应为1－12＋13－14＋…＋12n －1－12n ；等式右边的特征：第1个有1项，第2个有2项，第3个有3项，故第n 个有n 项，且有前几个的规律不难发现第n 个等式右边应为1n ＋1＋1n ＋2＋…＋12n. 答案 1－12＋13－14＋…＋12n －1－12n ＝1n ＋1＋1n ＋2＋…＋12n4.(2013·陕西，13)观察下列等式 (1＋1)＝2×1(2＋1)(2＋2)＝22×1×3(3＋1)(3＋2)(3＋3)＝23×1×3×5 ……照此规律，第n 个等式可为____________________________________________. 解析 观察规律，等号左侧为(n ＋1)(n ＋2)…(n ＋n )，等号右侧分两部分，一部分是2n，另一部分是1×3×…×(2n －1).答案 (n ＋1)(n ＋2)…(n ＋n )＝2n×1×3×…×(2n －1)5.(2014·福建，16)已知集合{a ，b ，c }＝{0，1，2}，且下列三个关系：①a ≠2；②b ＝2；③c ≠0有且只有一个正确，则100a ＋10b ＋c 等于________.解析 可分下列三种情形：(1)若只有①正确，则a ≠2，b ≠2，c ＝0，所以a ＝b ＝1与集合元素的互异性相矛盾，所以只有①正确是不可能的；(2)若只有②正确，则b ＝2，a ＝2，c ＝0，这与集合元素的互异性相矛盾，所以只有②正确是不可能的；(3)若只有③正确，则c ≠0，a ＝2，b ≠2，所以b ＝0，c ＝1，所以100a ＋10b ＋c ＝100×2＋10×0＋1＝201. 答案 2016.(2014·山东，4)用反证法证明命题“设a ，b 为实数，则方程x 3＋ax ＋b ＝0至少有一个实根”时，要做的假设是( ) A.方程x 3＋ax ＋b ＝0没有实根 B.方程x 3＋ax ＋b ＝0至多有一个实根 C.方程x 3＋ax ＋b ＝0至多有两个实根 D.方程x 3＋ax ＋b ＝0恰好有两个实根解析 至少有一个实根的否定是没有实根，故做的假设是“方程x 3＋ax ＋b ＝0没有实根”. 答案 A7.(2016·浙江，20)设函数f (x )＝x 3＋11＋x，x ∈[0，1]，证明： (1)f (x )≥1－x ＋x 2； (2)34＜f (x )≤32. 证明 (1)因为1－x ＋x 2－x 3＝1－（－x ）41－（－x ）＝1－x 41＋x，由于x ∈[0，1]，有1－x 41＋x ≤1x ＋1，即1－x ＋x 2－x 3≤1x ＋1， 所以f (x )≥1－x ＋x 2.(2)由0≤x ≤1得x 3≤x ，故f (x )＝x 3＋1x ＋1≤x ＋1x ＋1＝x ＋1x ＋1－32＋32＝（x －1）（2x ＋1）2（x ＋1）＋32≤32，所以f (x )≤32.由(1)得f (x )≥1－x ＋x 2＝⎝ ⎛⎭⎪⎫x －122＋34≥34，又因为f ⎝ ⎛⎭⎪⎫12＝1924＞34，所以f (x )＞34.综上，34＜f (x )≤32.8.(2015·四川，21)已知函数f (x )＝－2x ln x ＋x 2－2ax ＋a 2，其中a >0. (1)设g (x )是f (x )的导函数，讨论g (x )的单调性；(2)证明：存在a ∈(0，1)，使得f (x )≥0恒成立，且f (x )＝0在区间(1，＋∞)内有唯一解.(1)解 由已知，函数f (x )的定义域为(0，＋∞)，g (x )＝f ′(x )＝2(x －1－ln x －a )，所以g ′(x )＝2－2x ＝2（x －1）x，当x ∈(0，1)时，g ′(x )＜0，g (x )单调递减； 当x ∈(1，＋∞)时，g ′(x )＞0，g (x )单调递增. (2)证明 由f ′(x )＝2(x －1－ln x －a )＝0， 解得a ＝x －1－ln x ，令φ(x )＝－2x ln x ＋x 2－2x (x －1－ln x )＋(x －1－ln x )2＝(1＋ln x )2－2x ln x ，则φ(1)＝1＞0，φ(e)＝2(2－e)＜0， 于是，存在x 0∈(1，e)，使得φ(x 0)＝0， 令a 0＝x 0－1－ln x 0＝u (x 0)， 其中u (x )＝x －1－ln x (x ≥1)， 由u ′(x )＝1－1x≥0知，函数u (x )在区间(1，＋∞)上单调递增， 故0＝u (1)＜a 0＝u (x 0)＜u (e)＝e －2＜1， 即a 0∈(0，1)，当a ＝a 0时，有f ′(x 0)＝0，f (x 0)＝φ(x 0)＝0， 再由(1)知，f ′(x )在区间(1，＋∞)上单调递增， 当x ∈(1，x 0)时，f ′(x )＜0， 从而f (x )＞f (x 0)＝0；当x ∈(x 0，＋∞)时，f ′(x )＞0， 从而f (x )＞f (x 0)＝0；又当x ∈(0，1]时，f (x )＝(x －a 0)2－2x ln x ＞0， 故x ∈(0，＋∞)时，f (x )≥0，综上所述，存在a ∈(0，1)，使得f (x )≥0恒成立，且f (x )＝0在区间(1，＋∞)内有唯一解.9.(2015·江苏，20)设a 1，a 2，a 3，a 4是各项为正数且公差为d (d ≠0)的等差数列. (1)证明：2a 1，2a 2，2a 3，2a 4依次构成等比数列；(2)是否存在a 1，d ，使得a 1，a 22，a 33，a 44依次构成等比数列？并说明理由； (3)是否存在a 1，d 及正整数n ，k ，使得a n 1，a n ＋k 2，a n ＋2k3，a n ＋3k4依次构成等比数列？并说明理由.(1)证明 因为2a n ＋12a n ＝2a n ＋1－a n ＝2d(n ＝1，2，3)是同一个常数，所以2a 1，2a 2，2a 3，2a 4依次构成等比数列，(2)解 令a 1＋d ＝a ，则a 1，a 2，a 3，a 4分别为a －d ，a ，a ＋d ，a ＋2d (a ＞d ，a ＞－2d ，d ≠0).假设存在a 1，d ，使得a 1，a 22，a 33，a 44依次构成等比数列， 则a 4＝(a －d )(a ＋d )3，且(a ＋d )6＝a 2(a ＋2d )4.令t ＝d a ，则1＝(1－t )(1＋t )3，且(1＋t )6＝(1＋2t )4⎝ ⎛⎭⎪⎫－12＜t ＜1，t ≠0，化简得t 3＋2t 2－2＝0(*)，且t 2＝t ＋1. 将t 2＝t ＋1代入(*)式，t (t ＋1)＋2(t ＋1)－2＝t 2＋3t ＝t ＋1＋3t ＝4t ＋1＝0，则t ＝－14.显然t ＝－14不是上面方程的解，矛盾，所以假设不成立.因此不存在a 1，d ，使得a 1，a 22，a 33，a 44依次构成等比数列. (3)解 假设存在a 1，d 及正整数n ，k ，使得a n1，a n ＋k2，a n ＋2k3，a n ＋3k4依次构成等比数列，则a n1(a 1＋2d )n ＋2k＝(a 1＋d )2(n ＋k )，且(a 1＋d )n ＋k(a 1＋3d )n ＋3k＝(a 1＋2d )2(n ＋2k ).分别在两个等式的两边同除以a 2（n ＋k ）1及a 2（n ＋2k ）1，并令t ＝d a 1⎝ ⎛⎭⎪⎫t ＞－13，t ≠0， 则(1＋2t )n ＋2k＝(1＋t )2(n ＋k )，且(1＋t )n ＋k(1＋3t )n ＋3k＝(1＋2t )2(n ＋2k ).将上述两个等式两边取对数，得(n ＋2k )ln(1＋2t )＝2(n ＋k )ln(1＋t )， 且(n ＋k )ln(1＋t )＋(n ＋3k )ln(1＋3t )＝2(n ＋2k )ln(1＋2t ).化简得2k [ln(1＋2t )－ln(1＋t )] ＝n [2ln(1＋t )－ln(1＋2t )]，且3k [ln(1＋3t )－ln(1＋t )]＝n [3ln(1＋t )－ln(1＋3t )]. 再将这两式相除，化简得ln(1＋3t )ln(1＋2t )＋3ln(1＋2t )ln(1＋t ) ＝4ln(1＋3t )ln(1＋t )(**).令g (t )＝4ln(1＋3t )ln(1＋t )－ln(1＋3t )ln(1＋2t )－3ln(1＋2t )ln(1＋t )， 则g ′(t )＝2[（1＋3t ）2ln （1＋3t ）－3（1＋2t ）2ln （1＋2t ）＋3（1＋t ）2ln （1＋t ）]（1＋t ）（1＋2t ）（1＋3t ）.令φ(t )＝(1＋3t )2ln(1＋3t )－3(1＋2t )2ln(1＋2t )＋3(1＋t )2ln(1＋t )， 则φ′(t )＝6[(1＋3t )ln(1＋3t )－2(1＋2t )ln(1＋2t )＋(1＋t )ln(1＋t )]. 令φ1(t )＝φ′(t )，则φ1′(t )＝6[3ln(1＋3t )－4ln(1＋2t )＋ln(1＋t )]. 令φ2(t )＝φ1′(t )，则φ2′(t )＝12（1＋t ）（1＋2t ）（1＋3t ）＞0.由g (0)＝φ(0)＝φ1(0)＝φ2(0)＝0， φ′2(t )＞0，知φ2(t )，φ1(t )，φ(t )，g (t )在⎝ ⎛⎭⎪⎫－13，0和(0，＋∞)上均单调. 故g (t )只有唯一零点t ＝0，即方程(**)只有唯一解t ＝0，故假设不成立. 所以不存在a 1，d 及正整数n ，k ，使得a n1，a n ＋k2，a n ＋2k3，a n ＋3k4依次构成等比数列.10.(2014·天津，20)已知q 和n 均为给定的大于1的自然数.设集合M ＝{0，1，2，…，q －1}，集合A ＝{x |x ＝x 1＋x 2q ＋…＋x n qn －1，x i ∈M ，i ＝1，2，…，n }.(1)当q ＝2，n ＝3时，用列举法表示集合A ； (2)设s ，t ∈A ，s ＝a 1＋a 2q ＋…＋a n qn －1，t ＝b 1＋b 2q ＋…＋b n qn －1，其中a i ，b i ∈M ，i ＝1，2，…，n .证明：若a n ＜b n ，则s ＜t .(1)解 当q ＝2，n ＝3时，M ＝{0，1}，A ＝{x |x ＝x 1＋x 2·2＋x 3·22，x i ∈M ，i ＝1，2，3}.可得，A ＝{0，1，2，3，4，5，6，7}. (2)证明 由s ，t ∈A ，s ＝a 1＋a 2q ＋…＋a n qn －1，t ＝b 1＋b 2q ＋…＋b n qn －1，a i ，b i ∈M ，i ＝1，2，…，n 及a n <b n ，可得s －t ＝(a 1－b 1)＋(a 2－b 2)q ＋…＋(a n －1－b n －1)q n －2＋(a n －b n )qn －1≤(q －1)＋(q －1)q ＋…＋(q －1)qn －2－qn －1＝（q －1）（1－q n －1）1－q－q n －1＝－1<0.所以，s <t .。