3.3垂径定理1((浙教版2014))

《3・3垂径定理》♦教材分析本节是《圆》这一章的重要内容，也是本章的基础。

它揭示了垂直于弦的直径和这条弦及这条弦所对的弧Z间的内在关系，是圆的轴对称性的具体化；也是今后证明线段相等、角相等、弧相等、垂直关系的重要依据；同时也为进行圆的有关计算和作图提供了方法和依据；由垂径定理的得出，使学生的认识从感性到理性，从具体到抽象，有助于培养学生思维的严谨性。

同时，通过本节课的教学，对学生渗透类比、转化、数形结合、方程、建模等数学思想和方法，培养学生实验、观察、猜想、抽象、概括、推理等逻辑思维能力和识图能力。

所以它在教材屮处于非常重要的位置。

【知识与能力目标】1.通过实验观察，讣学生理解圆的轴対称性；2.学握垂径定理，理解其探索和证明过程；3.能初步运用垂径定理解决有关的计算和证明问题.【过程与方法目标】在研究过程屮，进一步体验“实验一归纳一猜想一证明”的方法；在解题过程中，注重发散思维的培养，同一个问题会从不同的角度去分析解决.【情感态度价值观目标】通过圆的对称性，培养学生对数学的审美观，并激发学生对数学的热爱.【教学重点】使学生掌握垂径定理、记住垂径定理的题设和结论.【教学难点】对垂径定理的探索和证明，在解决问题时想到用垂径定理.教师准备：圆规，三角尺，PPT课件，多媒体学生准备：圆规，三角尺，练习本♦教学过程一、温故知新1、我们所学的圆是不是轴对称图形呢？2、我们所学的圆是不是中心对称图形呢?思考：活动：探究圆的轴对称性•如图（1）,若将OO沿直径AB对折，观察两部分是否重合? 让学生用自己進备好的圆形纸片亲自实验，教师引导学生努力发现：1.圆是轴对称图形，过圆心的任意一条直线（或直径所在的直线）都是它的对称轴.2.如图，仞是（DO的一条弦，做直径使CD LAB,垂足为£（1）这个图形是轴对称图形吗？如果是，它的对称轴是什么？（2）你能发现图中有那些相等的线段和弧？为什么？3、引入新知：如图（2）,左图中AB 是的弦，直径CQ 与弦AB 相交，那么沿直径 CD 所在的直线折叠之后，图形可以重合吗？右图中，是O0的弦，直径CD 丄AB,垂足 为E 此时再沿直径CD 所在直线折輕，图形可以重合吗？（重合，说明此图也是轴对称图 形，称这种处于特殊位置的直径称为垂直于弦的直径），引出本节课研究的内容.猜想，证明，形成垂径定理1、 提问：继续观察图（2）的右图，根据圆的对称性，把圆沿直径CD 所在的直线折叠 之后，圆中的线段和弧会出现怎样的位置关系？同时出现怎样的数量关系？2、 猜想：可能出现的位置关系是：线段AE 和线段BE 重合，弧4C 和弧重合，弧AD 和弧3D 重合.可能出现的数量关系是：AE = BE, AC = BC, AD = BD3、证明：利用等腰三角形三线合一的性质或者三角形全等的知识来证明线段AE 与线段BD 相等, 利用圆的对称性证明对应弧相等•板书：4、引导学生归纳总结垂径定理的文字表述，板书：垂直于眩的直径平分眩，并且平分眩所对的两条弧.（二）分析垂径定理的条件和结论1、 再次明确垂径定理的条件和结论加深学生的印象.2、 利用反例、变式图形对定理进一步引中，揭示定理的本质属性，以加深学生对定理 CD 是圆0的直径1 CD 丄AB,垂足为E ） AE = BD AC = BC AD=BD c本质的了解.练习：在下列图形中，能使用垂径定理的图形有哪些?3、引申定理：定理中垂直于弦的直径可以是直径、半径，也可以是过圆心的直线或线段.(三)例题例1已知：如图(3),在＜30中，弦A3的长为8cm,圆心。

知识提要1．圆是轴对称图形，每一条过圆心的直线都是圆的对称轴．2．垂直于弦的直径平分这条弦，并且平分弦所对的弧．注：用垂径定理进行计算或证明时，常常连结半径或作出弦心距，构造直角三角形求解．3．平分弦(不是直径)的直径垂直于弦，并且平分弦所对的弧．4．平分弧的直径垂直平分弧所对的弦．(见了弧的中点常连结圆心，如第13题)5．垂径定理解读：(1)过圆心；(2)平分弦(不是直径)；(3)垂直于弦；(4)平分弦所对的优弧；(5)平分弦所对的劣弧．若一条直线具备这五项中任意两项，则必具备另外三项．例1：[2017·眉山]如图，AB 是⊙O 的弦，半径OC ⊥AB 于点D ，且AB ＝8 cm ，DC ＝2 cm ，则OC ＝__5__cm.【解析】 如答图，连结OA ，∵OC ⊥AB ，∴AD ＝12AB ＝4 cm ，设⊙O 的半径为R ， 由勾股定理，得OA 2＝AD 2＋OD 2，∴R 2＝42＋(R －2)2，解得R ＝5，∴OC ＝5 cm.例2：如图，AB 为⊙O 的直径，弦CD ⊥AB 于点E ，连结AC ，AD ，△ACD 是边长为23的等边三角形，则⊙O 的半径为__2__．【解析】 如答图，连结OC ，∵AB 是⊙O 的直径，CD ⊥AB ，∴CE ＝12CD ， ∵AC ＝CD ＝23，∴CE ＝3，∴AE ＝AC 2－CE 2＝（23）2－（3）2＝3.例题分析垂径定理设⊙O 的半径为r ，则OC ＝r ，∴OE ＝AE －AO ＝3－r ，在Rt △OCE 中，由勾股定理得OE 2＋CE 2＝OC 2，∴(3－r )2＋(3)2＝r 2，解得r ＝2， ∴⊙O 的半径为2.例3：如图，⊙O 的直径为10 cm ，弦AB ＝8 cm ，P 是弦AB 上的一个动点，求OP 的长度范围．解：如答图，过点O 作OE ⊥AB 于点E ，连结OB .∵AB ＝8 cm ，∴AE ＝BE ＝12AB ＝12×8＝4(cm)． ∵⊙O 的直径为10 cm ，∴OB ＝12×10＝5(cm)，∴OE ＝OB 2－BE 2＝52－42＝3(cm)． ∵垂线段最短，半径最长，∴3 cm≤OP ≤5 cm.一、选择题1．下列命题正确的是( C )①垂直于弦的直径平分弦；②平分弦的直径必垂直于弦，并且平分弦所对的两条弧； ③平分弦的直线必过圆心；④弦所对的两条弧的中点连线垂直平分弦；A ．①②B ．①③C ．①④D ．②③2. 如图，已知⊙O 的半径为2cm ，弦AB 长23cm ，则这条弦的中点C 到弦所对劣弧的中点D 的距离为( A)A ．1cmB ．2cm C.2cm D.3cm3. 如图，⊙O 的半径是3，P 是弦AB 的延长线上一点，连结OP .若OP ＝4，∠APO ＝30°，则弦AB 的长为( A)A ．25 B.5 C ．213 D.134. 如图，如果AB 为⊙O 的直径，弦CD ⊥AB ，垂足为E ，那么下列结论错误的是( D)A ．CE ＝ED B.BC ︵＝BD ︵ C ．∠BAC ＝∠BAD D ．OE ＝BE5. 如图，将半径为2cm 的圆形纸片折叠后，圆弧恰好经过圆心O ，则折痕AB 的长为(C)A ．2cm B.3cm C ．23cm D ．25cm同步练习6. [18 ·张家界]如图AB 是⊙O 的直径，弦CD ⊥AB 于点E ，OC ＝5 cm ，CD ＝8 cm 则AE ＝(A)A ．8 cmB ．5 cmC ．3 cmD ．2 cm【解析】A ∵弦CD ⊥AB 于点E ，CD ＝8 cm ，∴CE ＝12CD ＝4 cm ，又∵OC ＝5 cm ， ∴在Rt △COE 中，OE ＝OC 2－CE 2＝52－42＝3 cm ，∴AE ＝OA ＋OE ＝5＋3＝8 cm.7. [2018·衢州]如图，AC 是⊙O 的直径，弦BD ⊥AO 于E ，连结BC ，过点O 作OF ⊥BC 于F ，若BD ＝8 cm ，AE ＝2 cm ，则OF 的长度是( D )A ．3 cm B. 6 cm C ．2.5 cm D. 5 cm【解析】D 如答图，连结AB ，∵AC ⊥BD ，∴BE ＝ED ＝8÷2＝4，∵AE ＝2，根据勾股定理可得AB ＝25，又∵OF ⊥BC ，根据垂径定理可知BF ＝CF ，故可得知OF 为△ABC 的中位线，∴OF ＝12AB ＝ 5. 8. (甘南州中考)⊙O 过点B ，C ，圆心O 在等腰直角三角形ABC 内部，∠BAC ＝90°，OA ＝1，BC ＝6，则⊙O 的半径为( C )A.10 B ．23 C.13 D ．3 2【解】C 过点A 作AD ⊥BC 于点D ，由题意，可知AD 必过点O ，连结OB ，如解图． ∵△BAC 是等腰直角三角形，AD ⊥BC ，∴AD ＝BD ＝CD ＝3，∴OD ＝AD －OA ＝2. 在Rt △OBD 中，根据勾股定理，得OB ＝BD 2＋OD 2＝13.9. 已知⊙O 的半径OA ＝1，弦AB ，AC 的长分别是2，3，则∠BAC 的度数为( D )A ．15°B ．60°C ．75°D ．15°或75°【解】D 如解图①，过圆心O 作OM ⊥AB 于点M ，ON ⊥AC 于点N ，连结OA .∵AM ＝12AB＝22，OA ＝1，∴OM ＝22.∴AM ＝MO ，∴∠BAO ＝45°.同理，∠CAO ＝30°.∴∠BAC ＝15°. 如解图②.同理可知∠BAC ＝75°.综上所述，∠BAC 的度数是15°或75°.10．如图，在半径为5的⊙O 中，AB ，CD 是互相垂直的两条弦，垂足为P ，且AB ＝CD ＝8，则OP 的长为( C )A ．3B ．4C ．3 2D ．4 2【解析】C 如答图，过点O 作OM ⊥AB 于点M ，ON ⊥CD 于点N ，连结OB ，OD . 由垂径定理、勾股定理，得OM ＝ON ＝52－42＝3.∵弦AB ，CD 互相垂直，∴∠DPB ＝90°.∵OM ⊥AB ，ON ⊥CD ，∴∠OMP ＝∠ONP ＝90°， ∴四边形MONP 是矩形，∵OM ＝ON ，∴四边形MONP 是正方形，∴OP ＝2OM ＝3 2.二、填空题1. 已知在⊙O 中，直径AB 垂直于弦CD 于点E ，AB 被CD 分成长度分别为5 cm 和13 cm 的两段，则圆心O 到CD 的距离为4cm.2. 如图，M 是CD 的中点，EM 过圆心O .若CD ＝4，EM ＝8，则CED ︵所在圆的半径为174．3. 如图，在平面直角坐标系中，O 为坐标原点，点P 在第一象限，⊙P 与x 轴交于O ，A 两点，点A 的坐标为(6，0)，⊙P 的半径为13，则点P 的坐标为__(3，2)__．【解析】 如答图，过点P 作PD ⊥x 轴于点D ，连结OP .∵A (6，0)，PD ⊥OA ，∴OD ＝12OA ＝3.∵OP ＝13，OD ＝3，∴PD ＝OP 2－OD 2＝ （13）2－32＝2，∴点P 的坐标为(3，2)．4. 如图所示，某游乐场的摩天轮⊙P 的最高处A 到地面l 的距离是23m ，最低处B 到地面l 的距离是3m ，从B 处乘摩天轮绕一周需3分钟，小明从B 处乘摩天轮一周的过程中，当他到地面l 的距离恰好是18m 的时候应为第__1或2________分钟．5. 已知半径为2的⊙O 有两条互相垂直的弦AB 和CD ，其交点E 到圆心O 的距离为1，则AB 2＋CD 2＝__28 ______．6. 把球放在长方体纸盒内，球的一部分露在盒外，其截面如图所示，已知EF ＝CD ＝16 cm ，则球的半径为10cm.【解】 设圆心为O ，过点O 作OH ⊥EF 于点H ，延长HO 交BC 于点I ，连结OE ，设⊙O的半径为r (cm)．易知HI ＝CD ＝16，∴OH ＝16－r .易知EH ＝12EF ＝8，OE ＝r ， ∴由勾股定理，得r 2＝82＋(16－r )2，解得r ＝10(cm)．三、解答题1. 如图，⊙O 的直径AB 与弦CD 相交于E ，已知AE ＝1cm ，BE ＝5cm ，∠DEB ＝30°，求：(1)CD 的弦心距OF 的长；(2)弦CD 的长．解：(1)∵BO ＝12(AE ＋BE)＝12(1＋5)＝3，∴OE ＝3－1＝2，在Rt △EFO 中，∵∠OEF ＝30°，∴OF ＝1，即CD 的弦心距OF 为1cm ；(2)连结OD ，如图，在Rt △DFO 中，OD ＝3，∴DF ＝OD 2－OF 2＝32－12＝22，∵OF ⊥CD ，∴CD ＝2DF ＝42，∴CD 的长为42cm .2. 已知：如图，A 、B 、C 为⊙O 上三点，点D 、E 分别为AB ︵、AC ︵的中点，连结DE ，分别交AB 、AC 于点F 、G ，求证：AF ＝AG .解：连OD 、OE ，交AB 、AC 于M 、N ，∵OD ＝OE ＝r ，∴∠ODE ＝∠OED ，而D ，E 分别为弧AB ，弧AC 的中点，∴OD 、OE 分别垂直于AB 、AC ，则有∠DFB ＝∠EGC ，∴∠AFG ＝∠AGF ，∴AF ＝AG .3. 如图，射线PG 平分∠EPF ，O 为射线PG 上的一点，以O 为圆心，10为半径作⊙O ，分别与∠EPF 两边相交于点A ，B 和点C ，D ，连结OA ，此时有OA ∥PE.(1)求证：AP ＝AO ；(2)若弦AB ＝12，求OP 的长．解：(1)证明：∵PG 平分∠EPF ，∴∠DPO ＝∠BPO.∵OA ∥PE ，∴∠DPO ＝∠POA ，∴∠BPO＝∠POA ，∴AP ＝AO.(2)如图，过点O 作OH ⊥AB 于点H ，则AH ＝HB.∵AB ＝12，∴AH ＝6.由(1)可知PA ＝OA ＝10，∴PH ＝PA ＋AH ＝16.在Rt △OAH 中，OH ＝OA 2－AH 2＝102－62＝8，∴OP ＝PH 2＋OH 2＝8 5.4. 如图，⊙O 的直径AB 和弦CD 交于点E ，已知AE ＝6 cm ，EB ＝2 cm ，∠CEA ＝30°，求CD 的长．【解】 过点O 作OF ⊥CD 于点F ，连结OC .∵AE ＝6 cm ，EB ＝2 cm ，∴AB ＝8cm ，∴OA ＝12AB ＝4 cm ，∴OE ＝AE －OA ＝2 cm. 在Rt △OEF 中，∵∠CEA ＝30°，∴OF ＝12OE ＝1 cm. 在Rt △CFO 中，∵OF ＝1 cm ，OC ＝OA ＝4 cm ，∴CF ＝OC 2－OF 2＝15 cm.∵OF ⊥CD ，∴DF ＝CF ，∴CD ＝2CF ＝215 cm.5. 如图，隧道的截面由圆弧AED 和矩形ABCD 构成，矩形的长BC 为12m ，宽AB 为3m ，隧道的顶端E(圆弧AED 的中点)高出道路(BC)7m.(1)求圆弧AED 所在圆的半径；(2)如果该隧道内设双行道，现有一辆超高货运卡车高6.5m ，宽2.3m ，问这辆货运卡车能否通过该隧道．解：(1)设圆心为点O ，半径为R m ，连结OE 交AD 于F 点，连结OD ，由垂径定理，得OF 垂直平分AD ，DF ＝6，OF ＝R －(7－3)＝R －4，由勾股定理，得DF 2＋OF 2＝OD 2，即：62＋(R －4)2＝R 2，解得R ＝6.5，即圆弧AED 所在圆的半径为6.5m ；(2)能通过，但要小心．车宽GH ＝2.3，圆的半径OH ＝6.5，由勾股定理，得OG ＝ 6.52－2.32≈6.08，G 点与BC 的距离为7－6.5＋6.08＝6.58＞6.5；能通过．。

3.3垂径定理 教学目标 １．使学生理解圆的轴对称性．２．掌握垂径定理．３．学会运用垂径定理解决有关弦、弧、弦心距以及半径之间的证明和计算问题． 教学重点垂径定理是圆的轴对称性的重要体现，是今后解决有关计算、证明和作图问题的重要依据，它有着广泛的应用，因此，本节课的教学重点是：垂径定理及其应用．教学难点 垂径定理的推导利用了圆的轴对称性，它是一种运动变换，这种证明方法学生不常用到，与严格的逻辑推理比较，在证明的表述上学生会发生困难，因此垂径定理的推导是本节课的难点．教学关键理解圆的轴对称性．教学环节的设计这节课我通过七个环节来完成本节课的教学目标，它们是：复习提问，创设情境；引入新课，揭示课题；讲解新课，探求新知；应用新知，体验成功； 目标训练，及时反馈；总结回顾，反思内化；布置作业，巩固新知．一、复习提问，创设情境1．教师演示：将一等腰三角形沿着底边上的高对折，启发学生共同回忆等腰三角形是轴对称图形，同时复习轴对称图形的概念；２．提出问题：如果以这个等腰三角形的顶点为圆心，腰长为半径作圆，得到的圆是否是轴对称图形呢？（教师用教具演示，学生自己操作） 二、引入新课，揭示课题1．在第一个环节的基础上，引导学生归纳得出结论：圆是轴对称图形，每一条直径所在的直线都是对称轴．强调：（1）对称轴是直线，不能说每一条直径都是它的对称轴； （2）圆的对称轴有无数条．判断：任意一条直径都是圆的对称轴（ ）设计意图：让学生更好的理解圆的轴对称轴新性，为下一环节探究新知作好准备．三、讲解新课，探求新知先按课本进行合作学习1．任意作一个圆和这个圆的任意一条直径CD ；2．作一条和直径CD 的垂线的弦，AB 与CD 相交于点E ．提出问题：把圆沿着直径CD 所在的直线对折，你发现哪些点、线段、圆弧重合？ 在学生探索的基础上，得出结论：（先介绍弧相等的概念） ①EA=EB ；② AC=BC ，AD=BD ．理由如下：∵∠OEA=∠OEB=Rt ∠，根据圆的轴轴对称性，可得射线EA 与EB 重合， ∴点A 与点B 重合，弧AC 和弧BC 重合，弧AD 和弧BD 重合．∴ EA=EB ， AC=BC，AD=BD ． 思考：你能利用等腰三角形的性质，说明OA 平分CD 吗？（课内练习1） 注：老教材这个内容放在圆心角、圆周角之后，垂径定理完全可以不用圆的轴对称性来证，可用等腰三角形的性质来证明，现在只能证前面一个（略）． AB C D O E ⌒ ⌒ ⌒ ⌒ A⌒ ⌒ ⌒ ⌒然后把此结论归纳成命题的形式：垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧．垂径定理的几何语言∵CD 为直径，CD ⊥AB （OC ⊥AB ） ∴ EA=EB ， AC=BC ，AD=BD ． 四、应用新知，体验成功 例1 已知AB ，如图，用直尺和圆规求作这条弧的中点．(先介绍弧中点概念)作法：⒈连结AB.⒉作AB 的垂直平分线 CD ， 交弧AB 于点E.点E 就是所求弧AB 的中点．变式一： 求弧AB 的四等分点．思路：先将弧AB 平分，再用同样方法将弧AE 、弧BE 平分．（图略）有一位同学这样画，错在哪里？1．作AB 的垂直平分线CD2．作AT 、BT 的垂直平分线EF 、GH （图略）教师强调：等分弧时一定要作弧所对的弦的垂直平分线．变式二：你能确定弧AB 的圆心吗？ 方法：只要在圆弧上任意取三点，得到三条弦，画其中两条弦的垂直平分线，交点即为圆弧的圆心．例2 一条排水管的截面如图所示．排水管的半径OB=10，水面宽AB=16，求截面圆心O 到水面的距离OC ．思路：先作出圆心O 到水面的距离OC ，即画 OC ⊥AB ，∴AC=BC=8，在Rt △OCB中，68102222=-=-=BC OB OC ∴圆心O 到水面的距离OC 为6．例3 已知：如图，线段AB 与⊙O 交于C 、D 两点，且OA=OB ．求证：AC=BD ．思路：作OM ⊥AB ，垂足为M ， ∴CM=DM∵OA=OB ， ∴AM=BM ， ∴AC=BD ．概念：圆心到圆的一条弦的距离叫做弦心距．小结：1．画弦心距是圆中常见的辅助线；2．半径（r ）、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路，它们之间的关系：弦长222d r AB -=．注：弦长、半径、弦心距三个量中已知两个，就可以求出第三个．五、目标训练,及时反馈1．已知⊙0的半径为13，一条弦的AB 的弦心距为5，则这条弦的弦长等于 ．⌒ ⌒ ⌒ ⌒O A B C ⌒ ⌒ ⌒答案：242．如图，AB 是⊙0的中直径，CD 为弦，CD ⊥AB 于E ，则下列结论中不一定成立的是（ ）A ．∠COE=∠DOEB ．CE=DEC ．OE=BED ．BD=BC答案：C3．过⊙O 内一点M 的最长弦长为10cm ，最短弦长为8cm ，那么OM 长为（ ）A ．3B ．6cmC ． cmD ．9cm答案：A注：圆内过定点M 的弦中，最长的弦是过定点M 的直径，最短的弦是过定点M 与OM 垂直的弦，此结论最好让学生记住，课本作业题也有类似的题目．4．如图，⊙O 的直径为10，弦AB 长为8，M 是弦AB 上的动点，则OM 的长的取值范围是（ ）A ．3≤OM ≤5B ．4≤OM ≤5C ．3<OM<5D ．4<OM<5答案：A5． 已知⊙O 的半径为10，弦AB ∥CD ，AB=12，CD=16，则AB 和CD 的距离为 ． 答案：2或24 注：要分两种情况讨论：（1）弦AB 、CD 在圆心O 的两侧；（2）弦AB 、CD 在圆心O 的同侧．6．如图，已知AB 、AC 为弦，OM ⊥AB 于点M ， ON ⊥AC 于点N ，BC=4，求MN 的长． 思路：由垂径定理可得M 、N 分别是AB 、AC 的中点，所以MN=21BC=2． 六、总结回顾，反思内化师生共同总结：１．本节课主要内容：（1）圆的轴对称性；（2）垂径定理．2．垂径定理的应用：（1）作图；（2）计算和证明．3．解题的主要方法：（1）画弦心距是圆中常见的辅助线；（2）半径（r ）、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路，它们之间的关系：弦长222d r AB -=．七、布置作业， 巩固新知P75作业题1~6，第7题选做．⌒ ⌒。

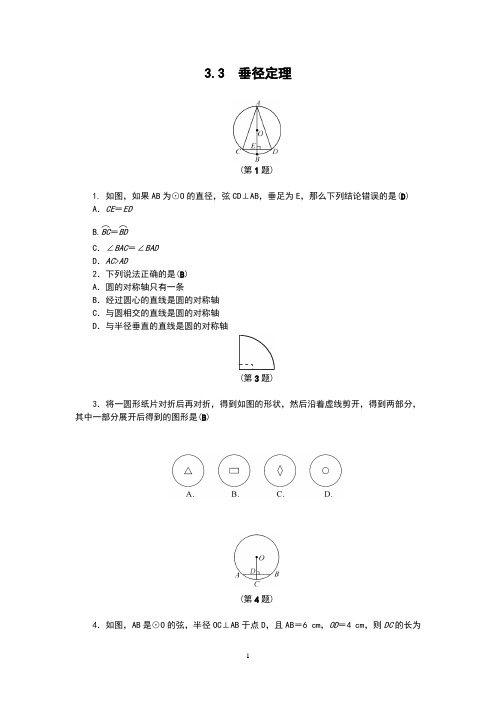
3.3 垂径定理(第1题)1. 如图，如果AB 为⊙O 的直径，弦CD⊥AB，垂足为E ，那么下列结论错误的是(D ) A ．CE ＝ED B.BC ︵＝BD ︵C ．∠BAC ＝∠BAD D ．AC >AD2．下列说法正确的是(B ) A ．圆的对称轴只有一条B ．经过圆心的直线是圆的对称轴C ．与圆相交的直线是圆的对称轴D ．与半径垂直的直线是圆的对称轴(第3题)3．将一圆形纸片对折后再对折，得到如图的形状，然后沿着虚线剪开，得到两部分，其中一部分展开后得到的图形是(B )(第4题)4．如图，AB 是⊙O 的弦，半径OC⊥AB 于点D ，且AB ＝6 cm ，OD ＝4 cm ，则DC 的长为(D )A ．5 cmB ．2.5 cmC ．2 cmD ．1 cm5. 如图，若⊙O 的半径为13 cm ，点P 是弦AB 上的一个动点，且到圆心的最短距离为5 cm ，则弦AB 的长为__24__cm.,(第5题)),(第6题))6. 在直径为1000 mm 的圆柱形油槽内装入一些油后，截面如图所示．若油面宽AB ＝800 mm ，则油的最大深度为__200__mm.(第7题)7．某市新建的滴水湖是圆形人工湖，为测量该湖的半径，小杰和小丽沿湖边选取A ，B ，C 三根木柱，使A ，B 之间的距离与A ，C 之间的距离相等，并测得BC 长为240 m ，A 到BC 的距离为5 m ，如图．请你帮助他们求出滴水湖的半径．【解】 设圆心为点O ，连结OA ，OB ，OC ，AB ，AC ，OA 交BC 于点D . ∵AB ＝AC ，OB ＝OC ，OA ＝OA ， ∴△OBA ≌△OCA (SSS )， ∴∠BOD ＝∠COD . 又∵OB ＝OC ，∴BD ＝DC ，OA ⊥BC .∴BD ＝12BC ＝120.设OB ＝x .∵AD ＝5，在Rt△OBD 中，OB 2＝BD 2＋OD 2， ∴x 2＝(x －5)2＋1202， 解得x ＝1442.5.即滴水湖的半径为1442.5 m.(第8题)8．如图，⊙O 的直径为10cm ，弦AB 为8cm ，P 是弦AB 上一点．若OP 的长是整数，则满足条件的点P 有(D )A ．2个B ．3个C ．4个D ．5个【解】 过点O 作OM⊥AB 于点M ，连结OA. ∵OA ＝5，AM ＝12AB ＝4，∴OM ＝3.∴3≤OP ≤5，∴OP 的长为3，4或5.当OP ＝3时，点P 只能与点M 重合；当OP ＝4时，点P 可以在AM 上，也可以在BM 上，∴有2个点P ；当OP ＝5时，点P 与点A 或点B 重合．即满足条件的点P 有5个．(第9题)9．如图，点A ，B 是⊙O 上两点，AB ＝10.点P 是⊙O 上的动点(P 与A ，B 不重合)，连结AP ，PB.过点O 分别作OE⊥AP 于点E ，OF ⊥PB 于点F ，则EF ＝__5__．【解】 ∵OE⊥AP，OF ⊥PB ， ∴E ，F 分别是AP ，PB 的中点． ∴EF 是△APB 的中位线，∴EF ＝12AB ＝5.(第10题)10．如图，AB 是⊙O 的直径，弦CD 与AB 交于点P ，且AP∶PB＝1∶5，OP ＝2，∠DPB ＝30°，求CD 的长．【解】 过点O 作OE ⊥CD ，连结OD . 在Rt△POE 中，∵∠EPO ＝30°，∴OE ＝12OP ＝1.∵AP ∶PB ＝1∶5，AO ＝BO ，OP ＝2， ∴AB ＝6，∴OD ＝3. 在Rt△OED 中，DE ＝OD 2－OE 2＝32－12＝2 2， 又∵OE ⊥CD ， ∴CE ＝ED ， ∴CD ＝4 2.(第11题)11．如图，在Rt△AOB 中，∠O ＝90°，OA ＝6，OB ＝8.以点O 为圆心，OA 为半径作圆交AB 于点C ，求BC 的长．【解】 过点O 作AB 的垂线，垂足为E ，连结OC .∵AB ＝OA 2＋OB 2＝62＋82＝10，∴OE ＝OA ·OB AB ＝6×810＝4.8，∴AE ＝AO 2－OE 2＝62－4.82＝3.6.∴AC ＝2AE ＝7.2，∴BC ＝AB －AC ＝10－7.2＝2.8.(第12题)12．如图，在⊙O 中，AB 是直径，CD 是弦，过点C 作CD 的垂线交AB 于点E ，过点D 作CD 的垂线交AB 于点F.求证：AE ＝BF.【解】 过点O 作ON⊥CD 于点N ， 则N 是CD 的中点． ∵CE ⊥CD ，DF ⊥CD ， ∴CE ∥NO ∥DF ， ∴EO ＝FO ，∴AO －EO ＝BO －FO ，即AE ＝BF.初中数学试卷金戈铁骑 制作。

教学设计课程基本信息学科数学年级九年级学期秋季课题 3.3垂径定理（第一课时）教科书书名：《义务教育教科书数学（九年级上册）》出版社：浙江教育出版社教学目标1. 经历探索垂径定理的过程.2. 探索并掌握垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧.3. 会运用垂径定理解决一些简单的几何问题.教学内容教学重点：垂径定理教学难点：垂径定理的推导过程以及垂径定理的灵活运用教学过程一：创设情境引入新课问题1：如图，剪一个圆形纸片，沿着它的任意一条直径对折，重复做几次，你发现了什么？由此你能得到什么结论？我们发现在折叠的过程中，直径两侧的部分会完全重合，因此我们得到结论：圆是轴对称图形任何一条直径所在直线都是它的对称轴．问题2：如图，在⊙O中任意作一条弦AB，观察下面的图形，它还是轴对称图形吗，若是，你能作出它的对称轴吗？二：师生互动共创新知已知：如图，CD是⊙O的直径，CD⊥AB，求证：AE=BE，AĈ=BĈ，AD̂=BD̂.分析：利用半径来构造等腰三角形来证明AE=BE；弧等可以利用同圆或等圆中两弧的端点重合来证明.垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧.几何语言：∵CD是直径，CD⊥AB，∴AE=BE，AĈ=BĈ，AD̂=BD̂. 三：应用新知层层深入B OACD下列图形是否适合用垂径定理呢？例1 已知AB̂，用直尺和圆规作这条弧的中点 分析：要平分弧，找到这条弧的中点，让我们联想到了垂径定理的 基本图形，所以第一步我们先连结AB ，然后再画出垂直弦AB 的过圆心的一条直线即可，所以第二步，作AB 的垂直平分线CD ， 交弧AB 于点E.例2 一条排水管的截面如图所示，已知排水管的半径OB=10，水面宽AB=16，求截面圆心O 到水面的距离.分析:为求O 到AB 的距离，我们先过点O 作OC ⊥AB ，即求OC的长度，观察图形发现OC 在直角三角形OBC 中，其中半径 OB=10，由于OC ⊥AB ，由垂径定理可得BC 等于AB 的一半等于8， 那么根据勾股定理即可得到OC 的长度.变式：一条排水管的截面如图所示。

3.3 垂径定理（1）教学案教学目标知识目标：1．理解圆是轴对称图形，每一条直径所在的直线都是对称轴．2．掌握圆的性质（垂径定理），并会用它解决有关弦、弧、弦心距及半径之间关系的证明和计算．能力目标：经历折纸、画图、归纳等过程，培养学生的探索能力和应用能力．情感目标：通过合作学习，探索圆的性质；让学生亲身体验、直观感知，并操作确认，激发学生自主学习和应用数学的意识．教学重点难点重点：探索圆的轴对称性和圆的性质．难点：用圆的轴对称性推导出圆的性质及其应用．课堂教与学互动设计【创设情境，引入新课】复习提问：（1）什么是轴对称图形？（2）正三角形是轴对称性图形吗？有几条对称轴？（3）圆是否为轴对称图形？如果是，它的对称轴是什么？•你能找到多少条对称轴？──引入新课【合作交流，探究新知】一、自主探索1．在透明纸上任意作一个圆和这个圆的任意一条直径，•然后沿着直径所在的直线把纸折叠，你发现了什么？2．结论：圆是_________图形，_________的直线都是对称轴．二、合作学习1．在圆形纸片（如图所示）上任意画一条直径CD，然后在CD上任意取一点E，过E画弦AB⊥CD于点E，把圆形纸片沿直径对折，观察直径CD两侧，你发现哪些点、线互相重合？有哪些圆弧相等？2．请你用命题的形式表达你的结论．3．请你对上述命题写出已知、求证，并给出证明．4．圆的性质（垂径定理）：垂直于弦的直径平分这条弦且平分弦所对的弧．三、概括性质1．直径垂直于弦..⎧⇒⎨⎩直径平分弦直径平分弦所对的弧例如：CD是直径，AB⊥CD，EA=EB，CA CB=，DA DB=．2．分一条弧成相等的两条弧的点，叫做这条弧的中点．例如，上图中，•点C•是AB的中点，D是ADB的中点．【例题解析，当堂练习】例1 （课本例1）已知AB（如图），用直尺和圆规求作这条弧的中点．练一练如图，同心圆O中，大圆的弦AB与小圆交于C，D两点，判断线段AC与BD的大小关系，并说明理由．。