2021届吉林省抚松五中高三四盟校期中联考理数试题Word版含解析

∴ ，则 .
18．
（1）
（2） ，
（3） ，
（1）首先根据题意得到制作一次视频合格的概率 ，再求进行3次制作，恰有一次合格作品的概率即可.
（2）根据二项分布求解数学期望与方差即可.
A．第一象限B．第三象限C．直线 上D．直线 上
3．在二项式 的展开式中，含 的项的系数是（ ）
A． B． C． D．
4．数列 为等差数列，且 ，则 （ ）
A．1B．3C．6D．12
5．长春54路有轨电车建成于上个世纪30年代，大概是现存最美的电车路线了，见证着这座城市的历史与发展.学生甲和学生乙同时在长影站上了开往西安大路方向的电车，甲将在创业大街站之前任何一站下车，乙将在景阳大路站之前任何一站下车，他们都至少坐一站再下车，则甲比乙后下车的概率为（ ）
故选：A
4．D
根据定积分的几何意义求 ，再应用等差中项的性质求目标式的值.
解：∵ 表示半径为2的四分之一圆面积(处于第一象限)，
∴ ，又 为等差数列，
∴ ，则 .
故选：D.
5．B
先求出甲、乙下车的情况共有 种可能，再求出甲比乙后下车共有15种可能，最后利用几何概型公式求解即可.
解：甲将在长影站上车，将在创业大街站之前任何一站下车,可能在6个站下车，
（1）
由ADEF为正方形，则ED⊥AD，
∵面 面 ，ED⊂面ADEF，面 面 ，
∴ED⊥面ABCD，BC⊂面ABCD，则ED⊥BC，
在直角梯形ABCD中，|AB|＝|AD|＝2，|CD|＝4，则 ，|BD|＝2 ，
在△BCD中， ，则BC⊥BD，
∵DE∩BD＝D，DE、BD面BDE，
∴BC⊥BDE，又BC⊂面BEC，
17．

吉林省 2021 版数学高三上学期理数期中考试试卷（II）卷姓名:________班级:________成绩:________一、 选择题 (共 12 题；共 24 分)1. （2 分） (2017 高二下·新乡期末) 已知集合 A={0，1，2，3，4}，B={x|（x+5）（x﹣m）＜0}，m∈Z，若 A∩B 有三个元素，则 m 的值为（ ）A . ﹣2B.2C . ﹣3D.32. （2 分） 若 ab,c 为实数，则下列命题正确的是（）A . 若 a>b，则B . 若 a<b<0，则C . 若 a<b<0，则 D . 若 a<b<0，则3. （2 分） 化简 A.1 B.2=（ ）C.D . -14. （2 分） (2019 高一下·大庆期中) 已知实数，且A.，则以下不等式恒成立的是（ ）第 1 页 共 11 页B.C.D.5. （2 分） (2019·黑龙江模拟) 已知等差数列 列 的前 项和为（ ）满足：，且 ， ， 成等比数列，则数A.B.C. 或 D. 或6. （2 分） (2019 高一上·绵阳期中) 已知函数 f（x）=x+2x ， g（x）=x+lnx，f（x）=x+为，则的大小关系为（ ）的零点分别A.B.C.D.7. （2 分） (2017 高二上·定州期末) 已知函数 f（x）=（a＞0，且 a≠1）在 R 上单调递减，且关于 x 的方程|f（x）|=2﹣x 恰好有两个不相等的实数解，则 a 的取值范围是（ ）A . （0， ]B.[ ， ]第 2 页 共 11 页C . [ ， ]∪{ } D . [ ， ）∪{ } 8. （2 分） 函数 f（x）=Asin（ωx+ϕ）+k 在一个周期内的图象如图，函数 f（x）解析式为（ ）A . f（x）=4sin（ x+ ）﹣1 B . f（x）=2sin（2x﹣ ）+1C . f（x）=4sin（ x+ ）D . f（x）=2sin（2x﹣ ）+19. （2 分） (2020 高二下·钦州期中) 已经知道函数 （）A . 最大值为 9B . 最小值为C . 函数在区间上单调递增D.是它的极大值点10. （2 分） 已知函数 A. B.，若第 3 页 共 11 页在上，则下列说法不正确的是， 则实数 a 等于（ ）C.2 D.411. （2 分） (2018 高二上·北京期中) 不等式A.，的解集是（ ）B.，C.D.12. （2 分） (2019 高三上·长治月考) 已知函数 象有三个不同的交点，则直线 斜率的取值范围为（ ），过点的直线 与的图A.B.C.D.二、 填空题 (共 4 题；共 4 分)13. （1 分） (2016 高一下·防城港期末) 若向量 、 满足 + • =________．=（2，﹣1）， =（1，2），则14. （1 分） (2017 高二下·保定期末) （+xcosx）dx=________．15. （1 分） (2018·南阳模拟) 若非零向量 ， 满足 的投影为________．第 4 页 共 11 页，则在 方向上16. （1 分） (2017 高二下·寿光期末) 设曲线 y=xn+1（n∈N+）在点（1，1）处的切线与 x 轴的交点的横坐 标为 xn ， 则 log2017x1+log2017x2+…+log2017x2016 的值为________．三、 解答题 (共 6 题；共 55 分)17. （10 分） (2020·随县模拟) 等差数列 的前 项和为 ，数列 是等比数列，，，.（1） 求数列 和 的通项公式；（2） 设，求数列 的前 项和 .18. （10 分） (2019 高三上·广东期末) 如图，在，且.中，角 ， ， 的对边分别为 ， ，（1） 求的大小；（2） 若 积的最大值.，点 、 在 的异侧，，，求平面四边形面19. （10 分） (2020 高二下·洛阳期末) 函数 .的图象在处的切线方程为：（1） 求 和 的值；（2） 若满足：当时，，求实数 的取值范围.20. （5 分） (2019 高一下·仙桃期末) 满足，的面积分别为．第 5 页 共 11 页，点 在内且（Ⅰ）求的值；（Ⅱ）求的最小值．21. （5 分） (2016 高二下·南昌期中) 设 l 为曲线 C：y= 在点（1，0）处的切线． （Ⅰ）求 l 的方程； （Ⅱ）证明：除切点（1，0）之外，曲线 C 在直线 l 的下方．22. （15 分） (2016 高一上·吉林期中) 已知函数 f（x）=k﹣ （其中 k 为常数）； （1） 求：函数的定义域； （2） 证明：函数在区间（0，+∞）上为增函数； （3） 若函数为奇函数，求 k 的值．第 6 页 共 11 页一、 选择题 (共 12 题；共 24 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、 11-1、 12-1、二、 填空题 (共 4 题；共 4 分)13-1、 14-1、 15-1、参考答案第 7 页 共 11 页16-1、三、 解答题 (共 6 题；共 55 分)17-1、 17-2、18-1、第 8 页 共 11 页18-2、 19-1、19-2、第 9 页 共 11 页20-1、21-1、 22-1、第 10 页 共 11 页22-2、22-3、第11 页共11 页。

2021年高三数学上学期期中联考试题 理(IV)本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟第Ⅰ卷（选择题，共60分）一.选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1、若复数（为虚数单位）是纯虚数，则实数（ ）A. B. C.0 D.12．已知全集21{|230},{|0|}3x U x x x A x x -=-+-≤=>-，则C U A=（ ） A ．{x|l<x<2} B ．{x|l ≤x ≤2}C ．{x|2≤x<3}D ． {x|2≤x ≤3或x=1}3．设集合和集合都是自然数集合，映射,把集合中的元素映射到集合中的元素,则在映射下，象20的原象是（ ）A.2B.3C.4D.54．已知数列的通项公式为。

令,则数列{}的前10项和T 10=（ ）A ．70B ．75C ．80D ．855.，其中为向量与的夹角，若，，，则等于（ ）A ．B ．C ．或D ．6．已知数列满足，，则等于（ ）A ．B ．C ．D ．7、在△ABC 中，角所对的边分别是，已知，且，则△ABC 的面积是（ ）8、化简（ ）A. B. C. D.9、函数的图象大致是（ ）10．已知函数的图像为曲线，若曲线存在与直线垂直的切线，则实数的取值范围为（ ）A ．B ．C ．D ．11、设函数,若实数满足,则( )A. B. C. D.12、已知函数 是定义在R 上的奇函数，其导函数为 ，且x<0时， 恒成立，则的大小关系为（ ） A. 2015(2015)2014(2014)(1)f f f <<B ． 2015(2015)(1)2014(2014)f f f <<C ． (1)2015(2015)2014(2014)f f f <<D ． (1)2014(2014)2015(2015)f f f <<第Ⅱ卷（非选择题 共90分）二.填空题 (本题共4小题，每小题5分，共20分，把答案填在答题卷中的横线上)13．已知点和向量,若,则点的坐标为14．已知是偶函数，则的图像的对称轴是直线 .15．已知实数若，则___________.16．设为的导函数，是的导函数，如果同时满足下列条件：①存在，使；②存在，使在区间单调递增，在区问单调递减．则称为的“上趋拐点”；如果同时满足下列条件：①存在，使；②存在，使在区间单调递减，在区间单调递增．则称为的“下趋拐点”．给出以下命题，其中正确的是 （只写出正确结论的序号）①为的“下趋拐点”；②在定义域内存在“上趋拐点”；③在（1，+∞）上存在“下趋拐点”，则的取值范围为；④，是的“下趋拐点”，则的必要条件是．三、解答题（本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤）17．（本小题10分）已知函数，（Ⅰ）解关于的不等式；（Ⅱ）若函数的图像恒在函数图像的上方，求实数的取值范围．18．（本小题12分）已知数列的前项和为，且.（Ⅰ）求数列的通项公式；（Ⅱ）设，求数列的前项和．19．（本小题12分）函数在一个周期内的图象如图所示,为图象的最高点,、为图象与轴的交点,且为正三角形. (Ⅰ)求的值及函数的值域;(Ⅱ)若,且,求的值.20、（本小题12分）在△ABC中，角所对的边分别是，且．(Ⅰ)求角的大小；(Ⅱ)已知，求的值．21.（本小题12分）已知函数(Ⅰ)若，求函数的极值和单调区间；(Ⅱ)若在区间上至少存在一点，使得成立，求实数的取值范围.22．（本小题12分）已知函数.（I）若函数有极值1，求实数的值；（II）若函数在区间上是增函数，求实数的取值范围；（III）证明：.xx 学年第一学期赣州市十三县(市)期中联考高三数学（理科）参考答案一．选择题（共60分）题号 1 2 3 4 5 6 7 8 9 10 11 12答案A D CB B D DC A C AD 二．填空题（共20分）13. 14. 15. 3 16. ①③④三．解答题（共70分）17. 解：（Ⅰ）由得，…………1分…………2分…………3分故不等式的解集为…………5分（Ⅱ）∵函数的图象恒在函数图象的上方∴恒成立，即恒成立…………7分∵，…………9分∴的取值范围为．…………10分18. （Ⅰ）当时，由得：．…………1分由 ①（ ）②…………2分上面两式相减，得：．（ ） …………4分所以数列是以首项为，公比为的等比数列． 得：．……6分（Ⅱ）． …………7分． ……9分121n n T c c c ⎛=++⋅⋅⋅+=+++⋅⋅⋅+ ⎝ …………12分19. 解：(Ⅰ)由已知可得:=3cos ωx+…………2分又由于正三角形ABC 的高为2,则BC=4 …………3分所以,函数482824)(πωωπ===⨯=，得，即的周期T x f …………5分所以,函数 …………6分(Ⅱ)因为(Ⅰ)有…………7分由x 0 …………8分所以, …………9分故)22532254(324sin )34cos(4cos )34([sin 3200⨯+⨯=+++=ππππππx x …………10分 …………11分…………12分20. 解：(Ⅰ)sin sin sin cos cos sin tan tan cos cos cos cos A B A B A B A B A B A B++=+=， ，∴，………2分∴，…………4分 ∵，∴B=.………………………………………6分(Ⅱ)，……………………… 7分∵，∴，即，∴，………………………8分 而，∴.……………10分∴ . ……………………………………………… 12分21.解：（1） 因为，……………1分当，，令，得，令，得；令，得……………2分所以时，的极小值为1. ……………3分的递增区间为，递减区间为；……………4分（2）因为，且，令，得到，①当，即时， 在区间上单调递减，故在区间上的最小值为，由，得，即.……………6分 ②当，即时，ⅰ）若，则对成立，在区间上单调递减，所以，在区间上的最小值为，显然，在区间上的最小值小于0不成立. ……………8分ⅱ）若，即时，则有（右表）， 所以在区间上的最小值为， ……………10分 由 ，得，解得，即.…………11分综上，由①②可知：符合题意. ……………12分22．解：（Ⅰ） F′（x ）=a ﹣=（x ＞0），……………1分当a≤0时，F′（x ）＜0，F （x ）在（0，+∞）递减，无极值；当a ＞0时，由F′（x ）＞0，可得x ＞，由F′（x ）＜0，可得0＜x ＜，……………2分 x=取得极小值．由F （x ）有极值﹣1，即有1﹣ln=1，解得a=1；……………3分（Ⅱ）G （x ）=f[sin （1﹣x ）]+g （x ）=asin （1﹣x ）+lnx ，G′（x ）=﹣acos （1﹣x ）+，……………4分因为G （x ）在（0，1）上递增，即有﹣acos （1﹣x ）+≥0在（0，1）上恒成立，即a≤在（0，1）上恒成立．……………5分令h （x ）=xcos （1﹣x ），0＜x ＜1，h′（x ）=cos （1﹣x ）+xsin （1﹣x ）＞0， h （x ）在（0，1）递增，0＜xcos （1﹣x ）＜1，即有＞1，……………6分 则有a≤1．……………7分（III ）由（II ）知，当a=1时，在区间上是增函数，所以,所以，……………8分令，即，则……………9分所以()()()222211123sinln ln ...ln 132421n k n n n k =+<+++⨯⨯++∑ ()()()()2ln 2ln32ln3ln 2ln 4...2ln 1ln ln 2n n n =-+--+++--+⎡⎤⎣⎦……………10分 ()()1ln 2ln 1ln 2ln 2ln ln 22n n n n +=++-+=+<+……………11分 故。

5
5 ，且 为第二象限角，则 tan 的值等于（ 13
5
）
B. 12
C. 5
12
D. 5
12
3、若 z 1 2i ，则 (A)1
4i （ z z 1
-1
） (C) i (D)-i
(B)
4、在等差数列{an}中，a3+3a8+a13=120，则 a8=（ A．24 B．22 C．20 D．25
7、已知曲线 f（x） = A. 3
2
ax 2 在点 1, f 1 处切线的斜率为 1，则实数 a 的值为（ x+1
C. 3
4
B. 3
2
D. 4
3
1 + log x 2 8、函数 f ( x )= 的零点所在区间是（ x
（A） 0,1 （B） 1, 2 （C） 2,3
）
5、若函数 f(x)＝ax2＋ax－1 在 R 上满足 f(x)＜0 恒成立，则 a 的取值范围是( A．a≤0 B．a＜－4 C．－4＜a＜0 D．－4＜a≤0 ）
)
1 6、幂函数 y f ( x ) 的图象经过点 (4, ), 则f (2) =（ 2
A． 1
4
B． 1
2
C． 2
2
D． 2 ）
长白县实验中学高三上学期期中考试数学（文）试卷
一：选择题（每小题 5 分，共 60 分） 1、已知集合 A {x || x | 2} ， B {1,0,1, 2,3} ，则 A B （
A. {0,1} B. {0,1, 2} C. {1, 0,1} ）
D. {1,0,1,2}
2、若 sin A. 12
13、充分不必要．

【 A. 3 B. -3 C.
3
】
D. 3
6、已知向量 a, b 满足 a 2, b 1 ，且对一切实数 x， a xb a b 恒成立，则 a, b 的夹 角的大小为 π A． 6 【
B．
】
π 3
C．
2π 3
D．
5π 6
7、设直角坐标系 xoy 平面内的三点 A 1, 2 ， B a, 1 ， C b, 0 ，其中 a 0 ， b 0 ， 若 A ， B ， C 三点共线，则 A．4 8、函数 B．6 的图象大致是
，都有
，求 的取值范围.
21. (本小题满分 12 分)已知函数 f ( x) ( x 2)e x ． （1）求函数 f ( x) 的单调递增区间； （2）若 g ( x ) f ( x ) 2e x ax 2 ， h( x) x ，且对于任意的 x1 ， x2 (0, ) ，都有
A．
1 5
B．
1 5
C．
7 5
D．
7 5
11、已知 单位，得到
，把
的图象向右平移 个单位，再向上平移 2 个 成立，则 【 】Biblioteka 的图象；若对任意实数 ，都有
A. 12、 已知函数
B. 3
C. 2
D.
， 若关于 的方程 【 D. 】
有 8 个不等的实数根，则 的取值范围是 A. 二、填空题 （每空 5 分，共 20 分） 评卷人 得分 B. C.
1
1 ,当 x 2,0 时， 15、 设函数 f x 是定义在 R 上的奇函数， 且对任意的 x R, f x 2 f x
f x log2 ( x 3) ，则 f 2017 f (2015) =_____________________。

吉林省2021年高三上学期期中数学试卷（理科）A卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）若全集U={x|0≤x＜6，x∈N}，集合A={1，3，5}，B={x|x2+4=5x}，则∁UA∪∁UB等于（）A . {2，3，4，5}B . {0，2}C . {0，2，3，4，5}D . {0，2，3，4}2. （2分）由曲线y=x2 ， y=x3围成的封闭图形面积为（）A .B .C .D .3. （2分） (2016高一下·衡阳期中) 若| |= ，| |=2且（﹣）⊥ ，则与的夹角是（）A .B .C .D .4. （2分） (2019高一下·集宁月考) 从集合的所有子集中，任取一个，这个集合恰是集合子集的概率是（）A .B .C .D .5. （2分）设、都是非零向量，下列四个条件中，一定能使成立的是（）A . =-B .C . =2D .6. （2分）函数的零点所在的区间是（）A .B .C .D .7. （2分） 5人站成一排，甲、乙两人相邻的不同站法的种数为（）A . 24B . 36C . 48D . 608. （2分） (2017高三上·连城开学考) 若a= ，b= ，c= ，则a，b，c大小关系是（）A . a＜c＜bB . a＜b＜cC . c＜b＜aD . c＜a＜b9. （2分）(2019·南昌模拟) 《莱茵德纸草书》是世界上最古老的数学著作之一，书中有一道这样的题目：把120个面包分给5个人，使每人所得成等差数列，且使较多的三份之和的是较少的两份之和，则最少的一份面包个数为（）A . 46B . 12C . 11D . 210. （2分） (2017高一下·红桥期末) 如图所示，是一个空间几何体的三视图，则这个空间几何体是（）A . 长方体B . 球C . 圆锥D . 圆柱11. （2分） (2015高三上·合肥期末) 若实数x，y满足约束条件，则目标函数z=x+y的最大值为（）A . 2B . 1C . ﹣1D . ﹣212. （2分）已知定义域为的奇函数.当时,，则不等式的解集为（）A .B .C .D .二、填空题 (共4题；共4分)13. （1分）(2019·乌鲁木齐模拟) 在平面直角坐标系xOy中，若直线与曲线b，相切于点，则的值为________．14. （1分） (2016高一上·黑龙江期中) 已知y=f（x）是奇函数，若g（x）=f（x）+2且g（1）=1，则g （﹣1）=________15. （1分）设 a>0 ，若曲线与直线x=a,y=0, 所围成封闭图形的面积为 a2 ，则 a= ________.16. （1分） (2016高一上·青浦期中) 已知﹣1＜a＜b＜2，则a﹣b的范围是________．三、解答题 (共7题；共60分)17. （5分）已知a是实数，函数f（x）=是奇函数，求f（x）在（0，+∞）上的最小值及取到最小值时x的值．18. （15分） (2020高二上·西湖期末) 如图所示，在四棱锥中，底面是且边长为的菱形，侧面为正三角形，其所在平面垂直于底面，若为的中点，为的中点.（1）求证：平面；（2）求证：；（3）在棱上是否存在一点，使平面平面，若存在，确定点的位置；若不存在，说明理由19. （10分）(2017·太原模拟) 已知数列{an}的前n项和Sn=2n+1﹣2，数列{bn}满足bn=an+an+1（n∈N*）．（1）求数列{bn}的通项公式；（2）若cn=log2an（n∈N*），求数列{bn•cn}的前n项和Tn ．20. （5分） (2017高一下·桃江期末) 某校从参加考试的学生中抽出60名学生，将其成绩（均为整数）分成六组[40，50），[50，60）…[90，100]后，画出如下部分频率分布直方图．观察图形的信息，回答下列问题：（Ⅰ）求成绩落在[70，80）上的频率，并补全这个频率分布直方图；（Ⅱ）估计这次考试的及格率（60分及以上为及格）和平均分；（Ⅲ）设学生甲、乙的成绩属于区间[40，50），现从成绩属于该区间的学生中任选两人，求甲、乙中至少有一人被选的概率．21. （5分）已知函数f（x）=x3+bx2+ax+d的图象过点P（0，2），且在点M（﹣1，f（﹣1））处的切线方程为6x﹣y+7=0．（Ⅰ）求函数y=f（x）的解析式；（Ⅱ）求函数y=f（x）的单调区间．22. （10分） (2017·长春模拟) 已知在平面直角坐标系xOy中，以O为极点，x轴的正半轴为极轴，建立极坐标系．曲线C1的极坐标方程为ρ=4cosθ，直线l：（为参数）．（1）求曲线C1的直角坐标方程及直线l的普通方程；（2）若曲线C2的参数方程为（α为参数），曲线P（x0 ， y0）上点P的极坐标为，Q为曲线C2上的动点，求PQ的中点M到直线l距离的最大值．23. （10分）设定义域为R的函数f（x）= ．（1）在如图所示的平面直角坐标系内作出函数f（x）的图象，并写出函数f（x）的单调区间（不需证明）；（2）求函数f（x）在区间[1，4]上的最大值与最小值．参考答案一、选择题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题；共60分)17-1、18-1、18-2、18-3、19-1、19-2、20-1、21-1、22-1、22-2、23-1、23-2、。

绝密★启用前吉林省白山市普通高中2021届高三毕业班下学期第四次高考模拟联合考试数学(理)试题 (解析版)2021年5月一、单选题1.已知集合 A ={x ∈Z|−3<x <5} , B ={y|y =2x,x ∈A} ,则 A ∩B 的元素个数为（ ）A. 3B. 4C. 5D. 6 【答案】 B【考点】交集及其运算【解析】【解答】因为 A ={−2,−1,0,1,2,3,4} , B ={−4,−2,0,2,4,6,8} ,所以 A ∩B ={−2,0,2,4} .元素个数是4． 故答案为：B ．【分析】根据题意由交集的定义即可得出答案。

2.在 △ABC 中,若 AB =1,AC =5,sinA =35 ,则 AB ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ = （ ） A. 3 B. ±3 C. 4 D. ±4 【答案】 D【考点】平面向量数量积的运算【解析】【解答】由于 sinA =35 ,所以 cosA =±√1−sin 2A =±45 , 所以 AB ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =|AB ⃗⃗⃗⃗⃗ |⋅|AC ⃗⃗⃗⃗⃗ |⋅cosA =±4 . 故答案为：D【分析】首先由同角三角函数的关系式代入数值计算出cosA的值,再由数量积的的运算性质计算出答案即可。

3.函数f(x)=x3−7x2+1的图象在点(4,f(4))处的切线斜率为（）A. -8B. -7C. -6D. -5【答案】A【考点】导数的几何意义【解析】【解答】因为f′(x)=3x2−14x,所以所求切线的斜率为f′(4)=3×16−14×4=−8.故答案为：A【分析】根据题意对函数求导并把数值代入到导函数的解析式,计算出结果即为切线的斜率。

4.跑步是一项有氧运动,通过跑步,我们能提高肌力,同时提高体内的基础代谢水平,加速脂肪的燃烧,养成易瘦体质.小林最近给自己制定了一个200千米的跑步健身计划,他第一天跑了8千米,以后每天比前一天多跑0.5千米,则他要完成该计划至少需要（）A. 16天B. 17天C. 18天D. 19天【答案】B【考点】二次函数的性质,等差数列的前n项和【解析】【解答】依题意可得,他从第一天开始每天跑步的路程（单位：千米）依次成等差数列,且首项为8,公差为0.5,设经过n天后他完成健身计划,则8n+n(n−1)2×12≥200,整理得n2+31n−800≥0.因为函数f(x)=x2+31x−800在[1,+∞)为增函数,且f(16)<0, f(17)>0,所以n≥17.故答案为：B【分析】根据题意把实际问题转化为数学问题再由等差数列前n项和公式整理即可得出关于n的方程,结合二次函数的性质即可得出n的取值范围。

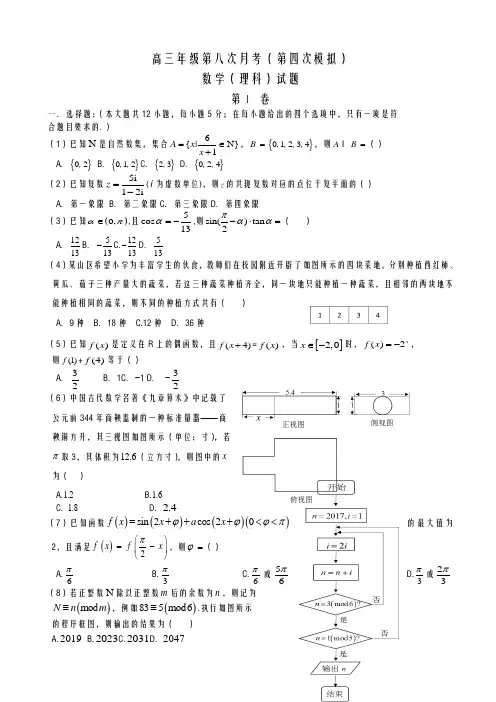
高三年级第八次月考（第四次模拟）数学（理科）试题第Ⅰ 卷一． 选择题：（本大题共12小题，每小题5分；在每小题给出的四个选项中，只有一项是符 合题目要求的．） （1）已知N 是自然数集，集合N}16{∈+=x x|A ，{}01234,,,,B =，则A B =I （） A ．{}02, B ．{}012,,C ．{}23,D ．{}024,, （2）已知复数5i12iz =-(i 为虚数单位)，则z 的共轭复数对应的点位于复平面的（） （3）已知()πα,0∈,且5cos 13α=-,则sin()tan 2παα-⋅=（ ）A ．13 B ．13- C.13-D ．13（4）某山区希望小学为丰富学生的伙食，教师们在校园附近开辟了如图所示的四块菜地，分别种植西红柿、黄瓜、茄子三种产量大的蔬菜，若这三种蔬菜种植齐全，同一块地只能种植一种蔬菜，且相邻的两块地不能种植相同的蔬菜，则不同的种植方式共有（ ） A ．9种 B ．18种 C.12种 D ．36种（5）已知()f x 是定义在R 上的偶函数，且(4)f x +=()f x ，当[]2,0x ∈-时，()2x f x =-， 则(1)f +(4)f 等于（） A ．32 B ．1C ．−1 D ． −32（6）中国古代数学名著《九章算术》中记载了 公元前344年商鞅监制的一种标准量器——商 鞅铜方升，其三视图如图所示（单位：寸），若π取3，其体积为12.6（立方寸），则图中的x为（ ）A.1.2B.1.6C. 1.8D. 2.4 （7）已知函数()()()()sin 2cos 20f x x a x ϕϕϕπ=+++<<的最大值为2，且满足()2f x f x π⎛⎫=- ⎪⎝⎭，则ϕ=（） A.6πB.3πC.6π或56πD.3π或23π（8）若正整数N 除以正整数m 后的余数为n ，则记为()mod N n m ≡，例如()835mod6≡.执行如图所示的程序框图，则输出的结果为（ ）A.2019B.2023C.2031D. 2047（9）如图，在矩形ABCD 中，2,1AB AD ==，以A 为顶点且 过点C 的抛物线的一部分在矩形内；若在矩形ABCD 内随机地 投一点，则此点落在阴影部分内的概率为（ ） A.12 B.32 C.53 D.34（10）已知,x y 满足,2,2.y x x y x y m ≥⎧⎪+≤⎨⎪-≥⎩若2z x y =+有最大值4，则实数m 的值为（）A ．4-B ．2-C ．1-D ．1（11）已知点2F 、P 分别为双曲线()222210,0x y a b a b-=>>的右焦点与右支上的一点，O为坐标原点，若()212OM OP OF =+uuu r uu u r uuu r ，2222OF F M =uuu r uuuu r ，且22222OF F M a b ⋅=+uuu r uuuu r ，则该双曲线的离心率为（）A ．31+B ．32C ．3D ．23 （12）已知函数()f x ax =，()ln g x x =，存在(]0,t e ∈，使得()()f t g t -的最小值为3，则函数()ln g x x =图象上一点P 到函数()f x ax =图象上一点Q 的最短距离为（ ）A ．1eB ．4411e e ++ C.44211e e ++D ．44311e e ++第Ⅱ 卷二．填空题：（本题共4小题，每小题5分，共20分）（13）若0,0a b >>，且()ln 0a b +=，则11a b+的最小值是__________ （14）若()2018220180122018(12)x a a x a x a x x R +=++++∈L ，则12a -+222a −332a +…+201820182a 的 值为（15、B 、C 是球O 的球面上三点，2AB =，23AC =，60ABC ∠=o ，且棱锥O ABC -的体积为463，则球O 的表面积为___________ （16）已知ABC ∆外接圆O 的半径为1，且BO BA BC λμ=+uu u r uu r uu u r.若60ABC ∠=o，则λμ+的最大值为__________三．解答题：（本大题共6小题，其中17-21小题为必考题，每小题12分；第22—23题为选考题，考生根据要求做答，每题10分） （17）（本小题满分12分）已知数列{}n a 中，11a =，其前n 项和为n S ，且满足()22221n n n S a n S =≥-.（Ⅰ）求证：数列1n S ⎧⎫⎨⎬⎩⎭的通项公式；（Ⅱ）证明：当2n ≥时，1231113232n S S S S n ++++<L . （18）（本小题满分12分）某水产品经销商销售某种鲜鱼，售价为每公斤20元，成本为每公斤15元.销售宗旨是当天进货当天销售.如果当天卖不出去，未售出的全部降价处理完，平均每公斤损失3元.根据以往的销售情况，将日需求量按[50,150)，[150,250)，[250,350)，[350,450)，[450,550]进行分组，得到如图所示的频率分布直方图.在频率分布直方图的需求量分组中，以各组区间的中点值代表该组的各个值. （Ⅰ）求未来连续三天内，该经销商有连续两 天该种鲜鱼的日销售量不低于350公斤，而另 一天日销售量低于350公斤的概率；（Ⅱ）该经销商计划每日进货300公斤或400 公斤，以每日利润Y 的数学期望值为决策依据. 他应该选择每日进货300公斤还是400公斤？ （19）（本小题满分12分）如图，在四棱锥-P ABCD 中，底面ABCD 为菱形，PA ⊥平面ABCD ，2AB =，60ABC ∠=o ，E F ，分别是BC PC ，的中点． （Ⅰ）证明:AE PD ⊥；（Ⅱ）设H 为线段PD 上的动点，若线段EH 长的最小值为5，求二面角--E AF C 的余弦值． （20）(本小题满分12分)已知圆C ：224x y +=与x 轴交于1F ，2F (2F 在原点右侧)两点，动点P 到1F ，2F 两点的距离之和为定值()22a a >，且12cos F PF ∠的最小值为−13．（Ⅰ）求动点P 的轨迹方程；（Ⅱ）过2F 且斜率不为零的直线l 与点P 的轨迹交于A ，B 两点，若存在点E ，使得2EA EA AB +⋅uu r uu r uu u r是与直线l 的斜率无关的定值，则称E 为“恒点”．问在x 轴上是否存在这样的“恒点”?若存在，请求出该点的坐标；若不存在，请说明理由．（21）(本小题满分12分)已知函数()ln f x x =.（Ⅰ）设()()1gx f x ax =-+，讨论()g x 的单调性；（Ⅱ）若不等式()()f x a e x b ≤-+恒成立，其中e 为自然对数的底数，求ba的最小值.请考生在22、23二题中任选一题作答，如果多做，则按所做第一题记分. （22）（本小题满分10分）选修4-4：坐标系与参数方程已知曲线C 的参数方程为2cos 2sin x y θθ=⎧⎪⎨=⎪⎩(θ为参数).以平面直角坐标系xOy 的原点O 为极点，x 轴的正半轴为极轴,取相同的单位长度建立极坐标系，设直线l 的极坐标方程为()cos 2sin 6ρθθ-=. （Ⅰ）求曲线C 的直角坐标方程及直线l 的普通方程；（Ⅱ）设P 为曲线C 上任意一点，求点P 到直线l 的距离的最值. （23）（本小题满分10分）选修4-5：不等式选讲 已知函数()2,()3f x x g x x m =-=-++()m R ∈ （Ⅰ）解关于x 的不等式()20(R)f x a a +->∈；（Ⅱ）若函数()f x 的图象恒在函数()g x 图象的上方，求m 的取值范围.高三年级第八次月考（第四次模拟）数学（理科）答案一．选择题 1 2 3 4 5 6 7 8 9 10 11 12 BCABDBDCBBAD二．填空题13. 4 14. -1 15.48π 16. 三．解答题18.（Ⅰ）由频率分布直方图可知，日销售量不低于350公斤的概率为(0.0025＋0.0015)×100＝0.4，则未来连续三天内，有连续两天的日销售量不低于350公斤，而另一天日销售量低于350公斤的概率P ＝0.4×0.4×(1－0.4)＋(1－0.4)×0.4×0.4＝0.192．.....4分（Ⅱ）当每日进货300公斤时，利润Y1可取－100，700，1500，此时Y1的分布列为：Y1－100 700 1500P 0.1 0.2 0.7此时利润的期望值E(Y1)＝－当每日进货400公斤时，利润Y2可取－400，400，1200，2000，此时Y2的分布列为：Y2－400 400 1200 2000P 0.1 0.2 0.3 0.4此时利润的期望值E(Y2)＝1200；因为E(Y1)＜E(Y2)，所以该经销商应该选择每日进货400公斤．......12分19.证明：20．【解析】(1)由已知，22x y +=4与x 轴交于1F (−2，0)，2F (2，0)，则|1F 2F | =4，由题意知|P 1F |+|P 2F |=2a ，cos ∠1F P 2F =222121212||||||2||||PF PF F F PF PF +-=22121212(||||)||2||||PF PF F F PF PF +-−1=2124162||||a PF PF -−1≥224162a a -−1=1−28a =−13，当且仅当|P 1F |=|P 2F |=a时等号成立，因而2a =6，由椭圆的定义知，P 的轨迹为椭圆，且1F ，2F 分别为其左、右焦点，2b =2a −2c =2，所以所求轨迹方程为26x +22y =1 …6分(2)如图，设直线l 的方程为x= my+2，A(1x ，1y )，B(2x ，2y )，由222162x my x y =+⎧⎪⎨+=⎪⎩，得(m 2+3)y 2+4my −2=0，则1y +2y =−243m m +，1y 2y =−223m +．（8分） 假设存在这样的“恒点”E(t ，0)，则2EA EA AB +⋅u u u r u u u r u u u r =EA EB ⋅u u u r u u u r=(1x −t ，1y )·(2x −t ，2y )=(m 1y +2−t ，1y )·(m 2y +2−t ，2y )=(m 2+1) 1y 2y +(2−t)m(1y +2y )+(2−t)2 =2222224(2)33m t m m m ----++++(2−t)2=2222(6)312103t m t t m -+-++．若2EA EA AB +⋅u u u r u u u r u u u r是与直线l 的斜率无关的定值，则其为与m 无关的定值，则32t −18=32t −12t+10，得t=73， 此时定值为(73)2−6=−59，“恒点”为(73，0)．（12分） 21. 【解析】（Ⅰ）函数定义域为()0,+∞，由题意得()ln 1g x x ax =-+，则()'1g x a x=-， ①当0a ≤时，()'0g x >，则()g x 在()0,+∞上单调递增；②当0a >时，令()'0g x =，解得1x a=，当10,x a ⎛⎫∈ ⎪⎝⎭时，()'0g x >，()g x 在10,a ⎛⎫ ⎪⎝⎭上单调递增， 当1,x a ⎛⎫∈+∞⎪⎝⎭时，()'0g x <，()g x 在1,a ⎛⎫+∞ ⎪⎝⎭上单调递减 …4分 （Ⅱ）设函数()()ln F x x a e x b =---，其中e 为自然对数的底数， ∴()'1F x e a x=+-，0x >， 当a e ≤时，()'0F x >，()f x 在()0,+∞上是增函数，∴()0F x ≤不可能恒成立， 当a e >时，由()'10F x e a x =+-=，得1x a e=-, ∵不等式()0F x ≤恒成立，∴()max 0F x ≤， 当10,x a e ⎛⎫∈ ⎪-⎝⎭时，()'0F x >，()F x 单调递增， 当1,x a e ⎛⎫∈+∞⎪-⎝⎭时，()'0F x <，()F x 单调递减， ∴当1x a e =-时，()F x 取最大值，()1ln 10F a e b a e ⎛⎫=----≤ ⎪-⎝⎭， ∴满足()ln 10a e b -++≥即可，∴()1ln b a e ≥---， ∴()()1ln a e b a e a a---≥>， 令()()1ln x e G x x---=，x e >，()()()()()'221ln ln xx e x e x e e x e G x x x e x -++-----==- 令()()()ln H x x e x e e =---，()()'ln 1H x x e =-+， 由()'0H x =，得1x e e=+， 当1,x e e ⎛⎫∈++∞ ⎪⎝⎭时，()'0H x >，()H x 是增函数， 当1,x e e e ⎛⎫∈+ ⎪⎝⎭时，()'0H x <，()H x 是减函数，∴当1x e e =+时，()H x 取最小值11H e e e e ⎛⎫+=-- ⎪⎝⎭，∵x e →时，()0H x →，2x e >时，()0H x >，()20H e =， ∴当(),2x e e ∈时，()'0G x <，()G x 是减函数，当()2,x e ∈+∞时，()'0G x >，()G x 是增函数，∴2x e =时，()G x 取最小值，()11122G e e e--==-， ∴b a 的最小值为1e- …12分。

2021届吉林省吉林市高三四模数学（理）试题一、单选题1．已知全集{0,1,2,3,4}U A B =⋃=，(){1,3}U A C B =，则集合B =（ ）A ．{1,3}B ．{1,2,3,4}C ．{0,2,4}D ．{0,1,2,3,4}【答案】C【分析】由题设，结合韦恩图，即可求集合B . 【详解】由{0,1,2,3,4}U A B =⋃=，(){1,3}U AC B =，∴{0,2,4}B =. 故选：C.2．已知α是第二象限角，则（ ） A ．cos 0α> B ．sin 0α<C ．sin 20α<D ．tan 0α>【答案】C【分析】由已知结合三角函数的定义及象限角的范围，及正弦的二倍角公式判断即可. 【详解】由α是第二象限角，可得cos 0α<，sin 0α>，tan 0α<sin 22sin cos 0ααα∴=<故选：C3．已知a R ∈，i 是虚数单位，若复数21(1)z a a i =-++为纯虚数，则a =（ ）A ．0B ．1或-1C ．1-D ．1【答案】D【分析】直接由实部为0且虚部不为0列式求解. 【详解】21(1)z a a i =-++为纯虚数，∴21010a a ⎧-=⎨+≠⎩，即1a =. 故选：D .【点睛】本题考查复数的基本概念，是基础的计算题.4．甲，乙，丙三名运动员在某次测试中各射击20次，三人测试成绩的频率分布条形图分别如图1，图2和图3，若s 甲，s 乙，s 丙分别表示他们测试成绩的标准差，则（ ）A ．s s s <<乙甲丙B ．s s s <<乙甲丙C ．s s s <<乙甲丙D ．s s s <<乙甲丙【答案】D【分析】先分别求出甲，乙，丙三名运动员射击成绩的平均分，然后根据方差公式求出相应的方差，比较大小可得标准差的大小.【详解】甲的平均成绩为(78910)0.258.5+++⨯=,其方差为222220.25(78.5)(88.5)(98.5)(108.5) 1.25S ⎡⎤=⨯-+-+-+-=⎣⎦甲乙的平均成绩为70.380.290.2100.38.5⨯+⨯+⨯+⨯=, 其方差为222220.3(78.5)0.2(88.5)0.2(98.5)0.3(108.5) 1.45S =⨯-+⨯-+⨯-+⨯-=乙丙的平均成绩为70.280.390.3100.28.5⨯+⨯+⨯+⨯= 其方差为222220.2(78.5)0.3(88.5)0.3(98.5)0.2(108.5) 1.05S =⨯-+⨯-+⨯-+⨯-=丙. 所以s s s <<乙甲丙 故选： D5．已知随机变量(5,1)X N ~，且()0.6827P X μσμσ-<≤+≈，(22)0.9545P X μσμσ-<≤+≈，则(67)P X <≤为（ ）A ．0.1358B ．0.1359C ．0.2716D ．0.2718【答案】B【分析】由随机变量(5,1)X N ~可知5,1μσ==，利用正态分布的对称性求解即可 【详解】由随机变量(5,1)X N ~知，5,1μσ==， 所以(46)0.6827P X <≤≈，(37)0.9545P X <≤≈， 所以1(67)[(37)(46)]0.13592P X P X P X <≤=<≤-<≤=， 故选：B6．若点(1,1)P 为圆22(4)16x y -+=的弦AB 的中点，则弦AB 所在直线方程为（ ） A ．340x y +-= B ．320x y -+= C ．340x y +-= D ．320x y --=【答案】D【分析】求得圆心坐标为(4,0)C ，根据斜率公式求得PC k ，再根据圆的弦的性质，得到2AB k =，结合直线点斜式方程，即可求解. 【详解】因为圆22(4)16x y -+=， 所以圆心坐标为(4,0)C ，半径为4， 又由斜率公式，可得011413PC k -==--， 根据圆的弦的性质，可得1PC ABk k ，所以3AB k =，所以弦AB 所在直线方程为13(1)y x -=-，即320x y --=， 所以弦AB 所在直线方程为320x y --=. 故选：D7．设m n 、是两条不同的直线，αβ、是两个不同的平面，下列命题中正确的是（ ）A ．,,m n m n αβαβ⊥⊂⊥⇒⊥B ．//,,//m n m n αβαβ⊥⇒⊥C ．,,//m n m n αβαβ⊥⊥⇒⊥D ．,,m n m n αβαββ⊥=⊥⇒⊥【答案】B【分析】利用空间直线与直线、直线与平面、平面与平面的位置关系逐个判断可得答案. 【详解】对于A ，,,//m n m n αβαβ⊥⊂⊥⇒或α与β相交但不垂直或αβ⊥，故A 不正确；对于B ，因为//n β，过n 作平面γ交平面β于n '，所以//n n '，由//αβ，m α⊥可得m β⊥，所以m n '⊥，所以m n ⊥，故B 正确；对于C ，,,////m n m n αβαβ⊥⊥⇒或m 、n 相交且垂直或m 、n 相交但不垂直或m 、n 异面且垂直或m 、n 异面但不垂直，故C 不正确；对于D ，,,//m n m n αβαββ⊥=⊥⇒或n β⊂或n 与β相交但不垂直或n β⊥.故选：B8．已知,,a b c 分别为ABC 三个内角,,A B C 的对边，且cos 3sin 0a C a C b c --=，则A 为（ ）A ．6π B ．3πC ．23π D ．4π 【答案】B【分析】先利用正弦定理把cos 3sin 0a C a C b c --=都统一成角，然后消去角B ，再利用辅助角公式化为1sin()62A π-=，从而可求出角A 的值. 【详解】因为cos 3sin 0a C a C b c --=， 所以sin cos 3sin sin sin sin 0A C A C B C --=， 因为()B A C π=-+，所以sin sin[()]sin()sin cos cos sin B A C A C A C A C π=-+=+=+， 所以sin cos 3sin sin (sin cos cos sin )sin 0A C A C A C A C C -+-=，3sin sin cos sin sin 0A C A C C --=，因为sin 0C ≠3sin cos 1A A -=，所以1sin()62A π-=， 因为5666A πππ-<-<，所以66A ππ-=，得3A π=故选：B【点睛】关键点点睛：利用正弦定理，统一为角的问题，利用三角恒等变换化简，是解题的关键，属于中档题.9．已知1112332222log log log 0x x x ==<，则123,,x x x 的大小关系是（ ）A ．213x x x >>B ．321x x x >>C ．123x x x >>D ．312x x x >>【答案】A【分析】根据已知不等式，得到123,,x x x 之间的关系及与1的关系，利用不等式的比较方法即可得到结果.【详解】∵11123313222222log log log 0log 1log 1x x x ==<==，∴11x >，21>x ，31x <，212x x =，∴()111122110x x x x x x -=-=-<，∴12x x <，∴213x x x >>. 故选：A.10．一副三角板有两种规格，一种是等腰直角三角形，另一种是有一个锐角是30的直角三角形，如图两个三角板斜边之比为3:2.四边形ABCD 就是由三角板拼成的，2AB =，60ABC ∠=︒，则AB CD AC DB ⋅+⋅的值为（ ）A ．23B ．6-C ．623--D ．23-【答案】C【分析】建立直角坐标系,利用数量积的坐标表示求解即可. 【详解】建立如图所示直角坐标系：因为2AB =，60ABC ∠=︒， 所以23,6AC AD ==则()((2,0,0,23,3,3B C D -， 所以()()()(2,0,0,23,3,3,23,3AB AC CD DB ===--=+-，所以623AB CD AC DB -⋅+⋅=-故选：C11．已知函数()sin (0)f x x ωω=>在区间2,33ππ⎡⎤-⎢⎥⎣⎦上单调递增，且|()|1f x =在区间[]0,π上有且仅有一个解，则ω的取值范围是（ ） A ．30,4⎛⎫ ⎪⎝⎭B ．33,42⎡⎫⎪⎢⎣⎭C ．13,22⎡⎫⎪⎢⎣⎭D ．13,24⎡⎤⎢⎥⎣⎦【答案】D【分析】先利用整体代换思想以及正弦函数的单调递增区间求出函数()f x 的单调递增区间，结合集合的包含关系求出ω的范围，然后再利用正弦函数取最大值的性质可再得一个ω的范围，两个范围取交集即可求解. 【详解】令2,222x k k ππωππ⎡⎤∈-+⎢⎥⎣⎦，解得22,22k k x ππππωωωω⎡⎤∈-+⎢⎥⎣⎦，k Z ∈，而函数()sin (0)f x x ωω=>在区间2,33ππ⎡⎤-⎢⎥⎣⎦上单调递增， 所以223230ππωππωω⎧-≤-⎪⎪⎪≥⎨⎪>⎪⎪⎩，解得304ω<≤，当[]0,x π∈时，[]0,x ωω∈π，因为|()|1f x =在区间[]0,π上有且仅有一个解，所以232πωππωπ⎧≥⎪⎪⎨⎪<⎪⎩，解得1322ω≤<.综上所述，ω的取值范围是1324ω≤≤. 故选：D.【点睛】本题的核心是利用整体思想，首先根据正弦函数的单调性，以及已知单调性得ω的一个取值范围；然后根据取最值的个数，求得ω的另一个范围.这里要注意，|()|1f x =说明()1f x =±，而根据题意，|()|1f x =只有一个解，所以()f x 只能取一个值，而根据函数本身的图象可以发现()f x 只能等于1.如果能够取到1-，那么根据自变量的范围，此时()f x 肯定也可以取1，所以舍去.12．已知抛物线2:2(0)C y px p =>的焦点为F ，过点F 的直线l 交抛物线于,A B 两点，以线段AB 为直径的圆与y 轴交于,M N 两点，设线段AB 的中点为Q ，若抛物线C 上存在一点(3,)E t 到焦点F 的距离等于4.下面四个命题： ①抛物线的方程是22y x = ②抛物线的准线方程是1x =- ③sin QMN ∠的最小值是12④线段AB 长的最小值是4 其中正确的命题的个数是（ ） A ．4 B ．3C ．2D ．1【答案】B【分析】求得抛物线的焦点和准线方程，运用抛物线的定义可得p ，进而得到抛物线方程和准线方程；求得()0F ，1，设()11,A x y ，()22,B x y ，直线l 的方程为1x mx =+，联立抛物线方程，运用韦达定理和弦长公式可得线段AB 的最小值，可得圆Q 的半径，由中点坐标公式可得Q 的坐标，运用直角三角形的锐角三角函数的定义，可得所求sin QMN ∠的最小值.【详解】抛物线2:2(0)C y px p =>的焦点为,02p F ⎛⎫⎪⎝⎭，得抛物线的准线方程为2p x =-， 点(3,)E t 到焦点F 的距离等于4，可得342p+=，解得2p =， 则抛物线C 的方程为24y x =，准线为1x =-，故①错误，②正确；因为()10F ，， 设()11,A x y ，()22,B x y ，直线l 的方程为1x my =+， 由21 4x my y x=+⎧⎨=⎩，消去x 得2440y my --=， 所以124y y m +=，124y y =-，所以()21212242x x m y y m +=++=+，所以AB 的中点Q 的坐标为()2212m m +，， 221242244AB x x p m m =++=++=+，故线段AB 的最小值是4，即④正确；所以圆Q 的半径为222r m =+， 在等腰QMN 中，22221111sin 11222222Qx m QMN r m m +∠===-≥-=++， 当且仅当0m =时取等号， 所以sin QMN ∠的最小值为12，即③正确， 故选：B【点睛】关键点点睛：根据抛物线的定义可求出抛物线的方程，利用直线与抛物线相交联立方程消元，由韦达定理可求弦中点坐标，弦长，圆的几何性质求最值，属于中档题.二、填空题13．已知变量x和y需满足约束条件2526x yx yx-≥⎧⎪-≤⎨⎪≤⎩，则yzx=的最小值为___________.【答案】13【分析】作出可行域，根据yzx=的几何意义求解即可.【详解】作出可行域如图，yzx=可表示为可行域内一点与原点连线的斜率，由25020x yx y--=⎧⎨--=⎩解得31xy=⎧⎨=⎩，即(3,1)A,根据图象可知当yzx=过点A时，即13z=时，直线的斜率最小，故答案为：1314．宋元时期是我国古代数学非常辉煌的时期，涌现了一大批卓有成就的数学家，其中秦九韶､李冶､杨辉和朱世杰成就最为突出，被誉为“宋元数学四大家”.现从秦九韶的《数书九章》､李冶的《测圆海镜》《益古演段》､杨辉的《详解九章算法》､朱世杰的《算学启蒙》《四元玉鉴》这六部著作平均分给班级的3个数学兴趣小组，则有___________种不同的分配方式.【答案】90【分析】先从6部中选2部，再从剩下的4部中选2部，此时把6部书分成3份，然后分给3个数学兴趣小组即可【详解】解：由题意得，六部著作平均分给班级的3个数学兴趣小组的方法数有222322264236423390C C CA C C CA⋅==,故答案为：9015．已知函数1()ln 21x f x x =+-，设121()n F n f f f n n n -⎛⎫⎛⎫⎛⎫=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，其中*n N ∈且2n ≥，则(2021)F =___________.【答案】1010【分析】由于111()(1)ln ln 1212x x f x f x x x-+-=+++=-，然后利用倒序相加法求解即可【详解】解：因为1()ln 21x f x x=+- 所以111()(1)ln ln 1212x x f x f x x x-+-=+++=-， 因为1221()n n F n f f f f n n n n --⎛⎫⎛⎫⎛⎫⎛⎫=++++⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭， 所以121()2n n F n f f f f n n n n --⎛⎫⎛⎫⎛⎫⎛⎫=++++⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭， 所以2()1F n n =-，所以1()2n F n -=， 所以20211(2021)10102F -==， 故答案为：1010三、双空题16．如图所示，在长方1111ABCD A BC D -中，13,4,5AB AD AA ===，点E 是棱1CC 上的一个动点，若平面1BED 交棱1AA 于点F ，则四棱锥11B BED F -的体积为___________，截面四边形1BED F 的周长的最小值为___________.【答案】20 274【分析】根据锥体的体积计算，利用切割法可得四棱锥11B BED F -的体积；将几何体展开，根据两点之间直线最短，即可求出最短周长的截面，进而根据勾股定理即可求得结果.【详解】由题意可得1//D F BE ，利用切割法可得1111111111B BED F B BED B BFD D BEB D BFB V V V V V -----=+=+1111111322BB BC AB BB D A AB ⎡⎤=⋅⋅⋅+⋅⋅⎢⎥⎣⎦ ()115435432032=⨯⨯⨯+⨯⨯=； 将长方体展开，如图所示，当点E 为1BD 与1CC 的交点、点F 为1BD 与1AA 的交点时，截面周长最小， 此时截面的周长为12BD ，而在1BDD 中，()22153474BD =++=， 所以截面周长的最小值为274. 故答案为：20；274.四、解答题17．已知等比数列{}n a 的前n 项和为132n n S m +=-.（1）求m 的值，并求出数列{}n a 的通项公式；（2）令3(1)log nn n b a =-，设n T 为数列{}n b 的前n 项和，求2n T .【答案】（1）32m =，3nn a =；（2）2n T n =. 【分析】（1）法一：由已知n S 求1a 、n a ，根据等比数列的性质确定1a 的值，进而求出m ，写出{}n a 通项公式；法二：由n a 与n S 的关系，结合已知求得1a 、2a ，3a ，再根据等比中项的性质求m ，写出{}n a 通项公式；（2）由（1）写出{}n b 通项公式，由奇偶项和为定值，应用并项求和法求2n T . 【详解】（1）法一：当1n =时，1192a S m ==- 当2n ≥时，1133()322n nn n n n a S S m m +-=-=---=∵{}n a 是等比数列， ∴13a =，即932m -=，解得32m =综上，m 的值为32，数列{}n a 的通项公式为3nn a =. 法二：∵1192a S m ==-，2219a S S =-=，33227a S S =-= ∵{}n a 是等比数列， ∴2213a a a ，即9()27812m -⨯=，解得32m =，设{}n a 的公比为q ， ∴213a q a ==，11a =，则1333n n n a -=⨯=. （2）∵3(1)log (1)n nn n b a n =-=-⋅，∴21234212n n n T b b b b b b -=++++⋅⋅⋅++(1)2(3)4[(21)]2n n=-++-++⋅⋅⋅+--+(12)(34)[(21)2]n n =-++-++⋅⋅⋅+--+n =.18．已知斜三棱柱111ABC A B C -，侧面11ACC A 与底面ABC 垂直，90ABC ∠=︒，2BC =，22AC =，且1111,AA AC AA AC ⊥=.（1）试判断1A A 与平面1A BC 是否垂直，并说明理由；（2）求二面角1A BC C --的余弦值. 【答案】（1）不垂直，理由见解析；（2）3-. 【分析】取AC 中点O ，连接1AO ､BO ，可证明1AO ⊥平面ABC ，以OC 为x 轴，OB 为y 轴，1OA 为z 轴建立空间直角坐标系，（1）利用计算1AA BC⋅的值确定1A A 与平面1A BC 是否垂直；（2）根据二面角的向量法求解即可.【详解】取AC 中点O ，连接1AO ､BO ，又1AA AC =，得1AO AC ⊥，平面11ACC A ⊥平面ABC ，交线为AC ，又1AO ⊂平面11ACC A，则1AO ⊥平面ABC ， ∵90,2,22ABC BC AC ∠=︒==，∴2BC AB ==， ∵O 为AC 中点，∴OB AC ⊥以OC 为x 轴，OB 为y 轴，1OA 为z 轴建立如图所示的空间直角坐标系，如图 ，则12)A ，(2,0,0)C ，2,0)B ，(2,0,0)A -，1(22,0,2)C （1）1(2,0,2)AA =，(2,2,0)BC =-， 1220(2)2020AA BC ⋅=⨯-=≠，所以1AA 与BC 不垂直，即1AA 与平面1A BC 不垂直.(另解：求出平面ABC 法向量0(1,1,1)n =，1AA 与0n 不平行，则1AA 与平面1A BC 不垂直)（2）因为1AO ⊥平面ABC ，设平面ABC 的一个法向量(0,0,1)m = 设(,,)n x y z =为平面11BB C C 的一个法向量，(2,2,0)BC =-，1(2,0,2)CC =由10000n BC n CC ⎧=⋅=⎪⇒⎨⋅=⎪=⎩ 令1x =，则1,1yz，即(1,1,1)n =-，又因为cos ,m n <>== 由图知，二面角1A BC C --为钝角， 所以二面角1A BC C --的余弦值为 【点睛】方法点睛：向量法求二面角的方法就是分别求出二面角的两个面所在平面的法向量，然后通过两个平面的法向量的夹角得到二面角的大小，但要注意结合实际图形判断所求角是锐角还是钝角．19．江苏卫视推出的大型科学竞技真人秀《最强大脑（8）》现已进入联盟抢分赛环节，由12强选手组建的凌霄､逐日､登峰联盟三支队伍(每队四人)将进行“12进6”的登顶预备战，每局有两队参加，没有平局.按12强历次成绩统计得出，在一局比赛中，逐日联盟胜凌霄联盟的概率为35，逐日联盟胜登峰联盟的概率为45，凌霄联盟胜登峰联盟的概率为35.联盟抢分赛规则如下：按抽签决定由逐日联盟和凌霄联盟先进行第一局的比赛，然后每局的获胜队与未参加此局比赛的队伍进行下一局的比赛.在比赛中，有队伍先获胜两局，就算取得比赛的胜利，直接晋级6强的全国脑王争霸赛. （1）求只进行两局比赛，逐日联盟晋级6强的概率； （2）求只进行两局比赛，就能确定晋级6强联盟队的概率； （3）求逐日联盟晋级6强的概率. 【答案】（1）1225；（2）1825；（3）35.【分析】（1）记“只进行两局比赛，逐日联盟晋级6强”为事件A ，根据独立事件乘法公式，即可求得答案.（2）记“只进行两局比赛，就能确定晋级6强联盟队”为事件B ，则事件B 包含逐日联盟晋级或凌霄联盟晋级，代入数据，即可得答案.（3）记“逐日联盟晋级6强”为事件C .则事件C 包含三种情况：①逐日联盟胜凌霄联盟，逐日联盟胜登峰联盟；②逐日联盟胜凌霄联盟，逐日联盟负登峰联盟，登峰联盟负凌霄联盟，逐日联盟胜凌霄联盟；③逐日联盟负凌霄联盟，凌霄联盟负登峰联盟，登峰联盟负逐日联盟，逐日联盟胜凌霄联盟，分别求解，即可得答案. 【详解】（1）记“只进行两局比赛，逐日联盟晋级6强”为事件A . ∴()34125525P A =⨯= （2）记“只进行两局比赛，就能确定晋级6强联盟队”为事件B 则事件B 包含逐日联盟晋级或凌霄联盟晋级. ∴()342318555525P B =⨯+⨯= （3）记“逐日联盟晋级6强”为事件C .则事件C 包含三种情况： ①逐日联盟胜凌霄联盟，逐日联盟胜登峰联盟：34125525⨯= ②逐日联盟胜凌霄联盟，逐日联盟负登峰联盟，登峰联盟负凌霄联盟，逐日联盟胜凌霄联盟：3133275555625⨯⨯⨯= ③逐日联盟负凌霄联盟，凌霄联盟负登峰联盟，登峰联盟负逐日联盟，逐日联盟胜凌霄联盟：2243485555625⨯⨯⨯= ∴()1227483256256255P C =++= 20．已知点F 为椭圆2222:1(0)x y C a b a b+=>>的右焦点，椭圆上任意一点到点F 距离的最大值为3，最小值为1. （1）求椭圆C 的标准方程；（2）若M 为椭圆C 上的点，以M 为圆心，MF 长为半径作圆M ，若过点(1,0)E -可作圆M 的两条切线,EA EB (,A B 为切点)，求四边形EAMB 面积的最大值.【答案】（1）22143x y +=；（2【分析】（1）由题意可得关于,a c 的方程，解出即可得椭圆方程；（2）由椭圆的定义可得||4ME r r =->，将BE 用r 表示，四边形EAMB 面积表示为关于r 的表达式，利用导数与单调性的关系得最值即可.【详解】（1）根据题意椭圆上任意一点到点F 距离的最大值为3，最小值为1.所以31a c a c +=⎧⎨-=⎩，解得2,1a c ==，所以3b =因此椭圆C 的标准方程为22143x y +=（2）由（1）知，()1,0E-为椭圆的左焦点，根据椭圆定义知，||||4ME MF +=，设|r MF MB ==｜， ∵点E 在圆M 外，∴||4ME r r =->，∴12r ≤< 所以在直角三角形MEB 中，22||(4)242EB r r r =--=-，1||||422MEBSEB MB r r =⋅=-， 由圆的性质知，四边形EAMB 面积2242MEBS S r r ==-，其中12r ≤<.即()3222412S r r r =-+≤<.令()322412y r r r =-+≤<，则2682(34)y r r r r '=-+=--当413r <<时，0y '>，3224y r r =-+单调递增； 当423r <<时，0y '<，3224y r r =-+单调递减. 所以，在43r =时，y 取极大值，也是最大值此时32max44162243329S ⎛⎫⎛⎫=-+= ⎪ ⎪⎝⎭⎝⎭.【点睛】关键点点睛：（1）椭圆上长轴上的两个顶点到焦点的距离即为椭圆上的点到焦点的距离最值；（2）将四边形的面积表示为关于r 的函数，通过导数求最值即可. 21．已知函数11()ln 2a f x x ax a x -⎛⎫=-+> ⎪⎝⎭. （1）当曲线()y f x =在(2,(2))f 处的切线与直线:21l y x =+垂直时，求实数a 的值；（2）求函数()f x 的单调区间. （3）求证：()*1111111ln(1)1234123n n N n n++++<+<++++∈+.【答案】（1）1a =；（2）答案见解析；（3）证明见解析. 【分析】（1）由题意可得111(2)242a f a -'=-+=-，从而可求出a 的值； （2）由于221(x 1)(x )11(x)aa a af a x xx -----'=-+=，12a >，所以分101a a-<<和10aa-≤两种情况讨论导函数的正负，从而可求得函数的单调区间； （3）由（2）可知ln 1≤-x x 在(0,)+∞恒成立，所以11ln 1x x≤-，即1ln 1x x ≥-在(0,)+∞恒成立，因此当(0,)x ∈+∞时不等式11ln 1x x x 恒成立，用1k k+替换x 得11ln(1)ln 1k k k k<+-<+，然后给k 从取到n ，得到n 个式子相加可得结论 【详解】因为1()ln (0)af x x ax x x-=-+>， 所以211()a f x a x x-'=-+ （1）根据题意111(2)242a f a -'=-+=- 解得1a =，满足12a >，∴1a = （2）221(x 1)(x )11(x)aa a a f a x xx -----'=-+=当112a <<时，101a a-<<， 令()0f x '>，∴11a x a -<<，令()0f x '<，∴10ax a-<<或1x > 所以()f x 的递增区间是1(,1)a a -，递减区间是1(0,),(1,)aa-+∞ 当1a ≥时，10aa-≤， 令()0f x '>，∴01x <<，令()0f x '<，∴1x >所以()f x 的递增区间是(0,1)，递减区间是(1,)+∞综上所述：当112a <<时，()f x 的递增区间是1(,1)a a -，递减区间是1(0,),(1,)aa-+∞； 当1a ≥时，()f x 的递增区间是(0,1)，递减区间是(1,)+∞.（3）由（2）知当1a =时，()ln f x x x =-，并且max ()(1)1f x f ==-， 因此有ln 1≤-x x 在(0,)+∞恒成立， 用1x替换x 得11ln 1x x ≤-，即1ln 1x x ≥-在(0,)+∞恒成立，因此当(0,)x ∈+∞时不等式11ln 1xx x恒成立，令k *∈N 用1k k+替换x 得11ln(1)ln 1k k k k <+-<+， 所以11111[ln(1)ln ]1nn nk k k k k k k===<+-<+∑∑∑ 即1111111ln(n 1)1234123n N n n*+++⋅⋅⋅+<+<+++⋅⋅⋅+∈+， 【点睛】关键点点睛：此题考查导数的应用，考查导数的几何意义，利用导数求函数的单调区间，考查不等式的证明，解题的关键是由（2）可得当(0,)x ∈+∞时不等式11ln 1xx x恒成立，用1k k+替换x 得11ln(1)ln 1k k k k <+-<+，然后给k 从取到n ，得到n 个式子相加可得结论，考查计算能力，属于较难题22．在平面直角坐标系xOy 中，点P 是曲线11:1x t tC y t t ⎧=+⎪⎪⎨⎪=-⎪⎩(t 为参数)上的动点，以坐标原点O 为极点，x轴的正半轴为极轴建立极坐标系，曲线2C 的极坐标方程为sin 3cos ρθθ=-.（1）求曲线1C 的普通方程和曲线2C 的直角坐标方程； （2）若点P 在y 轴右侧，点Q 在曲线2C 上，求||PQ 的最小值.【答案】（1）1C ：22144x y -=，2C：30x y -+=；（2【分析】（1）由11:1x t tC y t t ⎧=+⎪⎪⎨⎪=-⎪⎩，消去t 即可；将cos sin x y ρθρθ=⎧⎨=⎩代入sin 3cos ρθρθ-=得到曲线2C 的直角坐标方程；（2）设点P 坐标为()11(,)0t t t t t+->，PQ 最小值，由点P到曲线2:30C x y -=的距离求解.【详解】（1）∵11:1x t tC y t t ⎧=+⎪⎪⎨⎪=-⎪⎩，消去t ,∴224x y -=，即曲线1C 的普通方程为∴22144x y -=.曲线2C的极坐标方程为sin 3cos ρθρθ-=由cos sin x y ρθρθ=⎧⎨=⎩得曲线2C的直角坐标方程为30x y -=. （2）∵P 是曲线1C 右支上的动点， ∴设点P 坐标为()11(,)0t t t t t+->， ∵Q 是曲线2C 上，∴PQ 最小值即点P到曲线2:30C x y -=的距离()d t ，则()d t ==， ∵0t >，∴42t t +≥=，当且仅当t =∴当t =时，()d t∴PQ 23．设函数()|2|||(0)f x x a x a a =-++>. （1）若1a =，求证：()3f x ≥；（2）对于(0,1)x ∀∈，()3f x ≤恒成立，求实数a 的取值范围. 【答案】（1）证明见解析；（2）(]0,1.【分析】（1）由1a =时，利用绝对值三角不等式求解；（2）法一根据0a >转化为323-x a x a a x +-≤-≤-对()0,1x ∈恒成立求解；法二根据0a >结合()0,1x ∈，分21a ≥，021a <<讨论求解；【详解】（1）当1a =时，()()()212-13f x x x x x =-++≥-+=， 当且仅当()()210x x -+≤，等号成立， ∴()3f x ≥.（2）对于(0,1)x ∀∈，()3f x ≤恒成立， ∵0a >，∴0x a +>，∴|2|3x a x a -++≤， ∴|2|3x a a x -≤--，∴323-x a x a a x +-≤-≤-对()0,1x ∈恒成立，∴3323a a x ≤⎧⎨≥-⎩，即11a a ≤⎧⎨≥-⎩，∵0a >，∴01a <≤. ∴实数a 的取值范围(]0,1法二：∵0a >，∴()2f x x a x a =-++， ∵()0,1x ∈， 当21a ≥时，即12a ≥时，()233f x a x x a a =-++=≤， ∴1a ≤，∴112a ≤≤， 当021a <<即102a <<时，第 21 页 共 21 页 ①当02x a <≤时，()233f x a x x a a =-++=≤， ∴1a ≤，∴102a <<， ②当21a x <<时，()223f x x a x a x a =-++=-≤， ∴()max 23f x a =-≤，∴1a ≥-，∴102a <<， 由①②可知∴102a <<. 综上：a 的取值范围(]0,1【点睛】方法点睛：恒（能）成立问题的解法：若()f x 在区间D 上有最值，则（1）恒成立：()()min ,00x D f x f x ∀∈>⇔>；()()max ,00x D f x f x ∀∈<⇔<；（2）能成立：()()max ,00x D f x f x ∃∈>⇔>；()()min ,00x D f x f x ∃∈<⇔<. 若能分离常数，即将问题转化为：()a f x >（或()a f x <），则 （1）恒成立：()()max a f x a f x >⇔>；()()min a f x a f x <⇔<； （2）能成立：()()min a f x a f x >⇔>；()()max a f x a f x <⇔<；。

吉林省2021版高三上学期期中数学试卷（理科）B卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）若直线x+2y+1=0与直线ax+y﹣2=0互相垂直，那么a的值等于（）A . -2B . -C . -D . 12. （2分） (2019高二下·柳州期中) 下列命题中，真命题的是（）A .B .C . 的充要条件是D . 若，且，则中至少有一个大于13. （2分）设变量x，y满足约束条件，则目标函数z=x+y﹣3的最小值为（）A . -2B . -C . -1D . 54. （2分）某调查机构调查了某地100个新生婴儿的体重，并根据所得数据画出了样本的频率分布直方图（如图所示），则新生婴儿的体重（单位：kg）在[3.2，4.0）的人数是（）A . 30B . 40C . 50D . 555. （2分）若集合M＝{y|y＝2x ，x∈R}，P＝{x|y＝}，则M∩P＝（）A . (1，＋∞)B . [1，＋∞)C . (0，＋∞)D . [0，＋∞)6. （2分）函数y=cosx在其定义域上的奇偶性是（）A . 奇函数B . 偶函数C . 既奇且偶的函数D . 非奇非偶的函数7. （2分） (2019高一上·上海月考) 已知非空集合M满足：对任意，总有，且，若，则满足条件的M的个数是（）A . 11B . 12C . 15D . 168. （2分） (2017高二下·肇庆期末) 若z=4+3i，则 =（）A . 1B . ﹣1C . + iD . ﹣ i9. （2分） (2017高一下·上饶期中) 下列算式中不正确的是（）A .B .C .D .10. （2分）(2018·榆林模拟) 设，则的大小关系为（）A .B .C .D .11. （2分） (2016高一上·公安期中) 下列函数中，其定义域和值域分别与函数y=10lgx的定义域和值域相同的是（）A . y=xB . y=lgxC . y=2xD . y=12. （2分）(2019·东北三省模拟) 我国古代数学名著《九章算术·商功》中阐述：“斜解立方，得两壍堵。

2021届吉林省五校联考高三上学期联合模拟考试数学〔理〕试题一、单项选择题1．假设集合(){}{}22log 2,60A x y x B x x x ==-=--≤，那么()R A B =〔 〕A ．(]2,2-B ．[]22-,C ．()2,3D ．(]2,3【答案】B【分析】首先求出集合A 、B ，再根据补集、交集的定义计算可得； 【详解】解：(){}{}{}2log 2202A x y x x x x x ==-=-= 所以{}|2R A x x =≤所以(){}|22R A B x x =-≤≤ 应选：B2．i 是虚数单位，那么21ii+-的虚部为〔 〕 A ．32-B ．12-C ．12D ．32【答案】D【分析】利用复数的运算法那么即可得出．【详解】解：复数2(2)(1)131(1)(1)22i i i z i i i i +++===+--+，那么z 的虚部是32．应选：D ．3．()52x +的展开式中3x 项的系数为〔 〕 A ．20 B ．40 C ．60 D ．80【答案】B【分析】首先写出展开式的通项，再代入计算可得；【详解】解：()52x +的展开式的通项5152r r r r T C x -+=，令53r -=，解得2r ，所以232335240T C x x ==，所以3x 项的系数为40，应选：B4．假设数列{}n a 满足12211,1,n n n a a a a a ++===+，那么称数列{}n a 为斐波那契数列.斐波那契螺旋线是根据斐波那契数列画出来的螺旋曲线，自然界中存在许多斐波那契螺旋线的图案，是自然界最 完美的经典黄金比例.作图规那么是在以斐波那契数为边的正方形拼 成的长方形中画一个圆心角为90︒的扇形，连起来的弧线就是斐波 那契螺旋线，如下图的5个正方形的边长分别为125,,,a a a ⋅⋅⋅， 在长方形ABCD 内任取一点，那么该点不在任何一个扇形内的概率为〔 〕 A ．1031156π-B ．14π-C ．7116π-D ．391160π-【答案】D【分析】由题意求得数列{}n a 的前6项，求得长方形ABCD 的面积，再求出4个扇形的面积和，由测度比是面积比得答案．【详解】解：由题意可得，数列{}n a 的前6项依次为：1，1，2，3，5，8，∴长方形ABCD 的面积为5840⨯=．4个扇形的面积之和为222239(1235)44ππ+++=． ∴所求概率391160P π=-． 应选：D ．5．向量()(),2,1,1a x b ==，假设a b a b +=+，那么实数〔 〕 A ．1 B ．2 C ．3 D ．4【答案】B【分析】由a b a b +=+，平方可得,a b 两个向量同向，利用坐标公式求解即可. 【详解】由a b a b +=+，平方得222222a a b b a a b b +⋅+=+⋅+， 即a b a b ⋅=⋅，那么a b ，同向，故有1210x ⨯-⨯=，得2x =， 应选：B.6．执行如下图的程序框图，输出的S 值为〔 〕 A ．13B ．23C ．1321D ．610987【答案】C【分析】按箭头执行运算，一次运算后不满足判断框中的条件继续执行循环，二次运算后满足判断框中的条件退出循环，得出答案.【详解】20,1,,13i S S i ==== ，不满足判断框中的条件继续执行循环，22()1133,2221213S i +===⨯+ ，满足判断框中的条件退出循环.应选：C【点睛】直到型循环，先执行循环体，直到满足条件退出循环，注意计算的准确性.7．将函数()sin(2)(0)f x x ϕϕπ=+<<的图象向右平移4π个单位长度后得到函数π()sin(2)6g x x =+的图象，那么函数()f x 的一个单调减区间可以为〔 〕A ．π5π[,]1212-B ．π5π[,]66- C ．π5π[,]36- D ．π2π[,]63【答案】A【分析】先利用三角函数的平移变换的应用得2()sin(2)3f x x π=+，再利用正弦型函数单调减区间的整体思想的应用求出结果即可． 【详解】把()sin(2)(0)f x x ϕϕπ=+<<的图象向右平移4π个单位长度后，得到()sin(2)2g x x ϕπ=-+=sin(2)6x π+的图象， 0ϕπ<<，23πϕ∴=，即2()sin(2)3f x x π=+.令2222,232k x k k ππ3ππ+≤+≤π+∈Z ，解得5,1212k x k k Z ππππ-≤≤+∈，令0k =，可得函数()f x 的一个单调减区间为,]1212π5π[-. 应选：A ．8．关于直线,m n 与平面,αβ，有以下四个命题：①//,m nαβ且αβ⊥，那么//m n ；②//,//m n αβ且//αβ，那么//m n ；③,//m n αβ⊥且αβ⊥，那么m n ⊥ ； ④,m n αβ⊥⊥且αβ⊥，那么m n ⊥.其中正确命题的个数是〔 〕 A ．1 B ．2C ．3D ．4【答案】A【分析】对①，利用特殊情况即可判断；对②，由线面平行的判定定理以及面面平行的性质定理即可判断；对③④，根据面面垂直两个面的法向量与方向向量的关系即可判断. 【详解】解：对①，当m β⊂时，由n β⊥得m n ⊥，故①错误；对②，由线面平行的判定定理以及面面平行的性质定理可知，,m n 可能平行，相交，异面，故②错误；对③，由,m ααβ⊥⊥知：m β或m β⊂ ， 又n β，,m n ∴平行、相交或异面，故③错误；对④，由,m n αβ⊥⊥知：m 为α的法向量 ，n 为β的法向量， 又αβ⊥，m n ∴⊥，故④正确.应选：A.9．0.90.70.9log 0.9,log 0.7,0.7a b c ===，那么,,a b c 的大小关系是〔 〕 A ．a b c << B ．b a c << C ．a c b << D ．c a b <<【答案】C【分析】可直接判断1b >，(),0,1a c ∈，再以0.7为“桥梁〞，比拟,a c 大小即可. 【详解】0.70.70.7log 0.9log 0.70.7a =<=，所以()0,0.7a ∈；0.90.9log 0.7log 0.91b =>=，所以1b >；0.910.70.70.7c =>=，所以()0.7,1c ∈，故a c b <<.应选：C.10．双曲线()2222:10,0y x C a b a b-=>>的上、下焦点分别为12,F F ，点P 在双曲线上，且2PF y ⊥轴，假设12PF F △的内切圆半径为45a，那么双曲线的离心率为〔 〕A ．95B ．85C ．75 D ．65【答案】A【分析】由双曲线的性质结合直角三角形的内切圆半径公式，即可得到离心率.【详解】y c =代入双曲线方程，得2bx a=±，所以2221,||2b b PF PF a a a==+，12Rt PF F 内切圆半径为222(2)425b b c a a a a c a +-+=-=所以99,55a c e ==. 应选：A.11．函数()()11sin 1x x f x x e e --+=-+-，那么关于x 的不等式()0f x >的解集为〔 〕A ．(),1-∞B ．()1,+∞C ．()1,eD ．(),e +∞【答案】B【分析】求出导函数，结合根本不等式可得()0f x '>，可得()f x 是R 上的增函数，进而可得结果.【详解】依题意可得111()cos(1)x x f x x e e --'=-++，因为11111122x x x x e e e e ----+≥⋅=， cos(1)[1,1]x -∈-，所以()0f x '>，()f x 是R 上的增函数，又(1)0f =， 所以()0()(1)1f x f x f x >⇔>⇔>. 应选：B.【点睛】关键点点睛：此题的关键点是：得出函数()f x 是R 上的增函数.12．在ABC 中，BAC ∠的平分线交BC 于点,2,6D BD DC BC ==，那么ABC ∆的面积的最大值为〔 〕 A ．6 B ．62 C ．12 D ．122【答案】C【分析】设AC x =，BAC θ∠=，那么2AB x =，结合正弦定理表示得1sin 2ABCSAB AC BAC =⋅⋅∠，由余弦定理可得x 与θ的关系式，联立前式由同角三角函数和二次函数性质化简即可求解【详解】如图，设设AC x =，BAC θ∠=，那么由正弦定理可得sin sin BD ABBAD ADB=∠∠①，sin sin CD ACCAD ADC=∠∠②，又ADB ADC π∠+∠=，所以sin sin ADB ADC ∠=∠，①②式联立可得21AB AC =，那么2AB x =，那么211sin 2sin sin 22ABC S AB AC BAC x x x θθ=⋅⋅∠=⋅⋅=⋅△，对ABC ，由余弦定理可得22222536cos 24AB AC BC x BAC AB AC x +--∠==⋅，那么()22422242424425362536036sin 1cos 1416x x x S x x x x x θθ⎛⎫⎛⎫--+ ⎪=⋅=⋅-=⋅-=- ⎪ ⎪⎝⎭⎝⎭()()()2422422199********+14420256161616x x x x x ⎡⎤=--+=--=---⎢⎥⎣⎦， 当220x =时，2S 有最大值，()2max 925614416S =⨯=，所以max 12S =， 应选：C【点睛】此题考查由三角形的边角关系求解面积最值，正弦定理、余弦定理解三角形，属于难题，此题中的角平分线性质可当结论进行识记：AD 为ABC 的角平分线，那么AB BDAC CD= 二、填空题13．函数()54,0ln .0x x f x x x +≤⎧=⎨>⎩，那么35f f ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭__________. 【答案】0【分析】从内层往外逐层代入即可求解. 【详解】解：3354155f ⎛⎫⎛⎫-=⨯-+= ⎪ ⎪⎝⎭⎝⎭，()31ln105f f f ⎛⎫⎛⎫-=== ⎪ ⎪⎝⎭⎝⎭， 故答案为：0.14．假设x ，y 满足约束条件20030y x y x y -≤⎧⎪-≤⎨⎪+-≥⎩，那么y z x =的最大值为__________.【答案】2【分析】画出可行域，z 表示可行域上的点到原点(0,0)的斜率，分析并计算z 的最大值. 【详解】作出可行域如下图，又z 为可行域内的点到原点(0,0)O 的斜率，由图得z 的最大值为AO k ， 又(1,2)A ，得z 的最大值为AO k 2=. 故答案为：2【点睛】此题考查了线性规那么，正确画出不等式组表示的平面区域是解题的根底，理解目标函数的意义是解题的关键．15．甲、乙两支排球队进行比赛，约定先胜3局者获得比赛的胜利，比赛随即结束.除第五局甲队 获胜的概率是12外，其余每局比赛甲队获胜的概率都是23，假设各局比赛结果相互独立，那么甲队以3:2获胜的概率是__________. 【答案】427【分析】甲队以3:2获得比赛胜利是指前四局比赛甲、乙两队2:2平，第五比赛甲胜，由此利用n 次独立重复试验中事件A 恰好发生k 次的概率计算公式能求出甲队以3:2获得比赛胜利的概率．【详解】解：甲、乙两支排球队进行比赛，约定先胜3局者获得比赛的胜利，比赛随即结束．除第五局甲队获胜的概率是12外，其余每局比赛甲队获胜的概率都是23．假设各局比赛结果相互独立．甲队以3:2获得比赛胜利是指前四局比赛甲、乙两队2:2平，第五比赛甲胜，∴甲队以3:2获得比赛胜利的概率为：22242114()()()33227P C ==．故答案为：427． 16．抛物线2:16C y x =的焦点为,F P 是抛物线C 上动点，点()4,6B -，当PBPF取最大值时，点P 的坐标为__________. 【答案】()1,4-【分析】根据抛物线的定义，PB PF 转化为PBPQ ，结合图像判断什么时候PB PF取最大值，进而求出点P 的坐标.【详解】由题意知，焦点为()4,0F ，且()4,6B -在抛物线的准线上， 设点P 在抛物线准线上的投影为点Q ，那么PF PQ =，故PB PB PFPQ=，要使PBPF取最大，只需PBQ ∠最小，此时直线PB 与抛物线相切，设直线PB ：()46x t y +=-，即64x ty t =--，联立21664y x x ty t ⎧=⎨=--⎩，得21696640y ty t -++=，由直线PB 与抛物线相切，得()()216496640t t ∆=-+=，即2t =或12t =-，结合图像，可知当12t =-时，PBQ ∠最小，故28160y y ++=，即4y =-，因此点P 的坐标为()1,4-. 故答案为：()1,4-.【点睛】直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要用到根与系数的关系. 三、解答题17．等差数列{}n a 满足253,25a S ==.〔1〕求数列{}n a 的通项公式； 〔2〕令11n n n b a a +=，求数列{}n b 的前n 项和n S . 【答案】〔1〕21n a n =-； 〔2〕21nn +. 【分析】〔1〕由253,25a S ==，列出方程组，求得1a 1,d 2，即可求得数列{}n a 的通项公式；〔2〕由〔1〕求得11111()22121n n n b a a n n +==--+，结合“裂项法〞求和，即可求解. 【详解】〔1〕设等差数列{}n a 的公差为d ，因为253,25a S ==，可得113545252a d a d +=⎧⎪⎨⨯+=⎪⎩，解得1a 1,d 2， 所以数列{}n a 的通项公式()12121n a n n =+-=-. 〔2〕由〔1〕知21n a n =-， 可得111111()(21)(21)22121n n n b a a n n n n +===--+-+， 所以数列{}n b 的前n 项和： 111()2121211111111[(1)()()](1)233557122n nS n n n n --++=-+-+-++=-=+. 【点睛】此题主要考查了等差数列的通项公式的求解，以及“裂项法〞求和的应用，其中解答中熟记等差数列的通项公式和前n 项和公式，以及合理利用“裂项法〞求和是解答的关键，着重考查推理与运算能力，属于根底题.18．为推动长春市校园冰雪运动，充分展示?长春市中小学“百万学子上冰雪〞行动方案?的工作成果，某 学校决定学生全员参与冰雪健身操运动.为了调查学生对冰雪健身操的喜欢程度，现从全校学生中随机抽 取了20名男生和20名女生的测评成绩〔总分值为100分〕组成一个样本，得到如下图的茎叶图，并且认为得分不低于80分的学生为喜欢.〔1〕请根据茎叶图填写下面的列联表，并判断能否有85%的把握认为该校学生是否喜欢冰雪健身操与性别有关？〔2〕从样本中随机抽取男生、女生各1人，求其中恰有1人喜欢冰雪健身操的概率； 〔3〕用样本估计总体，将样本频率视为概率，现从全校男生、女生中各随机抽取1人，求其中喜欢冰雪健身操的人数X 的分布列及数学期望. 参考公式及数据：()()()()()22n ad bc K a b c d a c b d -=++++【答案】〔1〕答案见解析；〔2〕12；〔3〕答案见解析.【分析】〔1〕分析数据，完成列联表，套公式计算2K ，对照参数下结论； 〔2〕利用等可能性的概率公式直接求概率；〔3〕分析题意，列举X 的所有可能取值，分别求概率，写出分布列，套公式求数学期望.【详解】〔1〕列联表如下：所以()()()()()()222405101510 2.667 2.07215252020n ad bc K a b c d a c b d -⨯-⨯==≈>++++⨯⨯⨯， 所以有85%的把握该校学生是否喜欢冰雪健身操与性别有关.〔2〕设事件A ：随机抽取男生、女生各1人，求其中恰有1人喜欢冰雪健身操，那么()1111510151011202012C C C C P A C C +==. 〔3〕X 的所有可能取值：0,1,2，那么()3130428P X ==⨯=，()11311142422PX ==⨯+⨯=， ()1112428P X ==⨯=，所以X 的分布列为X 的数学期望为：()34130128884E X =⨯+⨯+⨯=.19．等边三角形ABC 的边长为3，点,D E 分别是棱,AB AC 上的点，且满足12AD CE DB EA ==〔如图 ①〕，将ADE 沿DE 折起到1A DE △的位置，连接11,A B A C，点F 是棱1A B 上的动点，点P 是棱BC 上的动点〔如图②〕.〔1〕假设113A F FB =，求证：//CF 平面 1A DE ；〔2〕假设1A D DB ⊥，且直线1A P 与平面1A BD 求平面1A DP 与平面1A CE 所成锐二面角的余弦值. 【答案】(1)见详解；. 【分析】(1)通过边长的比例关系，先证明平面CHF ∥平面1A DE ，进而求证//CF 平面 1A DE ；(2)根据条件，建立空间直角坐标系，用空间向量的方法求平面1A DP 与平面1A CE 所成锐二面角的余弦值. 【详解】(1)证明：过点C 作BD 的垂线，交BD 于点H ，连接FH .由题意易得：DE BD ⊥，CH BD ⊥，CH ∴∥DE ，DE ⊂平面1A DE ，CH ⊄平面1A DE ，CH ∴∥平面1A DE ,又12AD DB =，13DH BH ∴=， 113A F FB =，1A D ∴∥FH ， 1A D ⊂平面1A DE ，FH ⊄平面1A DE ，FH ∴∥平面1A DE ，又CH ∈平面CHF ，FH ∈平面CHF ，且FHCH H =，∴平面CHF ∥平面1A DE ，CF ⊂平面CHF ， CF ∴∥平面 1A DE ；(2)由题意易得1A D 、BD 、DE 两两垂直，故以点D 为坐标原点，DB 为x 轴，DE 为y 轴，1DA 为z 轴， 建立如以下图所示的空间直角坐标系， 过点P 作BD 的垂线交BD 于点Q ，连接1A Q ， 易得PQ ⊥平面1A BD ，又因直线1A P 与平面1ABD 那么直线1A P 与平面1A BD1PQ AQ= 再由1AQ=)PQ DQ ==-= 得1DQ =.故在空间坐标系中：()10,0,1A ，()0,0,0D ，()P，12C ⎛⎫ ⎪⎪⎝⎭，()E ，设平面1A DP 的法向量(),,n x y z =，那么100n DA n DP ⋅=⎧⎨⋅=⎩ ，得0z x =⎧⎪⎨=⎪⎩，取1y =，那么()3,1,0n =-，同理平面1A CE的法向量(3,1,m =-，故平面1A DP 与平面1A CE所成锐二面角的余弦值为3n m n m⋅==+⋅20．椭圆()2222:10x y C a b a b+=>>的左、右焦点分别是12,F F ，短轴长是12.〔1〕求椭圆C 的标准方程；〔2〕点P 是椭圆上任意一点，直线1PF 交椭圆于点Q ，直线2PF 交椭圆于点R ，且满足1122,,PF FQ PF F R λμ== .求证：λμ+是定值. 【答案】(1)22143x y +=；(2) λμ+为定值103. 【分析】(1)由，易求得a ，b ，进而得到椭圆C 的标准方程；(2)根据题意，对P 是否为长轴顶点分类讨论，假设P 不是长轴顶点，设直线1PF ：1x my =-，直线2PF ：1x ny =+，通过联立方程组，以及根与系数关系，用m，n 来表示λμ+，进而证明λμ+为定值.【详解】(1)由题意得212b c a ⎧=⎪⎨⎪⎩ ，解得2a b =⎧⎪⎨=⎪⎩，故椭圆C 的标准方程的标准方程为：22143x y +=. (2)①当点P 是椭圆为长轴顶点时，易得103；②当点P 是椭圆不为长轴顶点时，设直线1PF ：1x my =-，直线2PF ：1x ny =+， 设()00,P x y ，()11,Q x y ，()22,R x y ，联立221431x y x my ⎧+=⎪⎨⎪=-⎩ ，得()2234690m y my +--=， ()223636340m m ∆=++>恒成立，由韦达定理得：012634m y y m +=+，012934y y m =-+， 同理得：022634n y y n +=-+，022934y y n =-+，联立11x my x ny =-⎧⎨=+⎩，得2,m n P m n m n +⎛⎫⎪--⎝⎭， 又因点P 在椭圆上，得()()()2224143m n m n m n ++=--，化简得22101639m n mn +=+， 由1122,,PF FQ PF F R λμ==，得0102,y y y y λμ-=-=， 故22000102y y y y y y λμ+=-- 2222433892m n m mn n ++=⋅-+ ， 又因22101639m n mn +=+，故4401010441033416449933933mn mn mn mn λμ⎛⎫++⎪⎝⎭+=⋅=⋅=⎛⎫++ ⎪⎝⎭， 综上：λμ+为定值103. 【点睛】(1)解答直线与椭圆的题目时，时常把两个曲线的方程联立，消去x (或y )建立一元二次方程，然后借助根与系数的关系，并结合题设条件建立有关参变量的等量关系． (2)涉及到直线方程的设法时，务必考虑全面，不要忽略直线斜率为0或不存在等特殊情形．21．函数()()xf x x e a =-.〔1〕假设函数()f x 过原点切线的斜率是3，求实数a 的值； 〔2〕假设()1ln x x f x ++≤恒成立，求实数a 的取值范围. 【答案】〔1〕2a =-；〔2〕0a ≤.【分析】〔1〕函数过某点处的切线，需设出切点，利用函数在切点处的导数等于切点处切线的斜率，得到关于a 的方程，求出a .〔2〕恒成立问题别离参数，转化为求函数1ln ()x x xg x e x++=-的最小值，求导，利用隐零点代换001lnx x =，求出()g x 的最小值，得到0a ≤. 【详解】〔1〕设切点为000(,()xx x e a - ，且'()(1)x f x x e a =+- ，那么切线方程为00000()[(1)]()x xy x e a x e a x x --=+--，由切线过原点，那么有00000()[(1)]()x xx e a x e a x --=+--，解得00x = ，所以000'()(1)3xf x x e a =+-= ，因此2a =- .〔2〕假设()1ln x x f x ++≤恒成立，即1ln ()x x x x e a ++≤-恒成立，即1ln xx xa e x++≤-恒成立， 令1ln ()xx x g x e x ++=-，那么22ln '()x x e xg x x+= ， 令2()ln x h x x e x =+，那么21'()(2)0x h x e x x x=++> 所以2()ln x h x x e x =+在(0,)+∞ 是增函数，又112211(1)0,()110ee h e h e e e e -=>=-=-<因此，01(,1)x e∃∈ ，使得02000()ln =0xh x x e x =+，所以，当0(0,)x x ∈ 时，()0h x < ,即)'(0g x < ，()g x 在0(0,)x 上是减函数当0(+)x x ∈∞，时，()0h x >，即'()0g x >，()g x 在0(+)x ∞，上是增函数， 那么000min 001ln ()()x x x g x g x e x ++==-，由02000()ln =0x h x x e x =+得01ln 0000001111ln ln ln x x x e x e x x x x =-==⋅又设()x x xe ϕ= ，易知()x x xe ϕ=在(0,)+∞ 是增函数，所以001lnx x = ， 故000min 001ln ()()=0x x x g x g x e x ++==-，因此0a ≤ . 【点睛】注意区别在某点和过某点的切线问题，恒成立别离参数转化为求最值问题，零点不可求，需用隐零点代换，最终得解，注意()x x xe ϕ=在(0,)+∞ 是增函数，所以001lnx x =. 22．在直角坐标系xoy 中，曲线1C的参数方程为23x y ⎧=-⎪⎪⎨⎪=⎪⎩〔t 为参数〕，.在以坐标原点为极点，x 轴非负半轴为极轴的极坐标系中，曲线2C 的极坐标方程为4cos ρθ=. 〔1〕写出1C 的普通方程和2C 的直角坐标方程； 〔2〕假设1C 与2C 相交于,A B 两点，求AOB 的面积.【答案】〔1〕1C ：30x y +-=；2C ：()2224x y -+=；〔2【分析】〔1〕消元将直线的参数方程转化为普通方程，根据公式将极坐标方程化为直角坐标方程；〔2〕首先求出圆心到直线的距离，即可求出弦AB 的长，再根据原点到直线的距离即为高，即可求出三角形的面积；【详解】解：〔1〕因为曲线1C的参数方程为32x y ⎧=⎪⎪⎨⎪=+⎪⎩〔t 为参数〕，所以1C 的普通方程为30x y +-=，因为曲线2C 的极坐标方程为4cos ρθ=，所以24cos ρρθ=，所以224x y x +=，即曲线2C 的直角坐标方程为()2224x y -+=〔2〕因为2C ：()2224x y -+=的圆心坐标()22,0C ，半径2r，所以圆心到直线30x y +-=的距离d =，所以AB =点O 到直线30x y +-=的距离2h ==1122AOBSAB h == 23．()|1|| -1|f x x a x a =+++．〔1〕当1a =时，求不等式()3f x ≥的解集;〔2〕假设1≥x 时，不等式()2f x x ≥+恒成立，求a 的取值范围．【答案】(1) (,2][1,)-∞-+∞．(2) [0)+∞，. 【分析】〔1〕将a =1代入f 〔x 〕中，去绝对值后分别解不等式即可；〔2〕x ∈〔0，1〕时，不等式f 〔x 〕＜x +2恒成立等价于当x ∈〔0，1〕时，|ax -1|＜1恒成立，然后分a ≤0和a ＞0讨论即可．【详解】解：〔1〕解法1：当1a =时，不等式()3f x ≥可化简为13x x ++≥. 当–1x <时，13x x ---≥，解得2x -≤，所以2x -≤； 当10x -≤<时，13x x +-≥，13≥，无解； 当0x ≥时，13x x ++≥，解得1≥x ，所以1≥x ﹒ 综上，不等式()3f x ≥的解集为(,2][1,)-∞-+∞．解法2：当1a =时，21(1)()11(10)21(0)x x f x x x x x x --<-⎧⎪=++=-≤<⎨⎪+≤⎩ 当1x <-时，213x --≥，解得2x -≤，所以2x -≤； 当10x -≤<时，13≥，无解；当0x ≥时，213x +≥，解得1≥x ，所以1≥x ． 综上，不等式()3f x ≥的解集为(,2][1,)-∞-+∞．〔2〕解法1：当1≥x 时，不等式()2f x x ≥+可化简为11ax a -+≥.令()(1)1g x a x =-+，那么()g x 的图像为过定点()11，斜率为a 的一条直线， 数形结合可知，当0a ≥时，11ax a -+≥在[1)+∞，上恒成立. 所以，所求a=解法2：当1≥x 时，不等式()2f x x ≥+可化简为11ax a -+≥. 由不等式的性质得11ax a -+-≤或11ax a -+≥， 即(1)2a x --≤或(1)0a x -≥.当1≥x 时，a R ∀⊂，不等式2(1)2a x -≤-不恒成立； 为使不等式(1)0a x -≥恒成立，那么0a ≥. 综上，所求a=【点睛】此题考查了绝对值不等式的解法和不等式恒成立问题，考查了转化思想，属中档题．。

吉林省2021年高考数学四模试卷（理科）（I）卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）(2018·内江模拟) 设为虚数单位，，若是纯虚数，则（）A . 2B .C . 1D .2. （2分）(2017·河南模拟) 已知集合A={x|x2﹣2x﹣3＞0}，B={x|lg（x﹣2）≤1}，则（∁RA）∪B=（）A . （﹣1，12）B . （2，3）C . （2，3]D . [﹣1，12]3. （2分） (2017高二下·保定期末) 函数f（x）=1+log2x与g（x）=2﹣x+1在同一直角坐标系下的图象大致是（）A .B .C .D .4. （2分） (2018高二上·长安期末) 现采用随机模拟的方法估计某运动员射击4次，至少击中3次的概率：先由计算机给出0到9之间取整数值的随机数，指定0,1表示没有击中目标，2,3,4,5,6,7,8,9表示击中目标，以4个随机数为一组，代表射击4次的结果，经随机模拟产生了20组随机数：7527 0293 7140 9857 0347 4373 8636 6947 1417 46980371 6233 2616 8045 6011 3661 9597 7424 7610 4281根据以上数据统计该运动员射击4次至少击中3次的概率为（）A . 0.852B . 0.8192C . 0.8D . 0.755. （2分） (2016高二上·岳阳期中) 执行如图所示的程序框图，如果输入的N是4，那么输出的p是（）A . 6B . 10C . 24D . 1206. （2分）(2019·延安模拟) 函数的图象向左平移个单位长度后，所得到的图象关于原点对称，则等于（）A .B .C .D .7. （2分）一个几何体的三视图如图，则该几何体的体积为（）A .B .C . 2D . 18. （2分）设，则=（）A . ﹣2014B . 2014C . ﹣2015D . 20159. （2分） (2020高三上·湛江月考) 新型冠状病毒肺炎的潜伏期X（单位：日）近似服从正态分布：，若，则可以估计潜伏期大于等于11天的概率为（）A . 0.372B . 0.256C . 0.128D . 0.74410. （2分）湖面上漂着一个小球，湖水结冰后将球取出，冰面上留下了一个半径为6 cm，深2 cm的空穴，则该球表面积为（）cm².A .B .C .D .11. （2分）(2017·黑龙江模拟) 焦点在y轴上的双曲线的一条渐近线方程为，则该双曲线的离心率为（）A .B .C .D .12. （2分）若函数的图像在上恰有一个极大值和一个极小值，则的取值范围是（）A .B .C .D .二、填空题 (共4题；共4分)13. （1分） (2019高三上·江西月考) 若，满足则的最大值为________14. （1分）已知 =（1，1）， =（4，1）， =（4，5），则与夹角的余弦值为________．15. （1分）(2020·德州模拟) 在条件① ，② ，③中任选一个，补充到下面问题中，并给出问题解答.已知的内角A，B，C的对边分别是a，b，c，且，，________.求边上的高16. （1分）(2017·西宁模拟) 2016年夏季大美青海又迎来了旅游热，甲、乙、丙三位游客被询问是否去过陆心之海青海湖，海北百里油菜花海，茶卡天空之境三个地方时，甲说：我去过的地方比乙多，但没去过海北百里油菜花海；乙说：我没去过茶卡天空之境；丙说：我们三人去过同一个地方．由此可判断乙去过的地方为________．三、解答题 (共7题；共75分)17. （10分） (2016高二上·宾阳期中) 已知公差不为0的等差数列{an}满足：a1=1且a2 ， a5 ， a14成等比数列．（1）求数列{an}的通项公式an和前n项和Sn；（2）证明不等式且n∈N*）18. （15分） (2017高二上·景德镇期末) 如图，李先生家住H小区，他工作在C科技园区，从家开车到公司上班路上有L1、L2两条路线，L1路线上有A1、A2、A3三个路口，各路口遇到红灯的概率均为；L2路线上有B1、B2两个路口，各路口遇到红灯的概率依次为，．（1）若走L1路线，求最多遇到1次红灯的概率；（2）若走L2路线，求遇到红灯次数X的数学期望；（3）按照“平均遇到红灯次数最少”的要求，请你帮助李先生从上述两条路线中选择一条最好的上班路线，并说明理由．19. （10分）(2014·江苏理) 如图，在三棱锥P﹣ABC中，D，E，F分别为棱PC，AC，AB的中点，已知PA⊥AC，PA=6，BC=8，DF=5．求证：（1）直线PA∥平面DEF；（2）平面BDE⊥平面ABC．20. （10分）(2018·陕西模拟) 已知为椭圆的左、右顶点，为其右焦点，是椭圆上异于的动点，且面积的最大值为 .（1）求椭圆的方程；（2）直线与椭圆在点处的切线交于点，当点在椭圆上运动时，求证:以为直径的圆与直线恒相切.21. （10分） (2018高二下·定远期末) 已知函数 .（1）求函数；（2）设函数，其中a∈(1，2)，求函数g(x)在区间[1，e]上的最小值.22. （10分）(2017·新余模拟) 已知直线l在直角坐标系xOy中的参数方程为为参数，θ为倾斜角），以坐标原点O为极点，x轴正半轴为极轴，建立极坐标系，在极坐标系中，曲线的方程为ρ﹣ρcos2θ﹣4cosθ=0．（1）写出曲线C的直角坐标方程；（2）点Q（a，0），若直线l与曲线C交于A、B两点，求使为定值的值．23. （10分）设函数f（x）=1+|2x﹣3|．（1）求不等式f（x）≥|3x+1|的解集；（2）若不等式f（x）﹣tx≥0的解集非空，求t的取值范围．参考答案一、选择题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题；共75分) 17-1、17-2、18-1、18-2、18-3、19-1、19-2、20-1、20-2、21-1、21-2、22-1、22-2、23-1、23-2、。

吉林省2021年数学高三上学期理数期中考试试卷（I）卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分） (2017高二下·彭州期中) 若复数Z满足Z（i﹣1）=2i（i为虚数单位），则为（）A . 1+iB . 1﹣iC . ﹣1+iD . ﹣1﹣i2. （2分）(2020·漯河模拟) 设全集，集合，则（）A .B .C .D .3. （2分）若实数满足则的最小值是（）A .B .C .D .4. （2分）(2018·黑龙江模拟) 我国古代数学著作《孙子算经》中有这样一道算术题：“今有物不知其数，三三数之剩一，五五数之剩三，七七数之剩六，问物几何？”人们把此类题目称为“中国剩余定理”．若正整数N 除以正整数m后的余数为n，则记为N≡n（modm），例如10≡2（mod4）．现将该问题以程序框图给出，执行该程序框图，则输出的n等于（）A . 13B . 11C . 15D . 85. （2分） (2020高一上·贵州期中) 已知关于的方程有两个不等实根，则实数的取值范围是A . ，B .C . ，D .6. （2分） (2019高一下·上杭月考) 圆心和圆上任意两点可确定的平面有（）A . 0个B . 1个C . 2个D . 1个或无数个7. （2分）函数f（x）=x5+x3的图象关于（）对称．A . y轴B . 直线y=xC . 坐标原点D . 直线y=﹣x8. （2分）(2018·南充模拟) 下列命题中的假命题是（）A . ，B . ，C . ，D . ，9. （2分）(2018·衡水模拟) 在平面直角坐标系中，已知双曲线的中心在原点，焦点在轴上，实轴长为8，离心率为，则它的渐近线的方程为（）A .B .C .D .10. （2分）已知定义在R上的函数f（x）满足f（x＋1）＝－f（x）。

抚松五中、长白县实验中学、长二中、长实验中学2021届高三数学上学期期中联考试题 理一、单项选择题〔每一小题5分，一共60分〕1、{}{}{}6,2,4,1,3,4,6U x N x P Q =∈<==，那么()U C P Q ⋂=【 】A. {}3,4B. {}3,6C. {}1,3D. {}1,42、以下关于命题的说法错误的选项是，那么〞的逆否命题为“假设A. 命题“假设，那么〞；“函数在区间上为增函B. “〞是数〞的充分不必要条件；C. 假设命题：，，那么，；“，〞是真命题D. 命题3、命题p ：对任意x ∈R ，总有22x x >；q ：“1ab >〞是“a >l ，b >l 〞的 充分不必要条件．那么以下命题为真命题的是【 】A ．p q ∧B ．p q ⌝∧C ．p q ∧⌝D ．p q ⌝∧⌝ 4、以下函数中，在其定义域内，既是奇函数又是减函数的是 【 】A ．f 〔x 〕=B ．f 〔x 〕=制卷人：打自企； 成别使； 而都那。

审核人：众闪壹； 春壹阑； 各厅…… 日期：2022年二月八日。

评卷人得分C ．f 〔x 〕=2﹣x﹣2xD ．f 〔x 〕=﹣tanx5、菱形ABCD 的边长为2，E 为AB 的中点，120ABC ∠=，那么DE BD ⋅的值是 【 】A. 3B. -3C. 3D.3-6、向量b a ,满足1,2==b a ，且对一实在数x ，b a b x a +≥+恒成立，那么b a ,的夹角的大小为【 】A ．6π B ．3π C ．32π D ．65π 7、设直角坐标系xoy 平面内的三点()1,2A -，(),1B a -，(),0C b -，其中0a >，0b >，假设A ，B ，C 三点一共线，那么12a b+的最小值为【 】A ．4B ．6C ．8D ．98、函数的图象大致是 【 】A. B.C. D.9、〔e 为自然对数的底数〕，54log 2,log 3y z ==那么以下结论正确的选项是 【 】A. x y z <<B. y z x <<C. z y x <<D.z x y <<10、假设331sin 7,sin()cos(2)1221sin 5παπαπαπαα+<<-+-+=-，那么sin cos αα-=【 】A ．15 B ．15±C ．75D ．75±11、，把的图象向右平移个单位，再向上平移2个单位，得到的图象；假设对任意实数，都有成立，那么【 】A. B. 3 C. 2 D.12、函数，假设关于的方程有8个不等的实数根，那么的取值范围是 【 】A.B. C. D.二、填空题〔每空5分，一共20分〕13、()f x 为偶函数，当0x <时，()ln()3f x x x =-+，那么曲线()y f x =在点(1,3)- 处的切线方程是_____________________。

2021届吉林省长春市第五中学高三上学期期中考试数学（理）试题一、单选题1．集合{}lg 0M x x =>，{}24N x x =≤，则M N =（ ）．A ．1,2B ．[)1,2C ．(]1,2D ．[]1,2【答案】C【分析】先求出集合,M N ，再求交集运算.【详解】{}()lg 01,M x x =>=+∞,{}[]242,2N x x =≤=-(]1,2MN =故选：C 2．若1m ii+-是纯虚数，则实数m 的值为（ ）． A ．1- B ．0C ．1D ．2【答案】C【分析】对复数进行化简根据实部为零，虚部不为零建立等量关系和不等关系即可得解. 【详解】由题1m ii+-是纯虚数， ()()()()()()21111111222m i i m m i i m m i m i i i i +++++++-===+--+为纯虚数， 所以m =1. 故选：C【点睛】此题考查复数的运算和概念辨析，关键在于熟练掌握复数的运算法则. 3．设(1,2)a =，(2,)b k =，若(2)a b a +⊥，则实数k 的值为（ ） A ．B ．C ．D ．【答案】C【解析】试题分析：因为2(4,4)a b k +=+，(2)412(4)12206a b a k k k +⊥⇒⨯++=+=⇒=-【解析】1．平面向量的坐标运算；2．非零向量0a b a b ⊥⇔⋅=；3．数量积公式的坐标形式；4．“0x <”是“()ln 10x +<”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件【答案】B【分析】先由()ln 10x +<解得10x -<<，从而可判断. 【详解】由()ln 10x +<，可解得011x <+<，即10x -<<，由“0x <”是“10x -<<”的必要不充分条件可得“0x <”是“()ln 10x +<”的必要不充分条件， 故选：B.【点睛】本题主要考查了充分性和必要性的判断，解题的关键是先解出对数不等式的等价条件，属于基础题.5．已知0.50.50.70.50.3log 0.2a b c ===，，，则a b c ，，的大小关系是（ ） A ．c a b << B ．b a c << C ．c b a << D ．a b c <<【答案】B【分析】由对数函数和幂函数的单调性可得1b a c <<<，即可得解. 【详解】因为0.5y x=在(0,)+∞上是增函数，所以0.50.50.50.30.51<<，即1b a <<，因为0.7log y x =在(0,)+∞上是减函数，所以0.70.7log 0.2log 0.71c =>= 所以1b a c <<<. 故选：B.【点睛】本题考查了利用对数函数和幂函数的单调性比较大小，属于基础题. 6．在等差数列 {}n a 中，若12015,a a 为方程 210160x x -+= 的两根，则210082014++=a a a （ ）A ．10B ．15C ．20D ．40【答案】B【解析】分析：根据题意和韦达定理求出12015a a +，由等差数列的性质求出210082014a a a ++的值.详解：12015,a a 为方程 210160x x -+= 的两根，1201510a a ∴+=，由等差数列的性质得1008210a =，即10085a =，2100820141008315a a a a ∴++==.故选：B.点睛：本题考查等差数列的性质以及韦达定理，属基础题. 7．将函数sin 64y x π⎛⎫=+ ⎪⎝⎭的图象上各点的横坐标伸长到原来的3倍（纵坐标不变），再向右平移8π个单位，所得函数图象的一个对称中心是（ ）． A ．,016π⎛⎫⎪⎝⎭ B ．,09π⎛⎫⎪⎝⎭C ．,04π⎛⎫⎪⎝⎭D ．,02π⎛⎫⎪⎝⎭【答案】D【分析】先利用三角函数的图像变换，可以得到变换后的函数解析式sin 2y x =，再由正弦函数的对称性代入计算即可. 【详解】函数sin 64y x π⎛⎫=+⎪⎝⎭的图象上各点的横坐标伸长到原来的3倍（纵坐标不变）， 则得到：sin 24y x π⎛⎫=+⎪⎝⎭， 再向右平移8π个单位，则得到：sin 2sin 284y x x ππ⎛⎫⎛⎫=-+= ⎪ ⎪⎝⎭⎝⎭，令2x k =π即,2k x k Z π=∈ 故选：D【点睛】本题考查了三角函数图像的变换以及三角函数的对称性，属于一般题. 8．函数()[]cos sin ,,=-∈-f x x x x x ππ的大致图象为（ ）A ．B ．C ．D ．【答案】D【分析】判断函数的奇偶性和对称性，利用2f π⎛⎫⎪⎝⎭的符号进行排除即可． 【详解】()()()cos sin cos sin f x x x x x x x f x -=-+=--=-， 函数()f x 是奇函数，图象关于原点对称，排除,A Ccos sin 102222f ππππ⎛⎫=-=-< ⎪⎝⎭，排除B ，故选D ．【点睛】本题考查函数的图象的判断与应用，考查函数的零点以及特殊值的计算，是中档题；已知函数解析式，选择其正确图象是高考中的高频考点，主要采用的是排除法，最常见的排出方式有根据函数的定义域、值域、单调性、奇偶性、周期性等性质，同时还有在特殊点处所对应的函数值或其符号，其中包括,,0,0x x x x +-→+∞→-∞→→等.9．设若20lg ,0()3,ax x f x x t dt x >⎧⎪=⎨+≤⎪⎩⎰，((1))1f f =，则a 的值是( )A ．-1B ．2C ．1D ．-2【答案】C 【详解】233003|aat dt t a ==⎰，33(1)lg10,(0),1, 1.f f a a a ===∴==故选：C10．若tan 3α=，()tan 21αβ-=-，则()tan αβ-=（ ） A ．2 B ．－2C 3D ．3【答案】A【分析】由tan()tan[(2)]αβαβα-=--结合两角差的正切公式求解即可. 【详解】tan(2)tan 13tan()tan[(2)]21tan(2)tan 1(1)3αβααβαβααβα-----=--===+-+-⨯故选：A【点睛】本题主要考查了利用两角差的正切公式化简求值，属于基础题.11．已知函数2|1|,0()log ,0x xf x x x +≤⎧=⎨>⎩，若方程()f x a =有四个不同的解1x ，2x ，3x ，4x ，且1234x x x x <<<，则()3122341x x x x x ++的取值范围是（ ）． A ．(1,)-+∞ B ．[1,1)-C ．(,1)-∞D ．(]1,1-【答案】D【分析】根据图象可得：11x a +=-，21x a +=，23log x a =-，24log x a =.(01)a <， 则31222342()22212122a a a a a x x x x x --++=-⋅+=-⋅.令2a t ，(1t ∈，2]，而函数2y t t=-.即可求解.【详解】解：函数()21,0|log ,0x x f x x x ⎧+⎪=⎨>⎪⎩，的图象如下：根据图象可得：若方程()f x a =有四个不同的解1x ，2x ，3x ，4x ，且1234x x x x <<<， 则11x a +=-，21x a +=，23log x a =-，24log x a =.(01)a <≤122x x +=-，32a x -=，42a x = ∴则31222344()22221222a a a a ax x x x x ---++=-⋅+=-⋅. 令2at ，(1t ∈，2]，而函数2y t t=-在(1，2]单调递增. 所以211t t -<-≤，则21212a a ∴-<-. 故选：D.【点睛】本题考查函数的图象与性质，考查函数与方程思想、转化与化归思想、数形结合思想，考查运算求解能力，求解时注意借助图象分析问题，属于中档题.二、多选题12．我国新冠肺炎疫情进入常态化，各地有序推进复工复产，下面是某地连续11天复工复产指数折线图，下列说法正确的是（ ）A ．这11天复工指数和复产指数均逐日增加;B ．这11天期间，复产指数增量大于复工指数的增量;C ．第3天至第11天复工复产指数均超过80%;D ．第9天至第11天复产指数增量大于复工指数的增量; 【答案】CD【分析】注意到折线图中有递减部分，可判定A 错误；注意考查第1天和第11天的复工复产指数的差的大小，可判定B 错误；根据图象，结合复工复产指数的意义和增量的意义可以判定CD 正确.【详解】由图可知，第1天到第2天复工指数减少，第7天到第8天复工指数减少，第10天到第11复工指数减少，第8天到第9天复产指数减少，故A 错误；由图可知，第一天的复产指标与复工指标的差大于第11天的复产指标与复工指标的差，所以这11天期间，复产指数增量小于复工指数的增量，故B 错误; 由图可知，第3天至第11天复工复产指数均超过80%，故C 正确; 由图可知，第9天至第11天复产指数增量大于复工指数的增量，故D 正确;【点睛】本题考查折线图表示的函数的认知与理解，考查理解能力，识图能力，推理能力，难点在于指数增量的理解与观测，属中档题.三、填空题13．在ABC 中，π3B =中，且43BA BC ⋅=ABC 的面积是______． 【答案】6【分析】由条件利用向量的数量积的定义可得83BA BC ⋅=可得面积.【详解】由cos BA BC BA BC B ⋅=⋅=即1cos32BA BC BA BC π⋅=⋅⨯=所以83BA BC ⋅=11sin B 6222ABCS BA BC =⋅⨯=⨯= 故答案为：614．已知()f x 为奇函数，且当0x >时单调递增，()30f =，则不等式()0xf x <的解集______．【答案】(3,0)(0,3)-⋃ 【分析】()0xf x <0()0x f x >⎧⇔⎨<⎩或0()0x f x <⎧⎨>⎩，利用()f x 的单调性及奇偶性即可得到答案.【详解】由题意(3)(3)0f f -=-=，当0x >时，由()0f x <得03x <<， 当0x <时，由()0f x >得30x -<<，所以()0xf x <0()0x f x >⎧⇔⎨<⎩或0()0x f x <⎧⎨>⎩，解得03x <<或30x -<<. 所以不等式的解集为(3,0)(0,3)-⋃. 故答案为：(3,0)(0,3)-⋃15．已知函数()y f x =的图像在点()()11M f ，处的切线方程是122y x =+，则()()11f f '+＝______．【答案】3【分析】根据导数的几何意义，可得'(1)f 的值，根据点M 在切线上，可求得(1)f 的值，即可得答案.【详解】由导数的几何意义可得，'1(1)2k f ==， 又()()11M f ，在切线上， 所以15(1)1222f =⨯+=，则()()11f f '+=3， 故答案为：3【点睛】本题考查导数的几何意义的应用，考查分析理解的能力，属基础题.16．某学生对函数()2cos f x x x =进行研究后，得出如下四个结论： （1）函数()f x 在[]π,0-上单调递增，在[]0,π上单调递减； （2）存在常数0M >，使()f x M x ≤对一切实数x 均成立；（3）点π,02⎛⎫⎪⎝⎭是函数()y f x =图像的一个对称中心；（4）函数()y f x =图像关于直线πx =对称；其中正确的是______（把你认为正确命题的序号都填上） 【答案】（2）【分析】根据奇偶性，奇函数在关于原点对称区间单调性相同，确定（1）错误； 取M=2，可判定（2）正确；202f x f x ππ++-⎛⎫⎛⎫≠⎪ ⎪⎝⎭⎝⎭可判断（3）不正确；取2233f ππ⎛⎫⎪=- ⎝⎭，4433f ππ⎛⎫⎪=-⎝⎭特殊值判定（3）错误. 【详解】()2cos f x x x =定义域为R ，()()2cos f x x x f x -=-=-，所以()2cos f x x x =是奇函数，在关于原点对称的区间上单调性相同，所以（1）错误； cos 1x ≤，令2M =，()f x M x ≤成立，所以（2）正确；()()2sin 2sin 4sin 022x x x x x x f x f x ππππ⎛⎫⎛⎫=-+++-+-=-≠ ⎪ ⎪⎝⎭⎝⎭， 所以点π,02⎛⎫⎪⎝⎭不是函数()y f x =图像的一个对称中心，所以（3）不正确； 2422cos 3333f ππππ⎛⎫= =-⎪⎝⎭，4844cos 3333f ππππ⎛⎫= =-⎪⎝⎭， 函数()y f x =图像不关于直线πx =对称，所以（4）不正确. 故答案为：（2）【点睛】此题考查与三角函数性质相关命题的判定，需要熟练掌握奇偶性、单调性、对称性在解题中的处理方法.四、解答题17．已知函数2()cos 2sin 1f x x x x =+-.(1)求函数()f x 的单调递增区间；(2)在ABC ∆中，内角A ，B ，C 所对的边分别为a ，b ，c ，若()2,C ,24f A c π===，求ABC ∆的面积.【答案】(1),,63k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦；(2)32+. 【分析】（1）利用三角函数恒等变换的应用化简函数解析式可得f （x ）＝2sin （2x 6π-），利用正弦函数的单调性即可求解其单调递增区间． （2）由题意可得sin （2A 6π-）＝1，结合范围2A 6π-∈（6π-，116π），可求A 的值，由正弦定理可得a ，由余弦定理b ，进而根据三角形的面积公式即可求解． 【详解】（1）∵()221f x sin x =+-=x ﹣cos2x ＝2sin （2x 6π-）， 令2k π2π-≤2x 6π-≤2k π2π+，k ∈Z ，解得k π6π-≤x ≤k π3π+，k ∈Z ， ∴函数f （x ）的单调递增区间为：[k π6π-，k π3π+]，k ∈Z ．（2）∵f （A ）＝2sin （2A 6π-）＝2，∴sin （2A 6π-）＝1，∵A ∈（0，π），2A 6π-∈（6π-，116π）， ∴2A 62ππ-=，解得A 3π=，∵C 4π=，c ＝2，∴由正弦定理a csinA sinC=，可得a2c sinA sinC ⋅=== ∴由余弦定理a 2＝b 2+c 2﹣2bc cos A ，可得6＝b 2+4﹣2122b ⨯⨯⨯，解得b ＝1（负值舍去）， ∴S △ABC 12=ab sinC 12=（1322+⨯=． 【点睛】本题主要考查了三角函数恒等变换的应用，正弦函数的单调性，正弦定理，余弦定理，三角形的面积公式在解三角形中的综合应用，考查了计算能力和转化思想，属于中档题．18．设各项都为正数的等差数列{}()n a n *∈N的前n 项和为nS，且11a =，534S S S =+．（1）求数列{}n a 的通项公式．（2）若数列32n n a b +=，设n T 为数列11n n b b +⎧⎫⎨⎬⎩⎭的前n 项和，求n T 的最小值．【答案】（1）21n a n =-；（2）16【分析】（1）设等差数列{}n a 的公差为d ，将534S S S =+用1,a d 表示即可得到公差d ，进一步得到通项公式；（2）由（1）得到1n b n =+，进一步得到111112n n b b n n +=-++，利用裂项相消法求得n T ，再利用n T 的单调性得到最小值.【详解】（1）设等差数列{}n a 的公差为d ，由534S S S =+，得543S S S -=，即5123a a a a =++，又11a =，所以141112d d d +=++++，解得2d =，所以1(1)221n a n n =+-⨯=- （2）由（1）可得312n n a b n +==+ 所以11111(1)(2)12n n b b n n n n +==-++++ 1111111123341222n T n n n =-+-++-=-+++ 又111023n n T T n n +-=->++，所以n T 单调递增，所以116n T T ≥= 所以n T 的最小值为16.19．已知数列{}n a 的前n 项和n S ，21n n S a =-，数列{}n b 是等差数列，且11b a =，43b a =．（1）求数列{}n a 和{}n b 的通项公式； （2）若121n n n n c a b b +=-，求数列{}n c 的前n 项和n T ． 【答案】（1）12n na ；nb n = （2）211321n n --++ 【分析】(1) 当1n =时11a =，由1n n n a S S -=-可得122n n n a a a -=-，可求出n a ，根据111b a ==，434b a ==，可求出n b(2)由条件()11121212112121n n n n n n n n c a b b n n -+-+⎛⎫=-=-=-- ⎪+⎝⎭，由等比数列的求和公式和裂项相消法可求和.【详解】（1）当1n =时，11121S a a ==-，得11a =当2n ≥时，21n n S a =- ……①1121n n S a --=- ……②由①－② 得122n n n a a a -=-，即12n n a a -=所以数列{}n a 是以1为首项，2为公比的等比数列,所以12n n a所以111b a ==，434b a ==．则等差数列{}n b 的公差为1d =所以n b n =（2）()11121212112121n n n n n n n n c a b b n n -+-+⎛⎫=-=-=-- ⎪+⎝⎭ 211111*********22231n n T n n -⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=++++--+-++- ⎪ ⎪ ⎪ ⎪⎢⎥+⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ 2111112213112112n n n n -⎛⎫- ⎪⎛⎫⎝⎭=⨯--=-+ ⎪++⎝⎭- 【点睛】关键点睛：本题考查利用递推关系求数列的通项公式和利用公式法以及裂项相消法求和，解答本题的关键是由()11n n n a S S n -=->求通项公式，和将n c 化为121121n n c n n -⎛⎫=-- ⎪+⎝⎭用等比数列的求和公式和裂项相消法求和，属于中档题. 20．已知ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且满足()()sin sin sin c b A B a A b B -+=-，4b =．（1）若a =B ；（2）若ABC 的周长为10，求ABC 的面积．【答案】（1）4B π=；（2. 【分析】（1）由已知结合正弦定理可得到A ，再由余弦定理及大角对大边即可得到B ；（2）由周长为10得到6a c +=，再由（1）中的222c b a bc +-=及4b =得到22416c a c -=-，解方程组得到c ，再由面积公式1sin 2ABC S bc A =运算即可. 【详解】（1）因为()()sin sin sin c b A B a A b B -+=-，所以()sin sin sin c b C a A b B -=-由正弦定理得()22c b c a b -=-，即222c b a bc +-= 由余弦定理，得cos A =222122c b a bc +-=，又(0,)A π∈，所以3A π=由正弦定理，sin sin a b A B =460sin B =，2sin 2B ==， 又b a <，B A <，所以4B π=.（2）因为ABC 的周长为10，4b =，所以6a c +=，由（1）知222c b a bc +-=，即22416c a c -=-所以解得75,22a c ==所以115sin 422222ABC S bc A ==⨯⨯⨯=. 21．设a ＞1，函数f （x ）=（1+x 2）e x -a ．（1）求f （x ）的单调区间；（2）证明f （x ）在（-∞，+∞）上仅有一个零点；（3）若曲线y=f （x ）在点P 处的切线与x 轴平行，且在点M （m ，n ）处的切线与直线OP 平行，（O 是坐标原点），证明：1m ≤-．【答案】（1）在（-∞，+∞）上为增函数；（2）见解析；（3）见解析【分析】（1）利用导数()0f x '≥得出函数单调区间．（2）利用零点存在性定理得出(0)0f f ⋅<，再结合()f x 的单调性即可得出仅有一个零点.（3）首先求得2(())1x f x e x '=+，设点00)(P x y ，，则020'()(1)xf x e x =+，根据()y f x =在点P 处的切线与x 轴平行求得01x =-，将01x =-代入()y f x =可得02a ey ，令()(1)m g m e m =-+，然后利用导数求函数最值的方法证明结论． 【详解】（1）f ′（x ）=e x （x 2+2x+1）=e x （x+1）2，∴f ′（x ）≥0，∴f （x ）=（1+x 2）e x -a 在（-∞，+∞）上为增函数．（2）∵f （0）=1-a ，a ＞1，∴1-a ＜0，即f （0）＜0，∵f）=（1+a）-a=（-1），a ＞1，∴1，＞0，即f）＞0，且由（1）问知函数在（-∞，+∞）上为增函数，∴f （x ）在（-∞，+∞）上有且只有一个零点．（3）f ′（x ）=e x （x+1）2，设点P （x 0，y 0）则f'（x ）=e x0（x 0+1）2， ∵y=f （x ）在点P 处的切线与x 轴平行，∴f ′（x 0）=0，即：e x0（x 0+1）2=0，∴x 0=-1，将x 0=-1代入y=f （x ）得y 0=2a e -．∴op 2a 2e k a 1e-==--， ∴()m 22f'm e (m 1)a e=+=-，要证1m ≤-，即证（m+1）3≤a-2e， 需要证（m+1）3≤e m （m+1）2，即证m +1≤e m ，因此构造函数g （m ）=e m -（m+1），则g ′（m ）=e m -1，由g ′（m ）=0得m=0．当m ∈（0，+∞）时，g ′（m ）＞0，当m ∈（-∞，0）时，g ′（m ）＜0，∴g （m ）的最小值为g （0）=0，∴g （m ）=e m -（m+1）≥0，∴e m ≥m+1，∴e m （m+1）2≥（m+1）3， 即：32a (m 1)e -≥+，∴1m ≤-．【点睛】在解决含参不等式问题时有时可结合分析法，执果索因，构造函数，利用导数研究函数的单调性，求出最值，进而得出相应的含参不等式，从而得出参数的取值范围．22．已知直线l的参数方程为122x t y ⎧=⎪⎪⎨⎪=+⎪⎩（t 为参数），曲线C 的参数方程为4cos 4sin x y θθ=⎧⎨=⎩（θ为参数）．（1）将曲线C 的参数方程化为普通方程；（2）若曲线C 上的点P 到直线l 的最大距离．【答案】（1）2216x y +=；（2）92. 【分析】（1）根据三角函数平方关系消参数得结果；（2）将直线l 化为普通方程，再利用圆心到直线的距离d 与半径r 的和为P 到直线l 的最大距离计算.【详解】（1）由曲线C ：4cos 4sin x y θθ=⎧⎨=⎩，得2216,x y += 所以曲线C 的普通方程为2216x y +=.（2）将l 化为普通方程，得1y =-10y --=， 圆心到直线l 的距离12d ==， 所以点P 到直线l 的最大距离为19422d r +=+=.。

一、单选题1. 若曲线在点处的切线方程为，则的最大值为（ ）A．B ．1C．D ．2. 冶铁技术在我国已有悠久的历史，据史料记载，我国最早的冶铁技术可以追溯到春秋时代已知某铁块的三视图如图所示，若将该铁块浇铸成一个铁球，则该铁球的表面积为（）A．B．C．D．3.已知幂函数上单调递增，则（ ）A ．0B．C．D．4. 计算的结果是（ ）A．B．C．D ．15. 几何体的俯视图为一边长为2的正三角形，则该几何体的各个面中，面积最大的面的面积为（）A ．3B．C ．2D．6. 筒车亦称“水转筒车"，是我国古代发明的一种水利灌溉工具，筒车发明于隋而盛于唐，距今已有1000多年的历史，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理（如图）.假设在水流量稳定的情况下，一个半径为4m 的筒车按逆时针方向做4min 一圈的匀速圆周运动，已知筒车的轴心O到水面的距离为，以筒车上的某个盛水筒P （视为质点）刚浮出水面开始计时，设转动时间为t （单位：min ），则下列说法正确的是（）①时，盛水筒P 到水面的距离为；吉林省五校联考2021-2022学年高三上学期联合模拟考试数学（理科）试题吉林省五校联考2021-2022学年高三上学期联合模拟考试数学（理科）试题二、多选题三、填空题②与时，盛水筒P 到水面的距离相等；③经过30min ，盛水筒P 共7次经过筒车最高点.A ．①②B ．②③C ．①③D ．①②③7. 现有5种不同的颜色，给四棱锥P-ABCD 的五个顶点涂色，要求同一条棱上的两个顶点颜色不能相同，一共有种方法.A ．240B ．360C ．420D ．4808. 以下函数图象中为奇函数的一项是（ ）A．B．C．D．9.已知双曲线经过点，则（ ）A．的实轴长为B．的焦距为C．的离心率为D ．的渐近线方程是10. 已知函数和分别为R 上的奇函数和偶函数，满足，，分别为函数和的导函数，则下列结论中正确的是（ ）A．B．当时，的值域为C ．当时，若恒成立，则a的取值范围为D ．当时，满足11. 若甲组样本数据，，…，（数据各不相同）的平均数为2，方差为4，乙组样本数据，，…，的平均数为4，则下列说法正确的是（ ）A ．a 的值为-2B ．乙组样本数据的方差为36C ．两组样本数据的样本中位数一定相同D ．两组样本数据的样本极差不同12. 复数满足，则下列说法正确的是（ ）A．在复平面内点落在第四象限B ．为实数C．D ．复数的虚部为13. 已知圆锥顶点为P ，底面的中心为O ，过直线OP 的平面截该圆锥所得的截面是面积为的正三角形，则该圆锥的体积为___________.四、解答题14.已知常数满足，其中，函数，则的最大值为_________，当取得最大值时，_______．15. 已知等比数列满足：，则______.16.在中，内角的对边分别为，且．(1)求；(2)若的面积的最小值为，求的最小值．17. 本学期某校举行了有关垃圾分类知识测试活动（满分10分，分值为整数），并从该校七年级和八年级中各随机抽取40名学生的测试成绩，整理如下：小明将样本中的成绩进行了数据处理，如表为数据处理的一部分：根据图表，解答问题：年级平均数众数中位数方差七年级7.577 2.8八年级82.35(1)填空：表中的______，______；(2)你认为______年级的成绩更加稳定，理由是______；(3)若规定6分及6分以上为合格，该校八年级共1200名学生参加了此次测试活动，估计参加此次测试活动成绩合格的学生人数是多少？18. 如图，在四棱锥P -ABCD 中，底面ABCD 为菱形，△PAD 为正三角形，平面PAD ⊥平面ABCD ，E ，F 分别是AD ，CD 的中点.(1)证明：BD ⊥PF ；(2)若AD =DB =2，求点C 到平面PBD 的距离；19. 如图1，在四边形中，.将沿翻折到的位置，使得平面平面，如图2所示.(1)设平面与平面的交线为，证明：.(2)若点在线段上（点不与端点重合），平面与平面夹角的正弦值为，求的值.20. 已知直线轴，垂足为轴负半轴上的点，点关于坐标原点的对称点为，且，直线，垂足为，线段的垂直平分线与直线交于点．记点的轨迹为曲线．(1)求曲线的方程．(2)已知点，不过点的直线与曲线交于M，N两点，以线段为直径的圆恒过点，试问直线是否过定点？若是，求出该定点坐标；若不是，请说明理由．21. 在中，所对的边分别为，且，其中是三角形外接圆半径，且不为直角.(1)若，求的大小；(2)求的最小值.。