运筹学通论I

第一讲 运筹学概述一、运筹学是什么？----------------------晕愁学其实，这绝对一种误解，事实上运筹学方法及应用早在中小学就比较系统地学过，并且在我们每时每刻的生活过程中都在利用。

北师大版小学语文第六册教材中就有一篇课文《田忌赛马》，在座的各位应该都不陌生。

这是战国时期运筹学思想成功应用的典型实例。

孙膑同志合理地利用当时的现有资源、条件和比赛规则，只建议田忌调换了赛马的出场顺序，就使得原来屡战屡败的战局得到了彻底的扭转，以获胜而告终。

形成了本文主题中“初战失败”、“孙膑献计”、“再赛获胜”的三部分内容。

运筹学思想体现的是，将现有资源的作用得到充分发挥，以获得最优的结果。

运筹让生活得更有条理的艺术。

谈起运筹学，是否会想到很通俗的例子——沏茶水。

沏茶，看起来是一件日常生活中再小不过的事情，却包含着运筹学的道理。

让我们来看一看，沏茶的过程可以分为烧开水、洗茶壶、放茶叶多道“工序”。

其中，烧开水所需的时间最长，洗茶壶、放茶叶的时间则较短。

善于运筹的人，应该是先将水烧上，在烧水的过程中，从从容容地把茶壶洗净，把茶叶放好。

而不善运筹的人，可能会先把茶壶洗净，把茶叶放好，才想起来水还没有烧；或者先把水烧开了，才急急忙忙去洗茶壶、放茶叶，搞得手忙脚乱。

另外还有一个例子我们外地生到上海的路线选择，虽然条条大路都能通到上海，但我们都有一个明确的目标，有些人的目标是准备用最短的时间到达，有些人的目标是用最少费用到达，这样基于不同的目标，就会选择不同的最佳路线。

这两个生活中的运筹学实例说明了运筹学应用的思想并不神秘，而现实的生活中，从沏茶、选择路线这样一件小事，到规模宏大的建设项目，都能运用运筹学的原理。

在人生大事的安排上，也同样需要下功夫好好运筹一番。

从技术是，也就是运筹学解决决策问题的工具方面，在初中的数学教材中有一个重要的内容是《线性规划》，其中比较详细地讲述了线性规划的数学表述形式和求解方法。

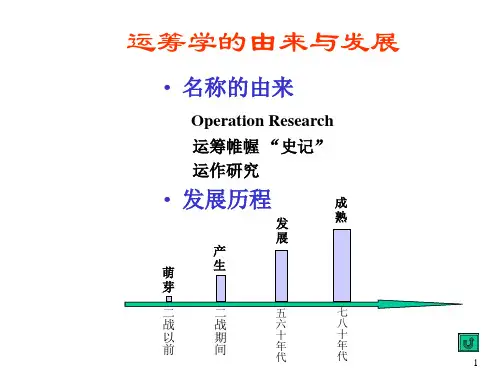
第一章绪论一运筹学的发展历史1学科起源：二战期间英美等国军事部门集中多学科人员，研究提高武器系统效能，如反空袭雷达控制系统，使雷达和高炮相配合。

诺将物理学家布莱克特（Blackett）领导研究小组“Operational Research”，多学科构成（布莱克特马戏团）。

战争结束后专家转移到企业和院校——学科形成。

2我国古代的运筹思想：齐王赛马——齐王“上中下”，田忌“下上中”丁渭修皇宫——北宋真宗宰相丁渭（澶chan州之盟的主和派），主持皇宫失火后的修复。

宫前大街取土、引汴河运料、完工后回填废土。

3我国近代以来：50年代开始钱学森、许志国等引进运筹学理论，华罗庚教授回国后从事优选法和统筹法研究推广（烧茶壶的故事）4翻译：来自汉高祖“夫运筹帷幄之中,决胜千里之外,吾不如子房;填国家,抚百姓,给饷馈,不绝粮道,吾不如萧何;连百万之众,战必胜,攻必取,吾不如韩信。

”台湾地区直译为“运作研究”。

二运筹学的特点运筹学存在多种定义，如“依照给定目标和条件，从众多方案中选择最优方案的最优化技术”，学科特点：最优化、定量化1 多种专家的协作2 科学的方法：从实际情况出发，通过假设的模型打到一个符合实际的结论3 目的在于解决实际问题。

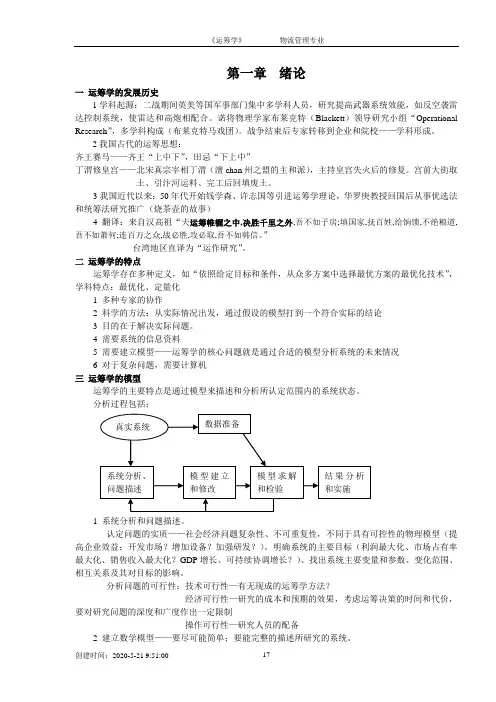
4 需要系统的信息资料5 需要建立模型——运筹学的核心问题就是通过合适的模型分析系统的未来情况6 对于复杂问题，需要计算机三运筹学的模型运筹学的主要特点是通过模型来描述和分析所认定范围内的系统状态。

分析过程包括：1 系统分析和问题描述。

认定问题的实质——社会经济问题复杂性、不可重复性，不同于具有可控性的物理模型（提高企业效益：开发市场？增加设备？加强研发？）。

明确系统的主要目标（利润最大化、市场占有率最大化、销售收入最大化？GDP增长、可持续协调增长？）、找出系统主要变量和参数、变化范围、相互关系及其对目标的影响。

分析问题的可行性：技术可行性—有无现成的运筹学方法？经济可行性—研究的成本和预期的效果，考虑运筹决策的时间和代价，要对研究问题的深度和广度作出一定限制操作可行性—研究人员的配备2 建立数学模型——要尽可能简单；要能完整的描述所研究的系统。

运筹学通论
等）
运筹学，即英文Optimization Theory，即优化理论，是指研究问题的基本模型、关系的最优求解的研究，运筹学关注的是怎样以最有效的方式满足特定的目标。

它兼具数学、计算机算法、和决策论等多种学科的元素，是计算机科学的主要分支之一，它主要用于求解各种复杂科学、技术和经济问题。

运筹学通论是运筹学的基础课，它具有广泛的应用范围，如操作研究、管理学、气象学、量子力学等。

运筹学通论从历史上讲，是运筹学的基础学科，包括传统的运筹学数学模型的求解的方法。

运筹学通论强调建立符合实际环境的有效数学模型、求解这些模型的方法以及得出可行解的评价方法。

它涉及多学科之间的交叉，如数学分析、模糊数学、模式识别、诊断论等等，广泛地应用在建筑、交通、制造业、农业、电气、计算机系统等各行各业，深受各方关注。

运筹学以其全面性来支持多种决策。

它把飞行计划制定、路线网络优化、系统控制设计等多种解决方案都整合到一起，利用数学方法对问题的层次结构及其相关的决策进行模拟和预测，可以有效解决各类复杂的问题，为社会的应用和管理提供有效的支持。

例如在运输、工厂调度等行业中，可以有效地管理仓储资源，进行合理的目标分配，提高运输效率，实现最大程度的节约。

总之，运筹学通论具有重要意义，它是计算机科学、管理学、决策论等诸多学科交叉、深入研究的重要学科，因而有越来越多的人将其作为上本、研究的重要基础。

运筹学习题集（第二章）判断题判断正误，如果错误请更正第二章线形规划的对偶理论1.原问题第i个约束是<=约束,则对偶变量yi>=0.2.互为对偶问题,或则同时都有最优解,或则同时都无最优解.3.原问题有多重解,对偶问题也有多重解.4.对偶问题有可行解,原问题无可行解,则对偶问题具有无界解.5.原问题无最优解,则对偶问题无可行解.6.设X,Y分别为｛minZ=CX｜AX>=b,X>=0｝和｛maxw=Yb｜YA<=C,Y>=0｝的可行解,则有(1)CX<=Yb;(2)CX是w的上界;(3)当X,Y为最优解,CX=Yb;(4)当CX=Yb 时,有YXs+YsX=0;(5)X为最优解且B是最优基时,则Y=C B B-1是最优解;(6)松弛变量Ys的检验数是λs,则X=-λs是基本解,若Ys是最优解, 则X=-λs是最优解.7.原问题与对偶问题都可行,则都有最优解.8.原问题具有无界解,则对偶问题可行.9.若X,Y是原问题与对偶问题的最优解.则X=Y.10.若某种资源影子价格为0,则该资源一定有剩余.11影子价格就是资源的价格.12.原问题可行对偶问题不可行,可用对偶单纯形法计算.13.对偶单纯形法比值失效说明原问题具有无界解.14.对偶单纯形法是直接解对偶问题的一种解法.15.减少一个约束,目标值不会比原来变差.16.增加一个约束,目标值不会比原来变好.17增加一个变量, 目标值不会比原来变差.18.减少一个非基变量, 目标值不变.19.当Cj(j=1,2,3,……，n)在允许的最大范围内同时变化时，最优解不变。

选择题在下列各题中，从4个备选答案中选出一个或从5个备选答案中选出2~5个正确答案。

第二章线性规划的对偶理论1.如果决策变量数列相等的两个线规划的最优解相同，则两个线性规划A约束条件相同B目标函数相同C最优目标函数值相同D以上结论都不对2.对偶单纯形法的最小比值规则是为了保证A使原问题保持可行B 使对偶问题保持可行C逐步消除原问题不可行性D逐步消除对偶问题不可行性3.互为对偶的两个线性规划问题的解存在关系A若最优解存在，则最优解相同B原问题无可行解，则对偶问题也无可行解C对偶问题无可行解，原问题可能无可行解D一个问题无界，则另一个问题无可行解E一个问题无可行解，则另一个问题具有无界解4.已知规范形式原问题（max）的最优表中的检验数为（λ1，λ2，……λn），松弛变量的检验数为（λn+1,λn+2,……λn+m）,则对偶问题的最优解为A—（λ1，λ2，……λn）B （λ1，λ2，……λn）C —（λn+1,λn+2,……λn+m）D （λn+1,λn+2,……λn+m）5.原问题与对偶问题都有可行解，则A原问题有最优解，对偶问题可能没有最优解B原问题与对偶问题可能都没有最优解C可能一个问题有最优解，另一个问题具有无界解D原问题与对偶问题都有最优解计算题线性规划问题和对偶问题2.1 对于如下的线性规划问题min z = 3x1 + 2x2 +x3s.t. x1 + x2+ x3 ≤ 15 (1)2x1 - x2+ x3≥ 9 (2)-x1 + 2x2+2x3≤ 8 (3)x1 x2x3 ≥ 01、写出题目中线性规划问题的对偶问题；2、分别求出原始问题和对偶问题的最优解（求解的次序和方法不限）；解答：1、写出题目中线性规划问题的对偶问题；解：max w = 15y1 + 9y2 + 8y3s.t. y1 + 2y- y3 ≤ 3 (1)y1 - y2+ 2y3≤ 2 (2)y1 + y2+ 2y3≤ 1 (3)y1≤0、y2 ≥0、y3 ≤02、分别求出原始问题和对偶问题的最优解（求解的次序和方法不限）；解：先将原问题化成以下形式，则有mi n z = 3x1 + 2x2 + x3s.t. x1 + x2+ x3+ x4= 15 (1)-2x1 + x23+ x5= -9 (2)-x1 + 2x2+2x3+x6= 8 (3)原始问题的最优解为（X 1 X 2 X 3 X 4 X 5 X 6）=（2，0，5，8，0，0），minz=11 对偶问题的最优解为（y 1 y 2 y 3 y 4 y 5 y 6）=（0，7/5，-1/5，0，19/5，0），maxw=112.2 对于以下线性规划问题max z = -x 1 - 2x 2s.t. -2x 1 + 3x 2 ≤ 12 (1) -3x 1 + x 2 ≤ 6 (2) x 1 + 3x 2 ≥ 3 (3) x 1 ≤ 0，x 2 ≥ 01、写出标准化的线性规划问题；2、用单纯形表求出这个线性规划问题的最优解和最优的目标函数值；3、写出这个（极大化）线性规划问题的对偶问题；4、求出对偶问题的最优解和最优解的目标函数值；5、第（2）个约束右端常数b 2=6在什么范围内变化，最优解保持不变。

我建议的学习经济学的课程表有人关于读书先后次序的相关疑问，我觉得这样的话就得排一个课程表了。

我按4年半，9个学期来排。

数学课程表根本是科大数学系的，经济学课程是我自己的经历。

当然是比拟需要专注、极高热情和兴趣才能按照这个课程表完成的。

下面这些推荐的书，并不是最好的，但是是能够在网上下载的。

后面我附录的科大数学系本科教材我认为是更好的选择，只是很多网上没资源。

只好退而求其次。

例如吉米多维奇习题集并不是理想的习题集，只是理想的习题集网上没有，例如波利亚的习题集或者方企勤的“数学分析习题集“。

第一学期1、数学分析教程〔上下册〕常庚哲史济怀编.pdf〔到一元微积分为止〕2、吉米多维奇〔数学分析习题集解〕.pdf〔相应局部〕3、项武义根底几何学之一.pdf4、项武义根底几何学之二.pdf5、曼昆微观经济学原理.pdf第二学期1、数学分析教程〔上下册〕常庚哲史济怀编.pdf〔到多元微积分为止〕2、吉米多维奇〔数学分析习题集解〕.pdf〔相应局部〕3、炯生_线性代数科大版.pdf〔参考书：线性代数与解析几何讲义-发来.pdf〕4、宏观经济学_曼昆第四版中文.pdf〔实际上常庚哲教师和炯生教师这两门课是科大数学系的招牌菜，奠定了科大数学系本科生在江湖上的竞争力来源，以及可以牛的本钱〕第三学期1、数学分析教程〔上下册〕常庚哲史济怀编.pdf〔剩余课程〕2、吉米多维奇〔数学分析习题集解〕.pdf〔相应局部〕3、炯生_线性代数科大版.pdf〔参考书：许以超_线性代数与矩阵论.pdf〕第四学期1、复变函数(史济怀).pdf2、近世代数引论.pdf4、丁+承治_常微分方程教程.pdf5、中级：微观经济学：现代观点〔里安〕.pdf第五学期1、实变函数与泛函分析〔上册〕复旦.pdf〔参考书：Analysis-实变函数论,.徐森林,.中科大版.2002.pdf〕2、“点集拓扑讲义“(第二版熊金城).pdf〔参考书：拓扑(熊金城，科大版).pdf〕3、老收藏-数学物理方程(复旦).pdf4、概率论第一册概率论根底〔复旦大学〕.pdf5、中级宏观：宏观经济学第八版_多恩布什.pdf第六学期1、实变函数与泛函分析〔下册〕复旦.pdf2、复旦大学 - 数理统计〔“概率论“第二册〕一、二分册合集.pdf〔参考书：数理统计引论希儒着.pdf〕3、小凯-数理经济学根底.pdf第七学期1、概率论第三册随机过程〔复旦大学〕.pdf2、运筹学清华大学.pdf3、最优控制理论与应用.pdf4、小凯经济学原理.pdf第八学期1、高级：[国外经济学教材库]微观经济学高级教程第三版·[美]哈尔·瓦里安着.pdf2、高级：高级宏观_布兰查德_费希尔_宏观经济学〔高级教程〕.pdf第九学期1、中一数理经济学.pdf2、龚六堂动态经济学方法.pdf3、高山晟“经济学中的分析方法“.pdf---------------------------------------------------------------------------- 附：中国科学技术大学数学系本科生必修课教材及参考书目录1、数学根底：教材：汪芳庭“数学根底“科学2、初等数论：教材：克勤“整数与多项式“高等教育参考书：承洞、承彪“初等数论“大学3、数学分析：教材：常庚哲“数学分析教程“〔第二版〕高等教育参考书：方企勤“数学分析习题集“高等教育许绍浦“数学分析教程“大学华罗庚“高等数学引论“科学S. M. Nikolsky，A course of mathematical analysis，Mir Publishers库朗“微积分与分析引论“科学卢丁“数学分析原理“高等教育斯皮瓦克“流形上的微积分“科学4、解析几何：教材：吴光磊“解析几何简明教程“高等教育参考书：丘维声“解析几何“大学5、线性代数：教材：烔生“线性代数“中国科学技术大学参考书：叶明训“线性空间引论“大学贤科“高等代数学“清华大学许以超“线性代数与矩阵论“高等教育A.I. Kostrikin，Introduction to algebra，Springer-VerlagM. Postnikov，Linear algebra and differential geometry，Mir Publishers Lang. Serge，Linear algebra，Springer-Verlag6、普通物理：教材：永令“力学“复旦大学玉民“根底物理学教程———热学“中国科学技术大学胡有秋“电磁学“高等教育郭光灿“光学“高等教育徐克尊“近代物理学“高等教育参考书：漆安慎“力学“高等教育允豪“热学“高等教育凯华“电磁学“高等教育凯华“光学“高等教育福家“原子物理学“高等教育中国科大物理教研室“美国物理试题汇编“中国科学技术大学7、常微分方程：教材：丁、承治“常微分方程教程“高等教育参考书：V.I.Arnold“常微分方程“科学庞特里亚金“常微分方程“高等教育袁相碗“常微分方程“大学A. Coddington，Theory of ordinary differential equations，McGraw-HillA.Φ.菲利波夫“常微分方程习题集“科技8、复变函数：教材：龚昇“简明复分析“大学参考书：H.嘉当“解析函数论初步“科学L.V.Ahlfors， ple* Analysis 3rd ed ，McGraw-Hill任尧福“应用复分析“复旦大学余家荣“复变函数“高等教育L.沃尔科维斯“复变函数论习题集“科技9、实变函数：教材：徐森林“实变函数论“中国科学技术大学参考书：维行“实变函数与泛函分析概要“〔第一册〕高等教育周民强“实变函数论“大学A.N. Kolmogorov，Theory of Functions and Functional Analysis，DOVERE. Hewitt，Real and Abstract Analysis，Springer Verlag鄂强“实变函数论的定理与习题“高等教育10、近世代数：教材：克勤“近世代数引论“中国科学技术大学参考书：熊全淹“近世代数“大学莫宗坚“代数学“〔上〕大学聂灵沼“代数学引论“高等教育N.Jacobson,Basic Algebra〔1〕Springer-VerlagA.I. Kostrikin，Introduction to algebra，Springer-Verlag11、概率论：教材：淳“概率论“中国科学技术大学讲义参考书：振明“概率论“科学王辛坤“概率论及其应用“科学12、微分几何：教材：家贵“微分几何“高等教育参考书：A.T.Fomenko Differential geometry and topology，Consultants Bureau 省身“微分几何“南开大学讲义多卡模“曲线和曲面的微分几何学“高等教育吴大任“微分几何讲义“高等教育A.C.菲金科“微分几何习题集“师大学13、拓扑学：教材：熊金城“点集拓扑讲义〔第二版〕“高等教育参考书：儿玉之宏“拓扑空间论“科学J.L.Kelley，General Topology，Springer-VerlagM.A.Armstrong“根底拓扑学“大学肇“点集拓扑学“大学肇“点集拓扑学题解与反例“大学14、泛函分析：教材：恭庆“泛函分析讲义“〔上册〕大学参考书：培德“泛函分析根底“大学夏道行“实变函数与泛函分析“〔下册〕高等教育维行“实变函数与泛函分析概要“〔下册〕高等教育A.N. Kolmogorov，Theory of Functions and Functional Analysis，DOVER А.Б.安托涅维奇“泛函分析习题集“高等教育15、偏微分方程：教材：祖墀“偏微分方程“中国科技大学参考书：齐民友“广义函数与数学物理方程“高等教育礼尚“数学物理方程讲义“高等教育Aleksei.A.Dezin ，Partial differential equations，Springer-Verlag 16、数理统计：教材：希孺“数理统计学教程“科技参考书：家鼎“数理统计学讲义“高等教育陆璇“数理统计根底“清华大学中国科学技术大学“数理统计习题集“中国科学技术大学讲义17、数值分析：教材：奚梅成“数值分析方法“中国科学技术大学参考书：林成森“数值计算方法“科学18、C语言程序设计：教材：谭浩强“C语言程序设计“清华大学19、数据构造：教材：黄生“数据构造“中国科学技术大学20、数据库：教材：黄生“数据构造“中国科学技术大学21、微机原理：教材：周佩玲“16位微机原理接口技术及其应用“中国科学技术大学22、电子电路：教材：翰荪“电路分析“高等教育23、模拟电子技术：教材：同怀“模拟电子线路“中国科学技术大学24、数字电子技术：教材：康华光“电子技术根底〔数字局部〕“高等教育25、理论力学：教材：金尚年“经典力学“复旦大学参考书：Landau，Mechanics，Heinemann26、电动力学：教材：郭硕鸿“电动力学“〔第二版〕高等教育参考书：Jackson，Classical Electrodynamics27、热力学与统计物理学：教材：汪志诚“热力学与统计物理“高等教育参考书：Landau，Statistical Physics Part1，Heinemann28、量子力学：教材：永德“量子力学讲义“中国科学技术大学讲义参考书：Landau，Quantum Mechanics (Non-relatisticTheory)，Heinemann--------------------------------------------------------------------------附：数学系研究生课程〔这就是号称国最好的数学系能够开出来的课程〕一、数学系研究生一级学科学科根底课课程设置一览表抽象代数；群和代数；代数拓扑；微分流形；黎曼曲面；微分几何；泛函分析；偏微分方程概论；随机数学概论；最优化计算方法；数值分析。

课程介绍一、运筹学产生的和发展1. 运筹学产生的原因✓科学技术的发展，利用和改造自然的规模扩大，生产规模扩大，生产组织形式复杂，出现了更复杂的管理方面的问题。

管理方面的新问题：如何有效和合理地利用有限的或稀缺的资源，使系统的整体目标达到最优。

2. 运筹学的起源✓运筹学的三个来源：军事、经济、管理✓1981年美国军事运筹学会出版的“System analysis and modeling in defence”一书中称孙武子是世界上第一个军事运筹学家。

✓第二次世界大战期间英、美等国军事部门成立的一些研究小组的研究活动。

最初人们称这类研究为“运作研究”(operational research)，或“运作分析”(operational analysis)。

✓研究的特点是集中一批跨多学科的研究人员，有组织地对一特定问题进行系统分析，提出提高某武器系统效率的操作方法和执行策略。

✓二战期间成功的运筹研究案例有：英国防空部门如何布置防空雷达，建立有效的空防预警系统；研究反潜飞机巡逻路线及深水炸弹引爆深度，击沉德军潜艇数提高4倍；研究如何使用机载雷达提高轰炸命中率，两年内使命中率提高3倍；研究船队在受敌机攻击时的躲避策略，使中弹率从47%下降到29%；✓数理经济对运筹学的影响Qusnay 的经济表Walras 提出的经济平衡问题V on Neumann 提出的广义经济平衡模型康托洛维奇(Kantorovich)发表的《生产组织和计划中的数学方法》✓管理科学-- 运筹学的关系✓管理理论中最有影响的三个学派中的两个（古典学派与系统学派）广泛应用定量分析与系统分析的方法。

✓古典学派的代表性人物Taylor, Gantt 等提出的动作分析、甘特图至今还在使用。

3. 运筹学的发展二战结束后运筹学在理论上得到全面的发展；线性规划、非线性规划、动态规划、网络分析、整数规划、对策论、排队论等分枝得到迅速的发展。

运筹学应用从军事部门迅速向工业部门转移。

运筹学讲义绪论（2学时）参考教材：（1）运筹学基础教程（魏权龄）（2）管理运筹学（韩伯棠）（3）管理运筹学通论（韩大卫）（4）运筹学（胡运权）先修课程：一元微积分、线性代数、概率统计学时：48+（8）主讲教师：狄军锋一、运筹学发展1、运筹学的产生✧最早与1938年出现于英国，简称OR(operational Research)✧夫运筹帷幄之中，决胜于千里之外，吾不如子房。

---史记✧古代运筹学思想：田忌赛马+丁谓挖沟+沈括运军粮✧二战中的运筹学：反潜艇策略、深水炸弹的起爆深度、诺曼底登陆✧运筹学在我国的发展：①50年代中期，钱学森、许国志等教授将运筹学由西方引入我国。

②管梅谷（1962年，山东师范大学）：“中国邮递员问题”③华罗庚：优选法（1970）和统筹法（1965）2、运筹学的定义：管理运筹学是一门应用科学，它广泛应用现有的科学技术和数学方法，解决管理中提出的专门问题，为决策者选择最优或较优的决策提供定量依据。

运筹学是一门新兴的交叉学科，来源于军事、管理和经济。

本课程主要介绍用于解决管理领域问题的运筹学，因此称为管理运筹学，也有人称为管理科学。

二、运筹学解决问题的思路提出问题→建模→求解→结果分析与调整→实施二、运筹学的学科内容：线性规划（LP）；*整数规划（IP）；*非线性规划(NP)；*多目标规划（MP）；动态规划（DP）；对策论（GT）；决策分析（DA）；存贮论（IC）；排队论（QT）；图论（Graph Theory）三、章节安排1、绪论（2学时）2、线性规划(14学时)3、动态规划（6学时）4、存储论（6学时）5、对策论（10学时）6、决策论（6学时）7、统筹方法（2学时）8、总复习（2学时）四、应用举例1、猴子运香蕉2、海盗分宝石3、猜生日第二*主要内容1、线性规划的一般形式、压缩形式、矩阵形式、向量形式2、线性规划问题的图解法（3）3、线性规划问题的标准形式4、单纯形方法（4）5、线性规划问题应用举例（3）6、运输问题的解法（4）§1 线性规划问题的基本模型一、 引例【引例1】某工厂在计划期内要安排生产Ⅰ、Ⅱ两种产品，已知生产单位产品需的设备台时，A 、B 两种原材料的消耗以及每种产品可获利润如下表所示。