运筹学实验一

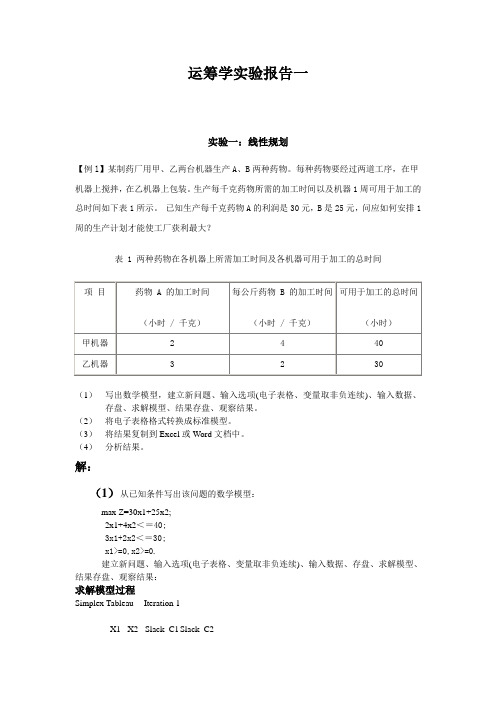
运筹学实验报告一实验一：线性规划【例l】某制药厂用甲、乙两台机器生产A、B两种药物。

每种药物要经过两道工序，在甲机器上搅拌，在乙机器上包装。

生产每千克药物所需的加工时间以及机器1周可用于加工的总时间如下表1所示。

已知生产每千克药物A的利润是30元，B是25元，问应如何安排1周的生产计划才能使工厂获利最大？表 1 两种药物在各机器上所需加工时间及各机器可用于加工的总时间（1）写出数学模型，建立新问题、输入选项(电子表格、变量取非负连续)、输入数据、存盘、求解模型、结果存盘、观察结果。

（2）将电子表格格式转换成标准模型。

（3）将结果复制到Excel或Word文档中。

（4）分析结果。

解：（1）从已知条件写出该问题的数学模型：max Z=30x1+25x2;2x1+4x2＜＝40;3x1+2x2＜＝30;x1>=0,x2>=0.建立新问题、输入选项(电子表格、变量取非负连续)、输入数据、存盘、求解模型、结果存盘、观察结果：求解模型过程Simplex Tableau -- Iteration 1X1 X2 Slack_C1 Slack_C2Basis C(j) 30.0000 25.0000 0 0 R. H. S. RatioSlack_C1 0 2.0000 4.0000 1.0000 0 40.0000 20.0000Slack_C2 0 3.0000 2.0000 0 1.0000 30.0000 10.0000C(j)-Z(j) 30.0000 25.0000 0 0 0Simplex Tableau -- Iteration 1X1 X2 Slack_C1 Slack_C2Basis C(j) 30.0000 25.0000 0 0 R. H. S. RatioSlack_C1 0 2.0000 4.0000 1.0000 0 40.0000 20.0000Slack_C2 0 3.0000 2.0000 0 1.0000 30.0000 10.0000C(j)-Z(j) 30.0000 25.0000 0 0 0Simplex Tableau -- Iteration 3X1 X2 Slack_C1 Slack_C2Basis C(j) 30.0000 25.0000 0 0 R. H. S. RatioX2 25.0000 0 1.0000 0.3750 -0.2500 7.5000X1 30.0000 1.0000 0 -0.2500 0.5000 5.0000C(j)-Z(j) 0 0 -1.8750 -8.7500 337.5000（2）将电子表格格式转换成标准模型。

运筹学lingo实验报告(一)运筹学lingo实验报告介绍•运筹学是一门研究在给定资源约束下优化决策的学科，广泛应用于管理、工程、金融等领域。

•LINGO是一种常用的运筹学建模和求解软件，具有丰富的功能和高效的求解算法。

实验目的•了解运筹学的基本原理和应用。

•掌握LINGO软件的使用方法。

•运用LINGO进行优化建模和求解实际问题。

实验内容1.使用LINGO进行线性规划的建模和求解。

2.使用LINGO进行整数规划的建模和求解。

3.使用LINGO进行非线性规划的建模和求解。

4.使用LINGO进行多目标规划的建模和求解。

实验步骤1. 线性规划•确定决策变量、目标函数和约束条件。

•使用LINGO进行建模，设定目标函数和约束条件。

•运行LINGO求解线性规划问题。

2. 整数规划•在线性规划的基础上，将决策变量的取值限制为整数。

•使用LINGO进行整数规划的建模和求解。

3. 非线性规划•确定决策变量、目标函数和约束条件。

•使用LINGO进行非线性规划的建模和求解。

4. 多目标规划•确定多个目标函数和相应的权重。

•使用LINGO进行多目标规划的建模和求解。

实验结果•列举各个实验的结果，包括最优解、最优目标函数值等。

结论•运筹学lingo实验是一种有效的学习运筹学和应用LINGO的方法。

•通过本实验能够提高对运筹学概念和方法的理解，并掌握运用LINGO进行优化建模和求解的技能。

讨论与建议•实验过程中是否遇到困难或问题，可以进行讨论和解决。

•提出对于实验内容或方法的建议和改进方案。

参考资料•提供参考书目、文献、教材、网站等资料，以便学生深入学习和研究。

致谢•对与实验指导、帮助或支持的人员表示感谢，如老师、助教或同学等。

以上为运筹学lingo实验报告的基本框架，根据实际情况进行适当调整和补充。

实验报告应简洁明了，清晰表达实验目的、内容、步骤、结果和结论，同时可以加入必要的讨论和建议，以及参考资料和致谢等信息。

实验报告项目名称所属课程名称运筹学项目类型实验(实训)日期3月18号班级学号姓名指导教师浙江财经学院教务处制一、实验概述（一）实验目的掌握使用Excel软件求解线性规划问题。

（二）实验要求用Excel软件完成案例求解并进行结果分析。

（三）实验工具Excel软件二、实验内容案例营养配餐问题♦有A、B两种食品，含有每天必须的营养成分C、D，每天至少需要营养成分C和D 分别为2和3个单位。

食品A、B的成分和单价如下表，试做花钱最少的食谱，并求其费用。

（一）线性规划模型♦1、确定决策变量：设A、B两种食品每天的购买量分别为x1,x2单位。

♦2、确定目标函数：min W=0.9x1+0.8x2♦3、确定约束条件：成分C约束：x1+2x2 ≥2成分D约束：3x1+x2 ≥3x1 ≥0,x2 ≥0（二）电子表格模型A购买量0.8B购买量0.6目标函数 1.2成分C约束 2成分D约束 3A购买量0.8B购买量0.6（三）结果分析Microsoft Excel 11.0 运算结果报告工作表[Book1.xls]Sheet1报告的建立: 2012/3/18 18:51:54目标单元格(最小值)单元格名字初值终值$B$5目标函数0 1.2可变单元格单元格名字初值终值$B$2A购买量00.8 $B$3B购买量00.6约束单元格名字单元格值公式状态型数值$B$7成分C约束2$B$7>=2到达限制值$B$8成分D约束3$B$8>=3到达限制值$B$10B购买量0.6$B$10>=0未到限制值0.6$B$9A购买量0.8$B$9>=0未到限制值0.8分析：由上表可知：目标函数的最小值为1.2，当产品A的购买量为0.8，产品B的购买量为0.6时取得最小值。

取得最小值时成分C的含量与成分D的含量均达到最低要求。

Microsoft Excel 11.0 极限值报告工作表 [Book1.xls]极限值报告 1报告的建立: 2012/3/18 18:54:24目标式单元格名字值$B$5 目标函数 1.2变量下限目标式上限目标式单元格名字值极限结果极限结果$B$2 A购买量0.8 0.8 1.2 #N/A #N/A$B$3 B购买量0.6 0.6 1.2 #N/A #N/A分析：有该表可知：产品A购买量下极限为0.8单位，取下极限时目标函数结果为1.2，上极限为无穷大，目标值也为无穷大；产品B购买量下极限为0.6单位，取下极限时目标函数结果为1.2，上极限为无穷大，目标值也为无穷大。

运筹学实验一-图文实验报告项目名称生产计划优化研究所属课程名称运筹学项目类型求解线性规划问题实验(实训)日期班级学号姓名指导教师浙江财经学院教务处制一、实验概述（一）实验目的安装E某cel软件“规划求解”加载宏，用E某cel软件求解线性规划问题。

（二）实验内容（1）建立电子表格模型：输入数据、给单元格命名、输入公式等；（2）使用E某cel软件中的规划求解功能求解模型；（3）结果分析；（4）在Word文档中书写实验报告，包括线性规划模型、电子表格模型和结果分析等。

（三）实验工具E某cel软件二、案例分析案例生产计划优化研究某柴油机厂年度产品生产计划的优化研究。

某柴油机厂是我国生产中小功率柴油机的重点骨干企业之一。

主要产品有2105柴油机、某2105柴油机、某4105柴油机、某4110柴油机、某6105柴油机、某6110柴油机。

柴油机生产过程主要分成三大类：热处理、机加工、总装。

与产品生产有关的主要因素有单位产品的产值、生产能力、原材料供应量及生产需求情况等。

每种产品的单位产值如表1所示。

各产品的单位产值序号123456产品型号及名称2105柴油机某2105柴油机某4105柴油机某4110柴油机某6105柴油机某6110柴油机单位产值（元）5400650012000140001850020000为简化问题，根据一定时期的产量与所需工时，测算了每件产品所需的热处理、机加工、总装工时，如表2所示。

单位产品所需工时序号123产品型号及名称2105柴油机某2105柴油机某4105柴油机热处理10.5811.0329.11机加工14.587.0523.96总装17.0815029.37456某4110柴油机某6105柴油机某6110柴油机32.2637.6340.8427.729.3640.4333.3855.153.5同时，全厂所能提供的总工时如表3所示。

各工序所能提供的工时工序名称全年提供总工时4所示。

原材料最大供应量原材料名称最大供应量生铁（吨）1562焦炭（吨）951废钢（吨）钢材（吨）530350热处理120000机加工95000总装180000产品原材料主要是生铁、焦炭、废钢、钢材四大类资源。

运筹学实验总结引言：运筹学是一门综合了数学、经济学和工程学等多学科知识的学科，它通过建立数学模型和运用各种优化方法，帮助我们在现实问题中寻找最优解决方案。

在这学期的运筹学课程中，我们进行了一系列实验。

这些实验不仅加深了对运筹学理论的理解，还提供了一种应用运筹学方法解决问题的实践平台。

在本文中，我将总结我参与的运筹学实验，并分享我的体会和收获。

实验一：线性规划问题求解在这个实验中，我们学习了线性规划的基本概念和求解方法。

我选择了一个典型的生产调度问题作为实验题目。

通过建立数学模型，并运用线性规划软件，我成功地解决了这个问题。

通过这个实验，我深刻理解了线性规划问题的本质，以及如何利用线性规划方法找到最优解。

实验二：整数规划问题求解整数规划是线性规划的扩展，它在决策问题中更加实用。

在这个实验中，我选择了货物配送路线问题作为研究对象。

通过构建整数规划模型，并运用求解软件，我得到了最佳的货物配送方案。

这个实验不仅对我的数学建模能力提出了要求，还培养了我的实际问题解决能力。

实验三：动态规划动态规划是一种重要的优化方法，它广泛应用于最优化问题的求解。

在这个实验中，我们学习了动态规划的基本原理和设计思想。

我选择了旅行商问题作为研究对象，通过建立递推关系和寻找最优子结构，我成功地解决了该问题。

这个实验让我意识到了动态规划方法的强大威力，同时也对我的算法设计能力提出了更高的要求。

实验四：模拟退火算法模拟退火算法是一种全局搜索优化算法，具有很强的应用能力。

在这个实验中，我选择了旅行商问题作为研究对象，通过模拟退火算法的迭代和优化，我得到了一个较好的解。

通过这个实验，我掌握了模拟退火算法的基本原理和实现过程，也了解到了算法的优越性。

实验五：遗传算法遗传算法是一种模拟自然选择和遗传机制的优化算法。

在这个实验中，我选择了装箱问题作为研究对象。

通过运用遗传算法的交叉、变异和适应度选择，我得到了一个较好的装箱方案。

这个实验不仅对我的算法设计能力提出了更高的要求，还让我意识到了遗传算法的创新性和解决复杂问题的能力。

运筹学实验：线性规划问题一、实验目的1、学习建立数学模型2、熟练运用计算软件求得模型最优解二、实验内容案例一：1.13、某饲养场饲养动物出售，设每头动物每天至少需700g 蛋白质、30g 矿物质、100mg 维生素。

现有五种饲料可供选用，各种饲料每kg 营养成分含量及单价如表1-20所示。

表1-20饲料 蛋白质（g ） 矿物质（g ） 维生素（mg ） 价格（元/kg ） 1 2 3 4 5 3 2 1 6 18 1 0.5 0.2 2 0.5 0.5 1.0 0.2 2 0.8 0.2 0.7 0.4 0.30.8 要求确定既满足动物生长的营养需要，又使费用最省的选用饲料的方案。

解：建立线性规划模型设x i 表示第i 中饲料数量 i=1,2,3,4,5Minz=0.2x 1+0.7x 2+0.4x 3+0.3x 4+0.8x 53x 1+2x 2+x 3+6x 4+18x 5>=700x 1+0.5x 2+0.2x 3+2x 4+0.5x 5>=30S.t. 0.5x 1+x 2+0.2x 3+2x 4+0.8x 5>=100x i >=0(i=1,2,3,4,5)运算截图如下所示：结果如下所示：案例二：1.18、宏银公司承诺为某建设项目从2003年起的4年中每年初分别提供以下数额贷款：2003年——100万元，2004年——150万元，2005年——120万元，2006年——110万元。

以上贷款资金均需于2002年底前筹集齐。

但为了充分发挥这笔资金的作用，在满足每年贷款额情况下，可将多余资金分别用于下列投资项目：（1）、于2003年初购买A种债券，期限3年，到期后本息合计为投资额的140%，但限购60万元；（2）、于2003年初购买B种债券，期限2年，到期后本息合计为投资额的125%，且限购90万元；（3）、于2004年初购买C种债券，期限2年，到期后本息合计为投资额的130%，但限购50万元；（4）、于每年年初将任意数额的资金存放于银行，年息4%，于每年年底取出。

运筹学实验报告一、实验目的：通过实验熟悉单纯形法的原理，掌握matlab循环语句的应用，提高编程的能力和技巧，体会matlab在进行数学求解方面的方便快捷。

二、实验环境：Matlab2012b,计算机三、实验内容（包含参数取值情况）：构造单纯形算法解决线性规划问题Min z=cxs.t. Ax=bxj>=0,j=1,…,n函数功能如下：function[S,val]=danchun(A1,C,N)其中，S为最优值，Val为最优解，A1为标准形式LP问题的约束矩阵及最后一列为资源向量（注：资源向量要大于零），A1=[A+b]；C是目标函数的系数向量，C=c；N为初始基的下标（注：请按照顺序输入，若没有初始基则定义N=[]）。

先输入A1,C,N三个必要参数，然后调用danchun（A1,C,N）进行求解。

在此函数中，首先判断N的长度是否为空，若为空，则flag=1，进入初始解问题的迭代求值，添加辅助问题，构建单纯形表，求g所对应的RHS值，若其>0,则返回该问题无解，若其=0，则返回A1,C,N三个参数，继续构造单纯形表求解。

A1为经过变换后的系数及资源向量，C为单纯形表的第一行，N为经过辅助问题求解之后的基的下标。

否则，直接构建单纯形表，对该问题进行求解，此时flag=2,多次迭代后找到解。

另外，若在大于零的检验数所对应的系数均小于零时，会显示“此问题无界”。

若找到最优解和最优值时，会输出“val”和“S=”以及具体数值。

四、源程序（在matlab中输入edit后回车，写在.M文件中，并保存为danchun.M）function[S,val]=danchun(A1,C,N)if(length(N)==0)gN=zeros(1,length(A1(:,1)));gC=[-C,gN,0];%原文题的检验数的矩阵G=[zeros(1,length(C)),-ones(1,length(gN)),0];val=zeros(1,length(C));%val为最优解；for i=(length(C)+1):length(C)+length(A1(:,1))%生成基变量gN(i-length(C))=i;endNn=gN;%%%%%%%ll=zeros(1,length(N));%比值最小原则%生成除了最上端两行的表的矩阵gb=A1(:,length(C)+1);A1(:,length(C)+1)=[];l=zeros(length(gN),length(gN));gA=[A1,l,gb];for i=1:length(gb)gA(i,gN(i))=1;endfor i=1:length(gN)%J为基本可行基所对应的检验数J(i)=G(gN(i));endfor i=1:length(gN)%找到基本可行基的检验数，将其赋值为0 if(J(i)~=0)G=G-(J(i)/gA(i,gN(i)))*gA(i,:);endendflag=1;elseflag=2;A=A1;Z=[-C,0];%单纯形表的第一行val=zeros(1,length(C));%val为最优解；ll=zeros(1,length(N));%比值最小原则end%%初始解问题while flag==1for i=1:length(gN)%J为基本可行基所对应的G的检验数J(i)=G(gN(i));JZ(i)=Z(gN(i));%JZ为基本可行基所对应的Z的检验数endfor i=1:length(gN)%找到基本可行基的检验数，将其赋值为0 if(J(i)~=0)G=G-(J(i)/gA(i,gN(i)))*gA(i,:);Z=Z-(JZ(i)/gA(i,gN(i)))*gA(i,:);endG1=G;%G1为检验数G1(:,length(G1))=[];D=max(G1);%找到检验数的最大值if(D<=0)%检验数都小于0if(G(length(G))>=1)disp('此情况无解');flag=0;elseif(G(length(G))>=0)for i=1:length(gN)if(max(gN)<=length(A1(1,:)));flag=2;for j=1:length(Nn)a=Nn(1);gA(:,a)=[];Z(a)=[];endA=gA;N=gN;break;endendendendelse%检验数大于0for i=1:length(G)if(G(i)==D)%找到最大的那个检验数所对应的元素for j=1:length(gN)if(gA(j,i)>0)ll(j)=gA(j,length(G))/gA(j,i);%求比值elsell(j)=10000;endendd=min(ll);for k=1:length(ll)%找到进基和离基if(ll(k)==d)gN(k)=i;gA(k,:)=gA(k,:)/gA(k,i);for m=1:k-1gA(m,:)=-(gA(m,i)/gA(k,i))*gA(k,:)+gA(m,:);endfor n=k+1:length(ll)gA(n,:)=-(gA(n,i)/gA(k,i))*gA(k,:)+gA(n,:);endbreak;endendendendendendwhile(flag==2)for i=1:length(N)%J为基本可行基所对应的检验数J(i)=Z(N(i));endfor i=1:length(N)%找到基本可行基的检验数，将其赋值为0if(J(i)~=0)Z=Z-(J(i)/A(i,N(i)))*A(i,:);endendZ1=Z;%Z1为检验数Z1(:,length(Z1))=[];D=max(Z1);%找到检验数的最大值if(D<=0)%检验数都小于0disp('已找到最优解和最优值')for i=1:length(N)val(N(i))=A(i,length(Z));endS=Z(length(Z));disp('val');disp(val);flag=0;else%检验数大于0for i=1:length(Z)if(Z(i)==D)%找到最大的那个检验数所对应的元素for j=1:length(N)if(A(j,i)>0)ll(j)=A(j,length(Z))/A(j,i);%求比值elsell(j)=10000;endendd=min(ll);if(d==10000)disp('此问题无界')flag=0;break;endfor k=1:length(ll)%找到进基和离基if(ll(k)==d)N(k)=i;A(k,:)=A(k,:)/A(k,i);for m=1:k-1A(m,:)=-(A(m,i)/A(k,i))*A(k,:)+A(m,:);endfor n=k+1:length(ll)A(n,:)=-(A(n,i)/A(k,i))*A(k,:)+A(n,:);endbreakendendendendendend五、运行结果与数据测试参考例题：例1：Min z=3x1+x2+x3+x4s.t. -2x1+2x2+x3=43x1+2x+x4=6Xj>=0,j=1,2,3,4在workspace中写入，形式如下：>> A=[-2 2 1 0 43 1 0 1 6]A =-2 2 1 0 43 1 0 1 6>> C=[3 1 1 1]C =3 1 1 1>> N=[3 4]N =3 4>> danchun(A,C,N)已找到最优解和最优值val0 2 0 4ans =6例2：初始解问题Min z=5x1+21x3s.t. x1-x2+6x3-x4=2x1+x2+2x3-x5=1xj>=0,j=1,…,5在workspace中写入，形式如下：>> A=[1 -1 6 -1 0 21 12 0 -1 1]A =1 -1 6 -1 0 21 12 0 -1 1 >> C=[5 0 21 0 0]C =5 0 21 0 0>> N=[]N =[]>> danchun(A,C,N)已找到最优解和最优值val0.5000 0 0.2500 0 0ans =7.7500六、求解实际问题（即解决附件中的实验题目）实验题目列出下列问题的数学模型，并用你自己的单纯形算法程序进行计算，最后给出计算结果。

实验一运筹学软件应用一、实验目的（1）学会使用Lindo和Lingo软件求解线性规划问题。

（2）会解读实验结果和Lindo软件的灵敏度分析结果报告。

二、实验内容验证下料问题不同目标函数的最优解情况。

三、主要步骤生产100套钢架，长2.9、2.1、1.5米各1根/套，原料长7.4米，如何下料？方案 1 2 3 4 5 6 7 8 2.9 2 1 1 1 0 0 0 0 2.1 0 2 1 0 3 2 1 0 1.5 1 0 1 3 0 2 3 4 料头 0.1 0.3 0.9 0 1.1 0.2 0.8 1.4给出下料问题的计算程序：Lindo程序：!min 0.1x1+0.3x2+0.9x3+0x4+1.1x5+0.2x6+0.8x7+1.4x8 min 1x1+1x2+1x3+1x4+1x5+1x6+1x7+1x8subject to2x1+1x2+1x3+1x4+0x5+0x6+0x7+0x8>1000x1+2x2+1x3+0x4+3x5+2x6+1x7+0x8>1001x1+0x2+1x3+3x4+0x5+2x6+3x7+4x8>100endgin x1gin x2gin x3gin x4gin x5gin x6gin x7gin x8Lingo程序：model:sets:E/1..8/:c,x;F/1..3/:b;link(F,E):a;endsetsmin=@sum(E(j):c(j)*x(j));@for(F(i):@sum(E(j):a(i,j)*x(j))>100); @for(E(j):x(j)>0);@for(E(j):@gin(x));data:!c=0.1,0.3,0.9,0,1.1,0.2,0.8,1.4;c=1,1,1,1,1,1,1,1;a=2,1,1,1,0,0,0,0,0,2,1,0,3,2,1,0,1,0,1,3,0,2,3,4;enddataend2、给出问题的计算程序：例子某工厂生产A、B两个产品，要经过2道工序，每单位B产品生产2单位副产品C，无生产费用。

工商管理学院2019-2020学年第二学期《管理运筹学》课程实验报告专业班级：工商管理1402学号：2019年6月30日【实验1：线性规划】（1） 对以下问题进行求解：12121212212max 32262+812,0z x x x x x x x x x x x =++≤⎧⎪≤⎪⎪-+≤⎨⎪≤⎪≥⎪⎩************************************************************************求解结果：结果分析：（1） 该问题的最优解为： 当x1=3.3333，x2=1.3333时， 此问题有最有解，max z=12.6667（2） 4个约束条件的右端项分别在什么范围变化，问题最优基不变： 当问题最优基不变时，4.0000>=b1<=7.0000 6.0000>=b2<=12.0000 -2.0000>=b3<=M1.3333>=b4<=M完成时间：2020/6/30 8:30:39************************************************************************（2）通过对以下问题的分析，建立线性规划模型，并求解:某工厂要用三种原材料C、P、H混合调配出三种不同规格的产品A、B、D。

已知产品的规格要求，产品单价，每天能供应的原材料数量及原材料单价分别见下表1和2。

该厂应如何安排生产，使利润收入为最大？************************************************************************建立的线性规划模型为：用i=1,2,3分别代表原材料C,P,H，用j=1,2,3分别代表A,B,C三种产品，设xij为生产第j 种产品使用的第i种原材料的质量。

Maxz=50*(x11+x21+x31)+35*(x12+x22+x32)+25*(x13+x23+x33)-65*(x11+x12+x13)-25*(x21+x22+x23)-35*(x31+x32+x33)x11>=0.5*(x11+x21+x31)x21<=0.25*(x11+x21+x31)x12>=0.25*(x12+x22+x32)x22<=0.5*(x12+x22+x32)xij>=0(i=1,2,3,j=1,2,3)生产A 种产品用C 0.5千克，P 0.25千克，H为60千克，B种产品用C 0. 25千克，P 0.5千克，H 0千克，不生产C产品时利润最大为903.7500元完成时间：2020/6/30 09:11************************************************************************【实验2：运输问题与指派问题】（1）对以下运输问题进行求解：************************************************************************ 求解结果与分析：完成时间：2020/6/30************************************************************************（2）对以下运输问题进行求解：设有三个化肥厂（A, B, C）供应四个地区（I, II, III, IV）的农用化肥。