高考数学大一轮复习 8.6双曲线 理
- 格式:ppt
- 大小:3.18 MB
- 文档页数:54



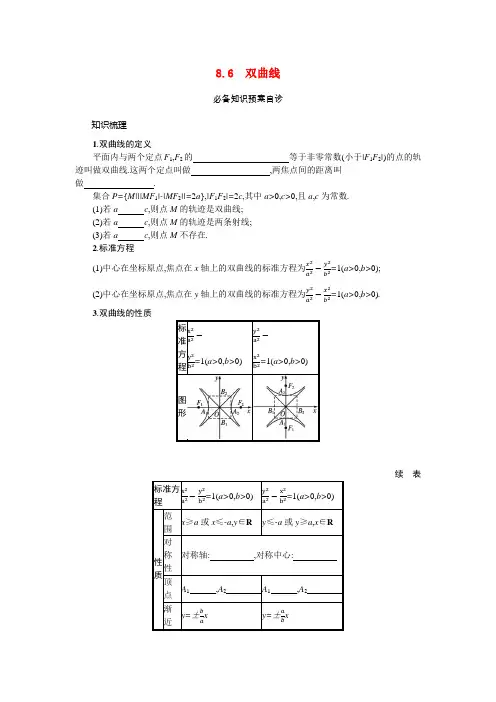
8.6双曲线必备知识预案自诊知识梳理1.双曲线的定义平面内与两个定点F1,F2的等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线.这两个定点叫做,两焦点间的距离叫做.集合P={M|||MF1|-|MF2||=2a},|F1F2|=2c,其中a>0,c>0,且a,c为常数.(1)若a c,则点M的轨迹是双曲线;(2)若a c,则点M的轨迹是两条射线;(3)若a c,则点M不存在.2.标准方程(1)中心在坐标原点,焦点在x轴上的双曲线的标准方程为x2a2−y2b2=1(a>0,b>0);(2)中心在坐标原点,焦点在y轴上的双曲线的标准方程为y2a2−x2b2=1(a>0,b>0).3.双曲线的性质图形续表2 2−y2b2=1(a>0,b>0)y2a2−x2b2=1(a>0,b>1.过双曲线x2a 2−y 2b 2=1(a>0,b>0)上一点M (x 0,y 0)的切线方程为x 0xa 2−y 0y b 2=1.2.双曲线x 2a 2−y 2b 2=1(a>0,b>0)的左、右焦点分别为F 1,F 2,点P (x 0,y 0)为双曲线上任意一点,且不与点F 1,F 2共线,∠F 1PF 2=θ,则△F 1PF 2的面积为b 2tanθ2.3.若点P (x 0,y 0)在双曲线x 2a2−y 2b 2=1(a>0,b>0)内,则被点P 所平分的中点弦的方程为x 0x a 2−y 0y b 2=x 02a 2−y 02b 2.4.双曲线中点弦的斜率公式设点M (x 0,y 0)为双曲线x 2a 2−y 2b2=1(a>0,b>0)的弦AB (不平行y 轴)的中点,则k AB ·k OM =b 2a2,即k AB =b 2x0a 2y 0.5.双曲线的焦半径公式双曲线x 2a 2−y 2b 2=1(a>0,b>0)的焦点为F 1(-c ,0),F 2(c ,0),当点M (x 0,y 0)在双曲线右支上时,|MF 1|=ex 0+a ,|MF 2|=ex 0-a ;当点M (x 0,y 0)在双曲线左支上时,|MF 1|=-ex 0-a ,|MF 2|=-ex 0+a.6.若P 是双曲线右支上一点,F 1,F 2分别为双曲线的左、右焦点,则|PF 1|min =a+c ,|PF 2|min =c-a.7.双曲线的同支的焦点弦中最短的为通径(过焦点且垂直于实轴所在直线的弦),其长为2b 2a;异支的弦中最短的为实轴,其长为2a.考点自诊1.判断下列结论是否正确,正确的画“√”,错误的画“×”.(1)平面内到点F1(0,4),F2(0,-4)距离之差的绝对值等于8的点的轨迹是双曲线.()(2)双曲线x2m2−y2n2=λ(m>0,n>0,λ≠0)的渐近线方程是x2m2−y2n2=0,即xm±yn=0.()(3)关于x,y的方程x2m −y2n=1(mn>0)表示焦点在x轴上的双曲线.()(4)与双曲线x2m −y2n=1(其中mn>0)共渐近线的双曲线方程可设为x2m−y2n=λ(λ≠0).()(5)若双曲线x2a2−y2b2=1(a>0,b>0)与x2b2−y2a2=1(a>0,b>0)的离心率分别是e1,e2,则1e12+1e22=1.()2.“m>0”是“方程x2m −y2m+2=1表示双曲线”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.已知双曲线C:x2a2−y2b2=1(a>0,b>0)过点(√2,√3),且实轴的两个端点与虚轴的一个端点组成一个等边三角形,则双曲线C的标准方程为()A.x212-y2=1 B.x29−y23=1C.x2-y23=1 D.x223−y232=14.(2019北京,5)已知双曲线x2a2-y2=1(a>0)的离心率是√5,则a=() A.√6 B.4C.2D.125.若双曲线x2a2−y2b2=1(a>0,b>0)的一条渐近线经过点(3,-4),则此双曲线的离心率为.关键能力学案突破考点双曲线的定义【例1】(1)已知点F2为双曲线C:x2a2−y2b2=1(a>0,b>0)的右焦点,直线y=kx交双曲线C于A,B两点,若∠AF2B=2π3,S△AF2B=2√3,则双曲线C的虚轴长为.(2)已知双曲线E :x 2a 2−y 2b 2=1(a>0,b>0)的左、右焦点分别为F 1,F 2,过点F 1的直线l 与双曲线的左、右两支分别交于A ,B 两点.若△ABF 2的内切圆与边AB ,BF 2,AF 2分别相切于点M ,N ,P ,且|AP|=4,则a 的值为 .解题心得双曲线定义的应用主要有两个方面:一是判定平面内动点轨迹是否为双曲线,进而求出曲线方程;二是在“焦点三角形”中,常利用正弦定理、余弦定理,结合||PF 1|-|PF 2||=2a ,运用平方的方法,建立与|PF 1|·|PF 2|的联系.对点训练1(1)(2020河南非凡联盟4月联考)已知双曲线C :x 2a 2−y 29=1(a>0)的左、右焦点分别为F 1,F 2,一条渐近线与直线4x+3y=0垂直,点M 在双曲线C 上,且|MF 2|=6,则|MF 1|=( )A.2或14B.2C.14D.2或10(2)(2020河北廊坊省级示范学校联考)设F 1,F 2分别为双曲线C :x 2a 2−y 2b 2=1(a>0,b>0)的左、右焦点,过点F 1的直线交双曲线C 的左支于A ,B 两点,且|AF 2|=3,|BF 2|=5,|AB|=4,则△BF 1F 2的面积为 .考点双曲线的标准方程【例2】(1)已知动圆M 与圆C 1:(x+4)2+y 2=2外切,与圆C 2:(x-4)2+y 2=2内切,则动圆圆心M 的轨迹方程为( )A.x 22−y 214=1(x ≥√2) B.x 22−y 214=1(x ≤-√2) C.x 22+y 214=1(x ≥√2) D.x 22+y 214=1(x ≤-√2)(2)在平面直角坐标系中,经过点P (2√2,-√2),渐近线方程为y=±√2x 的双曲线的标准方程为( )A.x 24−y 22=1 B.x 27−y 214=1C.x 23−y 26=1D.y 214−x 27=1(3)已知双曲线x 2a 2−y 2b 2=1(a>0,b>0)的左、右焦点分别为F 1,F 2,过点F 2且斜率为247的直线与双曲线在第一象限的交点为A ,若(F 2F 1⃗⃗⃗⃗⃗⃗⃗⃗ +F 2A ⃗⃗⃗⃗⃗⃗⃗ )·F 1A ⃗⃗⃗⃗⃗⃗⃗ =0,则双曲线的标准方程可能为( ) A.x 24−y 23=1B.x 23−y 24=1C.x 216−y 29=1D.x 29−y 216=1解题心得1.求双曲线标准方程的答题模板2.利用待定系数法求双曲线方程的常用方法 (1)与双曲线x 2a 2−y 2b 2=1共渐近线的方程可设为x 2a 2−y 2b 2=λ(λ≠0);(2)若双曲线的渐近线方程为y=±bax ,则双曲线的方程可设为x 2a2−y 2b 2=λ(λ≠0);(3)若双曲线过两个已知点,则双曲线的方程可设为x 2m +y 2n=1(mn<0)或mx 2+ny 2=1(mn<0).对点训练2(1)(2020河南安阳模拟)过双曲线x 2a 2−y 2b 2=1(a>0,b>0)的右焦点F (c ,0)作其渐近线y=√32x 的垂线,垂足为M ,若S △OMF =4√3(O 为坐标原点),则双曲线的标准方程为( )A.x 24−y 23=1 B.x 28−y 26=1 C.x 216−y 212=1D.x 232−y 224=1(2)过双曲线C :x 2a 2−y 2b 2=1的右顶点作x 轴的垂线,与双曲线C 的一条渐近线相交于点A.若以双曲线C 的右焦点F 为圆心,4为半径的圆经过A ,O 两点(O 为坐标原点),则双曲线C 的方程为( )A.x 24−y 212=1 B.x 27−y 29=1 C.x 28−y 28=1 D.x 212−y 24=1(3)经过点P (3,2√7),Q (-6√2,7)的双曲线的标准方程为 .考点双曲线的几何性质(多考向探究)考向1 求双曲线的渐近线方程【例3】(2020福建厦门一模)已知双曲线C :x 2a 2−y 2b 2=1(a>0,b>0)的一个焦点为F ,点A ,B 是双曲线C 的一条渐近线上关于原点对称的两点,以AB 为直径的圆过点F 且交双曲线C 的左支于M ,N 两点,若|MN|=2,△ABF 的面积为8,则双曲线C 的渐近线方程为( )A.y=±√3xB.y=±√33x C.y=±2xD.y=±12x解题心得求双曲线的渐近线方程的方法依据题设条件,求出双曲线方程x 2a 2−y 2b 2=1(a>0,b>0)中a ,b 的值或a 与b 的比值,进而得出双曲线的渐近线方程.对点训练3(2020山东德州高三第二次模拟)已知椭圆x 2a 2+y 2b 2=1(a>b>0)与双曲线x 2a 2−y 2b 2=12的焦点相同,则双曲线渐近线方程为( )A.y=±√33x B.y=±√3x C.y=±√22xD.y=±√2x考向2 求双曲线的离心率【例4】(2020广东汕尾一模)已知双曲线C :x 2a 2−y 2b 2=1(a>0,b>0),F 为双曲线C 的右焦点,A 为双曲线C 的右顶点,过点F 作x 轴的垂线,交双曲线C 于M ,N 两点.若tan ∠MAN=-34,则双曲线C 的离心率为( )A.3B.2C.43D.√2解题心得求双曲线离心率的值或取值范围的方法 (1)求a ,b ,c 的值,由e=ca =√1+b 2a 2直接求出e.(2)列出含有a ,b ,c 的齐次方程(或不等式),借助b 2=c 2-a 2消去b ,然后转化为关于e 的方程(或不等式)求解.对点训练4(2019全国2,理11)设F 为双曲线C :x 2a 2−y 2b 2=1(a>0,b>0)的右焦点,O 为坐标原点,以OF 为直径的圆与圆x 2+y 2=a 2交于P ,Q 两点.若|PQ|=|OF|,则C 的离心率为( )A.√2B.√3C.2D.√5考向3 与双曲线有关的取值范围问题【例5】已知M (x 0,y 0)是双曲线C :x 22-y 2=1上的一点,F 1,F 2是双曲线C 的两个焦点,若MF 1⃗⃗⃗⃗⃗⃗⃗⃗ ·MF 2⃗⃗⃗⃗⃗⃗⃗⃗ <0,则y 0的取值范围是( )A.(-√33,√33) B.(-√36,√36) C.(-2√23,2√23) D.(-2√33,2√33)解题心得与双曲线有关的取值范围问题的解题思路(1)若条件中存在不等关系,则借助此关系直接转化为不等式求解.(2)若条件中没有明显的不等关系,则要善于发现隐含的不等关系来解决. 对点训练5已知焦点在x 轴上的双曲线x 28-m+y 24-m=1,它的焦点到渐近线的距离的取值范围是 .考点双曲线与圆的综合问题【例6】已知点P 为双曲线C :x 2a 2−y 2b 2=1(a>0,b>0)上一点,F 1,F 2为双曲线C 的左、右焦点,若|PF 1|=|F 1F 2|,且直线PF 2与以双曲线C 的实轴为直径的圆相切,则双曲线C 的渐近线方程为( )A.y=±43x B.y=±34xC.y=±35xD.y=±53x对点训练6过双曲线x 2a 2−y 2b 2=1(a>0,b>0)的左焦点F 作圆O :x 2+y 2=a 2的两条切线,切点为A ,B ,双曲线的左顶点为C ,若∠ACB=120°,则双曲线的渐近线方程为( )A.y=±√3xB.y=±√33x C.y=±√2x D.y=±√22x8.6 双曲线 必备知识·预案自诊知识梳理1.距离的差的绝对值 双曲线的焦点 双曲线的焦距 (1)< (2)= (3)> 3.坐标轴 原点 (-a ,0) (a ,0) (0,-a )(0,a)a2+b22a2b考点自诊1.(1)×(2)√(3)×(4)√(5)√2.A由“方程x2m −y2m+2=1表示双曲线”得m(m+2)>0,即m>0或m<-2,又“m>0”是“m>0或m<-2”的充分不必要条件,故“m>0”是“方程x 2m −y2m+2=1表示双曲线”的充分不必要条件.故选A.3.C由双曲线C:x2a2−y2b2=1(a>0,b>0)过点(√2,√3),且实轴的两个端点与虚轴的一个端点组成一个等边三角形,可得{2a2-3b2=1,b a =√3,解得{a=1,b=√3.故双曲线C的标准方程为x2-y23=1.4.D∵双曲线的离心率e=ca =√5,c=√a2+b2,∴√a2+1a=√5,解得a=12.故选D.5.5 3由题意知直线y=-bax过点(3,-4),所以3ba=4,即ba=43,所以e=ca=√1+b2a2=√1+169=53.关键能力·学案突破例1(1)2√2(2)2(1)设双曲线C的左焦点为F1,连接AF1,BF1,由对称性可知四边形AF1BF2为平行四边形,因为∠AF2B=2π3,S△AF2B=2√3,所以S△AF1F2=2√3,∠F1AF2=π3.设|AF1|=r1,|AF2|=r2,则4c2=r12+r22-2r1r2cosπ3,又|r1-r2|=2a,故r1r2=4b2.又S△AF1F2=12r1r2sinπ3=2√3,所以b2=2,所以该双曲线的虚轴长为2√2.(2)由题意知|BM|=|BN|,|PF2|=|NF2|,|AM|=|AP|=4.根据双曲线的定义,知|BF1|-|BF2|=|MF1|-|NF2|=2a,|AF2|-|AF1|=2a,则|AF1|=|AF2|-2a,所以|BF1|-|BF2|=|AM|+|AF1|-|NF2|=|AM|+|AP|+|PF2|-2a-|NF2|=8-2a=2a,所以a=2.对点训练1(1)C(2)92(1)由题意知3a=34,故a=4,则c=5.由|MF2|=6<a+c=9,知点M在双曲线C的右支上.由双曲线的定义知|MF1|-|MF2|=2a=8,所以|MF1|=14.(2)因为|AF2|=3,|BF2|=5,|AF2|-|AF1|=2a,|BF2|-|BF1|=2a,所以|AF2|+|BF2|-|AB|=3+5-4=4=4a,所以a=1,所以|BF1|=3.又|AF2|2+|AB|2=|BF2|2,所以∠F2AB=90°,所以S△BF1F2=12|BF1||AF2|=12×3×3=92.例2(1)A(2)B(3)D(1)设动圆M的半径为r,由题意可得|MC1|=r+√2,|MC2|=r-√2,|C1C2|=8,所以|MC1|-|MC2|=2√2<|C1C2|,所以由双曲线的定义可知动点M在以C1(-4,0),C2(4,0)为焦点,实轴长为2√2的双曲线的右支上,所以a=√2,c=4,所以b2=16-2=14,故动圆圆心M的轨迹方程为x22−y214=1(x≥√2).(2)因为双曲线的渐近线方程为y=±√2x ,所以可设所求双曲线的方程为2x 2-y 2=k (k ≠0).又点P (2√2,-√2)在双曲线上,所以k=16-2=14,所以双曲线的方程为2x 2-y 2=14,所以双曲线的标准方程为x 27−y 214=1.故选B .(3)由(F 2F 1⃗⃗⃗⃗⃗⃗⃗⃗ +F 2A ⃗⃗⃗⃗⃗⃗⃗ )·F 1A ⃗⃗⃗⃗⃗⃗⃗ =0,可知(F 2F 1⃗⃗⃗⃗⃗⃗⃗⃗ +F 2A ⃗⃗⃗⃗⃗⃗⃗ )·(F 2A ⃗⃗⃗⃗⃗⃗⃗ −F 2F 1⃗⃗⃗⃗⃗⃗⃗⃗ )=0,即|F 2A ⃗⃗⃗⃗⃗⃗⃗ |2-|F 2F 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ |2=0,所以|F 2A|=|F 1F 2|=2c.又AF 2的斜率为247,所以cos ∠AF 2F 1=-725.在△AF 1F 2中,由余弦定理得|AF 1|=165c.由双曲线的定义得165c-2c=2a ,即c a=53,所以a ∶b=3∶4.所以此双曲线的标准方程可能为x 29−y 216=1.故选D .对点训练2(1)C (2)A (3)y 225−x 275=1(1)由题意易得|FM|=b ,又|OF|=c ,FM ⊥OM ,所以|OM|=√|OF |2-|FM |2=a.联立{ba =√32,12ab =4√3,解得{a =4,b =2√3, 所以双曲线的标准方程为x 216−y 212=1.故选C .(2)不妨设渐近线y=ba x 与直线x=a 交于点A ,则点A (a ,b ).依题意,c=4,√(4-a )2+b 2=4,a 2+b 2=c 2=16,解得a 2=4,b 2=12,故双曲线的标准方程为F 24−y 212=1.(3)设双曲线的方程为mx 2+ny 2=1(mn<0).因为所求双曲线经过点P (3,2√7),Q (-6√2,7), 所以{9m +28n =1,72m +49n =1,解得{m =-175,n =125.故所求双曲线的方程为y 225−x 275=1.例3B 不妨设点A ,B 在直线y=b a x 上,点F (c ,0),则设点A (x 0,b a x 0),B -x 0,-bax 0.因为以AB 为直径的圆过点F ,所以AF ⃗⃗⃗⃗⃗ ⊥BF ⃗⃗⃗⃗⃗ ,所以AF ⃗⃗⃗⃗⃗ ·BF ⃗⃗⃗⃗⃗ =c 2-x 02−b 2a2x 02=c 2-c 2a2x 02=0,所以x 0=±a.所以S △ABF =12·c·|2bax 0|=bc=8.由{x 2+y 2=c 2,x 2a 2-y 2b 2=1,得y=±b 2c ,则|MN|=2b 2F=2,即b 2=c.所以b=2,c=4,所以a=√c 2-b 2=2√3.所以双曲线C 的渐近线方程为y=±√33x.故选B .对点训练3A 由椭圆x 2a 2+y 2b 2=1(a>b>0)与双曲线x 2a 2−y 2b 2=12,即x 2a 22−y 2b 22=1的焦点相同,可得a 2-b 2=a 22+b 22,即a 2=3b 2,所以ba =√33.所以双曲线的渐近线方程为y=±√33x.故选A .例4B 由题意可知tan ∠MAN=2tan∠MAF1-tan 2∠MAF =-34,解得tan ∠MAF=3.令x=c ,则y=±b 2a , 可得tan ∠MAF=b 2ac -a =c 2-a 2ac -a=c+a a=3,则e=ca =2.故选B .对点训练4A 如图,设PQ 与x 轴交于点A ,由对称性可知PQ ⊥x 轴.∵|PQ|=|OF|=c ,∴|PA|=c2.∴PA 为以OF 为直径的圆的半径,A 为圆心,∴|OA|=c2. ∴Pc 2,c 2.又点P 在圆x 2+y 2=a 2上,∴c24+c 24=a 2,即c22=a 2,∴e 2=c2a 2=2,∴e=√2.故选A .例5A 因为点F 1(-√3,0),F 2(√3,0),x 022−y 02=1,所以MF 1⃗⃗⃗⃗⃗⃗⃗⃗ ·MF 2⃗⃗⃗⃗⃗⃗⃗⃗ =(-√3-x 0,-y 0)·(√3-x 0,-y 0)=x 02+y 02-3<0,即3y 02-1<0,解得-√33<y 0<√33.对点训练5(0,2) 因为双曲线x 28-m+y 24-m =1的焦点在x 轴上,所以{8-m >0,4-m <0,解得4<m<8.所以焦点到渐近线的距离d=√m -4∈(0,2).例6A 如图.由已知得|PF1|=|F1F2|=2c.因为直线PF2与以双曲线C的实轴为直径的圆相切,设切点为M,所以|OM|=a,OM⊥PF2,所以|MF2|=√c2-a2=b.由双曲线的定义可得|PF2|-|PF1|=2a,所以|PF2|=2a+2c,所以cos∠OF2M=bc =(2c)2+(2a+2c)2-(2c)22×2c×(2a+2c),整理得c=2b-a.又c2=a2+b2,解得ba=43.所以双曲线C的渐近线方程为y=±43x.故选A.对点训练6A如图,连接OA,OB.设双曲线x 2a2−y2b2=1(a>0,b>0)的焦距为2c(c>0),则点C(-a,0),F(-c,0).由双曲线和圆的对称性,可知点A与点B关于x轴对称,则∠ACO=∠BCO=12∠ACB=12×120°=60°.因为|OA|=|OC|=a,所以△ACO为等边三角形,所以∠AOC=60°.因为FA与圆O相切于点A,所以OA⊥FA.在Rt△AOF中,因为∠AOC=60°,所以|OF|=2|OA|,即c=2a,所以b=√c2-a2=√(2a)2-a2=√3a.所以双曲线x 2a2−y2b2=1(a>0,b>0)的渐近线方程为y=±√3x.。

高三数学第一轮复习:双曲线的定义、性质及标准方程【本讲主要内容】双曲线的定义、性质及标准方程双曲线的定义及相关概念、双曲线的标准方程、双曲线的几何性质【知识掌握】【知识点精析】1. 双曲线的定义:(1)第一定义:平面内与两定点F1、F2的距离之差的绝对值是常数(小于|F1F2|)的点的轨迹叫做双曲线,这两个定点叫做双曲线的焦点,两焦点的距离叫做焦距。
(2)第二定义:平面内到一个定点F的距离与到一条定直线l的距离的比等于常数(e>1)的点的轨迹叫做双曲线,定点F为焦点,定直线l称为准线,常数e称为离心率。
说明:(1)若2a等于2c,则动点的轨迹是射线(即F1F2、F2F1的延长线);(2)若2a大于2c,则动点轨迹不存在。
2. 双曲线的标准方程、图形及几何性质:标准方程)0b,0a(1byax2222>>=-中心在原点,焦点在x轴上yaxba b2222100-=>>(,)中心在原点,焦点在y轴上图形几何性质X围x a≤-或x a≥y a≤-或y a≥对称性关于x轴、y轴、原点对称(原点为中心)顶点()()1200A a A a-,、,()()1200A a A a-,、,轴实轴长122A A a=,虚轴长122B B b=离心率ecae=>()1准线2212:,:a al x l xc c=-=2212:,:a al y l yc c=-=实轴、虚轴长相等的双曲线称为等轴双曲线,焦点在x 轴上,标准方程为()2220x y a a -=≠;焦点在y 轴上,标准方程为()2220y x a a -=≠。
其渐近线方程为y=±x 。
等轴双曲线的离心率为e =4. 基础三角形:如图所示,△AOB 中,,,,tan b OA a AB b OB c AOB a===∠=。
5. 共渐近线的双曲线系方程:与双曲线x a y b22221-=(a>0,b>0)有相同渐近线的双曲线系可设为()22220x y a b λλ-=≠,若λ>0,则双曲线的焦点在x 轴上;若λ<0,则双曲线的焦点在y 轴上。


8.6 双曲线[课 时 跟 踪 检 测][基 础 达 标]1.(2017届合肥质检)若双曲线C 1:x 22-y 28=1与C 2:x 2a 2-y 2b2=1(a >0,b >0)的渐近线相同,且双曲线C 2的焦距为45,则b =( )A .2B .4C .6D .8解析:由题意得ba=2⇒b =2a ,C 2的焦距2c =45⇒c =a 2+b 2=25⇒b =4,故选B. 答案:B2.若双曲线x 2a 2-y 2b2=1(a >0,b >0)的离心率为3,则其渐近线方程为( )A .y =±2xB .y =±2xC .y =±12xD .y =±22x 解析:由条件e =c a =3,得c 2a 2=a 2+b 2a 2=1+b 2a 2=3,所以ba=2,所以双曲线的渐近线方程为y =±2x .故选B.答案:B3.已知双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的焦点为F 1,F 2,且C 上点P 满足PF 1→·PF 2→=0,|PF 1→|=3,|PF 2→|=4,则双曲线C 的离心率为( )A.102B . 5 C.52D .5解析:依题意得,2a =|PF 2|-|PF 1|=1,|F 1F 2|=|PF 2|2+|PF 1|2=5,因此该双曲线的离心率e =|F 1F 2||PF 2|-|PF 1|=5.答案:D4.(2017届长春质检)过双曲线x 2-y 215=1的右支上一点P ,分别向圆C 1:(x +4)2+y2=4和圆C 2:(x -4)2+y 2=1作切线,切点分别为M ,N ,则|PM |2-|PN |2的最小值为( )A .10B .13C .16D .19解析:由题可知,|PM |2-|PN |2=(|PC 1|2-4)-(|PC 2|2-1)=|PC 1|2-|PC 2|2-3=(|PC 1|-|PC 2|)(|PC 1|+|PC 2|)-3=2(|PC 1|+|PC 2|)-3≥2|C 1C 2|-3=13.答案:B5.(2018届河南六市第一次联考)已知点F 1,F 2分别是双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点,过F 1的直线l 与双曲线C 的左、右两支分别交于A ,B 两点,若|AB |∶|BF 2|∶|AF 2|=3∶4∶5,则双曲线的离心率为( )A .2B .4 C.13D .15解析:由题意,设|AB |=3k ,|BF 2|=4k ,|AF 2|=5k ,则BF 1⊥BF 2.∵|AF 1|=|AF 2|-2a =5k -2a ,|BF 1|-|BF 2|=5k -2a +3k -4k =4k -2a =2a ,∴a =k ,∴|BF 1|=6a ,|BF 2|=4a .又|BF 1|2+|BF 2|2=|F 1F 2|2,即13a 2=c 2,∴e =ca=13.答案:C6.(2018届合肥市第二次质量检测)双曲线M :x 2-y 2b2=1的左、右焦点分别为F 1、F 2,记|F 1F 2|=2c ,以坐标原点O 为圆心,c 为半径的圆与曲线M 在第一象限的交点为P ,若|PF 1|=c +2,则点P 的横坐标为( )A.3+12 B .3+22C.3+32D .332解析:由点P 在双曲线的第一象限可得|PF 1|-|PF 2|=2,则|PF 2|=|PF 1|-2=c ,又|OP |=c ,∠F 1PF 2=90°,由勾股定理可得(c +2)2+c 2=(2c )2,解得c =1+ 3.易知△POF 2为等边三角形,则x P =c2=3+12,选项A 正确. 答案:A7.(2018届湖南十校联考)设双曲线x 2a 2-y 2b 2=1(a >0,b >0)的两条渐近线与直线x =a 2c分别交于A ,B 两点,F 为该双曲线的右焦点.若60°<∠AFB <90°,则该双曲线的离心率的取值范围是________.解析:双曲线x 2a 2-y 2b 2=1的两条渐近线方程为y =±b a x ,x =a 2c 时,y =±abc ,不妨设A ⎝ ⎛⎭⎪⎫a 2c ,ab c ,B ⎝ ⎛⎭⎪⎫a 2c,-ab c ,因为60°<∠AFB <90°,所以33<k FB <1,所以33<abc c -a 2c<1,所以33<a b <1,所以13<a 2c 2-a2<1,所以1<e 2-1<3,所以2<e <2. 答案:(2,2)8.若点P 是以A (-3,0),B (3,0)为焦点,实轴长为25的双曲线与圆x 2+y 2=9的一个交点,则|PA |+|PB |=________.解析:不妨设点P 在双曲线的右支上,则|PA |>|PB |. 因为点P 是双曲线与圆的交点,所以由双曲线的定义知,|PA |-|PB |=25,① 又|PA |2+|PB |2=36,②联立①②化简得2|PA |·|PB |=16,所以(|PA |+|PB |)2=|PA |2+|PB |2+2|PA |·|PB |=52, 所以|PA |+|PB |=213. 答案:2139.(2017年全国卷Ⅰ)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的右顶点为A ,以A 为圆心,b 为半径作圆A ,圆A 与双曲线C 的一条渐近线交于M ,N 两点.若∠MAN =60°,则C 的离心率为________.解析:∵|AM |=|AN |=b ,∠MAN =60°, ∴△MAN 是等边三角形, ∴在△MAN 中,MN 上的高h =32b . ∵点A (a,0)到渐近线bx -ay =0的距离d =ab a 2+b 2=abc, ∴ab c =32b , ∴e =c a=23=233. 答案:23310.已知双曲线x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,点P 在双曲线的右支上,且|PF 1|=4|PF 2|,则双曲线的离心率e 的最大值为________.解析:由双曲线定义知|PF 1|-|PF 2|=2a , 又|PF 1|=4|PF 2|,所以|PF 1|=83a ,|PF 2|=23a ,在△PF 1F 2中,由余弦定理得cos ∠F 1PF 2=649a 2+49a 2-4c 22·83a ·23a =178-98e 2,要求e 的最大值,即求cos ∠F 1PF 2的最小值,当F 1、P 、F 2三点共线时,即∠F 1PF 2=π时,cos ∠F 1PF 2有最小值为-1,∴cos ∠F 1PF 2=178-98e 2≥-1,解得1<e ≤53,即e 的最大值为53.答案:5311.设A ,B 分别为双曲线x 2a 2-y 2b2=1(a >0,b >0)的左、右顶点,|AB |=43,焦点到渐近线的距离为 3.(1)求双曲线的方程; (2)已知直线y =33x -2与双曲线的右支交于M ,N 两点,且在双曲线的右支上存在点D ,使OM →+ON →=tOD →,求t 的值及点D 的坐标.解:(1)由题意知a =23,∵一条渐近线为y =b ax ,即bx -ay =0. ∴由焦点到渐近线的距离为3,得|bc |b 2+a 2= 3.又∵c 2=a 2+b 2, ∴b 2=3,∴双曲线的方程为x 212-y 23=1.(2)设M (x 1,y 1),N (x 2,y 2),D (x 0,y 0), 则x 1+x 2=tx 0,y 1+y 2=ty 0.将直线方程y =33x -2代入双曲线方程x 212-y 23=1得x 2-163x +84=0,则x 1+x 2=163,y 1+y 2=33(x 1+x 2)-4=12. ∴⎩⎪⎨⎪⎧x 0y 0=433,x 212-y 203=1,解得⎩⎨⎧x 0=43,y 0=3.∴t =4,点D 的坐标为(43,3).12.已知中心在原点,焦点在坐标轴上的双曲线C 经过A (-7,5),B (-1,-1)两点. (1)求双曲线C 的方程;(2)设直线l :y =x +m 交双曲线C 于M ,N 两点,且线段MN 被圆E :x 2+y 2-12x +n =0(n ∈R )三等分,求实数m ,n 的值.解:(1)设双曲线C 的方程是λx 2+μy 2=1(λμ<0),依题意有⎩⎪⎨⎪⎧49λ+25μ=1,λ+μ=1,解得⎩⎪⎨⎪⎧λ=-1,μ=2,所以双曲线C 的方程是2y 2-x 2=1. (2)将l :y =x +m 代入2y 2-x 2=1, 得x 2+4mx +(2m 2-1)=0,① Δ=(4m )2-4(2m 2-1)=8m 2+4>0.设M (x 1,y 1),N (x 2,y 2),MN 的中点P (x 0,y 0), 则x 1+x 2=-4m , 所以x 0=x 1+x 22=-2m ,y 0=x 0+m =-m ,所以P (-2m ,-m ).又圆心E (6,0),依题意k PE =-1, 故m6+2m=-1,即m =-2. 将m =-2代入①得x 2-8x +7=0, 解得x 1=1,x 2=7,所以|MN |=1+12|x 1-x 2|=6 2. 故直线l 截圆E 所得弦长为13|MN |=2 2.又E (6,0)到直线l 的距离d =22, 所以圆E 的半径R =22+22=10,所以圆E 的方程是x 2+y 2-12x +26=0. 所以m =-2,n =26.[能 力 提 升]1.已知双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的离心率为3,点(3,0)是双曲线的一个顶点.(1)求双曲线的方程;(2)经过双曲线右焦点F 2作倾斜角为30°的直线,直线与双曲线交于不同的两点A ,B ,求|AB |.解:(1)∵双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为3,点(3,0)是双曲线的一个顶点,∴⎩⎪⎨⎪⎧c a =3,a =3,解得c =3,b =6,∴双曲线的方程为x 23-y 26=1.(2)双曲线x 23-y 26=1的右焦点为F 2(3,0),∴经过双曲线右焦点F 2且倾斜角为30°的直线的方程为y =33(x -3). 联立⎩⎪⎨⎪⎧x 23-y 26=1,y =33x -,得5x 2+6x -27=0.设A (x 1,y 1),B (x 2,y 2), 则x 1+x 2=-65,x 1x 2=-275.所以|AB |=1+13×⎝ ⎛⎭⎪⎫-652-4×⎝ ⎛⎭⎪⎫-275=1635. 2.已知椭圆C 1的方程为x 24+y 2=1,双曲线C 2的左、右焦点分别是C 1的左、右顶点,而C 2的左、右顶点分别是C 1的左、右焦点,O 为坐标原点.(1)求双曲线C 2的方程;(2)若直线l :y =kx +2与双曲线C 2恒有两个不同的交点A 和B ,且OA →·OB →>2,求k 的取值范围.解:(1)设双曲线C 2的方程为x 2a 2-y 2b2=1(a >0,b >0),则a 2=4-1=3,c 2=4, 再由a 2+b 2=c 2,得b 2=1, 故双曲线C 2的方程为x 23-y 2=1.(2)将y =kx +2代入x 23-y 2=1,得(1-3k 2)x 2-62kx -9=0.由直线l 与双曲线C 2交于不同的两点,得⎩⎨⎧1-3k 2≠0,Δ=-62k2+-3k2=-k2,∴k 2<1且k 2≠13.①设A (x 1,y 1),B (x 2,y 2), 则x 1+x 2=62k 1-3k 2,x 1x 2=-91-3k 2.∴x 1x 2+y 1y 2=x 1x 2+(kx 1+2)(kx 2+2) =(k 2+1)x 1x 2+2k (x 1+x 2)+2 =3k 2+73k 2-1. 又∵OA →·OB →>2, 即x 1x 2+y 1y 2>2, ∴3k 2+73k 2-1>2, 即-3k 2+93k 2-1>0, 解得13<k 2<3.②由①②得13<k 2<1,故k 的取值范围为⎝ ⎛⎭⎪⎫-1,-33∪⎝ ⎛⎭⎪⎫33,1.。




第6课时双曲线1.了解双曲线的定义、几何图形和标准方程及简单性质.2.了解双曲线的实际背景及双曲线的简单应用.3.理解数形结合的思想.[对应学生用书P140]【梳理自测】一、双曲线的概念(教材改编)已知点F1(-4,0)和F2(4,0),一曲线上的动点P到F1,F2距离之差为6,该曲线方程是________.答案:x29-y27=1(x≥3)◆此题主要考查了以下内容:平面内与两个定点F1,F2(|F1F2|=2c>0)的距离的差的绝对值为常数(小于|F1F2|且不等于零)的点的轨迹叫做双曲线.这两个定点叫双曲线的焦点,两焦点间的距离叫做焦距.集合P={M||MF1|-|MF2||=2a},|F1F2|=2c,其中a、c为常数且a>0,c>0;(1)当2a<2c时,P点的轨迹是双曲线;(2)当2a=2c时,P点的轨迹是两条射线;(3)当2a>2c时,P点不存在.二、双曲线标准方程及性质1.(教材改编)双曲线x210-y22=1的焦距为( )A.3 2 B.4 2C.3 3 D.4 32.双曲线y2-x2=2的渐近线方程是( )A .y =±xB .y =±2xC .y =±3xD .y =±2x3.已知双曲线x 2a 2-y25=1的右焦点为(3,0),则该双曲线的离心率等于( )A .31414 B .324 C .32D .434.双曲线mx 2+y 2=1的虚轴长是实轴长的2倍,则m =________. 答案:1.D 2.A 3.C 4.-14◆此题主要考查了以下内容:1.一条规律根据方程中x 2与y 2的系数的正负来确定实轴与虚轴的位置,即焦点在实轴上. 2.两种方法(1)定义法:由题目条件判断出动点轨迹是双曲线,由双曲线定义,确定2a 、2b 或2c ,从而求出a 2、b 2,写出双曲线方程.(2)待定系数法:先确定焦点是在x轴上还是在y轴上,设出标准方程,再由条件确定a2、b2的值,即“先定型,再定量”;如果焦点位置不好确定,可将双曲线方程设为x2m -y2n=λ(λ≠0),再根据条件求λ的值.3.三个关注点——双曲线几何性质的关注点双曲线的几何性质从以下三点关注:(1)“六点”:两焦点、两顶点、两虚轴端点;(2)“四线”:两对称轴(实、虚轴),两渐近线;(3)“两形”:中心、顶点、虚轴端点构成的三角形,双曲线上的一点(不包括顶点)与两焦点构成的三角形.[对应学生用书P141]考向一双曲线的定义及标准方程(1)(2014·陕西师大附中模拟)设过双曲线x2-y2=9左焦点F1的直线交双曲线的左支于点P,Q,F2为双曲线的右焦点.若|PQ|=7,则△F2PQ的周长为( ) A.19 B.26C.43 D.50(2)已知双曲线x2a2-y2b2=1(a>0,b>0)和椭圆x216+y29=1有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为________.【审题视点】(1)利用双曲线定义|PF2|-|QF2|=2a及三角形周长的计算求解.(2)已知双曲线的焦点及离心率求双曲线方程.【典例精讲】(1)如图,由双曲线的定义可得⎩⎪⎨⎪⎧|PF 2|-|PF 1|=2a ,|QF 2|-|QF 1|=2a ,将两式相加得|PF 2|+|QF 2|-|PQ|=4a , ∴△F 2PQ 的周长为|PF 2|+|QF 2|+|PQ| =4a +|PQ|+|PQ|=4×3+2×7=26.(2)椭圆x 216+y 29=1的焦点坐标为F 1(-7,0),F 2(7,0),离心率为e =74.由于双曲线x 2a 2-y 2b 2=1与椭圆x 216+y 29=1有相同的焦点,因此a 2+b 2=7.又双曲线的离心率e =a 2+b 2a =7a ,所以7a =274,所以a =2,b 2=c 2-a 2=3,故双曲线的方程为x 24-y23=1.【答案】 (1)B (2)x 24-y23=1【类题通法】 (1)涉及到双曲线上的点到焦点的距离问题时,经常考虑双曲线的定义. (2)当已知双曲线的焦点不明确而又无法确定时,其标准方程可设为x 2m -y2n =1(mn >0),这样可避免讨论和复杂的计算;也可设为Ax 2+By 2=1(AB <0),这种形式在解题时更简便;(3)当已知双曲线的渐近线方程bx±ay =0,求双曲线方程时,可设双曲线方程为b 2x 2-a 2y 2=λ(λ≠0),据其他条件确定λ的值;(4)与双曲线x 2a 2-y 2b 2=1有相同的渐近线的双曲线方程可设为x 2a 2-y2b 2=λ(λ≠0),据其他条件确定λ的值.1.根据下列条件,求双曲线方程:(1)与双曲线x 29-y216=1有共同的渐近线,且过点(-3,23);(2)与双曲线x 216-y24=1有公共焦点,且过点(32,2).解析:(1)设所求双曲线方程为x 29-y216=λ(λ≠0),将点(-3,23)代入得λ=14,∴所求双曲线方程为x 29-y 216=14,即x 294-y24=1. (2)设双曲线方程为x 216-k -y24+k =1,将点(32,2)代入得k =4(k =-14舍去). ∴所求双曲线方程为x 212-y28=1.考向二 双曲线的性质及应用(1)(2014·哈尔滨模拟)已知P 是双曲线x 2a 2-y2b2=1(a >0,b >0)上的点,F 1,F 2是其焦点,双曲线的离心率是54,且PF 1→·PF 2→=0,若△PF 1F 2的面积为9,则a +b 的值为( )A .5B .6C .7D .8(2)F 1、F 2分别是双曲线x 2a 2-y2b 2=1(a >0,b >0)的左、右焦点,过F 1的直线l 与双曲线的左、右两支分别交于A 、B 两点.若△ABF 2是等边三角形,则该双曲线的离心率为( )A .2B .7C .13D .15【审题视点】 (1)利用PF 1→ ·PF 2→=0及e =54转化为a ,b 的方程组.(2)利用双曲线定义及余弦定理求a 与c 的关系. 【典例精讲】 (1)由PF 1→·PF 2→=0,得PF 1→⊥PF 2→,设|PF 1→|=m ,|PF 2→|=n ,不妨设m >n ,则m 2+n 2=4c 2,m -n =2a ,12mn =9,c a =54,解得⎩⎪⎨⎪⎧a =4,c =5, ∴b =3,∴a +b =7,故选C . (2)如图,由双曲线定义得,|BF 1|-|BF 2|=|AF 2|-|AF 1|=2a ,因为△ABF 2是正三角形,所以|BF 2|=|AF 2|=|AB|,因此|AF 1|=2a ,|AF 2|=4a ,且∠F 1AF 2=120°,在△F 1AF 2中,4c 2=4a 2+16a 2+2×2a ×4a ×12=28a 2,所以e =7,故选B .【答案】 (1)C (2)B【类题通法】 (1)求双曲线的离心率,就是求c 与a 的比值,一般不需要具体求出a ,c 的值,只需列出关于a ,b ,c 的方程或不等式解决即可.(2)双曲线的离心率与渐近线方程之间有着密切的联系,二者之间可以互求.2.(2014·济南模拟)过双曲线x 2a 2-y2b 2=1(a >0,b >0)的一个焦点F 作一条渐近线的垂线,若垂足恰在线段OF(O 为原点)的垂直平分线上,则双曲线的离心率为________.解析:如图所示,不妨设F 为右焦点,过F 作FP 垂直于一条渐近线,垂足为P ,过P 作PM⊥OF 于M.由已知得M 为OF 的中点,由射影定理知|PF|2=|FM||FO|,又F(c ,0),渐近线方程为bx -ay =0,∴|PF|=bcb 2+a2=b ,∴b 2=c 2·c ,即2b 2=c 2=a 2+b 2,∴a 2=b 2,∴e =c a = 1+b2a2= 2. 答案: 2考向三 直线与双曲线的综合应用已知双曲线C :x 2a2-y 2=1(a >0)与l :x +y =1相交于两个不同的点A 、B ,l与y 轴交于点P ,若PA →=512PB →,则a =________.【审题视点】 联立方程组,利用P 、A 、B 坐标之间的关系,建立a 的方程. 【典例精讲】 因为双曲线C 与直线l 相交于两个不同的点,故知方程组⎩⎪⎨⎪⎧x 2a2-y 2=1,x +y =1有两组不同的实数解,消去y 并整理,得(1-a 2)x 2+2a 2x -2a 2=0,实数a 应满足⎩⎪⎨⎪⎧a >0,1-a 2≠0,4a 4+8a 2(1-a 2)>0, 解得0<a <2且a≠1. 设A(x 1,y 1)、B(x 2,y 2), 由一元二次方程根与系数的关系, 得x 1+x 2=2a2a 2-1,①x 1x 2=2a2a 2-1,②又P(0,1),由PA →=512PB →,得(x 1,y 1-1)=512(x 2,y 2-1),从而x 1=512x 2,③ 由①③,解得⎩⎪⎨⎪⎧x 1=517·2a 2a 2-1,x 2=1217·2a 2a 2-1代入②, 得517×1217×⎝ ⎛⎭⎪⎫2a 2a 2-12=2a2a 2-1, 即2a 2a 2-1=28960,解得a =1713,⎝ ⎛⎭⎪⎫a =-1713舍去. 【答案】1713【类题通法】 (1)判断直线l 与双曲线E 的位置关系时,通常将直线l 的方程Ax +By +C =0(A 、B 不同时为0)代入双曲线E 的方程F(x ,y)=0,消去y(也可以消去x)得到一个关于变量x(或变量y)的一元方程.即⎩⎪⎨⎪⎧Ax +By +C =0F (x ,y )=0,消去y 后得ax 2+bx +c =0.由此转化为两点坐标的关系.(2)特殊情况考虑与渐近线平行的直线与双曲线的位置关系,数形结合求解.3.已知点A(-2,0),点B(2,0),且动点P 满足|PA|-|PB|=2,则动点P 的轨迹与直线y =k(x -2)有两个交点的充要条件为k∈________.解析:由已知得动点P 的轨迹为一双曲线的右支且2a =2,c =2,则b =c 2-a 2=1,∴P 点的轨迹方程为x 2-y 2=1(x >0),其一条渐近线方程为y =x.若P 点的轨迹与直线y =k(x -2)有两个交点,则需k∈(-∞,-1)∪(1,+∞).答案:(-∞,-1)∪(1,+∞)[对应学生用书P 142]双曲线与渐近线的关系不清致误(2014·浙江温州适应性测试)已知F 1,F 2为双曲线Ax 2-By 2=1的焦点,其顶点是线段F 1F 2的三等分点,则其渐近线的方程为( )A .y =±22xB .y =±24x C .y =±x D .y =±22x 或y =±24x 【正解】 依题意c =3a ,∴c 2=9a 2.又c 2=a 2+b 2, ∴b 2a 2=8,b a =22,a b =24.故选D . 【答案】 D【易错点】 (1)默认为双曲线焦点在x 轴其渐近线为y =±ba x ,而错选为A .(2)把双曲线认为等轴双曲线而错选为C .(3)把a ,b ,c 的关系与椭圆c 2=a 2-b 2混淆致错.【警示】 (1)对于方程x 2a 2-y 2b 2=1来说,求渐近线方程就相当于求ba 的值,但要分焦点的位置是在x 轴还是在y 轴上,此题没有给出焦点的位置,其渐近线斜率有四种情况.(2)渐近线为y =±b a x 所对应的双曲线为x 2a 2-y2b 2=λ(λ≠0).当λ>0时,表示焦点在x 轴上,当λ<0时,焦点在y 轴上.1.(2013·高考福建卷)双曲线x 24-y 2=1的顶点到其渐近线的距离等于( )A .25B .45C .255 D .455解析:选C .求出双曲线的顶点和渐近线,再利用距离公式求解.双曲线的渐近线为直线y =±12x ,即x±2y =0,顶点为(±2,0),∴所求距离为d =|±2±0|5=255. 2.(2013·高考广东卷)已知中心在原点的双曲线C 的右焦点为F(3,0),离心率等于32,则C 的方程是( )A .x 24-y 25=1B .x 24-y25=1 C .x 22-y 25=1 D .x 22-y25=1 解析:选B .求双曲线的标准方程需要确定焦点位置及参数a ,b 的值.右焦点为F(3,0)说明两层含义:双曲线的焦点在x 轴上;c =3.又离心率为c a =32,故a =2,b 2=c 2-a 2=32-22=5,故C 的方程为x 24-y25=1,选B .3.(2013·高考北京卷)双曲线x 2-y2m=1的离心率大于2的充分必要条件是( )A .m >12B .m ≥1C .m >1D .m >2解析:选C .用m 表示出双曲线的离心率,并根据离心率大于2建立关于m 的不等式求解.∵双曲线x 2-y2m=1的离心率e =1+m ,又∵e >2,∴1+m >2,∴m >1.4.(2013·高考湖北卷)已知0<θ<π4,则双曲线C 1:x 2cos 2θ-y 2sin 2θ=1与C 2:y2sin 2θ-x2sin 2θtan 2θ=1的( )A .实轴长相等B .虚轴长相等C .焦距相等D .离心率相等解析:选D .先根据θ的范围,确定双曲线方程的类型,判断焦点所在的坐标轴,然后分析双曲线C 1和C 2的实轴长、虚轴长、焦距、离心率是否相等.双曲线C 1的焦点在x 轴上,a =cos θ,b =sin θ,c =1,因此离心率e 1=1cos θ;双曲线C 2的焦点在y 轴上,由于0<θ<π4,所以a =sin θ,b =sin θtan θ,c =sin 2θ+sin 2θtan 2θ,因此离心率e 2=sin 2θ+sin 2θtan 2θsin θ=sin θ1+tan 2θsin θ=1cos θ. 故两条双曲线的实轴长、虚轴长、焦距都不相等,离心率相等。
8.6 双曲线一、学习目标1.理解双曲线的定义;2.掌握双曲线的标准方程及简单几何性质;3.会求双曲线的离心率和渐近线方程.二、知识要点1.双曲线定义:平面内,满足c F F a PF PF 222121=<=-的动点P 的轨迹;2.标准方程与几何性质:标准方程 )0,0(12222>>=-b a b y a x )0,0(12222>>=-b a b x a y 图 形性质 范围 a x -≤或a x ≥a y -≤或a y ≥顶点 ),0(),,0(),0,(),0,(2121b B b B a A a A -- )0,(),0,(),,0(),,0(2121b B b B a A a A --渐近线方程x ab y ±= x ba y ±= 对称性 既关于y x ,轴对称,又关于原点O 对称离心率),1(+∞∈=ace c b a ,,关系222b a c +=实轴a A A 221=,虚轴b B B 221=焦半径 a c PF -≥1焦点三角形设θ221=∠PF F ,则θtan 221b S PF F =∆三、课前热身:1.椭圆1322=-y x 的焦点坐标为______,离心率为_____,渐近线方程为_________.【答案】)0,2(±,332,x y 33±= 2. 双曲线221412x y -=的焦点到渐近线的距离为__________.【答案】323.已知方程22121x y λλ-=++表示双曲线,则λ的取值范围是________.【答案】),1()2,(+∞---∞4.设21,F F 是双曲线1811622=-y x 的焦点,P 是双曲线上一点,91=PF ,则=2PF ______. 【答案】175. 已知)0,5(-A ,)0,5(B ,动点6=-PB PA ,则点P 的轨迹方程是__________.【答案】116922=-y x (0>x ) 三、典例分析例1.(1)一动圆与两圆221x y +=和228120x y x +-+=都外切,则动圆圆心轨迹为( )A .圆B .椭圆C .双曲线的一支D .抛物线(2)已知F 是双曲线221412x y -=的左焦点,(1,4)A ,P 是双曲线右支上的动点,则||||PF PA +的最小值为 .【答案】(1)C ; (2)9.例2.(1)与椭圆14922=+y x 有公共焦点,且离心率为25的双曲线方程是__________.(2)已知双曲线的渐近线方程为023=±y x ,且过点)23,4(P ,则该双曲线的方程为____________.【答案】(1)1422=-y x ; (2)118822=-y x . 例3.(1)设21,F F 分别为双曲线22221(0,0)x y a b a b-=>>的左、右焦点.若在双曲线右支上存在点P ,满足212||||PF F F =,且2F 到直线1PF 的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( )A .340x y ±=B .350x y ±=C .430x y ±=D .540x y ±=(2)已知双曲线22221(,0)x y a b a b-=>的左焦点(,0)F c -,其中c 满足0c >,且222c a b =+,直线330x y c -+=与双曲线在第二象限交于点A ,若||||OA OF =(O 为坐标原点),则该双曲线的渐近线方程为( )A .102y x =±B .22y x =± C .62y x =±D .52y x =±【答案】(1)C ; (2)C.例4.(1)已知椭圆和双曲线有相同的焦点12,F F ,它们的离心率分别为12,e e ,P 是它们的一个公共点,且1223F PF π∠=.若123e e =,则2e =( ) A .6+12B .6+22C .6+32D .6+22(2)如图1F 、2F 是椭圆221:14x C y +=与双曲线2C 的公共焦点,A 、B 分别是1C 、2C 在第二、四象限的公共点,若四边形12AF BF 为矩形,则2C 的离心率是________.【答案】(1)B ; (2)62.五、课外作业基础题:1.双曲线2212x y -=左、右焦点坐标分别是( )A .()2,0-,()2,0B .()3,0-,)3,0C .()2,0-,)2,0D .()1,0-,()1,0【答案】B2.双曲线2214y x -=的渐近线方程为( )A .12y x =±B .14y x =±C .2y x =±D .4y x =±【答案】C3.已知双曲线()222210,0x y a b a b-=>>的右焦点为()2,0F ,渐近线方程为30x y ±=,则该双曲线实轴长为( )A .2B .1C .3D .23【答案】A4.已知定点(,0)P m ,动点Q 在圆O :2216x y +=上,PQ 的垂直平分线交直线 OQ 于M 点,若动点M 的轨迹是双曲线,则m 的值可以是( )A .2B .3C .4D .5【答案】D5.已知F 为双曲线2222:1x y C a b-=(a >0,b >0)的左焦点,A 为双曲线的右顶点,B (0,-b ),P 为双曲线左支上的动点,若四边形FBAP 为平行四边形,则双曲线的离心率为( )A .43 B .21+ C .231-D .83【答案】B6.已知F 是双曲线22221(0,0)x y a b a b -=>>的右焦点,直线l 经过点F 且与双曲线相交于,A B 两点,记该双曲线的离心率为e ,直线l 的斜率为k ,若2AF FB =,则( )A .2281e k -=B .2281e k -=C .2291e k -=D .2291k e -=【答案】C7. 已知双曲线2214y x -=,点1F ,2F 为其两个焦点,点P 为双曲线上一点,若12PF PF ⊥,则21F PF ∆的面积为________. 【答案】48.过双曲线22221(0,0)x y a b a b-=>>的右焦点2F 向其一条渐近线作垂线l ,垂足为P ,l 与另一条渐近线交于Q 点.若223F Q F P =,则该双曲线的离心率为_______. 【答案】39.设O 为坐标原点,12,F F 是双曲线22221(0,0)x y a b a b-=>>的焦点,若在双曲线上存在点P ,满足1260F PF ∠=︒,7OP a =,则该双曲线的渐近线方程为__________. 【答案】x y 2±=10.如图,已知双曲线()2222:10,0x y C a b a b-=>>的左、右焦点分别为1F 、2F ,以2OF 为直径的圆与双曲线C 的渐近线在第一象限的交点为P ,线段1PF 与另一条渐近线交于点Q ,且2OPF △的面积是OPQ △面积的2倍,则该双曲线的离心率为_________.【答案】2C 提高题:1.已知双曲线C :()222210,0x y a b a b-=>>的左右焦点为1F ,2F ,以12F F 为直径的圆与双曲线在第一象限的交点为A ,直线1AF 与双曲线的左支交于点B ,且2AB AF =,设双曲线的离心率为e ,则2e =( ) A .332+ B .322+ C .532+ D .522+【答案】D2.如图,已知椭圆1E 和双曲线2E 在x 轴上具有相同的焦点1F ,2F ,设双曲线2E 与椭圆1E 的上半部分交于A ,B 两点,线段2AF 与双曲线2E 交于点C .若22223AF BF CF ==,则椭圆1E 的离心率是( ) A .23B .12C 5D 3【答案】C。