20-附表六常用分布函数

1常用分布函数11常用分布函数1.1均匀分布X∼U(a,b)U(x|a,b)=xa1b−adt(a≤x≤b),其中，期望E(X)和方差Var(X)分别为：E(X)=a+b 2Var(X)=(b−a)2121.2正态分布X∼N(µ,σ2)标准正态分布X∼N(0,1)：Φ(x)=x−∞φ(t)dt=1√2πx−∞e−t22dt其中，期望E(X)和方差Var(X)分别为：E(X)=0Var(X)=1正态分布X∼N(µ,σ2)：F(x)=x−∞f(t)dt=1√2πσ2x−∞e−(t−µ)22σ2dt其中，期望E(X)和方差Var(X)分别为：E(X)=µVar(X)=σ21常用分布函数2 1.3指数分布X∼e(µ,λ)E(x|µ,λ)=xµλe−λ(t−µ)dt(x≥µ)其中，期望E(X)和方差Var(X)分别为：E(X)=µ+1λVar(X)=1λ21.4Gamma分布X∼Γ(a,b)G(x|a,b)=b aΓ(a)xt a−1e−bt dt(a>0,b>0;x≥0)其中，Γ(a)为Gamma函数：Γ(a)= ∞t a−1e−t dt,且期望E(X)和方差Var(X)分别为：E(X)=a bVar(X)=a b21.5Beta分布X∼β(a,b)I x(a,b)=1B(a,b)xt a−1(1−t)b−1dt其中，B(a,b)为Beta函数：B(a,b)=1t a−1(1−t)b−1dt=B(b,a)=Γ(a)Γ(b)Γ(a+b)1.6χ2分布X∼χ2(n)H(x|n)=12n2Γn2(n为正整数;x>0)其中，期望E(X)和方差Var(X)分别为：E(X)=nVar(X)=2n1常用分布函数3 1.7t分布X∼t(n)T(x|n)=1√nB12,n2X−∞1+t2n−n+12dt(n为正整数;−∞<x<∞),其中，期望E(X)和方差Var(X)分别为：E(X)=0(n>1时),Var(X)=nn−2(n>2时).1.8F分布X∼F(m,n)F(x|m,n)=mnm2Bm2,n2xt m2−11+mtn−m+n2dt (n,n为正整数;x>0),其中，期望E(X)和方差Var(X)分别为：E(X)=nn−2(n>2),Var(X)=2n2(m+n−2)m(n−2)2(n−4)(n>4).。

1.均匀分布（Uniform Distribution）: 这种分布的密度函数是一条平行于坐标轴的直线，表示所有取值的概率相同。

2.正态分布（Normal Distribution）: 这种分布又称高斯分布，是一种对称的分布，其概率密度函数是一个钟形曲线。

3.指数分布（Exponential Distribution）: 这种分布的密度函数是一条指数形的曲线，常用来描述随机事件的发生时间间隔。

4.卡方分布（Chi-square Distribution）: 这种分布常用于统计检验，其概率密度函数是一条单峰曲线。

5.t分布（t Distribution）: 这种分布常用于统计检验，其概率密度函数是一条单峰曲线，但比卡方分布的峰值低。

6.F分布（F Distribution）: 这种分布常用于统计检验，其概率密度函数是一条双峰曲线。

分布函数表示及解释一、什么是分布函数呢？哎呀，分布函数这东西呀，就像是一个超级神秘又超级有用的魔法地图呢。

想象一下，你在一个超级大的迷宫里，这个迷宫里到处都是各种各样的数据和数值，而分布函数就是那个能告诉你每个角落都有些啥的神奇指南。

比如说，我们有一堆学生的考试成绩。

这个分布函数就能告诉我们，有多少学生考了很低的分数，有多少学生考了高分数，就像把这些成绩按照不同的小盒子分类放好，然后告诉我们每个小盒子里有多少个成绩一样。

1. 从数学的角度来看它其实是一个很有规律的函数哦。

它会把那些随机变量的值，转化成一个概率的表示。

就像是把那些看起来乱乱的数字，整理成一个个有秩序的小方块，每个小方块都代表着一种可能性。

比如说，对于一个连续型的随机变量，这个分布函数就像是一个平滑的曲线，沿着这条曲线，我们能知道在某个区间内找到这个随机变量的概率是多少。

就好比我们在一条长长的河边找鱼，分布函数能告诉我们在某一段河水里找到鱼的可能性有多大。

2. 它的表示形式分布函数通常会用一个大写的字母来表示，比如说F(x)。

这里的x呢，就是那个随机变量啦。

这个函数的值域是在0到1之间的哦。

这就像是一个百分比的范围，0就表示完全没有可能，1就表示肯定会发生。

比如说，我们扔一个骰子，扔出1点的分布函数值，在理想情况下就是1/6，因为总共6个面，出现1点的可能性就是1/6呀。

3. 它的实际意义在现实生活中，分布函数的应用可多啦。

在统计人口年龄的时候，分布函数能告诉我们不同年龄段的人口比例。

在研究产品质量的时候，它能告诉我们有多少产品在合格范围内，有多少是次品。

这就像是一个超级管理员，把所有的数据都管理得井井有条。

二、怎么去解释分布函数呢？这就像是给一个陌生人介绍你的好朋友一样，要把分布函数的特点都讲清楚。

1. 从整体到局部我们可以先看整个分布函数的形状。

如果它是一个比较对称的形状，像正态分布那样，就说明这个随机变量的取值比较均匀地分布在中间值的两边。

excel常用统计学概率分布函数
理论分布 DIST Excel 函数无cumu参数cumu参数 1 cumu参数0二项分布BINOM.DIST 求左尾面积求概率泊松分布POISSON.DIST 求左尾面积求概率正态分布NORM.DIST 求左尾面积求概率密度标准正态分布NORM.S.DIST 求左尾面积求概率密度t 分布T.DIST 求左尾面积求概率密度t 分布T.DIST.2T 求双尾面积F 分布
F.DIST 求左尾面积求概率密度F 分布F.DIST.RT 求右尾面积卡方分布CHISQ.DIST 求左尾面积求概率密度卡方分布
CHISQ.DIST.RT 求右尾面积逆运算 INV Excel 函数正态分布
NORM.INV 求左尾临界值标准正态分布NORM.S.INV 求左尾临界值t 分布T.INV 求左尾临界值t 分布T.INV.2T 求双尾临界值F 分布F.INV 求左尾临界值F 分布 F.INV.RT 求右尾临界值卡方分布
CHISQ.INV 求左尾临界值卡方分布CHISQ.INV.RT 求右尾临界值已知累积概率（面积），求横坐标值已知横坐标值，求概率（面积）。

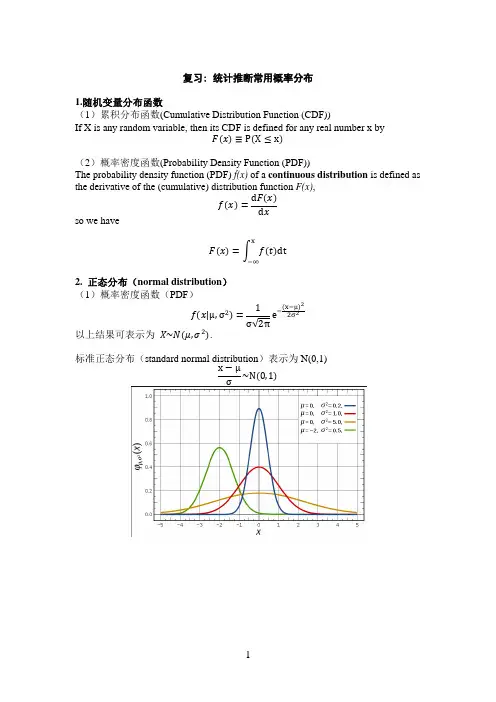
复习: 统计推断常用概率分布1.随机变量分布函数（1）累积分布函数(Cumulative Distribution Function (CDF))If X is any random variable, then its CDF is defined for any real number x byP X x（2）概率密度函数(Probability Density Function (PDF))The probability density function (PDF) f(x) of a continuous distribution is defined as the derivative of the (cumulative) distribution function F(x),ddso we havedt2. 正态分布（normal distribution ） （1）概率密度函数（PDF ）|µ,σ1σ√2πeµ以上结果可表示为 ~ ,.标准正态分布（standard normal distribution ）表示为N(0,1)x µ~N 0,1(2) 累积分布函数 (CDF)1σ√2πeµdt3. Chi-squared ( ）分布如果Z1, Z2 ..., Z n是相互独立的随机变量，且都服从于N(0,1)分布，那么服从自由度（degree of freedom, df）为n的χ 分布，记为X~χ n . （1）PDF of χ（2）CDF of χ4. t-分布(student's t-distribution)设)n (~Y )1,0(N ~X 2χ和，且X 和Y 相互独立，则称随机变量n Y X T /=服从df. 为n 的t-分布，记为T ～ t(n)。

（1）PDF of t-distribution（2）CDF of t-distribution5. F-分布X和Y是相互独立的χ 分布随机变量，d.f分别为m和n，则称随机变量n/ Y m/XF=服从df.为 (m, n)的F-分布，且通常写为F～F（m,n）。

分布函数形式分布函数是一个用于描述随机变量的概率分布的数学工具。

在概率论和统计学中，分布函数通常用于描述一个随机变量X小于或等于给定值x的概率。

在概率论中，随机变量X是指具有随机性质的变量，从而可以在一定范围内取值。

它的分布函数就是指这个随机变量X在各个取值点时的概率。

具体来说，分布函数F(x)是指随机变量X小于或等于给定值x的概率，即：F(x) = P(X ≤ x)其中P是概率，X是随机变量。

分布函数的取值范围通常是[0,1]。

也就是说，F(x)是指X的实现值小于或等于x时的概率。

分布函数的形式可以分为离散型和连续型两种：1.离散型分布函数（离散分布函数）其中P(X = xi)表示随机变量X取值为xi的概率。

对于离散型分布函数，它的取值范围就是随机变量取值的集合。

常见的离散型分布函数有伯努利分布、二项分布、泊松分布等。

其中f(x)是X的概率密度函数。

对于连续型分布函数，它的取值范围是从0到1之间的实数。

F(x) = P(X ≤ x) = ∑ P(X = xi) +∫f(x)dx其中P(X = xi)表示离散型变量的概率，f(x)表示连续型变量的概率密度函数。

在实际应用中，混合型分布函数比较常见。

分布函数的形式不同，对应的随机变量也会有不同的特点和应用范围。

在实际研究中，需要根据具体问题选择相应的分布函数来描述随机变量的概率分布。

随机变量的分布函数在概率论和统计学中都有广泛的应用。

在概率论中，它可作为随机变量在不同取值点的概率描述方法，可以较好地描述随机事件发生的概率；在统计学中，它则是描述样本分布的一种方法，可以用来判断数据是否符合某种特定分布规律，从而推断出总体的特性。

下面以常见的正态分布为例，简要介绍分布函数的应用。

正态分布是概率论和统计学中最为常见的一种连续型分布函数，它是许多自然现象和社会现象的概率模型。

正态分布函数的形式为：f(x) = 1/（σ√ (2π)）exp[-(x-μ)^2/2σ^2]μ表示正态分布的均值，σ^2表示正态分布的方差。