大学物理学第4章作业题

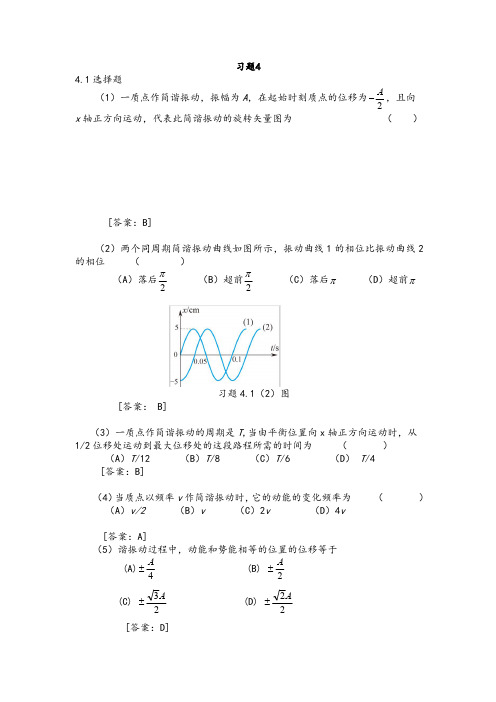
第四章机械振动4．1一物体沿x 轴做简谐振动，振幅A = 0.12m ，周期T = 2s ．当t = 0时，物体的位移x = 0.06m ，且向x 轴正向运动．求：（1）此简谐振动的表达式；（2）t = T /4时物体的位置、速度和加速度；（3）物体从x = -0.06m ，向x 轴负方向运动第一次回到平衡位置所需的时间． [解答]（1）设物体的简谐振动方程为x = A cos(ωt + φ)，其中A = 0.12m ，角频率ω = 2π/T = π．当t = 0时，x = 0.06m ，所以cos φ = 0.5，因此φ = ±π/3． 物体的速度为v = d x /d t = -ωA sin(ωt + φ)．当t = 0时，v = -ωA sin φ，由于v > 0，所以sin φ< 0，因此：φ = -π/3．简谐振动的表达式为：x = 0.12cos(πt – π/3)．（2）当t = T /4时物体的位置为;x = 0.12cos(π/2 – π/3) = 0.12cosπ/6 = 0.104(m)． 速度为；v = -πA sin(π/2 – π/3) = -0.12πsinπ/6 = -0.188(m·s -1)．加速度为：a = d v /d t = -ω2A cos(ωt + φ)= -π2A cos(πt - π/3)= -0.12π2cosπ/6 = -1.03(m·s -2)． （3）方法一：求时间差．当x = -0.06m 时，可得cos(πt 1 - π/3) = -0.5， 因此πt 1 - π/3 = ±2π/3．由于物体向x 轴负方向运动，即v < 0，所以sin(πt 1 - π/3) > 0，因此πt 1 - π/3 = 2π/3，得t 1 = 1s ．当物体从x = -0.06m 处第一次回到平衡位置时，x = 0，v > 0，因此cos(πt 2 - π/3) = 0， 可得 πt 2 - π/3 = -π/2或3π/2等．由于t 2> 0，所以πt 2 - π/3 = 3π/2， 可得t 2 = 11/6 = 1.83(s)．所需要的时间为：Δt = t 2 - t 1 = 0.83(s)．方法二：反向运动．物体从x = -0.06m ，向x 轴负方向运动第一次回到平衡位置所需的时间就是它从x = 0.06m ，即从起点向x 轴正方向运动第一次回到平衡位置所需的时间．在平衡位置时，x = 0，v < 0，因此cos(πt - π/3) = 0，可得 πt - π/3 = π/2，解得t = 5/6 = 0.83(s)．[注意]根据振动方程x = A cos(ωt + φ)，当t = 0时，可得φ = ±arccos(x 0/A )，（-π<φ<= π）， 初位相的取值由速度决定．由于v = d x /d t = -ωA sin(ωt + φ)，当t = 0时，v = -ωA sin φ，当v > 0时，sin φ< 0，因此 φ = -arccos(x 0/A )；当v < 0时，sin φ> 0，因此φ = arccos(x 0/A )π/3．可见：当速度大于零时，初位相取负值；当速度小于零时，初位相取正值．如果速度等于零，当初位置x 0 = A 时，φ = 0；当初位置x 0 = -A 时，φ = π．4．2已知一简谐振子的振动曲线如图所示，试由图求：（1）a ，b ，c ，d ，e 各点的位相，及到达这些状态的时刻t 各是多少？已知周期为T ； （2）振动表达式； （3）画出旋转矢量图． [解答]方法一：由位相求时间．（1）设曲线方程为x = A cos Φ，其中A 表示振幅，Φ = ωt + φ表示相位． 由于x a = A ，所以cos Φa = 1，因此Φa = 0．由于x b = A /2，所以cos Φb = 0.5，因此Φb = ±π/3；由于位相Φ随时间t 增加，b 点位相就应该大于a 点的位相，因此Φb = π/3．由于x c = 0，所以cos Φc = 0，又由于c 点位相大于b 位相，因此Φc = π/2．同理可得其他两点位相为：Φd = 2π/3，Φe = π．c 点和a 点的相位之差为π/2，时间之差为T /4，而b 点和a 点的相位之差为π/3，时间之差应该为T /6．因为b 点的位移值与O 时刻的位移值相同，所以到达a 点的时刻为t a = T /6． 到达b 点的时刻为t b = 2t a = T /3．图4.2到达c 点的时刻为t c = t a + T /4 = 5T /12． 到达d 点的时刻为t d = t c + T /12 = T /2． 到达e 点的时刻为t e = t a + T /2 = 2T /3．（2）设振动表达式为：x = A cos(ωt + φ)，当t = 0时，x = A /2时，所以cos φ = 0.5，因此φ =±π/3； 由于零时刻的位相小于a 点的位相，所以φ = -π/3， 因此振动表达式为． 另外，在O 时刻的曲线上作一切线，由于速度是位置对时间的变化率，所以切线代表速度的方向；由于其斜率大于零，所以速度大于零，因此初位相取负值，从而可得运动方程．（3）如图旋转矢量图所示．方法二：由时间求位相．将曲线反方向延长与t 轴 相交于f 点，由于x f = 0，根据运动方程，可得所以：．显然f 点的速度大于零，所以取负值，解得t f = -T /12．从f 点到达a 点经过的时间为T /4，所以到达a 点的时刻为：t a = T /4 + t f = T /6， 其位相为：． 由图可以确定其他点的时刻，同理可得各点的位相．4．3 有一弹簧，当其下端挂一质量为M 的物体时，伸长量为9.8×10-2m ．若使物体上下振动，且规定向下为正方向．（1）t = 0时，物体在平衡位置上方8.0×10-2m 处，由静止开始向下运动，求运动方程；（2）t = 0时，物体在平衡位置并以0.60m·s -1速度向上运动，求运动方程． [解答]当物体平衡时，有：Mg – kx 0 = 0， 所以弹簧的倔强系数为：k = Mg/x 0， 物体振动的圆频率为：s -1)． 设物体的运动方程为：x = A cos(ωt + φ)．（1）当t = 0时，x 0 = -8.0×10-2m ，v 0 = 0，因此振幅为：=8.0×10-2(m)；由于初位移为x 0 = -A ，所以cos φ = -1，初位相为：φ = π． 运动方程为：x = 8.0×10-2cos(10t + π)．（2）当t = 0时，x 0 = 0，v 0 = -0.60(m·s -1)，因此振幅为：v 0/ω|=6.0×10-2(m)；由于cos φ = 0，所以φ = π/2；运动方程为：x = 6.0×10-2cos(10t +π/2)．4．4 质量为10×10-3kg 的小球与轻弹簧组成的系统，按的规律作振动，式中t 以秒(s)计，x 以米(m)计．求： （1）振动的圆频率、周期、振幅、初位相； （2）振动的速度、加速度的最大值；（3）最大回复力、振动能量、平均动能和平均势能；cos(2)3t x A T ππ=-cos(2)03t T ππ-=232f t Tπππ-=±203a a t T πΦπ=-=ω==0||A x ==A =20.1cos(8)3x t ππ=+（4）画出这振动的旋转矢量图，并在图上指明t 为1，2，10s 等各时刻的矢量位置． [解答]（1）比较简谐振动的标准方程：x = A cos(ωt + φ)，可知圆频率为：ω =8π，周期T = 2π/ω = 1/4 = 0.25(s)，振幅A = 0.1(m)，初位相φ = 2π/3．（2）速度的最大值为：v m = ωA = 0.8π = 2.51(m·s -1)； 加速度的最大值为：a m = ω2A = 6.4π2 = 63.2(m·s -2)． （3）弹簧的倔强系数为：k = mω2，最大回复力为:f = kA = mω2A = 0.632(N)； 振动能量为:E = kA 2/2 = mω2A 2/2 = 3.16×10-2(J)， 平均动能和平均势能为:= kA 2/4 = mω2A 2/4 = 1.58×10-2(J)． （4）如图所示，当t 为1，2，10s 等时刻时，旋转矢量的位置是相同的．4．5 两个质点平行于同一直线并排作同频率、同振幅的简谐振动．在振动过程中，每当它们经过振幅一半的地方时相遇，而运动方向相反．求它们的位相差，并作旋转矢量图表示．[解答]设它们的振动方程为:x = A cos(ωt + φ)， 当x = A /2时，可得位相为:ωt + φ = ±π/3．由于它们在相遇时反相，可取Φ1 = (ωt + φ)1 = -π/3，Φ2 = (ωt + φ)2 = π/3，它们的相差为:ΔΦ = Φ2 – Φ1 = 2π/3，或者:ΔΦ` = 2π –ΔΦ = 4π/3．矢量图如图所示．4．6一氢原子在分子中的振动可视为简谐振动．已知氢原子质量m = 1.68×10-27kg ，振动频率v = 1.0×1014Hz ，振幅A = 1.0×10-11m ．试计算：（1）此氢原子的最大速度； （2）与此振动相联系的能量．[解答]（1）氢原子的圆频率为:ω = 2πv = 6.28×1014(rad·s -1)， 最大速度为:v m = ωA = 6.28×103(m·s -1)．（2）氢原子的能量为:= 3.32×10-20(J)．4．7 如图所示，在一平板下装有弹簧，平板上放一质量为1.0kg 的重物，若使平板在竖直方向上作上下简谐振动，周期为0.50s ，振幅为2.0×10-2m ，求：（1）平板到最低点时，重物对平板的作用力；（2）若频率不变，则平板以多大的振幅振动时，重物跳离平板？ （3）若振幅不变，则平板以多大的频率振动时，重物跳离平板？ [解答]（1）重物的圆频率为：ω = 2π/T = 4π，其最大加速度为：a m = ω2A ，合力为：F = ma m ，方向向上．重物受到板的向上支持力N 和向下的重力G ，所以F = N – G ． 重物对平板的作用力方向向下，大小等于板的支持力： N = G + F = m (g +a m ) = m (g +ω2A ) = 12.96(N)．（2）当物体的最大加速度向下时，板的支持为：N = m (g - ω2A )． 当重物跳离平板时，N = 0，频率不变时，振幅为：A = g/ω2 = 3.2×10-2(m)．（3）振幅不变时，频率为：3.52(Hz)．4．8 两轻弹簧与小球串连在一直线上，将两弹簧拉长后系在固定点A 和B 之间，整个系统放在光滑水平面上．设两弹簧的原长分别为l 1和l 2，倔强系统分别为k 1和k 2，A和B 间距为L ，小球的质量为m ．（1）试确定小球的平衡位置；k pE E =212m E mv=2ωνπ==（2）使小球沿弹簧长度方向作一微小位移后放手，小球将作振动，这一振动是否为简谐振动？振动周期为多少？[解答]（1）这里不计小球的大小，不妨设L > l 1 + l 2，当小球平衡时，两弹簧分别拉长x 1和x 2，因此得方程：L = l 1 + x 1 + l 2 + x 2；小球受左右两边的弹簧的弹力分别向左和向右，大小相等，即k 1x 1 = k 2x 2． 将x 2 = x 1k 1/k 2代入第一个公式解得：．小球离A 点的距离为：．（2）以平衡位置为原点，取向右的方向为x 轴正方向，当小球向右移动一个微小距离x 时，左边弹簧拉长为x 1 + x ，弹力大小为：f 1 = k 1(x 1 + x )， 方向向左；右边弹簧拉长为x 1 - x ，弹力大小为：f 2 = k 2(x 2 - x )， 方向向右．根据牛顿第二定律得：k 2(x 2 - x ) - k 1(x 1 + x ) = ma ，利用平衡条件得：，即小球做简谐振动．小球振动的圆频率为：．4．9如图所示，质量为10g 的子弹以速度v = 103m·s -1水平射入木块，并陷入木块中，使弹簧压缩而作简谐振动．设弹簧的倔强系数k = 8×103N·m -1，木块的质量为4.99kg ，不计桌面摩擦，试求：（1）振动的振幅；（2）振动方程．[解答]（1）子弹射入木块时，由于时间很短，木块还来不及运动，弹簧没有被压缩，它们的动量守恒，即：mv = (m + M)v 0．解得子弹射入后的速度为：v 0 = mv/(m + M) = 2(m·s -1)，这也是它们振动的初速度．子弹和木块压缩弹簧的过程机械能守恒，可得：(m + M ) v02/2 = kA 2/2， 所以振幅为：10-2(m)． （2）振动的圆频率为：= 40(rad·s -1)．取木块静止的位置为原点、向右的方向为位移x 的正方向，振动方程可设为：x = A cos(ωt + φ)．当t = 0时，x = 0，可得：φ = ±π/2；由于速度为正，所以取负的初位相，因此振动方程为：x = 5×10-2cos(40t - π/2)．4．10如图所示，在倔强系数为k 的弹簧下，挂一质量为M 的托盘．质量为m 的物体由距盘底高h 处自由下落与盘发生完全非弹性碰撞，而使其作简谐振动，设两物体碰后瞬时为t = 0时刻，求振动方程．[解答]物体落下后、碰撞前的速度为：物体与托盘做完全非弹簧碰撞后，根据动量守恒定律可得它们的共同速度为，这也是它们振动的初速度．设振动方程为：x = A cos(ωt + φ)，211212()k x L l l k k =--+211111212()k L l x l L l l k k =+=+--+2122d ()0d xm kk x t++=ω=22T πω==A v =ω=v =0m v v m M ==+图4.9 图4.10其中圆频率为：物体没有落下之前，托盘平衡时弹簧伸长为x 1，则：x 1 = Mg/k ．物体与托盘磁盘之后，在新的平衡位置，弹簧伸长为x 2，则：x 2= (M + m )g/k ． 取新的平衡位置为原点，取向下的方向为正，则它们振动的初位移为x 0 = x 1 - x 2 = -mg/k ．因此振幅为：初位相为：4．11 装置如图所示，轻弹簧一端固定，另一端与物体m 间用细绳相连，细绳跨于桌边定滑轮M 上，m 悬于细绳下端．已知弹簧的倔强系数为k = 50N·m -1，滑轮的转动惯量J = 0.02kg·m 2，半径R = 0.2m ，物体质量为m = 1.5kg ，取g = 10m·s -2．（1）试求这一系统静止时弹簧的伸长量和绳的张力；（2）将物体m 用手托起0.15m ，再突然放手，任物体m 下落而整个系统进入振动状态．设绳子长度一定，绳子与滑轮间不打滑，滑轮轴承无摩擦，试证物体m 是做简谐振动； （3）确定物体m 的振动周期；（4）取物体m 的平衡位置为原点，OX 轴竖直向下，设振物体m 相对于平衡位置的位移为x ，写出振动方程．[解答]（1）在平衡时，绳子的张力等于物体的重力T = G = mg = 15(N)．这也是对弹簧的拉力，所以弹簧的伸长为：x 0 = mg/k = 0.3(m)．（2）以物体平衡位置为原点，取向下的方向为正，当物体下落x 时，弹簧拉长为x 0 + x ，因此水平绳子的张力为：T 1 = k (x 0+ x )．设竖直绳子的张力为T 2，对定滑轮可列转动方程：T 2R – T 1R = Jβ， 其中β是角加速度，与线加速度的关系是：β = a/R ．对于物体也可列方程：mg - T 2 = ma ． 转动方程化为：T 2 – k (x 0 + x ) = aJ/R 2，与物体平动方程相加并利用平衡条件得：a (m + J/R 2) = –kx ，可得微分方程：，故物体做简谐振动． （3）简谐振动的圆频率为：s -1)． 周期为：T 2 = 2π/ω = 1.26(s)．（4）设物体振动方程为：x = A cos(ωt + φ)，其中振幅为：A = 0.15(m)． 当t = 0时，x = -0.15m ，v 0 = 0，可得：cos φ = -1，因此φ = π或-π， 所以振动方程为：x = 0.15cos(5t + π)，或x = 0.15cos(5t - π)．4．12一匀质细圆环质量为m ，半径为R ，绕通过环上一点而与环平面垂直的水平光滑轴在铅垂面内作小幅度摆动，求摆动的周期．[解答]通过质心垂直环面有一个轴，环绕此轴的转动惯量为：I c = mR 2．根据平行轴定理，环绕过O 点的平行轴的转动惯量为I = I c + mR 2 = 2mR 2．当环偏离平衡位置时，重力的力矩为：M = mgR sin θ， 方向与角度θ增加的方向相反．ω=A ==00arctan v x ϕω-==222d 0d /x kx t m J R +=+ω=根据转动定理得：Iβ = -M ，即，由于环做小幅度摆动，所以sin θ≈θ，可得微分方程：． 摆动的圆频率为：周期为：4．13 重量为P 的物体用两根弹簧竖直悬挂，如图所示，各弹簧的倔强系数标明在图上．试求在图示两种情况下，系统沿竖直方向振动的固有频率．[解答]（1）前面已经证明：当两根弹簧串联时，总倔强系数为k = k1k 2/(k 1 + k 2)，因此固有频率为（2）前面还证明：当两根弹簧并联时，总倔强系数等于两个弹簧的倔强系数之和，因此固有频率为．4．14质量为0.25kg 的物体，在弹性力作用下作简谐振动，倔强系数k = 25N·m -1，如果开始振动时具有势能0.6J ，和动能0.2J ，求：（1）振幅；（2）位移多大时，动能恰等于势能？（3）经过平衡位置时的速度．[解答]物体的总能量为：E = E k + E p = 0.8(J)．（1）根据能量公式E = kA2/2，得振幅为：．（2）当动能等于势能时，即E k = E p ，由于E = E k + E p ，可得：E = 2E p ，即，解得：= ±0.179(m)． （3）再根据能量公式E = mv m2/2，得物体经过平衡位置的速度为： 2.53(m·s -1)．4．15 两个频率和振幅都相同的简谐振动的x-t 曲线如图所示，求： （1）两个简谐振动的位相差；（2）两个简谐振动的合成振动的振动方程． [解答]（1）两个简谐振动的振幅为：A = 5(cm)， 周期为：T = 4(s)，圆频率为：ω =2π/T = π/2，它们的振动方程分别为：x 1 = A cos ωt =5cosπt /2， x 2 = A sin ωt =5sinπt /2 =5cos(π/2 - πt /2)即x 2=5cos(πt /2 - π/2)．位相差为：Δφ = φ2 - φ1 = -π/2． （2）由于x = x 1 + x 2 = 5cosπt /2 +5sinπt /2 = 5(cosπt /2·cosπ/4 +5sinπt /2·sinπ/4)/sinπ/4 合振动方程为：(cm)．22d sin 0d I mgR tθθ+=22d 0d mgRt Iθθ+=ω=222T πω===2ωνπ===2ωνπ===A =2211222kA kx =⨯/2x =m v =cos()24x t ππ=- (b)图4.134．16 已知两个同方向简谐振动如下：，．（1）求它们的合成振动的振幅和初位相； （2）另有一同方向简谐振动x 3 = 0.07cos(10t +φ)，问φ为何值时，x 1 + x 3的振幅为最大？φ为何值时，x 2 + x 3的振幅为最小？（3）用旋转矢量图示法表示（1）和（2）两种情况下的结果．x 以米计，t 以秒计．[解答]（1）根据公式，合振动的振幅为：=8.92×10-2(m)． 初位相为：= 68.22°．（2）要使x 1 + x 3的振幅最大，则：cos(φ– φ1) = 1，因此φ– φ1 = 0，所以：φ = φ1 = 0.6π． 要使x 2 + x 3的振幅最小，则 cos(φ– φ2) = -1，因此φ– φ2 = π，所以φ = π + φ2 = 1.2π．（3）如图所示．4．17质量为0.4kg 的质点同时参与互相垂直的两个振动：， ．式中x 和y 以米(m)计，t 以秒(s)计．（1）求运动的轨道方程；（2）画出合成振动的轨迹；（3）求质点在任一位置所受的力．[解答]（1）根据公式：，其中位相差为：Δφ = φ2 – φ1 = -π/2，130.05cos(10)5x t π=+210.06cos(10)5x t π=+A =11221122sin sin arctancos cos A A A A ϕϕϕϕϕ+=+0.08cos()36x t ππ=+0.06cos()33y t ππ=-2222212122cos sin x y xyA A A A ϕϕ+-∆=∆所以质点运动的轨道方程为：． （2）合振动的轨迹是椭圆．（3）两个振动的圆频率是相同的ω = π/3，质点在x 方向所受的力为，即F x = 0.035cos(πt /3 + π/6)(N)．在y 方向所受的力为，即F y = 0.026cos(πt /3 - π/3)(N)．用矢量表示就是，其大小为，与x 轴的夹角为θ = arctan(F y /F x )．4．18 将频率为384Hz 的标准音叉振动和一待测频率的音叉振动合成，测得拍频为3.0Hz ，在待测音叉的一端加上一小块物体，则拍频将减小，求待测音叉的固有频率．[解答]标准音叉的频率为v 0 = 384(Hz)， 拍频为Δv = 3.0(Hz)， 待测音叉的固有频率可能是v 1 = v 0 - Δv = 381(Hz)， 也可能是v 2 = v 0 + Δv = 387(Hz)．在待测音叉上加一小块物体时，相当于弹簧振子增加了质量，由于ω2 = k/m ，可知其频率将减小．如果待测音叉的固有频率v 1，加一小块物体后，其频率v`1将更低，与标准音叉的拍频将增加；实际上拍频是减小的，所以待测音叉的固有频率v 2，即387Hz ．4．19示波器的电子束受到两个互相垂直的电场作用．电子在两个方向上的位移分别为x = A cos ωt 和y = A cos(ωt +φ)．求在φ = 0，φ = 30º，及φ = 90º这三种情况下，电子在荧光屏上的轨迹方程．[解答]根据公式，其中Δφ = φ2 – φ1 = -π/2，而φ1 = 0，φ2 = φ．（1）当Δφ = φ = 0时，可得，质点运动的轨道方程为y = x ，轨迹是一条直线．（2）当Δφ = φ = 30º时，可得质点的轨道方程， 即，轨迹是倾斜的椭圆．（3）当Δφ = φ = 90º时，可得， 即x 2 + y 2 = A 2，质点运动的轨迹为圆．4．20三个同方向、同频率的简谐振动为，，．222210.080.06x y +=22d d x x x F ma m t==20.08cos()6m t πωω=-+22d d y y y F ma m t==20.06cos()3m t ωω=--πi+j x y F F F =F =2222212122cos sin x y xyA A A A ϕϕ+-∆=∆2222220x y xyA A A+-=222214x y A+=222/4x y A +=22221x y A A +=10.08cos(314)6x t π=+20.08cos(314)2x t π=+350.08cos(314)6x t π=+求：（1）合振动的圆频率、振幅、初相及振动表达式； （2）合振动由初始位置运动到所需最短时间（A 为合振动振幅）． [解答]合振动的圆频率为：ω = 314 = 100π(rad·s -1)． 设A 0 = 0.08，根据公式得：A x = A 1cos φ1 + A 2cos φ2 + A 3cos φ3 = 0，A y = A 1sin φ1 + A 2sin φ2 + A 3sin φ3 = 2A 0 = 0.16(m)， 振幅为：，初位相为：φ = arctan(A y /A x ) = π/2．合振动的方程为：x = 0.16cos(100πt + π/2)．（2）当时，可得：，解得：100πt + π/2 = π/4或7π/4．由于t > 0，所以只能取第二个解，可得所需最短时间为t = 0.0125s ．x A =A =/2x =cos(100/2)2t ππ+。

大学物理第四章习题答案大学物理第四章习题答案大学物理是一门让许多学生感到头疼的学科，尤其是对于那些对数学和计算不太擅长的学生来说。

而第四章是大学物理中的一个重要章节，涵盖了许多关于力学和运动的基本概念和原理。

在这篇文章中，我将为大家提供一些大学物理第四章习题的答案，希望能够帮助到那些正在学习这门课程的学生。

1. 一个物体以10 m/s的速度沿着水平方向运动，受到一个10 N的水平力的作用，求物体在2秒钟内的位移。

根据牛顿第二定律，物体的加速度可以通过力和质量的比值来计算。

在这个问题中，物体的质量未知，但我们可以通过已知的力和加速度来计算出质量。

由于力和加速度的关系是F = ma，我们可以将已知的力和加速度代入这个公式，解出物体的质量。

然后，我们可以使用物体的质量和已知的力来计算物体的加速度。

最后，我们可以使用物体的初始速度、加速度和时间来计算物体的位移。

2. 一个物体以5 m/s的速度沿着斜坡上升，斜坡的倾角为30度。

求物体在10秒钟内上升的高度。

在这个问题中，我们需要使用三角函数来计算物体在斜坡上升时的垂直位移。

首先，我们可以使用已知的速度和斜坡的倾角来计算物体在斜坡上的水平速度。

然后，我们可以使用已知的时间和水平速度来计算物体在斜坡上的水平位移。

最后，我们可以使用已知的斜坡的倾角和物体在斜坡上的水平位移来计算物体在斜坡上升时的垂直位移。

3. 一个物体以10 m/s的速度竖直向上抛出，求物体在2秒钟内的最大高度和总的飞行时间。

在这个问题中，我们需要使用物体的初速度和重力加速度来计算物体在竖直抛物线运动中的最大高度和总的飞行时间。

首先，我们可以使用已知的初速度和时间来计算物体在竖直方向上的位移。

然后，我们可以使用已知的初速度和重力加速度来计算物体在竖直方向上的最大高度。

最后，我们可以使用已知的重力加速度来计算物体在竖直方向上的总的飞行时间。

这些问题只是大学物理第四章中的一小部分，但它们涵盖了一些基本的概念和原理。

第四章热学基础选择题4—1 有一截面均匀的封闭圆筒,中间被一光滑的活塞隔成两边,如果其中一边装有0.1kg某一温度的氢气,为了使活塞停在圆筒的正中央,则另一边应装入同一温度的氧气的质量为（ C ）(A)1kg16; (B) 0.8kg; (C) 1.6kg; (D) 3.2kg.4—2 根据气体动理论,理想气体的温度正比于（ D ）(A) 气体分子的平均速率; (B)气体分子的平均动能;(C) 气体分子的平均动量的大小; (D)气体分子的平均平动动能.4—3 在一固定的容器内,理想气体的温度提高为原来的两倍,那么（ A ）(A) 分子的平均平动动能和压强都提高为原来的两倍;(B) 分子的平均平动动能提高为原来的四倍,压强提高为原来的两倍;(C) 分子的平均平动动能提高为原来的两倍,压强提高为原来的四倍;(D) 分子的平均平动动能和压强都提高为原来的四倍.4—4 一瓶氦气和一瓶氮气的密度相同,分子的平均平动动能相同,且均处于平衡态,则它们（ C ）(A) 温度和压强都相同;(B) 温度和压强都不相同;(C) 温度相同,但氦气的压强大于氮气的压强;(D) 温度相同,但氦气的压强小于氮气的压强.4—5 下面说法中正确的是（ D ）(A) 在任何过程中,系统对外界做功不可能大于系统从外界吸收的热量;(B) 在任何过程中,系统内能的增量必定等于系统从外界吸收的热量;(C) 在任何过程中,系统内能的增量必定等于外界对系统所做的功;(D) 在任何过程中,系统从外界吸收的热量必定等于系统内能的增量与系统对外界做功之和.4—6 如图所示,一定量的理想气体,从状态A 沿着图中直线变到状态B ,且A AB B p V p V =,在此过程中: （ B ）(A) 气体对外界做正功,向外界放出热量;(B) 气体对外界做正功,从外界吸收热量;(C) 气体对外界做负功,向外界放出热量;(D) 气体对外界做负功,从外界吸收热量.4—7 如图所示,一定量的理想气体从状态A 等压压缩到状态B ,再由状态B 等体升压到状态C .设2C B p p =、2A B V V =,则气体从状态A 到C 的过程中 （ B ）(A) 气体向外界放出的热量等于气体对外界所做的功;(B) 气体向外界放出的热量等于外界对气体所做的功;(C) 气体从外界吸收的热量等于气体对外界所做的功;(D) 气体从外界吸收的热量等于外界对气体所做的功.4—8 摩尔定容热容为2.5R （R 为摩尔气体常量）的理想气体,由状态A 等压膨胀到状态B ,其对外界做的功与其从外界吸收的热量之比为 （ C ）(A) 2:5; (B) 1:5; (C) 2:7; (D) 1:7.4—9 质量相同的同一种理想气体,从相同的状态出发,分别经历等压过程和绝热过程,使其体积增加一倍.气体温度的改变为 （ C ）(A) 绝热过程中降低,等压过程中也降低;(B) 绝热过程中升高,等压过程中也升高;(C) 绝热过程中降低,等压过程中升高;(D) 绝热过程中升高,等压过程中降低.4—10 一理想气体的初始温度为T ,体积为V .由如下三个准静态过程构成一个循环过程.先从初始状态绝热膨胀到2V ,再经过等体过程回到温度T ,最后等温压缩到体积V .在此循环过程中,下述说法正确的是 （ A ）(A) 气体向外界放出热量; (B) 气体对外界做正功;(C) 气体的内能增加; (D) 气体的内能减少.4—11 有人试图设计一台可逆卡诺热机,在一个循环中,可从400K 的高温热源吸收热量1800J ,向300K 的低温热源放出热量800J ,同时对外界作功1000J ,这样的设计是（ B ）(A) 可以的,符合热力学第一定律;(B) 可以的,符合热力学第二定律;(C) 不行的,卡诺循环所做的功不能大于向低温热源放出的热量;(D) 不行的,这个热机的效率超过理论最大值.4—12 对运转在1T 和2T 之间的卡诺热机,使高温热源的温度1T 升高T ∆,可使热机效率提高1η∆;使低温热源的温度2T 降低同样的值T ∆,可使循环效率提高2η∆.两者相比,有（ B ）(A) 12ηη∆>∆; (B) 12ηη∆<∆;(C) 12ηη∆=∆; (D) 无法确定哪个大.4—13 在o 327C 的高温热源和o27C 的低温热源间工作的热机,理论上的最大效率为（ C ）(A) 100%; (B) 92%; (C) 50%; (D) 25%.4—14 下述说法中正确的是 （ C ）(A) 在有些情况下,热量可以自动地从低温物体传到高温物体;(B) 在任何情况下,热量都不可能从低温物体传到高温物体;(C) 热量不能自动地从低温物体传到高温物体;(D) 热量不能自动地从高温物体传到低温物体.4—15 热力学第二定律表明 （ D ）(A) 热机可以不断地对外界做功而不从外界吸收热量;(B) 热机可以靠内能的不断减少而对外界做功;(C) 不可能存在这样的热机,在一个循环中,吸收的热量不等于对外界作的功;(D) 热机的效率必定小于100%.4—16 一个孤立系统,从平衡态A 经历一个不可逆过程变化到平衡态B ,孤立系统的熵增量B A S S S ∆=- 有 （ A ）(A) 0S ∆>; (B) 0S ∆<; (C) 0S ∆=; (D) 0S ∆≥.计算题4—17 容器内装满质量为0.1kg 的氧气,其压强为61.01310Pa ⨯,温度为o 47C .因为漏气,经过若干时间后,压强变为原来的一半,温度降到o 27C .求:(1) 容器的容积;(2) 漏去了多少氧气.解 (1) 由状态方程m pV RT M=,可得气体的体积,即容器的容积为 333360.18.31(47273)m 8.2010m 3210 1.01310m V RT Mp -⨯⨯+===⨯⨯⨯⨯ (2) 压强变为12p p =,温度降为()227327K T =+时,由状态方程,可得剩余气体的质量为36311113210 1.013108.20102kg 0.0533kg 8.31(27273)Mp V m RT ⨯⨯⨯⨯⨯⨯===⨯+ 漏掉的气体质量为1(0.10.0533)kg 0.0467kg m m m -∆=-=-=4—18 如图所示,a 、c 间曲线是1000mol 氢气的等温线,其中压强51410Pa p =⨯, 521010Pa p =⨯.在点a ,氢气的体积31 2.5m V =,求:(1) 该等温线的温度;(2) 氢气在点b 和点d 的温度b T 和d T .解 (1) 由状态方程m pV RT M=,可得在等温线上,气体的温度为 52111010 2.5K 301K 10008.31p V M T m R ⨯⨯==⨯= (2) 气体由点c 等体增压至点b ,压强增大为原来的10 2.54=倍,由等体方程21b cp p T T =,可得气体在点b 的温度为212.5 2.5301K 753K b c c p T T T p ===⨯= 气体由点a 等体减压至点d ,压强减小为原来的410,由等体方程21a d p p T T =,可得气体在点d 的温度为1244301K 120K 1010d a a p T T T p ===⨯= 4—19 22.010kg -⨯氢气装在334.010m -⨯的容器内,求当容器的压强为53.9010Pa⨯时,氢气分子的平均平动动能.解 由状态方程m pV RT M=,可得气体的温度为 MpV T mR=气体分子的平均平动动能为 t 353222233332223210 3.9010 4.010 J 3.8910J 2210 6.02310a MpV MpV kT k mR mN ε----===⨯⨯⨯⨯⨯=⨯=⨯⨯⨯⨯4—20 在一个具有活塞的容器中盛有一定量的气体.如果压缩气体,并对它加热,使它的温度从o 27C 升到o177C ,体积减少一半.求:(1) 气体的压强是原来压强的多少倍;(2) 气体分子的平均平动动能是原来平均平动动能的多少倍.解 (1) 由状态方程m pV RT M=,可得压缩后与压缩前的压强之比为 21212132(273177)(27327)p VT p V T +===+ 即压强增加为原来的三倍.(2) 子的平均平动动能t 32kT ε=与温度成正比,因此,压缩后与压缩前的分子的平均平动动能之比为 t22t112731773 1.5273272T T εε+====+ 即增加为原来的1.5倍.4—21 容器中储有氦气,其压强为71.01310Pa ⨯,温度为o 0C .求:(1) 单位体积中分子数n ;(2) 气体的密度;(3) 分子的平均平动动能.解 (1) 由p nkT =,可得单位体积中的分子数为73273231.01310m 2.6910m 1.3810273p n kT ---⨯===⨯⨯⨯ (2) 气体的密度为2727334 1.6710 2.6910kg m 18.0kg m mn ρ---==⨯⨯⨯⨯⋅=⋅(3) 分子的平均平动动能为2321t 33 1.3810273J 5.6510J 22kT ε-==⨯⨯⨯=⨯4—22 如图所示,一系统从状态A 沿ABC 过程到达状态C ,从外界吸收了350J 的热量,同时对外界做功126J .(1) 如沿ADC 过程,对外界作功为42J ,求系统从外界吸收的热量;(2) 系统从状态C 沿图示曲线返回状态A ,外界对系统做功84J ,系统是吸热还是放热?数值是多少?解 由热力学第一定律,ΔQ E A =+,可得从状态A 到状态C ,系统内能的增量为Δ350J 126J 224J ABC ABC E Q A =-=-=(1) 沿ADC 过程从状态A 到状态C ,系统吸收的热量为Δ224J 42J 266J ADC ADC Q E A =+=+=(2) 从状态C 沿图示曲线所示过程返回状态A ,系统吸收的热量为Δ224J 84J 308J CA CA Q E A =+=--=-308J<0CA Q =-,说明系统向外界放热308J .4-23 如图所示,一定量的空气, 起始在状态A ,其压强为52.010Pa ⨯,体积为332.010m -⨯沿直线AB 变化到状态B 后,压强变为51.010Pa ⨯,体积变为333.010m -⨯.求此过程中气体对外界所做的功.解 在此过程中气体作正功,大小为图示直线AB 下的面积()()()()5533121 2.010 1.010 3.010 2.010J 150J 2A B B A A p p V V -=+-=⨯+⨯⨯-⨯= 4—24 在标准状态下,1mol 的氧气经过一等体过程,到达末状态.从外界吸收的热量为336J .求气体到达末状态的温度和压强.设氧气的摩尔定容热容,m 52V C R =. 解 初始为标准状态,50 1.01310Pa p =⨯,230 2.2410m V -=⨯,0273K T =.气体经过等体过程吸受的热量等于内能的增量,,m V Q E C T =∆=∆.由此可得1mol 氧气经过等体过程后温度变化为,m 336 K 16.1K 2.58.31V Q T C ∆===⨯ 气体到达末状态时的温度为 0273K 16.1K 289K T T T =+∆=+=由等体方程,00p pT T =,可得气体到达末状态时的压强为5500 1.01310289 Pa 1.0710Pa 273p p T T ⨯==⨯=⨯ 4—25 在标准状态下,0.032kg 的氧气经过一等温过程,到达末状态.从外界吸收的热量为336J .求气体到达末状态的压强和体积.解 0.032kg 的氧气是1mol .标准状态为50 1.01310Pa p =⨯,230 2.2410m V -=⨯, 0273K T =.气体经过等温过程,吸受的热量等于其对外界所作的功:000000lnln V p Q A p V p V V p === 由此可得 520000336ln ln 0.1481.01310 2.2410V p Q V p p V -====⨯⨯⨯ 气体到达末状态的压强和体积分别为0.14850.14840 1.01310 Pa 8.710Pa p p e e --==⨯⨯=⨯0.14820.1483230 2.2410 m 2.6010m V V e e ----==⨯⨯=⨯4—26 1mol 的氦气,从温度为o 27C 、体积为232.010m -⨯,等温膨胀到体积为234.010m -⨯后,再等体冷却到o 27C -,设氦气的摩尔定容热容,m 32V C R =,请作出P V -图,并计算这一过程中,氦气从外界吸收的热量和对外界做的功.解 过程的P V -图如图所示.在等温过程AB 中,气体吸受的热量等于对外所做的功,为()232ln 4.010 8.3127327lnJ 1.7310 J 2.010BAB AB A AV Q A RT V --==⨯=⨯+⨯=⨯⨯ 在等体过程BC 中,气体做功为零,即0BC A =,吸受的热量为(),m 38.31(2727) J 673 J 2BC V C B m Q C T T M -=-=⨯⨯+=- 在整个过程ABC 中,气体吸受的热量和所作的功分别为()31.730.67 J 1.0610 J AB BC Q Q Q =+=-=⨯31.7310 J AB A A ==⨯4—27 将1mol 理想气体等压加热,使其温度升高72K ,气体从外界吸收的热量为31.610 J ⨯.求:(1) 气体对外界所做的功;(2) 气体内能的增量;(3) 比热容比.解 (1) 在此等压过程中气体对外界所做的功为8.3172 J 598 J A R T =∆=⨯=(2) 在此等压过程中气体内能的增量为33(1.610598)J 1.0010J E Q A ∆=-=⨯-=⨯(3) 气体的摩尔定压热容和定容热容分别为31111,m 1.6010J mol K 22.2J mol K 72p Q C T ----⨯==⋅⋅=⋅⋅∆ ()1111,m ,m 22.28.31J mol K 13.9J mol K V p C C R ----=-=-⋅⋅=⋅⋅比热容比为,m,m 22.2 1.6013.9p V C C γ=== 4—28 1mol 理想气体盛于气缸中,压强为51.01310Pa ⨯,体积为231.010m -⨯.先将此气体在等压下加热,使体积增大一倍.然后在等体下加热,使压强增大一倍.最后绝热膨胀使温度降为初始温度.请将全过程在p V -图中画出,并求在全过程中内能的增量和对外所做的功.设气体的摩尔定压热容,m 52p C R =. 解 过程的P V -图如图所示.因为末状态D 与初状态A 的温度相同,所以,从状态A 到状态D 的全过程中的内能增量为零:0E ∆=由热力学第一定律,ΔQ E A =+,由于0E ∆=,因此,全过中程气体吸受的热量等于对外界所做的功:()(),m ,m p B A V C B A Q C T T C T T ==-+-而,m ,m 5322V p C C R R R R =-=-= pV RT =于是()()5322B B A AC C B B A Q p V p V p V p V ==-+- 由于2B B A A p V p V =,24C C B B A A p V p V p V ==,因此5331111 1.01310 3.010 J 1.6710 J 22A A A Q p V -===⨯⨯⨯⨯=⨯ 4—29 1mol 的氮气,温度为o 27C ,压强为51.01310Pa ⨯.将气体绝热压缩,使其体积变为原来的15.求: (1) 压缩后的压强和温度;(2) 在压缩过程中气体所做的功( 1.4)γ=.解 (1) 在绝热过程中,pV γ为常数.压缩后的压强为 5 1.4500 1.013105Pa 9.6410Pa V p p V γ⎛⎫==⨯⨯=⨯ ⎪⎝⎭在绝热过程中,1V T γ-亦为常数.压缩后的温度为1(1.41)00(27273)5K 571K V T T V γ--⎛⎫==+⨯= ⎪⎝⎭(2) 将 1.4γ=代入,m ,mV V C RC γ+=,可得,m 52V C R =.在绝热压缩过程中,气体对外界所做的功,等于内能的减少:3055()8.31[571(27273)]J 5.6310J 22A E R T T =-∆=--=-⨯⨯-+=-⨯ 负号说明,在绝热压缩过程中,是外界对气体做功.4—30 一卡诺热机低温热源温度为o 7C ,效率为40%,若要把它的效率提高到50%,高温热源的温度应提高多少开?解 在效率为40%和50%的两种情况下,低温热源温度2T 相同.由211T T η=-,两种情况下的效率分别可表为 21122140%150%1T T T T T ηη==-==-+∆由此可得,高温热源的温度应提高 22112737K 93.3K 0.500.6033T T T +⎛⎫∆=-=== ⎪⎝⎭4—31 一卡诺热机,高温热源的温度为400K ,每一个循环从高温热源吸收75 J 热量,并向低温热源放出60 J 热量.求:(1) 低温热源温度;(2) 循环效率.解 (1) 对卡诺循环,有2211Q T T Q =,由此可得低温热源的温度为 221160400 K 320 K 75Q T T Q ==⨯=(2) 热机的循环效率为21601120%75Q Q η=-=-= 4—32 一卡诺机,在温度o 127C 和o 27C 两个热源间运转. (1)若一个正循环,从o 127C 热源吸收1200 J 热量,求向o 27C 的热源放出的热量;(2)若此循环逆向工作,从o 27C 的热源吸收1200 J 热量,求向o 127C 的热源放出的热量.解 (1) 对卡诺热机,2211Q T T Q =,由此可得,一个正循环向低温热源放出的热量为 2211272731200 J 900 J 127273T Q Q T +==⨯=+ (2) 对卡诺制冷机,有2211Q T Q T '=',由此可得,一个逆循环向高温热源放出的热量为 112241200 J 1600 J 3T Q Q T ''==⨯= 4—33 理想气体做卡诺循环,高温热源的热力学温度是低温热源热力学温度的n 倍,求在一个循环中,气体从高温热源吸收的热量有多少比例传给了低温热源.解 对卡诺热机,2211Q T T Q =,将12T n T =代入,可得 211Q Q n= 气体从高温热源吸收的热量有1n传给了低温热源. 4-34 质量为m ,摩尔质量为M 的理想气体,其摩尔定容热容为,m V C .在可逆的等体过程中温度从1T 升高到2T ,试证明在这一过程中气体的熵增量为2,m 1ln V T m S C M T ∆= 证 在气体的初态和末态间作可逆的等体曲线.气体沿此曲线,在温度升高d T 的元过程中,吸热为,m d d V m Q C T M=,熵增为,m d d d V Q m T S C T M T== 温度从1T 升高到2T ,气体的熵增量为 22112,m ,m 1d d ln S T V V S T T m T m S S C C M T M T ∆===⎰⎰ 4-35 质量为m ,摩尔质量为M 的理想气体,在可逆的等压过程中,温度从1T 升高到2T ,求在这一过程中,气体的熵增量.已知气体的摩尔定压热容为,m p C .解 在气体的初态和末态间作可逆的等压曲线.气体沿此曲线,在温度升高d T 的元过程中,吸热为,m d d p m Q C T M=,熵增为 ,m d d d p Q m T S C T M T== 温度从1T 升高到2T ,气体的熵增为22112,m ,m 1d d ln S T p p S T T m T m S S C C M T M T ∆===⎰⎰。

一．选择题 ［ B ］1、（基础训练1）一质点在如图4-5所示的坐标平面内作圆周运动，有一力)(0j y i x F F+=作用在质点上．在该质点从坐标原点运动到(0，2R ）位置过程中，力F对它所作的功为(A) 20R F ． (B) 202R F ．(C) 203R F ． (D) 204R F ．【提示】020220000d 2RRx y A F r F dx F dy F xdx F ydy F R =⋅=+=+=⎰⎰⎰⎰⎰［ C ］2、（基础训练3）如图4-6，一质量为m 的物体，位于质量可以忽略的直立弹簧正上方高度为h 处，该物体从静止开始落向弹簧，若弹簧的劲度系数为k ，不考虑空气阻力，则物体下降过程中可能获得的最大动能是(A) mgh ． (B) kg m mgh 222-．(C) k g m mgh 222+． (D) kg m mgh 22+．【提示】 当合力为零时，动能最大，记为km E ，此时00, mgmg kx x k==；以弹簧原长处作为重力势能和弹性势能的零点，根据机械能守恒，有：20012km mgh E kx mgx =+-，求解即得答案。

［ B ］3、（基础训练6）一质点由原点从静止出发沿x 轴运动，它在运动过程中受到指向原点的力作用，此力的大小正比于它与原点的距离，比例系数为k ．那么当质点离开原点为x 时，它相对原点的势能值是(A) 221kx -． (B) 221kx ． (C) 2kx -． (D) 2kx ． 【提示】依题意，F kx =-，x = 0处为势能零点，则021()2p xE kx dx kx =-=⎰［ B ］4、（自测提高2）质量为m ＝0.5 kg 的质点，在Oxy 坐标平面内运动，其运动方程为x ＝5t ，y =0.5t 2（SI ），从t = 2 s 到t = 4 s 这段时间内，外力对质点作的功为(A) 1.5 J ． (B) 3 J ． (C) 4.5 J ．(D) -1.5 J ．【提示】用动能定理求解。

第Ⅰ卷（选择题，共40分）一、本题共10小题，每小题4分，共40分，在每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确，全部选对的得4分，选不全的得2分，有选错或不答的得0分。

1．观察图一中烟囱冒出的烟和车上的小旗，关于甲、乙两车相对于房子的运动情况，下列 说法正确的是 （ ） A ．甲、乙两车一定向左运动 B ．甲、乙两车一定向右运动 C ．甲车可能运动，乙车向右运动 D ．甲车可能静止，乙车向左运动 2．如图二所示，在水平方向的匀强电场中，绝缘细线的一端固定在O 点，另一端系一带正电的小球在竖直平面内做圆周运动，小球所 受的电场力大小等于重力大小，比较a 、b 、 c 、d 这四点，小球（ ）A ．在最高点a 处动能较其他三点都小B ．在最低点c 处重力势能最小C ．在水平直径右端b 处机械能最大D ．在水平直径左端d 处总能量最大3．关于动物量和动能的以下说法中正确的是 （ ）A ．系统动量守恒的过程动能必定也守恒B ．系统动能守恒的过程动量必定也守恒C ．如果一个物体的动量保持不变，那么它的动能必然也不变D ．如果一个物体的动能保持不变，那么它的动能必然也不变 4．如图所示，P 、Q 是两个电量相等的异种电荷： 其中P 带正电，Q 带负电，O 是P 、Q 连线的 中点，MN 是线段PQ 的中垂线，PQ 与MN 所 在平面与纸面平行，有一磁场方向垂直于纸面， 一电子以初速度v o 一直沿直线MN 运动，则（ ）A ．磁场的方向垂直纸面向里B ．电子速度先增大后减少C ．电子做匀速直线运动D ．电子速度减少后增大5．如图四所示的甲、乙、丙三个电源的U —I 图线，甲和丙两图线平行，下列判断正确 的是（ ）A ．甲电源的电动势比乙大B ．乙电源的电动势和内阻都比丙电源大C．甲和丙电源的内阻相等D．甲电源内阻最大，丙电源内阻最小6．图五a、b所示的两个情景中，静水原先静止的甲、乙两船的质量相同、两船上的人的质量也分别相同。

习题四4-1 一宇航员要到离地球为5光年的星球去旅行，如果宇航员希望把这路程缩短为3光年，则他所乘的火箭相对于地球的速度应是多少？解 5光年是在地球上测得的原长，由于此长度相对宇航员也是高速运动的，所以他测得收缩了的长度为3光年. 即3=火箭相对于地球的速度应为45u c =4-2 一飞船以0.99c 的速率平行于地面飞行，宇航员测得此飞船的长度为400 m.. （1）地面上的观察者测得飞船长度是多少？（2）为了测得飞船的长度，地面上需要有两位观察者携带着两只同步钟同时站在飞船首尾两端处.那么这两位观察者相距多远？ （3）宇航员测得两位观察者相距多远？解（1）56.4(m)l l ===（2）这两位观察者需同时测量飞船首、尾的坐标，相减得到飞船长度，所以两位观察者相距是56.4 m.（3）地面上的两位观察者相距56.4 m ，这一距离在地面参考系中是原长，宇航员看地面是运动的，他测得地面上两位观察者相距为7.96(m)l l ===所以宇航员测得两位观察者相距7.96 m.4-3 已知π介子在其静止系中的半衰期为81.810s -⨯。

今有一束π介子以0.8u c =的速度离开加速器，试问，从实验室参考系看来，当π介子衰变一半时飞越了多长的距离？解：在π介子的静止系中，半衰期80 1.810s t -∆=⨯是本征时间。

由时间膨胀效应，实验室参考系中的观察者测得的同一过程所经历的时间为8310s t -∆==⨯因而飞行距离为7.2m d u t =∆=4-4 在某惯性系K 中，两事件发生在同一地点而时间相隔为4s 。

已知在另一惯性系'K 中，该两事件的时间间隔为6s，试问它们的空间间隔是多少？解：在K系中，04st∆=为本征时间，在'K系中的时间间隔为6st∆=两者的关系为t∆==所以259β=故两惯性系的相对速度为8110m su cβ-==⋅由洛伦兹变换，'K系中两事件的空间间隔为)k kx x u t'∆=∆+∆两件事在K系中发生在同一地点，因此有0kx∆=，故810mkx'∆==4-5 惯性系'K相对另一惯性系K沿x轴作匀速运动，取两坐标原点重合的时刻作为计时起点。