齿轮的分类与齿形曲线
- 格式:pps
- 大小:1.33 MB
- 文档页数:49




齿轮齿条分类
齿轮齿条的分类如下:
1. 按齿形:可分为直齿齿条和斜齿齿条,分别与直齿圆柱齿轮和斜齿圆柱齿轮配对使用。
2. 按齿线形状:可分为直齿、斜齿和曲线齿,其中最常用的是渐开线齿形。
3. 按制造工艺:可分为淬火、调质、研磨、铣齿、磨齿等。
4. 按精度等级:可分为1-13级精度。
5. 按结构:可分为内齿轮和外齿轮,其中内齿轮用于行星齿轮传动机构和齿轮联轴器等结构中。
6. 按轴线分布:可分为平行轴齿轮、相交轴齿轮和交错轴齿轮,其中交错轴齿轮包括蜗轮蜗杆和交错斜齿轮。
总的来说,齿轮齿条的分类方式多种多样,具体分类方式取决于不同的分类标准。






齿轮知识大全齿轮之种类:齿状有许多种类,依照齿轮轴性区分,有平行轴(parallel axis),直交轴(intersecting axis),错交轴(non-parallel and non-intersecting axis) 齿轮之分类齿轮之种类正,斜齿轮平行轴正,斜齿条内齿轮直交轴错交轴1.决定齿轮要传递多少的功率 P2.两配合的齿轮转速为何?N1, N23.算出速度比(velocity ratio)VR = N1 /N24.查表得模数大小(m),并使用最小且可能的齿数 N 代入式子去试验5.用速度比和pinion 齿数来决定 gear 的齿数N= VR×N16.由上可求得节圆直径D1 = m×N 1;D2 = m×N2 及中心轴距 C = (D1+D2)÷27.由上条件可计算出法向受力及切线速度 Vt 8.考虑齿面宽 F 及齿形系数u9.依据所需的负荷、硬度、弹性系数等机械性质,选择适当的材料伞形齿轮 Worm and Worm Wheel 95-99% 30-88% 95-99% 效率齿轮加工时的特殊用语: 1.齿形修整(tip relief)齿形修整有齿冠部份之修整及齿根部份之修整两种,大部分是轴类的齿冠修整较普遍使用,且一各国标准及齿轮级数不同,修整量也有不同.优点是可缓和干扰,降低噪音,增长齿轮寿命.但若修整量过大,将会发生咬合不良. 2.鼓形加工及削端加工鼓形加工及削端加工都是齿筋方向的修整方法.鼓形加工为使齿面之接触集中在齿幅之中央部位,而将齿筋修整成带有鼓形之状态,若鼓形加工过甚,对齿轮强度有不良影响.削端加工为将齿筋之两端轻微倒角,如此可得近似鼓形加工之效果. 3.扫外径及倒角(topping and semi-topping)以刀具加工齿轮时,顺便将齿轮外径削除称作 topping, 此种作法可降低外径偏差,削除齿尖所产生之毛边,增加美观.加工时将齿顶部份倒角切除,而没切削到外径,称做semi-topping , JIS 及DIN 规范各有不同.单件齿轮无法传达任何动力,至少要2个以上齿轮咬合一起才能传达动力. 1.一段减速机构速度传达比:Z1/Z2=N2/N1Z1:主动齿轮之齿数 Z2:被动齿轮之齿数 N1:主动齿轮之转数 N2:被动齿轮之转数速度传达比>1 增速齿轮机构速度传达比<1 减速齿轮机构速度传达比=1 等速齿轮机构此外,一段齿轮机构尚有齿条与正齿轮之组合(Rack and Pinion) 2.2段齿轮机构2段齿轮机够为一段齿轮机构使用两组之情形,2.3游星齿轮机构游星齿轮机构,入力轴与出力轴成为同一直线,另配置两个以上之游星齿轮,故可以分担负荷,所以游星齿轮机构,能缩小减速机的体积.但游星齿轮机构,结构复杂,加工精度要求高,又有内齿轮干扰问题,这是它的缺点.模数:表示齿轮轮齿大小的一个指标,一对咬合的齿轮其模数必需一致,否则两齿轮的轮齿规格不同,无法平顺的运转。
齿轮的齿形齿轮的齿形使用在产业机械上的齿轮大部分是渐开线齿形。
渐开线齿形的普及是因为这种齿形具有容易使用等许多优点。
渐开线齿形的特长加工工具制作容易(直线齿条齿形)即使中心距略有偏差仍可圆滑的旋转传动只要模数, 压力角相同, 可以使用同一工具加工齿数不同的齿轮。
什么是渐开线齿形?渐开线齿形(曲线)是由基圆( db )做出的曲线。
将缠绕在基圆圆柱上的线在绷紧状态下逐渐放开, 此时线的先端所描画出的曲线即为渐开线曲线。
(A - b - c - d - e)图中所示为圆周的 1/4, 90°部分,线的先端所描画的曲线。
图 3.1 渐开线曲线什么是基圆?正如其名,基圆是形成渐开线曲线的基础圆。
基圆的大小取决于压力角(α)和分度圆( d )的大小。
db = d cos α(3.1)基圆是形成渐开线齿形的基础圆。
分度圆是决定齿轮大小的基准圆。
基圆 / 分度圆是齿轮的重要几何尺寸。
渐开线齿形是在基圆的外侧形成的曲线。
在基圆上压力角为零度。
渐开线齿轮的啮合两个标准的渐开线齿轮的分度圆在标准的中心距下相切啮合。
两轮啮合时的模样,看上去就像是分度圆直径大小为 d1 , d2 的两个摩抆轮(Friction wheels)在传动。
但是,实际上渐开线齿轮的啮合取决于基圆而不是分度圆。
这就像将皮带交叉地套在两个基圆的外周上做旋转运动传递动力一样。
皮带驱动的场合, 当摩抆力小于传动力时, 皮带与皮带轮间产生滑动。
而使用齿轮的场合,因为轮齿的存在, 所以能不产生滑动确实地做旋转运动并传动动力。
基圆的公切线 A - B 被称为啮合线。
图 3.2 动力的传动两个齿轮齿形的啮合接触点按 P1 → P2 → P3 的顺序在啮合线上移动。
请注意驱动齿轮中黄色的轮齿。
这个齿开始啮合后的一段时间内,齿轮为两齿啮合。
(P1/P3)啮合继续,当啮合点移动到分度圆上的点 P2 时, 啮合轮齿只剩下了一个。
啮合继续进行, 啮合点移动到点 P3 时, 下一个轮齿开始在 P1 点啮合, 再次形成两齿啮合的状态。
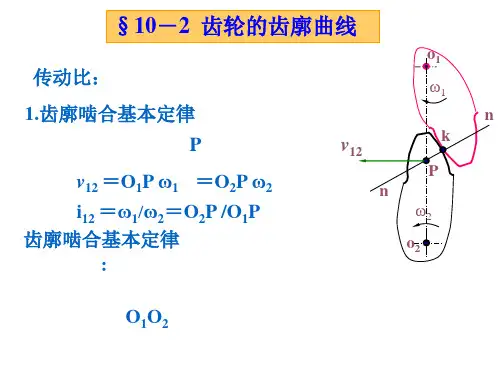
凡是满足齿廓啮合基本定律的一对齿廓称为共轭齿廓,论上可以作为共轭齿廓的曲线有很多种,但是考虑到设计、制造、测量、安装及使用等问题,目前常用的齿廓曲线有渐开线、摆线和圆弧等。
齿轮如果要能够有效率的传输动力就应该避免接触面的滑动摩擦而使用滚动摩擦. 在这个前提之下就不是所有的共軛曲线可以达成的. 其中最佳的就是渐开线与摆线. 这也就是为什么近代的齿轮都採用这两种设计的理由。
渐开线齿轮压力角在旋转的全程都为一定值. 这意味著渐开线齿轮的主动齿轮在推动从动齿轮个时候. 推动的力量与方向始终保持不变. 所以传输动力的大小相当稳定. 可是主动齿轮虽然保持著稳定的角速度. 但传到从动齿轮时虽然接触点通过每一齿的时间相同. (也就是每一齿的角速度相同). 但是在这一齿的角度中如果再分成10段. 则每一段的角速度就有差别。
所以如果把渐开线齿轮用在天文望远镜的角度调整上. 手调的主动齿轮为10齿. 旋转角度的被动齿轮为360齿. 那么在理论上手调的主动齿轮旋过1齿. 照理说从动应该转0.1度. 但实际上因为旋转的角度已经低于1齿. 因此角度并不正确. 这也就是为什么所有必须利用齿轮系精确调整角度的各种观测仪器仍然必须维持使用摆线齿轮的原因. 但是摆线齿轮的压力角在旋转中不稳定. 如果用来做为传动系统. 在每一齿的旋转传动中力量会忽大忽小. 不但造成转动的振动. 也对轴承造成伤害. 所以动力的传动都是使用渐开线齿轮. 渐开线齿轮的角速度稳不定. 而且齿数越少越严重. 因此渐开线齿轮很少低于16齿. 大动力机械传动用最小的我见过12齿. 传动不是那么重要的玩具一般不会低于9齿. 不过这只是传动考量的次要因素. 齿数越少的齿轮齿根越薄就越容易断裂.。
摆线齿轮的概念摆线齿轮是一种特殊类型的齿轮,其齿形曲线是一条摆线曲线。
摆线齿轮是由摆线生成器驱动的,它使得齿轮的转速和传递力矩保持恒定,同时也能提供平滑的传动。
摆线齿轮的概念最早由奥地利工程师Joseph Hermann Widmann 在1830年提出,并于1836年获得专利。
他的目标是开发一种平滑运动的齿轮,可以减少噪音和摩擦损失,并提高传动效率。
摆线齿轮的齿形曲线是一条特殊的数学曲线,它的形状类似于周期性变化的正弦波。
这种曲线具有具有非常平滑的形状,可以让齿轮在接触点的相对速度始终保持一致。
在传统的齿轮设计中,齿顶和齿谷处的接触点速度会有突变,这会导致齿轮传动中的冲击和噪音。
而摆线齿轮通过摆线生成器产生的曲线,在接触点速度的变化上比传统齿轮更加平滑,从而减少了冲击和噪音。
摆线齿轮的传动原理是通过在传动过程中齿的相对速度始终保持一致,从而实现平稳的传动。
这是因为摆线齿轮的齿形曲线在接触点处的切线始终与切向速度方向相切。
这种设计可以避免齿轮之间的相对滑动,减少了能量损失和摩擦。
摆线齿轮通常用于一些要求高精度和平稳传动的应用领域。
例如,摆线齿轮常被用于钟表、计时器、传输装置等精密机械中。
由于其传动过程平稳,因此可以减少噪音和振动,并延长传动系统的寿命。
另外,摆线齿轮还可以实现非整数传动比。
这意味着它可以用来传递复杂的运动关系,如调整机构和编织机器等。
摆线齿轮的非整数传动比可以通过改变齿轮的齿数、曲线的形状和齿轮之间的间隙来实现。
总结来说,摆线齿轮是一种利用摆线曲线齿形来实现平稳传动的特殊齿轮。
它具有平稳、高效、低噪音等优点,常被用于要求高精度和平稳传动的领域。
摆线齿轮不仅技术成熟,而且在一些特殊应用中具有独特的优势。