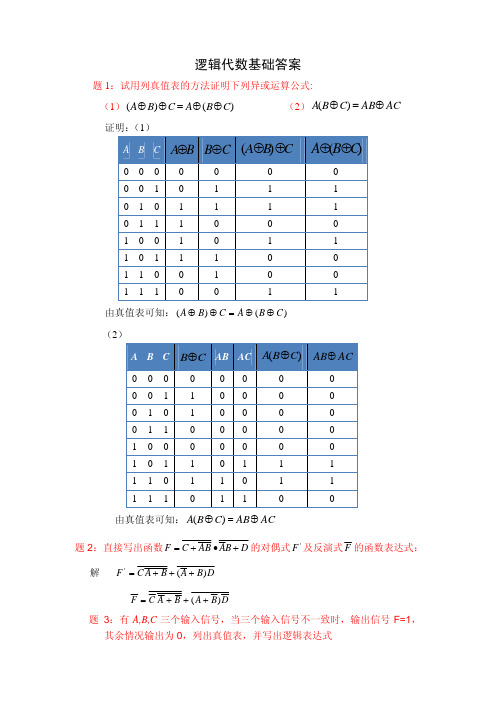
试用列真值表的方法证明下列异或运算公式

习 题 一1.1 把下列不同进制数写成按权展开形式。

（1） （3） 10) 267.3825 (8) 247.536 ( （2）（4）2) 1011.10101 (16) 24.D87 (A 1.2 将下列二进制数转换为等值的十六进制数和等值的十进制数。

（1） （2） （3）2)110010111(2)1101.0(2)101.1101(1.3 将下列十进制数转换成等效的二进制数和等效的十六进制数。

要求二进制数保留小数点以后4位有效数字。

（1） （2） （3） 10)156(10)39.0(10)67.82(1.4 将下列十六进制数化为等值的二进制数和等值的十进制数。

（1） （2） （3） （4） 16)5(B 16).3(CE B 16).7(FF F 16)00.10(1.5 完成下列二进制表达式的运算。

（1）10111+101.1O1 （3）10.0l ×1.01（2）1100-111.011 （4）1001.0001÷11.1011.6 已知010011.010111.01011010114321-=+=-=+=N N N N ，，，，试分别求出在8位机中它们的原码、反码和补码表示。

1.7 用原码、反码和补码完成如下运算。

（1）0000101-0011010 （2）010110-0.100110 1.8 将下列8421码转换成十进制数和二进制数。

BCD （1）011010000011 （2）01000101.1001 1.9 试用余3码和格雷码分别表示下列各数。

BCD （1） （2）10) 695 (2) 10001101 (习 题 二2.1 试用列真值表的方法证明下列异或运算公式。

1)7()( )6()()( )5(1)4(0 )3(1 )2(0 )1(⊕⊕=⊕=⊕⊕=⊕⊕⊕=⊕⊕=⊕=⊕=⊕=⊕B A B A B A AC AB C B A C B A C B A A A A A A A A A2.2 已知逻辑函数的真值表如表P2.1(a)、(b)，试写出对应的逻辑函数式。

第四章数学命题的数学设计一、真值表1、否定（非）：, 设P为一个命题，称P为P的否定式，记作p，其真值表如2、合取：设p,q表示两个命题，用逻辑联结词“与”把它们连接起来成为一个新命题“p与q”，记作qp∧。

真值表如下：3、析取：设p,q表示两个命题，用逻辑联结词“或”把它们连接起来成为一个新命题“p或q”，记作qp∨。

真值表如下：4、蕴涵（如果、、、那么、、、）：设p,q表示两个命题，用“如果、、、那么、、、”把它们连接起来成为一个新命题“如果p,那么q”，记作qp→。

真值表如下：5、当且仅当（等价式）：设p,q 表示两个命题，把q p ↔称为p,q 的等价式，其真值表如下真值表的作用证明重言式、两个命题等价，解决逻辑推理问题 例1 q p q p ∨≡∧例2 q p q p ∨≡→其真值表如下：三、推理规则1、合取规则：p 为真q 为真, q p ∧也为真。

2、分离规则：q p →为真，p 为真，q 也为真（充分条件假言规则）。

3、全称命题为真，则特称命题也为真。

4、r p ,,→→→则r q q p 。

5、是恒真命题r p r q q p ↔→↔∧↔)()(。

6、q(T) (T) p q(T)p ↔7、qp p q q p ↔→→8、(T)p (T) )(q T q p →（否定规则）9、pq q p →→10、(T)q (T) )(p T q p ∨（选言规则）11、qqp p q p ∧∧或（联言规则）12、三段论：推理形式为如果M 是P,S 是M,那么S 是P 。

它的逻辑式为：)()()(P S M S P M →→→∧→。

由真值表可知：)()()(P S M S P M →→→∧→1≡是恒真命题。

凡是恒真命题（重言式）都可作为推理规则。

前面提到的分离规则1)(≡→∧→q p q p ，选言规则1)(≡→∧∨q p q p ，联言规则1)(≡→∧p q p ，也都是恒真命题。

分别证明如下：11)()(31)()()()(21)()()()()(1≡∨≡∨∨≡∨∧≡→∧≡∨∨∨≡∨∧∨≡→∧∨≡∨∨∨≡∨∧∨≡∧∨≡→∧→q p q p p q p p q p q p q p q p q p q p q p q p q p q p q p p q p q q p 、、、四、证明方法1、直接证明：直接从所给论题入手，以公理、定义、定理等为论据，运用逻辑推理规则来论证论题为真的证明方法。

【题2.1】试用真值表的方法证明下列异或运算公式。

（1）A⊕0=A（2）A⊕1=A’（3）A⊕A=0（4）A⊕A’=1（5）(A⊕B)⊕C=A⊕(B⊕C)（6）A(B⊕C)=AB⊕AC（7）A⊕B’=(A⊕B)’=A⊕B⊕1【题2.2】证明下列逻辑恒等式（方法不限）（1）AB’+B+A’B=A+B（2）(A+C’)(B+D)(B+D’)=AB+BC’（3）((A+B+C’)C’D)+(B+C’)(AB’D+B’C’)=1（4）A’B’C’+A(B+C)+BC=(AB’C’+A’B’C+A’BC’)【题2.3】已知逻辑函数Y1和Y2的真值表如表P2.3(a)、P2.3(a)【题2.4】已知逻辑函数和的真值表如表P2.4(a)、（b）所示，试写出对应的逻辑函数式。

P2.4(b)【题2.5】列出下列逻辑函数的真值表。

（1）Y1=A’B+BC+ACD’（2）Y2=A’B’CD’+(B⊕C)’D+AD【题2.10】将下列各函数式化为最小项之和的形式。

（1）Y=A’BC+AC+B’C （2）Y=AB’C’D+BCD+A’D（2）Y=A+B+CD （4）Y=AB+((BC)’(C’+D’))’（5）Y=LM’+MN’+NL’（6）Y=((A⊙B)(C⊙D))’【题2.15】用卡诺图化简法化简以下逻辑函数（1）Y1=C+ABC（2）Y2=AB’C+BC+A’BC’D（3）Y3(A,B,C)=∑m（1，2，3，7）（4）Y4(A,B,C,D)=∑m（0，1，2，3，4，6，8，9，10，11，14）【题2.27】将下列逻辑函数化为或非—或非形式，并画出全部用或非逻辑单元组成的逻辑电路图。

（1）Y=AB’C+BC’（2）Y=(A+C)(A’+B+C’)(A’+B’+C)（3）Y=(ABC’+B’C)’D’+A’B’D（4）Y=((CD’)’(BC)’(ABC)’D’)’。

1.在数字系统中为什么要采用二进制？答案：因为数字信号有在时间和幅值上离散的特点，它正好可以用二进制的1和0来表示两种不同的状态。

难度：2 知识点：数字电路的基础知识（数字信号的特点）2.格雷码的特点是什么？为什么说它是可靠性代码？答案：格雷码的任意两组相邻代码之间只有一位不同，其余各位都相同，它是一种循环码。

这个特性使它在形成和传输过程中可能引起的错误较少，因此称之为可靠性代码。

难度：2 知识点：数字电路的基础知识码制格雷码的特点3.奇偶校验码的特点是什么？为什么说它是可靠性代码？答案：奇偶校验码可校验二进制信息在传送过程中1的个数为奇数还是偶数，从而发现可能出现的错误。

难度：2 知识点：数字电路的基础知识码制奇偶校验码的特点4. 逻辑代数与普通代数有何异同？答案：都有输入、输出变量，都有运算符号，且有形式上相似的某些定理，但逻辑变量的取值只能有0和1两种，而普通代数不限，且运算符号所代表的意义不同。

难度： 3 知识点：数字电路的基础知识逻辑代数与普通代数的区别5. 逻辑函数的三种表示方法如何相互转换？答案：通常从真值表容易写出最小项表达式，从逻辑图易于逐级推导出逻辑表达式，从与或表达式或最小项表达式易于列出真值表。

难度：3 知识点：数字电路的基础知识逻辑函数表示方法转换6. 为什么说逻辑等式都可以用真值表证明？答案：因为真值表具有唯一性。

难度：1 知识点：数字电路的基础知识逻辑等式与真值表7. 对偶规则有什么用处？答案：可使公式的推导和记忆减少一半，有时可利于将或与表达式化简。

难度： 2 知识点：数字电路的基础知识逻辑代数的基本定理对偶规则8. 将下列二进制数化为等值的十进制数：(1)（1011010）B (2) (110.110)B(3) (111001.1011)B答案：(1)（1011010）B =（90）D(2) (110.110)B =（6.75）D(3) (111001.1011)B =（57.6875）D难度：2 知识点：数字电路的基础知识数制的转换二/ 十进制转换9.将下列十六进制数化为等值的十进制数：(1)（78.8）H (2)（3AE.6B）H(3)（9ABCD）H答案：(1)（78.8）H =（120.5）D(2)（3AE.6B）H =（942.41796875）D(3)（9ABCD）H =（9×164+10×163+11×162+12×161+13×160）D难度：3 知识点：数字电路的基础知识数制的转换十六进制/十进制转换10.将下列十进制数化为等值的二进制数：(1)（748）D (2)（75.75）D(3)（108.85）D答案：(1)（748）D =（1011101100）B(2)（75.75）D =（1001011.11）B(3)（108.85）D =（1101100.11011001）B难度：3 知识点：数字电路的基础知识数制的转换十/二进制转换11.将下列十进制数化为等值的十六进制数：(1)（748）D (2)（75.75）D(3)（108.85）D答案：(1)（748）D =（2EC）H(2)（75.75）D =（4B.C）H(3)（108.85）D =（6C.D9）H难度：3 知识点：数字电路的基础知识数制的转换十/十六进制转换12.将下列二进制数化为等值的十六进制数：(1)（110111101001）B (2)（101101101.1101101）B(3)（110101.110）B答案：(1)（110111101001）B =（DE9）H(2)（101101101.1101101）B =（16D.DA）H(3)（110101.110）B =（35.C）H难度：3 知识点：数字电路的基础知识数制的转换二/十六进制转换13.将下列十六进制数化为等值的二进制数：(1)（8A7B6C）H , (2)（123EF.567）H, (3) (ABCD.789)H答案：(1)（8A7B6C）H =（1000 1010 0111 1011 0110 1100）B(2)（123EF.567）H =（0001 0010 0011 1110 1111 0101 0110 0111）B(3) (ABCD.789)H =（1010 1011 1100 1101.0111 1000 1001）B难度：3 知识点：数字电路的基础知识数制的转换十六/二进制转换14.写出下列BCD码对应的十进制数：(1)（10000111011001010100）8421BCD(2)（10010011.10000011）8421BCD(3)（100001110101.10010011）余3码答案：(1)（10000111011001010100）8421BCD =（87654）D(2)（10010011.10000011）8421BCD = （93.83）D(3)（100001110101.10010011）余3码=（542.60）D难度：4 知识点：数字电路的基础知识数制的转换BCD码/十进制数转换15.写出下列十进制数的8421BCD 代码：(1)（345678）D (2)（789.123）D(3)（108.206）D答案：(1)（345678）D =（0011 0100 0101 0110 0111 1000）8421BCD(2)（789.123）D =（0111 1000 1001.0001 0010 0011）8421BCD(3)（108.206）D =（0001 0000 1000.0010 0000 0110）8421BCD难度：3 知识点：数字电路的基础知识数制的转换十进制数/BCD码转换16.将下列8421BCD码转换位二进制数：(1)（000100100011.01000101）8421BCD(2)（011001111000）8421BCD答案：(1)（000100100011.01000101）8421BCD=（123.45）D=（111 1011.0111）B(2)（011001111000）8421BCD =（678）D=（10 1010 0110）B难度：3 知识点：数字电路的基础知识数制的转换BCD码/二进制数转换17.列出逻辑函数DACBCBAY++=的真值表。

第二章2.2 证明下列异或运算公式（1）A0A证明：左侧A0 A 0A得证（2）A1A证明：左侧 A 1 A 1A得证（3）A A0证明：左侧 A A A A得证（4）AA A证明：左侧 A A A AA得证（5）ABAB证明：右侧A B A BA B A BA B得证(6)(A B) C A (B C)证明：等式右侧 A (B C) A (BC BC)A(BC BC) A (BC BC)A(BC BC) A BC A BCA (B C)( B C)ABC A BCA (BB BC BC CC)ABC ABCABC ABC ABC ABC(A B AB)C (AB A B)C(A B)C (A B)C（将看成一个整体 (A B) ，用M来表示MC MCM C再替换 M ，则）(A B)C得证2.3 用逻辑代数法将下列逻辑函数式化简为最简与或表达式（1） L=AB(BC+A)解： L=AB(BC+A)=ABC+AB=AB(C+1)=AB(2)L=AB AB B解：L= AB AB B= AB (A1)B=AB B=AB B+A=A+B(3)L A ABC ABC BC BC解： L A ABC ABC BC BCA（1 BC ABC） C（B B）A C(4)L A B BD DCE AD解： L AB （A B）D DCEA B A BD DCEA B D DCEA B D (1CE)A B D(5)L( A B)AB A B AB解： L( A B)( A B)AB(A B)ABA B AB ABA B AB AB ABA (B B)B(A A )A B(6)L (A B C) (D E)(A B C DE )解： L(A B C) (D E)(A B C DE)（( A B C)(D E)）(ABC DE )（A BC DE）(ABC DE )（0 DE( ABC ) ABCDE DE )DE2.4 已知函数L(A ,B,C)ABC ABC ABC 。

异或的运算公式异或（Exclusive OR，简称 XOR）是一种逻辑运算，在数学和计算机科学中都有着广泛的应用。

异或运算的公式看起来可能有点复杂，但其实理解起来并不难。

咱们先来说说异或运算的定义。

异或运算对于两个操作数，如果它们相同则结果为0 ，如果它们不同则结果为1 。

用数学符号表示就是：若 a 和 b 是两个二进制数，那么 a ⊕ b = (a 且非 b) 或 (非 a 且 b) 。

举个简单的例子来说明一下，比如 0101 ⊕ 1010 ，从右往左依次比较每一位。

第一位是 1 和 0 ，不同，所以结果的第一位是 1 ；第二位是 0 和 1 ，不同，结果的第二位也是 1 ；第三位是 1 和 0 ，不同，结果的第三位还是 1 ；第四位是 0 和 1 ，不同，结果的第四位同样是 1 。

所以 0101 ⊕ 1010 的结果就是 1111 。

我记得之前在给学生们讲这个知识点的时候，有个小同学瞪着大眼睛一脸疑惑地问我：“老师，这异或运算到底有啥用啊？”我笑着跟他说：“别着急，咱们来做个小游戏。

”我拿出了一些卡片，上面写着不同的二进制数字，然后让同学们两两一组，通过异或运算来找出卡片中的“特殊数字”。

比如说，有三张卡片分别写着 0110 、 1001 和 0101 ，通过两两进行异或运算，就能发现0101 与另外两个数字的运算结果都不同，从而找出这个“特殊数字”。

同学们玩得可开心了，在游戏中也渐渐明白了异或运算的作用。

再来说说异或运算的一些性质。

异或运算满足交换律和结合律，也就是说 a ⊕ b = b ⊕ a ， (a ⊕ b) ⊕ c = a ⊕ (b ⊕ c) 。

这就好比我们换座位，不管怎么换，最终的排列组合效果是一样的。

在计算机编程中，异或运算常常被用来进行简单的加密和解密。

比如说，我们有一段明文信息，通过与一个特定的密钥进行异或运算，就可以得到密文。

接收方再用相同的密钥进行异或运算，就能还原出明文。

第20章习题 门电路和组合逻辑电路S10101B为实现图逻辑表达式的功能，请将TTL 电路多余输入端C 进行处理（只需一种处理方法），Y 1的C 端应接 ，Y 2的C 端应接 ，解：接地、悬空S10203G在F = AB +CD 的真值表中，F =1的状态有( )。

A. 2个 B. 4个 C. 3个 D. 7个 解：DS10203N某与非门有A 、B 、C 三个输入变量，当B =1时，其输出为( )。

A. 0 B. 1 C. D. AC 解：CS10204B在数字电路中，晶体管的工作状态为( )。

A. 饱和 B. 放大 C. 饱和或放大 D. 饱和或截止 解：DS10204I逻辑电路如图所示，其逻辑函数式为( )。

A. B.C. D.解：CS10204N已知F =AB +CD ，选出下列可以肯定使F = 0的情况( )。

A. A = 0，BC = 1 B. B = C = 1 C. C = 1，D = 0 D. AB = 0，CD = 0 解：DS10110B三态门电路的三种可能的输出状态是 ， ， 。

解：逻辑1、逻辑0、高阻态S10214B逻辑图和输入A ，B 的波形如图所示，分析当输出F 为“1”的时刻应是( )。

A. t 1B. t 2C. t 3解：AYS10211I图示逻辑电路的逻辑式为( )。

A. B. C. 解：BS10212I逻辑电路如图所示，其功能相当于一个( )。

A. 门B. 与非门C. 异或门 解：CS10216B图示逻辑电路的逻辑式为( )。

A. A +BB.C. AB + 解：CS10217B逻辑图如图（a ）所示，输入A 、B 的波形如图（b ），试分析在t 1瞬间输出F 为( )。

A. “1”B. “0”C. 不定 解：BS10218B图示逻辑符号的逻辑状态表为( )。

A. B. C.解：BS10219B逻辑图和输入A的波形如图所示，输出F的波形为( )。