第十三讲总纵强度计算实例.

第一章 总纵强度计算外力的确定§1.1船舶在静水中的剪力和弯矩一、概述1. 计算模型：自由-自由梁承受垂向载荷（两端处的N M ==0）[图示坐标系、载荷曲线以及微元体受力平衡]2. 静水载荷：q x w x b x ()()()=−单位长度垂向力重力浮力q x w x b x ()()()=−3. 静水剪力和弯矩（符号惯例同“结构力学”）由平衡状态下 w x b x ()()⎧⎨⎩⎫⎬⎭⇒q x ()⎯⎯⎯⎯⎯⎯⎯→N x M x ()()⎧⎨⎩⎫⎬⎭⎯边界条件微元体平衡ξ，可以采用以下2种方法之一计算（设x 轴原点取在船艉）： (1)积分法N x q x dxM x N x dx q x dx x q d x x x x x()()()()()()()====−⎧⎨⎪⎩⎪∫∫∫∫∫002000ξξ 说明：①当载荷分段解析时，相应的积分也需要分段进行；②式中的积分亦可由相应曲线下的面积表示。

(2)截面法取艉端至指定截面的一段船体为“隔离体”，根据平衡条件确定截面的剪力和弯矩。

二、重量曲线1. 船体重量组成——全船性重量、局部性重量（参阅书图1-3）2. 绘制重量曲线w x ()的方法和应遵循的原则 (1)绘制方法——先分后合[分：将船体重量划分为全船性重量与若干项局部性重量，分别处理；合：在同一站距内合并各项重量](2)原则静力等效（重量及重心纵向位置保持不变）分布范围大体一致⎧⎨⎩3. 举例（静力等效原则可以提供2个方程式） 例1：全船性重量（参阅书图1-5）[3个待定参数abc；静力等效原则可以提供2个方程式（应用负面积法）；根据统计资料直接给出b]例2：局部性重量（参阅书图1-6）[静力等效2条件→，P q L 11=ΔP q L 22=Δ]三、浮力曲线1. 对问题的分析（图示）⎯⎯⎯⎯⎯⎯←⎯⎯⎯⎯⎯←=)()()()()(图平衡水线图邦戎曲线：：剖面吃水船体单位长度浮力WL x d x x b γω⎭⎬⎫⎩⎨⎧⎯⎯⎯⎯⎯⎯⎯⎯←型值表）邦戎曲线（或型线图或），全船重量及重心位置（（浮态）船体在静水中平衡位置重力与浮力平衡条件g x W 2. 确定平衡水线的原理和方法(1)原理：全船重力与浮力相平衡（2个平衡方程）求解关于首、尾吃水和的（非线性）联立方程：d f d a f d d f d d f a f a1100(,)(,)==⎧⎨⎪⎩⎪ (2)逐步近似法（调整“倾差”）——求解上述联立方程的数值方法之一 ①等容倾斜原理：船体绕漂心F(水线面之形心)旋转任意角ψ（ψψ≈≈−tan x x Rg bm a ），其排水体积保持不变。

第二章船体总纵强度的计算知识点1剖面模数W=I/Z意义：表征船体抵抗弯曲变形能力的一种几何特性。

最小剖面模数——离中和轴最远的构件（最上层连续甲板即强力甲板；船底。

但船底离中和轴更近，则强力甲板处为最小剖面模数处，弯曲正应力最大）知识点2校核时候取危险剖面，即可能出现最大正应力的面（船中0.4倍船长范围内）。

危险剖面指：骨架式改变处剖面，材料分布变化处，上层建筑端壁处剖面）知识点3（填空）强度等值梁：有效参与弯曲的全部构件组成的梁，该梁在抵抗总弯曲和总纵强度性能上和船体等效。

纵向强力构件：纵向连续并能有效传递总弯曲应力的构件。

（可以计入船体梁的计算中，如船中0.4-0.5倍船长连续纵向构件）（间断构件看看即可，具体使用应该参考规范）知识点4剖面模数及第一次近似总纵弯曲应力计算过程（课件第二章15-21页）看看即可。

知识点5（简答）为什么要校核船体构件的稳定性？A．所有受压的甲板板列，与其他刚性构件相连的一部分完全有效。

B．而其余部分不能承受大于板极限载荷的压力。

C．不是所有纵向强力构件都完全有效参与抵抗总纵弯曲。

D．对船体结构的要求，既应该保证必要的强度，又要保证必要的稳定性。

（简答）怎样校核稳定性？计算临界应力：确定板的临界应力时的注意事项（课件45页）具体的计算方法：板的稳定性计算中只需记住一些简单的边界条件，不用记那些经验公式。

纵骨的稳定性计算只需记住当求得的欧拉应力超过材料的比例极限时要对欧拉应力进行修正，以考虑材料不服从虎克定律对稳定性的影响。

将实际应力与临界应力比较进行校核。

（填空）决定临界应力的条件：构建的几何尺寸、外力的作用方式、边界条件。

知识点6（判断）纵向骨架在计算载荷下不允许丧失稳定性，只有板可能失稳。

知识点7板的应力分布同一水平高度的应力沿着板宽分布不均匀，与纵向骨架相连的部分板宽内应力较高，而板宽的中间部分应力较低。

知识点8剖面折减将船体剖面中一部分失稳的板构件剖面积化为假想不失稳的刚性构件剖面积。

1一引起船体梁总纵弯曲的外力计算1 在船体总纵强度计算中，通常将船体理想化为一变断面的空心薄壁梁，简称船体梁。

船体梁在外力作用下沿其纵向铅垂面内所发生的弯曲，称为总纵弯曲。

船体梁抵抗总纵弯曲的能力，称为总纵强度。

2 船体总纵强度计算的传统方法：将船舶静置在波浪上，求船体梁横剖面上的剪力和弯曲力矩以及相应的应力，并将它与许用应力相比较以判断船体强度。

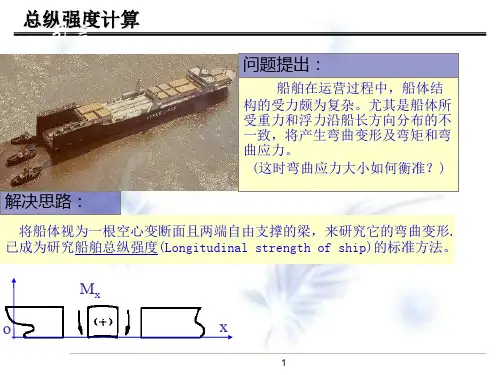
3 重力p(x)与浮力b(x)是引起船体梁总纵弯曲的主要外力。

载荷q(x)，剪力N(x)，弯矩M(x)。

4 中拱：船体梁中部向上拱起，首、尾两端向下垂。

中垂：船中部下垂，首、尾两端向上翘起。

5重量曲线：船舶在某一计算状态下，描述全船重量沿船长分布状况的曲线。

绘制重量曲线的方法：静力等效原则。

6 重量的分类：按变动情况来分，①不变重量，即空船重量，包括：船体结构、舾装设备、机电设备等各项固定重量。

②变动重量，即装载重量，包括货物、燃油、淡水、粮食、旅客、压载等各项可变重量。

按分布情况来分，①总体性重量，即沿船体梁全长分布的重量，通常包括：主体结构、油漆、锁具等各项重量。

②局部性重量，即沿船长某一区段分布的重量。

7 重量的分布原则：静力等效原则。

①保持重量的大小不变，这就是说要使近似分布曲线所围成的面积等于该项实际重量。

②保持重量重心的纵向坐标不变，即要使近似分布曲线所围的面积的形心纵坐标与该项重量的重心坐标相等。

③近似分布曲线的范围与该项重量的实际分布范围相同或大体相同。

8 浮力曲线：船舶在某一装载情况下，描述浮力沿船长分布状况的曲线29 载荷曲线：在某一计算状态下，描述引起船体梁总纵弯曲的载荷沿船长分布状况的曲线。

10 静水剪力、弯矩曲线：船体梁在静水中所受到的剪力和弯矩沿船长分布状况的曲线。

11 静波浪剪力和弯矩计算：船舶由静水进入波浪时，重量曲线p(x)并未改变，但水面线发生了变化，从而导致浮力的重新分布。

波浪下浮力曲线相对静水状态的浮力增量是引起静波浪剪力和弯矩的载荷。

第二章 总纵强度计算§2-1船体总纵弯曲应力第一次近似计算一、危险剖面的选择危险剖面：可能出现最大弯曲应力的剖面，由总纵弯曲力矩曲线可知，最大弯矩一般在船中0.4倍船长范围的，所以计算剖面一般应是此范围内的最弱剖面—既有最大的船口或其电开口的剖面，如机舱、货舱开口剖面。

除此之外，一般还要对船体骨架改变处剖面，上层建筑端壁处剖面，主体材料分布变化处剖面，以及由于重量分布特殊可能出现相当大的弯矩值的某些剖面。

二、纵向强力构件 1、 1、 纵向强力构件纵向连续并能有效的传递总纵弯曲应力的构件。

船中0.4~0.5倍船长区域内连续的纵向构件，上甲板板、外板、内底板、纵桁、中内龙骨等都是纵向强力构件。

船中非连续构件参加总纵弯曲的有效性取决于本身的长度及与主体的连续情况。

（1）、构件连续长度≥3h 计算剖面船口纵围板、纵桁等纵向构件可计入船体梁剖面计算中，但除外机座纵桁和其它加强纵桁不应计入。

（2）、构件长度L %15 的上层建筑。

（3）、不少于三个横舱壁或类似结构支柱的长甲板室。

2、 2、 间断构件（1）、相临舱口甲板。

（2）、纵桁板上的H h %20 的开口。

三、剖面模数及剖面要素计算 1、 1、 不同材料剖面面积折算根据变形相等的条件，承受相同的力P 即在计算时，可以船体梁仅由一种基本材料构件，而把与基本材料弹性横量E 不同和构件剖面面积乘以两材料的弹性横量之比E E i，同时又不改形心位置。

因此，对薄壁构件，相当于只对板厚作上述变换。

2、 2、 剖面要素的计算步骤（1）、画出船体计算剖面的剖面图并编号（i ）（2）、选定参数轴—离基线（0.45～0.5）型深处。

确定形心至参数轴距离（i Z ）。

（3）、计算剖面积（A ）、静力矩（B ）、惯性矩（C ）。

∑=i A A ∑=i i Z A B ∑+=)(02i Z A C i i（4）、求中和轴至参考轴的距离（ε）、任意构件至中和轴的距离（'i Z ）A B=εε-=i i Z Z '（5）、求对中和轴的惯性矩（I ）)(2)(222A B C A C I -=-=ε（6）、若甲板和船底距中和轴最远的距离分别为j Z 和d Z ，则甲板和船底的剖面模数分别为j j Z IW =d d Z I W =通常甲板的剖面模数比船底的剖面模数（d j W W <），所以有时也称j W 为船体的min W 。

第一章总纵强度计算外力的确定§1.1船舶在静水中的剪力和弯矩§1.2船舶静置于波浪中的剪力和弯矩§1.3船体波浪剪力和弯矩的数值计算§1.1船舶在静水中的剪力和弯矩一、概述二、重量曲线三、浮力曲线四、剪力弯矩的计算返回一、概述1. 计算模型：认为船舶是在重力和浮力作用下平衡于波浪上的一根梁q(x)=w(x)-b(x)q(x)单位长度垂向力；w(x)重力；b(x)浮力静水载荷、重力向下为正，浮力向上为正3、静水剪力和弯矩(1)剪力和弯矩符号，以下为一个船体梁断面建议大家复习一下微元体，由于选取的方式不同，将导致同一处的剪力或弯矩的大小相同，符号不同。

一般取左端面为准计算出剪力弯矩。

(2)积分法计算，设x 轴原点取在船艉⎪⎩⎪⎨⎧===∫∫∫∫dx dx x q dx x N x M q(x)dx x N x x00)()()()(计算思路：在平衡状态下，由w(x),b(x)得到q(x ）,通过微元体平衡，边界条件，得到N （x ）,M(x).返回二、重量曲线1. 船体重量组成—全船性重量、局部性重量一个重量分布曲线图2. 绘制重量曲线的方法——先分后合分：将船体重量划分为全船性重量与若干项局部性重量，分别处理；合：在同一站距内合并各项重量原则：a:静力等效—不改变重力大小及其对船肿的力矩大小。

b:分布范围大体一致全船性重量的分配方法1、围长法假设船体结构单位长度重量和剖面围长成比例。

A xlW xw h) () (⋅=船主体结构重量的总和，tfX剖面处围长，m船体全表面积2、抛物线法假定船体和舾装品构成的曲线可用抛物线和矩形之和表示。

总重量的一半作为均匀分布，另一半按抛物线分布。

用于无平行中体船。

3、梯形法重量分布用梯形曲线表示。

用于中间肥，两头尖瘦且中部有平行中体的船。

局部性重量的分布方法1、分布在两个理论站距内的重力⎩⎨⎧⋅=Δ⋅−+=aP L P P P P P 2/)(2121静力等效方程2、分布在三个理论站距内的重力先近似确定其中一个站距内的重力，然后可以比较简单地利用静力等效原则直接列出两个方程，从而求得不同理论站距内的分布载荷强度第一步：以1.5ΔL代替ΔL，使用静力等效方程求得P1、P2；第二步：将P1、P2分别向其相邻的两个理论站距内分布；最后，对中间理论站距迭加来自P1、P2的相应分布值。

FPSO总纵强度计算方法分析杨贵强【摘要】对常规运输船舶,一般用规范给出的经验公式进行评估,而FPSO因为船型、装载,尤其是必须承受的波浪条件与运输船舶显著不同,在恶劣海况下必须用直接计算法进行评估,概要介绍静水弯矩、波浪弯矩、横截面模数的计算方法,并给出FPSO工程计算实例.【期刊名称】《船海工程》【年(卷),期】2014(043)005【总页数】3页(P19-21)【关键词】FPSO;总纵强度;静水弯矩;波浪弯矩【作者】杨贵强【作者单位】中海油能源发展采油服务公司,天津300452【正文语种】中文【中图分类】U661.4为了保障FPSO在恶劣环境条件下作业和生存安全，必须具有足够的总纵强度。

航行船舶通常采用规范公式计算，钢质海船入级规范对于船舶的总纵强度计算有明确的规范公式计算方法，这些方法是以无限航区(北大西洋20年一遇的波浪条件)和过去成功的船舶设计实践为基础制定的，这也是FPSO初始设计的基础。

海洋工程结构一般采用直接计算法，即利用流体动力分析和详细的结构有限元分析。

两种计算方法在很多情况下结果差异很大，国际主要船级社普遍提高了对FPSO总纵强度的要求[1]。

1 总纵强度的概念通常把船体视为一变截面空心梁，沿船长方向作用着非均匀分布的重力和浮力以及流体扰动力。

总纵强度计算的主要工作是求解静水弯矩Ms、波浪弯矩Mw和船体横截面模数。

1)总弯矩Mt = Ms+Mw。

2)剖面模数W。

按船体舯剖面图给出的甲板、船底和舷侧以及纵舱壁板厚、纵向骨材的规格尺寸计算剖面模量。

3)许用应力[σ]。

规范规定：普通强度钢[σ]=175 MPa，FPSO通常采用的高强钢32[σ]=224 MPa，高强钢36[σ]=243 MPa。

4)应满足[σ]≥Mt/W条件。

2 静水弯矩2.1 主要因素影响由于重力和浮力分布不均匀而产生静水荷载、静水剪力和弯矩。

船体依靠水的浮力漂浮在水面上，水是船体梁的弹性基础。

计算时，假设船体静止在平静的水面上或波浪上。

2船体总纵强度计算船舶强度与结构设计第2章船体总纵强度计算根据梁弯曲理论：σ=M?Z I（2-1）对于一定计算状态，可求出作用于船体剖面上的弯矩M值。

为了计算剖面弯曲应力σ，还必须先计算剖面对水平中和轴的惯性矩I，以及剖面任意构件至水平中和轴的距离Z等剖面要素。

2.1 船体总纵弯曲应力第1次近似计算2.1.1 船体剖面要素计算由于船体结构对称于中纵剖面，一般只需对半个剖面进行剖面要素的计算。

具体步骤如下：首先，画出船体计算剖面的半剖面图，如图2-1所示。

然后，对纵向强力构件进行编号，并注意把所有至中和轴距离相同的构件列为一组进行编号；选取图2-1 船体横剖面图参考轴O′?O′，该轴可选在离基线0.45倍～0.50倍型深处。

最后，列表进行计算，并分别求出各组构件剖面积Ai，其形心位置至参考轴的距离Zi（按所选定的符号法则，在参考轴以上的构件Zi取为正），静力矩AiZi，惯性矩AiZi。

对于高度较大的垂向构件，如舷侧板等，还要计算其自身惯性矩i0=Aihi/12（hi为该构件的垂直高度，这种表达式也适用于倾斜板的剖面）。

则得：2219船舶强度与结构设计∑Ai=Ai（2-2）∑AZii=B 2i∑(AZ+i0)=C 剖面水平中和轴至参考轴的距离为：Δ=B(m) A（2-3）由移轴定理，剖面对水平中和轴的惯性矩为：B2I=2(C?ΔA)=2(C? （cm2 ·m2）A2（2-4）任意构件至中和轴的距离为：Zi′=Zi?Δ=Zi?B （m）A（2-5）最上层连续甲板和船底是船体剖面中离中和轴最远的构件，构成了船体梁的上下翼板。

构成船体梁上翼板的最上层连续甲板通常称为强力甲板。

设中和轴至强力甲板和船底的垂直距离分别为Zd和Zb，则强力甲板和船底处的剖面模数分别为：IIWd=，Wb= ZdZb（2-6）在一般船舶中，中和轴离船底较近，即Zd&gt;Zb，因此Wd&lt;Wb。

所以，有时也称强力甲板处剖面模数为船体剖面的最小剖面模数。