二阶低通滤波传递函数介绍
- 格式:doc
- 大小:173.50 KB
- 文档页数:4

二阶低通滤波器为了改进一阶低通滤波器的频率特性,可采用二阶低通滤波器。
一个二阶低通滤波器包含两个 如图所示为二阶低通滤波器的一般电路。
此一般电路对于二阶高通滤波器也同样适用。
图6—2-3所示的滤波器是同相 放大器。
在图6-2-3中,零频增益为気=!诗(6-2-5)在节点A 可得气打=叫(龄 + 耳 + FJ -u v Y 3-u n Y 2(6・24)在节点B 可得将式(6-2-8 )代人式(6-2-6),转变到复频域,可得一般二阶低通滤波器的传递函数为r ----- c oRC 支路,(6-2-7) (6 2呂)L;YR RATG(J )R KC仆3厲(&29)对于上图所示的二阶低通滤波器,其传递函数为在构成二阶低通滤波器时,只需选择巧,殇,蚝,%。
导纳的值即可。
例如,当选择 丫1 = 1/R 1 , 丫2 =1/R 2, Y3 = sC i Y 4=S C 2时,则构成图6 - 2 - 4所示的二阶低通滤波器门然角频率为(6-2-10)(6-242)式零频增益为粗尼系数为为了进一步简化计算,选取Q =C 2 = C.R, - = R.则式(6-2-14) ^(6-2-15)可进一步简化为1气=五f = 3 - G o采用频率归一化的方法.则上述二阶低通滤波器的传递函数为"VS 】如图6 -2 -5所示为二阶低通滤波器的幅频特性曲线,其阻带衰减特性的斜率为— 40dB / 10oct ,克服了一阶低通滤波器阻带衰减太慢的缺点。
二阶低通滤波器的各个参数,影响其滤波特性,如阻尼系数苫的大小,决定了幅频特性有无峰值,或 谐振峰的高低。
如图6 =2-6所示为苫对二阶低通滤波器幅频特性的影响。
GiwMdB) (6-243)为了简化计算■通常选G = C. = 式(6212人式(6213)可简化为1 c 7心阻(6-2-14) (6-2-15)(6-2-16) (6-2-17)(6*2-18)G(a))(dB)。
二阶低通滤波器为了改进一阶低通滤波器的频率待性,可采川二阶低通滤波器。
一个二阶低通滤波器包含两个RC 支路, 如图所示为二阶低通滤波器的•般虫路‘,此-•般电路对丁-二阶高通滤波器也同样适川。
图6-2-3所示的滤波器是同相放大器。
在图6—2—3中,零频增益为G 。
二 1 +普(625)在节点4可得叫人=你(齐+丫2 +岭)- %岭一叫岭=u A (y, + £ + «)-叭岭一晋(6-2-6)在节点B 可得« (人 + rj 叭岭二叫(均+岭)=亠才亠nt )it = --------- ---------- ------- —AG 必将式(6—2—8)代人式(6—2—6),转变到复频域,可得一般二阶低通滤波器的传递函数为(6-2-7) (6-2-8)在构成二阶低通滤波器时,只需选择巧,场,虹,%o 导纳的值即可。
例如,当选择Yi=1/Ri, 丫2 =1/R2, Y3=S GY4=S C2时,则构成图6-2-4所示的二阶低通滤波器。
对丁•上图所示的二阶低通滤波器,其传递两数为口然角频率为(6212)G(S )=特| :3($)■齐场 + + 匕 + 岭)+ Y 2Y.(\ -G O )(6-2-9)/($)式屮■零频增益为(6-2-10)(6211)G(eXdB)为了进一步简化计算,选取G = C 2 = C,R, = 则式(6-2-14).式(6・2・15)可进一步简化为I气一屁—3 - G 。
采用频率归一化的方法,则上述二阶低通滤波器的传递函数为如图6-2-5所示为二阶低通滤波器的輛频特性曲线,其阻带衰减特性的斜率为一40dB /10oct, 克服了一阶低通滤波器阻带衰减太慢的缺点。
二阶低通滤波器的各个参数,影响其滤波特性,如阻尼系数苫的大小,决定了幅频特性有无峰值,或 谐振峰的高低。
如图6=2-6所示为苫对二阶低通滤波器幅频特性的彩响。
阻尼系数为旺陌iR.C ;—加+J 斌"")、/证(6-2-13)(6-2-14) (6-2-15)(6-2-16) (6-2-17)(6-2-18)05G(®)(dB)。


简单二阶有源低通滤波器电路及幅频特性为了使输出电压在高频段以更快的速率下降,以改善滤波效果,再加一节RCo(1)通带增益当f=0时,各电容器可视为开路,通带内的增益为低通滤波环节,称为二阶有源滤波电路。
它比一阶低通滤波器的滤波效果更好二阶LPF的电路图如图6所示,幅频特性曲线如图7所示。
1-(2)二阶低通有源滤波器传递函数根据图8-2.06可以写出丄“盘斗丄〕俯二一礎通常有,联立求解以上三式,可得滤波器的传递函数臥)—九…(3)通带截止频率将s 换成j 3,令3 0 = 2n f o=1/(RC)可得当f=fp时,上式分母的模="丿厶I VoZ与理想的二阶波特图相比,在超过fO以后,幅频特性以-40 dB/dec的速率下降,比一阶的下降快。
但在通带截止频率fp -fO之间幅频特性下降的还不够快。
摘要设计一种压控电压源型二阶有源低通滤波电路,并利用MultisimIO仿真软件对电路的频率特性、特征参量等进行了仿真分析,仿真结果与理论设计一致,为有源滤波器的电路设计提供了EDA手段和依据。
关键词二阶有源低通滤波器;电路设计自动化;仿真分析;MultisimIO滤波器是一种使用信号通过而同时抑制无用频率信号的电子装置,在信息处理、数据传送和抑制干扰等自动控制、通信及其它电子系统中应用广泛。
滤波一般可分为有源滤波和无源滤波,有源滤波可以使幅频特性比较陡峭,而无源滤波设计简单易行,但幅频特性不如有源滤波器,而且体积较大。
从滤波器阶数可分为一阶和高阶,阶数越高,幅频特性越陡峭。
高阶滤波器通常可由一阶和二阶滤波器级联而成。
采用集成运放构成的RC有源滤波器具有输入阻抗高,输出阻抗低,可提供一定增益,截止频率可调等特点。
压控电压源型二阶低通滤波电路是有源滤波电路的重要一种,适合作为多级放大器的级联。
本文根据实际要求设计一种压控电压源型二阶有源低通滤波电路,采用EDA仿真软件Multisim1O对压控电压源型二阶有源低通滤波电路进行仿真分析、调试,从而实现电路的优化设计。

传递函数求截止频率截止频率是指在频率响应中,信号的幅度下降到原始幅度的一半的频率值。
在电子电路中,截止频率常常被用于描述滤波器的性能。
通过传递函数,可以通过数学方法求得截止频率。
传递函数是用来描述输入与输出之间关系的数学函数。
在滤波器中,传递函数可以表示为H(ω),其中ω是频率。
具体的计算截止频率的方法取决于滤波器的类型和传递函数的形式。
下面将介绍几种常见的滤波器类型及其传递函数,并讨论如何通过传递函数求得截止频率。
1.RC低通滤波器:RC低通滤波器是一种常见的电子滤波器,它可以通过一个电阻(R)和一个电容(C)组成。
其传递函数可以表示为:H(ω)=1/(1+jωRC)其中j是虚数单位。
对于RC低通滤波器,截止频率可以通过频率响应函数的幅度计算得出。
当传递函数的幅度下降到1/√2,即0.707倍时,对应的频率即为截止频率。
可以将传递函数的幅度表示为:H(ω),= sqrt(1 / (1 + (ωRC)^2))当,H(ω),=1/√2时,可以解得ωRC=1、因此,截止频率f_c=1/(2πRC)。
2.RL高通滤波器:类似地,RL高通滤波器可以通过一个电阻(R)和一个电感(L)组成。
其传递函数可以表示为:H(ω)=jωL/(jωL+R)对于RL高通滤波器,同样可以通过传递函数的幅度计算截止频率。
当传递函数的幅度下降到1/√2时,对应的频率即为截止频率。
传递函数的幅度可以表示为:H(ω),= sqrt((ωL)^2 / ((ωL)^2 + R^2))当,H(ω),=1/√2时,可以解得ωL=1、因此,截止频率f_c=1/(2πL)。
3.二阶巴特沃斯低通滤波器:二阶巴特沃斯低通滤波器是一种常用的滤波器,在无源滤波器设计中被广泛应用。
其传递函数可以表示为:H(ω)=1/((1+(jω/ω_c))^2)其中ω_c是截止角频率,与截止频率f_c之间有如下关系:ω_c=2πf_c。
对于二阶巴特沃斯低通滤波器,截止频率f_c与传递函数相关系数有关。

二阶低通滤波器参数计算摘要:一、引言二、二阶低通滤波器的定义和特点三、二阶低通滤波器参数的计算方法1.截止频率2.传递函数3.频率响应四、二阶低通滤波器参数计算的实际应用五、总结正文:一、引言在信号处理领域,滤波器是一种广泛应用的技术。
二阶低通滤波器是其中一种常见的滤波器类型,它的主要作用是在保留信号的低频部分的同时,衰减高频部分。
为了更好地理解和应用二阶低通滤波器,我们需要了解其参数计算方法。
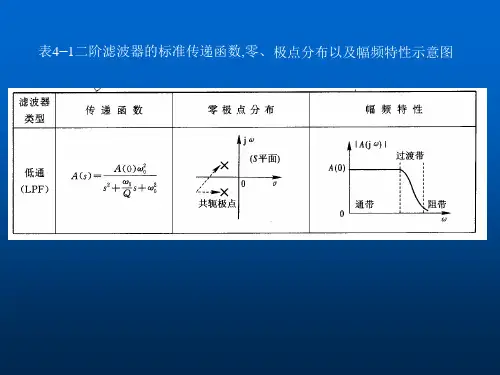
二、二阶低通滤波器的定义和特点二阶低通滤波器是一种具有两个极点的低通滤波器,它的传递函数为:H(s) = A(s) / (1 + ω_n^2s^2)。
其中,A(s) 是滤波器的幅频特性,ω_n 是滤波器的截止角频率,s 是复变量。
二阶低通滤波器的主要特点是,在截止频率ω_n 处,滤波器的幅频特性下降到一半。
三、二阶低通滤波器参数的计算方法1.截止频率截止频率ω_n 是二阶低通滤波器的关键参数,决定了滤波器能够通过的信号频率范围。
根据系统的物理特性(如电容、电感等)可以计算出截止频率ω_n。
2.传递函数二阶低通滤波器的传递函数H(s) 可以通过公式H(s) = A(s) / (1 +ω_n^2s^2) 计算。
其中,A(s) 是滤波器的幅频特性,可以通过对信号进行模拟滤波得到。
3.频率响应频率响应是描述滤波器对不同频率信号的处理效果的指标。
可以通过计算滤波器在各个频率点的幅频特性值,得到频率响应。
四、二阶低通滤波器参数计算的实际应用在实际应用中,二阶低通滤波器的参数计算可以帮助我们更好地设计和优化滤波器。
例如,在通信系统中,通过调整截止频率,可以实现对不同频率信号的滤波,从而提高信号质量。
五、总结本文介绍了二阶低通滤波器的参数计算方法,包括截止频率、传递函数和频率响应。
这些计算方法对于理解和应用二阶低通滤波器具有重要意义。

二阶低通滤波器标准形式低通滤波器是一种信号处理器件,它可以使通过的信号频率低于截止频率的信号通过,而高于截止频率的信号被抑制。
在实际应用中,常常使用二阶低通滤波器来实现这一功能。
二阶低通滤波器是指其传递函数具有二次多项式的形式。
标准形式是指传递函数可以化简为一个正规的、无平方项的形式。
这种形式的好处是可以方便地设计和分析滤波器的性能。
在二阶低通滤波器的标准形式中,其传递函数可以表示为以下形式:H(s) = K / (s^2 + s/Q + 1)其中,H(s)表示传递函数,K表示系统增益,s表示复频域变量,Q表示品质因数。
传递函数的分母是一个二次多项式,其形式为s^2 + s/Q + 1。
这是由于二阶低通滤波器主要考虑到截止频率和滚降率两个因素。
传递函数的分子为常数项K,用来调整滤波器的增益。
品质因数Q是一个反映滤波器相应特性的重要参数。
当Q值较大时,滤波器的幅频特性会呈现出较为尖锐的特性,有较小的过渡带宽,并呈现出较高的共振峰。
而Q值较小时,滤波器的幅频特性会呈现较为平缓的特性,具有较大的过渡带宽,但缺乏共振峰。
在实际设计中,我们可以通过调整系统增益K和品质因数Q来实现所需的滤波器性能。
增益K可以通过放大或衰减滤波器的输入或输出信号来调整。
而品质因数Q则可以通过调整滤波器的带宽来达到。
二阶低通滤波器的标准形式具有一些明显的特点。
首先,其传递函数的分母是一个二次多项式,这样可以方便地分析滤波器的阶数和频率响应。
其次,标准形式使得滤波器的设计和调整变得简单和直观。
最后,由于是一个常数增益的滤波器,可以方便地进行增益的补偿和调整。
除了标准形式外,二阶低通滤波器还可以有其他形式的表达。
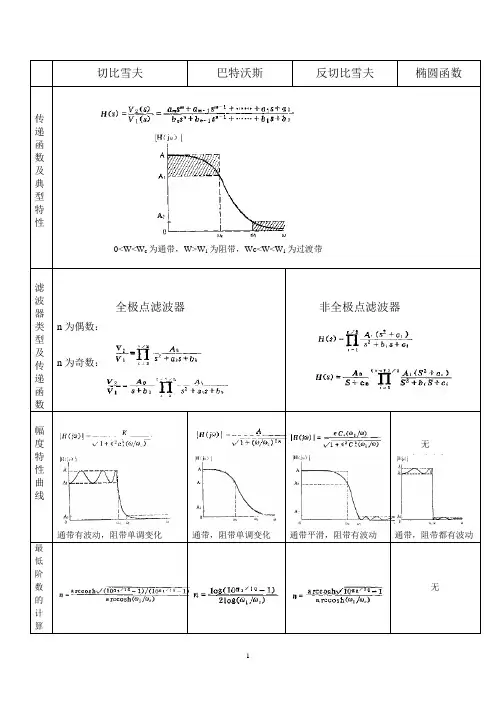
例如,可以表示为巴特沃斯形式、切比雪夫形式和椭圆形式等。
每种形式都有其特定的设计和性能特点,可以根据具体的应用需求选择适合的形式。
总之,二阶低通滤波器的标准形式是一种简化的滤波器表示形式,方便了低通滤波器的设计和分析。
设计人员可以通过调整系统增益和品质因数来实现所需的滤波器性能。

二阶低通滤波传递函数介绍在数字信号处理中,低通滤波器常用于去除不需要的高频噪声或频率成分,保留所需的低频信号。
二阶低通滤波器是指其传递函数为二阶多项式的低通滤波器。
传递函数一般采用有理函数形式,定义为输出与输入信号之间的比例关系。
对于一个二阶低通滤波器,其传递函数可以表示为:H(s)=K/(s^2+2ζω_0s+ω_0^2)其中,H(s)为传递函数,s为复变量,K为增益系数,ζ为阻尼比,ω_0为截止频率。
传递函数中的复变量s代表一个复平面上的频率变量,可以写成s=ο+jω的形式,其中ο为实部,j为虚数单位,ω为频率。
传递函数中的K、ζ、ω_0分别为滤波器的增益系数、阻尼比和截止频率。
增益系数K是用来调整滤波器的放大倍数,阻尼比ζ是用来控制滤波器的响应速度和稳定性,截止频率ω_0则决定了滤波器的频率特性。
当滤波器中的阻尼比ζ小于1时,系统呈现过阻尼的特性,当阻尼比ζ等于1时,系统呈现临界阻尼的特性,当阻尼比ζ大于1时,系统呈现欠阻尼的特性。
这三种特性分别对应着不同的频率响应曲线。
根据传递函数的形式,可以推导出二阶低通滤波器的幅频响应和相频响应。
幅频响应描述了信号在不同频率下经过滤波器后的变化程度,而相频响应描述了信号的相位在不同频率下经过滤波器后的变化程度。
通过分析滤波器的幅频响应和相频响应,我们可以了解该滤波器对输入信号的影响,并选择合适的滤波器参数以满足特定的应用需求。
1.平滑特性:二阶低通滤波器可以实现对信号的平滑处理,滤除高频噪声,使信号更加清晰。
2.相位延迟:由于滤波器会引起信号的相位变化,因此滤波器的相位延迟是需要考虑的重要因素。
在设计滤波器时,我们需要确保滤波器引入的相位延迟不会对信号的时域特性产生明显的影响。
3.截止频率选择:截止频率是决定滤波器性能的重要参数,它决定了滤波器对不同频率信号的响应程度。
合理选择截止频率可以实现对信号的有效滤波,避免对有用信号的损失。
4.抽样频率:在数字信号处理中,抽样频率是指输入信号的采样频率。

MEMS 陀螺的带宽为30HZ ,从采样频率100HZ 的数据序列中消除掉30HZ 以上的噪声。
巴特沃斯函数只是在ω=0处精确地逼近理想低通特性,在通带内随着ω增加,误差愈来愈大,在通带边界上误差最大,逼近特性并不很好,但是陀螺仪的有用输出信号本就在低频段,对通带边界的滤波要求不高,因此巴特沃斯滤波器就可以满足要求。
要求巴特沃斯滤波器通带上限截止频率fc=30HZ ,阻带下限截止频率fs=80HZ ,通带最大衰减3max =A db ,阻带最小衰减为15min =A db 。
由式(1)-(4)可得巴特沃斯低通滤波器为二阶。
1110max 1.0≈-=A ε (1)49.1995.0622.30lg 110110lg 110110lg 3.05.11.01.0max min =⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛--A A (2) 85.01.7lg 302802lg lg 2==⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛ππc s w w (3)75.185.049.1lg 110110lg lg max min 1.01.0==⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-->c s A A w w n (4) 用302⨯⨯πs 代替121)(2++=s s s H 中的s 得到去归一化后的滤波器传递函数为式(5)所示。
6.354944.2666.35494)(2++=s s s H (5) 采用的低通滤波电路如图2所示,滤波增益为1,此电路传递函数如式(6)所示,只需将巴特沃斯滤波器的传递函数与此传递函数的系数一一对应即可以整定出滤波电路的参数。
图2 二阶低通滤波典型电路32212312112212111111)(R R C C s C R C R C R s R R C C s H +⎪⎪⎭⎫ ⎝⎛+++-= (6)式(5)与式(6)对比可得:6.3549411221=R R C C (7) 4.266111231211=++C R C R C R (8) 6.3549413221=R R C C (9) 令C 1=0.1uf ,R 2=R 1= R 3,解得R 2=R 1= R 3=6.6K ,C 2=0.6uf ,至此巴特沃斯滤波器构造完成。
二阶rc低通滤波器截止频率设计
二阶RC低通滤波器是一种常见的电子电路,用于滤除输入信号中高于截止频率的频率成分。
设计二阶RC低通滤波器的关键是确定截止频率。
首先,了解截止频率是指在该频率上,信号的幅值经过滤波器后会被衰减到原始幅值的70.7%。
因此,要设计二阶RC低通滤波器的截止频率,我们需要确定衰减幅度。
其次,根据二阶RC低通滤波器的传递函数可知,截止频率与电阻值和电容值有关。
传递函数为H(s)=1/(s^2*R1*R2*C1*C2 + s*(R1*C1+R1*C2+R2*C1) + 1),其中s为复变量。
为了确定电阻和电容的取值,可以使用以下公式:
截止频率 f_c = 1 / (2*pi*sqrt(R1*R2*C1*C2))
阻尼因子ζ = (R1*C1+R1*C2+R2*C1) / (2*sqrt(R1*R2*C1*C2))
根据所给的任务名称,我们需要设计二阶RC低通滤波器的截止频率。
因此,可以根据所给的截止频率f_c计算出阻尼因子ζ,并根据ζ通过合适选择电阻和电容的数值来实现。
总结一下,设计二阶RC低通滤波器截止频率的步骤如下:
1. 确定所需的截止频率f_c。
2. 计算出阻尼因子ζ = (R1*C1+R1*C2+R2*C1) / (2*sqrt(R1*R2*C1*C2))。
3. 根据ζ的数值选择合适的电阻和电容数值来实现设计要求。
通过以上步骤,我们可以设计出满足所需截止频率的二阶RC低通滤波器。
二阶传递函数二阶传递函数(second-ordertransferfunction)是一类常见的、非常重要的信号处理函数,主要用于分析和模拟机理和系统。
其数学表示形式为:H(s) = K / (s^2 + as + b)其中,s为复数,K为系统的增益参数,a和b分别为两个系统的参数,可以用来控制信号的变化和调整系统的特性。
二阶传递函数通常用来模拟和设计滤波器,它在系统设计中有一定的价值。
它具有一定的特性:首先,它是稳定的,因此它能够稳定系统。
其次,它具有低延迟和高通频。
此外,它还有一定的正反馈机制,可以用来控制系统的特性。
二阶传递函数可以应用于各种系统中,包括模拟信号系统、数字信号系统、测量和控制系统、电子电路系统、空间系统、机械系统、飞行控制系统等。
在模拟电路设计中,二阶传递函数可以用来设计滤波器,它的特性可以很好地满足滤波器的要求,特别是在低频带的范围内。
而在数字信号处理中,二阶传递函数也可以用来控制传输系统的性能,可以实现有效的低通滤波、高通滤波和带阻滤波。
在飞行控制系统中,一般采用二阶传递函数来模拟系统的性能,并使得控制系统更加灵活。
此外,在三维视觉传感器中,可以采用二阶传递函数来降低控制噪声的影响,并获得更加精确的结果。
通过使用二阶传递函数,不仅可以提高系统的稳定性和性能,而且可以有效地控制信号的传输。
然而,二阶传递函数也有其不足之处。
它通常涉及到许多复杂的系统参数,需要一定的计算量,而且很多时候,它的响应周期会受到限制,这使得它的表现有一定的局限性。
因此,在使用传递函数进行系统设计时,需要仔细考虑系统的要求,并根据实际情况进行合理的设计。
只有这样,才能够发挥传递函数的优势,有效地满足系统的性能要求。
总之,二阶传递函数是一种重要而又有用的信号处理工具,它可以用于模拟各种系统,并有效地控制系统的性能。
虽然它存在一定的局限性,但通过正确的设计,仍然可以使系统受益。
二阶低通滤波器传递函数
二阶低通滤波器是一种常用的滤波器,它具有综合滤波和单频滤波的优劣。
下面就来说说它的传递函数:
1. 传递函数公式:二阶低通滤波器的传递函数有多种形式,如一般表达形式、指数衰减表达形式、Hilbert变换后表达形式等,但它们都可以被表示为:H(jw) =
1/(1 + j (2πf/f0) + (2πf/f0)^2)。
2. 分析含义:低通滤波器的传递函数反映了滤波器的频率响应特性,其中H是传递函数,j是虚数单位,w表示角频率,f表示输入信号的频率,f0表示截断频率。
由传递函数可以看出,当f < f0时,H(jw)的值接近1,说明滤波器对低于截断频率的输入信号具有很高的通过,也就是说滤波器是对低频信号具有很高的通过率;而对于f > f0时,H(jw)的值接近0,说明滤波器对高于截断频率的输入信号具有很高的阻抗,也就是说滤波器是对高频信号具有很高的阻抗率。
3. 冲激响应:冲激响应就是滤波器在激励信号时的频率响应,主要分为振幅响应和相位响应。
一般来说,对于低通滤波器来说,随着频率的升高,滤波器的振幅响应和相位响应都是衰减的,而当输入信号的频率低于截断频率时,滤波器的振幅响应和相位响应则会接近1和0.
4. 滤波器特性:滤波器的特性可以从其传递函数中来归纳总结,它包括截止特性、带宽、变化而破坏的特性、失真特性等。
总的来说,二阶低通滤波器的传递函数表示了滤波器的频率响应特性,包括冲激响应和滤波器的特性,所以它是搞清楚滤波器的行为的关键因素。
简单二阶有源低通滤波器电路及幅频特性为了使输出电压在高频段以更快的速率下降,以改善滤波效果,再加一节RC低通滤波环节,称为二阶有源滤波电路。
它比一阶低通滤波器的滤波效果更好。
二阶LPF的电路图如图6所示,幅频特性曲线如图7所示。
?图6 二阶低通电路(LPF)图7 二阶低通电路幅频特性曲线(1)通带增益当f = 0时,各电容器可视为开路,通带内的增益为(2)二阶低通有源滤波器传递函数根据图可以写出通常有,联立求解以上三式,可得滤波器的传递函数(3)通带截止频率将s换成jω,令ω0=2πf0=1/(RC)可得?当f=fp 时,上式分母的模解得截止频率:?与理想的二阶波特图相比,在超过f0以后,幅频特性以-40 dB/dec的速率下降,比一阶的下降快。
但在通带截止频率fp→f0之间幅频特性下降的还不够快。
摘要设计一种压控电压源型二阶有源低通滤波电路,并利用Multisim10仿真软件对电路的频率特性、特征参量等进行了仿真分析,仿真结果与理论设计一致,为有源滤波器的电路设计提供了EDA手段和依据。
关键词二阶有源低通滤波器;电路设计自动化;仿真分析;Multisim10滤波器是一种使用信号通过而同时抑制无用频率信号的电子装置,在信息处理、数据传送和抑制干扰等自动控制、通信及其它电子系统中应用广泛。
滤波一般可分为有源滤波和无源滤波,有源滤波可以使幅频特性比较陡峭,而无源滤波设计简单易行,但幅频特性不如有源滤波器,而且体积较大。
从滤波器阶数可分为一阶和高阶,阶数越高,幅频特性越陡峭。
高阶滤波器通常可由一阶和二阶滤波器级联而成。
采用集成运放构成的RC有源滤波器具有输入阻抗高,输出阻抗低,可提供一定增益,截止频率可调等特点。
压控电压源型二阶低通滤波电路是有源滤波电路的重要一种,适合作为多级放大器的级联。
本文根据实际要求设计一种压控电压源型二阶有源低通滤波电路,采用EDA仿真软件Multisim1O对压控电压源型二阶有源低通滤波电路进行仿真分析、调试,从而实现电路的优化设计。
二阶有源滤波器的传输函数
在有源滤波器的设计中,高阶滤波器的传输函数都可以分解成一阶和多个二阶传输函数的乘积。
一阶传输函数比较简单,二阶函数分析如下。
1、低通滤波器
2、高通滤波器
式中,HO为传输增益双称通频带增益:A为阻尼系数,WO为滤波器的固有频率,S=JW。
幅频特性H(W)、相频特性φ(W)和延迟特性T(W)表示了低、高通滤波器的全部特性。
H(S)是传输函数。
由图5.4-47可以看出,A取值不同,曲线的形状可以有很大不同,也就是对滤波器的滤波性能有很大影响。
当A=√2时,幅频响应有最大平坦区,是巴特沃斯滤波器;A﹤√2时,在WO附近有凸峰;通带内有等值波动。
A值越小,阻尼越小,凸峰越明显,通带内幅度等值波动越大,选择性越好。
是切比雪夫滤波器。
A值越大,阻尼越大,曲线变化趋于缓慢。
当A=√3时,幅频响应平坦区较小,具有线性相移的特性,是贝塞尔滤波器。
图5.4-47 幅频特性曲线
A)低通滤波器具 B)高通滤波器
3、带通滤波器。
二阶rc低通滤波器截止频率计算二阶RC低通滤波器是指由两个电阻和两个电容构成的滤波器电路,其传递函数为:H(s)=1/(1+sRC+s²R²C²)其中,s为复频域变量,R为电阻值,C为电容值。
截止频率是指滤波器对信号幅值进行削弱的频率点,计算二阶RC低通滤波器的截止频率需要先将传递函数化简为标准形式。
标准形式为:H(s)=ωn²/(s²+2ζωn+ωn²)其中,ωn为系统的自然频率,ζ为阻尼比。
通过比较两个传递函数的系数,可以得到ωn和ζ与RC的关系。
根据传递函数H(s)的系数,可以得到:ωn²=1/(R²C²)2ζωn=1/RC解这个方程组,可以得到ωn和ζ的具体值。
在计算截止频率时,通常取阻尼比ζ为1/√2,这样可以得到二阶RC低通滤波器的标准截止频率。
带入阻尼比ζ为1/√2,可以得到:ωn=1/(RC)这个式子表明,二阶RC低通滤波器的截止频率只与RC的乘积有关。
因此,二阶RC低通滤波器的截止频率计算方法为:f=1/(2πRC)其中,f为截止频率。
这个公式表明,截止频率只与电阻值和电容值有关,与滤波器的阶数无关。
例如,如果取R=10kΩ,C=1μF,则截止频率f=1/(2π*10k*1μ)≈15.92Hz。
使用这个截止频率可以确定在输入信号频率高于15.92Hz时,二阶RC低通滤波器对信号进行有效的滤波。
不过需要注意的是,以上只是理论计算的结果,实际使用时还需要考虑电路的误差、负载影响等因素。
同时,在设计滤波器时还需要根据具体应用需求选择适当的电阻和电容值,以达到期望的滤波效果。
因此,在实际设计中,通常会进行一些测试和调整,以获得更准确的截止频率。
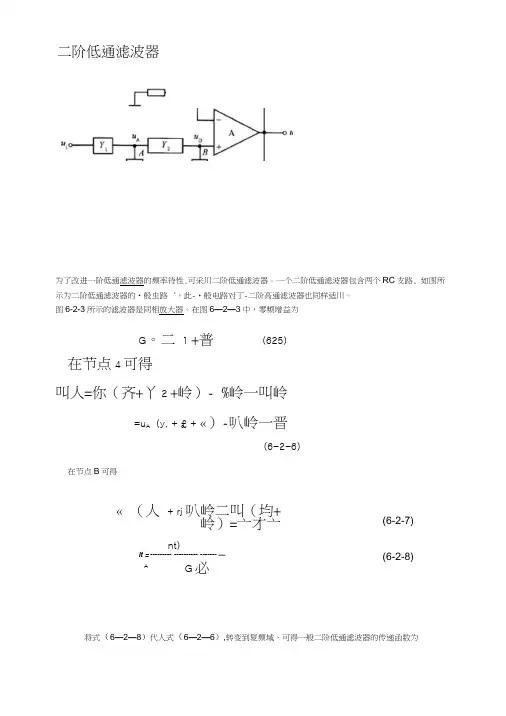
二阶低通滤波器
为了改进一阶低通滤波器的频率特性,可采用二阶低通滤波器。
一个二阶低通滤波器包含两个RC支路,如图所示为二阶低通滤波器的一般电路。
此一般电路对于二阶高通滤波器也同样适用。
图6-2-3所示的滤波器是同相放大器。
在图6-2-3中,零频增益为
在节点B可得
将式(6-2-8)代人式(6-2-6),转变到复频域,可得一般二阶低通滤波器的传递函数为
在构成二阶低通滤波器时,只需选择巧,殇,蚝,‰导纳的值即可。
例如,当选择Y1=1/R1,Y2=1/R2,Y3=sC1 Y4=sC2时,则构成图6-2-4所示的二阶低通滤波器。
对于上图所示的二阶低通滤波器,其传递函数为
如图6-2-5所示为二阶低通滤波器的幅频特性曲线,其阻带衰减特性的斜率为-40dB/10oct,克服了一阶低通滤波器阻带衰减太慢的缺点。
二阶低通滤波器的各个参数,影响其滤波特性,如阻尼系数苫的大小,决定了幅频特性有无峰值,或谐振峰的高低。
如图6=2-6所示为苫对二阶低通滤波器幅频特性的影响。