激光基本知识第二章答案解析

周炳琨激光原理第二章习题解答（完整版）1.试利用往返矩阵证明对称共焦腔为稳定腔，即任意傍轴光线在其中可以往返无限多次，而且两次往返即自行闭合。

证明：设从镜M1→M 2→M 1,初始坐标为⎪⎪⎭⎫⎝⎛θ00r ，往返一次后坐标变为⎪⎪⎭⎫⎝⎛θ11r =T⎪⎪⎭⎫ ⎝⎛θ00r ,往返两次后坐标变为⎪⎪⎭⎫⎝⎛θ22r =T •T ⎪⎪⎭⎫ ⎝⎛θ00r而对称共焦腔，R 1=R 2=L则A=1-2R L 2=-1B=2L ⎪⎪⎭⎫ ⎝⎛-2R L 1=0 C=-⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-+121R L 21R 2R 2=0 D=-⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛--211R L 21R L 21R L 2=-1所以，T=⎪⎪⎭⎫⎝⎛--1001故，⎪⎪⎭⎫ ⎝⎛θ22r =⎪⎪⎭⎫⎝⎛--1001⎪⎪⎭⎫ ⎝⎛--1001⎪⎪⎭⎫ ⎝⎛θ00r =⎪⎪⎭⎫⎝⎛θ00r 即，两次往返后自行闭合。

2．试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。

解：共轴球面腔的稳定性条件为0<g 1•g 2<1,其中g 1=1-1R L ,g 2=1-2R L （a 对平凹腔：R 2=∞,则g 2=1,0<1-1R L <1，即0<L<R1(b)对双凹腔：0<g 1•g 2<1, 0<⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-21R L 1R L 1<1 L R >1，L R >2或L R <1L R <2且LR R >+21(c)对凹凸腔：R 1=1R ,R 2=-2R ,0<⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛-21R L 1R L 1<1，L R >1且LR R <-||213．激光器的谐振腔由一面曲率半径为1m 的凸面镜和曲率半径为2m 的凹面镜组成，工作物质长0.5m ，其折射率为1.52，求腔长L 在什么范围内是稳定腔。

光的衍射、偏振、色散、激光【学习目标】1．了解光的衍射现象及观察方法． 2．理解光产生衍射的条件．3．知道几种不同衍射现象的图样．5．知道振动中的偏振现象，偏振是横波特有的性质． 6．明显偏振光和自然光的区别．7．知道光的偏振现象及偏振光的应用． 8．知道光的色散、光的颜色及光谱的概念． 9．理解薄膜干涉的原理并能解释一些现象．10．知道激光和自然光的区别． 11．了解激光的特点和应用．【要点梳理】 要点一、光的衍射 1．光的衍射现象当单色光通过很窄的缝或很小的孔时，光离开了直线路径，绕到障碍物的阴影里去，光所达到的范围会远远超过它沿直线传播所应照明的区域，形成明暗相间的条纹或光环． 2．产生明显衍射的条件障碍物的尺寸可以跟光的波长相近或比光的波长还要小时能产生明显的衍射．对同样的障碍物，波长越长的光，衍射现象越明显；对某种波长的光，障碍物越小，衍射现象越明显．由于波长越长，衍射性越好，所以要观察到声波的衍射现象就比观察到光波的衍射现象容易得多． 3．三种衍射现象和图样特征 (1)单缝衍射． ①单缝衍射现象．如图所示，点光源S 发出的光经过单缝后照射到光屏上，若缝较宽，则光沿着直线传播，传播到光屏上的AB 区域；若缝足够窄，则光的传播不再沿直线传播，而是传到几何阴影区，在AA BB ''、区还出现亮暗相间的条纹，即发生衍射现象．要点诠释：衍射是波特有的一种现象，只是有的明显，有的不明显而已． ②图样特征．单缝衍射条纹分布是不均匀的，中央亮条纹与邻边的亮条纹相比有明显的不同：用单色光照射单缝时，光屏上出现亮、暗相间的衍射条纹，中央条纹宽度大，亮度也大，如图所示，与干涉条纹有区别．用白光照射单缝时，中间是白色亮条纹，两边是彩色条纹，其中最靠近中央的色光是紫光，最远离中央的是红光．(2)圆孔衍射．①圆孔衍射的现象．如图甲所示，当挡板AB上的圆孔较大时，光屏上出现图乙中所示的情形，无衍射现象发生；当挡板AB上的圆孔很小时，光屏上出现图丙中所示的衍射图样，出现亮、暗相间的圆环．②图样特征．衍射图样中，中央亮圆的亮度大，外面是亮、暗相间的圆环，但外围亮环的亮度小，用不同的光照射时所得图样也有所不同，如果用单色光照射时，中央为亮圆，外面是亮度越来越暗的亮环．如果用白光照射时，中央亮圆为白色，周围是彩色圆环．(3)圆板衍射．在1818年，法国物理学家菲涅耳提出波动理论时，著名的数学家泊松根据菲涅耳的波动理论推算出圆板后面的中央应出现一个亮斑，这看起来是一个荒谬的结论，于是在同年，泊松在巴黎科学院宣称他推翻了菲涅耳的波动理论，并把这一结果当作菲涅耳的谬误提了出来但有人做了相应的实验，发现在圆板阴影的中央确实出现了一个亮斑，这充分证明了菲涅耳理论的正确性，后人把这个亮斑就叫泊松亮斑．小圆板衍射图样的中央有个亮斑——泊松亮斑，图样中的亮环或暗环间的距离随着半径的增大而减小．4．衍射光栅(1)构成：由许多等宽的狭缝等距离排列起来形成的光学仪器．(2)特点：它产生的条纹分辨程度高，便于测量．(3)种类：⎧⎨⎩透射光栅反射光栅．5．衍射现象与干涉现象的比较种类项目单缝衍射双缝干涉不同点产生条件只要狭缝足够小，任何光都能发生频率相同的两列光波相遇叠加条纹宽度条纹宽度不等，中央最宽条纹宽度相等条纹间距各相邻条纹间不等各相邻条纹等间距亮度中央条纹最亮，两边变暗清晰条纹，亮度基本相等相同点干涉、衍射都是波特有的现象，属于波的叠加；干涉、衍射都有明暗相间的条纹6．三种衍射图样的比较如图所示是光经狭缝、小孔、小圆屏产生的衍射图样的照片．由图可见：(1)光经不同形状的障碍物产生的衍射图样的形状是不同的．(2)衍射条纹的间距不等．(3)仔细比较乙图和丙图可以发现小孔衍射图样和小圆屏衍射图样的区别：①小圆屏衍射图样的中央有个亮斑——著名的“泊松亮斑”；②小圆屏衍射图样中亮环或暗环间距随着半径的增大而减小，而圆孔衍射图样中亮环或暗环间距随半径增大而增大；③乙图背景是黑暗的，丙图背景是明亮的．要点二、光的偏振1．光是横波光的干涉和衍射现象说明光具有波动性，但不能由此确定光究竟是横波还是纵波．要点诠释：电磁波是横波，电磁波中的电场强度E和磁感应强度B都与波的传播方向垂直．既然光是电磁波，也应该是横波，光的作用主要是由其电场强度E引起的．2．偏振现象(1)狭缝对横波、纵波的影响：如果在波的传播方向上放一带狭缝的木板，不管狭缝方向如何，纵波都能自由通过狭缝；对横波，只有狭缝的方向与横波质点的振动方向相同时，横波才能毫无阻碍地通过狭缝；当狭缝的方向与质点的振动方向垂直时，横波就不能通过狭缝，这种现象叫做横波的偏振．如图所示．(2)横波独有的特征：偏振现象是横波所特有的，故利用偏振现象可判断一列波是横波或是纵波．(3)光的偏振现象说明光波是横波．3．自然光和偏振光(1)自然光：从普通光源直接发出的自然光是无数偏振光的无规则集合，所以直接观察时不能发现光强偏向哪一个方向．这种沿着各个方向振动的光波强度都相同的光叫自然光．自然光介绍：太阳、电灯等普通光源发出的光，包含着垂直于传播方向上沿一切方向振动的光，而且沿着各个方向振动的光波的强度都相同。

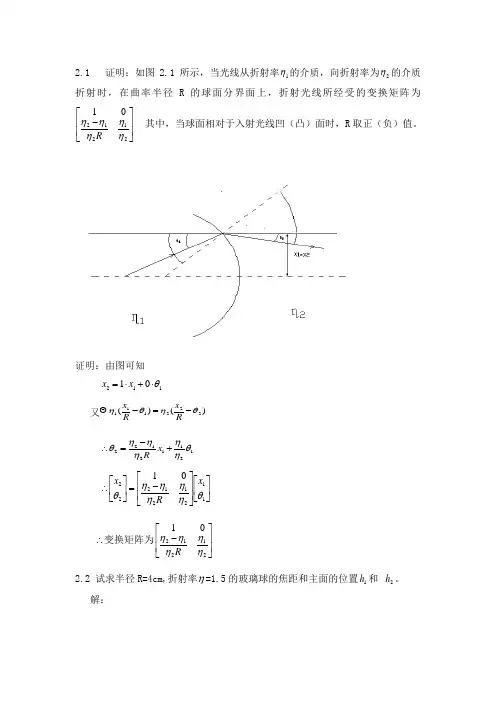
2.1 证明：如图2.1所示，当光线从折射率1η的介质，向折射率为2η的介质折射时，在曲率半径R 的球面分界面上，折射光线所经受的变换矩阵为⎥⎥⎦⎤⎢⎢⎣⎡-2121201ηηηηηR 其中，当球面相对于入射光线凹（凸）面时，R 取正（负）值。

证明：由图可知 11201θ⋅+⋅=x x 又)()(222111θηθη-=-RxR x 21121122x R ηηηθθηη-∴=+ ⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡∴11212122201θηηηηηθx Rx ∴变换矩阵为⎥⎥⎦⎤⎢⎢⎣⎡-2121201ηηηηηR 2.2 试求半径R=4cm,折射率η=1.5的玻璃球的焦距和主面的位置1h 和2h 。

解：变换矩阵⎥⎥⎦⎤⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=2112121221210110101n n R n n n l n n R n n n M 把11=n ，5.12=n ，cm R R 421=-=，cm l 8=代入，可得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡⨯-⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡--=3531316355.1145.115.10110815.145.1101M )(12f h A -=, f C 1-=, )(11f h D -= 求得 mm f 30-= mm h 201= mm h 202=2.3 焦距1f =5cm 和2f =-10c=m 的两个透镜相距5cm 。

第一个透镜前表面和第二个透镜后表面为参考平面的系统，其等效焦距为多少？焦点和主平面位置在何处？距1f 前表面20cm 处放置高为10cm 的物体，能在2f 后多远地方成像？像高为多少？ 解：（1）2110101010********1131101011110552A B L M CD f f ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥====⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-----⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦)(12f h A -=, f C 1-=, )(11f h D -=，求得cm f 5-= cm h 5.21= cm h 52-=第一个透镜前表面与前主面的距离为2.5cm ，第二个透镜后表面与后主面的距离为-5cm,前主面离焦点的距离为-5cm ，） （2）21201011===l x θ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡45252110235150235150111122θθθx x D C B A xcm l cm x 2,5.222-==（距2f 后表面-2cm ）2.4 一块折射率为η，厚度为d 的介质放在空气中，其两界面分别为曲率半径等于R 的凹球面和平面，光线入射到凹球面上。

激光原理知识点汇总第一章电磁场和物质的共振相互作用1.相干光的光子描述，光的受激辐射基本概念1)1960年7月Maiman报道第一台红宝石固体激光器，波长694.3nm。

2)光的基本性质：能量ε=hνh: Planck常数，ν :光波频率运动质量m=ε/c2=hv/c2静止质量0动量knhnchnmcp=•===22λππν3)光子的相干性：在不同的空间点、不同时刻的光波场某些特性的相关性相干体积相干面积，相干长度，相干时间光源单色性越好，相干时间越长：相格空间体积以及一个光波摸或光子态占有的空间体积度等于相干体积属于同一状态的光子或同一模式的光波是相干的4)黑体辐射的planck公式在温度T的热平衡下，黑体辐射分配到腔内每个模式上的平均能量1-=kThehEνν腔内单位体积、单位频率间隔内的光波摸式数338chnνπν=Planck公式：11833-==kThechνννπρ单色能量密度，k：Boltzmann常数Bohr定则：νhEE=-125)光的受激放大a.普通光源在红外和可见光波段是非相干光，黑体是相干光黑体辐射的简并度KTnmnmKTnmKTncmKTkThhEn50000,1,110,6.0,3001,60,30010,30,3001)exp(1353=≈=≈==≈==≈==→-==-μλμλμλλννb.让特定、少数模式震荡，获得高的光子简并度21212121338AWABchn===ννρνπρ6)光的自激振荡a.自激振荡概念分数单位距离光强衰减的百自损耗系数)(1)(zIdzzdI-=αdzzIIgzdI)(])([)(..α-=考虑增益和损耗])ex p[()(0zgIzIα-=αααsmsmIgIIIgIg)(1)(0-=→=+=光腔作用: (1)模式选择; (2）提供轴向光波摸的反馈；b.震荡条件等于号是阈值振荡ααα≥→≥-=000)(gIgI sm是工作物质长度llgL...........0δδα≥→=lg0单程小信号增益因子7)激光的特性：单色性、相干性、方向性、高亮性。

第二章开放式光腔与XX光束1.证明如图2.1所示傍轴光线进入平面介质界面的光线变换矩阵为证明：设入射光线坐标参数为，出射光线坐标参数为，根据几何关系可知傍轴光线则，写成矩阵形式得证2.证明光线通过图2.2所示厚度为d的平行平面介质的光线变换矩阵为。

证明：设入射光线坐标参数为，出射光线坐标参数为，入射光线首先经界面1折射，然后在介质2xx自由传播横向距离d，最后经界面2折射后出射。

根据1题的结论和自由传播的光线变换矩阵可得化简后得证。

3.试利用往返矩阵证明共焦腔为稳定腔，即任意傍轴光线在其中可以往返无限多次，而且两次往返即自行闭合证：设光线在球面镜腔内的往返情况如下图所示:其往返矩阵为:由于是共焦腔，则有R i = R2 = L将上式代入计算得往返矩阵T m [A D1"101〔01 一可以看出，光线在腔内往返两次的变换矩阵为单位阵，所以光线两次往返即自行闭合。

于是光线在腔内往返任意多次均不会溢出腔外，所以共焦腔为稳定腔。

4.试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。

解：共轴球面腔稳定性条件其中对平凹共轴球面镜腔有则，再根据稳定性条件可得。

对双凹共轴球面腔有，则根据稳定性条件可得。

对凹凸共轴球面镜腔有，则根据稳定性条件可得。

5•激光器的谐振腔由一面曲率半径为的凸面镜和曲率半径为的凹面镜组成，工作物质长，其折射率为1.52，求腔长L在什么范围内是稳定腔。

解：设两腔镜和的曲率半径分别为和，工作物质长，折射率当腔内放入工作物质时，稳定性条件中的腔长应做等效，设工作物质长为,工作物质左右两边剩余的腔长分别为和，贝y。

设此时的等效腔长为，则光在腔先经历自由传播横向距离，然后在工作物质左侧面折射，接着在工作物质中自由传播横向距离，再在工作物质右侧面折射，最后再自由传播横向距离，则。

］「1 ql1 °=1 町n J(0dj o 冷0 1-所以等效腔长等于1 ■01.17m<L ：：2.17m6. 图2.3所示三镜环形腔，已知，试画出其等效透镜序列图，并求 球面镜的曲率半径R 在什么范围内该腔是稳定腔。

2.19某共焦腔氦氖激光器，波长λ＝0.6328μm ，若镜面上基模光斑尺寸为0.5mm ，试求共焦腔的腔长，若腔长保持不变，而波长λ＝3.39μm ，问：此时镜面上光斑尺寸多大？ 解：20/ 1.24s L m ωπλ=≈0/1.16mms L ωλπ==2.20考虑一台氩离子激光器，其对称稳定球面腔的腔长L=1m ，波长λ= 0.5145μm ，腔镜曲率半径R=4m ，试计算基模光斑尺寸和镜面上的光斑尺寸。

解：1/42021/42242()(2)(22)(2) 4.65104L R L R L R L RL L mλωπλπ-⎡⎤--=⎢⎥-⎣⎦⎡⎤-==⨯⎢⎥⎣⎦1/42121/4222422()()(2)4.9810(2)L R R L L R L R L R L mRL L λωωπλπ-⎡⎤-==⎢⎥--⎣⎦⎡⎤==⨯⎢⎥-⎣⎦2.21腔长L ＝75cm 的氦氖平凹腔激光器，波长λ＝0.6328μm ，腔镜曲率半径R ＝1m ，试求凹面镜上光斑尺寸，并计算该腔基模远场发散角θ。

解：1/41/4212211121121/41/422112212212()0.295mm()()(1)()0.591()()(1)s s R R L g L Lw L R L R R L g g g R R L g LL w mmL R L R R L g g g λλππλλππ⎡⎤⎡⎤-===⎢⎥⎢⎥-+--⎣⎦⎣⎦⎡⎤⎡⎤-===⎢⎥⎢⎥-+--⎣⎦⎣⎦1/41/42221212120212121212(2)(2)220.0014rad=0.0782()()()(1)L R R g g g g L R L R L R R L L g g g g λλθππ⎡⎤⎧⎫--+-===⎨⎬⎢⎥--+--⎣⎦⎩⎭2.22设稳定球面腔的腔长L ＝16cm ，两镜面曲率半径为1R ＝20cm ，2R ＝－32cm ，波长λ=410-cm ，试求：（1）最小光斑尺寸0ω和最小光斑位置；（2）镜面上光斑尺寸1s ω、2s ω；（3）0ω和1s ω、2s ω分别与共焦腔（1R ＝2R ＝L ）相应值之比。

激光原理及应用部分课后答案1-4为使He-Ne 激光器的相干长度达到1KM ，它的单色性0λλ∆应是多少？2-2当每个模式内的平均光子数（光子简并数）大于1时，以受激辐射为主。

2-3如果激光器和微波激射器分别在um 10=λm 500n =λ和z 3000MH =ν输出1W 连续功率，问美秒从激光上能级向下能级跃迁的粒子数是多少？2-4当一对激光能级为E2和E1（f1=f2），相应的频率为v （波长为λ），能级上的粒子数密度分别为n2和n1,q 求：（1）当v=3000MHZ ，T=3000K 时，n2/n1=？（2）当λ=1um ，T=3000K 时，n2/n1=？（3）当λ=1um ，n2/n1=0时，温度T=？解：2-5激发态的原子从能级E2跃迁到E1时，释放出λ=5um的光子，求这个两个能级的能量差。

若能级E1和E2上的原子数分别为N1和N2，试计算室温T=300K的N2/N值。

2-7如果工作物质的某一跃迁是波长为100nm的远紫外光，自发辐射跃迁概率1621s10-=A，试问：（1）改跃迁的受激辐射爱因斯坦系数B21是多少？（2）为使受激辐射跃迁概率比自发辐射跃迁概率大三倍，腔内的单色能量密度νρ应为多少？2-9某一物质受光照射，沿物质传播1mm的距离时被吸收了1%，如果该物质的厚度是0.1m,那么入射光中有百分之几能通过该物质？并计算该物质的吸收系数α。

2-10激光在0.2m 长的增益介质中往复运动过程中，其增强了30%。

求该介质的小信号增益系数0G 。

假设激光在往复运动中没有损耗。

3-2CO2激光器的腔长L=100cm,反射镜直径D=1.5cm,两镜的光强反射系数分别为r1=0.985,r2=0.8.求由衍射损耗及输出损耗所分别引起的δ，τ。

3-4，分别按下图中的往返顺序，推导近轴光线往返一周的光学变换矩阵⎪⎪⎭⎫ ⎝⎛D C B A ，并证明这两种情况下的）（D A +21相等。

激光原理第二章习题解答(共15页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--《激光原理》习题解答 第二章习题解答1 试利用往返矩阵证明共焦腔为稳定腔，即任意傍轴光线在其中可以往返无限次，而且两次往返即自行闭合.证明如下：（共焦腔的定义——两个反射镜的焦点重合的共轴球面腔为共焦腔。

共焦腔分为实共焦腔和虚共焦腔。

公共焦点在腔内的共焦腔是实共焦腔，反之是虚共焦腔。

两个反射镜曲率相等的共焦腔称为对称共焦腔，可以证明，对称共焦腔是实双凹腔。

）根据以上一系列定义，我们取具对称共焦腔为例来证明。

设两个凹镜的曲率半径分别是1R 和2R ，腔长为L ，根据对称共焦腔特点可知：L R R R ===21因此，一次往返转换矩阵为⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-+-⎪⎪⎭⎫⎝⎛--=⎥⎦⎤⎢⎣⎡=211121222121221221221R L R L R L R L R R R L L R L D C B A T 把条件L R R R ===21带入到转换矩阵T ，得到：⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡=1001D C B A T 共轴球面腔的稳定判别式子()1211<+<-D A 如果()121-=+D A 或者()121=+D A ，则谐振腔是临界腔，是否是稳定腔要根据情况来定。

本题中 ，因此可以断定是介稳腔（临界腔），下面证明对称共焦腔在近轴光线条件下属于稳定腔。

经过两个往返的转换矩阵式2T ，⎥⎦⎤⎢⎣⎡=10012T 坐标转换公式为：⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡1111112221001θθθθr r r T r 其中等式左边的坐标和角度为经过两次往返后的坐标，通过上边的式子可以看出，光线经过两次往返后回到光线的出发点，即形成了封闭，因此得到近轴光线经过两次往返形成闭合，对称共焦腔是稳定腔。

第一章1、自发辐射：在没有外界影响时，它们会自发的从高能级E2向低能级E1跃迁，同时放出能量为hu的光子，这种与外界影响无关的、自发进行的辐射称为自发辐射。

2、受激辐射：如果原子系统的两个能级E2和E1满足辐射跃迁选择定则，当受到外来能量hu=E2-E1的光照射时，处在E2能级的原子有可能受到外来光的激励作用而跃迁到较低的能级E1上去，同时发射一个与外来光子完全相同的光子。

3、自发辐射和受激辐射的区别：①自发辐射是非相干光，受激辐射是相干光。

②自发辐射跃迁几率就是自发辐射本身，而受激辐射的跃迁几率决定于受激辐射系数与外来光单色辐射能量密度的乘积。

③当受激辐射系数B21一定时，外来光的单色辐射能量密度越大，受激辐射几率越高。

4、受激吸收：处于低能级E1的原子受到一个外来光子的激励作用，完全吸收该光子的能量而跃迁到高能级E2的过程，叫作受激吸收。

5、自发辐射、受激辐射、受激吸收之间的关系：在光和大量原子系统的相互作用中，三者之间三种过程是同时发生的。

A21n2dt+B21n2ρvdt=B12n1ρvdt（自发辐射光子数+受激辐射光子数=受激吸收光子数）6、自然增宽:在不受外界影响时，处于激发态的粒子会自发的向低能态跃迁。

也就是说，在自发辐射发光过程中，能量不断衰减，电偶极子的正负中心不再做简谐振动，从而导致光谱线有一定的宽度，叫做自然增宽。

(洛伦兹线型函数)7、均匀增宽介质和非均匀增宽介质的区别:均匀增宽：(1)自然加宽（普遍存在，但在固体工作物质中可忽略）—源于不确定性原理(2)碰撞加宽（存在于气体工作物质中）—源于气体分子碰撞导致的上能级粒子寿命变化(3)晶格振动加宽（存在于固体工作物质中）—源于固体中激光工作粒子在晶格附近的热振动。

非均匀增宽：(1)多普勒加宽（存在于气体工作物质中）——源于工作物质不断地运动而产生的多普勒频移(2)晶格缺陷加宽（存在于固体工作物质中）——源于固体加工时内部产生的晶格缺陷导致工作粒子所处状态不完全相同8、光谱线宽度:通常定义Δv=v2-v1,即相对光强为最大值的1/2处的频率间隔叫做光谱线的半(值)宽度，简称光谱线宽度。

激光原理与激光技术习题答案《激光原理与激光技术》堪误表见下方习题一(1)为使氦氖激光器的相干长度达到1m ，它的单色性∆λ/λ应为多大？解： 10101032861000106328--⨯=⨯=λ=λλ∆=.L R c(2) λ=5000Å的光子单色性∆λ/λ=10-7，求此光子的位置不确定量∆x解： λ=h p λ∆λ=∆2h p h p x =∆∆ m R p h x 5101050007102=⨯=λ=λ∆λ=∆=∆--(3)CO 2激光器的腔长L=100cm ，反射镜直径D=1.5cm ，两镜的光强反射系数分别为r 1=0.985,r 2=0.8。

求由衍射损耗及输出损耗分别引起的δ、τc 、Q 、∆νc (设n=1)解： 衍射损耗: 1880107501106102262.).(.a L =⨯⨯⨯=λ=δ-- s ..c L c 881075110318801-⨯=⨯⨯=δ=τ 686810113107511061010314322⨯=⨯⨯⨯⨯⨯⨯=πντ=--....Q cMHz .Hz ...c c 19101910751143212168=⨯=⨯⨯⨯=πτ=ν∆- 输出损耗: 1190809850502121.)..ln(.r r ln =⨯⨯-=-=δ s ..c L c 881078210311901-⨯=⨯⨯=δ=τ 686810964107821061010314322⨯=⨯⨯⨯⨯⨯⨯=πντ=--....Q c MHz .Hz ...c c 75107510782143212168=⨯=⨯⨯⨯=πτ=ν∆-(4)有一个谐振腔，腔长L=1m ，两个反射镜中，一个全反，一个半反，半反镜反射系数r=0.99，求在1500MHz 的范围内所包含的纵模个数，及每个纵模的线宽(不考虑其它损耗)解： MHz Hz .L c q 150105112103288=⨯=⨯⨯==ν∆ 11]11501500[]1[=+=+ν∆ν∆=∆q q005.0201.02===T δ s c L c 781067.6103005.01-⨯=⨯⨯==δτ MHz cc 24.01067.614.321217=⨯⨯⨯==-πτν∆(5) 某固体激光器的腔长为45cm ，介质长30cm ，折射率n=1.5，设此腔总的单程损耗率0.01π，求此激光器的无源腔本征纵模的模式线宽。

激光原理第二章习题答案1．估算2CO 气体在室温(300K)下的多普勒线宽D ν∆和碰撞线宽系数α。

并讨论在什么气压范围内从非均匀加宽过渡到均匀加宽。

解：2CO 气体在室温(300K)下的多普勒线宽D ν∆为11822770693103007.16107.161010.61044 0.05310HzD T M νν---⨯⎛⎫⎛⎫∆=⨯=⨯⨯⨯ ⎪ ⎪⨯⎝⎭⎝⎭=⨯ 2CO 气体的碰撞线宽系数α为实验测得，其值为49KHz/Pa α≈2CO 气体的碰撞线宽与气压p 的关系近似为L p να∆=当L D νν∆=∆时，其气压为930.053101081.6Pa 4910Dp να∆⨯===⨯所以，当气压小于1081.6Pa 的时候以多普勒加宽为主，当气压高于1081.6Pa 的时候，变为以均匀加宽为主。

2．考虑某二能级工作物质，2E 能级自发辐射寿命为s τ，无辐射跃迁寿命为τ。

假定在t=0时刻能级2E 上的原子数密度为2(0)n ，工作物质的体积为V ，自发辐射光的频率为ν，求：(1)自发辐射光功率随时间t 的变化规律；(2)能级2E 上的原子在其衰减过程中发出的自发辐射光子数；(3)自发辐射光子数与初始时刻能级2E 上的粒子数之比2η，2η称为量子产额。

解：(1) 在现在的情况下有可以解得：11()22()(0)s tn t n eττ-+=可以看出，t 时刻单位时间内由于自发辐射而减小的能级之上的粒子数密度为2/s n τ，这就是t 时刻自发辐射的光子数密度，所以t 时刻自发辐射的光功率为：222()()s dn t n ndt ττ=-+(2) 在t dt →时间内自发辐射的光子数为：所以(3) 量子产额为：3．根据红宝石的跃迁几率数据：7151332312121310.510,310,0.310,S sA sA s S S ---=⨯=⨯=⨯=估算13W 等于多少时红宝石对694.3nm λ=的光是透明的。

第一章1、激光与普通光源相比有三个主要特点：方向性好，相干性好，亮度高。

2、激光主要是光的受激辐射，普通光源主要光的自发辐射。

3、光的一个基本性质就是具有波粒二象性。

光波是一种电磁波，是一种横波。

4、常用电磁波在可见光或接近可见光的范围，波长为0.3~30μm,其相应频率为10^15~10^13。

5、具有单一频率的平面波叫作单色平面波，如果频率宽度Δν<<v 时，这种波叫作准单色波。

6、原子处于最低的能级状态称为基态，能量高于基态的其他能级状态叫作激发态。

7、两个或两个以上的不同运动状态的电子可以具有相同的能级，这样的能级叫作简并能级。

8、同一能级所对应的不同电子运动状态的数目，叫作简并度，用字母g表示。

9、辐射跃迁选择定则（本质：状态一定要改变），原子辐射或吸收光子，不是在任意两能级之间跃迁，能级之间必须满足下述选择定则：a、跃迁必须改变奇偶态；b、ΔJ=0，±1（J=0→J=0除外）；对于采用LS耦合的原子还必须满足下列选择定则：c、ΔL=0，±1（L=0→L=0除外）；d、ΔS=0，即跃迁时S不能发生改变。

10、大量原子所组成的系统在热平衡状态下，原子数按能级分布服从玻耳兹曼定律。

11、处于高能态的粒子数总是小于处在低能态的粒子数，这是热平衡情况的一般规律。

12、因发射或吸收光子从而使原子造成能级间跃迁的现象叫作辐射跃迁，必须满足辐射跃迁选择定则。

13、光与物质的相互作用有三种不同的基本过程：自发辐射，受激辐射，和受激吸收。

14、普通光源中自发辐射起主要作用，激光工作过程中受激辐射起主要作用。

15、与外界无关的、自发进行的辐射称为自发辐射。

自发辐射的光是非相干光。

16、能级平均寿命等于自发跃迁几率的倒数。

17、受激辐射的特点是：a、只有外来光子的能量hv=E2-E1时，才能引起受激辐射。

b、受激辐射所发出的的光子与外来光子的特性完全相同（频率相同，相位相同，偏振方向相同，传播方向相同）。