渐开线齿轮无侧隙啮合方程推导

1 设计应满足的条件1. 正确啮合条件一对渐开线齿廓能保证定传动比传动，但这并不表明任意两个渐开线齿轮都能搭配起来正确啮合传动。

为了正确啮合，还必须满足一定的条件。

图示一对渐开线齿轮同时有两对齿参加啮合，两轮齿工作侧齿廓的啮合点分别为K和K'。

为了保证定传动比，两啮合点K和K'必须同时落在啮合线N1N2上；否则，将出现卡死或冲击的现象。

这一条件可以表述为。

和分别为齿轮1和齿轮2相邻同侧齿廓沿公法线上的距离，称为法向齿距，用pn1、pn2表示。

因此，一对齿轮实现定传动比传的正确啮合件为两轮的法向齿距相等。

又由渐开线性质可知，齿轮法向齿距与基圆齿距相等，则该条件又可表述为两轮的基圆齿距相等，即将和代入上式得式中m1、m2和α1、α2分别为两轮的模数和压力角。

由于齿轮的模数和压力角都已标准化，要使上式成立，可以取来保证两轮的法向齿距相等。

因此，渐开线直齿圆柱齿轮的正确啮合条件最终表述为：两轮的模数和压力角分别相等。

2. 连续传动的条件（1）啮合传动过程齿轮传动是通过其轮齿交替啮合而实现的。

图所示为一对轮齿的啮合过程。

主动轮1顺时针方向转动，推动从动轮2作逆时针方向转动。

一对轮齿的开始啮合点是从动轮齿顶圆η2与啮合线N1N2的交点B2，这时主动轮的齿根与从动轮的齿顶接触，两轮齿进入啮合。

随着啮合传动的进行，两齿廓的啮合点将沿着啮合线向左下方移动。

一直到主动轮的齿顶圆η1与啮合线的交点B1，主动轮的齿顶与从动轮的齿根即将脱离接触，两轮齿结束啮合，B1点为终止啮合点。

线段为啮合点的实际轨迹，称为实际啮合线段。

当两轮齿顶圆加大时，点B1、B2分别趋于点N1、N2，实际啮合线段将加长。

但因基圆内无渐开线，故点B1、B2不会超过点N1、N2，点N1、N2称为极限啮合点。

线段是理论上最长的实际啮合线段，称为理论啮合线段。

2）连续传动条件连续传动条件为保证齿轮定传动比传动的连续性，仅具备两轮的基圆齿距相等的条件是不够的，还必须满足≥Pb。

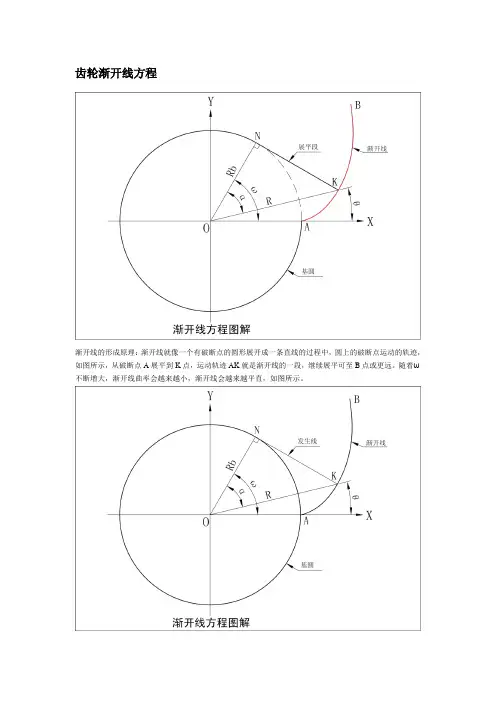
齿轮渐开线方程渐开线的形成原理：渐开线就像一个有破断点的圆形展开成一条直线的过程中，圆上的破断点运动的轨迹，如图所示，从破断点A展平到K点，运动轨迹AK就是渐开线的一段，继续展平可至B点或更远。

随着ω不断增大，渐开线曲率会越来越小，渐开线会越来越平直，如图所示。

渐开线方程的推理过程：如图所示，圆O为渐开线AB的基圆，半径为Rb,K为渐开线AB上的任一点；展平段KN为渐开线AB的发生线。

根据渐开线形成的原理可知，NO⊥NK，NK= N⌒A, ONK构成一个直角三角形。

以下过程将滚动角α（rad）作为已知变量进行推导：根据渐开线的形成原理可得N⌒A = NK，圆心角ω所对应的弧长：N⌒A =Rb*ω* PI /180, R=Rb/COS(α)。

先计算出OK与OX的夹角θ，根据渐开线函数公式θ=TAN(α)-α。

因为TAN(α)是N⌒A与Rb之比，相当于弧度值，所以此时α应换算为弧度值。

用PRO/E绘制方程曲线时，应将其转换为十进制角度。

即：θ=TAN(α)*180/PI-α，在PRO/E极坐标表示的方程中，θ用THETA表示。

A. 设α为压力角参数，将α用个人习惯的字母符号代替，如FAI。

设定一个参数值，如45°，即可写成：1. 压力角为参数“极坐标”表示的渐开线方程：FAI=T*45Rb=DB/2R=Rb/COS(FAI)THETA=TAN(FAI)*180/PI-FAIZ=0以上方程式是以压力角∠α作为变量参数。

若想使渐开线的长度控制在齿轮外径DW以内，就必须使渐开线K点与齿轮外径DW的边缘共线约束，可用∠α来控制。

因为齿轮的外径等于2*R=DW，基圆直径等于2*Rd=DB，渐开线K点与R的端点重合。

所以∠α应等于DB/DW的反余弦函数，即：∠α=ACOS(DB/DW)，此角就可使渐开线K点落在齿顶圆边缘的位置。

将其作为变量代入方程，即可写成：2. 齿顶圆压力角为参数控制的“极坐标”表示的渐开线方程A：以ACOS(DB/DW)作为已知变量进行推导，方程如下：FAI=T*ACOS(DB/DW)Rb=DB/2R=Rb/COS(FAI)THETA=TAN(FAI)*180/PI-FAIZ=0如果方程式是以滚角∠ω作为变量参数。

creo齿轮渐开线曲线方程介绍齿轮是机械传动中常见的一种元件，用于传递动力和转速。

在齿轮设计中，渐开线曲线是一种常用的曲线形状，它能够实现平稳的传动和减小齿轮的噪声。

本文将介绍creo软件中齿轮渐开线曲线的方程以及相关的设计原理和应用。

渐开线曲线的定义渐开线曲线是一种特殊的曲线形状，它的特点是齿轮齿面与传动方向垂直时，齿面上任意一点的切线与传动方向的夹角保持不变。

这种曲线形状能够实现平稳的传动和减小齿轮的噪声。

渐开线曲线方程的推导在creo软件中，我们可以通过一些参数来定义齿轮的渐开线曲线。

这些参数包括齿轮的模数、齿数、压力角等。

根据这些参数，我们可以推导出渐开线曲线的方程。

具体推导过程如下：1.首先，我们需要确定齿轮的基圆半径R。

基圆半径是齿轮齿面的中心线与齿轮齿面的交点到齿轮中心的距离。

2.接下来，我们可以根据齿轮的模数m和齿数z来计算齿轮的分度圆半径Rd。

分度圆半径是齿轮齿面的中心线与齿轮齿面的交点到齿轮中心的距离。

3.然后，我们可以根据齿轮的压力角α来计算齿轮的齿顶圆半径Rt和齿根圆半径Rb。

齿顶圆半径是齿轮齿面的最高点到齿轮中心的距离，齿根圆半径是齿轮齿面的最低点到齿轮中心的距离。

4.最后，我们可以根据齿轮的齿顶高度h和齿根高度c来计算齿轮的齿顶圆弧半径Rta和齿根圆弧半径Rba。

齿顶圆弧半径是齿轮齿面的最高点到齿轮中心的距离，齿根圆弧半径是齿轮齿面的最低点到齿轮中心的距离。

通过以上推导，我们可以得到齿轮渐开线曲线的方程。

渐开线曲线的设计原理渐开线曲线的设计原理是为了实现平稳的传动和减小齿轮的噪声。

在传动过程中，齿轮齿面上任意一点的切线与传动方向的夹角保持不变，这样可以减小齿轮的冲击和噪声。

此外，渐开线曲线还能够提高齿轮的传动效率和工作寿命。

渐开线曲线的应用渐开线曲线在齿轮设计中有着广泛的应用。

它可以用于各种类型的齿轮，如圆柱齿轮、锥齿轮、螺旋齿轮等。

渐开线曲线的应用可以提高齿轮传动的平稳性、减小齿轮的噪声、提高齿轮的传动效率和工作寿命。

渐开线齿轮几何参数学习总结一．渐开线1.1 渐开线的形成一条动直线（发生线）沿着一个固定圆（基圆）作纯滚动时，和该动直线固连点的轨迹线称渐开线。

由图一可知，固连点在动直线上的位置可分为A ，B ，C 三种情况。

A 点的轨迹线称缩短渐开线；C 点的渐开线称延伸渐开线；若C 点与基圆圆心重合，则延伸渐开线演变成了阿基米德螺旋线；B 点的轨迹线称圆的渐开线，简称渐开线。

三种渐开线总称广义渐开线。

A BC发生线基圆图一 基圆的形成现在工业上常用的渐开线齿轮齿形是圆的渐开线。

如未特别说明，下面提到的渐开线均指此类渐开线。

1.2 与渐开线有关的各种名称（1） 基圆—直线在其上滚动的定圆称为渐开线的基圆。

基圆的半径与直径分别用b r ，b d 表示。

（2） 发生线—沿基圆作纯滚动的直线称为渐开线的发生线（3） 压力角—渐开线齿形上任意一点K 的受力方向线与速度方向线之间的夹角称为K 点的压力角（4） 渐开角—渐开线上任意一点K 的向量半径与渐开线的起点的向量半径之间的夹角1.3 渐开线的性质（1） 发生线沿基圆滚过的长度，等于基圆上被滚过的圆弧长度。

即：⌒AN KN（2） 渐开线上任一点的法线一定是基圆的切线。

（3） 同一基圆所生成的任意两条反向渐开线间的公法线处处相等。

（4） 发生线与基圆的切点N 是渐开线K 点曲率中心，而发生线NK 是渐开线上K 点的曲率半径。

渐开线离基圆越圆的部分，其曲率越小，即渐开线越平直，渐开线越靠近基圆，其曲率越大，即渐开线越弯曲，曲率半径越小。

（5） 渐开线的形状与基圆大小有关。

基圆半径相等则渐开线完全相同，基圆半径越小，则渐开线越弯曲，基圆半径越大，则渐开线越平直，基圆半径为无穷大时，则渐开线变为一条直线。

（6） 基圆内无渐开线。

A1A2B1B2N1N212图二 渐开线的公法线 1.4 渐开线的方程 (1) 渐开线的极坐标方程k k k inv k kb r kαααθα-===tan cos r（2）渐开线的直角坐标方程αθααθcos cos cos sin x b r kinv y b r ===图三1.5 基于MATLAB 的渐开线齿轮齿廓建模 （1）程序流程图：输入ra,m,z,x,alpha将每个齿形视为三部分求出每部分极角范围采用极坐标分别绘制每段齿形采用循环绘制Z个齿（2）源程序function y=getinvolute(ra,m,z,x,alpha)rb=m*z*cosd(alpha)/2;for theta=0:0.1:2*pipolar(theta,rb);endhold onalpha1=acos(rb/ra);theta1=tan(alpha1)-alpha1;for i=0:zfor alpha2=0:0.01:alpha1theta2=tan(alpha2)-alpha2;rx=rb/cos(alpha2);polar(theta2+2*i*pi/z,rx);endendhold onfaib=(pi+4*x*tand(alpha))/z+2*(tand(alpha)-alpha/180*pi); x1=ra*cos(theta1);y1=ra*sin(theta1);x2=ra*cos(faib-theta1);y2=ra*sin(faib-theta1);k=(y2-y1)/(x2-x1);b=y1-k*x1;for i=0:zfor theta3=theta1:0.001:(faib-theta1)rzx=b/(sin(theta3)-k*cos(theta3));polar(theta3+2*i*pi/z,rzx);hold onendendfor i=0:zfor alpha4=0:0.01:alpha1theta4=faib-(tan(alpha4)-alpha4);rx2=rb/cos(alpha4);polar(theta4+2*i*pi/z,rx2);endendhold onaxis tightend（3）渐开线生成实例利用程序绘制的齿数为20，齿顶圆半径为22，模数为2，变位系数为0，20的齿轮齿廓曲线如下：压力角为二．渐开线标准直齿圆柱齿轮的基本参数及几何计算2.1 齿轮的基本参数h，径向间隙齿轮的基本参数为：齿数Z，模数m,压力角α，齿顶高系数*a系数*c，根据上述基本参数可推算出齿轮的几何尺寸。

齿轮啮合的基本条件公式
1. 齿轮正确啮合条件。

- 对于标准安装的渐开线齿轮，正确啮合条件是两轮的模数和压力角分别相等。

- 设齿轮1的模数为m_1，压力角为α_1；齿轮2的模数为m_2，压力角为α_2，则正确啮合条件公式为：
- m_1 = m_2=m（模数相等）
- α_1=α_2 = α（压力角相等），对于标准齿轮，α = 20^∘。

2. 连续传动条件。

- 齿轮连续传动的条件是重合度varepsilon≥slant1。

- 重合度varepsilon的计算公式为varepsilon=(1)/(2π)[z_1(tanα_a1-tanα') +
z_2(tanα_a2-tanα')]，其中z_1、z_2分别为两齿轮的齿数，α_a1、α_a2分别为两齿轮齿顶圆压力角，α'为啮合角。

- 齿顶圆压力角α_a的计算公式为cosα_a=(r_b)/(r_a)，其中r_b为基圆半径，r_a为齿顶圆半径。

对于标准齿轮，r_b = rcosα（r为分度圆半径），r_a=r + h_a^*m （h_a^*为齿顶高系数，对于标准齿轮h_a^*=1）。

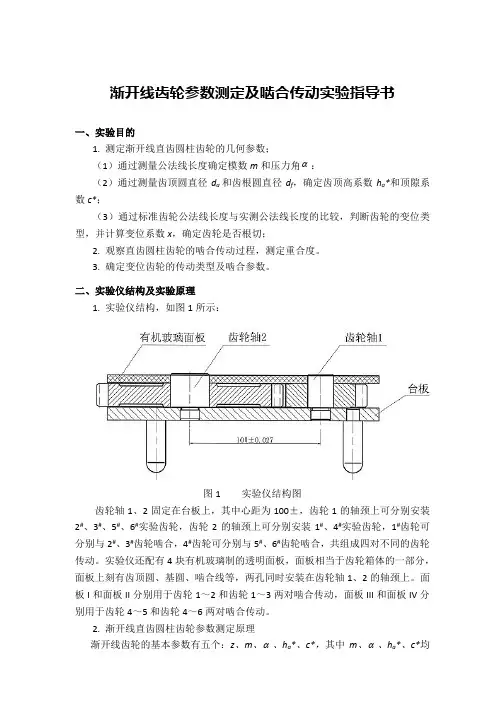
渐开线齿轮参数测定及啮合传动实验指导书一、实验目的1. 测定渐开线直齿圆柱齿轮的几何参数；（1）通过测量公法线长度确定模数m和压力角α：（2）通过测量齿顶圆直径d a和齿根圆直径d f，确定齿顶高系数h a*和顶隙系数c*；（3）通过标准齿轮公法线长度与实测公法线长度的比较，判断齿轮的变位类型，并计算变位系数x，确定齿轮是否根切；2. 观察直齿圆柱齿轮的啮合传动过程，测定重合度。

3. 确定变位齿轮的传动类型及啮合参数。

二、实验仪结构及实验原理1. 实验仪结构，如图1所示：图1 实验仪结构图齿轮轴1、2固定在台板上，其中心距为100±，齿轮1的轴颈上可分别安装2#、3#、5#、6#实验齿轮，齿轮2的轴颈上可分别安装1#、4#实验齿轮，1#齿轮可分别与2#、3#齿轮啮合，4#齿轮可分别与5#、6#齿轮啮合，共组成四对不同的齿轮传动。

实验仪还配有4块有机玻璃制的透明面板，面板相当于齿轮箱体的一部分，面板上刻有齿顶圆、基圆、啮合线等，两孔同时安装在齿轮轴1、2的轴颈上。

面板I和面板II分别用于齿轮1～2和齿轮1～3两对啮合传动，面板III和面板IV分别用于齿轮4～5和齿轮4～6两对啮合传动。

2. 渐开线直齿圆柱齿轮参数测定原理渐开线齿轮的基本参数有五个：z、m、α、h a*、c*，其中m、α、h a*、c*均应取标准值，z 为正整数。

对于变位齿轮，还有一个重要参数，即变位系数x ，变位齿轮及变位齿轮传动的诸多尺寸均与x 有关。

（1）通过测量公法线长度确定模数m 和压力角α，见图2。

① 确定跨齿数k ：20.5cot 180xk z ααπ=++o② 测量公法线长度k W '和1k W +'。

③ 确定模数m 、压力角α：图2 用游标卡尺测公法线长度根据渐开线性质：发生线沿基圆滚过的长度，等于基圆上被滚过的弧长。

(1)k b b W k p s '=-+ 1k b b W kp s +'=+所以1cos b k k p W W m πα+''=-=式中因α一般只为20。

2012-2-27最近我在研究渐开线齿轮的参数化建模问题。

经过一番搜索，在网上发现了一篇文章中关于用CATIA V5参数化建模的齿轮参数列表和计算公式。

序号参数类型或单位公式描述1 a 角度(deg) 标准值：20deg 压力角：（10deg≤a≤20deg）2 m 长度(mm) ——模数3 z 整数——齿数（5≤z≤200）4 p 长度(mm) m * π齿距5 ha 长度(mm) m 齿顶高=齿顶到分度圆的高度6 hf 长度(mm) if m > ，hf = m * ；else hf = m *齿根高=齿根到分度圆的深度7 rp 长度(mm) m * z / 2 分度圆半径8 ra 长度(mm) rp + ha 齿顶圆半径9 rf 长度(mm) rp - hf 齿根圆半径10 rb 长度(mm) rp * cos( a ) 基圆半径11 rr 长度(mm) m * 齿根圆角半径12 t 实数0≤t≤1渐开线变量13 xd 长度(mm) rb * ( cos(t * π) +sin(t * π) * t * π ) 基于变量t的齿廓渐开线X坐标14 yd 长度(mm) rb * ( sin(t * π) -cos(t * π) * t *π )基于变量t的齿廓渐开线X坐标15 b 角度(deg) ——斜齿轮的分度圆螺旋角16 L 长度(mm) ——齿轮的厚度此表来自网络，多谢网友分享。

（使用时个别地方还是要参考一下机械设计手册）我觉得，干咱们这一行的不仅要知其然，更要知其所以然。

下面我将渐开线的坐标公式做如下推导：渐开线的形成及其性质：如图1所示，当直线BK沿半径为br的圆周作纯滚动时，直线上任一点K的轨迹»AK就是该圆的渐开线。

这个圆称为渐开线的基圆，半径b r 称为基圆半径，直线BK 称为渐开线的发生线，k θ=AOK ∠称为渐开线上点K 的展角。

由渐开线的形成过程，可得渐开线的性质如下：（1） 发生线沿基圆滚过的长度，等于基圆上被滚过圆弧的长度，即»KB AB =。

2012-2-27最近我在研究渐开线齿轮的参数化建模问题。

经过一番搜索，在网上发现了一篇文章中关于用CATIA V5参数化建模的齿轮参数列表和计算公式。

序号参数类型或单位公式描述1 a 角度(deg) 标准值：20deg 压力角：（10deg≤a≤20deg）2 m 长度(mm) ——模数3 z 整数——齿数（5≤z≤200）4 p 长度(mm) m * π齿距5 ha 长度(mm) m 齿顶高=齿顶到分度圆的高度6 hf 长度(mm) if m > 1.25 ，hf = m * 1.25；else hf = m * 1.4齿根高=齿根到分度圆的深度7 rp 长度(mm) m * z / 2 分度圆半径8 ra 长度(mm) rp + ha 齿顶圆半径9 rf 长度(mm) rp - hf 齿根圆半径10 rb 长度(mm) rp * cos( a ) 基圆半径11 rr 长度(mm) m * 0.38 齿根圆角半径12 t 实数0≤t≤1渐开线变量13 xd 长度(mm) rb * ( cos(t * π) +sin(t *π) * t * π )基于变量t的齿廓渐开线X坐标14 yd 长度(mm) rb * ( sin(t * π) -cos(t * π) * t *π )基于变量t的齿廓渐开线X坐标15 b 角度(deg) ——斜齿轮的分度圆螺旋角16 L 长度(mm) ——齿轮的厚度此表来自网络，多谢网友分享。

（使用时个别地方还是要参考一下机械设计手册）我觉得，干咱们这一行的不仅要知其然，更要知其所以然。

下面我将渐开线的坐标公式做如下推导：渐开线的形成及其性质：如图1所示，当直线BK沿半径为br的圆周作纯滚动时，直线上任一点K的轨迹AK就是该圆的渐开线。

这个圆称为渐开线的基圆，半径b r 称为基圆半径，直线BK 称为渐开线的发生线，k θ=AOK ∠称为渐开线上点K 的展角。

由渐开线的形成过程，可得渐开线的性质如下：（1） 发生线沿基圆滚过的长度，等于基圆上被滚过圆弧的长度，即KB AB =。

【转】Pro/E齿轮渐开线方程的推导
2011-03-26 14:12
转载自knowwei
最终编辑knowwei
先看渐开线型成动画：
渐开线的数学定义：在平面上,一条动直线沿一个固定的圆作纯滚动时,此动直线上一点的轨
迹,称为渐开线。

以下图片为方程推导过程：
所以渐开线的圆柱座标方程为：
R=Rb*sqrt(1+ω^2)
θ=ω-atan(ω) ---- 注意此方程的角度为弧度制
在Pro/E中若以Datum Curve=>From Equation绘出渐开线的话，应该将ω转成十进制。

于是有:
A= t * 45 ---- 假设滚动角ω为0-45度，要留意滚动角也就是以后齿轮的压力角了
R= Rb * sqrt( 1+ ( A * pi/180 )^2 )
theta = A - atan ( A * pi/180 )
z = 0
上式中theta = A - atan ( A * pi/180 )为何是这样，而不是theta = A * pi/180 - atan ( A * pi/180 )。

留待各位思考吧！。

渐开线方程推导性质1：渐开线的形状仅取决于基圆；Propertyof the involute：推论1：齿轮的渐开线形状仅取决于m、z、a，即模数、齿数、压力角；性质2：基圆内无渐开线；性质3：发生线沿基圆滚过的长度，等于基圆上被滚过的长度，即KN AN；性质4：渐开线上任一点的法线恒与基圆相切；Illumination：图1渐开线方程推导青色带箭头的线――构成正交直角坐标系，O点为坐标原点；图中，绿色的圆――基圆、即渐开线发生圆，KN为渐开线发生线，基圆半径为rb；蓝色曲线AKB――渐开线，A为始端，B为终端，K为渐开线上任一动点；蓝色直线OK――连接基圆圆心O与动点K的矢径，OK；蓝色直线KV――动点K的速度矢量KV，垂直于矢径OK；绿色直线 KN――动点 K 的法线，根据渐开线的性质 4，设法线与基圆相切于 N ，连接 NO ；法线方向即为两齿轮啮合传动时、力矢的方向 KF ；紫色直线 NQ――切点 N 向 X 轴作垂线，垂足为 Q ； 紫色直线 KP――动点 K 向直线 NQ 作垂线，垂足为 P ； Definition ：KOA 称为展角，记为 κ；NOA 称为滚动角，记为 κ ；速度矢 KV 与力矢 KF 的夹角称为压力角，记为 κ ， 即图 1 中 VKN ；BecauseVKN OKN 90AndNOK OKN 90That isNOK VKN k滚动角＝展角+压力角；Evolution in polar coordinates ：在极坐标系中，渐开线方程可写为：r k OK br / cos(κ) k kkAN r b KN k r b k tan( κ)k即，r k br / cos(κ) κ τan( κ) kEvolution in Cartesian coordinates ：在直角坐标系中，渐开线方程可写为（关键是两条紫色的辅助线，注意：KNP 90 ONQ k）：x k OQ P Ky k NQ N P ON *cos( κ) N K *sin( κ) ON *cos( κ) A N *sin( κ) br *cos( κ) br * κ * sin( κ)即，x k br *cos(κ) βr * κ* sin( κ)ON *sin( κ) N K *cos( κ) ON *sin( κ) A N *cos( κ) br *sin( κ) br * κ * cos( κ)y k br *sin( κ) βr * κ* cos( κ)Supplement ：由以上推导可得出展角、滚动角、压力角三者之间的关系：κ τan( κ)kκ τan( κ)κ κ ktan( κ) κk即， 展角 滚动角滚动角；；＝ 压力角的正切－压力角； ＝ 压力角的正切；＝ 压力角+展角；压力角的正切 ＝ 压力角+展角；注 1：本文角度单位为弧度制；注 2：图 1 中的角 a ，b ，c 分别对应正文中的 κ, κ, κ ， 即压力角，展角，滚动角。