行阶梯形变换等价于矩阵乘法——LU分解
- 格式:pdf
- 大小:240.51 KB
- 文档页数:2

2矩阵代数1. 设A,B为可以相乘的矩阵,AB的每一列都是A的各列的线性组合,以B的对应列的元素为权。
同样,AB的每一行都是B的各行的线性组合,以A的对应行的元素为权。
例如,AB的第m列是以B的第m列为权的A的各列的线性组合;AB的第n行是以A的第n行为权的B的各行的线性组合。
2. 矩阵乘法恒等式:I m A = A = AI n3. 逆矩阵的概念仅对方阵有意义。
4. 若A可逆,则对每一R n中的b,方程Ax=b有唯一解x=A-1b5. 初等矩阵:将单位矩阵进行一次初等行变换所得的矩阵。
6. 对mxn矩阵A进行初等行变换所得的矩阵,等于对单位矩阵进行相同行变换所得初等矩阵与A相乘的结果。
设对单位矩阵I m进行初等行变换所得初等矩阵为E,对A进行相同初等行变换的结果可写为EA。
因为初等行变换可逆,所以必有另一行变换将E变回I。
设该“另一行变换”对应初等矩阵为F,结合上一行,F对E的作用可写为FE=I。
因此,每个初等矩阵均可逆。
7. 当n阶方阵A行等价于I n时,A可逆。
此时,将A变为I n的一系列初等行变换同时将I n变为A-1。
8. 求A-1:将增广矩阵[A I] 进行行化简,若A可逆,则[A I] ~ [I A-1]将 [A I] 行变换为[I A-1]的过程可看作解n个方程组:Ax=e1, Ax=e2, ... Ax=e n这n个方程组的“增广列”都放在A的右侧,就构成矩阵[A e1 e2 ... e n] = [A I]如果我们只需要A-1的某一列或某几列,例如需要A-1的j列,只需解方程组Ax=e j,而不需要求出整个A-1。
[注:根据此条可以导出利用克拉默法则求逆矩阵的公式]9. 可逆矩阵定理对于n阶方阵,以下命题等价:a) A可逆b) A与n阶单位矩阵等价c) A有n个主元位置d) 方程Ax=0仅有平凡解e) A各列线性无关f) 线性变换x|->Ax是一对一的g) 对R n中任意b,Ax=b至少有一个解(有且仅有唯一解?)h) A各列生成R ni) 线性变换x|->Ax将R n映上到R nj) 存在nxn阶矩阵B,使AB=BA=Ik) A T可逆l) A的列向量构成R n的一个基m) ColA=R nn) dim(Col(A))=no) rank(A)=np) Nul(A)=0q) dim(Nul(A))=0r) det(A)≠0 <=> A可逆s) A可逆当且仅当0不是A的特征值t) A可逆当且仅当A的行列式不等于零再次强调,以上命题仅对n阶方阵等价。




一:LU解法:# include<iostream>//命名空间的声明using namespace std;int i,j,k;//程序的入口点主函数int main(){//声明两个全局变量double s1=0,s2=0;//定义一个二维矩阵来存储该线性方程组的系数double A[4][4]={{2,-1,0,0},{-1,2,-1,0},{0,-1,2,-1},{0,0,-1,2}};//定义一个一维数组来存储该线性方程组的右端项double B[4]={1,0,0,1};//声明两个二维数组的长度分别是四行四列double L[4][4];double U[4][4];//利用双重for 循环使得下三角矩阵L的上三角元素以及上三角矩阵U的下三角元素都为0for( i=0;i<4;i++){for( j=i+1;j<4;j++){L[i][j]=0;U[j][i]=0;}}//利用双重for 循环将下三角矩阵L的对角线上的元素都初始化为1for( i=0;i<4;i++)for( j=0;j<4;j++)if(i==j)L[i][j]=1;//利用for 循环根据系数矩阵A 以及右端矩阵B 来计算下三角矩阵L 以及上三角矩阵U 的其他元素for( i=0;i<4;i++){for( j=i;j<4;j++)//求上三角矩阵u的第一行以及下三角矩阵l的第一列if(i==0){U[i][j]=A[i][j]/L[i][i];L[j][i]=A[j][i]/U[i][i];}//接下来再继续求u的行元素以及l的列元素else{//加入一个循环来求其中涉及到的求和式for( k=0;k<i;k++){s1+=L[i][k]*U[k][j];s2+=L[j][k]*U[k][i];}//上三角u的行元素以及下三角l的列元素U[i][j]=(A[i][j]-s1)/L[i][i];L[j][i]=(A[j][i]-s2)/U[i][i];//清空全局变量s1 s2 的值s1=s2=0;}}//最后利用for 循环分别将下三角矩阵L的所有元素全部输出for( i=0;i<4;i++){for(j=0;j<4;j++)cout<<L[i][j]<<" ";cout<<endl<<endl;}//换行语句cout<<endl<<endl;//利用for 循环将上三角矩阵U的所有元素全部输出for(i=0; i<4;i++){for(j=0;j<4;j++)cout<<U[i][j]<<" ";cout<<endl<<endl;}cout<<endl<<endl;return 0;}。

matlab的lu分解(实用版)目录1.MATLAB 的 LU 分解简介2.LU 分解的算法原理3.MATLAB 中进行 LU 分解的方法4.LU 分解的应用示例5.总结正文一、MATLAB 的 LU 分解简介LU 分解(LU Factorization)是一种常见的线性代数方法,用于将一个给定的矩阵分解为一个下三角矩阵和一个上三角矩阵的乘积。
这种分解方法在求解线性方程组、矩阵的特征值和特征向量等问题中具有广泛的应用。
MATLAB(Matrix Laboratory)是一款强大的数学软件,提供了丰富的矩阵操作和线性代数计算功能,其中就包括 LU 分解。
二、LU 分解的算法原理LU 分解的核心思想是高斯消元法,其基本步骤如下:1.对矩阵进行初等行变换,化为行最简阶梯形矩阵。
2.对阶梯形矩阵进行高斯消元,得到一个下三角矩阵和一个上三角矩阵。
3.将下三角矩阵和上三角矩阵组合成一个 LU 分解矩阵。
三、MATLAB 中进行 LU 分解的方法在 MATLAB 中,可以使用`lu`函数进行 LU 分解。
以下是一个简单的示例:```matlab% 定义一个矩阵 AA = [1 2 3; 4 5 6; 7 8 9];% 对矩阵 A 进行 LU 分解[L, U] = lu(A);% 输出 LU 分解结果disp("LU 分解结果:");disp(L);disp(U);```四、LU 分解的应用示例LU 分解在求解线性方程组方面具有广泛的应用。
例如,给定线性方程组:```AX = B```其中 A 是系数矩阵,X 是待求解的变量向量,B 是常数项向量。
可以通过 LU 分解求解该线性方程组。
具体步骤如下:1.对系数矩阵 A 进行 LU 分解,得到分解矩阵 L 和 U。
2.计算 U 的逆矩阵 U^-1。
3.将线性方程组改写为:```LUX = B```4.求解得到:```X = U^-1B```五、总结MATLAB 的 LU 分解功能为线性代数计算提供了极大的便利,可以帮助用户轻松地解决许多实际问题。

线性方程组解法总结与应用线性方程组是数学中的基础概念,广泛应用于各个领域,如物理学、经济学、工程学等。
解决线性方程组的问题对于理解和应用这些领域的知识至关重要。
本文将总结一些常见的线性方程组解法,并探讨其在实际问题中的应用。
一、高斯消元法高斯消元法是解决线性方程组的经典方法之一。
其基本思想是通过一系列的行变换将线性方程组转化为简化的行阶梯形式,从而求解方程组的解。
高斯消元法的优势在于其简单直观的操作步骤,适用于各种规模的线性方程组。
在实际应用中,高斯消元法常用于解决矩阵方程组的问题。
例如,在电力系统中,通过电流和电压的关系可以建立一个矩阵方程组,通过高斯消元法可以求解出电流和电压的值,从而实现对电力系统的分析和控制。
二、矩阵的逆与克拉默法则矩阵的逆是另一种常见的线性方程组解法。
当线性方程组的系数矩阵可逆时,可以通过求解矩阵的逆来得到方程组的解。
这种方法在计算机科学和工程学中得到广泛应用,例如在图像处理中,通过求解逆矩阵可以实现图像的旋转、缩放和变换。
克拉默法则是一种基于行列式的线性方程组解法。
它通过计算方程组的行列式和各个未知数的行列式来求解方程组的解。
克拉默法则的优势在于其简单的计算步骤,适用于规模较小的线性方程组。
在经济学中,克拉默法则常用于求解供求模型和投资决策模型等问题。
三、矩阵分解方法矩阵分解方法是一种将线性方程组转化为矩阵乘法的解法。
常见的矩阵分解方法包括LU分解、QR分解和奇异值分解等。
这些方法通过将系数矩阵分解为两个或多个矩阵的乘积,从而简化方程组的求解过程。
LU分解是将系数矩阵分解为一个下三角矩阵和一个上三角矩阵的乘积。
它的优势在于可以将线性方程组的求解过程分解为两个步骤,从而提高计算效率。
在计算机图形学中,LU分解常用于求解图像变换和光照模型等问题。
QR分解是将系数矩阵分解为一个正交矩阵和一个上三角矩阵的乘积。
它的优势在于可以将线性方程组的求解问题转化为最小二乘问题,从而提高求解的精度。

矩阵解方程组的方法全文共四篇示例,供读者参考第一篇示例:矩阵是线性代数中的重要概念,而矩阵解方程组也是线性代数中的基础内容之一。
在实际应用中,往往会遇到包含多个未知数和多个方程的方程组,如何通过矩阵的方法来高效地解决这些方程组成了一项重要的技能。
本文将介绍矩阵解方程组的方法,包括高斯消元法、矩阵求逆法以及克拉默法则等。
一、高斯消元法高斯消元法是解线性方程组的一种基本方法。
它的基本思想是通过对方程组进行一系列的行变换,将其转化为简化的阶梯形或行最简形,从而得到方程组的解。
下面通过一个具体的例子来说明高斯消元法的应用。
考虑如下的线性方程组:\begin{cases}2x + 3y - z = 1 \\3x + 2y + z = 3 \\x - y + 2z = 9\end{cases}首先将上述的方程组写成增广矩阵的形式:然后通过一系列的行变换,将增广矩阵转化为简化的阶梯形:\begin{bmatrix}1 & -1 &2 & | & 9 \\0 & 5 & -5 & | & -10 \\0 & 0 & 1 & | & 0\end{bmatrix}最后通过反向代入法,可以求得方程组的解为x=2, y=-2, z=0。
二、矩阵求逆法A = \begin{bmatrix}1 &2 \\2 & 1\end{bmatrix},X = \begin{bmatrix}x \\y\end{bmatrix},B = \begin{bmatrix}3 \\4\end{bmatrix}然后求解系数矩阵A 的逆矩阵A^{-1}:最后通过矩阵乘法,可以求得方程组的解为X = A^{-1}B =\begin{bmatrix}1 \\1\end{bmatrix}。
三、克拉默法则首先求解系数矩阵A 的行列式|A|:然后求解系数矩阵A 分别替换成结果矩阵B 的行列式|B_x| 和|B_y|:最后通过克拉默法则,可以求得方程组的解为x = \frac{|B_x|}{|A|} = \frac{-5}{-3} = \frac{5}{3},y = \frac{|B_y|}{|A|} = \frac{-2}{-3} = \frac{2}{3}。

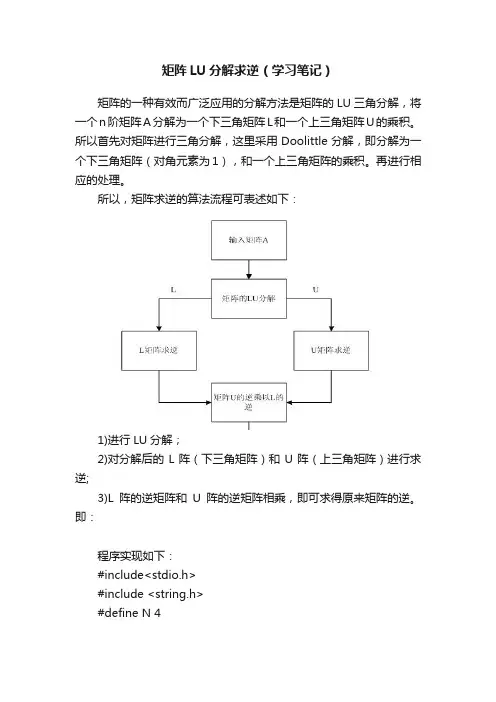
矩阵LU分解求逆(学习笔记)矩阵的一种有效而广泛应用的分解方法是矩阵的LU三角分解,将一个n阶矩阵A分解为一个下三角矩阵L和一个上三角矩阵U的乘积。
所以首先对矩阵进行三角分解,这里采用Doolittle分解,即分解为一个下三角矩阵(对角元素为1),和一个上三角矩阵的乘积。
再进行相应的处理。
所以,矩阵求逆的算法流程可表述如下:1)进行LU分解;2)对分解后的L阵(下三角矩阵)和U阵(上三角矩阵)进行求逆;3)L阵的逆矩阵和U阵的逆矩阵相乘,即可求得原来矩阵的逆。
即:程序实现如下:#include<stdio.h>#include <string.h>#define N 4void main(){float a[N][N];float L[N][N],U[N][N],out[N][N], out1[N][N];float r[N][N],u[N][N];memset( a , 0 , sizeof(a)); //初始化memset( L , 0 , sizeof(L));memset( U , 0 , sizeof(U));memset( r , 0 , sizeof(r));memset( u , 0 , sizeof(u));int n=N;int k,i,j;int flag=1;float s,t;////////////////////input a matrix////printf("input A=\n");for(i=0;i<n;i++)for(j=0;j<n;j++)scanf("%f",&a[i][j]);//////////////////figure the input matrix//////////////////////////printf("输入矩阵:\n");for(i=0;i<n;i++){for (j = 0; j < n; j++){printf("%lf ", a[i][j]);}printf("\n");}for(j=0;j<n;j++)a[0][j]=a[0][j]; //计算U矩阵的第一行for(i=1;i<n;i++)a[i][0]=a[i][0]/a[0][0]; //计算L矩阵的第1列for(k=1;k<n;k++){for(j=k;j<n;j++){s=0;for (i=0;i<k;i++)s=s+a[k][i]*a[i][j]; //累加a[k][j]=a[k][j]-s; //计算U矩阵的其他元素}for(i=k+1;i<n;i++){t=0;for(j=0;j<k;j++)t=t+a[i][j]*a[j][k]; //累加a[i][k]=(a[i][k]-t)/a[k][k]; //计算L矩阵的其他元素}}for(i=0;i<n;i++)for(j=0;j<n;j++){if(i>j){L[i][j]=a[i][j];U[i][j]=0;}//如果i>j,说明行大于列,计算矩阵的下三角部分,得出L的值,U的//为0else{U[i][j]=a[i][j];if(i==j)L[i][j]=1; //否则如果i<j,说明行小于列,计算矩阵的上三角部分,得出U的//值,L的为0elseL[i][j]=0;}}if(U[1][1]*U[2][2]*U[3][3]*U[4][4]==0){flag=0;printf("\n逆矩阵不存在");}if(flag==1){/////////////////////求L和U矩阵的逆for (i=0;i<n;i++) /*求矩阵U的逆 */{u[i][i]=1/U[i][i];//对角元素的值,直接取倒数for (k=i-1;k>=0;k--){s=0;for (j=k+1;j<=i;j++)s=s+U[k][j]*u[j][i];u[k][i]=-s/U[k][k];//迭代计算,按列倒序依次得到每一个值,}}for (i=0;i<n;i++) //求矩阵L的逆{r[i][i]=1; //对角元素的值,直接取倒数,这里为1for (k=i+1;k<n;k++){for (j=i;j<=k-1;j++)r[k][i]=r[k][i]-L[k][j]*r[j][i]; //迭代计算,按列顺序依次得到每一个值}}/////////////////绘制矩阵LU分解后的L和U矩阵///////////////////////printf("\nLU分解后L矩阵:");for(i=0;i<n;i++){printf("\n");for(j=0;j<n;j++)printf(" %lf",L[i][j]);}printf("\nLU分解后U矩阵:");for(i=0;i<n;i++){printf("\n");for(j=0;j<n;j++)printf(" %lf",U[i][j]);}printf("\n");////////绘制L和U矩阵的逆矩阵printf("\nL矩阵的逆矩阵:");for(i=0;i<n;i++){printf("\n");for(j=0;j<n;j++)printf(" %lf",r[i][j]);}printf("\nU矩阵的逆矩阵:");for(i=0;i<n;i++){printf("\n");for(j=0;j<n;j++)printf(" %lf",u[i][j]);}printf("\n");//验证将L和U相乘,得到原矩阵printf("\nL矩阵和U矩阵乘积\n"); for(i=0;i<n;i++){for(j=0;j<n;j++){out[i][j]=0;}}for(i=0;i<n;i++){for(j=0;j<n;j++){for(k=0;k<n;k++){out[i][j]+=L[i][k]*U[k][j];}}}for(i=0;i<n;i++){for(j=0;j<n;j++){printf("%lf\t",out[i][j]);}printf("\r\n");}//////////将r和u相乘,得到逆矩阵printf("\n原矩阵的逆矩阵:\n");for(i=0;i<n;i++){for(j=0;j<n;j++){out1[i][j]=0;}}for(i=0;i<n;i++){for(j=0;j<n;j++){for(k=0;k<n;k++){out1[i][j]+=u[i][k]*r[k][j];}}}for(i=0;i<n;i++){for(j=0;j<n;j++){printf("%lf\t",out1[i][j]); }printf("\r\n");}}}。

线性方程组的几种求解方法线性方程组是指由一系列线性方程组成的方程组。
求解线性方程组是在给定的约束条件下找到满足所有方程的解。
在数学和工程领域,线性方程组的求解是一项重要的任务,涉及到许多实际问题的建模和分析。
本文将介绍几种常见的线性方程组的求解方法。
1. 高斯消元法(Gaussian elimination)高斯消元法是求解线性方程组的最常用方法之一、它通过矩阵的初等行变换将线性方程组化简为阶梯形矩阵,然后通过回代求解未知数的值。
高斯消元法具有简单、直观的特点,适用于一般的线性方程组求解。
2. 列主元高斯消元法(Gaussian elimination with partial pivoting)列主元高斯消元法是高斯消元法的改进版本。
它在每一步选择主元时,选取列中绝对值最大的元素作为主元,以减小误差的传播。
这种方法可以提高数值稳定性,但相对于普通高斯消元法,计算量较大。
3. 克拉默法则(Cramer's rule)克拉默法则是一种用于求解线性方程组的代数方法。
它通过计算系数矩阵的行列式和各个未知数的代数余子式,得到每个未知数的值。
克拉默法则适用于方程组个数和未知数个数相等的情况,但由于计算行列式的复杂度高,不适用于大规模的线性方程组求解。
4. 矩阵分解法(Matrix factorization)矩阵分解法通过将系数矩阵分解为两个或多个特定形式的矩阵的乘积,从而简化线性方程组的求解。
常见的矩阵分解方法有LU分解、QR分解、Cholesky分解等。
矩阵分解法适用于大规模线性方程组的求解,具有高效、稳定的特点。
5. 迭代法(Iterative methods)迭代法是一种逐步逼近解的方法,通过迭代计算逐渐接近线性方程组的解。
常见的迭代法有雅可比迭代法、高斯-赛德尔迭代法和共轭梯度法等。
迭代法适用于大规模稀疏线性方程组的求解,具有快速收敛、节约存储空间的特点。
6. 特殊结构法(Special structure methods)对于具有特殊结构的线性方程组,可以利用其特殊性质设计相应的求解方法。
数值分析5LU分解法§3 LU分解法——Gauss消去法的变形知识预备:1矩阵的初等行变换、初等矩阵及其逆、乘积2矩阵的乘法3上三角矩阵的乘积、单位下三角矩阵的乘积4单位下三角矩阵的逆、可逆的上三角矩阵的逆一、Gauss消去法的矩阵解释23Gauss 消去法实质上是将矩阵A 分解为两个三角矩阵相乘。
我们知道,矩阵的初等行变换实质就是左乘初等矩阵。
第一轮消元:相当于对A (1)左乘矩阵L 1,即)2()1(1A A L = 其中)1(11)1(11)2()2(2)2(2)2(22)1(1)1(12)1(11)2(131211,,10111a a l a a a a a a a Al l lL i i nn n n n n =⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---=ΛΛO ΛΛΛΛOO ΛΛ第二轮消元:对应于)3()2(2A A L =4一般地1,,2,1)1()(-==+n k A A L k k k Λ ……………(1) 其中nk k i a a l l l L k kkk ikik nkk k k ,,2,1,,10111)()(1ΛO ΛO ++==⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--=+整个消元过程为U A A L L L L n n n 记)(1221=--Λ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=nnn n u u u u u u ΛO ΛΛ22211211………(2) 从而UL U L L L L U L L L L A n n n n ⋅===---------1112121111221)(ΛΛ其中L 是单位下三角矩阵,即5,1,,1,,3,2,,1111)()(21323121⎪⎪⎭⎫⎝⎛-===⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=n j n i l l l l l l L j jj j ija a ij n n ΛΛΛΛO ΛΛΛ (3)【注】消元过程等价于A 分解成LU 的过程回代过程是解上三角方程组的过程。
第五节、矩阵分解之LU分解
⼀、A的LU分解:A=LU
我们之前探讨过矩阵消元,当时我们通过EA=U将A消元得到了U,这⼀节,我们从另⼀个⾓度分析A与U的关系
假设A是⾮奇异矩阵且消元过程中没有⾏交换,我们便可以将矩阵消元的EA=U形式改写成A=LU形式,其中E与L互为逆矩阵,且L是下三⾓矩阵
这么写有什么好处?
当我们使⽤EA=U时,E是由E1E2...E n相乘得到的,我们发现E的每⼀⾏中都包含有前⾯操作的副操作,举个例⼦,将2个第⼀⾏加到第⼆⾏得到新的第⼆⾏,再将2个第⼆⾏加到第三⾏得到新的第三⾏,此时第三⾏中包含有4个第⼀⾏,这种累加效应让我们⽆法直接从E中看出消元的具体过程(尽管它包含了整个消元过程)。
⽽当我们使⽤A=LU时,U是⼀个上三⾓阵,L是⼀个下三⾓阵,消元的每⼀步并不会叠加在⼀起,这使得我们可以清楚地分析消元的过程。
LU分解在本质上是⾼斯消元法的⼀种表达形式,我们只需要将消元过程中的消元乘数写在相应的位置就可以得到L,使⽤这种⽅式可以减少消元的操作步骤,且使得消元思路清晰
⼆、EA=LU
前⾯的LU分解的条件是不进⾏⾏交换,现在我们来讨论⼀下允许⾏交换的情况
好吧,我觉得看到标题⼤家应该就知道⽅法了,就是现将A进⾏⾏交换然后再LU分解(E为置换矩阵)。
第四章 矩阵的分解将矩阵分解为具有某种特性的因子之积,从以我们所熟悉的Gauss 消去法为依据而导出的LU 分解,到上个世纪60、70年代以Givens 和Householder 变换发展起来的QR 分解,在矩阵理论的研究与应用中都具有十分重要的意义。
这些特殊的分解式一方面反映了原矩阵的某些数值特征,另一方面,分解的方法与过程也为某些数值计算方法和理论分析提供了有效的工具。
§4.1n 阶矩阵的三角分解和LU 分解在线性代数中我们已经学过应用Gauss 消去法求解n 元线性方程组b Ax =, 其中:()nn ija A ⨯=,()Tn x x x x ,,,21 =,()Tn b b b b ,,,21 =。
Gauss 消去法的基本思路是将系数矩阵化为上三角形矩阵,或将增广矩阵化为上阶梯形矩阵,而后回代求解。
现在应用所谓选主元素法来实施Gauss 消去法的消去过程,至于回代过程我们不做讨论。
设()A A =0,记A 的k 阶顺序主子式为k ∆()n k ,,2,1 =。
如果()00111≠=∆a ,令()()011011a a c i i = ()n i ,,3,2 =,构造Frobenius 矩阵:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=11121211 n n c c c L ,⎪⎪⎪⎪⎪⎭⎫⎝⎛---=-111212111 n n c c c L则()()()()()()()()()1002020220101201101100A a a a a a a a AL nn n n n =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=- (4.1.1) 因此,在()0A的第一列中除主元素()011a 外,其余元素均被化为零。
式(4.1.1)即为()()110A L A =,由于倍加变换不改变矩阵行列式的值,所以由()1A 得到A 的二阶顺序主子式为()()1220112a a =∆。
如果()()01220112≠=∆a a ,则必有()0122≠a 。
怎么计算lu分解的浮点计算个数
LU分解是一种常用的线性代数算法,它可以将一个矩阵分解为一个下三角矩阵L和一个上三角矩阵U的乘积。
在实际使用中,我们常常需要计算LU分解的浮点计算个数,以评估算法的效率和精度。
计算LU分解的浮点计算个数需要考虑以下几个方面:
1. 矩阵乘法:LU分解的计算过程中需要进行多次矩阵乘法运算,每次矩阵乘法需要进行n^3次浮点计算,其中n为矩阵的维数。
2. 行变换:为了避免除数为0的情况,LU分解需要进行行变换,每次行变换需要进行n^2次浮点计算。
3. 前向替换:在求解线性方程组时需要进行前向替换,每次前向替换需要进行n^2次浮点计算。
4. 后向替换:在求解线性方程组时需要进行后向替换,每次后向替换需要进行n^2次浮点计算。
因此,总的浮点计算个数为3n^3+2n^2。
需要注意的是,以上计算仅考虑了基本的LU分解算法,实际应用中还需要考虑如何优化算法以提高计算效率和精度。
- 1 -。
行阶梯形矩阵方法总结在线性代数的学习中,利用矩阵的初等行变换,把一个矩阵化为行阶梯形矩阵,是一种很重要的运算。
以下是整理ID行阶梯形矩阵方法总结,欢迎阅读!行阶梯形矩阵,Row—Echelon Form,是指线性代数中的矩阵。
阶梯形矩阵如果:所有非零行(矩阵的行至少有一个非零元素)在所有全零行的上面。
即全零行都在矩阵的底部。
非零行的首项系数(leading coefficient),也称作主元,即最左边的首个非零元素(某些地方要求首项系数必须为1),严格地比上面行的首项系数更靠右。
首项系数所在列,在该首项系数下面的元素都是零(前两条的推论)。
这个矩阵是行阶梯形矩阵:化简后的行阶梯形矩阵(reduced row echelon form),也称作行规范形矩阵(row canonical form),如果满足额外的条件:每个首项系数是1,且是其所在列的唯一的非零元素。
例如:注意,这并不意味着化简后的行阶梯形矩阵的左部总是单位阵。
例如,如下的矩阵是化简后的行阶梯形矩阵:因为第3列并不包含任何行的首项系数。
矩阵变换到行阶梯形通过有限步的行初等变换,任何矩阵可以变换为行阶梯形。
由于行初等变换保持了矩阵的行空间,因此行阶梯形矩阵的行空间与变换前的原矩阵的行空间相同。
行阶梯形的结果并不是唯一的。
例如,行阶梯形乘以一个标量系数仍然是行阶梯形。
但是,可以证明一个矩阵的化简后的行阶梯形是唯一的。
一个线性方程组是行阶梯形,如果其增广矩阵是行阶梯形。
类似的,一个线性方程组是简化后的行阶梯形或'规范形',如果其增广矩阵是化简后的行阶梯形。