《计量经济学》第5章数据
- 格式:doc
- 大小:147.50 KB
- 文档页数:5


计量经济学期中教学案例分析作业第五章案例分析班级:电子商务15-2 班姓名:郑瑞璇学号:2015213720一、问题的提出与模型的建立根据本章引子提出的问题,为了给制定医疗机构的规划提供依据,分析比较医疗机构与人口数量的关系,建立卫生医疗机构数与人口数的回归模型。
假定医疗机构数与人口数之间满足线性约束,则理论模型设定为Yi= 31+ 化Xi+uiYi表示医疗机构数;Xi表示人口数。
由2001年《四川统计年鉴》得到如表1所示数据。
表1 四川省2000年各地医疗机构数与人口数地区人口数(万人)X医疗机构数(个)Y地区人口数(万人)X医疗机构数(个)Y成都1013.36304眉山339.9827自贡315911宜宾508.51530攀枝花103934广安438.61589泸州463.71297达州620.12403德阳379.31085雅安149.8866绵阳518.41616巴中346.71223广元302.61021资阳488.41361遂宁3711375阿坝82.9536内江419.91212甘孜88.9594乐山345.91132凉山402.41471南充709.24064二、参数估计进入EViews软件包,确定样本范围,编辑输入数据,选择估计方程菜单,得到图一的估计结果。
[=]Equatron: UNTITLED Workfile: UNTITLED::Untitled\ ■巴翁Dependent Variable: YMethod: Least SquaresDate: 12/19/16 Time: 21:39Sample: 1 21 induced observations: 21Variable Coefficient Std. Error t-Statistic ProbC -562.9074 291.5642 -1.930646 0.06B5X5372028 0.644239 8339811 00Q00R-squared 0.78543& Mean dependentvar 1508143Adjusted R-squared 0.774145 S.D. dependent var 1310.975S.E. of regression 5230301 Akaike info criterion 15 79746Sum squared resid 7375164 Schwarz criterion 15.89694Log likelihood -16X8733 Hann自n-Ouinn criter 15.31905F-statistic 69.55245 Durbin-Watson stat 1 947198ProbfF-stati stic) 0000000图一回归结果估计结果Yi = -562.9074 + 5.3728Xit= (-1.9306)(8.3398)2R =0.7854 F=69.55三、检验模型的异方差本例用的是四川省2000年各州市的医疗机构数和人口数,由于各地区人口数不同,对医疗机构设置数量有不同的需求,这种差异使得模型很容易产生异方差,从而影响模型的估计与使用。



第五章经典单方程计量经济学模型:专门问题一、内容提要本章主要讨论了经典单方程回归模型的几个专门题。
第一个专题是虚拟解释变量问题。
虚拟变量将经济现象中的一些定性因素引入到可以进行定量分析的回归模型,拓展了回归模型的功能。
本专题的重点是如何引入不同类型的虚拟变量来解决相关的定性因素影响的分析问题,主要介绍了引入虚拟变量的加法方式、乘法方式以及二者的组合方式。
在引入虚拟变量时有两点需要注意,一是明确虚拟变量的对比基准,二是避免出现“虚拟变量陷阱”。
第二个专题是滞后变量问题。
滞后变量包括滞后解释变量与滞后被解释变量,根据模型中所包含滞后变量的类别又可将模型划分为自回归分布滞后模型与分布滞后模型、自回归模型等三类。
本专题重点阐述了产生滞后效应的原因、分布滞后模型估计时遇到的主要困难、分布滞后模型的修正估计方法以及自回归模型的估计方法。
如对分布滞后模型可采用经验加权法、Almon多项式法、Koyck方法来减少滞项的数目以使估计变得更为可行。
而对自回归模型,则根据作为解释变量的滞后被解释变量与模型随机扰动项的相关性的不同,采用工具变量法或OLS 法进行估计。
由于滞后变量的引入,回归模型可将静态分析动态化,因此,可通过模型参数来分析解释变量对被解释变量影响的短期乘数和长期乘数。
第三个专题是模型设定偏误问题。
主要讨论当放宽“模型的设定是正确的”这一基本假定后所产生的问题及如何解决这些问题。
模型设定偏误的类型包括解释变量选取偏误与模型函数形式选取取偏误两种类型,前者又可分为漏选相关变量与多选无关变量两种情况。
在漏选相关变量的情况下,OLS估计量在小样本下有偏,在大样本下非一致;当多选了无关变量时,OLS估计量是无偏且一致的,但却是无效的;而当函数形式选取有问题时,OLS估计量的偏误是全方位的,不仅有偏、非一致、无效率,而且参数的经济含义也发生了改变。
在模型设定的检验方面,检验是否含有无关变量,可用传统的t检验与F检验进行;检验是否遗漏了相关变量或函数模型选取有错误,则通常用一般性设定偏误检验(RESET检验)进行。

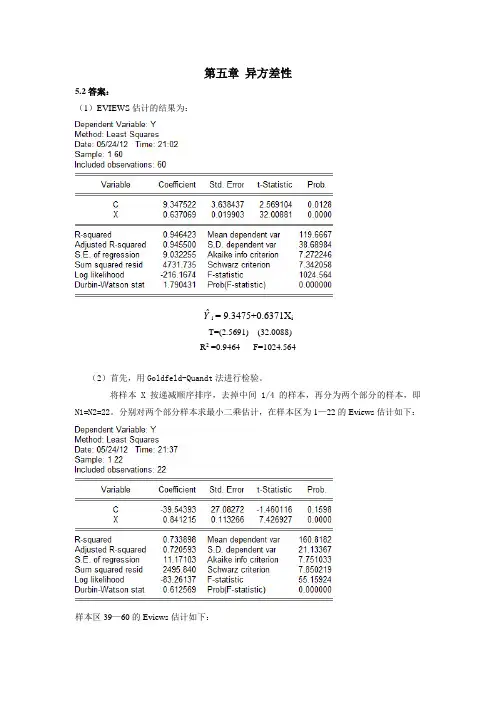
第五章异方差性5.2答案:(1)EVIEWS估计的结果为:Yˆi= 9.3475+0.6371X iT=(2.5691) (32.0088)R2 =0.9464 F=1024.564(2)首先,用Goldfeld-Quandt法进行检验。
将样本X按递减顺序排序,去掉中间1/4的样本,再分为两个部分的样本,即N1=N2=22。
分别对两个部分样本求最小二乘估计,在样本区为1—22的Eviews估计如下:样本区39—60的Eviews估计如下:得到两个部分各自的残差平方和,即∑e 12 =2495.840∑e 22 =603.0148求F 统计量为: F=∑∑e e 2221=2495.840/603.0148=4.1390给定α=0.05,查F 分布表,得临界值为F 0.05=(20,20)=2.12.比较临界值与F 统计量值,有F =4.1390>F 0.05=(20,20)=2.12,说明该模型的随机误差项存在异方差。
其次,用White 法进行检验结果如下:给定α=0.05,在自由度为2下查卡方分布表,得χ2=5.9915。
比较临界值与卡方统计量值,即nR2=10.8640>χ2=5.9915,同样说明模型中的随机误差项存在异方差。
(2)用权数W1=1/X,作加权最小二乘估计,得如下结果用White法进行检验得如下结果:F-statistic 3.138491 Probability 0.050925Obs*R-squared 5.951910 Probability 0.050999。
比较临界值与卡方统计量值,即nR2=5.9519<χ2=5.9915,说明加权后的模型中的随机误差项不存在异方差。
其估计的结果为:Yˆi= 10.3705+0.6309X iT=(3.9436) (34.0467)R2 =0.21144 F=1159.176 DW=0.95855.3答案:(1)EVIEWS估计结果:Yˆi= 179.1916+0.7195X iT=(0.808709) (15.74411)R2 =0.895260 F=247.8769 DW=1.461684 (2)利用White方法检验异方差,则White检验结果见下表:由上述结果可知,该模型存在异方差。

计量经济学张建强课后习题第五章5051、计量经济研究中常用的数据主要有两类:一类是时间序列数据,另一类是[ B ]A总量数据B横截面数据C平均数据D相对数据2、横截面数据是指[ A ]A同一时点上不同统计单位相同统计指标组成的数据B同一时点上相同统计单位相同统计指标组成的数据C同一时点上相同统计单位不同统计指标组成的数据D同一时点上不同统计单位不同统计指标组成的数据3、下面属于截面数据的是[ D ]A 19912003年各年某地区20个乡镇的平均工业产值B19912003年各年某地区20个乡镇的各镇工业产值C某年某地区20个乡镇工业产值的合计数D某年某地区20个乡镇各镇工业产值4、同一统计指标按时间顺序记录的数据列称为[ B ] A横截面数据B时间序列数据C修匀数据D原始数据5、回归分析中定义[ B ]A解释变量和被解释变量都是随机变量B解释变量为非随机变量,被解释变量为随机变量C解释变量和被解释变量都是非随机变量D解释变量为随机变量,被解释变量为非随机变量二、简答题、什么是计量经济学?它与统计学的关系是怎样的?计量经济学就是对经济规律进行数量实证研究,包括预测、检验等多方面的工作。
计量经济学是一种定量分析,是以解释经济活动中客观存在的数量关系为内容的一门经济学学科。
计量经济学与统计学密切联系,如数据收集和处理、参数估计、计量分析方法设计,以及参数估计值、模型和预测结果可靠性和可信程度分析判断等。
可以说,统计学的知识和方法不仅贯穿计量经济分析过程,而且现代统计学本身也与计量经济学有不少相似之处。
例如,统计学也通过对经济数据的处理分析,得出经济问题的数字化特征和结论,也有对经济参数的估计和分析,也进行经济趋势的预测,并利用各种统计量对分析预测的结论进行判断和检验等,统计学的这些内容与计量经济学的内容都很相似。
反过来,计量经济学也经常使用各种统计分析方法,筛选数据、选择变量和检验相关结论,统计分析是计量经济分析的重要内容和主要基础之一。

《计量经济学》第五章最新完整知识第五章多元线性回归模型在第四章中,我们讨论只有一个解释变量影响被解释变量的情况,但在实际生活中,往往是多个解释变量同时影响着被解释变量。
需要我们建立多元线性回归模型。
一、多元线性模型及其假定多元线性回归模型的一般形式是i iK K i i i x x x y εβββ++++= 2211令列向量x 是变量x k ,k =1,2,的n 个观测值,并用这些数据组成一个n ×K 数据矩阵X ,在多数情况下,X 的第一列假定为一列1,则β1就是模型中的常数项。
最后,令y 是n 个观测值y 1, y 2, …, y n 组成的列向量,现在可将模型写为:εββ++=K K x x y 11构成多元线性回归模型的一组基本假设为假定1. εβ+=X y我们主要兴趣在于对参数向量β进行估计和推断。
假定2. ,0][][][][21=?=n E E E E εεεε 假定3. n I E 2][σεε='假定4. 0]|[=X E ε我们假定X 中不包含ε的任何信息,由于)],|(,[],[X E X Cov X Cov εε= (1)所以假定4暗示着0],[=εX Cov 。
(1)式成立是因为,对于任何的双变量X ,Y ,有E(XY)=E(XE(Y|X)),而且])')|()([(])')((),(EY X Y E EX X E EY Y EX X E Y X Cov --=--=))|(,(X Y E X Cov =这也暗示βX X y E =]|[假定5 X 是秩为K 的n ×K 随机矩阵这意味着X 列满秩,X 的各列是线性无关的。
在需要作假设检验和统计推断时,我们总是假定:假定6 ],0[~2I N σε 二、最小二乘回归 1、最小二乘向量系数采用最小二乘法寻找未知参数β的估计量β,它要求β的估计β?满足下面的条件 22min ?)?(ββββX y X y S -=-? (2)其中()()∑∑==-'-=-?-nj Kj j ij i X y X y x y X y 1212ββββ,min 是对所有的m 维向量β取极小值。

第五章练习题参考解答练习题5.1 设消费函数为i i i i u X X Y +++=33221βββ式中,i Y 为消费支出;i X 2为个人可支配收入;i X 3为个人的流动资产;i u 为随机误差项,并且222)(,0)(i i i X u Var u E σ==(其中2σ为常数)。
试回答以下问题:(1)选用适当的变换修正异方差,要求写出变换过程;(2)写出修正异方差后的参数估计量的表达式。
5.2 根据本章第四节的对数变换,我们知道对变量取对数通常能降低异方差性,但须对这种模型的随机误差项的性质给予足够的关注。
例如,设模型为u X Y 21ββ=,对该模型中的变量取对数后得如下形式u X Y ln ln ln ln 21++=ββ(1)如果u ln 要有零期望值,u 的分布应该是什么? (2)如果1)(=u E ,会不会0)(ln =u E ?为什么? (3)如果)(ln u E 不为零,怎样才能使它等于零?5.3 由表中给出消费Y 与收入X 的数据,试根据所给数据资料完成以下问题: (1)估计回归模型u X Y ++=21ββ中的未知参数1β和2β,并写出样本回归模型的书写格式;(2)试用Goldfeld-Quandt 法和White 法检验模型的异方差性; (3)选用合适的方法修正异方差。
Y X Y X Y X 55 80 152 220 95 140 65 100 144 210 108 145 70 85 175 245 113 150 801101802601101607912013519012516584115140205115180981301782651301859514019127013519090125137230120200759018925014020574105558014021011016070851522201131507590140225125165651001372301081457410514524011518080110175245140225841151892501202007912018026014524090125178265130185981301912705.4由表中给出1985年我国北方几个省市农业总产值,农用化肥量、农用水利、农业劳动力、每日生产性固定生产原值以及农机动力数据,要求:(1)试建立我国北方地区农业产出线性模型;(2)选用适当的方法检验模型中是否存在异方差;(3)如果存在异方差,采用适当的方法加以修正。

计量经济学第一章use 打开数据 describe 查看数据集情况 summary 描述统计tabstat +[stats] 计算描述性统计量(指定) table+[contents] 类别变量+连续变量列联表 table/ tabulate 类别变量频次表 histogram 直方图第二章 一元回归线性模型:基本思想第三章 第四章 一元、多元线性回归模型:假设检验随机扰动项、参数的方差、标准误计算统计检验1模型的拟合优度检验:R2判定系数(可决系数)调整的可决系数:范围在0和1之间,越接近1,说明模型具有较高的拟合优度2方程的显着性检验:F 统计量,prob (F )F >F(k-1,n-k),拒绝原假设H0,即显着。
F<F(k-1,n-k),则暂时不拒绝,不显着。
显着性概率为0,小于给定显着性水平(0.05),表明模型对总体拟合显着 3变量的显着性检验:T 统计量 (服从n-2,n-k ),p 值Β2一般为0,T>2.306为显着,T<2.306为不显着(5%水平) 线性回归模型的基本假设:假设1:模型具有线性性(针对模型)。
Y 是参数βi 的线性组合,不一定要求是变量X 的线性组合。
假设2 :解释变量X 与u 不相关(针对扰动项)。
数学表达:cov(Xi,ui)=0通常说法:X 具有外生性假设3:给定X ,扰动项的期望或均值为零(针对扰动项)。
数学表达:E(?i |Xi)=0,i=1,2, …,n 假设4:同方差假定(针对扰动项)。
数学表达:Var (ui) = ??2 = Var (Yi) i=1,2, …,n. 假设5:无自相关(针对扰动项)。
数学表达:Cov(?i, ?j ) = 0= Cov(Y i, Y j ) i≠j 假设6:回归模型设定是正确的(表面是针对模型,实质上是针对扰动项)sort 排序 order 排序 drop 去除记录 keep 保留记录 generate 生产新变量 replace 给变量赋新值 rename 给变量重命名2R假设7:扰动项符合正态分布(针对扰动项)数学表达:?i~N(0, ??2 ) Y i~N(β0+β1X, ??2 )第五章线性回归模型拓展(函数形式,变量测度单位)第六章虚拟变量回归有截距,m个类别(取值),仅引入m-1个虚拟变量,无截距可以m个第七章模型设定误差1包含无关变量:后果(F,T检验)参数估计是无偏且一致的估计,但不是有效的估计,检验仍然有效,但方差增大,接收错误假设的概率较高。
计量经济学(第4版)数据表表2.1.1 某社区家庭每月收入与消费支出统计表表2.3.1 参数估计的计算表表2.6.1 中国各地区居民家庭人均全年可支配收入与人均全年消费性支出(元)资料来源:《中国统计年鉴》(2014)。
第2章练习12中国某年各地区税收Y和国内生产总值GDP的统计资料单位:亿元表3.2.1 2013年中国各地区城镇居民人均收入与人均消费性支出(元)资料来源:根据《中国统计年鉴》(2014)整理。
表3.5.1 2010年中国制造业各行业的总产出及要素投入资料来源:根据《中国统计年鉴》(2011年)整理。
表3.6.1 2013年中国居民人均收入与人均生活消费支出数据(元)表3.7.1 2012年中国农村居民对蛋类食物的消费及相关食物的价格指数蛋类消费量Q (千克)各类食品的消费价格指数(上年=100)居民消费价格指数P0(上年=100)人均消费支出X(元)蛋类P肉禽类P1水产类P2粮食P01油脂P02蔬菜P03北京11.0596.9106.7104.8102.6104.5112.0103.311878.92天津12.84101.7105.7106.7102.4103.7119.6102.78336.55河北10.4296.4101.1104.8102.9106.3114.9102.55364.14山西7.8296.2101.4107.4103.0105.2114.2102.65566.19内蒙古 6.4598.1105.3107.7105.7105.3112.3102.56381.97辽宁8.4896.2102.6107.3103.6105.0117.5102.55998.39吉林7.9094.6103.7108.5104.2105.7110.5102.46186.17黑龙江 6.3398.3105.4104.8104.6102.6115.3102.95718.05上海8.9298.2105.1105.8102.9103.8111.1102.811971.50江苏 6.9697.0102.5108.4102.3104.2109.0102.69138.18浙江 5.5697.6100.9108.8103.7103.7115.2102.310652.73安徽7.2394.398.7110.8104.2105.8113.3102.45555.99福建 5.3296.8102.0107.8103.0105.4116.5102.47401.92江西 4.2296.998.9112.6103.8104.2118.2103.05129.47山东12.3295.9101.6108.8102.5107.5111.2102.06775.95河南9.0694.499.4108.9104.1105.0113.2102.45032.14湖北 5.0298.6101.7111.1105.3105.2113.2103.05726.73湖南 4.92100.198.5110.9105.3102.5110.8101.65870.12广东 3.3998.2104.4107.3105.0106.0114.9102.97458.56广西 2.2297.3103.0104.9103.8108.2116.7103.34933.58海南 2.43102.7103.8102.2104.1106.2115.6103.24776.30重庆 5.18100.699.1106.7107.7106.0112.3102.65018.64四川 4.8797.799.9111.5104.9105.2118.1102.05366.71贵州 2.3595.7101.3107.6104.5104.4109.0102.83901.71云南 2.82100.1103.1104.9103.5102.9117.8102.34561.33西藏0.56102.4108.9102.8103.0105.5114.6103.42967.56陕西 3.9197.6101.5110.4103.3105.9111.7103.15114.68甘肃 3.9397.4104.2105.2102.3104.5108.5103.14146.24青海 1.5899.2107.6109.6102.8105.6112.8103.15338.91宁夏 3.4097.7104.8107.2101.0103.0108.7101.75351.36新疆 3.62102.1105.9105.2107.3105.3117.6104.75301.25资料来源:《中国统计年鉴》(2013)。
目 录第1章 绪 论第2章 经典单方程计量经济学模型:一元线性回归模型第3章 经典单方程计量经济学模型:多元线性回归模型第4章 经典单方程计量经济学模型:放宽基本假定的模型第5章 经典单方程计量经济学模型:专门问题第6章 联立方程计量经济学模型:理论与方法第7章 扩展的单方程计量经济学模型第8章 时间序列计量经济学模型第9章 计量经济学应用模型第1章 绪 论1什么是计量经济学?计量经济学方法与一般经济数学方法有什么区别?答:(1)计量经济学是经济学的一个分支学科,以揭示经济活动中客观存在的数量关系为主要内容,是由经济理论、统计学和数学三者结合而成的交叉学科。
(2)计量经济学方法通过建立随机的数学方程来描述经济活动,并通过对模型中参数的估计来揭示经济活动中各个因素之间的定量关系,是对经济理论赋予经验内容;而一般经济数学方法是以确定性的数学方程来描述经济活动,揭示的是经济活动中各个因素之间的理论关系。
2计量经济学的研究对象和内容是什么?计量经济学模型研究的经济关系有哪两个基本特征?答:(1)计量经济学的研究对象是经济现象,主要研究的是经济现象中的具体数量规律,即是利用数学方法,依据统计方法所收集和整理到的经济数据,对反映经济现象本质的经济数量关系进行研究。
(2)计量经济学的内容大致包括两个方面:一是方法论,即计量经济学方法或理论计量经济学;二是应用计量经济学。
任何一项计量经济学研究和任何一个计量经济学模型赖以成功的三要素是理论、方法和数据。
(3)计量经济学模型研究的经济关系的两个基本特征是随机关系和因果关系。
3为什么说计量经济学在当代经济学科中占据重要地位?当代计量经济学发展的基本特征与动向是什么?答:(1)计量经济学自20世纪20年代末30年代初形成以来,无论在技术方法还是在应用方面发展都十分迅速,尤其是经过20世纪50年代的发展阶段和60年代的扩张阶段,使其在经济学科占据重要的地位,主要表现在:①在西方大多数大学和学院中,计量经济学的讲授已成为经济学课程表中最具有权威的一部分;②从1969~2003年诺贝尔经济学奖的53位获奖者中有10位是与研究和应用计量经济学有关;③计量经济学方法与其他经济数学方法结合应用得到了长足的发展。
《计量经济学》各章数据
第5章自相关性
例5.3.1中国城乡居民储蓄存款模型(自相关性检验)。
表5.3.1列出了我国城乡居民储蓄存款年底余额(单位:亿元)和GDP指数(1978年=100)的历年统计资料,试建立居民储蓄存款模型,并检验模型的自相关性。
表5.3.1 我国城乡居民储蓄存款与GDP指数统计资料
5.5 案例分析:中国商品进口模型
商品进口是国际贸易交往的一种常用形式,对进口国来说,其经济发展水平决定商品进口情况。
这里,研究我国进口商品IM 与国内生产总值GDP 的关系。
有关数据见表5.5.1。
试建立中国商品进口模型。
表5.5.1 1989-2006年我国商品进口与国内生产总值数据(亿元)
思考与练习
10. 表1给出了美国1958-1969年期间每小时收入指数的年变化率(y )和失业率(x ) 请回答以下问题:
(1)估计模型t t
t u x b b y ++=1
1
0中的参数10,b b (2)计算上述模型中的DW 值。
(3)上述模型是否存在一阶段自相关?如果存在,是正自相关还是负自相关? (4)如果存在自相关,请用DW 的估计值估计自相关系数ρ。
(5)利用广义差分法重新估计上述模型。
自相关问题还存在吗?
表1 美国1958-1969年每小时收入指数变化率和失业率
11.考虑表2中所给数据:
表2 美国股票价格指数和GNP 数据
注:y-NYSE 10亿美元)
(1)利用OLS 估计模型:t t t u x b b y ++=10
(2)根据DW 统计量确定在数据中是否存在一阶自相关。
(3)如果存在一阶自相关,用DW 值来估计自相关系数ρˆ。
(4)利用估计的ρ
ˆ值,用OLS 法估计广义差分方程: t t t t t v x x b b y y +-+-=---)ˆ()ˆ1(ˆ1101ρρρ
(5)利用一阶差分法将模型变换成方程:
t t t t t v x x b y y +-=---)(111,或:t t t v x b y +∆=∆1
的形式,并对变换后的模型进行估计。
比较(4)、(5)的回归结果,你能得出什么结论?在变换后的模型中还存在自相关吗?
12.中国1980-2000年投资总额x 与工业总产值x 的统计资料如表3所示。
试问: (1)当模型设定为:t t t u x b b y ++=10时,是否存在自相关?如果存在自相关,利用
DW 求出ρ
ˆ。
(2)若按一阶自相关假设t t t v u u +=-1ρ,试用Durbin 两步估计法与广义最小二乘法估计原模型。
(3)采用差分形式1*--=t t t y y y 与1*--=t t t x x x 作为新数据,估计模型
t t t v x a a y ++=*10*
该模型是否存在序列相关?
表3 中国1980-2000年投资总额x 与工业总产值y 数据(亿元)
13.天津市城镇居民人均消费性支出(CONSUM ),人均可支配收入(INCOME ),以及消费价格指数(PRICE )见表4。
定义人均实际消费性支出Y= CONSUM/ PRICE ,人均实际可支配收入X= INCOME / PRICE 。
表4 天津市城镇居民人均消费与人均可支配收入数据
(1)利用OLS 估计模型:t t t 10
(2)根据DW 检验法、LM 检验法检验模型是否存在自相关。
(3)如果存在一阶自相关,用DW 值来估计自相关系数ρˆ。
(4)利用估计的ρ
ˆ值,用OLS 法估计广义差分方程: t t t t t v x x b b y y +-+-=---)ˆ()ˆ1(ˆ1101ρρρ
(5) 利用OLS 估计模型:t t t u x b b y ++=ln ln 10,检验此模型是否存在自相关,如何消除自相关?。