平面一般力系习题答案教学文案

习 题2-1 试计算图2-55中力F 对点O 之矩。

图2-55(a) 0)(=F O M (b) Fl M O =)(F (c) Fb M O -=)(F (d) θsin )(Fl M O =F(e) βsin )(22b l F M O +=F(f) )()(r l F M O +=F2-2 一大小为50N 的力作用在圆盘边缘的C 点上，如图2-56所示。

试分别计算此力对O 、A 、B 三点之矩。

图2-56mN 25.6m m N 625030sin 2505060cos 30sin 5060sin 30cos 50⋅=⋅=︒⨯⨯=︒⨯︒-︒⨯︒=R R M Om N 075.17825.1025.630cos 50⋅=+=⨯︒+=R M M O A m N 485.9235.325.615sin 50⋅=+=⨯︒+=R M M O B2-3 一大小为80N 的力作用于板手柄端，如图2-57所示。

(1)当︒=75θ时，求此力对螺钉中心之矩；(2)当θ为何值时，该力矩为最小值；(3) 当θ为何值时，该力矩为最大值。

图2-57(1)当︒=75θ时，（用两次简化方法）m N 21.20mm N 485.59.202128945.193183087.21sin 8025075sin 80⋅=⋅=+=⨯︒⨯+⨯︒⨯=O M (2) 力过螺钉中心 由正弦定理)13.53sin(250sin 30θθ-︒= 08955.03/2513.53cos 13.53sin tan =+︒︒=θ ︒=117.5θ(3) ︒=︒+︒=117.95117.590θ2-4 如图2-58所示，已知N 200N,300N,200N,150321='====F F F F F 。

试求力系向O 点的简化结果，并求力系合力的大小及其与原点O 的距离d 。

图2-58kN 64.1615110345cos kN 64.4375210145cos 321R321R-=+-︒-=∑='-=--︒-=∑='F F F F F F F F F F y y x x主矢RF '的大小 kN 54.466)()(22R =∑+∑='y x F F F 而 3693.064.43764.161tan RR ==''=x y F F α ︒=27.20α m N 44.21162.0511.045cos )(31⋅=-⨯+⨯︒=∑=F F M M O O Fmm 96.45m 04596.054.466/44.21/R==='=F M d O2-5 平面力系中各力大小分别为kN 60kN,260321===F F F ，作用位置如图2-59所示，图中尺寸的单位为mm 。

第二章平面基本力系答案一、填空题(将正确答案填写在横线上)1.平面力系分为平面汇交力系、平面平行力系和平面一般力系。

2.共线力系是平面汇交力系的特例。

3.作用于物体上的各力作用线都在同一平面内 ,而且都汇交于一点的力系,称为平面汇交力系。

4.若力FR对某刚体的作用效果与一个力系的对该刚体的作用效果相同,则称FR为该力系的合力,力系中的每个力都是FR的分力。

5.在力的投影中,若力平行于x轴,则F X＝ F或-F ;若力平行于Y轴,则Fy＝F或-F :若力垂直于x轴,则Fx=0;若力垂直于Y轴,则Fy＝ 0 。

6.合力在任意坐标轴上的投影，等于各分力在同一轴上投影的代数和。

7.平面汇交力系平衡的解析条件为：力系中所有力在任意两坐标轴上投影的代数和均为零。

其表达式为∑Fx＝0 和∑Fy＝0 ，此表达式有称为平面汇交力系的平均方程。

8.利用平面汇交力系平衡方程式解题的步骤是：（1）选定研究对象，并画出受力图。

（2）选定适当的坐标轴，画在受力图上；并作出各个力的投影。

（3）列平衡方程，求解未知量。

9.平面汇交力系的两个平衡方程式可解两个未知量。

若求得未知力为负值，表示该力的实际指向与受力图所示方向相反。

10.在符合三力平衡条件的平衡刚体上，三力一定构成平面汇交力系。

11.用力拧紧螺丝母，其拎紧的程度不仅与力的大小有关，而且与螺丝母中心到力的作用线的距离有关。

12.力矩的大小等于力和力臂的乘积，通常规定力使物体绕矩心逆时针转动时力矩为正，反之为负。

力矩以符号Mo(F) 表示，O点称为距心，力矩的单位是N.M 。

13.由合力矩定力可知，平面汇交力系的合力对平面内任一点的力矩，等于力系中的各分力对于同一点力矩的代数和。

14.绕定点转动物体的平衡条件是：各力对转动中心O点的矩的代数和等于零。

用公式表示为∑Mo(Fi) ＝0 。

15.大小相等、方向相反、作用线平行的二力组成的力系，称为力偶。

力偶中二力之间的距离称为力偶臂。

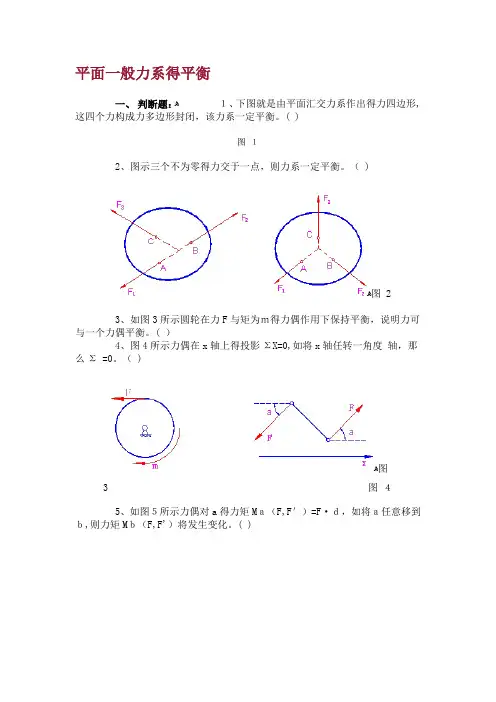
平面一般力系得平衡一、判断题：ﻫ１、下图就是由平面汇交力系作出得力四边形,这四个力构成力多边形封闭，该力系一定平衡。

( )图１2、图示三个不为零得力交于一点，则力系一定平衡。

（ )ﻫ图 23、如图3所示圆轮在力F与矩为ｍ得力偶作用下保持平衡，说明力可与一个力偶平衡。

( ）4、图4所示力偶在x轴上得投影ΣX=0,如将x轴任转一角度轴，那么Σ =0。

（ )ﻫ图3 图４5、如图５所示力偶对a得力矩Mａ（F,F＇）=F·ｄ，如将ａ任意移到ｂ,则力矩Mｂ（F,F'）将发生变化。

( )图 5 图６6、图６所示物体得A、B、C、D四点各有一力作用，四个力作出得力多7、如果两个力偶得力偶矩大边形闭合,则此物体处于平衡状态。

( ）ﻫ小相等，则此两个力偶等效.( ）ﻫ8、图示构件A点受一点力作用，若将此力平移到Ｂ点，试判断其作用效果就是否相同（）ﻫ图 7 图 89、图8所示梁,若求支反力时，用平面一般力系得平衡方程不能全部10、图9所示物体接触面间静摩擦系数就是ｆ,要使物体求出. （）ﻫ向右滑动。

试判断哪种施力方法省力。

( ）图9图1０11、力在坐标轴上得投影与该力在该轴上分力就是相同得。

( ）ﻫ1２、如果将图1０所示力F由A点等效地平移到B点，其附加力矩Ｍ＝13、平面任意力系，其独立得二力矩式平衡方程为∑Fｘ=0，Fa ( )。

ﻫ∑ＭA＝0, ∑MＢ=0，但要求矩心A、B得连线不能与x轴垂直。

（）ﻫ二、选择题ﻫ1、同一个力在两个互相平行得同向坐标轴上得投影（）。

ﻫA、大小相等，符号不同 B、大小不等,符号不同C、大小相等，符号相同Ｄ、大小不等,符号相同2、图11所示圆轮由O点支承，在重力Ｐ与力偶矩ｍ作用下处于平衡. 这说明( ）。

图 11A. 支反力R0与Ｐ平衡B。

m与Ｐ平衡C. m简化为力与Ｐ平衡ﻫD．R0与P组成力偶，其m（R０，P)=-P·r与m平衡３、图１2所示三铰刚架，在D角处受一力偶矩为m得力偶作用，如将该力力偶移到E角出,支座A、B得支反力（）.图12Ａ.A、B处都变化ﻫB。

第三章平面一般力系答案一、填空(将正确的答案填写在横线上)1、作用在物体上的各力的作用线都在同一平面内 ,并呈任意分布的力系,称为平面一般力系。

2、平面一般力系的两个基本问题是平面力系的简化 ,其平面条件的的应用。

3、力的平移定理表明,若将作用在物体某点的力平移到物体上的另一点,而不改变原力对物体的作用效果,则必须附加一力偶,其力偶距等于原来的力对新作用点的距。

4、平面一般力系向已知中心点简化后得到一力和一力偶距。

5平面一般力系的平衡条件为;各力在任意两个相互垂直的坐标轴上的分量的代数和均为零力系中所有的力对平面内任意点的力距的代数和也等零。

6.平面一般力系平衡方程中,两个投影式ΣFix=0 和ΣFiy=0 保证物体不发生移动 ;一个力矩式ΣMo(Fi)=0 保证物体不发生转动。

三个独立的方程,可以求解三个未知量。

7.平面一般力系平衡问题的求解中,固定铰链的约束反力可以分解为相互垂直的两个分力固定端约束反力可以简化为相互垂直的两个分力和一个附加力偶矩。

8.平衡方程ΣMA(Fi)=0、ΣMB(Fi)=0、ΣFiX=0适用于平面一般力系,使其用限制条件为AB连线与X轴不垂直。

9.平衡方程ΣMA(Fi)=0、ΣMB(Fi)=0、ΣMc(Fi)=0的使用限制条约为ABC不在同一直线上。

10.若力系中的各力作用现在同一平面内且相互平行,称为平面平行力系。

它是平面一般力系的特殊情况。

11.平面平行力系有两个独立方程,可以解出两个未知量。

12.平面平行力系的基本平衡方程是：ΣFi X=0，ΣM O(Fi)=0二、判断题（正确的打“√”，错误的打“×”）1.作用于物体上的力,其作用线可在物体上任意平行移动,其作用效果不变。

(×)2.平面一般力系的平衡方程可用于求解各种平面力系的平衡问题。

(√)3.若用平衡方程解出未知力为负值,则表明：(1)该力的真实方向与受力图上假设的方向相反。

(√)(2)该力在坐标轴上的投影一定为负值。

平面一般力系的平衡一、判断题：1.下图是由平面汇交力系作出的力四边形，这四个力构成力多边形封闭，该力系一定平衡。

（）图12.图示三个不为零的力交于一点，则力系一定平衡。

（）图23.如图3所示圆轮在力F和矩为m的力偶作用下保持平衡，说明力可与一个力偶平衡。

（）4.图4所示力偶在x轴上的投影ΣX=0，如将x轴任转一角度轴，那么Σ=0。

（）图3 图45.如图5所示力偶对a的力矩Ma（F，F＇）=F·d，如将a任意移到b，则力矩Mb（F，F＇）将发生变化。

（）图5 图66.图6所示物体的A、B、C、D四点各有一力作用，四个力作出的力多边形闭合，则此物体处于平衡状态。

（）7.如果两个力偶的力偶矩大小相等，则此两个力偶等效。

（）8.图示构件A点受一点力作用，若将此力平移到B点，试判断其作用效果是否相同（）图7 图89.图8所示梁，若求支反力时，用平面一般力系的平衡方程不能全部求出。

（）10.图9所示物体接触面间静摩擦系数是f，要使物体向右滑动。

试判断哪种施力方法省力。

（）图9 图1011.力在坐标轴上的投影和该力在该轴上分力是相同的。

（）12.如果将图10所示力F由A点等效地平移到B点，其附加力矩M ＝Fa （）。

13.平面任意力系，其独立的二力矩式平衡方程为∑Fx＝0，∑M A＝0，∑M B ＝0，但要求矩心A、B的连线不能与x轴垂直。

（）二、选择题1.同一个力在两个互相平行的同向坐标轴上的投影（）。

A.大小相等，符号不同B.大小不等，符号不同C.大小相等，符号相同D.大小不等，符号相同2.图11所示圆轮由O点支承，在重力P和力偶矩m作用下处于平衡。

这说明（）。

图11A．支反力R0与P平衡B．m与P平衡C．m简化为力与P平衡D．R0与P组成力偶，其m（R0，P）=-P·r与m平衡3. 图12所示三铰刚架，在D角处受一力偶矩为m的力偶作用，如将该力力偶移到E角出，支座A、B的支反力（）。

平面力系习题及答案平面力系习题及答案引言：在物理学中，平面力系是一个重要的概念。

它描述了在一个平面内作用的多个力的相互作用和平衡状态。

理解平面力系的性质和解决与之相关的习题是物理学学习的重要内容。

本文将介绍一些常见的平面力系习题，并提供详细的解答。

一、斜面上的物体考虑一个斜面上的物体，如何确定物体在斜面上的受力情况和平衡状态呢？解答：首先，我们需要将斜面上的力分解为垂直于斜面的分力和平行于斜面的分力。

根据牛顿第二定律，物体在垂直方向上的受力和平行方向上的受力应该平衡。

因此，可以根据斜面的倾角和物体的质量来确定这两个方向上的受力情况。

二、悬挂物体考虑一个悬挂在绳子上的物体，如何确定绳子和物体之间的受力情况和平衡状态呢？解答：首先，我们需要将绳子的拉力分解为垂直于绳子的分力和平行于绳子的分力。

根据牛顿第二定律，物体在垂直方向上的受力应该等于物体的重力，而在平行方向上的受力应该为零。

因此，可以根据物体的质量和绳子的角度来确定这两个方向上的受力情况。

三、平衡力系考虑一个平衡力系，如何确定各个力的大小和方向呢？解答：对于一个平衡力系，各个力的大小和方向应该满足力的平衡条件。

即，合力为零。

我们可以通过分析各个力的向量和方向，利用几何关系和三角函数来求解各个力的大小和方向。

四、平面力系的应用平面力系的概念和解题方法在实际生活中有很多应用。

例如，我们可以利用平面力系的原理来解决物体在斜坡上滑动的问题，或者解决悬挂物体的平衡问题。

此外，平面力系的概念也可以应用于机械设计和结构分析等领域。

结论：平面力系是物理学中一个重要的概念，理解和掌握平面力系的性质和解题方法对于物理学学习和实际应用都具有重要意义。

通过解决平面力系的习题，我们可以加深对物理学原理的理解，并提高解决实际问题的能力。

希望本文提供的平面力系习题及答案能对读者有所帮助。

平面一般力系习题在力学中，平面一般力系是指力作用在一个平面内的力的集合。

解决平面一般力系的习题，需要熟悉平面力的相关概念和定律，并能够应用力的平衡条件进行分析和计算。

下面将介绍一些关于平面一般力系的习题，并给出解答过程。

习题一：有两个力F1和F2作用在一个物体上，力F1的大小为10N，方向与x轴正方向夹角为30°；力F2的大小为8N，方向与y 轴正方向夹角为60°。

求合力的大小和方向。

解答：将力F1分解为x轴和y轴上的分力F1x和F1y，由三角函数可知F1x=F1*cos30°=10N*cos30°=10N*0.866≈8.66N，F1y=F1*sin30°=10N*sin30°=10N*0.5=5N。

将力F2分解为x轴和y轴上的分力F2x和F2y，由三角函数可知F2x=F2*sin60°=8N*sin60°=8N*0.866≈6.93N，F2y=F2*cos60°=8N*cos60°=8N*0.5=4N。

合力的分量为Fx=F1x+F2x=8.66N+6.93N≈15.59N，Fy=F1y+F2y=5N+4N=9N。

合力的大小为F=√(Fx²+Fy²)=√(15.59N²+9N²)≈18.07N。

合力的方向与x轴的夹角θ为tanθ=Fy/Fx=9N/15.59N≈0.577。

因此，合力的大小为约18.07N，方向与x轴的夹角约为0.577弧度。

习题二：一个物体受到三个力F1、F2和F3的作用，力F1的大小为8N，方向与x轴正方向夹角为60°；力F2的大小为6N，方向与y轴正方向夹角为45°；力F3的大小为10N，方向与x轴正方向夹角为120°。

求合力的大小和方向。

解答：将力F1分解为x轴和y轴上的分力F1x和F1y，由三角函数可知F1x=F1*cos60°=8N*cos60°=8N*0.5=4N，F1y=F1*sin60°=8N*sin60°=8N*0.866≈6.93N。