普朗克公式推导斯忒藩-玻尔兹曼定律和维恩位移定律

维恩位移定律推导维恩位移定律是热辐射领域中的一个基本定律，描述了黑体辐射中波长和温度之间的关系。

这个定律最初由德国物理学家维尔纳·维恩于1893年提出，并于1900年被瑞典物理学家维尔纳·普朗克用量子理论进行修正和推广。

维恩位移定律的推导主要是根据黑体辐射的性质和波动理论进行的，下面我们来详细阐述。

为了推导维恩位移定律，首先要了解黑体辐射的性质。

黑体是一种能够吸收所有入射辐射的物体，漫反射和完全吸收所有波长的光谱。

黑体辐射的光谱可以通过热诱导来观察，即将一个黑体加热到高温，使其发出可见光波长范围内的光。

然后，使用光谱仪来分析这些辐射，我们可以得到一个连续的能量分布。

根据电磁波理论，电磁辐射的能量与频率有关。

我们通过分析黑体辐射的能谱，可以得到一个关于频率（或波长）的分布函数。

这个函数描述了不同频率（波长）的电磁辐射的能量密度。

接下来，我们将使用波动理论来推导维恩位移定律。

根据波动理论，一个波动物体的波长和频率之间的关系可以通过传播速度来表示。

对于电磁波，它的传播速度等于光速。

根据光速的定义，我们知道v=c/λ，其中v是波长，c是光速。

考虑到黑体辐射中各个频率的辐射能量密度不同，我们以u(v)来表示单位频率内的能量密度。

维恩位移定律表明，黑体辐射的峰值频率与温度有关。

为了推导这个定律，我们假设黑体辐射服从玻尔兹曼分布定律。

根据玻尔兹曼分布定律，单位体积内不同频率（波长）的辐射能量密度与温度的关系为：u(v) = A * v^3 / (exp(Bv/T)-1)其中A和B是常数，v是频率，T是温度。

根据这个式子，我们可以看出温度越高，能量密度越大。

根据维恩位移定律，黑体辐射的峰值频率对应于最大的能量密度。

我们要找到这个峰值频率所对应的温度。

为了找到峰值频率，我们对玻尔兹曼分布定律的右侧取对数，并对v取导数，得到：ln(u(v)) = ln(A) + 3ln(v) - ln(exp(Bv/T)-1)对ln(u(v))关于v求导，并令导数等于零，可以得到最大值频率对应的v值。

大学物理 量子物理基础知识点1.黑体辐射（1）黑体：在任何温度下都能把照射在其上所有频率的辐射全部吸收的物体。

（2）斯特藩—玻尔兹曼定律：4o M T T σ（）= （3）维恩位移定律：m T b λ= 2.普朗克能量量子化假设（1）普朗克能量子假设：电磁辐射的能量是由一份一份组成的，每一份的能量是：h εν= 其中h 为普朗克常数，其值为346.6310h J s -=⨯⋅ （2）普朗克黑体辐射公式：2521M T ()1hckthc eλπλλ=-（,）3.光电效应和光的波粒二象性（1）遏止电压a U 和光电子最大初动能的关系为：212a mu eU = （2）光电效应方程： 212h mu A ν=+ （3）红限频率：恰能产生光电效应的入射光频率： 00V A K hν== （4）光的波粒二象性（爱因斯坦光子理论）：2mc hεν==；hp mc λ==；00m =其中0m 为光子的静止质量，m 为光子的动质量。

4.康普顿效应： 00(1cos )hm cλλλθ∆=-=- 其中θ为散射角，0m 为光子的静止质量，1200 2.42610hm m cλ-==⨯，0λ为康普顿波长。

5.氢原子光谱和玻尔的量子论：（1）里德伯公式: ()22111T T HR m n n m m nνλ==-=->（）()(), % （2）频率条件: k nkn E E hν-=(3) 角动量量子化条件：,1,2,3...e L m vr n n ===其中2hπ=，称为约化普朗克常量，n 为主量子数。

（4）氢原子能量量子化公式： 12213.6n E eVE n n=-=- 6.实物粒子的波粒二象性和不确定关系 （1）德布罗意关系式： h h p u λμ==（2）不确定关系: 2x p ∆∆≥； 2E t ∆∆≥7.波函数和薛定谔方程（1）波函数ψ应满足的标准化条件：单值、有限、连续。

（2）波函数的归一化条件: (,)(,)1Vr t r t d ψψτ*=⎰（3）波函数的态叠加原理: 1122(,)(,)(,)...(,)iiir t c r t c r t c r t ψψψψ=++=∑（4）薛定谔方程: 22(,)()(,)2i r t U r r t t ψψμ⎡⎤∂=-∇+⎢⎥∂⎣⎦8.电子自旋和原子的壳层结构（1）电子自旋： 1,2S s ==；1,2z s s S m m ==±注：自旋是一切微观粒子的基本属性.（2）原子中电子的壳层结构①原子核外电子可用四个量子数(,,,l s n l m m )描述：主量子数：0,1,2,3,...n = 它主要决定原子中电子的能量。

斯忒藩—玻尔兹曼定律摘要：一、斯忒藩—玻尔兹曼定律的背景与意义1.定律的起源2.对热力学与统计物理学的贡献二、斯忒藩—玻尔兹曼定律的公式与解释1.公式表述2.物理意义及推导过程三、斯忒藩—玻尔兹曼定律的应用领域1.气体动理论2.固体物理3.宇宙学四、斯忒藩—玻尔兹曼定律与其他定律的关系1.与麦克斯韦- 波尔兹曼分布律的联系2.与费米气体和玻色气体的区别正文：斯忒藩—玻尔兹曼定律，又称斯忒藩- 玻尔兹曼方程，是描述理想气体分子碰撞过程的一个基本定律。

它是以奥古斯特·斯忒藩和路德维希·玻尔兹曼两位物理学家的名字命名的，他们分别于1865 年和1872 年独立提出了这一定律。

这一定律在热力学和统计物理学领域有着重要的地位，并对气体动理论、固体物理以及宇宙学等领域产生了深远的影响。

斯忒藩—玻尔兹曼定律的公式表述为：Σ(i=1 至∞)pid2 =8πkT/√(NkT)，其中Σ表示对所有自由度求和，i表示自由度；pid2表示第i 个自由度的动能；k为玻尔兹曼常数；T为绝对温度；N为气体分子数。

该公式描述了在给定温度下，气体分子的总动能与分子数之间的关系。

在物理意义上，斯忒藩—玻尔兹曼定律表示了在一定温度下，气体分子的平均动能与分子数成正比。

当气体温度升高时，分子的平均动能也会增加。

这一定律揭示了气体动理论的基本规律，为研究气体性质提供了理论基础。

此外，斯忒藩—玻尔兹曼定律在固体物理、宇宙学等领域也有着广泛的应用。

在固体物理中，它有助于研究电子与晶格振动的相互作用，从而解释固体的热力学性质。

在宇宙学中，斯忒藩—玻尔兹曼定律可以用于估算宇宙背景辐射的温度，从而揭示宇宙的演化过程。

式中：W0 为黑体总辐射通量密度，单位（W²cm-2）；σ为斯忒藩-玻耳兹曼常量，（σ=（5.6697±0.0029）³10-2W²cm-2²k-4）式（2-7）为斯忒藩-玻耳兹曼定律，即黑体总辐射通量密度随温度的增加而迅速增大，它与温度的四次方成正比。

因此，温度只要有微小变化，就会引起辐射通量密度很大的变化，在用红外装置测定温度时，就是根据此定律作为理论依据的。

从图 2-10 中可以看到黑体辐射均有个极大值，它所对应的波长λmax，若对（2-6）式的 Wλ（λ，T）求波长的偏微分，并求极值，即可得到λmax。

?W? (?，T) ? 0??经整理可得：λmax²T=b（2 - 8）式中：λmax 为辐射通量密度的峰值波长；b 为常数，b=2897.8±0.4（μm²k）。

（2-9）式称为维恩位移定律，它说明随着温度的升高，辐射最大值对应的峰值波长向短波方向移动，表 2-4 给出不同温度时λmax 的数值。

表 2-4 不同温度时黑体辐射的峰值波长T(K) 273 300 310 1000 2000 3000 4000 5000 6000 7000λ maxμm 10.61 9.66 9.34 2.90 1.45 0.97 0.72 0.58 0.48 0.41上述讨论的是黑体辐射，自然界一般物体不是黑体，但在某一确定温度T 时，物体最强辐射所对应的波长λmax，也可以用维恩位移公式计算出近似值。

如：人体表面平均温度为37°（即 310K），其发射到空间的电磁辐射的峰值波长为外波段。

9.34即人体辐射的峰值波长位于热红二、地物的发射光谱特性任何地物当温度高于绝对温度OK 时，组成物质的原子、分子等微粒，在不停地做热运动，都有向周围空间辐射红外线和微波的能力。

通常地物发射电磁辐射的能力是以发射率作为衡量标准。

地物的发射率是以黑体辐射作为基准。

2023年光学教程第三版（姚启钧著）课后题答案下载2023年光学教程第三版（姚启钧著）课后题答案下载本教程以物理光学和应用光学为主体内容。

第1章到第3章为应用光学部分，介绍了几何光学基础知识和光在光学系统中的传播和成像特性，注意介绍了激光系统和红外系统;第4～8章为物理光学部分，讨论了光在各向同性介质、各向异性介质中的传播规律，光的干涉、衍射、偏振特性及光与物质的相互作用，并结合介绍了DWDM、双光子吸收、Raman放大、光学孤子等相关领域的应用和进展。

第9章则专门介绍航天光学遥感、自适应光学、红外与微光成像、瞬态光学、光学信息处理、微光学、单片光电集成等光学新技术。

光学教程第三版（姚启钧著）：内容简介绪论0.1 光学的研究内容和方法0.2 光学发展简史第1章光的干涉1.1 波动的独立性、叠加性和相干性1.2 由单色波叠加所形成的干涉图样1.3 分波面双光束干涉1.4 干涉条纹的可见度光波的时间相干性和空间相干性 1.5 菲涅耳公式1.6 分振幅薄膜干涉(一)——等倾干涉1.7 分振幅薄膜干涉(二)——等厚干涉视窗与链接昆虫翅膀上的彩色1.8 迈克耳孙干涉仪1.9 法布里一珀罗干涉仪多光束干涉1.10 光的干涉应用举例牛顿环视窗与链接增透膜与高反射膜附录1.1 振动叠加的三种计算方法附录1.2 简谐波的表达式复振幅附录1.3 菲涅耳公式的推导附录1.4 额外光程差附录1.5 有关法布里一珀罗干涉仪的(1-38)式的推导附录1.6 有同一相位差的多光束叠加习题第2章光的衍射2.1 惠更斯一菲涅耳原理2.2 菲涅耳半波带菲涅耳衍射视窗与链接透镜与波带片的比较2.3 夫琅禾费单缝衍射2.4 夫琅禾费圆孔衍射2.5 平面衍射光栅视窗与链接光碟是一种反射光栅2.6 晶体对X射线的'衍射视窗与链接与X射线衍射有关的诺贝尔奖附录2.1 夫琅禾费单缝衍射公式的推导附录2.2 夫琅禾费圆孔衍射公式的推导附录2.3 平面光栅衍射公式的推导习题第3章几何光学的基本原理3.1 几个基本概念和定律费马原理3.2 光在平面界面上的反射和折射光导纤维视窗与链接光导纤维及其应用3.3 光在球面上的反射和折射3.4 光连续在几个球面界面上的折射虚物的概念 3.5 薄透镜3.6 近轴物近轴光线成像的条件3.7 共轴理想光具组的基点和基面视窗与链接集成光学简介附录3.1 图3-6中P1和JP1点坐标的计算附录3.2 棱镜最小偏向角的计算附录3.3 近轴物在球面反射时物像之间光程的计算附录3.4 空气中的厚透镜物像公式的推导习题第4章光学仪器的基本原理4.1 人的眼睛4.2 助视仪器的放大本领4.3 目镜4.4 显微镜的放大本领4.5 望远镜的放大本领视窗与链接太空实验室——哈勃太空望远镜4.6 光阑光瞳4.7 光度学概要——光能量的传播视窗与链接三原色原理4.8 物镜的聚光本领视窗与链接数码相机4.9 像差概述视窗与链接现代投影装置4.10 助视仪器的像分辨本领视窗与链接扫描隧显微镜4.11 分光仪器的色分辨本领习题第5章光的偏振5.1 自然光与偏振光5.2 线偏振光与部分偏振光视窗与链接人造偏振片与立体电影 5.3 光通过单轴晶体时的双折射现象 5.4 光在晶体中的波面5.5 光在晶体中的传播方向5.6 偏振器件5.7 椭圆偏振光和圆偏振光5.8 偏振态的实验检验5.9 偏振光的干涉5.10 场致双折射现象及其应用视窗与链接液晶的电光效应及其应用5.11 旋光效应5.12 偏振态的矩阵表述琼斯矢量和琼斯矩阵附录5.1 从沃拉斯顿棱镜出射的两束线偏振光夹角公式(5-15)的推导习题第6章光的吸收、散射和色散6.1 电偶极辐射对反射和折射现象的解释6.2 光的吸收6.3 光的散射视窗与链接光的散射与环境污染监测6.4 光的色散6.5 色散的经典理论习题第7章光的量子性7.1 光速“米”的定义视窗与链接光频梳7.2 经典辐射定律7.3 普朗克辐射公式视窗与链接诺贝尔物理学奖7.4 光电效应7.5 爱因斯坦的量子解释视窗与链接双激光束光捕获7.6 康普顿效应7.7 德布罗意波7.8 波粒二象性附录7.1 从普朗克公式推导斯忒藩一玻耳兹曼定律附录7.2 从普朗克公式推导维恩位移定律习题第8章现代光学基础8.1 光与物质相互作用8.2 激光原理8.3 激光的特性8.4 激光器的种类视窗与链接激光产生106T强磁场8.5 非线性光学8.6 信息存储技术8.7 激光在生物学中的应用视窗与链接王淦昌与惯性的束核聚变习题主要参考书目基本物理常量表光学教程第三版（姚启钧著）：目录点击此处下载光学教程第三版（姚启钧著）课后题答案。

斯忒藩—玻尔兹曼定律
摘要：
1.斯忒藩- 玻尔兹曼定律的定义和概述
2.斯忒藩- 玻尔兹曼定律的公式和原理
3.斯忒藩- 玻尔兹曼定律在物理学中的应用
4.斯忒藩- 玻尔兹曼定律的意义和影响
正文：
1.斯忒藩- 玻尔兹曼定律的定义和概述
斯忒藩- 玻尔兹曼定律，又称为斯特藩- 玻尔兹曼定理，是由奥地利物理学家路德维希·玻尔兹曼和英国物理学家威廉·吉尔伯特·斯忒藩于1879 年提出的。

这一定律主要描述了在给定温度下，气体分子的平均动能与压强、体积之间的关系。

它是热力学的一个重要理论，为气体动力学理论的发展奠定了基础。

2.斯忒藩- 玻尔兹曼定律的公式和原理
斯忒藩- 玻尔兹曼定律的数学表达式为：PV = nRT，其中P 代表气体压强，V 代表气体体积，n 代表气体的物质的量，R 代表气体常数，T 代表气体的绝对温度。

该定律基于气体分子的统计力学原理，认为气体分子在给定温度下具有一定的平均动能，其压强与体积的变化会影响气体分子的碰撞频率和力度，进而影响气体的宏观性质。

3.斯忒藩- 玻尔兹曼定律在物理学中的应用
斯忒藩- 玻尔兹曼定律在物理学中有广泛的应用，例如在研究气体的压缩、膨胀、传热等过程，以及在设计热力学循环、制冷设备等方面都具有重要
意义。

此外，该定律也为气体动力学理论的发展提供了理论支持，为气体分子运动规律的研究奠定了基础。

4.斯忒藩- 玻尔兹曼定律的意义和影响
斯忒藩- 玻尔兹曼定律是热力学的一个重要理论，它揭示了气体分子在给定温度下的平均动能与压强、体积之间的关系，对于理解气体的宏观性质及其变化规律具有重要意义。

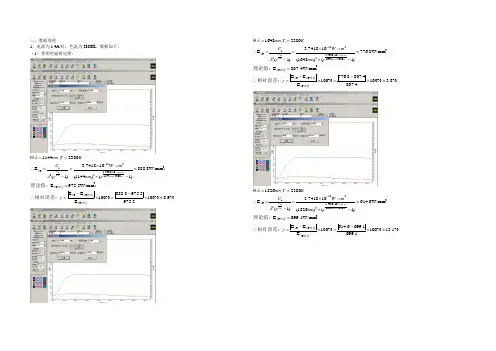
三、数据处理1、电流为1.4A 时，色温为2380K ，数据如下： （1）普朗克辐射定律：%9.8%1005.9755.9758.888%100E E E 975.5W/mmE W/mm8.888)1()1144(107418.3)1(E 2380,1144T T T 3T 323801144104388.1521251T 72≈⨯-=⨯-=∴=≈-⨯⋅⨯=-=∴==⨯⋅⨯-理论理论理论相对误差：；理论值：；λλλλλλγλλK nm Knm T C e nm cmW e C K T nm%8.3%1004.8074.8078.776%100E E E 807.4W/mmE W/mm8.776)1()1648(107418.3)1(E 2380,1648T T T 3T 323801648104388.1521251T 72≈⨯-=⨯-=∴=≈-⨯⋅⨯=-=∴==⨯⋅⨯-理论理论理论相对误差：理论值：λλλλλλγλλK nm Knm TC e nm cmW eC K T nm%1.12%1001.6991.6996.614%100E E E 699.1W/mmE W/mm 6.614)1()1826(107418.3)1(E 2380,1826T T T 3T 323801826104388.1521251T 72≈⨯-=⨯-=∴=≈-⨯⋅⨯=-=∴==⨯⋅⨯-理论理论理论相对误差：理论值：λλλλλλγλλKnm Knm TC enm cmW eC KT nm%2.6%1002.6682.6686.626%100E E E 668.2W/mmE W/mm 6.626)1()1878(107418.3)1(E 2380,1878T T T 3T 323801878104388.1521251T 72≈⨯-=⨯-=∴=≈-⨯⋅⨯=-=∴==⨯⋅⨯-理论理论理论相对误差：理论值：λλλλλλγλλKnm K nm TC enm cmW eC K T nm%5.4%1007.5617.5618.586%100E E E W/mm8.586E W/mm 7.615E 2070T T T 3T 3T ≈⨯-=⨯-=∴===理论理论理论相对误差：；实测值：；理论值：λλλλλγλnm（2）斯忒藩-玻耳兹曼定律：%6.3%1005.6705.6705.3103%100-)K mmW/10670.5)K mmW/103103.5K102085.3W/mm 7038.1,W/mm7038.1 ,K 102085.30K 238421442144132424134≈⨯-=⨯=∴⋅⨯=⋅⨯≈⨯==∴=⨯=⇒=--理论理论理论相对误差：（理论值：（波尔兹曼常数：又δδδγδδTE E T T T T(3)维恩位移定律%38.0%1002.896896.2885.2%100A A A Kmm 896.2A K2.885mm2380K m 1212T A TA 1212,0K 238max max max ≈⨯-=⨯-=∴⋅=⋅≈⨯=⋅=⇒=∴==理论理论理论相对误差：理论值：由维恩位移定律：γλλλn nm T2、电流为1.5A 时，色温为2420K ，数据如下： （1）普朗克辐射定律：%2.7%1001.10151.10158.941%100E E E W/mm1.0151E W/mm8.941)1()1036(107418.3)1(E 2420,1036T T T 3T 324201036104388.1521251T 72≈⨯-=⨯-=∴=≈-⨯⋅⨯=-=∴==⨯⋅⨯-理论理论理论相对误差：；理论值：；λλλλλλγλλK nm Knm T C e nm cmW e C K T nm%2.2%1003.10703.10704.1047%100E E E W/mm3.1070E W/mm4.1047)1()1200(107418.3)1(E 2420,1200T T T 3T 324201200104388.1521251T 72≈⨯-=⨯-=∴=≈-⨯⋅⨯=-=∴==⨯⋅⨯-理论理论理论相对误差：；理论值：；λλλλλλγλλK nm Knm T C e nm cmW e C K T nm%9.2%1007.8417.8419.816%100E E E W/mm7.841E W/mm9.816)1()1674(107418.3)1(E 2420,1674T T T 3T 324201674104388.1521251T 72≈⨯-=⨯-=∴=≈-⨯⋅⨯=-=∴==⨯⋅⨯-理论理论理论相对误差：；理论值：；λλλλλλγλλK nm Knm T C e nm cmW e C K T nm%9.3%1003.7823.7820.752%100E E E W/mm3.782E W/mm0.752)1()1762(107418.3)1(E 2420,1762T T T 3T 324201762104388.1521251T 72≈⨯-=⨯-=∴=≈-⨯⋅⨯=-=∴==⨯⋅⨯-理论理论理论相对误差：；理论值：；λλλλλλγλλK nm Knm T C e nm cmW e C K T nm%5.3%1008.6468.6467.669%100E E E W/mm8.646E W/mm7.669)1()1974(107418.3)1(E 2420,1974T T T 3T 324201974104388.1521251T 72≈⨯-=⨯-=∴=≈-⨯⋅⨯=-=∴==⨯⋅⨯-理论理论理论相对误差：；理论值：；λλλλλλγλλK nm Knm T C e nm cmW e C K T nm（2）斯忒藩-玻耳兹曼定律：%4.3%1005.6705.6705.4237%100-)K mmW/10670.5)K mmW/104237.5K104297.3W/mm 8602.1,W/mm8602.1 ,K 104297.3K 2420421442144132424134≈⨯-=⨯=∴⋅⨯=⋅⨯≈⨯==∴=⨯=⇒=--理论理论理论相对误差：（理论值：（波尔兹曼常数：又δδδγδδTE E T T T T(3)维恩位移定律%3.1%1002.896896.2933.2%100A A A Kmm 896.2A K2.933mm2420K m 1212T A TA 1212,K 2420max max max ≈⨯-=⨯-=∴⋅=⋅≈⨯=⋅=⇒=∴==理论理论理论相对误差：理论值：由维恩位移定律：γλλλn nm T3、电流为1.6A 时，色温为2470K ，数据如下： （1）普朗克辐射定律：%2.6%1007.11377.11375.1067%100E E E W/mm7.1137E W/mm 5.1067)1()1032(107418.3)1(E 2470,1032T T T 3T 324701032104388.1521251T 72≈⨯-=⨯-=∴=≈-⨯⋅⨯=-=∴==⨯⋅⨯-理论理论理论相对误差：；理论值：；λλλλλλγλλKnm Knm T C enm cmW e C K T nm%0.2%1001.11841.11843.1160%100E E E W/mm1.1184E W/mm3.1160)1()1200(107418.3)1(E 2470,1200T T T 3T 324701200104388.1521251T 72≈⨯-=⨯-=∴=≈-⨯⋅⨯=-=∴==⨯⋅⨯-理论理论理论相对误差：；理论值：；λλλλλλγλλK nm Knm T C e nm cmW e C K T nm%1003.9263.9263.926%100E E E W/mm3.926E W/mm 3.926)1()1648(107418.3)1(E 2470,1648T T T 3T 324701648104388.1521251T 72=⨯-=⨯-=∴=≈-⨯⋅⨯=-=∴==⨯⋅⨯-理论理论理论相对误差：；理论值：；λλλλλλγλλKnm Knm T C enm cmW e C K T nm%2.6%1000.7910.7918.741%100E E E W/mm0.791E W/mm8.741)1()1828(107418.3)1(E 2470,1828T T T 3T 324701828104388.1521251T 72≈⨯-=⨯-=∴=≈-⨯⋅⨯=-=∴==⨯⋅⨯-理论理论理论相对误差：；理论值：；λλλλλλγλλK nm Knm T C e nm cmW e C K T nm%8.5%1006.7016.7014.742%100E E E W/mm6.701E W/mm 4.742)1()1956(107418.3)1(E 2470,1956T T T 3T 324701956104388.1521251T 72≈⨯-=⨯-=∴=≈-⨯⋅⨯=-=∴==⨯⋅⨯-理论理论理论相对误差：；理论值：；λλλλλλγλλKnm K nm T C enm cmW e C K T nm（2）斯忒藩-玻耳兹曼定律：%8.2%1005.6705.6705.5137%100-)K mmW/10670.5)K mmW/105137.5K107221.3.0523W/mm 2,W/mm0523.2 ,K 107221.3K 2470421442144132424134≈⨯-=⨯=∴⋅⨯=⋅⨯≈⨯==∴=⨯=⇒=--理论理论理论相对误差：（理论值：（波尔兹曼常数：又δδδγδδTE E T T T T(3) 维恩位移定律%4.3%1002.896896.2994.2%100A A A Kmm 896.2A K2.994mm2470K m 1212T A TA 1212,K 2470max max max ≈⨯-=⨯-=∴⋅=⋅≈⨯=⋅=⇒=∴==理论理论理论相对误差：理论值：由维恩位移定律：γλλλn nm T4、电流为1.7A 时，色温为2500K ，数据如下： （1）普朗克辐射定律：%2.6%1000.12190.12199.1143%100E E E W/mm0.1219E W/mm9.1143)1()1034(107418.3)1(E 2500,1034T T T 3T 325001034104388.1521251T 72≈⨯-=⨯-=∴=≈-⨯⋅⨯=-=∴==⨯⋅⨯-理论理论理论相对误差：；理论值：；λλλλλλγλλK nm Knm T C e nm cmW e C K T nm%2.4%1007.12217.12218.1169%100E E E W/mm7.1221E W/mm 8.1169)1()1038(107418.3)1(E 2500,1038T T T 3T 325001038104388.1521251T 72≈⨯-=⨯-=∴=≈-⨯⋅⨯=-=∴==⨯⋅⨯-理论理论理论相对误差：；理论值：；λλλλλλγλλKnm Knm T C enm cmW e C K T nm%6.5%1008.8718.8712.823%100E E E W/mm8.871E W/mm2.823)1()1766(107418.3)1(E 2500,1766T T T 3T 325001766104388.1521251T 72≈⨯-=⨯-=∴=≈-⨯⋅⨯=-=∴==⨯⋅⨯-理论理论理论相对误差：；理论值：；λλλλλλγλλK nm Knm T C e nm cmW e C K T nm%1008.7778.7778.777%100E E E W/mm8.777E W/mm 8.777)1()1888(107418.3)1(E 2500,1888T T T 3T 325001888104388.1521251T 72=⨯-=⨯-=∴=≈-⨯⋅⨯=-=∴==⨯⋅⨯-理论理论理论相对误差：；理论值：；λλλλλλγλλKnm K nm T C enm cmW e C K T nm%8.5%1004.7104.7105.751%100E E E W/mm4.710E W/mm5.751)1()1982(107418.3)1(E 2500,1982T T T 3T 325001982104388.1521251T 72≈⨯-=⨯-=∴=≈-⨯⋅⨯=-=∴==⨯⋅⨯-理论理论理论相对误差：；理论值：；λλλλλλγλλK nm Knm T C e nm cmW e C K T nm（2）斯忒藩-玻耳兹曼定律：%6.1%1005.6705.6705.5820%100-)K mmW/10670.5)K mmW/105820.5K109063.3.0523W/mm 2,W/mm1808.2 ,K 109063.3K 2500421442144132424134≈⨯-=⨯=∴⋅⨯=⋅⨯≈⨯==∴=⨯=⇒=--理论理论理论相对误差：（理论值：（波尔兹曼常数：又δδδγδδTE E T T T T(3) 维恩位移定律%6.4%1002.896896.2030.3%100A A A Kmm 896.2A Kmm 030.32500K m 1212T A TA 1212,K 2500max max max ≈⨯-=⨯-=∴⋅=⋅≈⨯=⋅=⇒=∴==理论理论理论相对误差：理论值：由维恩位移定律：γλλλn nm T误差分析： 本次实验本不需要对仪器进行调整，只需按照步骤来操作软件。

维恩位移定律的推导介绍维恩位移定律是描述黑体辐射的一个基本定律，它是由奥地利物理学家维尔纳·维恩于1896年提出的。

维恩位移定律表明，黑体辐射的峰值波长与其温度呈反比关系。

在本文中，我们将详细推导维恩位移定律，并对其背后的物理原理进行深入探讨。

第一部分：黑体辐射什么是黑体辐射？黑体是指对所有入射辐射都吸收并完全辐射的物体。

根据黑体理论，一个完美的黑体能够以任意温度辐射能量，并且能够吸收所有入射能量，而不反射或透射任何能量。

黑体辐射的能谱分布黑体辐射的能量密度与波长有关，通常表示为能谱分布。

根据普朗克辐射定律，黑体辐射的能谱密度与波长的关系为: [B_{}(, T) = ] 其中，Bλ表示单位波长范围内的能谱密度，T表示黑体的温度，ℎ为普朗克常数，c为光速，k为玻尔兹曼常数。

第二部分：维恩位移定律的推导维恩位移定律描述了黑体辐射能谱分布的峰值波长与温度之间的关系。

下面是维恩位移定律的推导过程。

步骤1：寻找能谱密度的峰值波长我们首先需要找到能谱密度Bλ(λ,T)的峰值波长λmax，即使得能谱密度取最大值的波长。

为了求解λmax，我们需要对能谱密度的表达式进行求导。

为了简化推导，我们可以先对eℎcλkT进行展开，然后对λ5进行约化。

[B_{}(, T) = ]由于在求解峰值时，我们只关注相对位置，可以取倍数关系的常数ℎ，c和k的比值的倒数为1。

即令：ℎ=1，c=1，k=1。

[B_{}(, T) = ]步骤2：求解峰值波长将能谱密度分子项化简，最后得到能谱密度的简化表达式： [B_{}(, T) = ]对能谱密度求导，并令其等于零，即dBλdλ=0，我们可以求解得到λmax的值。

步骤3：推导维恩位移定律根据步骤2的结果，我们得到了能谱密度的峰值波长λmax。

下面我们将推导维恩位移定律的表达式。

由于ddλ(e1λT−1)<0，并且dBλdλ=0，我们可以得到: [() = 0] 这意味着λ−6e1λT(λT−1)+5λ−6e1λT=0。

斯特藩-玻尔兹曼定律（Stefan-Boltzmann law），又称斯特藩定律，是热力学中的一个著名定律，其内容为：一个黑体表面单位面积在单位时间内辐射出的总能量（称为物体的辐射度或能量通量密度）j*与黑体本身的热力学温度T（又称绝对温度）的四次方成正比，即:其中辐射度j*具有功率密度的量纲（能量/(时间·距离2)），国际单位制标准单位为焦耳/(秒·平方米)，即瓦特/平方米。

绝对温度T的标准单位是开尔文，ε为黑体的辐射系数；若为绝对黑体，则ε = 1.比例系数σ称为斯特藩-玻尔兹曼常数或斯特藩常量。

它可由自然界其他已知的基本物理常数算得，因此它不是一个基本物理常数。

该常数的值为：所以温度为 100 K 的绝对黑体表面辐射的能量通量密度为5.67 W/m2，1000 K 的黑体为56.7 kW/m2，等等。

斯特藩-玻尔兹曼定律是一个典型的幂次定律。

本定律由斯洛文尼亚物理学家约瑟夫·斯特藩（Jožef Stefan）和奥地利物理学家路德维希·玻尔兹曼分别于1879年和1884年各自独立提出。

提出过程中斯特藩通过的是对实验数据的归纳总结，玻尔兹曼则是从热力学理论出发，通过假设用光（电磁波辐射）代替气体作为热机的工作介质，最终推导出与斯特藩的归纳结果相同的结论。

本定律最早由斯特藩于1879年3月20日以Über die Beziehung zwischen der Wärmestrahlung und der Temperatur （《论热辐射与温度的关系》）为论文题目发表在维也纳科学院的大会报告上，这是唯一一个以斯洛文尼亚人的名字命名的物理学定律。

本定律只适用于黑体这类理想辐射源。

[编辑]斯特藩-玻尔兹曼定律的推导斯特藩-玻尔兹曼定律能够方便地通过对黑体表面各点的辐射谱强度应用普朗克黑体辐射定律，再将结果在辐射进入的半球形空间表面以及所有可能辐射频率进行积分得到。

维恩位移定律的证明维恩位移定律是描述黑体辐射谱的重要定律之一，它在物理学、天文学、化学等领域都有广泛的应用。

本文将介绍维恩位移定律的概念、历史背景以及证明过程。

一、维恩位移定律的概念维恩位移定律是描述黑体辐射谱的定律，它指出：黑体辐射谱峰值波长与黑体温度成反比。

简单来说，就是黑体温度越高，峰值波长越短。

这个定律由德国物理学家威廉·维恩于1893年提出，被认为是热力学和量子力学的重要成果之一。

二、历史背景在维恩提出位移定律之前，人们已经知道黑体辐射谱有一个峰值波长，但是并不清楚这个峰值波长与温度之间的关系。

维恩在研究黑体辐射谱时发现，在一定温度范围内，黑体辐射谱的峰值波长与温度成反比。

这个发现引起了物理学界的极大关注，成为了研究黑体辐射谱的重要突破之一。

三、证明过程为了证明维恩位移定律，我们需要从黑体辐射谱的性质入手。

黑体辐射谱是指一个完美吸收所有入射电磁波的物体所发出的电磁波谱。

根据普朗克公式，黑体辐射谱可以表示为：B(λ,T) = 2hc/λ^5 * 1/(e^(hc/λkT) - 1)其中，B(λ,T)表示在波长为λ处的辐射强度，T为黑体的温度，h、c、k分别为普朗克常数、光速和玻尔兹曼常数。

我们可以看出，黑体辐射谱的峰值波长λmax与温度T有关。

为了求出λmax与T的关系，我们需要对B(λ,T)求导，并令其等于0，即：d(B(λ,T))/dλ = -10hc/λ^6 * e^(hc/λkT)/(e^(hc/λkT) - 1) = 0化简后可得：λmaxT = 2.898×10^-3 m·K这个式子就是维恩位移定律的数学表达式。

它表明，黑体辐射谱的峰值波长λmax与温度T成反比。

这个定律的物理意义是，温度越高，黑体的辐射能量越大，发出的光波长越短，峰值波长也就越短。

四、应用与展望维恩位移定律在物理学、天文学、化学等领域都有广泛的应用。

在天文学中，它可以用来计算恒星的温度；在化学中，它可以用来研究分子的振动和转动状态。