当前位置：文档之家 › 高中数学必修二2.2.1线面与面面平行的判定

高中数学必修二2.2.1线面与面面平行的判定

  • 格式：pdf
  • 大小：175.46 KB
  • 文档页数：4

下载文档原格式

  / 4

合集下载

直线与平面平行的判定定理说课稿

直线与平面平行的判定定理说课稿

2.2.1<<直线与平面平行的判定>>说课稿各位评委老师：大家好！今天我说课的题目是直线与平面平行的判定。

下面我将从以下几方面来阐述我的教学。

一、教材分析“直线与平面的平行的判定”是普通高中课程标准数学实验教科书人教A版必修2第二章第二节第一讲的内容，是在学习了点、线、面的位置关系以后，进一步研究直线与平面的位置关系。

平行关系是本章的重要内容，线面平行是平行关系的初步，也是面面平行判定的基础，而且还映射着线面垂直的有关关系，具有承上启下的作用。

教材结合有关的实物模型，通过直观感知、操作确认归纳出直线与平面平行的判定定理，体现出了这节内容在物理学等中的广泛运用。

基于以上对教材的分析，根究高中新课标的要求，考虑到学生已有的知识结构和心理特征，我制订了如下教学目标。

二、教学目标1．知识与技能：能叙述并用数学语言表述线面平行的定义和判定定理，并运用判定定理进行简单的证明。

2．过程与方法：通过操作归纳出判定定理的过程中，培养学生观察、探究、发现的能力，提高空间想象能力、逻辑思维能力；3．情感与价值：通过亲身经历数学研究的过程，激发学生的学习兴趣，引导学生体会数学语言的简洁美，培养学生善于观察、勇于探索的良好习惯和严谨的科学态度。

为了达到上述教学目标，我认为本节课的重难点是：三、重点难点重点：直线和平面平行关系判定的形成过程，通过直观类比、探究发现来突出重点；难点：直线与平面平行判定定理的理解和应用，通过分组讨论、设计练习等教学手段来突破难点为了突出重点，突破难点使学生达到本节课的教学目标，我再从教学方法谈谈我的思路。

四、教学方法1、教法本节课在教法上主要采用启发式和探究式教学方法，以启发和引导为主，采用设疑的形式，引导学生通过直观感知、操作确认逐步发现知识的形成过程，利用课件来辅助教学，通过问题探究激发学生参与学习的积极性和主动性。

2、学法本节课在学法上，通过创设情境，让学生经历观察、想象、思考和应用的过程建构新的知识，再通过类比、联想，使建构的知识得以完善，而在这一过程中，师生交流、生生交流，从而形成民主、和谐、互动的气氛。

2.2.1线面平,面面平行的判定

2.2.1线面平,面面平行的判定
2.2.1直线与平面平行判定
复习提问
直线与平面有什么样的位置关系？
1.直线在平面内——有无数个公共点；
2.直线与平面相交——有且只有一个公共点；
3.直线与平面平行——没有公共点。
a
a

a


探究问题，归纳结论 如图,平面 外的直线 a平行于平面
的直线b。（1）这两条直线共面吗？
内
（2）直线
a


α
a
a
α
b b
β
β
3.如果平面α内有一条直线a平行于平面β，那么 α∥β. （×） 4.如果平面α内有无数条直线都平行于平面β，那 么α∥β. （×） 5.若两个平面分别经过两条平行直线，则这两个平 面平行。 a // b, a , b // （×）
a β α α
a
方法一：三角形的中位线定理
方法二：平行四边形的平行关系 线线平行
线面平行
面面平行
球场地面
两个平面的位置关系
位置关系 两平面平行
两平面相交
有一条公共直线
公共点
符号表示 图形表示
没有公共点
α∥ βα∩β=a源自一.预习检测1.如果平面 //平面 ,直线 a ,那么直线 a a // 和平面 的位置关系是________

2.如果平面 //平面 ,直线 a ,直线 b , 平行或异面 那么直线 和 b 的位置关系是_____________
β
b
两平面平行的判定

A
b a

地面



平面与平面平行的判定定理：
相交 直线与另一个平面平行, 一个平面内有两条_____ 则这两个平面平行. 即：a β β b β 线不在多，重在相 a∩b=P 交 //β a// b// a

高中数学教学课例《2.2.1直线与平面平行的判定》课程思政核心素养教学设计及总结反思

高中数学教学课例《2.2.1直线与平面平行的判定》课程思政核心素养教学设计及总结反思
设计意图：教学预设以生本教育观为指导，充分尊 重学生的学习主体地位．从建构主义理论来看，学生原 有认知结构是新授课的基础．本节课学生已有的知识储 备是直线与平面平行的定义．教学预设从数学学科内部 发展的顺序来说明本节课学习任务的确定，从数学学科 内部发展的需要来引起认知冲突并说明本课学习的必 要性，逻辑性强，利于知识系统的主动建构．
α 内平移 b，得到直线 c，不难发现 ac（强调直线 a， c 没有公共点）．
紧接着，提出问题，直线 a 能与平面 α 内的无数 条直线都平行吗？（能）
教师追问，直线 a 与平面 α 内的这无数条直线有 公共点吗？（没有）
教师带领全体同学思考一个问题：“反过来，直线 a 与平面 α 内的无数条直线都平行，则 a 与平面 α 平 行吗？”
导者，学习的主体是学生．
本节课的教学达到了预期的效果，学生基本上掌握
了直线与平面平行的判定定理的内容，会注意到定理中
的三个条件缺一不可。通过例题的讲解和练习的训练，
学生学会了证明直线与平面平行的方法，知道了利用判
定定理证明的关键是要去平面内去找一条直线与已知 课例研究综
直线平行，将空间问题转化为平面问题。本节课由于时 述
间与平面互相转化的思想。培养学生主动探究知识、合 作交流的意识，在体验数学美的过程中激发学生的学习 兴趣，从而培养学生勤于思考、勤于动手的良好习惯。
学生通过第一章课程的学习，对简单空间几何体的 结构特征有了初步认识，对几何体的直观图及三视图的 画法有了基本的了解．结合他们生活和学习中的空间实 例，学生对空间图形的基本关系也有了大致的了解，初 步具备了最朴素的空间观念．由于刚刚接触立体几何不 学生学习能 久，学习经验有限，学习立体几何所应具备的语言表达 力分析 能力及空间想象能力相对不足，他们从生活实例中抽象 概括出问题的数学本质的能力相对欠缺，从具体情境发 现并归纳出直线与平面平行的判定定理以及对定理的 理解是教学难点．教学时应注意及时纠正学生错误的地 方，这样有利于学生实现由平面图形到立体几何图形的 转变，更好的培养学生空间想象能力。

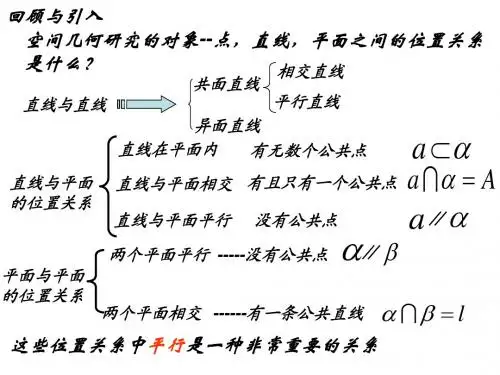
2.2.1线面平行的判定

2.2.1线面平行的判定

如图正方体ABCD-A’B’C’D’中， A’ 求证A’B’∥ 平面ABC’D’
A
练习：如图：S是平行四边形ABCD所在平面外一点， M是SC的中点， 求证：SA//平面BMD
S
M
D
O
C
A
B
∥
a∥
两个平面相交 ------有一条公共直线
l
这些位置关系中平行是一种非常重要的关系
§2.2.1 直线与平面平行的判定
question 直线与平面平行的定义是怎样的？ 直线与平面没有公共点 判断直线与平面没有公共点 -----判定直线与平面 平行的依据 观察生活中直线与平面平行，有何特点？
a

难
a b
观察直线a与平面平行吗
直线a 与直线b平行，b在 平面 内，那么a 与平行吗
1，直线a与b共面吗？ 2，直线a与平面 相交吗？
直线a与平面 平行！
定理：平面外一条直线与此平面内的一条直线
平行，则该直线与此平面平行
条件：平面外一条直线与此平面内的一条直线平行 结论： 该直线与此平面平行
直线与平面平行 的判定定理
特征：
从线线的平行 推导出线面平行
符号语言： a ∥b
a
a∥
b
例：求证：空间四边形相邻两边中点的连线平行于经过另 外两边所在的平面
A
F
E D

B
C
如图三棱锥S-ABC中E，F分别为SC， AC 的中点；求证：EF ∥ 平面SABLeabharlann S E C FBA
D’
C’ B’ D C B
回顾与引入 空间几何研究的对象--点，直线，平面之间的位置关系 是什么？ 相交直线

《2.2.1、平面与平面平行的判定,性质》

《2.2.1、平面与平面平行的判定,性质》

A1
D1 N
E F M B1
C1
D A B
C
课堂小结
1. 直线和平面平行的定义 2. 直线和平面平行的判定 3. 平面和平面平行的判定及推论
课堂练习1 课堂练习
已知有公共边AB的两个全等的矩形 已知有公共边 的两个全等的矩形ABCD和 ABEF不 的两个全等的矩形 和 不 在同一个平面内， ， 分别是对角线 分别是对角线AE， 的中点 在同一个平面内，P，Q分别是对角线 ，BD的中点
C1 B1 C B
思考
(1)若平面β内有一条直线与平面α平行， 若平面 平行， 平行吗？ 那么α ，β平行吗？ 平行， (2)若平面β 内有两条直线与平面α 平行， 若平面 平行吗？ 那么α ，β平行吗？ D1 C1 E A1 B1 D C F A B
思考
(1)若平面β内有一条直线与平面α平行， 若平面 平行， 平行吗？ 那么α ，β平行吗？ (2)若平面β 内有两条直线与平面α 平行， 若平面 平行， 平行吗？ 那么α ，β平行吗？ D1 C1 E A1 B1 D C F A B
α // c ③ ⇒α // β β // c
α // γ ④ β // γ ⇒α // β
α // γ ⑥ a// γ ⇒a// α
α // c ⑤
⇒α // a a// c
如图： 、 、 为不在同一直线上的 例1. 如图：A、B、C为不在同一直线上的 三点， 三点，AA1 ∥BB1 ∥CC1， ＝ ＝ 求证：平面ABC//平面 1B1C1. 平面A 求证：平面 平面 A1 B1 C A B
F
思路：在平面 内找PQ平行线 思路：在平面BCE内找 平行线。 内找 平行线。
课堂练习

高中数学必修二2.2-直线、平面平行的判定及其性质课堂练习及答案

高中数学必修二2.2-直线、平面平行的判定及其性质课堂练习及答案

2.2.直线、平面平行的判定及其性质2.2.1 直线与平面平行的判定●知识梳理1、直线与平面平行的判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。

简记为：线线平行，则线面平行。

符号表示：a αb β => a∥αa∥b●知能训练一．选择题1．已知m，n是两条不同直线，α，β，γ是三个不同平面，下列命题中正确的是（）A．若m∥α，n∥α，则m∥n B．若α⊥γ，β⊥γ，则α∥βC．若m∥α，m∥β，则α∥βD．若m⊥α，n⊥α，则m∥n2．若直线l不平行于平面α，且l⊄α，则（）A．α内存在直线与l异面B．α内存在与l平行的直线C．α内存在唯一的直线与l平行D．α内的直线与l都相交3．如图，M是正方体ABCD-A1B1C1D1的棱DD1的中点，给出下列命题①过M点有且只有一条直线与直线AB、B1C1都相交；②过M点有且只有一条直线与直线AB、B1C1都垂直；③过M点有且只有一个平面与直线AB、B1C1都相交；④过M点有且只有一个平面与直线AB、B1C1都平行．其中真命题是（）A．②③④B．①③④C．①②④D．①②③4．正方体ABCD-A1B1C1D1中M，N，Q分别是棱D1C1，A1D1，BC的中点．P在对角线BD1上，且BP＝BD1，给出下面四个命题：（1）MN∥面APC；（2）C1Q∥面APC；（3）A，P，M三点共线；（4）面MNQ∥面APC．正确的序号为（）A．（1）（2）B．（1）（4）C．（2）（3）D．（3）（4）5．在正方体ABCD-A1B1C1D1的各个顶点与各棱中点共20个点中，任取两点连成直线，所连的直线中与A1BC1平行的直线共有（）A．12条B．18条C．21条D．24条6．直线a∥平面α，P∈α，那么过P且平行于a的直线（）A．只有一条，不在平面α内B．有无数条，不一定在平面α内C．只有一条，且在平面α内D．有无数条，一定在平面α内7．如果直线a∥平面α，那么直线a与平面α内的（）A．一条直线不相交B．两条直线不相交C．无数条直线不相交D．任意一条直线不相交8．如图在正方体ABCD-A1B1C1D1中，与平面AB1C平行的直线是（）A．DD1B．A1D1C．C1D1D．A1D9．如图，在三棱柱ABC-A1B1C1中，点D为AC的中点，点D1是A1C1上的一点，若BC1∥平面AB1D1，则等于（）A．1/2B．1 C．2 D．310．下面四个正方体图形中，A、B为正方体的两个顶点，M、N、P分别为其所在棱的中点，能得出AB∥平面MNP的图形是（）A．①②B．①④C．②③D．③④11．如图，正方体的棱长为1，线段B′D′上有两个动点E，F，EF=，则下列结论中错误的是（）A．AC⊥BEB．EF∥平面ABCDC．三棱锥A-BEF的体积为定值D．异面直线AE，BF所成的角为定值二．填空题12．如图，在正方体ABCD-A1B1C1D1中，E，F，G，H，M分别是棱AD，DD1，D1A1，A1A，AB的中点，点N在四边形EFGH的四边及其内部运动，则当N只需满足条件时，就有MN⊥A1C1；当N只需满足条件时，就有MN∥平面B1D1C．13．如图，正方体ABCD-A1B1C1D1中，AB=2，点E为AD的中点，点F在CD上，若EF∥平面AB1C，则线段EF的长度等于．三．解答题14．如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AB⊥BC，D为AC的中点，AA1=AB=2．（1）求证：AB 1∥平面BC1D；（2）若BC=3，求三棱锥D-BC1C的体积．2.2.2 平面与平面平行的判定●知识梳理1、两个平面平行的判定定理：一个平面内的两条交直线与另一个平面平行，则这两个平面平行。

2.2.1《直线和平面平行判定》(新人教A版必修2)

2.2.1《直线和平面平行判定》(新人教A版必修2)
人教A版普通高中课程标准实验教科书数学必修2
2.2.1
直线与平面平行的判定
(第一课时)
湖南省泸溪县第一中学
说 课 流 程
1 教 材 分 析
2 学 情 分 析
3 教 学 目 标 分 析
4 教 法 学 法 分 析
5 教 学 过 程 分 析
6 设 计 说 明
一、教材分析
1 、 • 教 材 的 地 位 和 作 用
（3）若b , a // b, 则a //
3
辨 析 讨 论 深 化 理 解
判定定理的三个条件缺一不可 a a ∥ b a∥b
简记为：内外线线平行 （平面化）

线面平行
（空间问题）
定理运用、辨析： 1、判断下列命题是否正确，若正确，请简述理由，若不 正确，请给出反例.
(1)如果a、b是两条直线，且a∥b,那么a 平行于经过b的 任何平面；( )
教学过程 知识回顾： 一、直线与平面的位置关系
1、位置关系 （1）有无数个公共点 （2）有且只有一个公共点
直线在平面内
直线与平面相交 直线与平面平行
（3）没有公共点
教学过程
2、直线和平面位置关系的图形表示、符
号表示
a a
A
α
a
α
α
a //
a
a A
教学过程
1 创 设 情 境 感 知 概 念
直线和平面平行的判定定理：
2
观 察 归 纳 形 成 概 念
如果平面外的一条直线和此平面内的一条 直线平行，那么这条直线和这个平面平行.
a b
a b a∥b
a ∥

分组讨论：
判断下列命题是否正确，若不正确，请用图 形语言或模型加以表达

2.2.1线面平行、面面平行的判定

2.2.1线面平行、面面平行的判定

√ β∥γ
α∥γ
α∥β
× a∥c
⑤
α∥c
α∥a ⑥
×a∥γ
α∥γ
a∥α
例题分析
例2、如图：A、B、C为不在同一直线上的
三点，AA1 ∥ BB1∥ CC1 =求证：平面ABC//平面A1B1C1
C1 A1 B1 C A B
例3、已知正方体ABCD-A1B1C1D1，求证：平 面AB1D1∥平面C1BD。
2.2.1直线与平面平行的判定 2.2.2平面与平面平行的判定
(1)
直线和平面有哪些位置关系? a
a a
α
直线在平面α 内a α 有无数个交点
α
A
α
直线与平面α 平行 a∥α无交点
直线与平面α相交 a ∩ α= A 有且只有一个交点
定义：一条直线和一个平面没有公共点， 叫做直线与平面平行.
（2）怎样判定直线和平面平行？
小结
线面平行的判定定理 线线平行
线面平行
如果不在一个平面内的一条直线和平面内的 一条直线平行,那么这条直线和这个平面平行.
平面与平面平行的判定定理
一个平面内的两条相交直线与另一个平面平行， 则这两个平面平行。
定理的推论
如果一个平面内有两条相交直线分别平行于
另一个平面内的两条直线，那么这两个平面平行
（2）直线 a∥平面α，平面α内有无数条直线 交于 一点，那 么这无数条直线中与直线 a 平行的（ B ） （A）至少有一条 （C）有且只有一条 （B）至多有一条 （D）不可能有
例题分析
例1、求证：空间四边形相邻两边中点的连线平行于经过 另外两边所在的平面。 已知：空间四边形ABCD，E、F分别是AB、AD的中点。

必修二 2.2.1线面平行的判定定理

必修二 2.2.1线面平行的判定定理

B
M
C
∥ NF 即MC＝ 故MN∥CF
N B1
∴NFCM为平行四边形,
MN 平面AAC 1 1C
A1 F
C1
∴ MN∥平面AA1C1C,
例 4. 两个全等的正方形 ABCD 和 ABEF 所在平面相 交于AB，M∈AC，N∈FB，且AM=FN， 求证：MN∥平面BCE。
分析：只要在平面BEC内找到一条直线与MN平行
反思2：能够运用定理的条 件是要满足六个字， “面外、面内、平行”。
a b b//a
a //
反思3:运用定理的关键是找平行线。找平行线又经 常会用到三角形中位线定理。
思考交流：
如图，正方体 ABCD A1B1C1D 中， P 是棱A1B1 1 的中点，过点 P 画一条直线使之与截面A1BCD1 平行.
D1 A1 D A P B1 C C1
B
例2. 如图，四面体ABCD中，E，F，G，H分别是AB， BC，CD，AD的中点. (1)E、F、G、H四点是否共面？ (2)试判断AC与平面EFGH的位置关系； (3)你能说出图中满足线面平行位置 E 关系的所有情况吗？ B H D A
G F C
解：(1)E、F、G、H四点共面。 ∵在△ABD中，E、H分别是AB、 AD的中点.
操作确认
将一本书平放在桌面上，翻动书页， 书页的边AB所在直线与桌面所在平面 具有什么样的位置关系？
A B
操作确认
门扇转动的一边与门框所在的平面之间 的位置关系．
A1
A
B

B1
抽象概括：
线面平行的判定定理：平面外的一条直线和平面内 的一条直线平行，则该直线和这个平面平行。
a

高中数学必修2第二章点、线、面的位置关系知识点+习题+答案

高中数学必修2第二章点、线、面的位置关系知识点+习题+答案

D B A α 相交直线：同一平面内，有且只有一个公共点； ] ]； a 来表 a a 线线平行 A ·α C ·B · A · α P· αLβ 共面直线p线面平行 面面平行 作用：可以由平面与平面平行得出直线与直线平行叫做垂足。

叫做垂足。

的垂线，则这两个ba第 3 页 共 3 页aa b a b //,a a a ÞþýüË^^1、性质定理：垂直于同一个平面的两条直线平行。

符号表示：符号表示：b a b a //,Þ^^a a 2、性质定理：一条直线与一个平行垂直，那么过这条直线的平面也与此平面垂直 符号表示：b a b a ^ÞÌ^a a ,2.3.4平面与平面垂直的性质1、性质定理：、性质定理： 两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直。

符号表示：b b a a b a ^Þïþïýü=^Ì^a l l a a ,2、性质定理：垂直于同一平面的直线和平面平行。

符号表示：符号表示：符号表示：一、异面直线所成的角一、异面直线所成的角1.已知两条异面直线,a b ，经过空间任意一点O 作直线//,//a a b b ¢¢， 我们把a ¢与b ¢所成的锐角（或直角）叫异面直线,a b 所成的角。

所成的角。

2.角的取值范围：090q <£°；垂直时，异面直线当b a ,900=q二、直线与平面所成的角二、直线与平面所成的角1. 定义：平面的一条斜线和它在平面上的射影所成的锐角，叫这条斜线和这个平面所成的角2.角的取值范围：°°££900q 。

三、两个半平面所成的角即二面角：三、两个半平面所成的角即二面角： 1、从一条直线出发的两个半平面所组成的图形叫做二面角。

高一数学 人教A版必修2 第二章 2.2.1、2直线与平面平行、平面与平面平行的判定 课件

高一数学 人教A版必修2 第二章 2.2.1、2直线与平面平行、平面与平面平行的判定 课件

(1)直线EG∥平面BDD1B1；
证明 如图，连接SB.
∵点E，G分别是BC，SC的中点，
∴EG∥SB.
又∵SB⊂平面BDD1B1，EG⊄平面BDD1B1，
∴EG∥平面BDD1B1.
证明
(2)平面EFG∥平面BDD1B1. 证明 连接SD. ∵点F，G分别是DC，SC的中点， ∴FG∥SD. 又∵SD⊂平面BDD1B1，FG⊄平面BDD1B1， ∴FG∥平面BDD1B1. 又EG∥平面BDD1B1， 且EG⊂平面EFG，FG⊂平面EFG，EG∩FG＝G， ∴平面EFG∥平面BDD1B1.
证明
反思与感悟 解决线面平行与面面平行的综合问题的策略 (1)立体几何中常见的平行关系是线线平行、线面平行和面面平行，这三 种平行关系不是孤立的，而是相互联系、相互转化的. (2) 线线平行 ―判――定―→ 线面平行 ―判――定―→ 面面平行
所以平行关系的综合问题的解决必须灵活运用三种平行关系的判定定理.
第二章 §2.2 直线、平面平行的判 定及其性质
2.2.2 平面与平面平行的判定
学习目标
1.通过直观感知、操作确认，归纳出平面与平面平行的判定定理. 2.掌握平面与平面平行的判定定理，并能初步利用定理解决问题.
问题导学
知识点 平面与平面平行的判定定理
思考1 三角板的两条边所在直线分别与平面α平行，这个三角板所在平 面与平面α平行吗？ 答案 平行.
证明
Байду номын сангаас
命题角度2 以柱体为背景证明线面平行 例3 在三棱柱ABC－A1B1C1中，D，E分别是棱BC，CC1的中点，在线 段AB上是否存在一点M，使直线DE∥平面A1MC？请证明你的结论.
解答
引申探究 将本例改为在三棱柱ABC－A1B1C1中，若M为AB的中点， 求证：BC1∥平面A1CM. 证明 如图，连接AC1交A1C于点F， 则F为AC1的中点. 又因为M是AB的中点，连接MF， 所以BC1∥MF. 因为MF⊂平面A1CM，BC1⊄平面A1CM， 所以BC1∥平面A1CM.

2.2.1线面平行的判定

2.2.1线面平行的判定

直线在平面内
直线与平面相交
直线与平面平行
二、直线与平面平行的判定 若将一本书平放在桌面上，翻动书的封面， 观察封面边缘所在直线l与桌面所在的平面具有怎 样的位置关系？
l
观察
直线和平面平行
思考 如图，设直线b在平面α内，直线a在平面 α外，猜想在什么条件下直线a与平面α平行.
a
a//b
α
b
直线和平面平行
判定定理 如果平面外一条直线和这个平面内的一条 直线平行，那么这条直线和这个平面平行． 数学符号表示：a , b , a // b a // 四边形相邻两边中点的 连线，平行于经过另外两边的平面．
E 已知：空间四边形 ABCD 中， 、 F 分别是 AB 、 AD 的中点.
思想方法 通过直线间的平行，推证直线与平面平 行，即将直线与平面的平行关系（空间问题） 转化为直线间的平行关系（平面问题）.
作业:教材 P62 习题 3，4； 《红对勾》11课时1—11（解）
判定定理的证明
a 已知： b ，
a // b ，

b
求证： // a
证明：因为 a // b
所以经过a、b确定一个平面． 因为 a ，而a ， 所以 与是两个不同的平面． 因为b，b 所以 =b
未完
判定定理的证明
下面用反证法证明a与没有公共点：
假设a与有公共点P，而=b，得Pb，
所以 点P是a、b的公共点，这与a//b矛盾.
所以a//
求证： EF //平面
BCD ．
证明：连结 BD．, A E E B , A F F D
E F // B D , 又 E F 平 面 B C D , B D 平 面 B C D

高中数学必修2课件2.2.1直线和平面平行与平面和平面平行的判定

高中数学必修2课件2.2.1直线和平面平行与平面和平面平行的判定

2
一、直线和平面 1.直线和平面的位置关系： ①直线在平面内 —— 如果一条直线和一个平面有两个 公共点，那么这条直线就在这个平面内. ②直线和平面相交—— 一条直线和一个平面有且只有 一个公共点，叫做直线与平面相交. 这个公共点叫做直线与平面的交点。 ③直线和平面平行 —— 一条直线与一个平面没有公共点 叫做直线与平面平行。 a
P b
a
a
线线平行，则面面平行



8
4.结论： 平行于同一平面的两个平面平行.
// , // //
两个平面平行的判定方法:
⑴ 定义法

金太阳教育网

品质来自专业 信赖源于诚信
⑵ a // , b // , a b P // a 、b ⑶ a // a, b // b
11
金太阳教育网

小结:
品质来自专业 信赖源于诚信
线线平行，则线面平行 直线和平面平行的判定: 如果平面外的一条直线和平面内的一条直线平 行，那么这条直线和这个平面平行。
l // m, l , m
l
l //

m
12
两个平面平行的判定方法:
⑴ 定义法 ⑵ a // , b // , a b P // a 、b ⑶ a // a, b // b
D
C
又EF 平面BCD, BD 平面BCD，
EF // 平面BCD
5
二、两个平面 1.两个平面的位置关系: 两个平面平行—— 如果两个平面没有公共点，那么这 两个平面互相平行. 两个平面相交—— 有一条公共直线.


金太阳教育网

2.2.1、2线线、线面平行的判定

2.2.1、2线线、线面平行的判定
Ma b N cd
α
β
γ
e f
分析：
在四边形ABC1D1中， AB∥C1D1且AB＝C1D1故四边 形ABC1D1为平行四边形。
C
D A B
即AD1∥BC1
证明： ∵ABCD-A1B1C1D1是正方体 ∴D1C1//A1B1，D1C1=A1B1, AB//A1B1，AB=A1B1 ∴D1C1//AB，D1C1=AB ∴D1C1BA为平行四边形 ∴ D1A//C1B 又D1A 平面C1BD C1B 平面C1BD ∴D1A//平面C1BD 同理D1B1//平面C1BD
，
P
E
N D C M B
A
边听边练边落实
在正方体ABCD—A1B1C1D1中，M、N、P分别是C1C、 B1C1、C1D1的中点，求证：平面MNP∥平面A1BD.
边听边练边落实
直棱柱ABCD A1 B1C1 D1中，底面ABCD为 正方形，边长为 2，侧棱AA1 3，M、N分 别为A1 B1、A1 D1的中点，E、F分别是B1C1、 C1 D1的中点。 求证：平面AMN // 平面EFDB
探 究 如图，平面α外有直线 a平行于平面α内的直线 b。 （1）这两条直线共面吗？ 共面
（2）直线a 与平面α相交吗？
a
不可能相交

b
直线和平面平行的判定定理：
平面外一条直线与此平面内的一条直 线平行，则该直线与此平面平行。
符号表示： a//b
a α a//α b α
简述为： 线线平行，则线面平行
我们知道，若一个平面内所有直线都与另一平 面平行，那么这两个平面一定不可能相交，所以两 面平行。只要有一条直线与另一面相交，则两面不 平行。 面面问题

2.2.1线面平行的判定

2.2.1线面平行的判定

§2.2.1 直线与平面平行的判定【学习目标】1. 通过生活中的实际情况，建立几何模型，了解直线与平面平行的背景；2. 学会直线与平面平行的判定定理，并会用其证明线面平行.【重点难点】重点：直线和平面平行的判定定理。

难点：直线和平面平行的判定定理。

【想一想】直线与平面的位置关系有3种，其中平行是最重要的关系之一，那么如何判定直线和平面是平行的呢？本节课我们就来研究这个问题。

【复习回顾】1.直线与平面的位置关系2.直线与平面平行的定义：若一条直线和一个平面___________公共点，则它们平行。

讨论：根据定义如何判定直线和平面是平行的呢？好判断吗？【自主探究】一、直线与平面平行的背景分析实例1：如图5-1，一面墙上有一扇门，门扇的两边是平行的.当门扇绕着墙上的一边转动时，观察门扇转动的一边l与墙所在的平面位置关系如何？实例2：将课本的一边AB紧靠桌面，并绕AB转动，观察AB的对边CD在各个位置时，是不是都与桌面所在的平面平行？思考：通过实例，你能得到什么样的结论？【合作交流】【典型例题】例1.有一块木料如图5-4所示，P为平面BCEF内一点，要求过点P在平面BCEF内作一条直线与平面ABCD平行，应该如何画线？例2.求证：空间四边形相邻两边中点的连线，平行于经过另外两边所在的平面.变式1.如果E，F是线段AB，AD的三等分点，则EF 与平面BCD平行吗？四等分点呢？你得到了什么结论？变式2.如果G，H分别是线段BC，CD的中点，试证明EG //平面ACD.你还能找到哪些直线和平面平行？【巩固练习】1.在正方体ABCD—A1B1C1D1中，E为DD1的中点，试判断BD1与平面AEC的位置关系，并说明理由。

【个人收获与问题】知识：思想与方法：我的问题：【当堂检测】1. 下列命题正确的个数是（）（1）若直线l上有无数个点不在平面α内，则l// α（2）若直线l与平面α平行，则l平面α内的任意一直线平行（3）两条平行线中的一条直线与一个平面平行，那么另一条也与这个平面平行（4）若一直线ａ和平面α内一直线平行，则ａ// αA.0个B．1个C．2个D．3个2.在四面体A-BCD中，M,N分别是△ACD, △BCD的重心，则四面体的4个面中与MN 平行的面是___________________.证明：3.已知AB、BC、CD是不在同一平面内的三条线段，E、F、G分别为AB、BC、CD的中点.求证：AC∥平面EFG，BD∥平面EFG.。

2.2.1直线和平面平行的判定定理

2.2.1直线和平面平行的判定定理

P
第1题图
M
B
C
O
A
D
思考： 已知点P是平行四边形ABCD所在平面外一点， E, F 分别是AB，PD的中点，求证：AF//平面PEC
再见！
从中你能得出什么结论？ 猜一 A B 猜 CD 是桌面外一条直线， AB是桌面内一条
直线， CD ∥ AB ，则CD ∥桌面 猜想：如果平面外一条直线和这个平面内的一 条直线平行，那么这条直线和这个平面平行。
直线和平面平行的判定定理
如果平面外一条直线和这个平面内的一条直线 平行，那么这条直线和这个平面平行。 a a b a∥ b a∥ b
A
E
D
O
B
C
B
练一 练
两个全等的正方形ABCD、ABEF不在同 一平面内,M、N是对角线AC、BF的中点 求证：MN ∥面BCE A
D
F
M
N B E
C
M、N 是AC，BF上的点且AM=FN， 求证：MN ∥面BCE
A D N B E F
M
C
P
Q
A D N B
F
M
E C
p
知识小结
1．证明直线与平面平行的方法： （1）利用定义；直线与平面没有公共点 （2）利用判定定理． 线线平行 线面平行
复习引入
直线与平面有几种位置关系？
有三种位置关系：在平面内，相交、平行．
其中平行是一种非常重要的关系，不仅应用较 多，而且是学习平面和平面平行的基础．
a
a ∩=A
a
a ∥
引入新课
怎样判定直线与平面平行呢？ 根据定义，判定直线与平面是否平行，只需判 定直线与平面有没有公共点．但是，直线无限延长， 平面无限延展，如何保证直线与平面没有公共点呢？ a
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2.2.1 线面与面面平行的判定
【使用说明及学法指导】
1．先自学课本，理解概念，完成导学提纲；
2．小组合作，动手实践。

【学习目标】
1. 通过生活中的实际情况，建立几何模型，了解直线与平面平行的背景；
2. 理解和掌握直线与平面平行的判定定理，并会用其证明线面平行.
3. 能借助于长方体模型讨论直线与平面、平面与平面的平行问题；
4. 理解和掌握两个平面平行的判定定理及其运用；
【重点】直线与平面平行、平面与平面平行的判定定理及应用
【难点】直线与平面平行、平面与平面平行的判定定理及应用
一、自主学习
1.预习教材P54～ P57,完成下列问题
复习：直线与平面的位置关系有______________，_______________，_________________.
讨论：直线和平面的位置关系中，平行是最重要的关系之一，那么如何判定直线和平面是平行的呢？根据定义好判断吗？
2.导学提纲
探究1：直线与平面平行的背景分析
实例1：如图，一面墙上有一扇门，门扇的两边是平行的.当门扇绕着墙上的一边转动时，观察门扇转动
的一边l与墙所在的平面位置关系如何？
实例2：如图，将一本书平放在桌面上，翻动书的封面，观察封面边缘所在直线l与桌面所在的平面具有怎样的位置关系？
结论：
探究2：直线与平面平行的判定定理
问题：探究1两个实例中的直线l为什么会和对应的平面平行呢？你能猜想出什么结论吗？能作图把这一
结论表示出来吗？
直线与平面平行的判定定理
定理：
反思：思考下列问题
⑴用符号语言如何表示上述定理；⑵上述定理的实质是什么？
探究3：两个平面平行的判定定理
问题1：平面可以看作是由直线构成的.若一平面内的所有直线都与另一个平面平行，则这两个平面平行
吗？由此你可以得到什么结论？
问题2：一个平面内所有直线都平行于另外一个平面好证明吗？能否只证明一个平面内若干条直线和另外
一个平面平行，那么这两个平面就平行呢？
试试：在长方体中，回答下列问题
面,AA∥面BB C C，则面AA B B∥面BB C C吗？
⑴如下图，AA AA B B
面，则A ADD
面吗？
面∥DCC D
⑵如下图6-2，AA∥EF，AA∥DCC D
面，EF∥DCC D
⑶如下图，直线A C和B D相交，且A C、B D都和平面ABCD平行(为什么)，则平面A B C D∥平面ABCD吗？
反思：由以上3个问题，你得到了什么结论？
两个平面平行的判定定理：
如图所示，∥.
反思：
⑴定理的实质是什么? ⑵用符号语言把定理表示出来.
二、典型例题
例1. 有一块木料如图5-4所示，P为平面BCEF内一点，要求过点P在平面BCEF内作一条直线与平面ABCD平行，应该如何画线？
例2. 如图5-5，空间四边形ABCD 中，,E F 分别是,AB AD 的中点，求证：EF ∥平面BCD . 例3. 已知正方体1111ABCD A B C D ，如图，求证：平面11AB D ∥1CB D .
三、拓展探究
1. 正方形ABCD 与正方形ABEF 交于AB ，M 和
N 分别为AC 和BF 上的点，且AM FN ，如图5-6
所示.求证：MN ∥平面BEC . 2. 如图，正方体中，,,,M N E F 分别是棱A B ，A D ，B C ，C D 的中点，求证：平面AMN ∥平面EFDB .
四、课堂小结1．知识：2．数学思想、方法：
五、课后巩固
1．如图在正方体中，E 为1DD 的中点，判断1BD 与平面AEC 的位置关系，并说明理由.
N
M F
E
D C
B A F E
M N B C
A D
C
B
A
D
2．课本第62页A组3题、7题、8题。