- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-
14
思考:曼哈顿岛的价值
美国曼哈顿岛是世界地产业的黄金地段,包括 华尔街、联合国总部。1624年,Peter Minuit 花了US$24从印地安人手中购得曼哈顿。你 认为这宗答
到2003年底,复利期数达379年。若年复利 率为8%,到2003年底,这US$24的价值变为:
-
9
B、后付年金现值
例:某人在60岁时拟存入一笔钱以作今后20年 的生活费。计划今后每年末支取3000元,20年 后正好取完。设利率10%,问现在应存入多少?
01 2
A 1 (1 i)1
AA
A
(1
1 i)2
1 A (1 i)n1
A
(1
1 i)
n
-
n-1 n AA
10
P V A ( 1 1 A i) A ( 1 1 i)2 A ( 1 1 i)n 1 A ( 1 1 i)n
100000元
114240元
年份0
1
唐先生的财务顾问麦先生指出,如果他接受第一个报价,他可以将这 100000元,以12%的利率存入银行,这样一年以后他可以得到 112000元,因为112000小于114240,他建议唐先生接受后者.
-
6
(二)年金终值和现值
1、定义: 每期金额相等P29 2、分类: 后付年金
B、现值
递延年金的现值与 普通年金一样吗?
-
12
递延年金的现值
01
2
m
m+1 m+2 m+n-1 m+n
A
A
A
A
A
P=A·(P/A,i·n) ·(P/F,i,m)
-
13
(4)永续年金的终值和现值
A、没有终值
B、现值
A
P=
i
例:拟建永久性奖学基金,每年颁发10000元,若利率为10%, 基金额度应多少?
2.复利现值(Present value)
相当于原始本金,它是指今后某一特定时间收 到或付出一笔款项,按折现率i计算的现在时
点的价值。
PV=FV(1+i)-n
=FV *复利值现系数
=FV *(P/F, i,n)
P V IFi,n
-
5
例:一个简单的售房决策
唐先生考虑出售在市郊的一处房产,有人报价10万元并立即支付, 他准备接受这一报价;另有人报价11.424万元,但是一年后付款.两 个买主都有诚意,并且均有支付能力,那么唐先生应该选择哪个报 价呢?
例题解答
10000 5000 1000
0
1
2
3
PV=10000×PVIF4%,1+5000×PVIF4%,2+1000×PVIF4%,3
=10000×0.9615+5000×0.9246+1000×0.8890 =15127元
例题
H先生在30年前就有存硬币的嗜好,30年来, 硬币装满了5个布袋,共计15000元,平均每 年储存价值500元。如果他每年年末都将硬币 存入银行,存款的年利率为5%,那么30年后 他的存款帐户将有多少钱?这与他放入布袋 相比,将多得多少钱?
-1000
3
4
5
项目可行吗?
500 乙
-1000
400
300
200
选择甲还是乙?
-
100
3
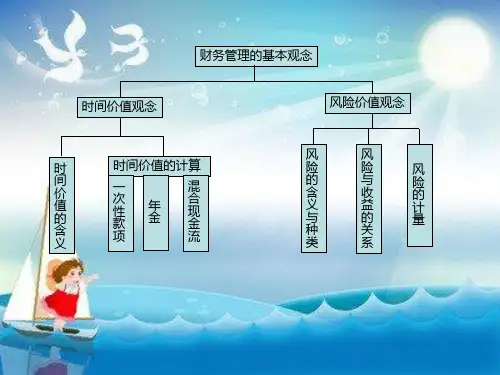
二、时间价值的计算
单利(Simple interest):在规定的时间内,对本 金计算利息
复利(Compound interest)在规定的时间内, 对本金和产生的利息计算利息
例:100元,按10%的单利存2年: 本利和=P+SI=P+P*i*n=100+100*10%*2=120 按10%的复利存2年:
第二章 财务管理的价值观念
-
1
第一节 货币的时间价值
一、时间价值的含义
1、时间价值的概念
2、 时间价值的表现形式
(1)绝对数 利息额
(2)相对数 利息率(纯利率)
投资者要求的最低投资报酬率
贴现率
-
2
3、时间价值的作用。解决了不同时点资金价值
的换算关系
100
200
300
400
500
甲0
1
2
A(1+i)n-1
-
8
即:FVA=A+A(1+i)+A(1+i)2+A(1+i)3
+ ---+ A(1+i)n-2 + A(1+i)n-1
则有:
FVAA(1i)n 1 i
年金终值系数 FVIFA(i,n)或(F/A,i,n )
上例中:FVA=1000× FVIFA(6%,10)
查表可得:FVA=13181元
例题解答
30年后的终值FVA=500×FVIFA(5%,30) =500×66.4388=33219.42 利息=33219.42-15000=18219.42
例题
某项目在营运后各年的现金流量如下(单 位:万元),贴现率为10%。
12345678 100 100 100 200 200 150 150 150
•根据你的理解,此项目的总回报是多少?
例题解答
PV=100×PVIFA10%,3+200×PVIFA10%,2 ×PVIF10%,3+150×PVIFA10%,3×PVIF10%,5
即P : VA A11/1 (i)n i
年金现值系数 PVIFA(i,n)或(P/A,i,n)
上例中,PVA=3000×PVIFA(10%,20) =3000×8.5136=25542
-
11
(2)先付年金的终值和现值 A、终值 比普通年金终值计算加一期,减A
B、现值
比普通年金终值计算减一期,加A
(3)递延年金的终值和现值 A、终值 与普通年金计算一样
先付年金 递延年金 永续年金 3、年金终值和现值的计算
-
7
(1)后付年金终值与现值的计算 A、后付年金终值
例:有一零存整取储蓄计划,每年末存入1000 元,连续存10年,设利率6%,问10年期满的 总价值?
01 2 3 AA A
n-1 n AA
A(1+i)0 A(1+i)1
A(1+i)n-3
A(1+i)n-2
本利和 =(P+P*i)(1+i)=100(1+10%)(1+10%)=121
时间价值的计算一般采用复利的概念
-
4
(一)复利终值与现值
1,复利终值(Future value)
一定量的本金按复利计算若干期后的本利和。
FV=PV(1+i)n
== PV*复利终值系数
== PV*(F/P,i,n)
F V IFi,n
V 2 0 0 3 U S $ 2 4 ( 1 8 % ) 3 7 9 U S $ 1 1 1 . 6 3 9 万 亿
你不一定认为 便宜吧!
-
16
例题
若贴现率为 4%,在第 一年末收到10000元, 第 二 年 末 收 到 5000 元 , 第 三 年 末 收 到 1000 元 , 则所有收到款项的现值 是多少?