北京清华大学附属中学2010-2011学年初二第二学期数学期末

北京一零一中2010-2011学年度第二学期期末考试初二数学试题及答案考试时间:120分钟满分:140分一、选择题:在每小题给出的四个选项中,只有一项符合题意,请把你认为正确的选项填入表格内。

本大题共10小题,共40分。

1. 下列根式中,是最简二次根式的是(A.8B.12C. 6D. 272. 在平面直角坐标系中,点P (2,-3关于原点对称的点'P 的坐标是( A. (-2,3 B. (3,-2 C. (-2,-3 D. (2,3 3. 关于x 的一元二次方程22(110a x x a -++-=的一个根是0,则a 的值为(A. 1B. -1C. 1或-1D. 04. 在下列图形中,既是轴对称图形,又是中心对称图形的是( A. 等腰梯形 B. 正三角形 C. 平行四边形 D. 菱形5. 下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是( A. 3,4,5 B. 6,8,10 C. 325 D. 1,126. 如图1所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B 恰好碰到地面,经测量AB =2米,则树高为(A.5米 B.3米 C. (5+1米 D. 3 米7. 如图2,在正方形A B C D 的外侧作等边A D E △,则A E B ∠的度数为( A. 10° B. 12.5° C. 15° D. 20°8. 如图3,△ABC 中,ABDE //交AC 于D ,交BC 于E ,若AD =2,CD =3,DE =4,则A B =(A.83B.203C.125D. 69. 如图4,等边三角形A B C 的边长为3,D 、E 分别是A B 、A C 上的点,且2AD AE ==,将A D E △沿直线D E 折叠,点A 的落点记为A ',则四边形A D A E '的面积1S 与A B C △的面积2S 之间的关系是(A.1212S S =B.1278S S =C.1234S S =D.1289S S =A E D BCA '图410. 如图5,矩形ABCD 中,AB >AD ,AB =a ,AN 平分∠DAB ,DM ⊥AN 于点M ,CN ⊥AN 于点N 。

北京市东城区（南片)2010—2011学年第二学期期末统一测试初二数学（总分：100分；时间:100分钟)亲爱的同学,这份试卷将再次记录你的自信、沉着、智慧和收获．请认真审题，看清要求，仔细答题，要相信“我能行”.一、精心选一选（本题共10小题，每小题3分,共30分) 1。

已知分式11-+x x 的值为0，那么x 的值为 A. 1 B 。

—1 C. ±1 D. 0 2。

下列函数中，自变量x 的取值范围为3≥x 的是 A. 31-=x y B 。

31-=x y C. y= x —3D. 3-=x y3。

反比例函数xky =的图象经过点(—2，4），则函数的图象在 A 。

第一、三象限 B. 第一、四象限 C. 第二、三象限 D 。

第二、四象限A 。

32，30B 。

31,30C 。

32，32D 。

30，305。

下面计算正确的是 A 。

3333=+ B.3327=÷C.532=⋅D.24±=6。

下列各组数中不能作为直角三角形的三边长的是A 。

1.5，2，3 B. 7，24,25 C 。

6，8，10 D 。

9，12,157。

如图，将矩形ABCD 沿BE 折叠，点A 落在点A’处，若∠CBA’=30°，则∠BEA'等于 A 。

30° B 。

45° C 。

60° D 。

75°8。

如图，菱形ABCD 的周长为20，点A 的坐标是（4，0),则点B 的坐标为A. （3,0) B 。

（4,0） C 。

（0,3）D 。

（0，4）9. 如图，点A 在反比例函数xky =的图象上，AB ⊥x 轴于点B ，点C 在x 轴上,且CO=OB ，△ABC 的面积为2,则此反比例函数的解析式为A 。

xy 4=B. xy 3=C. xy 2=D 。

xy 1=10。

如图，正方形硬纸片ABCD 的边长是4，点E 、F 分别是AB 、BC 的中点，若沿左图中的虚线剪开，拼成如下图的一座“小别墅”，则图中阴影部分的面积是A 。

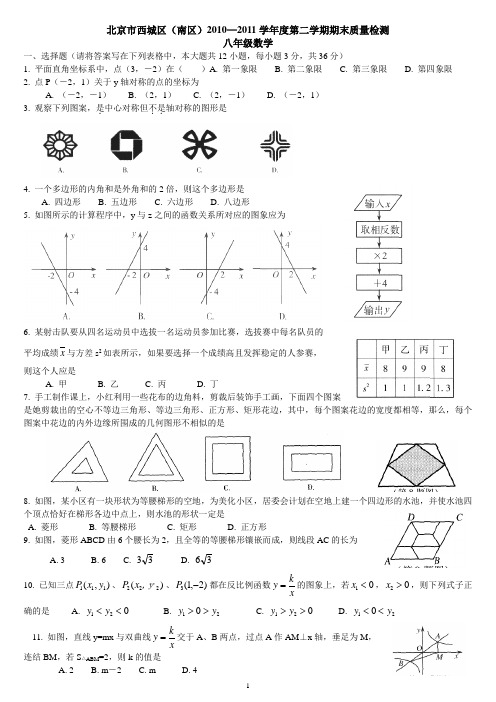
北京市西城区（南区）2010—2011学年度第二学期期末质量检测八年级数学一、选择题（请将答案写在下列表格中，本大题共12小题，每小题3分，共36分）1. 平面直角坐标系中，点（3，－2）在（ ）A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限2. 点P （－2，1）关于y 轴对称的点的坐标为A. （－2，－1）B. （2，1）C. （2，－1）D. （－2，1） 3. 观察下列图案，是．中心对称但不是．．轴对称的图形是4. 一个多边形的内角和是外角和的2倍，则这个多边形是A. 四边形B. 五边形C. 六边形D. 八边形5. 如图所示的计算程序中，y 与z 之间的函数关系所对应的图象应为6. 某射击队要从四名运动员中选拔一名运动员参加比赛，选拔赛中每名队员的平均成绩x 与方差s 2如表所示，如果要选择一个成绩高且发挥稳定的人参赛， 则这个人应是A. 甲B. 乙C. 丙D. 丁7. 手工制作课上，小红利用一些花布的边角料，剪裁后装饰手工画，下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边，其中，每个图案花边的宽度都相等，那么，每个图案中花边的内外边缘所围成的几何图形不相似的是8. 如图，某小区有一块形状为等腰梯形的空地，为美化小区，居委会计划在空地上建一个四边形的水池，并使水池四个顶点恰好在梯形各边中点上，则水池的形状一定是A. 菱形B. 等腰梯形C. 矩形D. 正方形9. 如图，菱形ABCD 由6个腰长为2，且全等的等腰梯形镶嵌而成，则线段AC 的长为A. 3B. 6C. 33D. 3610. 已知三点),(111y x P 、)(222，y x P 、)2,1(3-P 都在反比例函数xk y =的图象上，若01<x ，02>x ，则下列式子正确的是 A. 021<<y yB. 210y y >>C. 021>>y yD. 210y y <<11. 如图，直线y=mx 与双曲线xk y =交于A 、B 两点，过点A 作AM ⊥x 轴，垂足为M ，连结BM ，若S △ABM =2，则k 的值是A. 2B. m －2C. mD. 412. 如图是某条公共汽车线路收支差额y 与乘客量x 的函数图象（实线部分，收支差额=车票收入－支出费用）。

学年度初二下学期期末考试数学试卷一、选择题（每题分，共分）、已知一直角三角形的木板，三边长度的平方和为，则斜边长为（）、、、、、某服装销信商在进行市场占有率的调查时，他最应该关注的是（）、服装型号的平均数、服装型号的众数、服装型号的中位数、最小的服装型号、有三个角相等的四边形是（）、矩形、菱形、正方形、矩形、菱形、正方形作为结论都不对、如图，等腰梯形中，，∠＝°，，△的周长为，则等腰梯形的周长是（）、、、、、有一组数据如下：，，，，，，，。

那么这组数据的中位数是（）、或、、、、正比例函数与反比例函数的图象相交于、两点，轴于，轴于（如图），则四边形的面积为（）、、、、、某工厂为了选择名车工参加加工直径为的精密零件的技术比赛，随机抽取甲、乙两名车工加工的个零件，现测得的结果如下表，请你比较、的大小（）、、、、、若，则下列方程一定是一元二次方程的是（）、、、、二、填空题（每空分，共分）、如图，在平行四边形中，为边的中点，平分∠交于，是上任意一点，∠＝°，，则＋的最小值为。

、已知，则分式的值为。

、函数的自变量的取值范围是，其图像与轴的交点坐标为。

、如图，将一块边长为的正方形纸片的顶点折叠至边上的点，使，折痕为，则的长为。

三、解答题（共分）、（分）计算：、（分）已知实数满足，求的值。

、（分）解分式方程；、（分）解方程、（分）某公司对应聘者进行面试，按专业知识，工作经验，仪表形象给应聘者打分，这三个方面的重要性之比为，对应聘的王丽、张瑛两人打分如右表：如果两人中只录取一人，若你是人事主管，你会录用谁？说说你的理由。

、（分）如图，在菱形中，∠°，的垂直平分线对角线于点，为垂足，连结，求∠的度数。

、（分）如图所示，已知、两个乡镇相距千米，有一个自然保护区与相距千米，与相距千米，以点为圆心，千米为半径是自然保护区的范围，现在要在、两个乡镇之间修一条笔直的公路，请问：这条公路是否会穿过自然保护区？试通过计算加以说明。

北京市朝阳区2010～2011学年度八年级第二学期期末统一考试数 学 试 卷2011. 7（考试时间90分钟 满分100分）成绩一、选择题（每小题3分，共24分）在下列各题的四个选项中，只有一个是符合题意的，请将正确选项前的字母填在题后的括号内. 1.在函数=y x 的取值范围是（ ）A. 2-≠xB.2->xC. 2-≥xD. 2>x 2．下列由线段a ，b ，c 组成的三角形中，不是直角三角形的是（ ）A ．a ＝3，b ＝4，c ＝5B ．a ＝5，b ＝12，c ＝13C ．a ＝1，b ＝1，cD ．a ＝8，b ＝10，c ＝12 3．下列计算正确的是（ ） A．29= B2=- C6= D2=4．甲、乙、丙、丁四名射击运动员都参加了同一场预选赛，他们射击成绩的平均数及方差如下表所示：如果选出一个成绩较好且状态稳定的运动员去参赛，那么应选（ ） A ．甲B ．乙C ．丙D ．丁5． 一元二次方程032=-x x 的解为（ ）A ．3=xB ．01=x ，32=xC ．01=x ，32-=xD ．11=x ，32=x 6．若反比例函数xy 1=的图象上有两点1(1)A y ，、2(2)B y ，，则下列说法正确的是（ ） A. 21y y > B. 21y y ≥ C. 21y y < D. 21y y ≤7．一个物体所受到的压强P 与所受压力F 及受力面积S 之间的计算公式为SFP =. 当一个物体所受压力F ＝5时，该物体所受压强P 与受力面积S 之间的关系用图象表示大致为（ ）A. B. C. D.8. 已知关于x 的一元二次方程22410x x k ++-=有两个非零的整数根，k 为正整数，则k 的值为（ ） A ．123k =，，． B ．1k = C ．2k = D ．3k =二、填空题（每小题3分，共24分）9．计算：(1 = .10. 北京时间2011年6月4日，李娜夺得法网女单冠军，她是第一位揽获大满贯单打桂冠的中国人、亚洲人. 法网开赛前，李娜的微博就已经拥有了约160万粉丝，而到法网决赛之前，这一数字已经升至170多万. 在李娜夺冠之后的短短3个小时内，她的微博粉丝数激增至196万，截至6月5日23时，李娜的粉丝数已经达到了约212万. 这组数据：160万、170万、196万、212万的极差是__________． 11．如图，矩形ABCD 的两条对角线相交于点O ，∠AOD ＝110°，则1∠＝ °．12．分式方程19332+-=+x x x 的解是 . 13. 命题“如果一个梯形的两条对角线相等，那么这个梯形是等腰梯形” （第11题）的逆命题是 命题（填“真”或“假”）.14. 已知关于x 的一元二次方程052=++k x x 有一个根是1，则=k .SP八年级数学试卷第3页（共8页）15．如图，在Rt △ABC 中，∠ACB =90°，∠A =45°，BC =6，点D 在边AC 的三等分点处，连接BD ，E为AB 中点，F 为BD 中点，则△CEF 的周长为 .（第15题） （第16题）16．为庆祝建党90周年，美化社区环境，某小区要修建一块艺术草坪. 如图，该草坪依次由部分互相重叠的一些全等的菱形组成，且所有菱形的较长的对角线在同一条直线上，前一个菱形对角线的交点是后一个菱形的一个顶点，如菱形ABCD 、EFGH 、CIJK …，要求每个菱形的两条对角线长分别为4m 和6m . （1）若使这块草坪的总面积是39m 2，则需要 个这样的菱形；（2）若有n 个这样的菱形（n ≥2，且n 为整数），则这块草坪的总面积是 m 2．三、解答题（17-19题每题4分，20-23题每题5分，24题6分，25-26题每题7分，共52分） 17．计算：485316123+-． 18. 解方程：0742=-+x x （要求：用配方法）．19. 解方程：0)1(232=--x x ....A20．结合创建“全国文明城区”活动，我区某中学以班为单位进行“文明礼仪伴我行”知识竞赛，抽取各班学号分别为5、10和15的三名同学组成班级代表队参赛. 统计各班竞赛成绩后绘制成统计图，根据图中信息回答下列问题：（1）请补全竞赛成绩统计图①；（2）这次各班竞赛成绩的平均数是 ，中位数是 ，众数是 ； （3）请结合这次竞赛成绩，谈谈你对这所中学在文明礼仪教育方面的想法（写出一条即可）： .21．已知：如图，在□ABCD 中，E 、F 是对角线AC 上的两点，且AE ＝CF .求证：四边形BEDF 是平行四边形．竞赛成绩统计图②(分)八年级数学试卷第5页（共8页）22．列方程解应用题去冬今春，我国长江中下游地区遭受严重旱情，为了协助当地群众抗旱保春耕，某军区给水工程团派出工程人员及设备奔赴120千米外的某地执行抗旱打井任务，一辆装载设备的卡车先走，30分钟后，工程人员乘坐一辆客车从同一地点出发，结果两车同时到达指定地点. 已知卡车的速度是客车速度的43，求这两种车的速度.23．如图，已知在梯形ABCD 中，AD ∥BC ，∠ABC ＝60º，BD 平分∠ABC ，且BD ⊥DC ，CD ＝4． （1）求AD 的长；（2）求梯形ABCD 的面积．24. 如图，在平面直角坐标系中有一点A （－1, 3），OA 与x 轴的负半轴OM 的夹角∠AOM ＝60°，OB 平分∠AOM ，且OB ＝OA . （1）若点A 在反比例函数xky =的图象上，①求该反比例函数的解析式；②请说明点B 一定也在该反比例函数的图象上； （2）求△AOB 的面积;（3）设直线AB 的解析式为b ax y +=，若b ax xk+>，则x 的取值范围为 .八年级数学试卷第7页（共8页）25．将边长OA =8，OC =10的矩形OABC 放在平面直角坐标系中，顶点O 为原点，顶点C 、A 分别在x 轴和y 轴上.在OA 边上选取适当的点E ，连接CE ，将△EOC 沿CE 折叠. （1）如图①，当点O 落在AB 边上的点D 处时，点E 的坐标为 ；（2）如图②，当点O 落在矩形OABC 内部的点D 处时，过点E 作EG ∥x 轴交CD 于点H ，交BC 于点G. 求证：EH ＝CH ；（3）在（2）的条件下，设H （m ，n ），写出m 与n 之间的关系式 ； （4）如图③，将矩形OABC 变为正方形，OC ＝10，当点E 为AO 中点时，点O 落在正方形OABC 内部的点D 处，延长CD 交AB 于点T ，求此时AT 的长度．图① 图②图③26．四边形ABCD 和CEFH 都是正方形，连接AE ，M 是AF 中点，连接DM 和EM .（1）如图①，当点B 、C 、H 在一条直线上时，线段DM 与EM 的位置关系是 ，DMEM = ；（2）如图②，当点B 、C 、F 在一条直线上时，（1）中的结论还成立吗？如果成立，请证明；如果不成立，说明理由.图②图①八年级数学试卷第9页（共8页）朝阳区2010～2011学年度八年级第二学期期末统一考试数学试卷参考答案及评分标准2011.7一、选择题（每小题3分，共24分）二、填空题（每小题3分，共24分）9.210. 52万 11. 35 12. 2=x 13. 真14. 6-15. 13231++ 16. （1）4；（2）)39(+n . （说明：（1）1分，（2）2分）三、解答题（17-19题每题4分，20-23题每题5分，24题6分，25-26题每题7分，共52分） 17. 解：原式3203236+-=, ……………………………………………………………………3分324=. …………………………………………………………………………………4分18．解： 742=+x x ，47442+=++x x ，11)2(2=+x ， ………………………………………………………………………2分112±=+x ，∴1121+-=x ，1122--=x . ………………………………………………………4分19. 解：方程化为.02232=+-x x ……………………………………………………………………1分.2,2,3=-==c b a.020234)2(422<-=⨯⨯--=-=∆ac b ………………………………………………3分（分） ∴方程无实数根. ………………………………………………………………………………4分20. （1）……………………………………………………1分（2）84，85，90 ……………………………………………………………………………………4分 （3）如：大部分学生较好的掌握了文明礼仪知识. ……………………………………………………5分21. 解：连接BD 交AC 于点O ， ∵四边形ABCD 是平行四边形，∴AO ＝CO ，BO ＝DO . …………………………2分 又∵AE ＝CF ，∴AO －AE ＝CO －CF ，即EO ＝FO . ……………………………………………………………4分 ∴四边形EBFD 是平行四边形. …………………………………………………………………5分22. 解：设客车的速度为x 千米/时，则卡车的速度为x 43千米/时， 由题意，有2112043120+=x x ， …………………………………………………………………2分 解得 80=x . ……………………………………………………………………………………3分经检验，80=x 是原方程的解. ………………………………………………………………4分∴6043=x . ……………………………………………………………………………………5分 答：客车的速度为80千米/时，卡车的速度为60千米/时.23.解：（1）∵BD 平分∠ABC ，∠ABC ＝60°，∴∠1＝∠2＝21∠ABC ＝30°. 又∵BD ⊥DC ，∴∠C ＝60°. ∴∠ABC＝∠C .∴AB ＝CD ＝4. …………………………………………………………………………1分 ∵AD ∥BC ，∴∠1＝∠3.八年级数学试卷第11页（共8页）图②又∵∠1＝∠2，∴∠2＝∠3.∴AD ＝AB ＝4. ……………………………………………………………………………2分（2）作DE ⊥BC 于点E ，在Rt △DBC 中，∠1＝30°，∴BC ＝2CD ＝8. ……………………………………………………………………………………3分 在Rt △DEC 中，∠C ＝60°，∴∠4＝30°. ∴EC ＝21CD ＝2. ∴3222=-=EC CD DE . ……………………………………………………………………4分 ∴=ABCD S 梯形312)(21=⋅+DE BC AD .…………………………………………………………5分24. 解：（1）① 把点A （－1，3）代入xky =中，∴3-=k . 即反比例函数的解析式为xy 3-=. ………………………………………………1分 ② 作BC ⊥OM 于点C ，作AD ⊥OM 于点D ，由题意知，2==OA OB .∵OB 平分AOM ∠，且︒=∠60AOM ，∴︒=∠30BOM . ∴Rt △BOC 中，121==OB BC ，3=OC . ∴B （3-，1）. ………………………………2分 把3-=x 代入xy 3-=中，得1=y . ∴点B 一定也在反比例函数xy 3-=的图象上. （2）.1=-+=∆∆∆BO C AO D ABCD AO B S S S S 梯形 …………………………………………………………4分 （3）3-<x 或01<<-x . ……………………………………………………………………………6分25. （1）（0，5）；…………………………………………………1分 （2）证明：（如图②）由题意可知∠1＝∠2.∵EG ∥x 轴，∴∠1＝∠3. ∴∠2＝∠3.∴EH ＝CH . …………………………………………3分（3）.52012+=n m ……………………………………………………………………………………5分 （4）解：（如图③）连接ET ，由题意可知，ED ＝EO ，ED ⊥TC ，DC ＝OC ＝10， ∵E 是AO 中点，∴AE ＝EO . ∴AE ＝ED .在Rt △ATE 和Rt △DTE 中，⎩⎨⎧==,,ED AE TE TE ∴Rt △ATE ≌Rt △DTE （HL ）.∴AT ＝DT . ……………………………………………………………………………………6分 设x AT =，则x BT -=10，x TC +=10， 在Rt △BTC 中，222TC BC BT =+, 即222)10(10)10(x x +=+-，解得 5.2=x ，即5.2=AT . …………………………………………………………………7分26.（1）DM ⊥EM ，1； ……………………………………………………………………………………2分（2）结论仍然成立.证明：延长DM 交BF 于点N ，连接ED 、EN ，∵四边形ABCD 、ECHF 都是正方形， ∴AD ＝DC ，EC ＝EF ，AD ∥BC ，∠DCB ＝∠CEF ＝90°，∠1＝∠EFC ＝45°. ∴∠DAM ＝∠NFM .∵M 是AF 的中点，∴AM ＝FM . 在△AMD 和△FMN 中，⎪⎩⎪⎨⎧∠=∠=∠=∠,,,FMN AMD FM AM NFM DAM ∴△AMD ≌△FMN （ASA ）. ……………………………………………………………4分∴AD ＝FN ，DM ＝NM . 又∵AD ＝DC ，∴DC ＝FN .∵点B 、C 、F 在一条直线上，∠1＝45°，∠DCB ＝90°， ∴∠2＝45°.图③八年级数学试卷第13页（共8页）∴∠2＝∠EFC .在△EDC 和△ENF 中，⎪⎩⎪⎨⎧=∠=∠=,,2,EF EC EFC FN DC ∴△EDC ≌△ENF （SAS ）. ………………………………………………………………5分 ∴ED ＝EN ，∠3＝∠4.∴∠3＋∠CEN ＝∠4＋∠CEN ＝∠CEF ＝90°，即∠DEN ＝90°. ∵ED ＝EN ，DM ＝NM ，∴DM ⊥EM . …………………………………………………………………………6分 ∴.EM DM = ∴1=EMDM. …………………………………………………………………………………7分说明：各解答题的其他正确解法请参照以上标准给分.祝各位老师暑假愉快！。

一、选择题（每题3分，共30分）1. 下列数中，是正数的是（）A. -3B. 0C. 1/2D. -1/22. 下列各数中，绝对值最小的是（）A. -2B. 0C. 2D. -13. 已知 a > 0，b < 0，则下列不等式中正确的是（）A. a > bB. a < bC. -a > -bD. -a < -b4. 下列代数式中，正确的是（）A. (a + b)² = a² + b²B. (a - b)² = a² - b²C. (a + b)² = a² +2ab + b²D. (a - b)² = a² - 2ab + b²5. 若a² = b²，则下列说法正确的是（）A. a = bB. a = -bC. a = b 或 a = -bD. a 与 b 无关6. 在直角坐标系中，点P的坐标是（-3，4），点Q的坐标是（3，-4），则线段PQ的长度是（）A. 6B. 8C. 10D. 127. 一个长方形的长是6cm，宽是4cm，它的周长是（）A. 20cmB. 24cmC. 30cmD. 36cm8. 下列图形中，是轴对称图形的是（）A. 正方形B. 等腰三角形C. 长方形D. 以上都是9. 已知一次函数y=kx+b的图象经过点（2，3）和点（-1，1），则该函数的解析式是（）A. y = 2x + 1B. y = -2x + 1C. y = 2x - 1D. y = -2x - 110. 若 a、b、c 是等差数列，且 a + b + c = 12，a² + b² + c² = 42，则 b 的值是（）A. 4B. 6C. 8D. 10二、填空题（每题3分，共30分）11. 3的平方根是______，它的立方是______。

北京市西城区（北区）2010–2011学年度第二学期抽样测试八年级数学 2011.6（时间100分钟，满分100分）题号 一 二 三 四 五 总分 得分一、精心选一选（本题共30分，每小题3分） 1．函数5+=x y 中，自变量x 的取值范围是（ ）．A ． x ＞5-B ． x ≥5-C ． x ≤5-D ．x ≠5- 2．下列各组数中，以它们为边长的线段不能．．构成直角三角形的是（ ）． A ．6，8，10 B ．8，15，17 C ．1，3，2 D ．2，2，32 3．下列函数中，当x >0时，y 随x 的增大而增大的是（ ）．A ．x y 3-=B ．4+-=x yC ．xy 5-= D ．x y 21=4．对角线相等且互相平分的四边形一定是（ ）．A ．等腰梯形B ．矩形C ．菱形D ．平行四边形5．已知关于x 的方程0162=-+-m x x 有两个不相等的实数根，则m 的取值范围是（ ）．A ．10<mB ．10=mC ．10>mD ．10≥m 6．如图，等腰梯形ABCD 中，AD ∥BC ，BD 平分∠ABC ， ∠DBC =30°，AD =5，则BC 等于（ ）． A ．5 B ．7.5 C ．35 D ．107．用配方法解方程0142=+-x x ，下列变形正确的是（ ）．A ．4)2(2=-x B ．4)4(2=-x C ．3)2(2=-x D ．3)4(2=-x 8．右图为在某居民小区中随机调查的 10户家庭一年的月均用水量（单位：t ） 的条形统计图，则这10户家庭月均用水 量的众数和中位数分别是（ ）． 户数1 2 3 4A BCDC ．7，7D ．7，6.59．如图，反比例函数ky x =（0x >）的图象与一次函数y ax b =+的图象交于点A （1,6）和点B （3,2）， 当xkb ax <+时，x 的取值范围是（ ）． A ．13x << B ．1<x 或3x > C ．01x << D ．01x <<或3x >10．如图，正方形ABCD 中，AB =4，点E ，F 分别在AD ，DC 上，且△BEF 为等边三角形，则△EDF与△BFC 的面积比为（ ）．A ．2:1B ．3:1C ．3:2D ．5:3二、细心填一填（本题共16分，每小题2分）11．若03)2(2=-++y x ，则y x -的值为___________．12．在“2011年北京郁金香文化节”中，北京国际鲜花港的6103⨯株郁金香为京城增添了亮丽的色彩．若这些郁金香平均每平方米种植的数量为n （单位：株/平方米），总种植面积为S （单位：平方米），则n 与S 的函数关系式为____________________．（不要求写出自变量S 的取值范围） 13．如图，矩形ABCD 中，对角线AC ，BD 交于点O ，∠AOD =120°，BD =8，则AB 的长为___________．14．已知012=--x x ，则代数式111--x x 的值为__________．15．菱形ABCD 中，AB =2，∠ABC =60°，顺次连接菱形ABCD 各边的中点所得四边形的面积为____________． 16．如图，□ABCD 中，点E 在AB 边上，将△EBC 沿CE 所在直线折叠， 使点B 落在AD 边上的点B′处，再将折叠后的图形打开，若△AB ′E 的周长为4cm ，△B ′DC 的周长为11cm ，则B ′D 的长为_________cm ．17．正方形网格中，每个小正方形的边长为1．图1所示的矩形是由4个全等的直角梯形拼接而成的（图形的各顶点都在格点上；拼接时图形互不重叠，不留空隙），如果用这4个直角梯形拼接成一个等腰梯形，那么（1）仿照图1，在图2中画出一个拼接成的等腰梯形；（2）这个拼接成的等腰梯形的周长为________． ABC DOFDCEBAA BCDB'E A OBxy18．如图，在平面直角坐标系xOy 中，1(1,0)A ,2(3,0)A ,3(6,0)A ,4(10,0)A ,……，以12A A 为对角线作第一个正方形1121AC A B ，以23A A 为对角线作第二个正方形2232A C A B ，以34A A 为对角线作第三个正方形3343A C A B ，……，顶点1B ，2B ，3B ，……都在第一象限，按照这样的规律依次进行下去，点5B 的坐标为__________；点n B 的坐标为_________________．三、认真算一算（本题共16分，第19题8分，第20题8分） 19．计算：（1）1284(72)2+--； （2）21(23)(73)(73)++-+．20．解方程：（1）237x x x -=+； （2）2(1)3(1)x x x -=-． 解： 解：yxO A 1A 2A 4A 3C 1B 3B 2B 1C 2C 3四、解答题（本题共21分，第21题6分，第22、23、24题每题5分）21．已知：如图，□ABCD 中，对角线AC ，BD 相交于点O ，延长CD 至F ，使DF =CD ，连接BF 交AD 于点E ．（1）求证：AE =ED ；（2）若AB =BC ，求∠CAF 的度数． 证明：（1）解：（2）22．甲，乙两人是NBA 联盟凯尔特人队的两位明星球员，两人在前五个赛季的罚球命中率如下表所示：甲球员的命中率（%） 87 86 83 85 79 乙球员的命中率（%）8785848084（1）分别求出甲，乙两位球员在前五个赛季罚球的平均命中率；（2）在某场比赛中，因对方球员技术犯规需要凯尔特人队选派一名队员进行罚球，你认为甲，乙两位球员谁来罚球更好？（请通过计算说明理由）解：（1）（2） EFADCBO23．为了增强员工的团队意识，某公司决定组织员工开展拓展活动．从公司到拓展活动地点的路程总长为126千米，活动的组织人员乘坐小轿车，其他员工乘坐旅游车同时从公司出发，前往拓展活动的目的地．为了在员工们到达之前做好活动的准备工作，小轿车决定改走高速公路，路程比原路线缩短了18千米，这样比按原路线行驶的旅游车提前24分钟到达目的地．已知小轿车的平均速度是旅游车的平均速度的1.2倍，求这两种车平均每小时分别行驶多少千米．解：24．已知：如图，梯形ABCD 中，AD ∥BC ，∠B =90°，AD =a ，BC =b ，DC =b a +，且a b >，点M 是AB 边的中点．（1）求证：CM ⊥DM ；（2）求点M 到CD 边的距离．（用含a ，b 的式子表示） 证明：（1） A BCDM五、解答题（本题共17分，第25、26题6分，第27题5分） 25．已知：如图1，直线13y x =与双曲线ky x=交于A ，B 两点，且点A 的坐标为（6,m ）． （1）求双曲线ky x=的解析式； （2）点C （,4n ）在双曲线ky x=上，求△AOC 的面积；（3）过原点O 作另一条直线l 与双曲线ky x=交于P ，Q 两点，且点P 在第一象限．若由点A ，P ，B ，Q 为顶点组成的四边形的面积为20，请直接写出．．．．所有符合条件的点P 的坐标． 解：（1）（2）（3） yxCBOA图 1AOBxy备用图26．已知：如图1，平面直角坐标系xOy 中，四边形OABC 是矩形，点A ，C 的坐标分别为（6，0），（0，2）．点D 是线段BC 上的一个动点（点D 与点B ，C 不重合），过点D 作直线y ＝－12x ＋b 交折线O －A －B 于点E ．（1）在点D 运动的过程中，若△ODE 的面积为S ，求S 与b 的函数关系式，并写出自变量的取值范围； （2）如图2，当点E 在线段OA 上时，矩形OABC 关于直线DE 对称的图形为矩形O′A′B′C′，C′B ′分别交CB ，OA 于点D ，M ，O ′A ′分别交CB ，OA 于点N ，E ．探究四边形DMEN 各边之间的数量关系，并对你的结论加以证明；（3）问题（2）中的四边形DMEN 中，ME 的长为____________．解：（1）（2）（3）答：问题（2）中的四边形DMEN 中，ME 的长为____________．图1yxOAB C 图2E DCB A O xyO'C'B'A'MN27．探究问题1 已知：如图1，三角形ABC中，点D是AB边的中点，AE⊥BC，BF⊥AC，垂足分别为点E，F，AE，BF交于点M，连接DE，DF．若DE=k DF，则k的值为_____．图1CF MEBDA图2CEMFADB图3CEMFADB拓展问题2 已知：如图2，三角形ABC中，CB=CA，点D是AB边的中点，点M在三角形ABC的内部，且∠MAC=∠MBC，过点M分别作ME⊥BC，MF⊥AC，垂足分别为点E，F，连接DE，DF．求证：DE=DF．推广问题3 如图3，若将上面问题2中的条件“CB=CA”变为“CB≠CA”，其他条件不变．．．．．．，试探究DE与DF 之间的数量关系，并证明你的结论参考答案及评分标准一、精心选一选（本题共30分，每小题3分） 题号 1 2 3 4 5 6 7 8 9 10 答案BDCBADCBDA二、细心填一填（本题共16分，每小题2分）11．5-； 12．6310n S⨯=； 13．4； 14．1-； 15．3；16． 3.5； 17．（1）如图1所示（答案不唯一）；（2）1222+；（每问1分） 18．（18，3），2(1)1(,)22n n ++．（每空1分）三、认真算一算（本题共16分，第19题8分，第20题8分） 19．（1）解：1284(72)2+-- =2722(72)+-- ----------------------------------------------------------2分 =272272+-+ -------------------------------------------------------------3分 =732+． ---------------------------------------------------------------------------4分（2）解：21(23)(73)(73)++-+=144334+++ -----------------------------------------------------------------------2分=8434+ --------------------------------------------------------------------------------3分 =23+． -------------------------------------------------------------------------------4分20．（1）解：2470x x --=1a =，4b =-，7c =-，224(4)41(7)44b ac -=--⨯⨯-=． -----------------------------------------1分图1242b b ac x a -±-==4442±， ----------------------------------------------2分 211x =±，所以原方程的根为1211x =+，2211x =-． --------------------------4分（2）解：因式分解，得 (1)(23)0x x -+=． ------------------------------------------1分 10x -=或230x +=， ---------------------------------------------------------2分解得 11x =，232x =-． --------------------------------------------------------4分 阅卷说明：两个实数根各1分．四、解答题（本题共21分，第21题6分，第22、23、24题每题5分） 21．证明：（1）如图2．∵四边形ABCD 是平行四边形，∴ AB ∥CD ，AB =CD ． -------------------------1分 即AB ∥DF ．∵DF =CD ， ∴AB =DF ．∴四边形ABDF 是平行四边形． -----------------------------------------------2分 ∵AD ，BF 交于点E ，∴AE =DE ． -------------------------------------------------------------------------3分解：（2）∵四边形ABCD 是平行四边形，且AB =BC ，∴四边形ABCD 是菱形． ---------------------------------------------------------4分 ∴AC ⊥BD ． -------------------------------------------------------------------------5分 ∴∠COD =90°． ∵四边形ABDF 是平行四边形， ∴AF ∥BD ．∴∠CAF =∠COD =90°． ---------------------------------------------------------6分22．解：（1）878683857984x ++++==， ----------------------------------------------1分EFADC BO图28785848084845x ++++==乙． ----------------------------------------------2分所以甲，乙两位球员罚球的平均命中率都为84%．（2）222222(8784)(8684)(8384)(8584)(7984)85s -+-+-+-+-==甲，-------3分222222(8784)(8584)(8484)(8084)(8484) 5.25s -+-+-+-+-==乙． -----4分由x x =甲乙，22s s >甲乙可知，乙球员的罚球命中率比较稳定，建议由乙球员来罚 球更好． -------------------------------------------------------------------------------------5分23．解：设旅游车平均每小时行驶x 千米，则小轿车平均每小时行驶1.2x 千米．12612618241.260x x --=． ------------------------------------------------------------------2分 解得90x =． --------------------------------------------------------------------------------3分经检验，90x =是原方程的解，并且符合题意． ---------------------------------4分 ∴1.2108x =．答：旅游车平均每小时行驶90千米，小轿车平均每小时行驶108千米． ----5分24．证明：（1）延长DM ，CB 交于点E ．（如图3）∵梯形ABCD 中，AD ∥BC ， ∴∠ADM =∠BEM ． ∵点M 是AB 边的中点，∴AM =BM ．在△ADM 与△BEM 中， ∠ADM =∠BEM ， ∠AMD =∠BME ， AM =BM ，∴△ADM ≌△BEM ． ------------------------------------------------------------1分 ∴AD =BE =a ，DM =EM ． ∴CE =CB +BE =b a +． ∵CD =a b +， ∴CE =CD ．EA DMBC图3∴CM ⊥DM ． ----------------------------------------------------------------------2分解：（2）分别作MN ⊥DC ，DF ⊥BC ，垂足分别为点N ，F ．（如图4）∵CE =CD ，DM =EM ，∴CM 平分∠ECD ．∵∠ABC = 90°，即MB ⊥BC ，∴MN =MB ． --------------------------------------------------------------------------3分 ∵AD ∥BC ，∠ABC =90°， ∴∠A =90°．∵∠DFB =90°， ∴四边形ABFD 为矩形． ∴BF = AD =a ，AB = DF ．∴FC = BC －BF =b a -．∵Rt △DFC 中，∠DFC =90°，∴222DF DC FC =-=22()()a b b a +--=4ab ．∴ DF=2ab ． ---------------------------------------------------------------------4分 ∴MN=MB =12AB =12DF =ab ． 即点M 到CD 边的距离为ab ． -----------------------------------------------5分五、解答题（本题共17分，第25、26题6分，第27题5分） 25．解：（1）∵点A (6,)m 在直线13y x =上， ∴1623m =⨯=． --------------------------------------------------------------------1分∵点A (6,2)在双曲线ky x=上， ∴26k=， 12k =． ∴双曲线的解析式为12y x=． ---------------2分（2）分别过点C ，A 作CD ⊥x 轴，AE ⊥x 轴，垂足分别为点D ，E ．（如图5） ∵点C (,4)n 在双曲线12y x=上， DEAOBCxy图5FNECB M D A图4∴124n=，3n =，即点C 的坐标为(3,4)． ---------------------------------3分 ∵点A ，C 都在双曲线12y x=上， ∴11262AOE COD S S ∆∆==⨯=． ∴AOC S ∆=COEA S 四边形AOE S ∆-=COEA S 四边形COD S ∆-=CDEA S 梯形，∴AOC S ∆=DE AE CD ⋅+)(21=)36()24(21-⨯+⨯=9． --------------------4分（3）)3,4(P 或)34,9(P ． -----------------------------------------------------------------6分 阅卷说明：第（3）问两个点坐标各1分．26．解：（1）∵矩形OABC 中，点A ，C 的坐标分别为(6,0)，(0,2)， ∴点B 的坐标为(6,2)．若直线b x y +-=21经过点C (0,2)，则2=b ； 若直线b x y +-=21经过点A (6,0)，则3=b ；若直线b x y +-=21经过点B (6,2)，则5=b ．①当点E 在线段OA 上时，即32≤<b 时，（如图6） ---------------------1分∵点E 在直线b x y +-=21上， 当0=y 时，b x 2=，∴点E 的坐标为)0,2(b ．∴S =b b 22221=⋅⋅． --------------------------------------------------------------2分②当点E 在线段BA 上时，即53<<b 时，（如图7） ---------------------3分∵点D ，E 在直线b x y +-=21上， 当2=y 时，42-=b x ； 当6=x 时，3-=b y ，∴点D 的坐标为)2,42(-b ，点E 的坐标为)3,6(-b ． ∴D BE O AE CO D O ABC S S S S S ∆∆∆---=矩形图6yxOAB C DEE DC B AOxy图7)]3(2)][42(6[216)3(212)42(2126-----⋅--⋅--⨯=b b b bb b 52+-=． -------------------------------------------------------------------4分 综上可得：2223),535).b b S b b b <≤⎧=⎨-+<<⎩ ( (（2）DM =ME =EN =ND ．证明：如图8．∵四边形OABC 和四边形O′A′B′C′是矩形， ∴CB ∥OA ， C ′B ′∥O ′A ′， 即DN ∥ME ，DM ∥NE ．∴四边形DMEN 是平行四边形，且∠NDE =∠DEM ．∵矩形OABC 关于直线DE 对称的图形为矩形O′A′B′C′， ∴∠DEM =∠DEN ． ∴∠NDE =∠DEN ． ∴ND =NE ．∴四边形DMEN 是菱形．∴DM =ME =EN =ND ． ------------------------------------------------------5分（3）答：问题（2）中的四边形DMEN 中，ME 的长为 2. 5 ． -----------6分27．问题1 k 的值为 1 ． ---------------------------------------------------------------------1分问题2 证明：如图9．∵CB =CA ，∴∠CAB =∠CBA ． ∵∠MAC =∠MBC ，∴∠CAB －∠MAC =∠CBA －∠MBC ， 即∠MAB =∠MBA ． ∴MA =MB ．∵ME ⊥BC ，MF ⊥AC ，垂足分别为点E ，F ， ∴∠AFM =∠BEM =90°．在△AFM 与△BEM 中， ∠AFM =∠BEM ， ∠MAF =∠MBE ，图9CEMF AD B图8E DCB AO xyO'C'B'A'MNMA =MB ，∴△AFM ≌△BEM ． -------------------------------------------------------2分 ∴AF =BE ．∵点D 是AB 边的中点， ∴BD = AD ．在△BDE 与△ADF 中，BD = AD ， ∠DBE =∠DAF ， BE = AF ，∴△BDE ≌△ADF ．∴DE =DF ． ---------------------------------------------------------------------3分问题3 解：DE =DF ．证明：分别取AM ，BM 的中点G ，H ，连接DG ，FG ，DH ，EH ．（如图10）∵点D ，G ，H 分别是AB ，AM ，BM 的中点， ∴DG ∥BM ，DH ∥AM ，且DG =12BM ，DH =12AM ． ∴四边形DHMG 是平行四边形． ∴∠DHM =∠DGM ，∵ME ⊥BC ，MF ⊥AC ，垂足分别为点E ，F ， ∴∠AFM =∠BEM =90°． ∴FG =12AM = AG ，EH =12BM = BH ． ∴FG = DH ，DG = EH ， ------------------------------------------------------4分 ∠GAF =∠GFA ，∠HBE =∠HEB ． ∴∠FGM =2∠FAM ，∠EHM =2∠EBM ． ∵∠FAM =∠EBM ， ∴∠FGM =∠EHM ．∴∠DGM +∠FGM =∠DHM +∠EHM ，即∠DGF =∠DHE ． 在△EHD 与△DGF 中，EH = DG ， ∠EHD =∠DGF ， HD = GF ，图10GHBD A FM E C∴△EHD≌△DGF．∴DE=DF．---------------------------------------------------------------------5分。

新八年级下册数学期末考试题(答案)一、填空题（本大题共6个小题，每小题3分，共18分） 1. 若二次根式1-a 有意义，则a 的取值范围是 .2. 正比例函数kx y =（0≠k ）的图象过点（-1，3），则k = .3.一个五边形的内角和等于 .4. 分解因式：12-a = .5. 如图，在平行四边形ABCD 中，AB =5cm ，BC =7cm ，BE 平分∠ABC 交AD 边于点E ， 则线段DE 的长度为 cm ．6. 若一次函数m x m y --=)1(是 ．二、选择题（本大题共8个小题，每小题只有一个正确选项，每小题4分，共32分）7. 下列二次根式中，属于最简二次根式的是（ ） A. 7 B .31C .8D . 98. 以下列各组数为边长，不能构成直角三角形的是（ ）A . 5，12，13B . 1，2C .1 2D . 4，5，69. 甲、乙两个同学在四次数学模拟测试中，平均成绩都是112分，方差分别是s 2甲＝5，s 2乙＝12，则甲、乙两个同学的数学成绩比较稳定的是（ ）A . 甲B .乙C .甲和乙一样D .无法确定 10.下列各式中，运算正确的是（ ） A .532=+ B ．336)2(a a = C ． 1)2019(0=- D ．2)2(2-=-11．如图，已知：函数b x y +=2和2-=ax y 的图象交于点P （﹣3，﹣4），则根据图象可得不等式b x +2＞2-ax 的解集是（ ） A ．x ＞﹣4 B ．x ＞﹣3 C ．x ＞﹣2 D ．x ＜﹣312. 如图，四边形ABCD 的对角线AC 和BD ABCD 是平行四边形的条件是（ ） A . OC OA =，AD ∥BC B . ∠ABC =∠ADC ，AD ∥BC C . DC AB =，AD =BC D ．∠ABD =∠ADB ，∠BAO =∠DCODABCODb x y +=2 2-ax13. 在某市举办的“划龙舟，庆端午”比赛中，甲、乙两队在比赛时的路程s （米）与时间t （分钟）之间的函数关系图象如图所示，根据图象得到下列结论，其中错误的是（ ）A ．这次比赛的全程是500米B ．乙队先到达终点C ．比赛中两队从出发到1.1分钟时间段，乙队 的速度比甲队的速度快D ．乙与甲相遇时乙的速度是375米/分钟14. 如图，D 、E 分别是AB 、AC 的中点，过点C 作F ,则下列结论正确的是 ( )A ．CF EF =B . DE EF =C ．CF ＜BD D ．EF ＞DE 三、解答题（本大题共9个小题，共70分） 15.（本小题6分）计算：218÷2112⨯-2)3(24-+16. （本小题6分）如图，一根竹子高0.9丈，折断后竹子顶端落在离竹子底端3尺处，折断处离地面的高度是多少尺？（这是我国古代数学著作《九章算术》中的一个问题，其中的丈、尺是长度单位，1丈=10尺）.17.（本小题7分）如图， ABCD 的对角线AC ,BD 相交于点O ，E ，F 分别是OA ，OC 的中点.求证△ADE ≌△CBFF 地面？尺3尺B FCADE Ox - 218．（本小题7分）某同学参加“希望之星”英语口语大赛，7名评委给该同学的打分（单位：分）情况如下表：（2）计算该同学所得分数的平均数.19.（本小题7分）A 、B 两地相距200千米，甲车从A 地出发匀速开往B 地,乙车同时从B 地出发匀速开往A 地，两车相遇时距A 地80千米．已知乙车每小时比甲车多行驶30千米，求甲、乙两车的速度． 20．（本小题8分）如图，直线1l 的解析式为2+-=x y ，1l 与x 轴交于点B ，直线2l 经过点D （0，5），与直线1l 交于点C （﹣1，m ），且与x 轴交于点A .（1）求点C一、精心选一选（本题共 30 分，每小题 31. 在函数 y ＝中，自变量 x A ．x ≠2B ．x ＞21 2. 当 x ＜0 时，反比例函数 y ＝－3x的图象（A. 在第二象限内，y 随 x 的增大而增大B. 在第二象限内，y 随 x 的增大而减小C. 在第三象限内，y 随 x 的增大而增大D. 在第三象限内，y 随 x 的增大而减小3. 若 ＋（y ＋3）2＝0，则 y的值为（ ）．x4A. －33x -43 B. －4C.D ．－224. 下列各组数中，以 a 、b 、c 为边长的三角形不．是．直角三角形的是（ ）．A ．a ＝3，b ＝4，c ＝5，B ．a ＝5，b ＝12，c ＝13 3C ．a ＝1，b ＝2，c ＝ D．a ＝ 2，b ＝2，c ＝35. 初二 1 班的数学老师布置了 10 道选择题作为课后练习老师把每位同学答对的题数进行了统计，绘制成条形 统计图（如右图），那么该班 50 名同学答对题数的众数和中位数分别为（）．A ．8，8B ．8，9C ．9，9D ．9，8 6. 如图，四边形 A BCD 的对角线 A C 、BD 相平分，要使它成为正方形，需要添加的条件是（ ）． A ．AB ＝CD B ．AC ＝BD C ．AC ⊥BD D ．AC ＝BD 且 AC ⊥BD 7. 用配方法解方程 x 2－6x ＋2＝0 时，下列配方正确的是（）．355 21 10 甲乙A ．（x －3）2＝9B ．（x －3）2＝7C ．（x －9）2＝9D ．（x －9）2＝74 8. 如图，正比例函数 y ＝x 与反比例函数 y ＝的图象交于 A 、B 两点x过点 A 作 A C ⊥x 轴于点 C ，则△BOC 的面积是（ ） A ．4 B ．3 C ．2 D ．19. 将矩形纸片 ABCD 按如图所示的方式折叠，恰好得到菱形 AECF ．若 AD ＝，则菱形 AECF的面积为（）．A ．2 B.4 C.4 D.8第 9 题图 第 10 题图 10. 如图，在矩形 ABCD 中，A C 是对角线，将矩形 ABCD 绕点 B 顺时针旋转 90°到 BEFG位置，H 是 E G 的中点，若 A B ＝6，BC ＝8，则线段 C H 的长为（）．A ．2B ．C ．2D ． 二、细心填一填（本题共 16 分，每小题 2 分）11. 如图，在△ABC 中，∠C ＝90°，∠B ＝36°，D 为 AB 的中点，则 ∠DCB ＝ °．12. 如图，菱形 ABCD 中，对角线 AC 、BD 交于点 O ，若 AC ＝6cm ，BD＝8cm ，则菱形 A BCD 的周长为 cm ．13. 甲、乙两地相距 100km ，如果一辆汽车从甲地到乙地所用时间为x （h ）汽车行驶的平均速度为 y （Km/h ），那么 y 与 x 之间的函数关系式为 （不要求写出自变量的取值范围）．14. 如图，梯形 ABCD 中，AD ∥BC ，AB ＝CD ，DE ∥AB 交 BC 于点 E若∠B ＝60°，AD ＝2，BC ＝4，则△DEC 的面积等于 ． 15. 甲和乙一起去练习射击，第一轮 10 枪打完后两人的成绩如下图所示，通常新手的成绩不太稳定，那么根据图中的信息，估计甲和乙两人中的新手是 ， 他们成绩的方差大小关系是 S 2 S 2（填“＜”、“＞”或“＝”）．3 412 12 516. 正方形网格中，每个小正方形的边长为 1．如果把图 1 中的阴影部分图形剪开，拼接成一个新正方形，那么这个新正 方形的边长是 ，请你在图 2 中画出这个正方形． 17. 矩形 ABCD 中，AB ＝6，BC ＝2，过顶点 A 作一条射线，将图 1图 21矩形分成一个三角形和一个梯形，若分成的三角形的面积是矩形面积的 4的梯形的上底为．，则分成18. 如图，边长为的正方形 A BCD ，对角线 A C 、BD 交于点 O ，过点 O 作 O E 1⊥AB 于点 E 1，再过点 E 1 作 E 1A 1⊥AC 于点 A 1，接着过点 A 1 作 A 1E 2⊥AB 于点 E 2，继续过点 E 2 作 E 2A 2⊥AC 于点 A 2，…， 按此方法继续下去，可以分别得到 E n 、A n 点，则 A 2E 3 的长为 A n E n ＋1 的长为 ．三、认真算一算（本题共 16 分，第 19 题 8 分，第 20 题 8 分）19．计算：（1） ＋－（ － ）；（2）2 2 27 5 7 5解：解：20. 解下列方程：（1）3x 2－8x ＋2＝0； （2）x （x ＋2）－3（x ＋2）＝0． 解： 解：20 3四、解答题（本题共 12 分，每小题 6 分）21. 已知：如图，□ABCD 中，E 、F 点分别在 BC 、AD 边上，BE ＝DF ．（1） 求证：AE ＝CF ；（2） 若∠BCD ＝2∠B ，求∠B 的度数；（3） 在（2）的条件下，过点 A 作 AG ⊥BC 于点 G ，若 AB ＝2，AD ＝5， 求□ABCD 的面积．证明：（1）（2）（3）k 22. 在平面直角坐标系 xOy 中，若一次函数 y ＝ax ＋b 的图象与反比例函数 y ＝x相交于 A （1，2）、B （－2，m ）两点． （1） 求反比例函数和一次函数的解析式；的图象（2） 在所给的坐标系中，画出这个一次函数以及反比例函数在第一象限中的图象（可以不列表），并指出 x 为何值时，一次函数的值大于反比例函数的值． 解：（1）（2）五、解答题（本题共11 分，第23 题 5 分，第24 题 6 分）23.列方程解应用题某工程队承包了一条24 千米长的道路改造工程任务．为了减少施工带来的影响，在确保工程质量的前提下，该工程队实际施工速度是原计划每天施工的1.2 倍，结果提前20 天完成了任务，求原计划平均每天改造道路多少千米？解：24.某班准备从小明、小红两位同学中选出一名班长，为此分别进行了一次演讲答辩和民主测评活动，由五位老师作为评委，对“演讲答辩”情况进行评分，全班50 名同学参加了民主测评，结果分别记录如下：根据以上信息，解决下列问题：（1）小红同学在演讲答辩中，评委老师给分的极差是分；（2）补全三张表格中小红、小明同学的各项得分；（3）a 在什么范围时，小明的综合得分高于小红的综合得分，能当选为班长．解：（3）六、实验与探究（本题 6 分）25. 一张等腰直角三角形纸片 ABC ，∠A ＝90°，AB ＝AC ＝2．另有一张等腰梯形纸片 DEFG ，DG ∥EF ，DE ＝GF ．现将两张纸片叠放在一起（如图 1），此时梯形的下底 EF 与 BC 边完全重合，梯形的两腰分别落在 AB 、AC 上，且 D 、G 恰好分别是 AB 、AC 的中点． （1） 求 BC 的长及等腰梯形 DEFG 的面积；解：（2） 实验与探究（备用图供实验、探究使用）如图 2，固定△ABC ，将等腰梯形 D EFG 以每秒 1cm 速度沿射线 BC 方向平行移动，直到点 E 与点 C 重合时停止．设运动时间为 x 秒时，等腰梯形平移到D 1EFG 1 的位置．①当 x 为何值时，四边形 DBED 1 是菱形，并说明理由． ②设△ABC 与等腰梯形 D 1EFG 1 重叠部分的面积为y ，直接写出 y 与 x 之间的函数关系式． 解：①210 ②七、解答题（本题共 9 分，第 26 题 5 分，第 27 题 4 分）k26. 如图，反比例函数 y ＝在第一象限内的图象上有两点 A 、B ，已知点 A （3m ，m ）、x点 B （n ，n ＋1）（其中 m ＞0，n ＞0），OA ＝2.（1） 求 A 、B 点的坐标及反比例函数解析式；（2） 如果 M 为 x 轴上一点，N 为坐标平面内一点，以 A 、B 、M 、N 为顶点的四边形是矩形，请直接写出符合条件的 M 、N 点的坐标，并画出相应的矩形． 解：（1）（2）27.如图，正方形ABCD 中，BD 是对角线，E、F 点分别在BC、CD 边上，且△AEF 是等边三角形．（1）求证：△ABE≌△ADF；（2）过点D 作DG⊥BD 交BC 延长线于点G，在DB 上截取DH＝DA，连结HG．请你参考下面方框中的方法指导，证明：GH＝GE．证明：（1）（2）5 12 5 3 3 5 5 35 - b ± b 2 - 4ac 2a - (-8) ± 40 2⨯3 八年级数学试题答案及评分参考一、精心选一选（本题共 30 分，每小题 3 分）二、细心填一填（本题共 16 分，每小题 2 分）10011．3612．20 13．y ＝（若写成 x y ＝100 不得分）14． x15．乙，＜（每空 1 分）16． ，见图 1（每空 1 分）17．1 或 3（每个答案 1 分）18． 2 ， 8 n +1（每空 1 分）三、认真算一算（本题共 16 分，第 19题 8 分，第 20 题 8 分）19．（1）解： + －（ － ）；＝2 +2 － + …………………………………3 分＝3（2） 解：原式+ ． .......................................... 4 分＝＝＝1+ ……………………………………………………3 分．………………………………………………………4 分20．（1）解：a ＝3，b ＝－8，c ＝2．b 2－4ac ＝（－8）2－4×3×2＝40＞0． ........................... 1 分x ＝ ＝ ， .......................... 2 分x 1＝ 4 - 10 ,x 2＝3 ． ........................................................................4 分 （2）解：因式分解，得（x －3）（x +2）＝0． ......................... 1 分（x －3）＝0 或（x +2）＝0， ................................... 2 分 x 1＝3， x 2＝－2． ......................................................................................... 4 分3220 3 ( 2)2 + 22( 7 )2 + 2 2 22 4 + 1033 3 四、解答题（本题共 12 分，每小题 6 分）21. 证明：（1）∵四边形 ABCD 是平行四边形，∴AD ∥BC ，AD ＝BC ． ....................................................................... 1 分 即 AF ∥EC ． ∵BE ＝DF ，∴AD －DF ＝BC －BE ． 即 AF ＝EC∴四边形 AFCE 是平行四边形，……2 分 ∴AE ＝CF ． ....................... 3 分 （2） ∵四边形 ABCD 是平行四边形，∴AB ∥DC ．∴∠BCD +∠B ＝180°． ....................................................................... 4 分 ∵∠BCD ＝2∠B ， ∴∠B ＝60°． .......................................... 5 分（3） ∵AG ⊥BC ，∴∠AGB ＝90°．在 Rt △AGB 中，∠B ＝60°，AB ＝2，∴AG ＝ . 而 BC ＝AD ＝5，∴S □ABCD ＝BC ·AG ＝5 ................................................................................ 6 分k 22. 解：（1）由题意可知，点 A （1，2）在反比例函数 y ＝∴k ＝2．的图象上，x2 ∴反比例函数解析式为 y ＝ x. ………………………………………2 分点 B （－2，m ）在反比例函数图象上， 2∴－2＝ .m∴m ＝－1．∴B 的坐标为（－2，－1）． ............................... 3 分 ∵一次函数图象过 A （1，2）、B （－2，－1）两点， ∴一次函数的解析式为 y ＝x +1． ............................. 4 分 （2） 图象见图 3． .............................................. 5 分x ＞1 时，一次函数的值大于反比例函数的值． ............... 6 分2图 3五、解答题（本题共 11 分，第 24 题 5 分，第 25 题 6 分）23. 解：设原计划平均每天改造道路 x 千米． …………………………1 分24 由题意得：x24－1.2x＝20 ..................................................................... 3 分解得：x ＝0.2． .............................................. 4 分经检验：x ＝0.2 是原方程的解． 答：原计划平均每天改造道路 0.2 千米． ………………………… 5 分 24．解：（1）7． .................................................. 1 分（2） 演讲答辩得分表（单位：分）民主测评统计表综合得分表 …………………………………………………… 5 分 阅卷说明：每空 1 分． （3） 当 89－a ＞92－5a 时，小明同学的综合得分高于小红同学的综合得分，此时，解得 a ＞0.75． ∴当 0.75＜a ≤0.8 时，小明当选班长． ……………… 6 分六、实验与探究（本题 6 分）25．解：（1）在 R t △ABC 中，∠BAC ＝90°，AB ＝AC ＝2 （如图 4），∴∠B ＝45°，BC ＝4．（EF ＝4） ............................................................ 1 分2 2 2 又∵D 、G 分别为 AB 、AC 的中点， 1∴DG ＝ 2 1 ∴BD ＝ 2BC ＝2． AB ＝ .过 D 作 DM ⊥BC 于点 M ，则 DM ＝1． 1∴S 梯形 DEFG ＝ 2（DG +EF ）·DM ＝3．…2 分（2） ①当 x ＝秒时，四边形 D BED 1 为菱形．…3 分理由如下（如图 5）： 依题意可得 BE ＝x ，由 BD ∥ED 1，DD 1∥BE ，∴四边形 DBED 1 是平行四边形．当 BE ＝DB ＝ 菱形．时，四边形DBED1 为 即 x ＝ 时，四边形 D BED 1 为菱形．………4 分 ②分两种情况： i ） 当 0＜x ≤2 时， 点 D 1 在线段 DG 上（见图 6）， 重叠部分的面积为：y ＝3－x ； ............... 5 分 ii ）当 2＜x ≤4 时，点 D 1 在线段 DG 的延长线上（见图 7），设 AC 与 ED 1 交于点 N ，过 N 作 NH ⊥EF 于点 H ．重叠部分的面积为： y ＝ 1（4－x ）24 ＝1 x 2－2x +4. …6 分4图 7七、解答题（本题共 9 分，第 26 题 5 分，第 27 题 4 分） 26. 解：（1）过 A 作 AC ⊥x 轴于点 C ．由题意 A （3m ，m ），在 Rt △OAC 中，OA 2＝OC 2+AC 2．22 23 ∴（3m ）2+m 2＝（2 解得 m ＝2．）2，且 m ＞0．∴A 的坐标为（6，2）． .................................... 1 分k又点 A 在 y ＝的图象上，∴k ＝6×2＝12．x12 ∴反比例函数解析式为 y ＝.x12 点 B （n ，n +1）（其中 n ＞0）在 y ＝∴n （n +1）＝12．解得 n 1＝3，n 2＝－4（负舍）．的图象上，x∴点的坐标为 B （3，4）． .................................. 2 分 （2）M 、N 点的坐标分别为14M 1（ 3 ，0），N 1（51 ，2）或 M 2（ 33，0）10 N 2（3，－2）（见图 8）． ....................... 5 分阅卷说明：①写出一组 M 、N 点的坐标得 2 分；②只写出 M （一个或两个）点的坐标得 1 分； ③只写出 N （一个或两个）点的坐标得 1 分．27. 证明：（1）∵正方形 ABCD （如图 9），∴AB ＝AD ，∠ABC ＝∠ADC ＝90°．…1 分又△AEF 是等边三角形，∴AE ＝AF ．∴Rt △ABE ≌Rt △ADF ． .......................................................................... 2 分 （2）设正方形的边长为 a ，CE ＝x （0＜x ＜a ）． 在正方形 ABCD 中，BD 是对角线，DG ⊥BD ，∴∠1＝∠2＝45°．∴DA ＝DC ＝DH ＝CG ＝a ，DG ＝ 在 Rt △DHG 中，HG 2＝DH 2+DG 2， DC ＝ a ．∴HG ＝ a .又由（1）可得 BE ＝DF ，则 CE ＝CF ＝x ，BE ＝DF ＝a －x ．102 2 2 在 R t △ECF 中，EF ＝x ．∴AF ＝EF ＝ x ． 在 Rt △ADF 中， AF 2＝AD 2+DF 2．∴ （ x ）2＝a 2+（a －x ）2，整理，得x2+2ax－2a2＝0．解得x＝2新人教版数学八年级下册期末考试试题【答案】人教版八年级下学期期末数学试卷一、精心选一选（每小题4分，共40分）1x的取值范围是（）A、x≥5B、x≤5C、x≥﹣5D、x＜5答案：B考点：二次根式的意义。

清华大学附属中学2010-2011学年度第二学期期末试卷八年级数学一、选择题 （共8道小题，每小题4分，共32分）1、下列方程是关于x 的一元二次方程的是 （ ）A 、02=++c bx axB 、2112=+x x C 、1222-=+x x x D 、)1(2)1(32+=+x x2、右图是万花筒的一个图案，图中所有小三角形均是全等三角形，其中把菱形ABCD 以A 为中心旋转多少度后可得图中另一阴影的菱形 （ ）A ．顺时针旋转60°B ．顺时针旋转120°C ．逆时针旋转60°D ．逆时针旋转120°3、关于x 的方程2(6)860a x x --+=有实数根，则整数a 的最大值是 （ ）A ．6B ．7C ．8D ．94、如图所示，直角三边形三边上的半圆面积从小到大依次记为1S 、2S 、3S ，则1S 、2S 、3S 的关系是（ ）A ．321S S S =+B ．232221S S S =+C ．321S S S >+D ．321S S S <+5、将量角器按如图所示的方式放置在三角形纸板上，使点C 在半圆上．点A 、B 的读数分别为86°、30°，则ACB ∠的大小为 （ ）A ．15︒B ．28︒C ．29︒D ．34︒6、正方形ABCD 在坐标系中的位置如图所示，将正方形ABCD 绕D 点顺时针方向旋转90后，B 点的A ．(22)-，B ．(41)，C ．(31)，D ．(40)，7、正比例函数2y kx =与反比例函数1k y x-=在同一坐标系中的图像不可能是 （ ）8、如图，已知直线b x y +=3与2-=ax y 的交点的横坐标为2-，根据图象有下列3个结论：①0>a ；②0>b ；③2->x 是不等式23->+ax b x 的解集．其中正确的个数是 （ ）A ．0B ．1C ．2D ．3二、填空题（共6道小题，每小题4分，共24分）9、已知关于x 的一元二次方程2(1)10m x x -++=有实数根，则m 的取值范围是 ． 10、反比例函数2524n n y x --=的图像在所在象限内y 随x 的增大而增大，则n = ．11、在半径为5cm 的圆中，位于圆心同侧的两条平行弦的长度分别为6cm 和8cm ，则这两条弦之间的距离为12、若正比例函数2y kx =与反比例函数(0)k y k x=≠的图象交于点(,1)A m ，则k 的值是___________． 13、如图，在ABC ∆中，0120BAC ∠=，以BC 为边向形外作等边三角形BCD ∆，把ABD ∆绕着点D 按顺时针方向旋转600后得到ECD ∆，若3AB =，2AC =，则AD 的长为___________．14、如图，在ABC ∆中，090ACB ∠=，10AC BC ==，在DCE ∆中，090DCE ∠=，6DC EC ==，点D 在线段AC 上，点E 在线段BC 的延长线上，将DCE ∆绕点C 旋转060得到''DCE ∆（点D 的对应点为点'D ，点E 的对应点为点'E ），连接'AD 、'BE ，过点C 作'CN BE ⊥，垂足为N ，直线CN 交线段'AD 于点M ，则MN 的长为 。

2023北京清华附中初二（下）期末数 学一、选择题（本题共8小题，共24分）1. 下列方程中，属于一元二次方程的是（ ）A. 2230x x −−=B. 22x xy −=C. 212+=x xD. 2(1)x x −= 2. 将抛物线2y x 向下平移2个单位，所得抛物线的表达式为（ ） A. 22y x =+ B. 22y x =− C. 2(2)y x =+ D. 2(2)y x =−3. 用配方法解方程22250x x −−=时，原方程变形正确的是（ ）A. 2(1)6x +=B. 2(2)9x −=C. 2(1)6x −=D. 2(2)9x +=4. 抛物线22()1y x =−+的顶点坐标是（ ）A. 1,2B. ()2,1C. ()2,1−D. ()2,1−−5. 某商店购进一种商品，单价为30元．试销中发现这种商品每天的销售量P （件）与每件的销售价x （元）满足关系：1002P x =−．若商店在试销期间每天销售这种商品获得200元的利润，根据题意，下面所列方程正确的是（ ）A. ()()301002200x x −−=B. ()1002200x x −=C. ()()301002200x x −−=D. ()()302100200x x −−=6. 已知抛物线()2221y x =−+，()13,A y −，()23,B y ，()34,C y 是抛物线上三点，则1y ，2y ，3y 由小到大依序排列是（ ）A. 123y y y <<B. 213y y y <<C. 321y y y <<D. 231y y y <<7. 已知关于x 的方程220x x m −+=有两个不相等实数根，则m 可以取以下哪个数值（ ）A. 3B. 2C. 1D. 0 8. 已知二次函数()20y ax bx c a =++≠的图象如图所示，当0y <时，x 的取值范围是（ ）A. 12x −<<B. 2x >C. 1x <−D. 1x <−或2x >二、填空题（本题共12小题，共28分）9. 已知抛物线2y x x m =++与y 轴的交点在原点下方，则整数m 的值可以是______.(写出一个符合条件的值即可)10. 若关于的一元二次方程260x x k −+=有两个相等的实数根，则k = ______ ．11. 若二次函数()230y ax bx a =+−≠的图象经过点()1,4，则代数式a b +的值为______． 12. 关于x 的一元二次方程()22390m x x m +++−=有一根为0，则m = ______ ． 13. 抛物线243y x x =++在x 轴上截得的线段的长度是________．14. 已知m 是方程2430x x −−=的一个实数根，则242023m m −+的值是______ ．15. 已知等腰三角形的两边长分别是一元二次方程x 2﹣6x +8＝0的两根，则该三角形的周长为 ___． 16. 已知抛物线2()y a x h k =−+上部分点的横坐标x 和纵坐标y 的几组数据如下： x 1− 1 3y 2 2− 2点()1(2,),,P m Q x m −是抛物线上不同的两点，则1x =_________．17. 在平面直角坐标系中，已知点(),P m n ，m ，n 满足()()22221315m n m n ++++=，则OP 的长为______ ．18. 关于x 的方程220x x c +−=无实数根，则二次函数22y x x c =+−的图象的顶点在第______ 象限． 19. 已知抛物线()229y x a a x =−++的顶点在坐标轴上，则=a ______ ． 20. 如图，已知二次函数()20y ax bx c a =++≠的图象如图所示，有下列结论：①0abc >；②b a c −>；③420a b c ++>；④3a c >−；⑤()()1a b m am b m +>+≠．其中正确的是______(填序号)．三、解答题（本题共10小题，共68分）21. 用适当的方法解方程：（1）2(1)9x −=；（2）2240x x +−=；（3）()2(4)40x x x −+−=； （4）22310x x −+=．22. 已知抛物线22y x bx c =++过点()1,3和()1,5−，求该抛物线的解析式．23. 用一面足够长的墙为一边，其余各边用总长42米的围栏建成如图所示的生态园，中间用围栏隔开，由于场地限制，垂直于墙的一边长不超过7米(围栏宽忽略不计)，若生态园的面积为144平方米，求生态园垂直于墙的边长．24. 已知一个二次函数图象上部分点的横坐标x 与纵坐标y 的对应值如表所示： x ⋯ 3− 2−1− 0 1 ⋯ y ⋯ 0 3− 4− 3− 0 ⋯（1）这个二次函数的解析式是______ ；（2）在给定的平面直角坐标系中画出这个二次函数的图象；（3）当40x −<<时，y 的取值范围为______ ．25. 排球场的长度为18m ，球网在场地中央且高度为2.24m ，排球出手后的运动路线可以看作是抛物线的一部分，建立如图所示的平面直角坐标系，排球运动过程中的竖直高度(y 单位：m)与水平距离(x 单位：)m 近似满足函数关系2()(0)y a x h k a =−+<．（1）某运动员第一次发球时，测得水平距离x 与竖直高度y 的几组数据如下： 水平距离/m x0 2 4 6 11 12 竖直高度/m y 2.38 2.62 2.7 2.62 1.72 1.42①根据上述数据，求抛物线解析式；②判断该运动员第一次发球能否过网______ (填“能”或“不能”)．（2）该运动员第二次发球时，排球运动过程中的竖直高度(y 单位：)m 与水平距离(x 单位：)m 近似满足函数关系20.02(5) 2.88y x =−−+，请问该运动员此次发球是否出界，并说明理由．26. 如图，抛物线()20y ax bx c a =++≠经过点()0,3A ，()2,3B ，()1,0C −，直线()0y mx n m =+≠经过点B ，C ，部分图象如图所示，则：（1）该抛物线的对称轴为直线______ ；（2）关于x 的一元二次方程20ax bx c ++=的解为______ ；（3）关于x 的一元二次方程2ax bx c mx n ++=+的解为______ ；（4）若关于x 的一元二次方程20ax bx c k ++−=无实数根，则k 的取值范围是______ ．27. 已知关于x 的一元二次方程()()223240mx m x m +−+−=． （1）求证：方程总有两个实数根；（2）若m 为整数，当此方程有两个互不相等的正整数根时，求m 的值．28. 在平面直角坐标系xOy 中，抛物线()2240y mx mx m m =+++≠．（1）求抛物线的顶点坐标；（2）若抛物线与x 轴的交点为A 、(B 点A 在点B 的左侧)，且4AB =，①求抛物线的解析式；②已知点P 坐标为()3,4，点Q 在抛物线的对称轴上，将抛物线224y mx mx m =+++在第二象限内的部分记为图象G ，如果直线PQ 与图象G 只有一个公共点，请结合图象，直接写出点Q 的纵坐标t 的取值范围是______ ．29. 在正方形ABCD 中，点E 为边CD 上一点(不与点C 、D 重合)，AF BE ⊥于点F ，CG BE ⊥于点G ．（1）如图1，求证：AF BG =；（2）如图2，若F 为BG 中点，连接DF ，用等式表示线段AD ，DF 之间的数量关系，并证明； （3）若13AD =，5BF =，直接写出线段DF 的长是______ ．30. 对于线段AB 外一点M ，给出如下定义：若点M 满足222MA MB AB −=，则称M 为线段AB 的垂点，特别地，对于垂点M ，若MA AB =或MB AB =时，称M 为线段AB 的等垂点，在平面直角坐标系xOy 中，已知点()1,1A −，()1,1B ．（1）如图1，在点()0,4C ，()1,2D ，()3,2E −，()1,1F −−中，线段AB 的垂点是______ ；（2）已知点(),1P t ，()20Q t +,． ①如图2，当0=t 时，若直线12y x b =−+上存在线段PQ 的等垂点，求b 的值； ②如图3，若ABC 边上（包含顶点）存在线段PQ 的垂点，直接写出t 的取值范围是______ ．参考答案一、选择题（本题共8小题，共24分）1. 【答案】A【分析】方程经整理后能化为形如20(0)ax bx c a ++=≠，且a 、b 、c 是常数，这样的方程称为一元二次方程，根据此定义即可作出判断．【详解】A 、是一元二次方程，符合题意；B 、含有两个未知数，不是一元二次方程，故不符合题意；C 、不是整式方程，故不是一元二次方程，故不符合题意；D 、是一元一次方程，故不符合题意；故选：A ．【点睛】本题考查了一元二次方程的概念，理解概念是关键．2. 【答案】B【分析】根据平移的规律：上加下减，求出得到的抛物线的解析式即可．【详解】解：将抛物线2y x 向下平移2个单位，则所得抛物线的表达式为22y x =−，故选：B ．【点睛】此题主要考查了函数图象的平移，要求熟练掌握平移的规律：左加右减，上加下减．并用规律求函数解析式．3. 【答案】C【分析】把常数项5−移项后，应该在左右两边同时加上一次项系数一半的平方即可．【详解】解：22250x x −−=，即2250x x −−=，移项得：225x x −=，配方得：2216x x −+=，即2(1)6x −=，故选：C ．【点睛】本题考查用配方法求解一元二次方程，记住移项变号，两边同时加一次项系数一半的平方是解答此题的关键．4. 【答案】B【分析】根据抛物线解析式22()1y x =−+，可直接写出顶点坐标．【详解】解：22()1y x =−+的顶点坐标为()2,1，故选：B ．【点睛】此题考查了二次函数2()y a x h k =−+的性质，对于二次函数2()y a x h k =−+，顶点坐标是(,)h k ，对称轴是x h =．5. 【答案】A【分析】本题的等量关系是每件商品的利润×每天的销售量=每天的总利润．依据这个等量关系可求出方程．【详解】设每件商品的售价应定为x 元，每天要销售这种商品p 件．根据题意得：（x-30）（100-2x ）=200，整理得：x 2-80x+1600=0.故选A【点睛】解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解．6. 【答案】D【分析】将()13,A y −，()23,B y ，()34,C y 三个点分别代入抛物线()2221y x =−+求得1y ，2y ，3y ，即可得到答案【详解】将()13,A y −，()23,B y ，()34,C y 三个点分别代入抛物线()2221y x =−+得：151y =，23y =，39y =，∴231y y y <<故选：D ．【点睛】本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．7. 【答案】D【分析】方程有两个不相等的实数根，则有240b ac ∆=−>，据此即可得到关于m 的不等式，解不等式即可得到m 的取值范围． 【详解】解：()2242444b ac m m ∆=−=−−⨯=−，∴要使方程有两不相等实数根，则有440m −>，1m ∴<；∴m 可以取0，故选D ．【点睛】本题主要考查了一元二次方程的相关知识，解题的关键是明确一元二次方程的根与判别式之间的关系．8. 【答案】A【分析】根据已知图象可以得到图象与x 轴的交点是(1,0),(2,0)−，又0y <时，图象在x 轴下方，由此可以求出x 的取值范围．【详解】解：由图象可知，当0y <时，x 的取值范围是12x −<<，故选：A ．【点睛】本题考查了二次函数与不等式，解答此题的关键是求出图象与x 轴的交点，然后由图象找出当0y <时，自变量x 的范围，注意数形结合思想的运用.二、填空题（本题共12小题，共28分）9. 【答案】2(−答案不唯一)【分析】先求出与y 轴的交点坐标，根据抛物线与y 轴的交点在原点下方求出m 的取值范围即可求解．【详解】解：当0x =时，00y m m =++=，∴与y 轴的交点坐标为()0m ，，物线与y 轴的交点在原点下方，0m ∴<，m ∴的值可以是：2(−答案不唯一)．故答案为：2(−答案不唯一)．【点睛】本题考查了抛物线与y 轴的交点坐标，求出抛物线与y 轴的交点坐标是解答本题的关键． 10. 【答案】9【分析】根据关于的一元二次方程260x x k −+=有两个相等的实数根得到2(6)40k ∆=−−=，即可求出答案． 【详解】解：关于的一元二次方程260x x k −+=有两个相等的实数根， 2(6)40k ∴∆=−−=，即3640k ，解得：9k =，故答案为：9．【点睛】此题考查了一元二次方程根的判别式，根据一元二次方程根的情况求出k 的值是解题的关键． 11.【答案】7【分析】根据二次函数图象上点的坐标特征，把点()1,4直接代入解析式即可得到答案．【详解】解：∵二次函数()230y ax bx a =+−≠的图象经过点()1,4， ∴4=+3a b −，∴7a b +=，故答案为：7．【点睛】本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式，熟练掌握知识点是解题的关键．12. 【答案】3【分析】将0x =代入22390m xx m 中求得m 的值，然后根据一元二次方程的定义确定符合题意的m 的值即可． 【详解】解：关于x 的一元二次方程()22390m x x m +++−=有一根为0， 290m ∴−=，30m +≠，解得：3m =，故答案为：3．【点睛】本题考查一元二次方程的解及其定义，特别注意二次项系数不能为0．13. 【答案】2【分析】先设出抛物线与x 轴的交点，再根据根与系数的关系求出x 1+x 2及x 1×x 2的值，再由完全平方公式求解即可．【详解】设抛物线与x 轴的交点为：(x 1,0),(x 2,0)，∵x 1+x 2=−4,x 1×x 2=3，∴|x 1-x 221212()?4x x x x +−4=2，∴抛物线243y x x =++在x 轴上截得的线段的长度是2.故答案为2.【点睛】本题考查了抛物线与x 轴的交点，解题的关键是先求出坐标再计算线段长度.14. 【答案】2026【分析】根据一元二次方程的解的定义，将m 代入已知方程，即可求得24m m −的值，即可得解．【详解】解：m 是方程2430x x −−=的一个根，2430m m ∴−−=，解得，243m m −=，242023202332026m m ∴−+=+=，故答案是：2026．【点睛】本题考查的是一元二次方程的根即方程的解的定义．一元二次方程的根就是一元二次方程的解，就是能够使方程左右两边相等的未知数的值．即用这个数代替未知数所得式子仍然成立．15. 【答案】10【分析】解一元二次方程，得出三角形的边长，用三角形存在的条件分类讨论，解得等腰三角形的三边长，再计算周长即可．【详解】解：x 2﹣6x +8＝0（x -4）(x -2)=0解得x =4或x =2,当等腰三角形的三边为2，2，4时，不符合题意三角形三边关系，不能组成三角形，故舍去，当等腰三角形的三边为2，4，4时，符合题意三角形三边关系，能组成三角形，此时周长为2+4+4=10 故答案为：10．【点睛】本题考查等腰三角形的性质、三角形三边关系，解一元二次方程等知识，是重要考点，掌握相关知识是解题关键．16. 【答案】4【分析】根据表格数据确定抛物线的对称轴，再由点()1(2,),,P m Q x m −是抛物线上不同的两点，且纵坐标相同，利用对称轴求解即可．【详解】解：根据表格可得：当1x =−与3x =时的函数值相同， ∴抛物线的对称轴为1312x −+==， ∵点()1(2,),,P m Q x m −是抛物线上不同的两点，且纵坐标相同，∴1212x −+=， 解得：14x =，故答案为：4．【点睛】题目主要考查二次函数的基本性质及利用对称轴求解，熟练掌握二次函数基本性质是解题关键． 17. 2【分析】设22t m n =+，可得24120t t +−=，求出t 的值，然后根据勾股定理即可求出OP 的长．【详解】解：设22t m n =+，则由原方程，得()()1315t t ++=，整理，得24120t t +−=，即()()620t t +−=，解得6(t =−舍去)或2t =．()P m n ,，2222OP m n ∴=+=，2(OP ∴=负值不合题意，舍去)． 2．【点睛】本题考查了一元二次方程的解法，两点间的距离公式，换元有助于问题解决．18. 【答案】二【分析】由程220x x c +−=无实数根，可知抛物线与x 轴没有交点，由二次项系数大于0可知抛物线在x 轴的上方，然后结合对称轴即可求解．【详解】解：∵关于x 的方程220x x c +−=无实数根，∴二次函数22y x x c =+−的图象与x 轴没有交点，∵10a =>，∴二次函数22y x x c =+−的图象开口向上，∴抛物线在x 轴上方， ∵对称轴为直线12b x a=−=−，∴抛物线顶点在第二象限．故答案为：二．【点睛】本题考查了二次函数的图象与性质，以及二次函数与坐标轴的交点问题，一元二次方程与二次函数的关系，熟练掌握二次函数的图象与性质是解答本题的关键．19. 【答案】17−+17−−或0或2−【分析】分顶点在x 轴上时，顶点在y 轴上时，两种情况讨论，即可求解．【详解】解：当抛物线()229y x a a x =−++的顶点在x 轴上时，Δ0=， 即()2[2]490a a ∆=+−⨯=， 解得17a =−+或17a =−−当抛物线()229y x a a x =−++的顶点在y 轴上时，()2022a ab x a +=−==， 解得0a =或2a =−． 故答案为：17−+17−−或0或2−．【点睛】本题考查了二次函数的性质，熟练掌握二次函数的性质是解题的关键．20. 【答案】②③⑤【分析】根据抛物线的开口向下，对称轴及与y 轴交点位置判断出0a <， 0b >，0c >，据此可判断①；根据图当=1x −时所对应点的位置可判断②；由抛物线的对称性以及图象可判断③；由对称轴为12b x a=−=及=1x −时的函数值可判断④；由于抛物线的顶点坐标及()1x m m =≠时的函数值可判断⑤． 【详解】解：由于抛物线的开口向下，因此0a <，由于抛物线的对称轴是直线10x =>，所以a 、b 异号，而0a <，所以0b >，由于抛物线与y 轴的交点在y 轴的正半轴，因此0c >，所以0abc <，因此①不正确；由图象可知，当=1x −时，0y a b c =−+<，即b a c −>，因此②正确；由抛物线的对称性以及图象可知，2x =与0x =对应的函数值相同，等于c ，c 大于0，当2x =时，420y a b c =++>，因此③正确； 因为对称轴为12b x a=−=，即20a b +=， 而当=1x −时，0y a b c =−+<，所以30a c +<，即3a c <−，因此④不正确；由于抛物线的顶点坐标为()1,a b c ++，即1x =时，y 的值最大，即a b c ++最大，当()1x m m =≠时，2y am bm c a b c =++<++，即()()1a b m am b m +>+≠，因此⑤正确；综上所述，正确的结论有：②③⑤，故答案为：②③⑤．【点睛】本题主要考查了二次函数的图象与系数的关系，二次函数的图象与性质，解答此题的关键是熟练掌握：抛物线的开口方向确定a 的正负，对称轴的位置及a 的符号确定b 的符号，与y 轴交点的位置确定c 的符号．三、解答题（本题共10小题，共68分）21. 【答案】（1）14x =，22x =−（2）115x =−+215x =−（3）14x =，22x =（4）11x =，212x =． 【分析】（1）运用直接开方法解一元二次方程即可；（2）运用配方法，直接开方法解一元二次方程即可；（3）运用提公因式法分解因式解一元二次方程即可；（4）运用因式分解法解一元二次方程即可．【小问1详解】解：2(1)9x −=，等式两边同时开方，13x −=±，14x ∴=，22x =−，∴原方程的解为；14x =，22x =−．【小问2详解】解：2240x x +−=移项，224x x +=，配方得，22141x x ++=+，整理得，2(1)5x +=， 等式两边同时开方，15x +=， 115x ∴=−+215x =−；【小问3详解】解：()2(4)40x x x −+−= ∴()()4240x x −−=，40x ∴−=或240x −=，∴14x =，22x =；【小问4详解】解：22310x x −+=()()1210x x −−=，∴10x −=或210x −=，∴11x =，212x =． 【点睛】本题主要考查解一元二次方程的方法，掌握直接开方法，配方法，因式分解法解一元二次方程是解题的关键．22. 【答案】222y x x =−+【分析】待定系数法求解析式即可． 【详解】解：抛物线22y x bx c =++过点()1,3和()1,5−，2325b c b c ++=⎧∴⎨−+=⎩，解得：12b c =−⎧⎨=⎩， ∴抛物线的解析式为：222y x x =−+．【点睛】本题考查求二次函数的解析式，熟练掌握待定系数法求解析式是解题的关键．23. 【答案】生态园垂直于墙的边长为6米．【分析】设生态园垂直于墙的边长为x 米，则可得生态园平行于墙的边长，从而由面积关系即可得到方程，解方程即可；【详解】解：设生态园垂直于墙的边长为x 米，则平行于墙的边长为()423x −米，依题意，得()423144x x −=．解得16x =，28x =．由于287x =>，所以不合题意，舍去．所以6x =符合题意．答：生态园垂直于墙的边长为6米．【点睛】本题考查了一元二次方程在实际生活中的应用，理解题意并根据等量关系正确列出方程是解题的关键．24. 【答案】（1）223y x x =+−（2）见解析 （3）45y −<<【分析】（1）利用表中数据和抛物线的对称性可得到二次函数的顶点坐标为()1,4−−，可设解析式为2(1)4y a x =+−，然后再选择一个合适的值代入求解即可；（2）根据表格在网格中描出点的坐标，然后用圆滑的曲线连接即可；（3）根据4x =−，0时的函数值，再结合2y (x 1)4=+−可知当=1x −时，4y =−最小，即可写出y 的取值范围．【小问1详解】解：由题意可得二次函数的顶点坐标为()1,4−−，设二次函数的解析式为：2(1)4y a x =+−，把点()0,3−代入2(1)4y a x =+−，得1a =，故抛物线解析式为2y (x 1)4=+−，即223y x x =+−；【小问2详解】如图所示：【小问3详解】2(1)4y x =+−，∵对称轴为=1x −，∴4y =−最小，∴当4x =−时，2(41)45y =−+−=，当0x =时，=3y −，∴当40x −<<时，y 的取值范围是45y −<<．【点睛】本题主要考查二次函数的图像与性质，熟练掌握二次函数的图像与性质是解题的关键．25. 【答案】（1）①20.02(4) 2.7y x =−−+；②不能（2）该运动员此次发球没有出界，见解析【分析】（1）①由表格中数据得出顶点坐标，设函数解析式为顶点式，再把()4,2.7代入解析式求出a 即可；②当9x =时求出y 的值与2.24比较即可；（2）令20.02(5) 2.88y x =−−+中的0y =，解方程求出x 的值与18比较即可．【小问1详解】解：（1）①由表中数据可得顶点()4,2.7，设2(4) 2.7(0)y a x a =−+<，把()0,2.38代入得16 2.7 2.38a +=，解得：0.02a =−，∴所求函数关系为20.02(4) 2.7y x =−−+；②不能．当9x =时，()20.0294 2.7 2.2 2.24y =−−+=<， ∴该运动员第一次发球能过网，故答案为：不能；【小问2详解】判断：没有出界．第二次发球：20.02(5) 2.88y x =−−+，令0y =，则20.02(4) 2.880x −−+=，，解得17(x =−舍)，217x =，21718x =<，∴该运动员此次发球没有出界．【点睛】本题考查二次函数的应用，解题关键是正确求出函数解析式．26. 【答案】（1）1x =（2）11x =−，23x =（3）12x =，21x =−（4）4k >【分析】（1）根据抛物线()20y ax bx c a =++≠经过点()0,3A ，()2,3B 即可得到抛物线的对称轴； （2）由物线的对称轴为直线1x =及线()20y ax bx c a =++≠经过点()1,0C −，得到该抛物线还过点()3,0，即抛物线与x 轴相交于点()3,0和()1,0C −，即可得到关于x 的一元二次方程20ax bx c ++=的解； （3）根据抛物线()20y ax bx c a =++≠经过点()2,3B ，()1,0C −，直线()0y mx n m =+≠经过点B ，C ，即可得到2ax bx c mx n ++=+的解；（4）设该抛物线的解析式为()()13y a x x =+−，利用待定系数法求出抛物线的解析式为2(1)4y x =−−+，得到该抛物线的最大值为4，由一元二次方程20ax bx c k ++−=无实数根，即可得到k 的取值范围是4k >．【小问1详解】 解：抛物线()20y ax bx c a =++≠经过点()0,3A ，()2,3B ， ∴该抛物线的对称轴为直线0212x +==， 故答案为：1x =；【小问2详解】 由（1）知：该抛物线的对称轴为直线1x =，抛物线()20y ax bx c a =++≠经过点()1,0C −， ∴该抛物线过点()3,0，∴抛物线与x 轴相交于点()3,0和()1,0C −，∴一元二次方程20ax bx c ++=的解为11x =−，23x =，故答案为：11x =−，23x =；【小问3详解】抛物线()20y ax bx c a =++≠经过点()2,3B ，()1,0C −，直线()0y mx n m =+≠经过点B ，C ， ∴一元二次方程2ax bx c mx n ++=+的解为12x =，21x =−，故答案为：12x =，21x =−；【小问4详解】设该抛物线的解析式为()()13y a x x =+−，该抛物线经过点()0,3A ，()()30103a ∴=+−，解得1a =−，()()221323(1)4y x x x x x ∴=−+−=−++=−−+，∵10a =−<，∴抛物线开口向下，∴该抛物线的最大值为4，一元二次方程20ax bx c k ++−=无实数根，则k 的取值范围是4k >，故答案为：4k >【点睛】此题考查了二次函数的图象和性质、二次函数和一元二次方程、二次函数的最值等知识， 熟练掌握二次函数的图象和性质是解题的关键．27. 【答案】（1）见解析 （2）1−【分析】（1）根据方程的系数，结合根的判别式24b ac ∆=−，可得出220m ∆=+≥（），进而可证出方程总有两个实数根；（2）利用因式分解法，可求出方程的两个实数根，结合m 为整数且原方程有两个互不相等的正整数根，即可得出m 的值．【小问1详解】证明：()2(23)424m m m ∆=−−⨯⨯− 224129816m m m m =−+−+244m m =++2(2)m =+，2(2)0m +≥，0∴∆≥，∴方程总有两个实数根；【小问2详解】解：()()223240mx m x m +−+−=，()()220mx m x ⎡⎤∴+−−=⎣⎦，12m x m−∴=，22x =． m 为整数，且原方程有两个互不相等的正整数根，1m ∴=−．答：m 的值为1−．【点睛】本题考查了根的判别式以及因式分解法解一元二次方程，解题的关键是：（1）牢记“当0∆≥时，方程有两个实数根”；（2）利用因式分解法，求出方程的两个实数根．28. 【答案】（1）()1,4−（2）①223y x x =−−+；②4t =或4833t ≤<【分析】（1）将224y mx mx m =+++配方即可求解；（2）①由抛物线的对称轴为=1x −，且4AB =（点A 在点B 的左侧）可得()30A −，，()10B ，，代入抛物线即可求解；②分过点P 的直线与x 轴平行、过点P 的直线过()03，、过点P 的直线过()30−，三种情况分别求解即可． 【小问1详解】解：224y mx mx m =+++()2214m x x =+++2(1)4m x =++，∴抛物线的顶点坐标为()14−，； 【小问2详解】解：①抛物线的对称轴为=1x −，且4AB =（点A 在点B 的左侧），∴()30A −，，()10B ，， 将()10B ，代入224y mx mx m =+++得：240m m m +++=， ∴1m =−，∴抛物线的解析式为：223y x x =−−+；②图象G 对应的部分抛物线如图所示：当过点P 的直线与x 轴平行时，直线PQ 与图象G 只有1个交点，此时4t =；当过点P 的直线过()03，时，直线PQ 与图象G 只有1个交点，设直线PQ 的表达式为：3y kx =+，将()34，代入得：334k +=， ∴13k =， ∴133y x =+， 当=1x −时，83t =； 当过点P 的直线过()30−，时，直线PQ 与图象G 的交点在x 轴上， 此时直线PQ 的表达式为：223y x =+， 当=1x −时，43t =， 综上：4t =或4833t ≤<． 【点睛】本题考查的是抛物线与轴的交点，主要考查函数图象上点的坐标特征，要求学生非常熟悉函数与坐标轴的交点、顶点等点坐标的求法，及这些点代表的意义及函数特征．29. 【答案】（1）见解析．（2）AD DF =，理由见解析．（3193【分析】（1）通过证明ABF BCG ≌△△即可求得答案．（2）过点F 分别作AB ，AD 的垂线，分别交AB ，AD 于点H ，N ，设BC 的中点为M ，连接FM ，设5BF a =，可求得5BF CG FG a ===，根据勾股定理，求得BM 的长度，进而求得AB ，AD ，BC 的长度，根据1122ABF S AB FH AF BF =⋅=⋅，可求得FH 的长度，进而可求得FN 的长度，进一步可求得DF 的长度，即可求得答案．（3）过点F 分别作AB ，AD 的垂线，分别交AB ，AD 于点H ，N ，求得AF 的长度，根据1122ABF S AB FH AF BF =⋅=⋅求得FH 的长度，根据勾股定理，进而求得AH 的长度，进而可求得答案． 【小问1详解】∵四边形ABCD 是正方形，∴90ABC ∠=︒，AB BC =．∵AF BE ⊥，CG BE ⊥，∴90AFB BGC ∠=∠=︒．∴90ABF BCG CBG ∠=∠=︒−∠．在ABF △和BCG 中AFB BGC ABF BCG AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()AAS ABF BCG ≌．∴AF BG =．【小问2详解】AD DF =．理由如下：如图所示，过点F 分别作AB ，AD 的垂线，分别交AB ，AD 于点H ，N ，设BC 的中点为M ，连接FM ．根据题意可知90AHF ANF ∠=∠=︒．∵四边形ABCD 是正方形，∴90DAB ∠=︒．∴四边形AHFN 是矩形．∴AH FN =，AN HF =．∵F 为BG 中点，∴BF GF =．∵F 为BG 的中点，M 为BC 的中点，∴FM CG ∥，12FM CG =． ∴90BFM BGC ∠=∠=︒．∵ABF BCG ≌△△，∴BF CG =．∴BF CG FG ==． 设5BF a =．∴1522FM CG a ==． ∴()222255522a BM BF FM a a ⎛⎫=+=+= ⎪ ⎪⎝⎭． ∴25AB AD BC BM a ====． ∵5AF BG a ==，1122ABF S AB FH AF BF =⋅=⋅， ∴115?25?522a FH a a ⨯=⨯． ∴2FH a =．∴2AN FH a ==．∴523DN AD AN a a a =−=−=． ∵()2222(25)24AH AF FH a a a =−=−． ∴4FN AH a ==． ∴()()2222345DF DN FN a a a =+=+=．∴AD DF =．【小问3详解】 193.理由如下：如图所示，过点F 分别作AB ，AD 的垂线，分别交AB ，AD 于点H ，N ．由（2）证明可知，四边形AHFN 是矩形．∵AF BE ⊥，13AB AD ==，5BF =，∴222213512AF AB BF =−=−=． ∵1122ABF S AB FH AF BF =⋅=⋅， ∴111312522FH ⨯=⨯⨯．∴6013FH =． ∴6013AN FH ==． ∴60109131313DN AD AN =−=−=． ∵22226014412()1313AH AF FH =−=−=， ∴14413FN AH ==． ∴222210914432617()()1931313DF DN FN =+=+= ∴线段DF 193． 193【点睛】本题主要考查正方形的性质、矩形的判定及性质、勾股定理、全等三角形的判定及性质、三角形的中位线定理，牢记正方形的性质、矩形的判定定理及性质、勾股定理、全等三角形的判定定理及性质、三角形的中位线定理是解题的关键．30. 【答案】（1）()1,2D ，()1,1F −−（2）①b 的值为72或32−；② 41t −≤< 【分析】（1）按照线段AB 的垂点的定义进行计算验证即可得到答案；（2）①当0=t 时，点()0,1P ，()2,0Q ，设点M 是直线12y x b =−+上存在的线段PQ 的等垂点，则1,2M m m b ⎛⎫−+ ⎪⎝⎭，过点M 作MG y ⊥轴于点G ，过点M '作M H y '⊥轴于点H ，证明()AAS PMG QPO ≌，则1MG OP ==，2PG OQ ==，得到3OG =，则点()1,3M ，即可求出172m b =⎧⎪⎨=⎪⎩；同理可得()1,1M '−−，即可求出132m b =−⎧⎪⎨=−⎪⎩；最终得到b 的值；②说明线段PQ 的垂点一定在直线2y x b '=+上，把()0,4C 代入2y x b '=+，得4b '=，当()20Q t +,在直线24y x =+上时，()0224t =++，解得4t =−，把()1,1B 代入2y x b '=+，得1b '=−，当(),1P t 在直线21y x =−上时，121t =−，解得1t =，即可得到t 的取值范围．【小问1详解】解：∵(1,1)A −，()1,1B ，()22114AB ⎡⎤∴=−−=⎣⎦，()222222(10)(14)(10)140CA CB ⎡⎤−=−−+−−−+−=⎣⎦， 222CA CB AB ∴−≠，∴点C 不是线段AB 的垂点；()222222(11)(21)(11)214DA DB ⎡⎤−++−−−+−=⎣⎦=， 222DA DB AB ∴−=，∴点D 是线段AB 的垂点；()222222(31)(21)(31)2112EA EB ⎡⎤−++−−−−+−−=⎣⎦=， 222EA EB AB ∴−≠，∴点E 不是线段AB 的垂点；()222222(11)(11)(11)114FA FB ⎡⎤−−++−−−−−+−−⎣==⎦， 222FA FB AB ∴−=，∴点F 是线段AB 的垂点；综上所述，点D 、F 是线段AB 的垂点；故答案为：()1,2D ，()1,1F −−；【小问2详解】解：①当0=t 时，点()0,1P ，()2,0Q ，设点M 是直线12y x b =−+上存在的线段PQ 的等垂点，则1,2M m m b ⎛⎫−+ ⎪⎝⎭， 过点M 作MG y ⊥轴于点G ，过点M '作M H y '⊥轴于点H ， MP PQ ∴=，MP PQ ⊥，90PGM QOP ∴∠=∠=︒，90MPG PMG ∴∠+∠=︒，90QPO MPG ∠+∠=︒，PMG QPO ∴∠=∠，∴()AAS PMG QPO ≌，1MG OP ∴==，2PG OQ ==，123OG OP PG ∴=+=+=，()1,3M ∴，1132m m b =⎧⎪∴⎨−+=⎪⎩， 解得：172mb =⎧⎪⎨=⎪⎩；同理可得：()1,1M '−−，1112m m b =−⎧⎪∴⎨−+=−⎪⎩， 解得：132m b =−⎧⎪⎨=−⎪⎩；b ∴的值为72或32−；②(),1P t ，()20Q t +,． ∴2210t tk +−==−，∴线段PQ 的垂点一定在直线2y x b '=+上，把()0,4C 代入2y x b '=+，得4b '=，当()20Q t +,在直线24y x =+上时，()0224t =++， 解得：4t =−，把()1,1B 代入2y x b '=+，得1b '=−，当(),1P t 在直线21y x =−上时，121t =−，解得：1t =，t ∴的取值范围是41t −≤<；故答案为：41t −≤<．【点睛】此题考查了一次函数的图象和性质、全等三角形的判定和性质、勾股定理求平面内两点间的距离等知识，数形结合和分类讨论是解题的关键．。