当前位置：文档之家 › 指数函数图象及性质

指数函数图象及性质

  • 格式：ppt
  • 大小：1.66 MB
  • 文档页数：22

下载文档原格式

  / 22

合集下载

指数函数图像及性质(上课 )

指数函数图像及性质(上课 )

指数函数的定义： 函数形如 y a x (a 0且a 1)叫做指数函数， 其中X为自变量，定义域为R
例1、下列函数中，哪些是指数函数？
1
y4
x
2
x
yx
y4
x 1
4
3
y 4
4
二、实践操作，探求新知
动手画一画下列函数的图像：（1、2组画（1）、 （2），3、4组画（3）、（4））
五、小结归纳，拓展深化
（1）通过本节课的学习，你学到了哪些知识 ？
（2）你又掌握了哪些研究数学的学习方法？
六、布置作业,提高升华
(1)必做题 ：课本P73，1、2 (2)选做题：课本P77，4,5
指数函数及其性质
• 新知导学 • 1．指数函数的定义x a • 一般地，函数y＝_____(a＞0，且a≠1)叫做 指数函数，其中x是________ 自变量 ． • [名师点拨] 指数函数y＝ax(a＞0，且a≠1)的 结构特征： • (1)底数：大于零且不等于1的常数； • (2)指数：仅有自变量x； • (3)系数：ax的系数是1.
0.3
不同底数幂比大小 ，利用指数函数图像 与底的关系比较
不同底但同指数
6
1.70.3 与0.93.1
底不同，指数也不同
利用函数图像 或中间变量进行 比较
•2 •指数函数的图象问题 x和y＝(a－ • (1) 当 a ＞ 1 时，函数 y ＝ a •2 1)x2的图象只可能是( )
(2)图中的曲线是指数函数 y＝ax 的图象， 已知 a 的值取 3， 1 4 3 10，3，5四个值，则相应的曲线 C1，C2，C3，C4 的 a 的值依次 是( )
6．求下列函数的值域： (1)y＝2

指数函数的图像与性质

指数函数的图像与性质

.
回顾反思
知识小结： ①指数函数概念； ②指数函数图像、性质； ③简单应用，重点是研究比 较大小。 方法小结：数形结合思想 “数缺形时少直观，形缺数时难入微。 数形结合千般好，隔离分开万事休”
y 2 x ( x R )
(-2,0.25)
(-1,0.5)
(0,1)
1
y=1
1 2 3 4
-4
-3
-2
-1
0 -1
x
图像探究
2、 用列表 、 描点的方法作出函数
y ( ) ( x R )的图像 。 2
x
1
x y
… …
-3
-2
-1
0 1
4 3 2 1 (0,1)
1
2
3
…
8
(-2,4)
指数函数的图象与性质
问题引入
1. 细胞分裂过程 细胞个数 2 4 8
第一次
第二次 第三次 第x次
………… ……
2
x
细胞个数y关于分裂次数x的关系为
y2
x
问题引入
2.《庄子》：“一尺之棰，日取其半，万世不竭”
第 x 天还剩下原来的多少？ １
1
第一天 第二天 第三天 第x天
2பைடு நூலகம்
1 4
=1 =

1.指数函数的定义 底数为常数
指数为自变量
函数 y = a x( a 0且 a 1) 叫作指数函数,函 数定义域是Ｒ
概念剖析
探究 1：为什么规定指数函数
结论一:
y a x的底数 a 0且 a 1? x (1)若 a 0，则当 x 0 时 , a 0 ;
则当 x 0时， a x 无意义 .

指数函数的图像与性质

指数函数的图像与性质

2.比较a 与a 的大小（a 0且a 1 ）。
3.设 y1 a , y2 a 确定x为何值时，有：
3 x 1 2 x
1 2
1 3
，其中 a 0且a 1，
（ 1 ）y1 y2
（2）y1 y2
例 3：如图是指数函数①y＝ax (a>0，且 a≠1)， ②y＝bx (b>0， 且 b≠1)， ③y＝cx (c>0，且 c≠1)， ④y＝dx (d>0，且 d≠1)的图象，则 a，b，c，d 与 1 的大小关系为( ) A．a< b<1< c<d B．b< a<1< d< c C ．1<a< b< c<d D．a< b<1< d< c

x
指数函数y (a 2) 为减函数
0 a 2 1
可得a的取值范围为（ 2,3）
5 a 与 a 变式训练：比较 的大小，其中
a 0且a 1
练习：
0.7 0.9 0.8 a 0 . 8 , b 0 . 8 , c 1 . 2 , 1.已知
b<a<c 则 a , b, c 的大小关系是____________________.
y
(0,1)
y=1 x
(0,1)
当 x > 0 时，y > 1. 当 x < 0 时，. 0< y < 1
0
x
0 y > 1； 当 x < 0 时，
当 x > 0 时， 0< y < 1。
定义域: R 性 值 域: ( 0,+ ∞ ) 恒 过 点： ( 0 , 1 ) ,即 x = 0 时, y = 1 . 质 在 R 上是单调 增函数 在 R 上是单调 减函数

指数函数及图像与性质

指数函数及图像与性质
x x
（-1，3）

第一
_______________象限.
24
课堂小结
通过本节课的学习，你学到了哪些知识？又掌握了哪些方法？
定义
结构特征
指数函数
图像
a 1, 0 a 1
简单应用
比大小
性质
Hale Waihona Puke 性质及底对图像的影响再 见
解：在同一坐标系中
1 x 指数函数 y 2 与 y ( ) 2
x
的图像如图：
x
x
1 x 可以看出，当函数 y 2 与 y ( ) 的自变量的取 2
值互为相反数时，其函数值是相等的，因而两个函 数的图像关于 y 轴对称
21
观察下面几个函数图像，你能得出什么规律？
22
抽象概括
一般地，当函数y=ax(a＞0，a≠1， x∈R)与函数y=a-x的自变量的取值互为相 反数时，它们的函数值是相等的，故而
O
x
例题讲解
例 1 比较下列各题中两个数的大小： (1) 3
0.8
,
-0.1
3
0.7
(2) 0.75
,
0.75
0.1
解：方法一：直接用科学计算器计算各数的 值，再对两个数值进行大小比较
方法二 利用指数函数的性质对两个数值进行大小比较
(1) 因为 y 3x 是 R 上的增函数， 0.7 0.8 ，
0

1 3
2 3

3 2
例 4 (1)求使不等式 4 32 成立的 x 的集合；
x
(2)已知 a a ，求实数 a 的取值范围.
2
4 5
(1)求使不等式

指数函数图像与性质ppt课件

指数函数图像与性质ppt课件

探究:
为什么要规定a 0且a 1呢？
0
1
a
分类讨论
(1) 若a 0 , ax 不一定有意义，
如：a
2, x
1 ,ax
1
(2) 2
2,显然无意义；
2
(2) 若a 0 , x 0 时ax 0，x 0时ax均无意义；
(3) 若 a 1 ，1x 1，没有研究的必要 .
范例
例1．已知指数函数 f (x) ax(a>0且a≠1)的
函 数 y a x (a 1)
y ax (0 a 1)
图象
定义域 值域
单调性 过定点
函数值变 化情况
R
(0,+∞)
在R上是增函数 （0，1）
x > 0时，y > 1 x < 0时，0< y <1
R
(0,+∞)
在R上是减函数 （0，1）
x > 0时，0< y <1 x < 0时，y > 1
普通高中课程标准实验教科书·人教A版数学必修一（2.1.2）
2
1
0
1
关于y轴对称
x
观察右边图象，回答下列问题：y
(
1
)x
y
(1 3
)x
2
问题一：
图象分布在哪几个象限？
y=3X
Y y=2x
答四个图象都在第＿Ⅰ＿、＿Ⅱ＿象限。
问题二：
O
Y=1
X
图象的上升、下降与底数a有什么联系？
答：当底数＿a >＿1 时图象上升；当底数＿0<＿a＿<＿1时图象下降．
问题三： 图象中有一个最特殊的点？

指数函数的图像及性质

指数函数的图像及性质

∴1－3c>3a－1，即3c＋3a<2. 【答案】 D
求与指数函数有关的函数的定义域与值域
求下列函数的定义域和值域：
(1) y＝( 1 )2x－x2；(2)y＝9x＋2×3x－1.
2
思路点拨：这是与指数函数有关的复合函数，可以利 用指数函数的概念和性质来求函数的定义域、值域，对于 形式较为复杂的可以考虑利用换元法(如(2))．
素材2.1 设函数f x =a－ (a 0且a 1)，
x
若f 2 = 4，则a = f (2)与f 1的大小关系 是 ；
，
xa x 2 函数y = 0 a 1的 | x| 图象的大致形状是

解析：
1由f 2 4，得a
－2
1 4，所以a ， 2
另一部分是：y=3x
(x<0)
向左平移
1个单位
y=3x+1 (x<-1).
图象如图：
(2)由图象知函数在（-∞，-1］上是增函数，
在（-1，+∞）上是减函数. (3)由图象知当x=-1时,函数有最大值1,无最小值. 探究提高
在作函数图象时,首先要研究函数与某一
基本函数的关系.然后通过平移或伸缩来完成.
考点探究
点评： 利用单调性可以解决与指数函数有关的值域 问题．指数函数本身是非奇非偶函数，但是与指数函数有
关的一些函数则可能是奇函数或偶函数．要注意使用相关
的概念和性质解决问题．
考点探究
2 2.已知 f(x)是定义在 R 上的奇函数，且当 x∈(0，1)时，f(x)＝ x . 4 ＋1 (1)求 f(x)在(－1，1)上的解析式； (2)证明：f(x)在(0，1)上是减函数．

指数函数及其图像与性质_图文

指数函数及其图像与性质_图文

小试牛刀
例2.判断下列函数在其定义域上的单调性
(1)y=4x; 解：
知识积累：
y
指数函数y=2x的性质 x
（1）函数的定义域为R，值域为(0，∞); （2）图像都在x轴的上方，向上无限延伸，
向下无限接近x轴； （3）函数图象都经过（0,1）点； （4）函数图像自左至右呈上升趋势。
动手试一试
列表：
x
…
-3
…
8
图像：
指数函数y= 的图像
-2
-1.5
-1
-0.5
指数函数及其图像与性质_图文.ppt
直观感知：核裂变
如果裂变次数为x ，裂变后的原子核为 y，则y与x之间的关 系是什么？
y=2x
你还能举出一些类似的例子吗？ （如细胞分裂……）
归纳结论
指数函数的概念：
一般地，设a>0且a≠1，形如y=ax的函数称为指数函数。 定义域：R
学以致用
问题：对于其它a的值，指数函数的图像又 是怎样的呢？
及时复习~~积沙成塔
指数函数的图像和性质：
y=ax
a
a>1
0<a<1
图
像
性 质
(1)函数值都是正的； (2)x=0时，y=1； (3)当x>0时，y>1;当x<0时， 0<y<1； (4)f(x)=2x在（-∞，+ ∞）上是增函数。
（1）函数值都是正的； （2）x=0时，y=1； （3）当x>0时， 0<y<1 ;当x<0时， y>1 ； （4）f(x)=2x在（-∞，+ ∞）上是增函数。
0
0.5

指数函数的图像和性质 课件

指数函数的图像和性质 课件

1 02
为了便于研究，规定： (a>0且a≠1)
课堂练习
判断下列函数是否是指数函数
y 2 3x
y (4)x
y 3x1
y x
y 4x
y xx
二、指数函数的图像和性质
1.作出下列两组函数的 图象:
画函数图象的步骤：
列表
描点
连线
1.列表
x
-2
y=2x 1/4
y=(1/2)x 4
x格
1
麦粒数y
2
2
3
4
8
4
…x
16 … y= ?
实例2 创设情境、导入新课
庄子曰：一尺之棰，日取其半，万世不竭。
一尺长的棍子，第一天取掉其一半，第二天取
其剩余的一半……，请写出取x次后，木棰的剩留
量y与x的函数关系式。
第1次 第2次 第3次 第4次
第X次
1
2
1
1
4
1 8 木棒长度y与经历次数x的
y16
总数为：=18446744073709551615(粒) ，1000粒约40克 麦粒有7000多亿吨（现每年全球的小麦总量约6.5亿吨）
实例1 创设情境、导入新课
1．现在假设棋盘上第一格给2粒麦子，第二格给 4粒，第三格给8粒……，到第x格时，请大家写 出需要给的麦子粒数y与格子数x的关系式。
y = 2x
2.1.2指数函数及其性质
实例1 创设情境、导入新课
棋盘上的麦粒
在印度有一个古老的传说：舍罕王打算奖赏 国际象棋的发明人--宰相 西萨·班·达依尔。国王 问他想要什么， 他对国王说："陛下，请您在这 棋盘的第1个小格里，赏给我1粒麦子，在第2个 小格里给2粒，第3小格给4粒，以后每一小格都 比前一小格加一倍。请您把这样摆满棋盘上所有 的64格的麦粒，都赏给您的仆人吧!"国王觉得这 要求太容易满足了，命令给他这些麦粒。当人们 把一袋一袋的麦子搬来开始计数时，国王才发现： 就是把全印度甚至全世界的麦粒全拿来，也满足 不了那位宰相的要求。

4.2 指数函数的性质与图像

4.2 指数函数的性质与图像

③若a=1，则对于任何x R，
a x=1，是一个常量，没有研究的必要性.
为了避免上述各种情况，所以规定a>0且a1。
在规定以后，对于任何x R，a x 都有意义，
因此指数函数的定义域是R
探究2：下列函数中，那些是指数函数？
y ax (a 0且a 1) (1) (5) (7) (8)
(1) y=4x (2) y=x4
(3) y= - 4x (4) y=( - 4 ) x
(5) y=πx (6) y=2·4x
(7) y = 2 -x (8) y = ( 2a – 1 ) x
指数函数是形式上的定义，
像前面加个系数形如 (a>1/2且a≠1)
y=kax不是指数函数
幂函数与指数函数的对比
式子
名称
a
x
y
指数函数: y=ax 底数 指数 幂 幂函数: y= xa 指数 底数 幂
分析：在解决实际应用问题时候，首先
要根据题目要求进行恰当的假设，并注 意自变量的取值范围。其次试写几个特 殊的例子，利用归纳法得出关系式子。
每经过1年剩留的这种物质是原来的84%
（1）.先求出函数关系式：
设这种物质最初的质量是1，经过x年，剩留 量是y，那么：
经过1年，剩留量 y 1 84% 0.841
42084(元)
答:即现在只要在银行存入42084（元）就可以了。
小结：1.指数函数的定义：函数 y a x (a 0且a 1)
叫做指数函数，其中x是自变量，函数定义域是R。 2.指数函数的的图象和性质：
a>1
0<a<1
图
6
5
象
4 3
2
11

课件6：4.1.2　指数函数的性质与图像

课件6：4.1.2　指数函数的性质与图像
∴ ＝在［-1，1］上单调递增，
∴
1
0< ≤≤.

由二次函数的图象知，
1
当∈[ , ]时，
函数＝（ + 1） −
2
1
2在[ , ]上为增函数，
故当＝时，max＝2 + 2 − 1，
∴ 2 + 2 − 1＝14，解得＝3或＝-5（舍去）.
②若0<<1，∵ ∈［-1，1］，
∴
2 −2−3

1
2
∴ y＝
≤
1 −4
＝16.又∵
2
2 −2−3

1
2
2 −2−3

1
的值域为（0，16］.
2
>0，
形如y＝af（x）的函数的定义域和值域的求法
（1）函数y＝af（x）的定义域与函数f（x）的定义域相同；
（2）求函数y＝af（x）的值域，需先确定函数f（x）的
值域，再根据指数函数y＝ax的单调性确定函数y＝af（x）
图象；
③函数＝|()|的图象是将函数 = ()的图象在轴下
方的部分沿轴翻折到上方，轴上方的部分不变.
若直线＝2与函数＝| − 1|（>0，且≠1）
1
0,
的图象有两个公共点，则的取值范围是（ 2 ） .
（3）图象的识别问题
例5 如图所示的是指数函数①y＝ax；②y＝bx；③y＝
1
−4
（1） 2
＝
（2）
＝
；
2
1 −2−3
.
2
解：（1）由-4≠0，得≠4，
∴ =2
1
−4
的定义域为{|∈R，且≠4}.
1

指数函数图像和性质

指数函数图像和性质

[例 3]
比较下列各组数的大小： 1；
3－1.8 3－2.6 5 －2 (1)4 与4 ；(2)(8) 3 与
－2
4 －2 1 0.3 3 (3)0.6 与(3) ；(4)(3) 与 3－0.2. [思路点拨] (1)，(2)，(4)利用指数函数的单调性比
较；(3)利用中间值 1 比较．
4 －2 40 3 (3)∵0.6 >0.6 ＝1，(3) <(3) ＝1，
－2
0
4 －2 ∴0.6 >(3) 3 ；
－2
1 0.3 (4)∵(3) ＝3－0.3， 又∵－0.3<－0.2，∴3－0.3<3－0.2， 1 0.3 －0.2 ∴(3) <3 .
[一点通] 比较指数式大小的方法
(1)单调性法：比较同底数幂的大小，可构造指数函数，
（1） 1.72.5 , 1.73; （2） 0.8-01，0.8-02 指数相同底数不同 幂式比较大小，利用 （4幂函数单调性比较 ） 与
（3）
与
（5）(0.3) -0.3 与 (0.2) -0.3 （6）1.70.3,0.93.1
利用函数图像 不同底但同指数 或中间变量进行 比较 底不同，指数也不同
－0.28,
0.67
－3.1
.
解：(1)0.90.1,0.90.2可看作函数y＝0.9x的两个函数值， 由于底数0.9<1， 所以指数函数y＝0.9x在R上是减函数， 因为0.1<0.2，
所以0.90.1>0.90.2；
当 x > 0 时， 0< y < 1。
定义域: R 性 值 域: ( 0,+ ∞ ) 恒 过 点： ( 0 , 1 ) ,即 x = 0 时, y = 1 . 质 在 R 上是单调 增函数 在 R 上是单调 减函数

计算指数函数的图像和性质

计算指数函数的图像和性质

计算指数函数的图像和性质指数函数是数学中一类重要的函数，它的图像和性质具有一定的规律和特点。

在本文中，我们将通过对指数函数的图像和性质进行探讨，来深入理解指数函数的特点。

一、指数函数的定义和基本性质指数函数是以底数为常数的幂函数，其一般形式可以表示为 y = a^x，其中 a 是底数，x 是自变量，y 是因变量。

指数函数的定义域为全体实数，且底数 a 为正实数且不能为1。

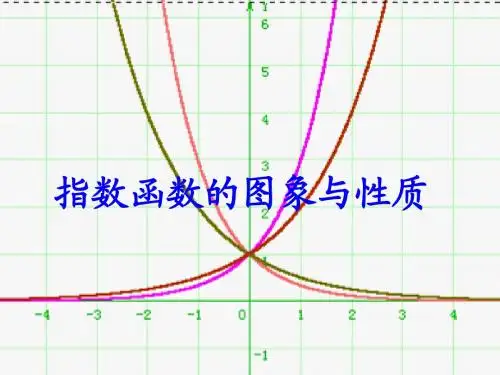
1. 图像特点当底数 a 大于1时，指数函数的图像呈现递增趋势，且越靠近 y 轴正半轴，函数增长越快。

当底数 a 介于0和1之间时，指数函数的图像呈现递减趋势，且越靠近 y 轴正半轴，函数递减越慢。

同时，指数函数的图像都经过点 (0,1)，这是因为当 x=0 时，指数函数的值总是等于1。

2. 增减性与奇偶性指数函数在定义域内始终为正数，且当底数a 大于1时，函数递增；当底数 a 介于0和1之间时，函数递减。

指数函数不具备奇偶性，因为 y = a^x 的图像关于 y 轴和原点都不对称。

3. 极限性质当 x 趋向于正无穷大或者负无穷大时，指数函数 a^x 会趋向于正无穷大或者0。

具体而言，当 a 大于1时，a^x 的极限为正无穷大；当 a介于0和1之间时，a^x 的极限为0。

二、指数函数的常见变形及其图像除了一般形式的指数函数 y = a^x 外，指数函数还存在常见的变形形式，如 y = a^(x-h)+k、y = -a^x、y = a^(-x) 等。

这些变形函数经过平移、翻转等操作后，其图像特点和性质也会发生变化。

举例来说，当指数函数的底数 a 大于1时，函数 y = a^(x-h)+k 相比于一般形式的指数函数，会在 x 轴方向上发生平移，横坐标平移 h 个单位；在 y 轴方向上发生平移，纵坐标平移 k 个单位。

而函数 y = -a^x 则对原始的指数函数进行关于x 轴翻转得到，使得其图像在y 轴下方。

三、指数函数的应用指数函数在数学和实际应用中有着广泛的应用，下面我们列举几个常见的应用场景。

指数函数及其性质(指数函数的概念与图象)_图文

指数函数及其性质(指数函数的概念与图象)_图文

3 9 27 …
1
o -3 -2 -1 1 2 3
x
函数图象特征
x
… -3
-2
1Leabharlann y=2-x … 8 4 2
y=3-x … 27 9 3 Y
0 1 2 3…
1
1/ 2
1/4
1/8
…
1思考13：/ 若1不/9用描17/点2法…，
这两个函数的图象又该
如何作出呢？
Y=1
X O
观察右边图象，回答下列问题： 问题一：
指数函数及其性质(指数函数的概念与图象)_ 图文.ppt
一、问题引入
问题一、比较下列指数的异同，能不能把它们看成函数值？ ①、
②、
函数值？？什 么函数？
函数图象特征
x … -3 -2 -1 0 y=2x … 1/8 1/4 1/2 1 y=3x … 1/27 1/9 1/3 1
y
12 24
3… 8…
图象分别在哪几个象限？
y=3X
Y y=2x
答：四个图象都在第＿Ⅰ＿、＿Ⅱ＿象限
问题二： 图象的上升、下降与底数a有联系吗O ？
Y=1
X
答：当底数＿＿时图象上升；当底数＿＿＿＿时图象下降．
底数a由大变小时函数图像在第一象限内按＿＿顺＿＿
时针方向旋转.
问题三： 图象中有哪些特殊的点？
答：四个图象都经过点＿＿＿＿．
2.1.2
• 第二课时
指数函数及其性 质
指数函数的性质
2.函数
是指数函数吗？
指数函数的解析式
中， 的系数是1.
有些函数貌似指数函数，实际上却不是.
有些函数看起来不像指数函数，实际上却是.
应用2

指数函数的图像和性质

指数函数的图像和性质

指数函数的图像和性质
指数函数是一种特殊函数，其定义域为实数集合R，值域也是实数集合R。

指
数函数的图像是一条弧线，朝右上方抛物线式延伸，底点在坐标原点处。

其图像如下所示：
指数函数具有以下性质：
一、指数函数是定义在实数集合上的单值函数，其图象是一条朝右上方延伸的
弧线，且在坐标原点处有底点，函数值随x增大而增大，函数图像上每一点到底点的距离都不变；
二、指数函数对任何正实数都有定义，指数函数f(x)=a^x（a为正实数）的图
谱具有单调性，当a的值不同时，指数函数的函数图象具有相似的特点；
三、指数函数具有不变性，不论x的取值范围如何，函数的函数图象仍不改变；
四、指数函数的切线斜率随着x的增大而增大；
五、指数函数的斜率在同一条线上增加或减少；
六、不论指数函数是升幂函数还是降幂函数，其图象都是从坐标原点开始，一
条朝右上方延伸的弧线。

以上就是指数函数的图像与性质，根据以上描述，指数函数的函数图像与以及
其性质可以得出：指数函数是从坐标原点开始，一条朝右上方延伸的弧线，有着单调性，不变性，切线斜率随着x的增大而增大等性质。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

8 4 2 y ? ??1 ??x …
1
?2 ?
1 2
11 48
…
y
y ? ?? 1 ??x ?2?
y ? 2x
1
-3 -2 -1 0 1 2 3
x
y
y ? ?? 1 ??x ?2?
y ? ?? 1 ??x ?3?
y ? 3x y ? 2x
y=1 1
0
1
x
（1）函数 y ? 2 x 的图象与函数 y ? ??1 ??x 有什
问题1:
某种细胞分裂时, 由1个分裂成2个,2 个分 裂成4个…一个这样的细胞分裂 x次后, 得到 的细胞分裂的个数y与x的函数关系是什么?
细胞分裂过程
细胞个数
第一次
21
第二次
22
第三次
…………
23
第x次
……
2x
细胞个数 y与分裂次数 x之间的关系式为 y =2x
问题2：
将一根长度为1的木棒每次截去一半, 依次截下 去, 问截取x次后, 剩下的木棒长度y.
（4） y ? 4 x?1 （5） y ? 3? x （6） y ? 2 ?3x
（1）、（5）
指数函数的图象
用描点法画出函数 y ? 2 x 和 y ? ?? 1 ??x的图象.
表1：
?2?
x … -3 -2 -1 0 1 2 3 …
y =2x
…
1 8
1 4
1 2
1
2
4
8…
表2：
x … -3 -2 -1 0 1 2 3 …
?2?
么关系？可否利用 y ? 2 x 的图象画出
y ? ?? 1 ??x 的图象？
?2?
（2）两个函数图象有什么共同点？
（3）两个函数的图象有何不同之处？
通过作图，我们发现y=a x的图象大致分两 种类型，即0＜a＜1和a＞1，图象如下：
y =a x y (0＜a ＜1)
y
y=a x
(a＞ 1)
例1、求下列函数的定义域 1 (1) y? 3 x?2； (2) y ? ?? 1 ?? x . ?2?
解:（1）由 x? 2 有意义，得x-2≥0即x ≥2，
∴原函数定义域为{x | x ≥2 } .
（2）由
1 x
有意义，得x≠0，
∴原函数定义域为{x | x ∈R且x≠0}.
π0 例2、已知指数函数 f (x) ? a x(a ? 0，且a ? 1) 的图 象经过点（3，?）,求 f (0), f (1), f (?3)的值.
( 3 ) 由指数函数性质知：
1 .7 0.3 ? 1 .7 0 ? 1而 0 .9 3.1 ? 0 .9 0 ? 1
? 1.7 0.3 ? 0.9 3.1
④ a 0.8 , a 0.6
当 0 ? a ? 1时 , a 0.8 ? a 0.6
当 a ? 1时 , a 0 .8 ? a 0 .6
比较两个指数式大小方法： （1）构造指数函数，利用
答：经过20年后，我国人口数约为16亿。
点评：有关“增长率”问题：
设该： 量原增有长量到为yN，，则每次y增?长N率(为1p?
，经过 x
p)x (x ?
次增长，
N)
即： y ? ka x (k ? R, k ? 0; a ? 0, a ? 1)
“指数型函数”模型
1.本节课学了哪些知识?
（1）指数函数概念
解：因为 f (x) ? a x的图象经过点（3，?），所以
f (3) ? ?，
1
即a3 ? ? ,解得 a ? ? 3，于是
x
f ( x) ? ? 3，
所以，f (0)
?
?
0
? 1，f (1)
?
?
1 3
?
3
? ，f (?3)
??
?1
?
1
?
.
例3、比较下列各式大小
①、 1.7 2.5 ,1.7 3 ③、 2x
和
y
?
?? 1 ?? x ?2?
的结构特征。
指数函数的定义 ：
一般，函数 y ? a x (a ? 0，且a ? 1) 叫做指数函数，其中x是自变量，定义域 为R.
为什么规定 a ? 0，且 a ? 1 ？
判断：下列函数中哪些是指数函数？
（1） y ? 4 x （2） y ? x4 （3） y ? ? 4x
(4)数形结合、分类讨论、
由特殊到一般
（2）指数函数图像和性质
（3）“指数型”函数增长模型 ? 定义域
2、研究函数的一般方法：
概念
图象
性质
? ?? ? ? ?
值域 特殊点 单调性
应用
?? 奇偶性
P59 A组 习题2.1
B组 3
5、7、8、
②、0 . 8 ? 2 , 0 . 8 ? 3
④ a 0.8 , a 0.6 ( a ? 0 , a ? 1)
解.（1） 函数 y ? 1.7 x 在 R 上是增函数； ? 2.5 ? 3, ? 1 .7 2.5 ? 1 .7 3
(2) 函数y ? 0.8x在R上是减函数；? ? 2 ? ? 3 ? 0.8?2 ? 0.8?3
(0,1) y= 1
y= 1 (0,1)
0
x
0
x
指数函数的图象和性质
y=ax
a＞1
y
0 ＜a ＜1
y
图 象
(1)定义域 (2)值域
性 (3)定点 质 (4)单调性
(5)函数值 的分布情 况
1
o
x
1
o
x
R ( 0 , + ∞)
在R上是增函数
当x＞0时，y＞1 当x＜0时，0＜y＜1
在R上是减函数
当x＞0时， 0＜y＜1 当x＜0时， y＞1
…
13亿
13+13×1℅=13×(1+1℅)(亿)
13×(1+1℅)+13×(1+1℅)
×1℅= 13?(1?1℅) 2(亿)
13×(1+1℅ ) 2 +13×(1+1℅ ) 2 ×1℅ =13×(1+1℅) 3(亿)
…
经过 x 年
y ? 13×(1+1℅) x (亿)
∴ 经过20年，人口约为13×（1+1℅ ) 20 ? 16（亿）
指数函数单调性比较； （2）引入中间量，比如“1”
例4、截止到1999年底，我国人口约13亿，如果今后能将人 口年平均增长率控制在1℅，那么经过20年后，我国人口数 最多为多少（精确到亿）？
解：设今后人口年平均增长率为1℅，经过 x年后，我国
人口数为 y亿。
年份
人口数
1999年底 2000年底 2001年底 2002年底
次数 1次
2次
3次 4次 …
x次
剩下长度
1
2
1 ? 1 ? ?? 1 ??2 2 2 ?2?
??1 ??2 ? 1 ? ??1 ??3 ?2? 2 ?2?
?? 1 ??3 ? 1 ? ?? 1 ??4 ?2? 2 ?2?
…
( 1 )x?1 ? 1 ? ( 1 )x 2 22
该木棒截x次后，剩下的木棒长度y与x的关系式是 y ? (1)x 2