当前位置：文档之家 › 单室模型——血管外给药

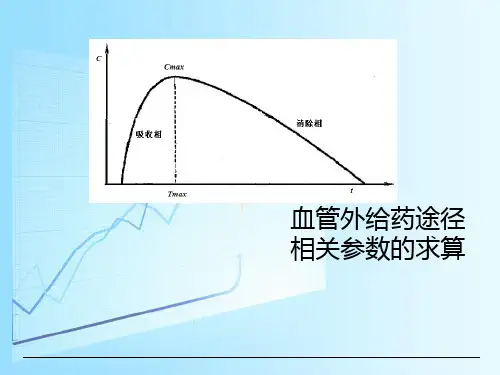
单室模型——血管外给药

  • 格式：pptx
  • 大小：522.39 KB
  • 文档页数：102

下载文档原格式

  / 102

合集下载

第八章 单室模型

第八章 单室模型

表观分布容积(V)
V X 0 / C0
Drug with low Vd
Drug with high Vd
high tissue binding
血药浓度－时间曲线下面积AUC
AUC Cdt 0 C0e dt


kt
0
C0 k
X0 Vk
清除率(Cl)
dX kX dt kV Cl C C
药物应主要经肾排泄， 药物较多以原型经肾排泄，且此过程符
合一级动力学过程。
1．尿排泄速度与时间的关系（速度法）

原型药物从尿液中排泄
X Xu
ke
其中，X为t时间体内药物的量，Xu为t时间排泄于 尿中原型药物累积量。
速度方程：
dXu = keX dt
dXu -kt = ke· X0e dt
lgC

k 2.303
t
3、基本参数(k和C0)求解
作图法：
C
lgC

k 2.303
t
t
最小二乘法：
（线性回归法）
4、其它参数的求解
半衰期(t1/2)
C0 k 0.693 lg t1/ 2 lg C0 t1/ 2 2 2.303 k

t1/2的临床意义:
(1)是体内药量或血药浓度下降一半所需要 的时间，反映药物在机体贮留的时间。
得
Xu

ke X 0 kt Xu e k
上式两边取对数得
lg( X u

k Xu ) t lg X u 2.303
式中 ( X u X u ) 项为待排泄原型药物的量， 简称亏量。

第八章 单室模型(血管外).

第八章 单室模型(血管外).

（二）曲线下面积AUC
1.积分法
AUC 0 M e kt e k t dt 0

a

M kt M e d kt 0 k ka M M 0 1 0 1 k ka M M k ka FX 0 kV
ci 1 ci cn AUC 0 ti 1 t i 2 k i 0
n 1
（三）k和ka的计算
1.残数法： 是药物动力学中把一条曲线分解成若干指数成分，从 而求药动学参数的方法。 在单室模型和二室模型中均有应用。 总之，凡C-T曲线为多项指数时，均可采用此方法。
该式为待排泄的原型药物量与时间t的关系。
当ka>k,t充分大时，e
u
-ka t
0
X k kt X Xu e ka k
X k k lg( X X u ) lg t ka k 2.303
u u a
u a
以
lg( X u X u ) 对t作图，从直线的斜率可求出K。
对上式积分得
( X A )t VCt KV Cdt
0
t
其中,(XA)t为t时间体内已吸收的药量，Ct为t时的血药浓度
( X A )t VCt KV Cdt
0
t
当t→∞时
( X A ) KV Cdt
0
其中,(XA) ∞为体内完全被吸收的药量。
( XA)t VCt kV 0 Cdt Ct k 0 Cdt 吸收分数 XA kV Cdt k Cdt 0
dX u / dt 故 C= keV
（dX u / dt） k dX u 1 d . ke dt ke dt

第八章 单室模型-3血管外给药

第八章 单室模型-3血管外给药

-katmax 再将e 再将
= 药时曲线方程得： 药时曲线方程得：
-ktmax k/kae
代入
残数法 （K/Ka） K/Ka）
药动学中将一曲线分段分解成若干指数函数 Feathering / peeling / stripping 应用： 应用：血药浓度曲线由多指数函数表达
K/ Ka估算 （残数法） 残数法）
Wagner-Nelson法（W-N） 法 ）
又称待吸收百分数法 一室模型法 又称待吸收百分数法；一室模型法 待吸收百分数 是求算Ka的经典方法 是求算 的经典方法
注
意
点
若以(Xa)t/(Xa)∞ 对释放百分数作图 ， 可得出 对释放百分数作图， ① 若以 体外释放百分数和体内吸收百分数之间关系。 体外释放百分数和体内吸收百分数之间关系 。 ② 若 [1- (Xa)t/(Xa)∞]对 t作图为一直线 ， 属于零 作图为一直线， 对 作图为一直线 级吸收；即本法可用于一些零级吸收过程。 级吸收；即本法可用于一些零级吸收过程。 本法只适用于单室模型， ③ 本法只适用于单室模型，对于双室模型要用 L-N（Loo-Riegelman）法 Loo-Riegelman）
滞后时间： 滞后时间：
A:图解法 图解法
B 参数计算法： 参数计算法：
C = Ae-kt – Ae-ka t 尾段直线 lnC = – Kt +lnC0 残数线 ln (C0e-kt – C) = – Kat+ lnA 在两直线的交点处： 在两直线的交点处： lnC = ln (C0e-kt – C) 则： lnC0 - Kt = lnA – Kat 所以： 所以：t = (lnA-lnC0) / (Ka-K)
备注： 备注： 1. 第一段和第二段曲线 ，血药 浓度由k 共同支配， 浓度由 a 和 k共同支配 ， 呈双指数 共同支配 下降。 下降。 2. 第三段为消除相，血药浓度只受 第三段为消除相， k支配，呈单指数下降。 支配，呈单指数下降。 3. V吸 和V除 是指吸收速度和消除 速度， 速度，等于浓度和速率常数的乘积 （V吸= kaXa、V除= kX）；而ka和k ） 是恒定不变的。 是恒定不变的。

第八章 单室模型

第八章 单室模型

地西泮治疗癫痫发作所需血药浓度为 0.5~2.5μg/mL,已知V=60L,t1/2=55h。今对一患 者先静脉注射10mg，半小时后以每小时10mg速 度滴注，经2.5h是否达到治疗所需浓度？
0.570 μg/mL
第三节 血管外给药 （一、血药浓度）
血管外给药途径包括口服、肌肉注射或皮下注 射，透皮给药，粘膜给药等
Ci 1 Ci Cn [ti 1 - ti ] 2 k
求算时间从0→t的AUC时，不加后缀相
C2
C0
k lg C t lgC0 2.303
C1
t1 t2
t
t
静注： AUC = C0/k
AUC
n 1 i 0
Ci 1 Ci Cn [ti 1 - ti ] 2 k
tc (h) 0.5 1.5 2.5 4.5 9 18 30 ……
（二） 亏量法
dX u ke X dt
拉氏变换
ke X 0 Xu (1 - e k
- kt
)
当t→∞时，最终经肾排泄的原型药物总量为：
X
u
ke X 0 ke X 0 - k (1 - e ) k k
ke X 0 X k
1、tmax由ka、k决定，与剂量无关 2、Cmax与剂量有关
血药浓度-时间曲线下面积（AUC）
AUC 0 Cdt 0 ka FX 0 FX 0 -kat -kt (e - e ) V (ka - k ) kV
AUC也可由实验数据用梯形法求得：
AUC
n 1 i 0
dX a = -k a X a dt dX = k a X a - kX dt
吸收相
消除相

单室模型

单室模型

静脉滴注
3.达到稳态浓度某一分数所需的时间 达到稳态浓度某一分数所需的时间
C = k0/kV(1 - e-kt) = Css(1 - e-kt)， ， C/Css = 1 - e-kt → fss （达坪分数）， e-kt = 1 – fss 达坪分数）， -kt = ln (1 - fss) t = -ln(1 - fss)/k = -1.44 t1/2ln(1 - fss)。 。 t = -1.44 t1/2ln(1 - fss)。 。 n = t/t1/2 = -1.44 ln(1 - fss)， ， ln(1 - fss) = - 0.693 n， ， fss = 1 － e-0.693 n 表. 半衰期数与达稳态分数的关系 n 1 2 3 4 5 6 7 fss(%) 50.0 75.0 87.5 93.7 96.8 98.4 99.2
静脉滴注
静脉滴注停滴以后的药-时关系 二.静脉滴注停滴以后的药 时关系 静脉滴注停滴以后的药 静脉滴注停滴以后的药-时关系通式 时关系通式(C 静脉滴注停滴以后的药 时关系通式 0是停滴时的给药浓 为静滴结束后的时间) 度，t为静滴结束后的时间 为静滴结束后的时间 ln C = ln C0 - kt， ， C0 = k0 / kV(1 - e－kT )， ， ln C = ln k0/kV×(1 － e－kT)－ kt × － ln C = ln k0/kV － kt 某药的k 例．某药的 = 0.01 h-1， V = 10 L，以2 mg/h的速度 ， ， 的速度 滴注6 ，问终止滴注2 后体内的血药浓度为多少 后体内的血药浓度为多少？ 滴注 h，问终止滴注 h后体内的血药浓度为多少？ 解：ln C = ln k0/kV(1－e －kT)－kt = 0.058 － － C = 1.14 µg/ml。 。

药代动力学第十章 重复给药

药代动力学第十章 重复给药

C ss A （
1 1 e

）e
t
B （
1 1 e

）e
t
血管外给药
CN （
1 1 e
）e k
a
kat
L （
1 1 e
）e
t
M（
1 1 e
）e
t
五、利用叠加原理预测重复给药血药浓度
第二节 平均稳态血药浓度
(Average Steady State Concentration)
单剂量静脉注射给药，AUC等于

0
C dt ＝
0
X0 V
e
－ kt
dt ＝
X0 kV
所以


0
C ss d t ＝ C d t ＝ 0

X0 kV
单室模型药物，多剂量静注给药达稳态
后，一个周期内的AUC等于单剂量给药 的AUC。
平均稳态血药浓度 C


0
ss
C ss
C ss d t
等于给药剂量的1.44倍。
二、血管外给药平均稳态血药浓度
多剂量血管外给药 C s s
C ss
0 C s s d t


＝
1


0

k t e kt e a k 1－ ek V (ka k ) 1－ e a
ka FX 0
dt
经积分得
C ss ＝ FX 0 kV


1



(
0
Le
t t
1 e

Me
t t

第八章 单室模型


X u 代替 dX u t dt
2
• 具体实例见教科书 p176 （用速度法和亏量法求药 动学参数）。
第二节 静脉滴注
一、血药浓度
1、模型的建立
• 是以恒定速度向血管内给药的方式。单室模型以静 脉滴注方式进入体内，在滴注时间T之内，体内除有 消除过程外，同时存在一个恒速增加药量的过程， 当滴注完成后，体内才只有消除过程 • 因此这种模型包括两个过程：（1）药物以恒定速度 k0 进入体内；（ 2 ）体内药物以 k 即一级速度从体内 消除。其模型如下图：
静脉注射计算公式汇总：
C C0 e
lgC
kt
X=X0 e
lgC 0
V = X0 / C0
-kt
kt
2.303
t1/2 = 0.693/k
斜率(-k/2.303)和截距（lgC0）
• T (min) 2 5 10 15 20 • C(mg/100ml) 10.20 7.20 3.80 2.05 1.11 • ㏒C 1.0086 0.8570 0.5798 0.3118 0.0453
Clr keV
• 从(8-37)可得：
dX u Clr C dt
………………..(8-40)
• 从(8-40)可知，用尿药排泄速度对相应的集 尿间隔内中点时间tc的血药浓度C作图（前 有讲述），可得到一条直线，直线的斜率 即为肾清除率（见教科书p176）。
• 在实际工作中，用实验所测得的 ，对 集 ti ti 1 尿期中点时间tc（ ）的血药浓度作图。
lg( X u X u ) k t lg X u 2.303

…………..(8-36)
上式中， ( X u X u ) 项称为待排泄原型药物 量，或称为亏量。

药动学公式总结

药动学公式汇总一、单室模型静脉注射1、C-t 与lgC-t 关系：（掌握）2、消除某一分数所需t 1/2个数：（掌握）t=3.32t 1/2lgC 0/C3、相关参数：（掌握）4、尿排泄速度与时间的关系（熟悉） （1）速度法 关系求 k（2）亏量法 lgX u -t 关系求k二、单室模型静脉滴注（掌握）1、C-t 与lgC-t 关系： （1）稳态后停滴)e (1k X k X kt 0e u --=X = X 0·e -kt C = C 0·e -kt0lg 303.2lg C t k C +-=k k t 693.02ln 2/1==00C X V =k C t e C AUC kt 0-00d ·==⎰∞kV C t X ==d /d TBCl AUC TBCl 0X =X k t X e u d d =0e u ·lg 303.2 d d lg X k t k t X +-=t tX →d d lg u k X k X 0e u =∞∞∞+=u u u lg 303.2-)-lg(X t k X X C X k e r Cl =0lgC a 303.2=-=k b )-1(-0kt e kVk C =kV k 0ss C ='-0kt e kVk C =kV k t k C 0log '303.2-log +=0e u ·lg 303.2 lg X k t k t X c +-=∆∆303.2k b -=（2）稳态前停滴2、达稳态分数： f ss =1-e -kt t=- 3.32 t 1/2 lg(1-f ss )三、单室模型血管外给药1、C-t 与lgC-t 关系（掌握）2、达峰时间与峰浓度（掌握）3、相关参数（掌握）梯形法求AUC ： 残数法求k 与ka （熟悉） 假设ka>k ，若t 充分大时，或4、尿排泄速度与时间的关系（熟悉）(1)速度法 关系求k 与k a'--0)-1(kt kT e e kV k C =)-1(log '303.2log -0kT e kVk t k C +=()t k kt e e k k V FX k Ca --a 0a -)-(=k k k k t a a max lg -303.2=m ax 0max kt e VFX C -=kV FX e e k k V FX k t k kt a 0--a 0a 0)-()-(AUC =⎰=∞k C t t C C ni i i i n i ++=++-=∑]-[2AUC 1110)-(lg 303.2-lg a 0a k k V FX k k C +=303.2k b -=)(log 303.2)(log a 0a a a 0a k k V FX k k C e k k V FX k kt -+-=⎭⎬⎫⎩⎨⎧---)-(log 303.2log a 0a a r k k V FX k t k C +=303.2a k b -=tt X →d d lg u k k FX k k t k t X e -log 303.2-d d lg a 0a u +=kk FX k k t k t X e c -log 303.2-lg a 0a u +=∆∆（2）亏量法 lgX u -t 关系求k 与k a四、重复给药多剂量函数（掌握）1、单室静注C-t 关系与达坪分数（掌握）坪辐 达坪分数 2、单室模型血管外给药C-t 关系（掌握）3、相关参数（熟悉）达坪分数3、平均稳态血药浓度（掌握） ττt C C SS ss d 0⎰= kk k X t k X X -lg 303.2-)-lg(a a u u u ∞∞+=ττi i k --nk e - 1e - 1=r kt k τ--nk τ0n e e - 1e - 1C C -=k τ--nk τ0max n e - 1e - 1C )(C =k τk τ--nk τ0min n e e - 1e - 1C )(C -=kt k τ-0ss e e - 11C C -=k τ-0ss max e - 11C V X =k τ-k τ-0ss min e e - 11C V X = 0min max V X C C ss ss =-τnk ss n n ss e C Cf --==1)()- 11- 11()(C 0n t k k nk kt k nk a a a a a e e e e e e k k V FX k ----------=ττττ)- 11- 11()(C 0ss t k k kt k a a a a e e e e k k V FX k ------=ττ时当e k 0a →-ττnk ss n n ss e C C f --==1)(])1()1(lg[303.2a a a max ττk k e k e k k k t ----⋅-=)-1(--0max max τk kt ss e e V FX C =)-11--11()-(a --a 0a minττk k ss e e k k V FX k C =)-1(--0min ττk k ss e e V FX C ≈)1lg(32.3)(21n ss f t n --=τ（1）静脉注射给药平均稳态血药浓度（2）血管外给药平均稳态血药浓度4、蓄积因子（掌握） （1）单室静注（2）血管外给药5、血药浓度波动程度 （了解）6、负荷剂量（掌握） 静注或口服：τk eX R X X --==1100*0 若t 1/2=τ，0*02X X = 静滴：（1）先静注再静滴： （2）快速静滴T min ，滴速为k 0* ，再按k 0恒速滴注)(44.12100ττt V FX Vk FX C ss ⨯==t 1/2/τ称为给药频数。

执业药师《药剂学》重点总结（三十四）

5.多剂量给药 6.单室模型静脉注射 ⼆、达稳态后⾎药浓度-时间关系式 三、稳态平均⾎药浓度 稳态平均⾎药浓度是多剂量给药情况下的⼀个⾮常有⽤的参数，所谓平均并不是稳态⾎药浓度（C∞）max与稳态最⼩⾎药浓度（C∞）max的算术平均值，它是稳态时的⼀个剂量间隔内（即从0→τ）的⾎药浓度曲线下⾯积与剂量间隔时间τ的⽐值。

（⼀）单室模型静脉注射 单室模型药物静脉注射达稳态时，稳态平均⾎药浓度为 从式中还可以看出，由于V及K都是所⽤药物的特定常数，故只能通过调整给药剂量X0和给药时间τ来获得理想的稳态平均⾎药浓度。

（⼆）单室模型⾎管外给药 根据稳态平均⾎药浓度的定义，单室模型⾎管外给药的稳态平均⾎药浓度为： 五、⾸剂量与维持剂量 在多剂量给药时，达稳态需要⼀段较长的时间，因此希望第⼀次给予⼀个较⼤的剂量，使⾎药浓度达到有效治疗浓度⽽后⽤维持剂量来维持共有效治疗浓度。

2. ⾮线性药物动⼒学和统计矩法 ⼀、⾮线性药物动⼒学 线性微分⽅程组来描述这些体内过程的规律性，⽆论是具备单室或双室模型特征的药物，当剂量改变时，其相应的⾎药浓度随剂量的改变⽽成⽐例的改变，药物的⽣物半衰期与剂量⽆关，⾎药浓度-时间曲线下总⾯积与剂量成正⽐等。

⾮线性动⼒学是在药物浓度超过某⼀界，参与药物代谢的酶发⽣了饱和现象所引起的。

可以⽤描述酶的动⼒学⽅程式即的⽶⽒⽅程（Michaelis-Menten）来进⾏研究。

[医学教育搜集整理] 该⽅程式基于物质在酶或载体参与下形成另⼀化学物质。

由于该过程需在某⼀特定酶或载体参与下进⾏，所以这些过程具有专属性强的特点。

药物的⽣物转化、肾⼩管的分泌以及某些药物的胆汁分泌过程都有酶的参与，所以具有⾮线性动⼒学特征。

3. ⽣物利⽤度和药物动⼒学模型判别⽅法 ⼀、⽣物利⽤度 ⽣物利⽤度（bioavailability）是指制剂中的药物进⼊体循环的相对数量和相对速度，即⽣物利⽤度包含药物的吸收速度与吸收程度两个⽅⾯的问题。

血管外给药途径


☆注意事项：
• 应用残数法，必须是在ka>k的情况下，这符合大多数药物。 • 因为一般药物制剂的吸收半衰期（t1/2a）总是短于消除半 衰期（t1/2），若出现k＞ka的情况，通过残数法先求的是
ka ，作残数线法得出的是k 。
• 此外，为保证残数线能作出，必须在吸收相内多次取样。 否则，残数值误差太大，一般以不少于3点为宜；在ka>k 的前提下，取样时间t应充分大，这样才能使e-kat→0。
t1/2＝0.693/k＝0.693/0.462＝1.5h
以lgCr － t直线回归，残数线的斜率为－ 1.505， 所以ka＝－1.505×（－2.303）＝3.465h-1
t1/2a＝0.693/ka＝0.693/3.465＝0.2h
截距为3.9，所以kaFXa/Vd(ka-k)=103.9得到，F=100%
0.2 时间（h） 血药浓度 （μg/ml） 1.65 2.33 2.55 2.51 2.40 2.00 1.27 0.66 0.39 0.4 0.6 0.8 1.0 1.5 2.5 4.0 5.0
假定该药物在体内的表观分布容积为30L，吸收进入 体内的药量Xa为100mg，试求算该药物的k，ka，t1/2， t1/2(a)及F值。
ka
C，Vd
k
Xa: t 时吸收部位的药量 X：t 时体内的药量 Ka：一级吸收速率常数 K：一级消除速率常数 F：生物利用度
_ _ X0 _ S X a X 0 ka X a X a S ka _ _ _ _ _ _ ka X a ka X 0 S X 0 k X k X X a a S k S ka S k 逆变换后：
c A e kt e kat
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

k FX
C
a
(e e ) O
kt
kat
V (k k)
a
3、达峰时间、峰浓度与曲线下面积
（1）达峰时间（tmax）和达峰浓度（Cmax） 在上面曲线中，一般将 峰左边称为吸收相，此时吸收速度大于消除速 度，曲线呈上升状态，主要体现药物的吸收情 况； 峰右边称为吸收后相（即消除相），此时的吸 收速度一般小于消除速度。
a
从上式看出： 对于某一给定的药物，ka ↑ ，到 达最大
血药浓度的时间↓ 。将tmax代替（2-3-7）式 中的t，可以得最大血药浓度：
k FX
C MAX
a
V (k
(e O
kt max
k)
e katmax )（2-3-11）
a
k
e ktmax
a
k
e katmax
k
e kat max
e kt max
112
8
• e 0.07 t
7.3
8 7.3 e 0.07 t
112
上式取对数，得
0.07t ln 0.52
则： t ln 0.52 9.30(h) 0.07
因此第二次给药最迟应于首次给药后约9h 服用。实际上，为保证药效可适当提前，如 间隔在8～8.5h服第二剂药较为合理。
从（2-3-7）式可以看出，单室模型血管外途 径给药 ，药物按一级速度吸收进入体内时， 血药浓 度-时间关系为单峰曲线，如下 图所示。
例十：已知某单室模型药物口服的生物利用 度为70%，ka=0.8h-1,V=10L,k=0.07h-1,如 口服剂量为200mg，试求服药后3小时的血 药浓度是多少？如该药物在体内的最低有效 血药浓度为8μg/ml，问第二次服药在什么时 间比较合适？
解：（1）将题中已知条件代入（2-3-7），得
C a
e O
kt
a
e O
kat
V(k k) V(k k)
a
a
对时间取微分
（2-3-8）
dC k 2FX
k kFX
a
e O
kat
a
e O
kt
dt V (k k) V (k k)
a
a
由于血药浓度在(tmax)时达到最大血药浓度 (Cmax)，dC／dt=0，所以
k 2FX
k kFX
a
因此曲线在一定程度上反映了药物的消除情况。 在到达峰顶的一瞬间，吸收速度恰好等于消除速
度，其峰值就是峰浓度(Cmax)，这个时间称为 达峰时 (tmax)。这两个参数可通过建立数学关
系式进行估算。
k FX
C
a
(e e ) O
kt
式，得：
k FX
k FX
0.8 0.7 200
8
(e e ) 0.07t
0.8 t
(0.8 0.07)10
上式是一个超越方程，只能寻求近似解。由于当t
e e 取适当大的值时, 0.07t
0.8t ，因此，上式
e 中 0.8t 可以忽略不计，则上式可以简化为：
0.8 0.7 200
8
e 0.07 t
(0.8 0.07)10
血管外给药途径包括: 口服、肌内注射或皮下注射，透皮给药， 粘膜给药等。
与血管内给药相比，血管外给药特点： ①给药后，药物在体内存在一个吸收过程 ②药物逐渐进入血液循环，不像静脉给药时， 药物直接进入血液循环。
一、血药浓度
1.模型的建立 血管外给药后，药物的吸收和消除常用一级 过程描述，即药物以一级速度过程吸收进入 体内，然后以一级速度过程从体内消除，这 种模型称之为一级吸收模型，如下图所示。
k FX
X a
(e e ) O
kt
kat
k k
a
（2-3-6）
上式两端除以药物的表观分布容积V得：
k FX
C
a
(e e ) O
kt
kat
V (k k)
a
（2-3-7）
单室模型血管外途径给药， 体内药物浓度C与时间t的关系
上式表示单室模型血管外途径给药，体内药 物浓度C与时间t的关系。 当某药的药动学参数为ka，k，V及F时可通 过（2-3-6）式、（2-3-7）式计算出任何时 间体内药量或血药浓度，以便进行临床血药 浓度的监测及其给药方案的调整。
F
X0
Xa
ka X
k
单室模型血管外给药示意图
上图中,X0是给药剂量；F 为吸收率；Xa为吸收部
位的药量；ka为一级吸收速度常数；X为体内药量； k为一级消除速度常数。
2.血药浓度与时间的关系
在血管外给药的一级吸收模型中，吸收部位 药物的变化速度与吸收部位的药量成正比， 用微分方程表示为：
dX
k X a
（2-3-1）
dt
a
a
体内药物的变化速度dX／dt应等于吸收速度 与消除速度之差，即：
dX
k X kX
dt
a
a
（2-3-2）
两次拉氏变换得：
S X a X k X a
O
a
（2-3-3）
SX k Xa kX a （2-3-4）
由上式解出
s kX
X
a
ka
代入（2-3-3）式
0.8 0.7 200
C
(e e ) 0.073
0.83
(0.8 0.07)10
112(0.810 0.091) 7.3
11.03(mg / L) 11.03(g / ml )
（2）在临床用药时，一般情况下，为达到有效治 疗目的，需维持体内血药浓度始终高于最低有效 浓度，因此第二次给药最好在血药浓度降至 8ug/ml之前。现在需求第一次服药后血药浓度降 至8ug/ml时所需的时间，这是一个已知浓度C,反 过来求t值的问题，即：
e O
ka tmax
a
e O
ktmax
V(k k)
V(k k)
a
a
k e 简化，得： a
ktmax
k
e katmax
（2-3-9）
两边取对数
tmax由ka和k决定
2.303 k
t
lg a
max k k k
（2-3-10）
a
k FX
C
a
(e e ) O
kt
kat
V (k k)
k
a
代入（2-3-11）得
k FX
C MAX
a
(e e ) O
kt max
kX
X
a
O
(S k)(S k )
a
上式应用拉氏变换表，得到体内药量与时间 的双指数方程如下：
kX
X (e e ) a
O
kt
kat
k k
a
（2-3-5）
上式表示单室模型血管外给药体内药量X与 时间t的关系式。由于血管外给药，吸收不 一定很充分，所以习惯上在给药剂量X0项前 加上“吸收系数 F”（0≤ F ≤ l），表示 吸收占剂量的分数值，即吸收率，或称其为 “生物利用度”。则上式变成：