下载文档原格式
VI3-D网格划分本章包含《Practical Finite Element Analysis》一书中的材料。
Matthias Goelke检查了本章并添加了一些材料。
7.1 3-D单元的适用场合当结构的3个维度尺寸在同一量级时应该使用3-D单元。
单元形状：四面体、楔形、六面体、金字塔用户需要输入的数据：无单元类型：实体实际应用：齿轮箱、发动机体、曲轴等6缸曲轴箱六面体网格曲轴四面体网格3-D单元类型：7.2 实体单元的自由度2-D薄壳和1-D梁单元都支持6个自由度，但所有实体单元都只有3个平动自由度（无转动自由度）。
例如一个10节点四面体单元总共有10 x 3 = 30个自由度。
为什么实体单元只有3个平动自由度而无转动自由度（物理解释）？考虑一张纸片（2-D几何）或者一把长的铁尺（1-D几何）。
他们容易被弯曲和扭转（转动自由度）。
但是如果是除尘刷或者压纸之类的实体。
他们通常不会承受很大的弯曲或扭转。
因此，实体单元只有3个平动自由度而无转动自由度。
7.3 四面体网格划分技术有两种四面体网格划分方法。
1）自动划分：这种方法局限于简单几何，并且要求CAD模型没有错误。
用户只需要选择实体，软件会自动根据单元长度、质量指标进行划分。
优点：很快很简单。
缺点：生成的单元和节点数量很多。
无法进行网格流向和网格模式控制（例如：螺栓、点焊、接触面模拟）。
2）2-D（三角形）到3-D（四面体）：这是最常用的方法。
在表面几何曲面上进行四边形和三角形网格3-D单元四面体楔形六面体金字塔线性四面体4节点线性楔形6节点线性六面体8节点线性金字塔5节点非所有软件均支持抛物线四面体10节点抛物线楔形15节点抛物线六面体20节点抛物线金字塔13节点划分。
在四面体网格划分时四边形被自动切割为三角形作为四面体单元的基础。
2-D（三角形）到3-D（四面体）网格划分的步骤：第一步：研究几何。
第二步：分割（孤立）曲面以便进行任务分配（如果有时间限制的话）。
三角网格细分法在重建隧道三维结构中的应用(1)摘要曲面造型一直是计算机图形学的重要研究内容之一。
曲面的显示效果涉及到数据的存储结构及对数据的操作方法等多方面的知识。
网格细分是曲面的一种表示方法，但却是目前广泛使用的一种曲面造型方法。
而三角网格细分的许多算法已经成功地应用于许多领域。
本文介绍了曲面造型的相关理论，重点介绍了Loop细分算法及其在重建隧道三维结构中应用。
关键词曲面; 网格; 细分; 逼近; 隧道0 引言隧道的施工安全，常常与隧道的掌子面观察紧密联系。
现行观察一般是人工纪录和掌子面状况描绘或者照像，这种描绘往往由于人为因素，使获得的数据缺乏一致性和可比性。
而照片在冲洗过程中，由于相片本身的分辨率也会导致冲照片在洗过程中出现信息畸变、丢失的现象，而且不能数字化和及时处理。
因此在对隧道开挖过程中的掌子面图象进行处理后，就需要根据所获得的特征参数，重建、显示隧道的三维结构，并用以指导隧道的施工。
但三维结构在重建过程中，重建的效率是十分重要的。
本文利用曲面网格的相关理论，并结合三角网格细分算法来进行遂道三维结构的重建，以加快生成速度和提高隧道三维结构显示的质量。
1 曲面网格的构建空间曲面的构建一般采用参数方式。
若用双参数构建曲面，其数学形式为：S=S(u,v)=[x(u,v),y(u,v),z(u,v)] (a≤u≤b,c≤v≤d)当u,v在各自的定义域内变化时，S（u,v）在空间坐标系中变化，且O-UV坐标系中的任意一点(u,v)均与O-XYZ坐标系中的点(X,Y,Z)呈一一映射关系。
当v不变而u变化时，得到u线；反之，则得到v线。
所有的u线和v线所形成的网叫参数曲线网。
由曲线p(u,c),p(u,d),p(a,v),p(b,v)四条边界曲所围成的部分，被称为网格，它定义在矩形域（(a≤u≤b,c≤v≤d)）上。
矩形定义域一般采用正方形（0≤u≤1,0≤v≤1）。
Coons曲面，Bezier曲面，B样条曲面均可用这种方式来建构。
三维⽹格细分算法（Catmull-ClarksubdivisionLoopsubdivis。
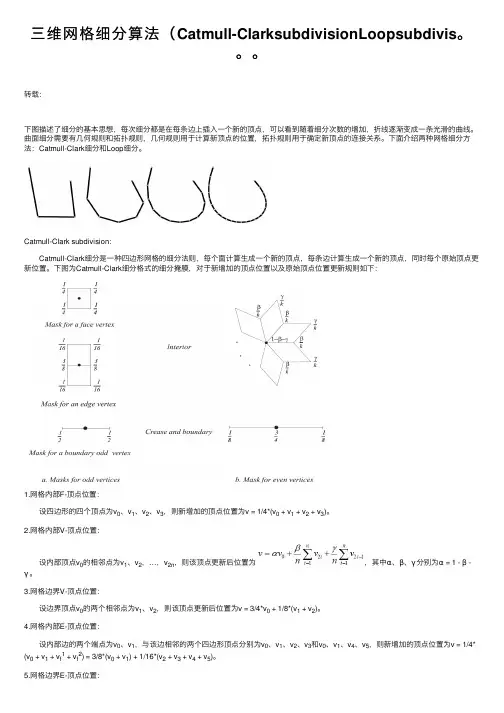
转载：下图描述了细分的基本思想，每次细分都是在每条边上插⼊⼀个新的顶点，可以看到随着细分次数的增加，折线逐渐变成⼀条光滑的曲线。
曲⾯细分需要有⼏何规则和拓扑规则，⼏何规则⽤于计算新顶点的位置，拓扑规则⽤于确定新顶点的连接关系。
下⾯介绍两种⽹格细分⽅法：Catmull-Clark细分和Loop细分。
Catmull-Clark subdivision： Catmull-Clark细分是⼀种四边形⽹格的细分法则，每个⾯计算⽣成⼀个新的顶点，每条边计算⽣成⼀个新的顶点，同时每个原始顶点更新位置。
下图为Catmull-Clark细分格式的细分掩膜，对于新增加的顶点位置以及原始顶点位置更新规则如下：1.⽹格内部F-顶点位置： 设四边形的四个顶点为v0、v1、v2、v3，则新增加的顶点位置为v = 1/4*(v0 + v1 + v2 + v3)。
2.⽹格内部V-顶点位置： 设内部顶点v0的相邻点为v1、v2，…，v2n，则该顶点更新后位置为，其中α、β、γ分别为α = 1 - β -γ。
3.⽹格边界V-顶点位置： 设边界顶点v0的两个相邻点为v1、v2，则该顶点更新后位置为v = 3/4*v0 + 1/8*(v1 + v2)。
4.⽹格内部E-顶点位置： 设内部边的两个端点为v0、v1，与该边相邻的两个四边形顶点分别为v0、v1、v2、v3和v0、v1、v4、v5，则新增加的顶点位置为v = 1/4* (v0 + v1 + v f1 + v f2) = 3/8*(v0 + v1) + 1/16*(v2 + v3 + v4 + v5)。
5.⽹格边界E-顶点位置： 设边界边的两个端点为v0、v1，则新增加的顶点位置为v = 1/2*(v0 + v1)。
效果：function [VV, FF, S] = CC_subdivision(V, F, iter)% Catmull_Clark subdivisionif ~exist('iter','var')iter = 1;endVV = V;FF = F;for i = 1:iternv = size(VV,1);nf = size(FF,1);O = outline(FF);original = 1:nv;boundary = O(:,1)';interior = original(~ismember(original, boundary));no = length(original);nb = length(boundary);ni = length(interior);%% SvEtmp = sort([FF(:,1) FF(:,2);FF(:,2) FF(:,3);FF(:,3) FF(:,4);FF(:,4) FF(:,1)],2);[E, ~, idx] = unique(Etmp, 'rows');Aeven = sparse([E(:,1) E(:,2)], [E(:,2) E(:,1)], 1, no, no);Aodd = sparse([FF(:,1) FF(:,2)], [FF(:,3) FF(:,4)], 1, no, no);Aodd = Aodd + Aodd';val_even = sum(Aeven,2);beta = 3./(2*val_even);val_odd = sum(Aodd,2);gamma = 1./(4*val_odd);alpha = 1 - beta - gamma;Sv = sparse(no,no);Sv(interior,:) = ...sparse(1:ni, interior, alpha(interior), ni, no) + ...bsxfun(@times, Aeven(interior,:), beta(interior)./val_even(interior)) + ...bsxfun(@times, Aodd(interior,:), gamma(interior)./val_odd(interior));Sboundary = ...sparse([O(:,1);O(:,2)],[O(:,2);O(:,1)],1/8,no,no) + ...sparse([O(:,1);O(:,2)],[O(:,1);O(:,2)],3/8,no,no);Sv(boundary,:) = Sboundary(boundary,:);%% SfSf = 1/4 .* sparse(repmat((1:nf)',1 ,4), FF, 1);i0 = no + (1:nf)';%% Seflaps = sparse([idx;idx], ...[FF(:,3) FF(:,4);FF(:,4) FF(:,1);FF(:,1) FF(:,2);FF(:,2) FF(:,3)], ...1);onboundary = (sum(flaps,2) == 2);flaps(onboundary,:) = 0;ne = size(E,1);Se = sparse( ...[1:ne 1:ne]', ...[E(:,1); E(:,2)], ...[onboundary;onboundary].*1/2 + ~[onboundary;onboundary].*3/8, ...ne, ...no) + ...flaps*1/16;%% new faces & new verticesi1 = no + nf + (1:nf)';i2 = no + 2*nf + (1:nf)';i3 = no + 3*nf + (1:nf)';i4 = no + 4*nf + (1:nf)';FFtmp = [i0 i4 FF(:,1) i1; ...i0 i1 FF(:,2) i2; ...i0 i2 FF(:,3) i3; ...i0 i3 FF(:,4) i4];reidx = [(1:no)'; no+(1:nf)'; no+nf+idx];FF = reidx(FFtmp);S = [Sv; Sf; Se];VV = S*VV;endendLoop subdivision： Loop细分是⼀种三⾓形⽹格的细分法则，它按照1-4三⾓形分裂，每条边计算⽣成⼀个新的顶点，同时每个原始顶点更新位置。
第五章三维实体网格划分本章讲述三维实体网格划分。
包括三部分内容：●生成四面体网格零件：对实体指定线性或者2次四面体网格。
●四面体网格填充器：通过从曲面网格生成四面体网格来对实体划分网格。
●扫描实体网格：通过从曲面网格生成六面体或者楔形网格对实体划分网格。
5．1 生成3D零件网格本节说明如何使用四面体网格划分方法生成3D网格。
在【Generative Structural Analysis】（通用结构分析）工作台和【Advanced Meshing Tools】（高级网格划分工具）工作台都有本命令。
根据用户安装的产品不同，显示的选项是不同的：●【Generative Structural Analysis】（通用结构分析）或者【FEM Surface】（曲面网格划分）系列产品。
●【FEM Solid】（有限元实体划分）系列产品。
5.1.1 【Generative Structural Analysis】（通用结构分析）或者【FEM Surface】（曲面网格划分）系列产品在通常的用户中，一般安装的是第一种情形。
在这种设置下，无论是在通用结构分析工作台还是高级划分工具工作台，定义3D网格的零件时，弹出的对话框只有两个选项卡。
（1）点击【Meshing Methods】（网格划分方法）工具栏内的【Octree Tetrahedron Mesher】（四面体网格划分器）按钮，如图5－1所示。
如果用户在【Generative Structural Analysis】（通用结构分析）工作台，则需要点击【Model Manager】工具栏内的【Octree Tetrahedron Mesher】（四面体网格划分器）按钮，如图5－2所示。
图5－1【Octree Tetrahedron Mesher】（四面体网格划分器）按钮图5－2（2）在图形区选择要划分网格的实体零件。
选择后弹出【OCTREE Tetrahedron Mesh】（四面体网格划分器）对话框，如图5－3所示。
三维网格模型分割的研究及其在人体测量中的应用三维网格模型分割的研究及其在人体测量中的应用摘要：在计算机科学领域中，三维网格模型分割是将3D模型分成各个独立的部分的过程。
现代科技中的三维扫描技术使得三维网格模型的获取变得越来越容易，因此三维网格模型分割也变得更加重要。
本文旨在探讨三维网格模型分割技术的研究进展，并着重讨论其在人体测量中的应用。
在本文中，我们将首先介绍三维网格模型分割的定义和研究背景，重点讨论三维网格模型分割算法的分类和性能指标。
然后，我们将深入探讨三维网格模型在人体测量中的应用，包括医学影像处理、虚拟现实和机器人定位导航等。
特别地，我们将详细讨论利用三维网格模型分割技术实现人体测量的方法和应用。
该论文所涉及的实验数据基于一个标准化的三维模型库，包含来自不同人群和不同种族的模型。
我们使用各类三维网格模型分割算法对这个模型库进行了实验比较，并得出了各个算法的优缺点。
结果表明，三维网格模型分割技术在人体测量中具有很好的应用潜力。
关键词：三维网格模型分割；人体测量；医学影像处理；虚拟现实；机器人定位导航。
I. 引言三维网格模型是用来描述物体表面的三维形状和纹理信息的一种数字化表示方法。
随着三维扫描技术的发展和基于三维网格模型的计算机应用的广泛应用，三维网格模型分割技术成为了一个热门研究课题。
三维网格模型分割是将三维网格模型分成各个独立的部分的过程，它是三维网格分析和应用中的一个核心问题。
分割后的每个部分都可以单独进行处理，并且可以对不同部分进行不同的操作，例如形状分析、局部纹理分析和对称性分析等。
本文旨在探讨三维网格模型分割技术的研究进展，并重点讨论其在人体测量中的应用。
II. 三维网格模型分割算法三维网格模型分割算法可以按照不同的分类方式进行划分，下面是主要的分类方法。
A. 基于图论的算法基于图论的算法将三维网格模型看做图的形式，将分割看做是图上的一个划分问题。
这种算法可以通过求解最小割问题实现。
三维网格分割的经典方法摘要：本文针对三维网格分割问题，提出一个经典的方法。
该方法基于微分几何和测地距离。
在算法中，将面片类型相同的顶点分割在一起。
测地距离利用顶点之间的最短路径表示，这里可以利用一些经典的算法求最短路径，如Dijkstra 算法。
但是当网格的数量很多时，Dijkstra 算法的效率很低。
因此，此算法避免了在整个网格上应用最短路径算法，在局部网格中求最短路径，从而减少了计算量。
本文在人造物体的三维网格模型以及分子结构中验证了该方法的有效性。
关键字：几何算法 面片分割 测地距离简介3D 物体的三维网格表示法具有很多的应用。
例如，在图像分析中，表示利用深度图像重建的物体表面。
此外，在复杂物体和场景的建模和可视化中也有广泛的应用。
在网格面片的分析中，网格分割已经成为一个关注的问题。
网格分割也就是将网格上相互接近并且具有相似曲率的顶点分成一组。
网格分割在很多方面具有重要的应用。
特征提取，模型匹配等。
Mangan 和Whitaker 提出三维网格分割的分水岭算法。
Razdan 和Bae 扩展了此算法，将基于点元（voxel-based ）和分水岭算法相结合，来分割三角网格。
这两种方法在分割中都需要计算整个曲率，然后在局部曲率最小处建立初始分割。
然而，在某些物体中，局部曲率的最小值是很难确定的。
因此，在这里提出一个初始分割的新方法。
在该算法中，应用基于面片的类型信息的网格区域增长方法，对顶点进行初始分割。
利用高斯曲率和平均曲率对顶点所在的面片进行分类。
这里利用离散微分几何计算高斯曲率和平均曲率。
通过本文提出的新方法来求得测地距离。
文章结构：第二部分，介绍网格面片的曲率分析和面片分类。
第三部分，详述本文的分割算法。
第四部分，实验以及其分割结果。
第五部分，结论。
2 面片分析在面片分析中，首先计算高斯曲率和平均曲率，然后利用它们进行面片分类。
顶点P 0的高斯曲率K 的计算公式如下：，A K θρ∆= ，∑-=∆i i 2θπθ ∑=ii A A ， A 为相邻三角形T i ( i =1，2，3，…)的面积总和。
第五章三维实体网格划分本章讲述三维实体网格划分。
包括三部分内容：●生成四面体网格零件：对实体指定线性或者2次四面体网格。
●四面体网格填充器：通过从曲面网格生成四面体网格来对实体划分网格。
●扫描实体网格：通过从曲面网格生成六面体或者楔形网格对实体划分网格。
5．1 生成3D零件网格本节说明如何使用四面体网格划分方法生成3D网格。
在【Generative Structural Analysis】（通用结构分析）工作台和【Advanced Meshing Tools】（高级网格划分工具）工作台都有本命令。
根据用户安装的产品不同，显示的选项是不同的：●【Generative Structural Analysis】（通用结构分析）或者【FEM Surface】（曲面网格划分）系列产品。
●【FEM Solid】（有限元实体划分）系列产品。
5.1.1 【Generative Structural Analysis】（通用结构分析）或者【FEM Surface】（曲面网格划分）系列产品在通常的用户中，一般安装的是第一种情形。
在这种设置下，无论是在通用结构分析工作台还是高级划分工具工作台，定义3D网格的零件时，弹出的对话框只有两个选项卡。
（1） 点击【Meshing Methods】（网格划分方法）工具栏内的【Octree Tetrahedron Mesher】（四面体网格划分器）按钮，如图5－1所示。
如果用户在【Generative Structural Analysis】（通用结构分析）工作台，则需要点击【Model Manager】工具栏内的【Octree Tetrahedron Mesher】（四面体网格划分器）按钮，如图5－2所示。
图5－1【Octree Tetrahedron Mesher】（四面体网格划分器）按钮图5－2（2） 在图形区选择要划分网格的实体零件。
选择后弹出【OCTREE Tetrahedron Mesh】（四面体网格划分器）对话框，如图5－3所示。
三维网格分割的经典方法摘要：本文针对三维网格分割问题，提出一个经典的方法。
该方法基于微分几何和测地距离。
在算法中，将面片类型相同的顶点分割在一起。
测地距离利用顶点之间的最短路径表示，这里可以利用一些经典的算法求最短路径，如Dijkstra 算法。
但是当网格的数量很多时，Dijkstra 算法的效率很低。
因此，此算法避免了在整个网格上应用最短路径算法，在局部网格中求最短路径，从而减少了计算量。
本文在人造物体的三维网格模型以及分子结构中验证了该方法的有效性。
关键字：几何算法 面片分割 测地距离简介3D 物体的三维网格表示法具有很多的应用。
例如，在图像分析中，表示利用深度图像重建的物体表面。
此外，在复杂物体和场景的建模和可视化中也有广泛的应用。
在网格面片的分析中，网格分割已经成为一个关注的问题。
网格分割也就是将网格上相互接近并且具有相似曲率的顶点分成一组。
网格分割在很多方面具有重要的应用。
特征提取，模型匹配等。
Mangan 和Whitaker 提出三维网格分割的分水岭算法。
Razdan 和Bae 扩展了此算法，将基于点元（voxel-based ）和分水岭算法相结合，来分割三角网格。
这两种方法在分割中都需要计算整个曲率，然后在局部曲率最小处建立初始分割。
然而，在某些物体中，局部曲率的最小值是很难确定的。
因此，在这里提出一个初始分割的新方法。
在该算法中，应用基于面片的类型信息的网格区域增长方法，对顶点进行初始分割。
利用高斯曲率和平均曲率对顶点所在的面片进行分类。
这里利用离散微分几何计算高斯曲率和平均曲率。
通过本文提出的新方法来求得测地距离。
文章结构：第二部分，介绍网格面片的曲率分析和面片分类。
第三部分，详述本文的分割算法。
第四部分，实验以及其分割结果。
第五部分，结论。
2 面片分析在面片分析中，首先计算高斯曲率和平均曲率，然后利用它们进行面片分类。
顶点P 0的高斯曲率K 的计算公式如下：，A K θρ∆= ，∑-=∆i i 2θπθ ∑=ii A A ， A 为相邻三角形T i ( i =1，2，3，…)的面积总和。
ρ为常量3。
如图1所示。
平均曲率定义为沿面法向方向的散度（divergence ），n H ∇=。
面片的平均曲率的法向量的计算公式如下[5、6、7]：∑∈-+=-)())(cot (cot 41i N j i j j j P P A n H βα其中，N(i)为顶点Pi 的邻接多边形的集合。
( P j -P i )为边ij e ，j βα和j 分别为在N(i)中，边ij e 所对的两个角。
A 为N(i)中所有三角型的面积总和。
如图2所示，顶点P i 的平均曲率的近似表示。
利用高斯曲率和平均曲率对一个顶点所在的面片进行分类。
面片的类型T的定义如下，)),sgn(1()),sgn(1(31εεk H T -+++=其中sgn 为分段函数（符号函数）(a tolerance signum function)，⎪⎩⎪⎨⎧<-≤>+=εεεεx x x x :1:0:1),sgn(3 网格分割算法设物体O 的网格结构为M ，M 由两部分组成，V 和E 。
},,{},,1|{},,,1|{q p i e i v i v v e N i e E N i v V =====其中，i v 为顶点，v N ,1≤≤q p 且q p ≠，V 是顶点集，E 为连接顶点的边的集合。
e v N N ,分别为M 中顶点和边的总数。
在该方法中，定义了四种分割类型：1. 峰值类型（peak-type ），2. 凹值类型（pit-type ），3. 最小面片类型（minimal surface-type ），4. 平面类型（flat-type ）。
对峰面、脊面(ridge)、马鞍面峰值(saddle ridge)的相应顶点进行峰值类型的分割，对凹面、谷面(valley)、马鞍凹面(saddle valley)的相应顶点作凹值类型的分割，对最小面片的相应顶点作最小面片类型的分割，平面类型的分割及对平面片的相应顶点进行操作。
该方法分为三个阶段：a) 分割初始化，b) 计算分割中心，c) 顶点分割和分割合并。
3.1 分割初始化这一步，初步形成上述四种类型的分割。
对于模型中其他类型的相应顶点并不考虑。
本文应用区域增长法来完成分割初始化。
图3为分割初始化算法。
算法中涉及了两个函数，Segment_Initializing 和Mesh_Growing 。
Segment_Initializing 用来建立顶点分割集队列元素（无ID 号），然后迭代的调用Mesh_Growing 函数对没有分割的顶点进行分割。
Mesh_Growing 函数自动的寻找具有相同面片类型的连通顶点。
最后初始分割集的生成。
每一个初始分割都包含具有任意一种面片的类型的连通顶点。
3.2 分割中心的计算设k S 为包括vk N 个顶点的集合（k V ）的初始分割。
令k ck V v ∈为k S 的中心顶点。
中心顶点设为：在集合k V 中，到所有顶点的平均测地距离最短。
由于平均距离和距离总和是可以等价的，中心点又可表示为，}min{∑i ik ck v v ，k ik V v ∈，⋅表示测地距离。
测地距离可以利用顶点的最短路径来近似的表示。
为了解决这个问题，首先建立一个带权矩阵，该矩阵既可以表示k V 中网格之间的联系，也可以表示相邻顶点间的欧几里得距离（即两点间距离公式求得）。
令k A 为k V 的vk vk N N ⨯的带权方阵，[]jk ik k v v A ,为方阵k A 的元素，其中k jk ik V v v ∈,。
k A 的定义如下，[]⎪⎩⎪⎨⎧∞∈∈=otherwise E v v if E v v if v v v v A jk ik jk ik jk ik jk ik k ,},{,0},{,,其中，||为欧几里得距离，E 为边的集合。
对k A 利用Dijkstra 算法求所有点对的最短路径（测地距离）。
此时所得到的方针k A 中元素均为最小值。
中心顶点ck v 满足在矩阵k A 中纵行距离和以及横行距离和均最小。
ck v ]},[min |{jk ik k ck v v A v ∑=图4为求图的中心顶点的例子。
3.3 分割在这一步，将未被分割的顶点i v 分割到距分割中心距离最小的分割集k S 中。
由此，我们可以知道顶点分割集[i]中是无标记的。
图5展示了i v 的分割算法。
首先建立一个集合D c ，D c 中存储顶点i v 到它的相应类型的所有分割中心的欧几里得距离。
如果初始分割的类型中，没有满足i v 的类型，D c 为空。
如果说在网格中，没有凹值类型的顶点，但具有低谷值类型和马鞍凹面类型的顶点，在这种情况下，不需建立凹值类型的初始分割集。
但是稍后，需要为低谷值类型和马鞍凹面类型的顶点新建立一个凹值类型的分割。
第二步，核对D c 。
如果D c 为空，则新建立一个包括i v 的分割，然后将这个分割添加到初始分割集中。
如果D c 非空，我们继续执行下一步。
第三步，选择一个距离域值p dist _，用于下一步中局部网格的生成。
p dist _为D c 中第p 个最短距离，p 的初始值为1。
p 每次加一或减一。
第四步，建立一个新的顶点集V t ，集合中的所有顶点到点i v 的距离都小于p dist _。
第五步，检查Vt 中局部网格的连通性。
首先，创建V t 的邻接矩阵来表示V t 中顶点的连通性。
设it v 为集合V t 中的顶点，i=1,…,N t ，N t 为集合V t 中顶点的总数。
令S t 为V t 的t t N N ⨯的邻接矩阵，矩阵中元素的定义如下，⎩⎨⎧∈=otherwise E v v if v v A jt iy jt iy t ,0},{,1],[ 在t A 中以i v 为根结点，进行深度优先搜索。
由此，可以得到与i v 相连通和非连通集合。
在这两个集合中分别可分割成中心顶点、以分割顶点、未分割顶点。
然后，从V t 中删除与i v 非连通的所有顶点。
对于与i v 相连通的顶点集，检查分割中心是否与i v 相连通。
如果连通，则执行第六步，否则更新p 值重复第三步。
第六步，在顶点集V t 中应用Dijkstra 算法计算i v 与分割中心以及其他顶点的最短路径。
然后将i v 分割到与分割中心距离最小的分割集中。
所有的顶点分割完后，以分割中心为根结点，利用深度优先搜索检查是否所有的顶点都是连通的。
非连通的顶点则从分割集中删除。
可能出现一种情况，某些顶点不属于任何一个分割集。
因此，我们利用网格增长算法将相似类型的顶点分成一组。
若得到的分割集太小（过分割问题），可以将这些小的分割集删除掉，或者是将它与其邻近的分割集相合并，但是要满足合并的两个分割集的整个曲率的差值应小于一个阈值。
一个分割的整个曲率即为该分割集中所有顶点曲率的平均值。
4 实验为了验证该方法的有效性，本文中进行了蛋白质三维网格模型和人工合成网格模型的分割。
这里在蛋白质结构的三维体柱结构中应用the marching cube algorithm ，对每种蛋白质三维网格结构的重构。
实验中建立了人造的模型，这些模型具有显著的特征，例如，低谷面、峰面、马鞍面，试验结果很容易的看出对这些特征的分割。
本文利用图形学建模软件Maya 来创建人造模型。
图3则标明了每个模型的信息。
图6 为蛋白质分割的结果显示。
图7为人造模型的分割结果显示。
对于每个模型，用不同的颜色表示不同的分割部分。
从试验结果可以看出，采用本算法可以很准确对显著特征进行分割。
这些分割结果可以应用在其他的网格分析中，例如，蛋白质的docking 应用。
5 结论本文利用微分几何和测地距离，提出一个新的网格分割方法。
在局部网格中应用Dijkstra算法。
此外，在分割检验和分割初始化过程中，分别应用了深度优先搜索和区域增长法。
对于网格面片的曲率，应用离散微分几何来求得。
从实验中可以看出，该方法能够准确的分割物体的显著特征，并得到满意的结果。
目前，该方法已经应用在蛋白质docking系统中。
