期权定价模型及其求解

伊藤过程dS=μSdt+σSdz上式是描述股票价格行为的最广泛使用的一种模型形式简单，比较容易处理，对实际情况的合理近似。

σ称为股票价格波动率，μ称为预期收益率伊藤定理：设变量x 遵循ITO 过程dx=a(x,t)dt+b(x,t)dz ，则x 和t 的函数G(x,t)遵循如下过程：bdz xG dt b x G t G a x G dG ∂∂+∂∂+∂∂+∂∂=)21(222其中，dz 是与上述过程中同样的维纳过程。

G 实际上也遵循一个ITO 过程。

的分布这是到期时刻股价对数或因此，相互独立其中，，则时刻的股价为，时刻的股价为设离散时间形式均为常数，因此可写为和其中得定理，由应用令由)](),)(2/([ln ~ln )](),)(2/[(~ln ln ),1,0(~,)(),,0(~,)2(ln ln G S T S )2(1,0,1G IT O ln 22222/12T 2222t T t T r S N S t T t T N S S z N t z t N z t T t zt S S t dzdt dG S S G t G S S S G Sdz Sdt dS T T T ---+----∆∆=∆∆∆-=∆∆+∆-=-=∆+-=-=∂∂=∂∂=∂∂=+=σσσσμεεσσμσμσσμσμ按照风险中性假设，当我们希望以无风险利率r 来贴现期权的价值时，即r 0=r ，股票的期望收益率也应该为无风险利率，即μ=r ，则：)]0,[max(ˆ)(K S E e c T t T r -=--)](),)(2/([ln ~ln 22t T t T r S N S T ---+σσ我们有了lnS T 的概率分布，就可以得到S T 的概率分布，即其密度函数，有了S T 的密度函数，E[max(ST-K,0)]就是一个积分过程，通过积分我们就可以得到结果，即著名的Ｂ-Ｓ公式。

具体积分过程如下：⎰⎰∞-∞---=====----T x T S S T xT T u d u f S F u d u f x F ex f x S e S f ln 22/1222/12)()()(ln )()()()2()(,ln )2()(ln 22)(2)(ln σσμμσπσπ则：令2)(ln 22)(ln 22/1222/12)2(1)2(1)(ln )()(σσμμσπσπ------=⨯=⨯=⨯=T S T S eS S eS S f S dx dx x dF S f T TTT T T以上是到期股价T S 的密度函数。

二、期权价值评估的方法（一）期权估价原理1、复制原理基本思想复制原理的基本思想是：构造一个股票和贷款的适当组合，使得无论股价如何变动投资组合的损益都与期权相同，那么创建该投资组合的成本就是期权的价值。

基本公式每份期权价格（买价）＝借钱买若干股股票的投资支出＝购买股票支出－借款额计算步骤（1）确定可能的到期日股票价格Su和Sd上行股价Su=股票现价S×上行乘数u下行股价Sd=股票现价S×下行乘数d（2）根据执行价格计算确定到期日期权价值Cu和Cd：股价上行时期权到期日价值Cu=上行股价-执行价格股价下行时期权到期日价值Cd=0（3）计算套期保值率：套期保值比率H=期权价值变化/股价变化=(CU-Cd)/(SU-Sd)（4）计算投资组合的成本（期权价值）=购买股票支出-借款数额购买股票支出=套期保值率×股票现价＝H×S0借款数额=价格下行时股票收入的现值＝（到期日下行股价×套期保值率）/（1+r）= H×Sd/（1+r）2、风险中性原理基本思想假设投资者对待风险的态度是中性的，所有证券的预期收益率都应当是无风险利率；假设股票不派发红利，股票价格的上升百分比就是股票投资的收益率。

因此：期望报酬率（无风险收益率）＝（上行概率×股价上升时股价变动百分比）+（下行概率×股价下降时股价变动百分比）＝p×股价上升时股价变动百分比+（1-p）×股价下降时股价变动百分比计算步骤（1）确定可能的到期日股票价格Su和Sd（同复制原理）（2）根据执行价格计算确定到期日期权价值Cu和Cd（同复制原理）（3）计算上行概率和下行概率期望报酬率＝（上行概率×股价上升百分比）+（下行概率×股价下降百分比）（4）计算期权价值期权价值＝(上行概率×Cu+下行概率×Cd)/（1+r）（二）二叉树期权定价模型1、单期二叉树定价模型基本原理风险中性原理的应用计算公式（1）教材公式期权价格＝U=股价上行乘数＝1＋股价上升百分比d=股价下行乘数＝1－股价下降百分比（2）理解公式：（与风险中性原理完全一样）2、两期二叉树模型基本原理把到期时间分成两期，由单期模型向两期模型的扩展，实际上就是单期模型的两次应用。

第11章 布莱克-舒尔茨-默顿期权定价模型一、基本思路1. 基本思路我们为了给股票期权定价，必须先了解股票本身的走势。

因为股票期权是其标的资产（即股票）的衍生工具，在已知执行价格、期权有效期、无风险利率和标的资产收益的情况下，期权价格变化的唯一来源就是股票价格的变化，股票价格是影响期权价格的最根本因素。

用几何布朗运动表示股票价格的变化过程，具体形式如下：dS dt dz Sμσ=+ 或者表示为dS Sdt Sdz μσ=+伊藤引理表明，当股票价格服从上述随机过程时，作为衍生品的期权价格f 将服从22221()2f f f f df S S dt Sdz S t SS μσσ∂∂∂∂=+++∂∂∂∂ 两式表明：股票价格及其衍生品——期权价格都只受到同一种不确定性的影响，只是两者对随机因素变化的反应程度不同而已。

从数学上看，将两式联立，解方程组可消掉随机项。

其金融含义可看作：买入股票、卖空期权构造一个短期内没有不确定性的投资组合。

在一个无套利市场中，该投资组合必然只能获得无风险利率收益。

由此可得到一个期权价格满足的微分方程，此即为BSM 期权定价模型的微分形式，具体为222212f f f rS S rf t S S σ∂∂∂++=∂∂∂ 由于该公式中不包含反映投资者风险偏好的参数——预期收益，因此可以在风险中性世界里求解该微分方程。

求解该方程可得到期权定价公式。

无股利欧式看涨期权的价格为 ()12()()r T t c SN d Xe N d --=-其中，21221d d d ===- 根据无股利欧式看涨期权和看跌期权平价公式()21()()r T t p Xe N d SN d --=--- 可求出无股利欧式看跌期权定价公式()21()()r T t p Xe N d SN d --=---无收益美式看涨期权是不会提前执行的，因此无收益美式看涨期权定价公式和欧式看涨期权定价公式相同，()12()()r T t C SN d Xe N d --=-对于有收益欧式期权，需要在股票价格中抛去收益的现值，对有收益的美式看涨期权，需要考虑其提前执行的情况，由于不存在美式期权之间的平价公式，因此无法给出美式看跌期权的确切公式。

期权定价理论知识期权定价理论是金融市场中重要的工具，它用于确定期权的合理价格。

期权是一种金融衍生品，它赋予持有者在未来某个时间点购买或卖出标的资产的权利，但并不强制执行。

期权的价格由多种因素决定，包括标的资产价格、行权价格、期权到期时间、标的资产的波动性以及无风险利率等。

在期权定价理论中，最著名的模型是布莱克-斯科尔斯期权定价模型（Black-Scholes Option Pricing Model）。

该模型是由费希尔·布莱克和米伦·斯科尔斯于1973年提出的，并且因此获得了诺贝尔经济学奖。

该模型基于一些假设，如市场是完全有效、无风险利率是恒定的等。

根据布莱克-斯科尔斯期权定价模型，期权的价格可以通过以下公式计算：C = S * N(d1) - X * e^(-rt) * N(d2)其中，C表示看涨期权价格，S表示标的资产价格，N(d1)和N(d2)分别是标准正态分布函数，X表示行权价格，r表示无风险利率，t表示期权到期时间。

公式中的d1和d2可以通过以下公式计算：d1 = (ln(S/X) + (r + (σ^2)/2)*t) / (σ * √t)d2 = d1 - σ * √t该模型通过考虑标的资产价格、行权价格、期权到期时间、标的资产的波动性和无风险利率等因素，来确定一个看涨期权的合理价格。

类似地，可以用类似的方法计算看跌期权的价格。

虽然布莱克-斯科尔斯期权定价模型是一个重要的理论框架，但它在实际应用中存在一些限制。

例如，该模型假设市场是完全有效的，但实际市场存在各种交易成本、税收和限制等，这些因素都可能影响期权的价格。

此外，该模型假设无风险利率是恒定的，但实际上利率是变化的。

因此，在实际应用中，需要根据实际情况进行调整和修正。

总之，期权定价理论是金融市场中重要的理论工具，它为期权的定价和交易提供了基础。

布莱克-斯科尔斯期权定价模型是其中最著名的模型之一，它通过考虑标的资产价格、行权价格、期权到期时间、标的资产的波动性和无风险利率等因素来确定期权的合理价格。

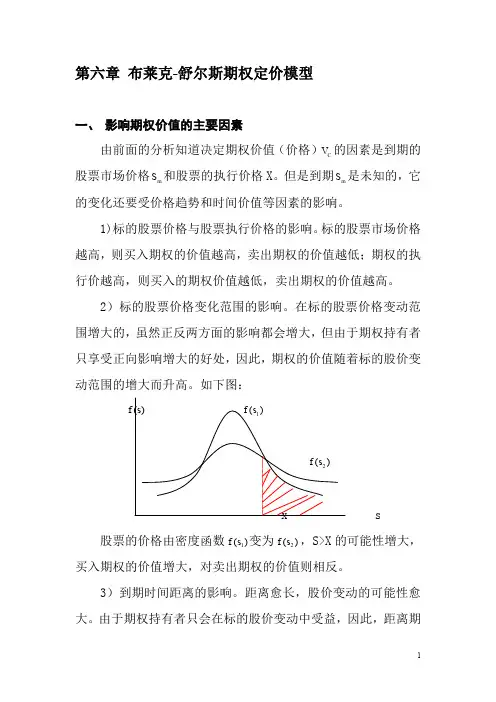
第六章 布莱克-舒尔斯期权定价模型一、 影响期权价值的主要因素由前面的分析知道决定期权价值（价格）C V 的因素是到期的股票市场价格m S 和股票的执行价格X 。

但是到期m S 是未知的，它的变化还要受价格趋势和时间价值等因素的影响。

1)标的股票价格与股票执行价格的影响。

标的股票市场价格越高，则买入期权的价值越高，卖出期权的价值越低；期权的执行价越高，则买入的期权价值越低，卖出期权的价值越高。

2）标的股票价格变化范围的影响。

在标的股票价格变动范围增大的，虽然正反两方面的影响都会增大，但由于期权持有者只享受正向影响增大的好处，因此，期权的价值随着标的股价变动范围的增大而升高。

如下图： )(s f )(1s f)(2s fx s股票的价格由密度函数)(1s f 变为)(2s f ，S>X 的可能性增大，买入期权的价值增大，对卖出期权的价值则相反。

3）到期时间距离的影响。

距离愈长，股价变动的可能性愈大。

由于期权持有者只会在标的股价变动中受益，因此，距离期权到期的时间越长，期权的价值就越高。

4）利率的影响。

利率越高，则到期m S 的现值就越低，使得买入期权价值提高，而卖出期权价值降低。

5）现金股利的影响。

股票期权受到股票分割或发放股票股利的保护，期权数量也适应调整，而不受影响，但是期权不受现金股利的保护，因此当股票的价格因公司发放现金股利而下降时，买入期权的价值下降，卖出期权的价值便上升。

二、布莱克-舒尔斯期权定价模型的假设条件B-S 模型是反映欧式不分红的买入期权定价模型，它的假定条件，除了市场无摩擦（例如无税、无交易成本、可以无限制自由借贷等）以外，还有：1． 股票价格是连续的随机变量，所以股票可以无限分割。

2． T 时期内各时段的预期收益率r i 和收益方差σi 保持不变。

3． 在任何时段股票的复利收益率服从对数正态分布，即在t 1-t 2时段内有：()()()2221211()ln ,()S t N t t t t S t μσ⎛⎫-- ⎪⎝⎭因为股票的价格可以用随机过程{},...2,1)(=t t S 表示，其中S （t ）表示第t 日股票的价格，它是一个随机变量. 则第t 日股票的收益率（年收益率）为R t ：3651)1()(t R t S t S +=-股票的年收益率（单利）R 应该是：)3651()3651)(3651()364()365()1()0()2()1()0()365(136521R R R S S S S S S S S R +++===+为了简化计算两边同时取自然对数可得：∑=+=+3651)3651()1(t tR In R In设r ，r 1，r 2，…，r 365为和R ，R 1，R 2，…，R 365相对应的连续复利。

如何评估期权的价值期权是一种金融衍生品，它赋予购买者在未来某个特定时间内以特定价格购买或者卖出某一标的资产的权利，而并非义务。

在金融市场中，期权的价值评估对于投资者和交易者来说至关重要。

合理的期权定价模型可以帮助投资者做出明智的决策，并降低投资风险。

本文将详细介绍如何评估期权的价值。

一、期权定价模型期权的价值评估主要使用两种经典的定价模型：Black-Scholes模型和Binomial模型。

1. Black-Scholes模型Black-Scholes模型是最常用的期权定价模型之一，基于以下几个关键因素对期权进行定价：- 标的资产的价格（S）：即期权对应的股票、商品或指数的当前价格；- 行权价格（K）：即期权买卖方约定的交易价格；- 到期时间（T）：即期权有效期限；- 无风险利率（r）：市场上的无风险利率，使用国债利率或短期利率作为参考；- 标的资产的波动率（σ）：标的资产价格的波动程度。

通过以上因素，Black-Scholes模型可以计算出一个期权理论价格，即市场上合理的期权价格。

2. Binomial模型Binomial模型是另一种常用的期权定价模型，它基于二叉树的计算方法。

该模型通过构建一个期权价格的二叉树，从期权到期时的所有可能价格路径中，使用回溯法计算出期权的价值。

二、评估期权的价值在实际应用中，我们可以使用以下几种方法来评估期权的价值：1. 市价法市价法是最常用的评估期权价值的方法，即根据市场上实际交易的期权价格来确定期权的价值。

这种方法可以反映市场对该期权的整体认知和供需状况，并具有一定的市场有效性。

2. 基于历史波动率的模型在Black-Scholes模型中，波动率是期权定价的一个重要参数。

我们可以根据过去的历史波动率来估计未来的波动率，然后将其代入到Black-Scholes模型中进行计算。

这种方法适用于市场波动率相对稳定的情况下。

3. 基于隐含波动率的模型隐含波动率是指使市场观察到的期权价格与Black-Scholes模型计算得出的价格相匹配的波动率。

BLACKSCHOLES期权定价模型计算公式套用数据Black-Scholes期权定价模型是一种用于计算欧式期权价格的数学模型，它基于以下假设：资产价格的波动性是已知且恒定的、市场无摩擦、无风险利率是已知且恒定的、欧式期权只能在到期日行使以获得支付。

根据Black-Scholes模型，欧式期权的价格可以通过以下公式计算：C=S*N(d1)-X*e^(-rT)*N(d2)P=X*e^(-rT)*N(-d2)-S*N(-d1)其中C表示认购期权的价格P表示认沽期权的价格S表示标的资产的当前价格X表示期权的行权价格r表示无风险利率T表示剩余期限，单位为年份d1 = (ln(S/X) + (r + σ^2/2)T) / (σ * √T)d2=d1-σ*√TN(d)和N(-d)是标准正态分布函数。

标准正态分布函数可以通过查找Z表或使用计算机程序进行近似计算。

在应用Black-Scholes模型时，需要提供以下数据：1.标的资产的当前价格（S）2.期权的行权价格（X）3.无风险利率（r）4.剩余期限（T）（以年为单位）5.标的资产的波动率（σ）下面举一个实例来说明如何使用Black-Scholes模型计算期权价格。

假设只股票的当前价格为100美元，期权的行权价格为105美元，无风险利率为5%，剩余期限为6个月（0.5年），股票的波动率为20%。

首先，根据给定的数据，计算d1和d2：d1 = (ln(100/105) + (0.05 + 0.2^2/2) * 0.5) / (0.2 * √0.5) d2=d1-0.2*√0.5然后，使用标准正态分布函数计算N(d1)、N(d2)、N(-d1)和N(-d2)的值。

假设N(d1)=0.6、N(d2)=0.5、N(-d1)=0.4和N(-d2)=0.3接下来，根据公式可计算出认购期权和认沽期权的价格：C=100*0.6-105*e^(-0.05*0.5)*0.5=7.16美元P=105*e^(-0.05*0.5)*0.3-100*0.4=3.84美元因此，在给定的条件下，该认购期权的价格为7.16美元，认沽期权的价格为3.84美元。

资产定价中的期权定价模型在金融市场中，期权是一种重要的金融衍生品。

期权的持有者在未来某一时间点上有权进行一定的交易，而其出售者则有相应的义务。

如何对期权进行定价，一直是金融学研究的重点之一。

期权定价模型可以帮助投资者合理地评估期权的价格，从而作出科学的投资决策。

在资产定价中，期权定价模型也起到了重要的作用。

期权定价模型主要有两种：Black-Scholes模型和Binomial模型。

Black-Scholes模型是最为著名的期权定价模型之一。

它是由费雪-布莱克和马顿·斯科尔斯在1973年提出的。

Black-Scholes模型假设以下四个条件：1. 证券市场是完全有效的，即不存在任何套利机会。

2. 股票价格的波动率是固定的，并且是已知的。

3. 股票市场的收益率符合对数正态分布。

4. 没有交易费用和税收。

基于以上条件，Black-Scholes模型可以通过求解偏微分方程来计算欧式看涨欧式看跌期权的理论价格。

该模型得出的期权价格，主要取决于以下几个因素：期权行权价格、期权到期时间、标的资产价格、无风险收益率和波动率。

其中，隐含波动率是一个重要的变量，它是指在当前市场条件下，使得理论价格等于市场价格的波动率。

Binomial模型又称二项式模型，是Cox、Ross和Rubinstein在1979年提出的。

Binomial模型基于离散时间、离散状态的假设，即时间轴和股价轴都是离散的。

该模型将给定时刻的资产价格看作是一个上涨或下跌的分支过程，从而形成一个二叉树结构。

通过在概率树上求解，可以计算出欧式期权、美式期权等的理论价格。

与Black-Scholes模型相比，Binomial模型更适用于处理近期股价波动较大的市场情况。

需要注意的是，Black-Scholes模型和Binomial模型都有其适用的范围。

在实际应用中，我们需根据特定的市场情况来选择相应的期权定价模型。

同时，期权定价模型也存在一定的局限性，如市场波动性的假设、隐含波动率的估计等问题。

期权定价理论期权定价理论是衡量期权合约价格的数学模型。

它基于一系列假设和推导出的公式，通过评估期权的相关因素来确定其合理的市场价格。

这些因素包括标的资产价格、期权执行价格、期限、波动率以及无风险利率等。

期权的定价理论中最著名的模型是布莱克-斯科尔斯模型（Black-Scholes Model）。

该模型基于以下假设：市场无摩擦，即不存在交易费用和税收；标的资产价格服从连续时间的几何布朗运动；期权可以在任意时间点以市场价格进行买卖。

布莱克-斯科尔斯模型通过以下公式计算欧式期权的价格：C = S0 * N(d1) - X * e^(-r * T) * N(d2)其中，C是期权的市场价格，S0是标的资产的当前价格，N()是标准正态分布函数，d1和d2分别是两个维度上的标准正态分布变量，X是期权的行权价格，r是无风险利率，T是期权剩余时间。

布莱克-斯科尔斯模型的原理是通过构建组合，使得期权价格与标的资产价格的变动相对冲，从而消除风险。

通过调整组合中的权重，可以确定合理的期权价格。

这一模型在市场上得到广泛应用，被视为期权定价的标准模型之一。

除了布莱克-斯科尔斯模型外，还有其他一些期权定价模型，如考虑股息的期权定价模型、跳跃扩散模型等。

这些模型在不同情况下，可以更准确地预测期权价格。

需要注意的是，期权定价理论是基于一系列假设和前提条件建立的。

市场实际情况中可能存在不符合这些假设的情况，因此实际期权价格可能与模型计算结果存在一定的差异。

此外，期权定价也受到市场供求关系、交易量以及市场情绪等因素的影响。

总之，期权定价理论是一种基于数学模型的方法，用于评估期权合约的合理价格。

布莱克-斯科尔斯模型是最著名的期权定价模型之一，通过构建相对冲抗风险的组合来确定期权价格。

然而，需要注意实际市场中的差异和其他影响因素。

期权定价理论是金融衍生品定价的核心理论之一，它对金融市场的有效运行和风险管理起着重要作用。

期权是一种约定，赋予期权持有人在未来某个特定时间以特定价格买入或卖出某个标的资产的权利，而不是义务。

期权定价的方法和模型综述本文从期权定价理论发展的历史和现状着手，系统地分析了期权定价的各种方法和模型，指出其优点和不足，并对期权定价理论的发展前景进行了展望。

关键词：期权定价无套利复制鞅方法期权就是选择权，期权的持有人在确定的时间、按确定的价格向出售方购销一定数量的基础资产，但他不承担必须购入（销售）的义务。

作为一种有效风险管理工具，期权日益活跃在现代金融市场中，其定价问题也一直是金融工程和数学金融学研究的重点之一。

期权定价问题的研究最早可以追溯到1900年，Bachelier在其博士论文中首次提出了股票价格的布朗运动假设并运用它来对欧式买权进行定价，然而模型中有几点与实际市场不符：股票价格可能为负、离到期日足够远的买权价格可能大于股票价格、股票的期望报酬为零。

1969年著名经济学家Sanuelson与Merton合作，提出了把期权价格做为基础资产价格函数的观点，不过在1973年B-S模型提出之前大部分模型都没有实用价值。

随着B-S 公式的问世，金融市场也变得空前繁荣，刺激了大量的学者对期权的定价机制、方法、模型进行研究，本文从三个方面综述期权定价理论的发展。

期权定价的方法无套利复制定价。

这种方法主要归功于Black-Scholes(1973)、Moerton(1973)，其基本原则就是无套利思想。

在一个无套利的市场中，具有相同未来收益的资产组合应当具有相同的价格，通过构造一个投资组合使得其未来收益与未定权益(如期权)的未来收益相同。

简单地说，构造一个就是复制该未定权益的投资组合，那么这个自筹资策略的初始成本就是期权当前的价值。

Black-Scholes正是根据上述思路得到了描述期权价格变化的随机微分方程，即所谓的B-S方程，最终利用得到了期权定价模型的解析解，也就是著名的Black-Scholes公式，正是这个公式使Scholes与Moerton分享了1997年的诺贝尔经济学奖。

期权定价的鞅方法。