第3讲_流体静力学基本方程式的应用
- 格式:ppt
- 大小:707.00 KB
- 文档页数:20


流体静力学方程式流体静力学是研究流体在静止状态下的力学性质的学科。
它是流体力学的一个分支,研究流体静止时的压力、密度、重力等因素对流体的影响。
本文将介绍流体静力学的方程式及其应用。
正文流体静力学方程式是描述流体静止时的力学行为的数学表达式。
主要包括两个方程式:流体静力平衡方程和流体连续性方程。
一、流体静力平衡方程流体静力平衡方程是基于力的平衡原理得出的。
它可以用来描述流体内外压力的均衡状态。
在一个封闭的容器中,流体的压力在各个方向上必须保持平衡。
这个平衡关系可以用以下方程式表示:P = ρg其中,P是压力场的梯度,ρ是流体的密度,g是重力加速度。
这个方程式表明流体中各个点的压力梯度与密度和重力加速度之间存在着一定的关系。
二、流体连续性方程流体连续性方程是基于流体质量守恒原理得出的。
它描述了流体在任意两个点之间质量的守恒关系。
对于一个不可压缩的流体(密度恒定),流体连续性方程可以用以下方程式表示:·v = 0其中,·v表示流体速度场的散度。
这个方程式表明流体在任意两个点之间的流量守恒,流出的质量等于流入的质量。
这两个方程式是流体静力学中的基本方程,通过它们可以计算流体静止时的压力分布和速度分布。
在实际的工程应用中,它们被广泛用于分析和设计涉及流体静力学的系统,如水坝、水管等。
总结起来,流体静力学方程式是描述流体静止时力学行为的基本数学表达式。
通过流体静力平衡方程和流体连续性方程,我们可以了解流体静态时的压力分布和速度分布,进而应用于实际工程中的设计和分析。
这些方程式为我们提供了深入理解流体静力学的基础,有助于我们更好地应对与流体静力学相关的问题。




第三讲 流体静力学一、 静止流体中的应力特性静止流体中,流体质点之间没有相对运动,切应力必然为0,又由于流体分子之间的引力很小,流体质点之间几乎不能承受拉力。
因此,在静止流体中,只能存在指向作用面的法向应力。
即n p =-p n (3-1)式中的p n 就是工程流体力学中的流体静压力。
上式也可以写成张量形式P ==000000p p p -⎡⎤⎢⎥-⎢⎥⎢⎥-⎣⎦=-p 00000011⎡⎤⎢⎥1⎢⎥⎢⎥⎣⎦= -p I (3-2) 式中I 为单位张量。
静止流体中任意一点处的应力无论来自何方均相等,即任意一点处的静压力与作用方向无关。
二、 欧拉平衡方程惯性坐标系中,任何流体处于静止状态的必要条件是:作用在物体上的合外力为0,即0∑=F (4-3)在静止流场中任取一个流体团作为研究对象,作用在其上的质量力可表示为d ρττ⎰⎰⎰f (a ) 表面力可表示为d d AAp A p A -=-⎰⎰⎰⎰n n (b )根据第一个平衡条件(3-3)可得d d =0Aρτp A τ-⎰⎰⎰⎰⎰f n (c ) 根据高斯定理可知,若物理量p 在封闭空间τ中连续且存在连续的一阶导数,则有d =d Ap A p ττ∇⎰⎰⎰⎰⎰n (d )将(d )式代入(c )式则可得d 0ρp ττ-∇=⎰⎰⎰()f 由于流体团是任意选取的,所以要使上式成立,则被积函数在该体积内任意点上的数值必须为0,于是有=0ρp -∇f或1=p ρ∇f (3-4)这就是欧拉平衡微分方程式,其在直角坐标系中可写为111x y z p f ρx pf ρy p f ρz ⎧∂=⎪∂⎪⎪∂=⎨∂⎪⎪∂=⎪∂⎩(3-5) 同时,合力矩为0是自动满足的。
三、 静压流场的质量力条件(自学)对于所有的静止流体,(3-4)式均成立,现对其两端同时取旋度可得1111==+=p p p p ρρρρ⎛⎫⎛⎫⎛⎫∇⨯∇⨯∇∇⨯∇∇⨯∇∇⨯∇ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()f上式中应用了标量函数梯度的旋度为0这一结论,现证明之p ∇⨯∇()=p p p xy z ⎛⎫∂∂∂∇⨯++ ⎪∂∂∂⎝⎭i j k=x y z p p p xy z∂∂∂∂∂∂∂∂∂∂∂∂ij k =p p p p p p y z z y x z z x x y y x ⎛⎫⎛⎫∂∂∂∂∂∂∂∂∂∂∂∂⎛⎫---+-⎪ ⎪ ⎪∂∂∂∂∂∂∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭i j k =0(矢量)将上式与(3-4)式进行点乘则有()1=p p ρρ⎡⎤⎛⎫∇∇⨯∇⨯∇⎢⎥ ⎪⎝⎭⎣⎦f f 上式右端为矢量的混合积,由混合积的定义可知由于三个矢量中有两个同名,所以其值为0,可得()=0∇⨯f f (3-6)由此可以得出结论:流体静止的必要条件是质量力必须满足()=0∇⨯ff 。
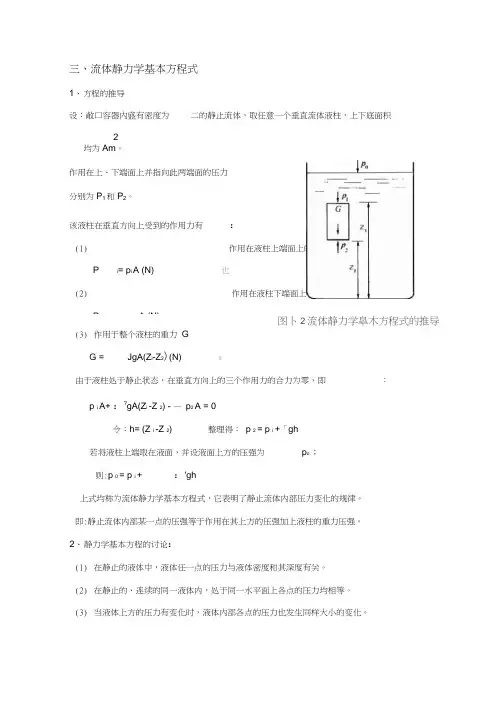
图卜2流体静力学皐木方程式的推导(3) 作用于整个液柱的重力 GG = JgA(Z i -Z 2)(N) 0由于液柱处于静止状态,在垂直方向上的三个作用力的合力为零,即 :p i A+ :?gA(Z i -Z 2) - — p 2 A = 0令:h= (Z i -Z 2) 整理得: p 2 = p i +「gh若将液柱上端取在液面,并设液面上方的压强为p o ; 则:p 0 = p i + :'gh上式均称为流体静力学基本方程式,它表明了静止流体内部压力变化的规律。
即:静止流体内部某一点的压强等于作用在其上方的压强加上液柱的重力压强。
2、 静力学基本方程的讨论:(1) 在静止的液体中,液体任一点的压力与液体密度和其深度有关。
(2) 在静止的、连续的同一液体内,处于同一水平面上各点的压力均相等。
(3) 当液体上方的压力有变化时,液体内部各点的压力也发生同样大小的变化。
三、流体静力学基本方程式1、 方程的推导设:敞口容器内盛有密度为 二的静止流体,取任意一个垂直流体液柱,上下底面积2均为Am 。
作用在上、下端面上并指向此两端面的压力分别为P 1和P 2。
该液柱在垂直方向上受到的作用力有: (1) 作用在液柱上端面上的总压力 P iPi = p i A (N) 也 (2) 作用在液柱下端面上的总压力 P 2P = p A (N)压强差的也大小可利用一定高度的液体柱来表示。
p P (5) 整理得:z 1g1二z 2g 也为静力学基本方程P g (6) 方程是以不可压缩流体推导出来的,对于可压缩性的气体,只适用于压强变 化不大的情况。
3、静力学基本方程的应用(1)测量流体的压差或压力①U 管压差计U 管压差计的结构如图。
对指示液的要求:指示液要与被测流体不互溶,不起 A化学作用,且其密度:7指应大于被测流体的密度:、。
通常采用的指示液有:水、油、四氯化碳或汞等。
I测压差:设流体作用在两支管口的压力为 p 1和P 2,且P i > P 2 , A-B 截面为等压面 即:P A 二P B 根据流体静力学基本方程式分别对 U 管左侧和U 管右侧进行计算整理得: P i - P 2 =:〔'指一'Rg讨论: (a )压差(p i -P 2)只与指示液的读数 R 及指示液冋被测流体的密度差有关。

静力学基本方程的应用静力学基本方程的应用流体静力学是流体力学的一个分支,研究是流体力学的一个分支研究相对静止流体(液体或气体)的压力、密度、温度分布以及流体对器壁或物体的作用力。
①静止流体;②质量力只有重力;③z轴垂直地面。
•压强的定义(-)(工程上的测压表相应地分为两类:用于被测系统压强高于外界大气压强的称为用于被测系统压强低于外界大气压的称为(1) 液柱压力计(压差计):(1)U型管压力计(压差计)(a) 普通U 型管压差计;(b) 倒U 型管压差计(c) 倾斜U 型管压差计;(d) 微差压差计种(倾例1.用3种压差计普通U型管压差计、倾斜U型管压差计和微压差计)测量气体的微小压差Δp=100Pa,试问:①用普通U型管压差计,以苯为指示液,其读数R为多少?用倾斜U型管压差计,α30,以苯为指示液,读数R为②=30°,以苯为指示液,读数R`多少?若用微压差计,其中加入苯和水两种指示液,扩大室截面③若用微压差计其中加入苯和水两种指示液扩大室截面积远远大于U型管截面积,此时读数R``为多少?R``是用苯为指示液的普通U型管压差计读数的多少倍?=879kg/m3,水的密度ρa=998kg/m3已知苯的密度为ρb已知:①气体的微小压差Δp=100Pa;②3种压差计•U型管压差计:指示剂——苯普通型管压差计指示剂•倾斜U型管压差计:指示剂——苯,α=30°•微压差计:指示剂——苯和水③指示剂密度:•水——ρa=998kg/m3=879kg/m3•苯——ρ求:•3种压差计的读数:R 、R` 和R``?•:``=?R R?解:计算时忽略气体密度的影响。
①普通U型管压差计②倾斜U型管压差计ab③微压差计hb R``a普通U型管压差计:R = 0.0116 m型管压差计R00116倾斜U型管压差计:R` = 0.0232 m微压差计:R``= 0.0857 mR :R` :R`` = 0.0116 : 0.0232 : 0.0857= 1 : 2 : 7.39其他形式的液体式压力计:①补偿式微压计扩大两个容器的截面积,消除毛细作用;毛细作用利用微测机构提高读数准确度;测压时把一个液面补偿到零点的位置以减少一次读数,提高测量的准确性。

第一节 流体静力学基本方程式流体静力学是研究流体在外力作用下达到平衡的规律。
在工程实际中,流体的平衡规律应用很广,如流体在设备或管道内压强的变化与测量、液体在贮罐内液位的测量、设备的液封等均以这一规律为依据。
1-1-1流体的密度一、密度单位体积流体所具有的质量,称为流体的密度,其表达式为:Vm =ρ (1-1) 式中 ρ——流体的密度,kg/m 3;m ——流体的质量,kg ;V ——流体的体积,m 3。
不同的流体密度不同。
对于一定的流体,密度是压力P 和温度T 的函数。
液体的密度随压力和温度变化很小,在研究流体的流动时,若压力和温度变化不大,可以认为液体的密度为常数。
密度为常数的流体称为不可压缩流体。
流体的密度一般可在物理化学手册或有关资料中查得,本教材附录中也列出某些常见气体和液体的密度值,可供查用。
二、气体的密度气体是可压缩的流体,其密度随压强和温度而变化。
因此气体的密度必须标明其状态,从手册中查得的气体密度往往是某一指定条件下的数值,这就涉及到如何将查得的密度换算为操作条件下的密度。
但是在压强和温度变化很小的情况下,也可以将气体当作不可压缩流体来处理。
对于一定质量的理想气体,其体积、压强和温度之间的变化关系为将密度的定义式代入并整理得'''Tp p T ρρ= (1-2) 式中 p ——气体的密度压强,Pa ;V ——气体的体积,m 3;T ——气体的绝对温度,K ;上标“'”表示手册中指定的条件。
一般当压强不太高,温度不太低时,可近似按下式来计算密度。
RTpM =ρ (1-3a ) 或 000004.22Tp p T Tp p T M ρρ== (1-3b ) 式中 p ——气体的绝对压强,kPa 或kN/m 2;M ——气体的摩尔质量,kg/kmol ;T ——气体的绝对温度,K ;R ——气体常数,8.314kJ/(kmol ·K )下标“0”表示标准状态(T 0=273K ,p 0=101.3kPa )。


流体流动知识点一、 流体静力学基本方程式或 注意:1、应用条件:静止的连通着的同一种连续的流体。
2、压强的表示方法: 绝压—大气压=表压 表压常由压强表来测量;大气压—绝压=真空度 真空度常由真空表来测量。
3、压强单位的换算:1atm=760mmHg===cm2=4、应用:水平管路上两点间压强差与U 型管压差计读数R 的关系: 处于同一水平面的液体,维持等压面的条件必须时静止、连续和同一种液体 二、定态流动系统的连续性方程式––––物料衡算式二、 定态流动的柏努利方程式––––能量衡算式以单位质量流体(1kg 流体)为基准的伯努利方程:讨论点:1、流体的流动满足连续性假设。
)(2112z z g p p -+=ρgh p p ρ+=0gRp p A )(21ρρ-=-常数常数=====≠ρρρρuA A u A u w s A ΛΛ222111,常数常数======uA A u A u V s A ΛΛ2211,ρ21221221///圆形管中流动,常数d d A A u u A ===ρf h u P gZ We u P gZ ∑+++=+++2222222111ρρ2、理想流体,无外功输入时,机械能守恒式:3、可压缩流体,当Δp/p 1<20%,仍可用上式,且ρ=ρm 。
4、注意运用柏努利方程式解题时的一般步骤,截面与基准面选取的原则。
5、流体密度ρ的计算:理想气体 ρ=PM/RT混合气体混合液体上式中:x vi ––––体积分率;x wi ––––质量分率。
6、gz 、u 2/2、p/ρ三项表示流体本身具有的能量,即位能、动能和静压能。
∑h f 为流经系统的能量损失。
We 为流体在两截面间所获得的有效功,是决定流体输送设备重要参数。
输送设备有效功率Ne=We·w s ,轴功率N=Ne/η(W )7、以单位重量流体为基准的伯努利方程, 各项的单位为m : [m] 22112212g 22f P u P u Z He Z H g g gρρ+++=+++ 以单位体积流体为基准的伯努利方程,各项的单位为Pa :[]22e f a f f u W gh p h p p h ρρρρρ∆=+∆++∑∆=∑而2222222111u P gZ u P gZ ++=++ρρvn n v v m x x x ρρρρ+++=Λ2211f e H gu g p Z H +∆+∆+∆=22ρnwn w m w m x x x ρρρρ+++=Λ22112212112222f u u gZ P We gZ P h ρρρρρρ+++=+++∑3、流型的比较:①质点的运动方式;②速度分布,层流:抛物线型,平均速度为最大速度的倍;湍流:碰撞和混和使速度平均化。
第3讲流体静力学基本方程式的应用引言流体静力学是研究静止液体或气体中力学平衡的一种分支学科。
它通过应用流体基本方程,如质量守恒方程和动量守恒方程,来分析静止流体的行为。
本文将介绍流体静力学基本方程式的应用。
流体静力学基本方程式流体静力学的基本方程式包括质量守恒方程、动量守恒方程和静力平衡方程。
下面我们将分别介绍这些方程的应用。
质量守恒方程的应用质量守恒方程描述了流体在静态情况下质量的守恒。
在应用中,质量守恒方程常被用于分析容器中静态液体的体积与密度的关系。
具体地,考虑一个封闭的容器,容器内充满了液体。
假设液体的体积为V,密度为ρ。
根据质量守恒方程,我们有:A1V1ρ1 = A2V2ρ2其中,A1和A2分别表示容器两个截面的面积,V1和V2分别表示液体在两个截面的体积,ρ1和ρ2分别表示液体在两个截面的密度。
通过这个方程,我们可以计算出液体在不同截面的体积与密度之间的关系。
动量守恒方程的应用动量守恒方程描述了流体在静态情况下动量的守恒。
在应用中,动量守恒方程常被用于分析液体在容器中的压力分布。
具体地,考虑一个封闭的容器中的液体,在容器的底部施加一个外力P。
根据动量守恒方程,我们有:P1A1 + P2A2 + F = 0其中,P1和P2分别表示液体在容器底部和顶部的压强,A1和A2分别表示容器底部和顶部的截面面积,F表示外力。
通过这个方程,我们可以计算出液体在不同位置的压强。
静力平衡方程的应用静力平衡方程描述了流体在静态情况下受力平衡的条件。
在应用中,静力平衡方程常被用于分析液体的浮力。
具体地,考虑一个浸泡在液体中的物体,它受到液体的浮力和重力的作用。
根据静力平衡方程,我们有:ρfVf + ρgVg = mg其中,ρf表示液体的密度,Vf表示物体受浸泡液体位于的部分的体积,ρg表示物体的密度,Vg表示物体未受浸泡液体部分的体积,m表示物体的质量,g表示重力加速度。
通过这个方程,我们可以计算出液体对物体的浮力大小。
流体静力学基本方程式的适用条件流体静力学是研究静止的流体力学现象的学科,主要研究流体静力学基本方程式的解法和应用。
流体静力学基本方程式包括质量守恒方程、动量守恒方程和能量守恒方程。
这些方程式适用于静止的流体,即不受外力而处于平衡状态的流体。
下面我们将详细介绍流体静力学基本方程式的适用条件。
一、质量守恒方程质量守恒方程是研究流体静力学的基本方程式之一,它描述了流体内质量的守恒。
质量守恒方程的适用条件如下:1. 流体是静止的,即流体的速度为零。
2. 流体是连续的,即流体是连续的物质,不存在空隙。
3. 流体是不可压缩的,即流体的密度不随时间和位置的变化而变化。
4. 流体是单相的,即流体内的物理和化学性质是均匀的。
二、动量守恒方程动量守恒方程是研究流体静力学的基本方程式之一,它描述了流体内动量的守恒。
动量守恒方程的适用条件如下:1. 流体是静止的,即流体的速度为零。
2. 流体是连续的,即流体是连续的物质,不存在空隙。
3. 流体是不可压缩的,即流体的密度不随时间和位置的变化而变化。
4. 流体是单相的,即流体内的物理和化学性质是均匀的。
5. 流体是粘性的,即流体内存在摩擦力。
三、能量守恒方程能量守恒方程是研究流体静力学的基本方程式之一,它描述了流体内能量的守恒。
能量守恒方程的适用条件如下:1. 流体是静止的,即流体的速度为零。
2. 流体是连续的,即流体是连续的物质,不存在空隙。
3. 流体是不可压缩的,即流体的密度不随时间和位置的变化而变化。
4. 流体是单相的,即流体内的物理和化学性质是均匀的。
5. 流体是绝热的,即流体内不存在热传导。
以上是流体静力学基本方程式的适用条件,下面我们将通过实例来进一步说明。
实例:一艘船停泊在湖面上,船底面积为10平方米,船重为50吨,水的密度为1000千克/立方米。
求船底受到的水的压力。
解析:根据质量守恒方程可知,流体在静止状态下,密度不随位置和时间的变化而变化,因此可以将水的密度视为恒定值1000千克/立方米。