四年级数学包含与排除
- 格式:doc
- 大小:20.50 KB
- 文档页数:2


和倍问题基本公式和÷(倍数和)=1倍数1倍数⨯倍数=几倍数例1 某校四年级选出48人到区里参加珠算竞赛,其中女同学是男同学的2倍,问:这个学校参加珠算竞赛的男、女生各多少人?练1 五年级学生参加文艺小组和科技小组的共有108人,参加文艺小组的人数是参加科技小组人数的2倍,参加两个小组的各有多少人?练2 师徒二人共加工零件42件,师傅加工数是徒弟的5倍,师徒各加工多少件?例2 小明买了14张画片,小刚买了10张画片,小明送给小刚几张后,小刚的画片张数是小明的3倍?练1 甲、乙两个数之和为72,甲数除乙数商是2,甲、乙两个数各是多少?练2 父子年龄的和是50岁,再过5年父亲的年龄是儿子的4倍,父子现在的年龄各是多少岁?例3 甲、乙二人共有钱810元,甲比乙的3倍还多10元,甲、乙二人各有钱多少元?练1 两个数的和是29,大数除以小数商是4,余数也是4,两个数各是多少?练2 一个除法算式,商是18,余数是4,被除数与除数的和是270,问:除数、被除数各是多少?例4 两个整数相除得商数是12,余数是26,被除数、除数、商数及余数的和等于454。
除数是多少?被除数是多少?练1 被除数比除数的3倍多1,并且被除数、除数、商、余数的和是81,求被除数、除数各是多少?练2 某公社有两个仓库共存粮84吨,已知甲仓库存粮比乙仓库的4倍少1吨,甲、乙两仓库各存粮多少吨?练3 甲站有车192辆,乙站有车48辆,每日从甲站开往乙站的有21辆,从乙站开往甲站的有24辆。
问:如此经过几天后,甲站车辆是乙站车辆的7倍?例5 白、红、黄三种棋子共56颗,白棋子是红棋子的2倍,红棋子是黄棋子的2倍,三种棋子各是多少颗?练1 红、黄、白三种棋子共48颗,红的是黄的3倍,白的是黄的2倍,三种棋子各是多少颗?练2 三个生产队合挖一条长1902米的水渠,第一队挖的是第二队的2倍,第三队挖的是第二队的3倍,三个队各挖了多少米?例6 甲、乙、丙三个数,甲数是乙数的2倍多100,乙数是丙数的2倍多50,已知三个数的和是950,三个数各是多少?练1 胜利化肥厂3天共生产2540袋,第二天生产的比第一天生产的2倍少60袋,第三天生产的比第一天生产的3倍少100袋,三天各生产了多少袋?练2 甲、乙、丙三人,甲的年龄比乙的年龄的2倍还大3岁,乙的年龄比丙的2倍小2岁,三个人年龄之和是109岁,分别求出三个人的年龄。

(二十九)包含与排除(上)《奥赛天天练》第二十一讲《包含与排除》。
包含与排除问题也叫重叠问题,从三年级奥数课堂开始由浅入深逐步学习,此类问题说明及容斥原理具体内容,请查阅:三年级奥数解析(三十九)重叠问题与容斥原理四年级奥数解析(二十九)容斥原理这一讲将在三、四年级学习的基础上,进一步学习运用容斥原理二解答稍复杂的包含与排除问题。
【容斥原理二】如果被计数的事物有A、B、C三类,则:三类元素总个数二A类元素个数+B类元素个数+C类元素个数一既是A类乂是B类的元素个数一既是A类乂是C类的元素个数一既是B类乂是C类的元素个数+既是A类乂是B类又是C类的元素个数。
【原理证明】如下图,三个圆片两两重叠,用红色圆片面积表示A类事物元素个数、黄色圆片面积表示B类事物元素个数、蓝色圆片面积表示C类事物元素个数,三个圆片覆盖的总面积就表示三类元素的总个数:A、B、C三个圆片共同重叠的正中间的一块,覆盖了三层圆片,重叠了2次;剩下的重叠部分都覆盖了两层圆片,重叠了1次。
三个圆片覆盖的总面积就等于三个圆片的面积之和减去重叠部分的面积,重叠1次的减去重叠面积,重叠2次的减去重叠面积的2倍。
但用三个圆片的总面积依次减去AB的重叠部分、AC的重叠部分和BC的重叠部分,重叠1次的面积正好减去了,可三个圆片共同重叠的部分既属于AB的重叠部分,也属于AC的重叠部分,同时属于BC的重叠部分。
这一块儿面积重叠2次,却减去了3次,多减了1次,要补上去。
所以:三类元素总个数二A类元素个数+B类元素个数+C类元素个数一既是A类乂是B类的元素个数一既是A类乂是C类的元素个数一既是B类乂是C类的元素个数+既是A类乂是B类又是C类的元素个数。
【题目】:在参加数学竞赛的46人中,做对第二题的有32人,做对笫4题的有24人,两道题都做对的有20人,两道题都没有做对的有儿人?【解析】:用做对第2题与做对第4题的人数和,减去两题都做对的人数(重叠部分),求出的就是这两题中至少做对了一题的人数:32+24-20=36 (人)。

包含与排除知识要点在一些计数问题中,经常遇到有关集合元素个数的计算。
求两个集合并集的元素的个数,不能简单地把两个集合的元素个数相加,而要从两个集合个数之和中减去重复计算的元素个数,即减去交集的元素个数,用式子可表示成:A B A B A B=+-U I (其中符号“U”读作“并”,相当于中文“和”或者“或”的意思;符号“I”读作“交”,相当于中文“且"的意思。
),则称这一公式为包含与排除原理,简称容斥原理。
图示如下:I,即阴影面积。
A表示小圆部分,B表示大圆部分,C表示大圆与小圆的公共部分,记为:A B1、先包含——A B+重叠部分A BI计算了2次,多加了1次;2、再排除——A B A B+-I把多加了1次的重叠部分A BI减去。
两者容斥【例 1】 把长38厘米和53厘米的两根铁条焊接成一根铁条。
已知焊接部分长4厘米,焊接后这根铁条有多长?包含与排除原理告诉我们,要计算两个集合A B 、的并集A B U 的元素的个数,可分以下两步进行: 第一步:分别计算集合A B 、的元素个数,然后加起来,即先求A B +(意思是把A B 、的一切元素都“包含”进来,加在一起);第二步:从上面的和中减去交集的元素个数,即减去C A B =I (意思是“排除”了重复计算的元素个数)。
A 类、B 类与C 类元素个数的总和=A 类元素的个数+B 类元素个数+C 类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数。
用符号表示为:A B C A B C A B B C A C A B C =++---+U U I I I I I图示如下:图中小圆表示A 的元素的个数,中圆表示B 的元素的个数,大圆表示C 的元素的个数。
1. 先包含——A B C ++A B I 、B C I 、C A I 重叠了2次,多加了1次。
2. 再排除——A B C A B B C A C ++---I I I重叠部分A B C I I 重叠了3次,但是在进行A B C A B B C A C ++---I I I 计算时都被减掉了。

包含与排除(容斥原理)学生姓名:年级:小升初科目:数学授课教师:贺琴授课时间:学生签字:包含与排除(容斥原理)集合是指具有某种属性的事物的全体,它是数学中的最基本的概念之一。
如某班全体学生可以看作是一个集合,0、1、2、3、4、5、6、7、8、9便组成一个数字集合。
组成集合的每个事物称为这个集合的元素。
如某班全体学生组成一个集合,每一个学生都是这个集合的元素,数字集合中有10个元素。
两个集合中可以做加法运算,把两个集合A、B合并在一起,就组成了一个新的集合C。
计算集合C的元素的个数的思考方法主要是包含与排除:先把A、B的一切元素都“包含”进来加在一起,再“排除”A、B两集合的公共元素的个数,减去加了两次的元素,即:C=A+B-AB。
在解包含与排除问题时,要善于使用形象的图示帮助理解题意,搞清数量关系的逻辑关系。
有些语言不易表达清楚的关系,用了适当的图形就显得很直观、很清楚,因而容易进行计算。
1、六年级96名学生都订了报纸,有64人订了少年报,有48人订了小学生报。
两种报纸都订的有多少人?[分析]用左边的圆表示订少年报的64人,右边的圆表示订小学报的48人,中间重叠部分表示两种报刊都订的人数。
显然,两种报刊都订的人数被统计了两次:64+48=112人,比总人数多112-96=16人,这16人就是两种报刊都订的人数。
【练习】1、一个班的52人都在做语文和数学作业。
有32人做完了语文作业,有35人做完了数学作业。
语文、数学作业都做完的有多少人?2、六年级有122人参加语文、数学考试,每人至少有一门功课得优。
其中语文得优的有65人,数学得优的有87人。
语文、数学都得优的有多少人?3、某班有50名学生,在一次测验中有26人满分,在第二次测验中有21人满分。
如果两次测验都没得过满分的学生有17人,那么,两次测验都得满分的有多少人?2、某校教师至少懂得英语和日语中的一种语言。
已知有35人懂英语,34人懂日语,两种语言都懂的有21人。

四年级思维拓展之包含与排除1.把长38厘米和53厘米的两根铁条焊接成一根铁条。
已知焊接部分长4厘米,焊接后这根铁条有多长?2.某小学三年级四班,参加语文兴趣小组的有28人,参加数学兴趣小组的有29人,有12人两个小组都参加。
这个班有多少人参加了语文或数学兴趣小组?3.在前100个自然数中,能被2或3整除的数有多少个?4.某科室有12人,其中6人会英语,5人会俄语,5人会日语,有3人既会英语又会俄语,有2人既会俄语又会日语,有2人既会英语又会日语,有1人英、日、俄这三种语言全会,只会一种外语的人比一种外语也不会的人多多少人?5.全班有46名同学,仅会打乒乓球的有18人,既会打乒乓球又会打羽毛球的有7人,既不会打乒乓球又不会打羽毛球的有6人。
问:仅会打羽毛球的有多少人?6.某班共有46人,参加美术小组的有12人,参加音乐小组的有23人,有5人两个小组都参加了。
这个班既没参加美术小组也没参加音乐小组的有多少人?7.有100位旅客,其中有10人既不懂英语又不懂俄语,有75人懂英语,83人懂俄语。
问既懂英语又懂俄语的有多少人?8.三年级科技活动组共有63人。
在一次剪贴汽车模型和装配飞机模型的定时科技活动比赛中,老师到时清点发现:剪贴好一辆汽车模型的同学有42人,装配好一架飞机模型的同学有34人。
每个同学都至少完成了一项活动。
问:同时完成这两项活动的同学有多少人?9.在春光小学“创造杯”展览会上,展品中有26件不是六年级的,有25件不是五年级的.已知五、六年级展品共35件,那么五年级的展品有____件.10.四1班有48名学生,在一节自习课上,写完语文作业的有30人,写完数学作业的有20人,语文数学都没写完的有6人。
(1)问语文数学都写完的有多少人?(2)只写完语文作业的有多少人?参考答案1.【解答】分析:焊接部分为两根铁条的重合部分,由包含排除法知,焊接后这根铁条长:38+53-4=87(厘米)。
2.【解答】分析:如图所示,A圆表示参加语文兴趣小组的人,B圆表示参加数学兴趣小组的人,A与B重合的部分C(阴影部分)表示同时参加两个小组的人。

复习盈亏问题1、少先队员到山上植树,如果每人载4棵,还剩18棵树苗,如果每人栽8棵,则少6棵树苗。
问:有多少名少先队员?多少棵树苗?2、活动课某班同学们参加拔河比赛,分成若干组,每组8人。
后来改成12人,结果少两组。
问全班有多少人?3、老师给大班小朋友分桃子,若8位小朋友每人分到3个,其余小朋友各分到5个,则还余54,若每人分到7个则正好分完。
问小朋友人数和桃子总数?4同学们秋游去公园划船,如果租船增加1条,那么正好每条船坐6人,如果少一条那么正好每条船坐8人。
问这个班共有多少人?包含与排除1、同学们到图书馆借书。
四(1)同学每人都借到课外书,其中借文艺书有40人,借科技书的有30人,两种书都借的有25,四(1)班共有多少人?2、四年级二班有46人,其中会弹琴的有30人,会拉小提琴的有28人,则这个班既会弹钢琴又会拉小提琴的有多少人?3、期末考试小芳的语文成绩和自然成绩加起来是187分,语文成绩和数学成绩加起来195分,数学成绩和自然成绩加起来是190分,那么小芳的语文成绩是多少?4、小玲会唱19首歌,小丽会唱24首歌,两人一共会唱的歌有36首,两人会唱的歌有几首?5、一个班级有48人,班主任在会上问:“谁做完语文作业的?这时有37人举手,又问”谁做完数学作业的有42人举手。
最后问“谁语文、数学作业都没有做完的?没有人举手。
这个班级语文、数学作业都玩的有多少?6、某班级40人在一次体育达标测试中,立定跳远达标的有26人,50米跑达标的有24人,两项都达标的有15人,有多少人两项都没有达标?7、四年级有48人,23人参加科技小组,26人参加文艺小组,12人两个小组都参加了。
有多少人两个小组都没有参加?8、一个旅行团有40人,其中会英语的有24人,会俄语的有18人,两样都不会的有14人,那么,两样都会的有多少人?9、某校进行体育竞赛,项目有短跑、游泳、跳高。
其中参加短跑的有75人,游泳的有52人,跳高的有38人,同时参加短跑与游泳的有26人、短跑与跳高有22人、游泳与跳高的有10人;三项都参加的有2人。



学生姓名: 年级:小升初科目:数学授课教师:贺琴授课时间: 学生签字:包含与排除(容斥原理)集合就是指具有某种属性得事物得全体,它就是数学中得最基本得概念之一。
如某班全体学生可以瞧作就是一个集合,0、1、2、3、4、5、6、7、8、9便组成一个数字集合。
组成集合得每个事物称为这个集合得元素。
如某班全体学生组成一个集合,每一个学生都就是这个集合得元素,数字集合中有10个元素。
两个集合中可以做加法运算,把两个集合A、B合并在一起,就组成了一个新得集合C。
计算集合C得元素得个数得思考方法主要就是包含与排除:先把A、B 得一切元素都“包含"进来加在一起,再“排除”A、B两集合得公共元素得个数,减去加了两次得元素,即:C=A+B-AB。
在解包含与排除问题时,要善于使用形象得图示帮助理解题意,搞清数量关系得逻辑关系、有些语言不易表达清楚得关系,用了适当得图形就显得很直观、很清楚,因而容易进行计算。
1、六年级96名学生都订了报纸,有64人订了少年报,有48人订了小学生报。
两种报纸都订得有多少人?[分析]用左边得圆表示订少年报得64人,右边得圆表示订小学报得48人,中间重叠部分表示两种报刊都订得人数。
显然,两种报刊都订得人数被统计了两次:64+48=112人,比总人数多112—96=16人,这16人就就是两种报刊都订得人数。
【练习】1、一个班得52人都在做语文与数学作业、有32人做完了语文作业,有35人做完了数学作业、语文、数学作业都做完得有多少人?2、六年级有122人参加语文、数学考试,每人至少有一门功课得优、其中语文得优得有65人,数学得优得有87人。
语文、数学都得优得有多少人?3、某班有50名学生,在一次测验中有26人满分,在第二次测验中有21人满分。
如果两次测验都没得过满分得学生有17人,那么,两次测验都得满分得有多少人?2、某校教师至少懂得英语与日语中得一种语言、已知有35人懂英语,34人懂日语,两种语言都懂得有21人。
四年级第二学期讲义第十一讲 包含与排除一、 知识要点日常生活或数学问题中,在把一些数据按照某个标准分类时,常常出现其中的一部分数据同时属于两种或两种以上不同的类别,这样在计算总数时就会出现重复计算的情况,这类问题就叫做重叠问题,容斥原理就是重叠问题的解题原理,也叫包含与排除原理。
在数学里,我们把具有某种相同性质的对象放在一起考虑,这些相同性质的对象便组成了一个“集合”,每个集合总是由一些成员组成的,集合中的这些成员叫做这个集合的元素。
名词解释:(1)由所有属于集合A 或属于集合B 的元素所组成的集合,叫做集合A 、B 的并集(又叫A 与B 的和)。
记作A B ,记号“ ”读作“并”,A B 读作“A 并B ”。
(2)A 、B 两个集合公共的元素,也就是那些既属于A ,又属于B 的元素,它们所组成的集合叫做A 和B 的交集,记作“A B ”,记号“ ”读作“交”,A B 读作“A 交B ”。
二、 典型例题例1、四(1)班同学中有37人喜欢打乒乓球,26人喜欢打羽毛球,21人既爱打乒乓球又爱打羽毛球。
问全班喜欢打乒乓球或羽毛球活动的有多少人?例2、四年级一班在期末考试中,语文得“优”的有15人,数学得“优”的有17人,老师请得“优”的同学都站起来,数了数有24人。
两科都得“优”的有几人?例3、图新小学四年级二班有24人参加了美术小组,有18人参加了音乐小组,其中11人两个小组都参加,还有5人什么组都没参加。
这个班共有学生多少人?例4、某班学生参加音乐组的有11人,参加美术组的有8人,参加英语组的有12人,既参加音乐组又参加美术组的有5人,既参加音乐组又参加英语组的有3人,既参加美术组又参加英语组的有4人,三个组都参加的只有1人,问:至少参加一个组的有多少人?例5、有82名参加数学与作文课外班的学生,其中参加作文班的有60人,参加数学班的有48人。
那么两种课外班都参加的有多少人?例6、全班有46名同学,仅会打乒乓球的有18人,会打乒乓球又会打羽毛球的有7人,不会打乒乓球又不会打羽毛球的有6人。
(二十九)包含与排除(上)《奥赛天天练》第二十一讲《包含与排除》。
包含与排除问题也叫重叠问题,从三年级奥数课堂开始由浅入深逐步学习,此类问题说明及容斥原理具体内容,请查阅:三年级奥数解析(三十九)重叠问题与容斥原理四年级奥数解析(二十九)容斥原理这一讲将在三、四年级学习的基础上,进一步学习运用容斥原理二解答稍复杂的包含与排除问题。
【容斥原理二】如果被计数的事物有A、B、C三类,则:三类元素总个数= A类元素个数+B类元素个数+C类元素个数—既是A类又是B类的元素个数—既是A类又是C类的元素个数—既是B类又是C类的元素个数+既是A类又是B类又是C类的元素个数。
【原理证明】如下图,三个圆片两两重叠,用红色圆片面积表示A类事物元素个数、黄色圆片面积表示B类事物元素个数、蓝色圆片面积表示C类事物元素个数,三个圆片覆盖的总面积就表示三类元素的总个数:A、B、C三个圆片共同重叠的正中间的一块,覆盖了三层圆片,重叠了2次;剩下的重叠部分都覆盖了两层圆片,重叠了1次。
三个圆片覆盖的总面积就等于三个圆片的面积之和减去重叠部分的面积,重叠1次的减去重叠面积,重叠2次的减去重叠面积的2倍。
但用三个圆片的总面积依次减去AB的重叠部分、AC的重叠部分和BC的重叠部分,重叠1次的面积正好减去了,可三个圆片共同重叠的部分既属于AB的重叠部分,也属于AC的重叠部分,同时属于BC的重叠部分。
这一块儿面积重叠2次,却减去了3次,多减了1次,要补上去。
所以:三类元素总个数= A类元素个数+B类元素个数+C类元素个数—既是A类又是B类的元素个数—既是A类又是C类的元素个数—既是B类又是C类的元素个数+既是A类又是B类又是C类的元素个数。
《奥赛天天练》第21讲,模仿训练,练习1【题目】:在参加数学竞赛的46人中,做对第二题的有32人,做对第4题的有24人,两道题都做对的有20人,两道题都没有做对的有几人?【解析】:如下图:用做对第2题与做对第4题的人数和,减去两题都做对的人数(重叠部分),求出的就是这两题中至少做对了一题的人数:32+24-20=36(人)。
涉及互相重复的两类或三类对象的计数问题.解题可利用计算所有对象总个数的容斥原理,以及图示包含与排除关系.1.某班有40名学生,其中有15人参加数学小组,18人参加航模小组,有10人两个小组都参加.那么有多少人两个小组都不参加?【分析与解】至少参加一个小组的同学有15+18-10=23人,所以有40-23=17人两个小组都不参加.2.某班45个学生参加期末考试,成绩公布后,数学得满分的有10人,数学及语文均得满分的有3人,这两科都没有得满分的有29人.那么语文成绩得满分的有多少人?【分析与解】数学、语文至少有一门得满分的学生有45-29=16人.所以语文成绩得满分的有16-10+3=9人.3.50名同学面向老师站成一行.老师先让大家从左至右按1,2,3,…,49,50依次报数;再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转.问:现在面向老师的同学还有多少名?【分析与解】在转过两次后,面向老师的同学分成两类:第一类是标号既不是4的倍数,又不是6的倍数;第二类是标号既是4的倍数又是6的倍数.1 50之间,4的倍数有504⎡⎤⎢⎥⎣⎦=12,6的倍数有506⎡⎤⎢⎥⎣⎦=8,即是4的倍数又是6的倍数的数一定是12的倍数,所以有5012⎡⎤⎢⎥⎣⎦=4.于是,第一类同学有50-12-8+4=34人,第二类同学有4人,所以现在共有34+4=38名同学面向老师.4.在游艺会上,有100名同学抽到了标签分别为1至100的奖券.按奖券标签号发放奖品的规则如下:①标签号为2的倍数,奖2支铅笔;②标签号为3的倍数,奖3支铅笔;③标签号既是2的倍数,又是3的倍数可重复领奖;④其他标签号均奖1支铅笔.那么游艺会为该项活动准备的奖品铅笔共有多少支?【分析与解】 1~100,2的倍数有1002⎡⎤⎢⎥⎣⎦=50,3的倍数有1003⎡⎤⎢⎥⎣⎦=33个,因为既是2的倍数,又是3的倍数的数一定是6的倍数,所以标签为这样的数有1006⎡⎤⎢⎥⎣⎦=16个. 于是,既不是2的倍数,又不是3的倍数的数在1~100中有100-50-33+16=33. 所以,游艺会为该项活动准备的奖品铅笔共有:50×2+33×3+33×1=232支.5. 有一根长为180厘米的绳子,从一端开始每隔3厘米作一记号,每隔4厘米也作一记号,然后将标有记号的地方剪断.问绳子共被剪成了多少段?【分析与解】 只需先计算剪了多少刀,再加上1即为剪成的段数. 从一端开始,将绳上距离这个端点整数厘米数的点编号,并将距离长度作为编号.有1~180,3的倍数有1803⎡⎤⎢⎥⎣⎦=60个,4的倍数有1804⎡⎤⎢⎥⎣⎦=45个,而既是3的倍数,又是4的倍数的数一定是12的倍数,所以这样的数有18012⎡⎤⎢⎥⎣⎦=15个. 注意到180厘米处的无法标上记号,所以剪了(60-1)+(45-1)-(15-1)=89,所以绳子被剪成89+1=90段.6. 东河小学画展上展出了许多幅画,其中有16幅画不是六年级的,有15幅画不是五年级的.现知道五、六年级共有25幅画,那么其他年级的画共有多少幅? 【分析与解】 将东河小学分成3个部分,六年级、五年级、其他年级,那么有五年级和其他年级共作画16幅,六年级和其他年级共作画15幅.而五、六年级共作画25幅,所以其他年级的画共有(16+15-25)÷2=3幅.7.有若干卡片,每张卡片上写着一个数,它是3的倍数或4的倍数,其中标有3的倍数的卡片占23,标有4的倍数的卡片占34,标有12的倍数的卡片有15张.那么,这些卡片一共有多少张?【分析与解】 设这些卡片的总数为“1”,而标有12的倍数的卡片既属于3的倍数又属于4的倍数.所以有"2""3"15"1"34+-=,解得“1”对应36张. 即这些卡片一共有36张.8.在从1至1000的自然数中,既不能被5除尽,又不能被7除尽的数有多少个?【分析与解】 l ~1000之间,5的倍数有10005⎡⎤⎢⎥⎣⎦=200个,7的倍数有10007⎡⎤⎢⎥⎣⎦=142个,因为既是5的倍数,又是7的倍数的数一定是35的倍数,所以这样的数有100035⎡⎤⎢⎥⎣⎦=28个. 所以既不能被5除尽,又不能被7除尽的数有1000-200-142+-28=686个.9.五年级三班学生参加课外兴趣小组,每人至少参加一项.其中有25人参加自然兴趣小组,35人参加美术兴趣小组,27人参加语文兴趣小组,参加语文同时又参加美术兴趣小组的有12人,参加自然同时又参加美术兴趣小组的有8人,参加自然同时又参加语文兴趣小组的有9人,语文、美术、自然3科兴趣小组都参加的有4人.求这个班的学生人数. 【分析与解】 设参加自然兴趣小组的人组成集合A ,参加美术兴趣小组的人组成集合日,参加语文兴趣小组的人组成集合C .A =25,B =35,C =27,B C =12,A B =8,A C =9,A B C =4. A B C =A B C A B A C B C A B C ++---+ .所以,这个班中至少参加一项活动的人有25+35+27-12-8-9+4=62,而这个班每人至少参加一项.即这个班有62人.10.如图8-1,已知甲、乙、丙3个圆的面积均为30,甲与乙、乙与丙、甲与丙重合部分的面积分别为6,8,5,而3个圆覆盖的总面积为73.求阴影部分的面积.【分析与解】 设甲圆组成集合A ,乙圆组成集合B ,丙圆组成集合C .A B C ===30,A B =6,B C =8,A C =5,A B C =73, 而A B C =A B C +--A B B C A C A B C --+ .有73=30×3-6-8-5+A B C ,即A B C =2,即甲、乙、丙三者的公共面积(⑧部分面积)为2.那么只是甲与乙(④),乙与丙(⑥),甲与丙(⑤)的公共的面积依次为6-2=4,8-2=6,5-2=3,所以有阴影部分(①、②、③部分之和)的面积为73-4-6-3-2=58.11.四年级一班有46名学生参加3项课外活动.其中有24人参加了数学小组,20人参加了语文小组,参加文艺小组的人数是既参加数学小组也参加文艺小组人数的3.5倍,又是3项活动都参加人数的7倍,既参加文艺小组也参加语文小组的人数相当于3项都参加的人数的2倍,既参加数学小组又参加语文小组的有10人.求参加文艺小组的人数.【分析与解】 设参加数学小组的学生组成集合A ,参加语文小组的学生组成集合B ,参加文艺小组的学生组成集合G .三者都参加的学生有z 人.有A B C =46,A =24,B =20,C =3.5,A C =7A B C ,B C =2A B C ,A B =10.因为A B C A B C A B A C B C A B =++---+ ,所以46=24+20+7x-10-2x-2x+x ,解得x=3,即三者的都参加的有3人.那么参加文艺小组的有3⨯7=21人.12.图书室有100本书,借阅图书者需在图书上签名.已知这100本书中有甲、乙、丙签名的分别有33,44和55本,其中同时有甲、乙签名的图书为29本,同时有甲、丙签名的图书为25本,同时有乙、丙签名的图书为36本.问这批图书中最少有多少本没有被甲、乙、丙中的任何一人借阅过?【分析与解】 设甲借过的书组成集合A ,乙借过的书组成集合B ,丙借过的书组成集合C .A =33,B =44,C =55,A B =29,A C =25,B C =36.本题只需算出甲、乙、丙中至少有一人借过的书的最大值,再将其与100作差即可. A B C A B C A B A C B C A B C =++---+ ,当A B C 最大时,A B C 有最大值.也就是说当三人都借过的书最多时,甲、乙、丙中至少有一人借过的书最多. 而A B C 最大不超过A 、B 、C 、A B 、B C 、A C 6个数中的最小值,所以A B C 最大为25.此时A B C =33+44+55-29-25-36+25=67,即三者至少有一人借过的书最多为67本,所以这批图书中最少有33本没有被甲、乙、丙中的任何一人借阅过.13.如图8-2,5条同样长的线段拼成了一个五角星.如果每条线段上恰有1994个点被染成红色,那么在这个五角星上红色点最少有多少个?【分析与解】 如下图,下图中“ ”位置均有两条线段通过,也就是交点,如果这些交点所对应的线段都在“ ”位置恰有红色点,那么在五角星上重叠的红色点最多,所以此时显现的红色点最少,有1994×5-(2-1)×10=9960个.14.甲、乙、丙同时给100盆花浇水.已知甲浇了78盆,乙浇了68盆,丙浇了58盆,那么3人都浇过的花最少有多少盆?【分析与解】只考虑甲乙两人情况,有甲、乙都浇过的最少为:78+68-100=46盆,此时甲单独浇过的为78-46=32盆,乙单独浇过的为68-46=22盆;欲使甲、乙、丙三人都浇过的花最少时,应将丙浇过的花尽量分散在两端。
小学四年级数学下册思维通用版容斥问题习题及答案知识点总结:容斥问题涉及到一个重要原理——包含与排除原理,也叫容斥原理。
即当两个计数部分有重复包含时,为了不重复计数,应从它们的和中排除重复部分。
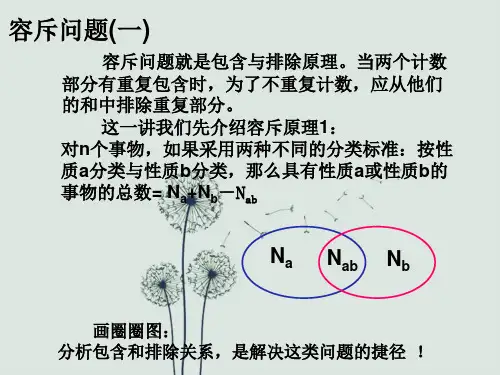
容斥原理:对n 个事物,如果采用不同的分类标准,按性质a 分类与性质b 分类(如图),那么具有性质a 或性质b 的事物的个数=Na +Nb -Nab 。
【经典例题1】空军突击队共有 25 名士兵,每个人都擅长射击和武术中的一项或者两项。
如果士兵中擅长射击的有 20 人,擅长武术的有 12 人。
则两项均擅长的士兵有多少人? 【思路分析】擅长射击的人数与擅长武术的人数之和为 20+12=32(人),大于空军突击队总人数 25 人,出现这种情况的原因是两项均擅长的人数被计算了两次,即多算了一次。
所以,两项均擅长的人数有 32-25=7(人) 射击20人 武术12人?人NaNbNab25人【本题解答】20+12-25=7(人)答:两项均擅长的士兵有7人。
【扩展训练】1、动物王国里有一个奇怪的猫村,已知猫村有60只猫咪,其中有漂亮尾巴的27只,漂亮毛色的45只。
所有猫毛色或尾巴至少一项都有的有60只,那么两样都漂亮的有多少只?2、佳佳是以为国旗爱好者,他从全世界193个国家的国旗中,挑出了43面带星星图案或带月亮图案的国旗,发现其中将星展图案的国能有34面。
带月亮图案的国旗有18面。
那么,既带星星图案又带月亮图案的国旗有多少面?3、学校成立“滑滑社团”,要求必须至少会滑冰、滑雪中的一项,才有资格成为的人团员。
已知有 2015 名符合上述要求的人前来报名,其中不会滑冰的有406 人,不会滑雪的有 460 人。
那么,其中两种运动都组会的有多少人?【经典例题2】某班 30 名同学中,有17人参加音乐小组,有12人参加美术小组,既参加音乐小组又参加美术小组的有7人,那么既不参加音乐小组又不参加美术小组的有多少人?【思路分析】如下图所示。
包含与排除基础卷1.五年级有168人参加语文、数学考试,每人至少有一门功课获优,其中语文获优的有87人,数学获优的有109人,问:语文、数学都获优的有多少人?2.某班有56名学生,在一次测试中有25人得满分,在第二次测试中有23人得满分,如果两次测试都没有得过满分的学生有18人,那么两次测试中都得满分的人有多少?3.某学校外语教研组有15名懂英语的教师,12名懂日语的教师,两种语言都懂的教师有8人,问:改教研组共有多少名教师?4.某班在一次测试中有28人语文获优,30人数学获优,其中语文、数学双优的有13人,另外还有8人语文、数学均未获优,这个班共有多少个学生?5.数学小组有20名同学一起做两道数学思想题,做对第一题的有10人,做对第二道题的有15人。
两题都做错的有2人,求:两题都做对的人数?6.有一个100名游客的旅游团,有60人懂英语,58人懂日语,既懂英语又懂日语的有34人,英语、日语都不懂的有多少人?提高卷1.五年级(1)班有学生56人,每人至少完成一门作业,其中45人完成了数学作业,42人完成了语文作业,这个班两种作业都做完的有多少人?2.某校挑选18名学生参加市春季运动会,获第一名的有12人,获第二名的有11人,两个名次都取得的有9人,这次运动会上既没取得第一名,也没取得第二名的有多少人?3.某学校组织同学参加足球和乒乓球比赛,参加足球比赛的有20人,参加乒乓球比赛的有18人,同时参加足球与乒乓球比赛的有13人,问:参加比赛的共有多少人?4.80个英语、日语老师中,懂英语的有65人,懂日语的有35人,其中必有既懂英语又懂日语的老师,问:只懂英语的老师有多少人?5.五年级112名同学参加语文、数学考试,每人至少有一门获优,已知语文获优60人,数学获优者73人,求只有语文一门获优的人数。
6.五(1)班有56名同学,每人至少会打乒乓球或羽毛球的一种,只会打乒乓球的28人,会打乒乓球又会羽毛球的有16人,仅会打羽毛球的有多少人?。
第35讲容斥原理前事不忘,后事之师。
《战国策·赵策》圣哲学校蔡雨欣一、专题简析:容斥问题涉及到一个重要原理——包含与排除原理,也叫容斥原理。
即当两个计数部分有重复包含时,为了不重复计数,应从它们的和中排除重复部分。
容斥原理:对n个事物,如果采用不同的分类标准,按性质a分类与性质b分类(如图),那么具有性质a或性质b的事物的个数=Na+Nb-Nab。
Nab NbNa二、精讲精练:例1:一个班有48人,班主任在班会上问:“谁做完语文作业?请举手!”有37人举手。
又问:“谁做完数学作业?请举手!”有42人举手。
最后问:“谁语文、数学作业都没有做完?”没有人举手。
求这个班语文、数学作业都完成的人数。
练习一1、五年级有122名学生参加语文、数学考试,每人至少有一门功课取得优秀成绩。
其中语文成绩优秀的有65人,数学优秀的有87人。
语文、数学都优秀的有多少人?2、四年级一班有54人,订阅《小学生优秀作文》和《数学大世界》两种读物的有13人,订《小学生优秀作文》的有45人,每人至少订一种读物,订《数学大世界》的有多少人?例2:某班有36个同学在一项测试中,答对第一题的有25人,答对第二题的有23人,两题都答对的有15人。
问多少个同学两题都答得不对?练习二1、五(1)班有40个学生,其中25人参加数学小组,23人参加科技小组,有19人两个小组都参加了。
那么,有多少人两个小组都没有参加?2、一个班有55名学生,订阅《小学生数学报》的有32人,订阅《中国少年报》的有29人,两种报纸都订阅的有25人。
两种报纸都没有订阅的有多少人?例3:某班有56人,参加语文竞赛的有28人,参加数学竞赛的有27人,如果两科都没有参加的有25人,那么同时参加语文、数学两科竞赛的有多少人?练习三1、一个旅行社有36人,其中会英语的有24人,会法语的有18人,两样都不会的有4人。
两样都会的有多少人?2、一个俱乐部有103人,其中会下中国象棋的有69人,会下国际象棋的有52人,这两种棋都不会下的有12人。
1.某班学生去图书室借书,每人都借了课外书,统计结果是:借语文书的有39人,借数学书的32人,语文、数学两种书都借的有26人。
全班学生共几人?
2.桥南小学三年级学生采集标本,采集昆虫标本的有27人,采集植物标本的有21人,两种标本都采集的有8人。
全班共有学生多少人?
3.一个班有学生54人,参加数学课外活动的有38人,参加语文课外活动的有29人。
至少有多少人两样活动都参加了?
4.某班36个同学在一次测验中,答对第一题的有25人,答对第二题的有23人,两题都答对的有15人。
问:有几个同学两题都不对,
5.一个班42名学生都订了报纸,订阅《中国少年报》的有32人,订阅《小学生报》的有27人。
有多少人订阅两种报纸?
6.有40名运动员,其中有25人会摔跤,有20人会击剑,有10人击剑、摔跤都不会。
问:既会摔跤又会击剑的运动员有多少人?
7.某校开运动会,参加比赛项目的人数如下:参加田赛的有26人,参加径赛的有30人,其中既参加田赛又参加径赛的有12人,田赛和径赛都没参加的有4人。
这个班共有学生多少人?
8.在50名出国人员中,有4人既不懂英语,也不懂日语,但其中有37人懂英语,有43人懂日语。
有多少人既懂英语又懂日语?
9.明明幼儿园大班里,会弹钢琴的有25人,会拉手风琴的有20人,既会弹钢琴又会拉手风琴的有15人,这两样都不会的有10人,这个班一共有多少人?
10.全班有50名同学,只参加数学小组的有27人,既参加教学小组又参加作文小组的有5人,两个小组都没参加的有4人,求只参加作文小组的有几人?
11.有50名同学参加了短跑和跳远的达标测试,短跑达标的有38名,跳远达标的有31名,两项都达标的有22名。
这两项都没达标的有几名?
12.学校田径队有40人上场参加比赛。
有18人参加田赛,有28人参加径赛,请问只参加田赛与只参加径赛的人数共是多少?
13.某班成立英语和微机小组,有25人参加英语小组,其中10人既参加了英语小组又参加了微机小组,没有参加微机小组的有18人。
请问有多少人两个小组都没参加?
14.某班52名同学,在一次测验中.答错第一题的有29人,答错第二题的有14人,这两道题都答对的有16人。
问有几个同学这两道题都没答对?
15.某班开展课外活动,每名学生至少参加一个小组。
参加文艺小组的有38人,参加体育小组的有32人,既参加文艺小组又参加体育小组的有12人,这个班一共有学生多少人?
16.某校先后举行了数学、语文、自然三科竞赛,参加竞赛时学生中,至少参加一科的有:数学498人,语文525人,自然499人;至少参加两科的有:数学、语文330人、数学、自然297人,语文、自然328人;三科都参加的有234人。
求参加竞赛的学生总数。
17.26名男同学中喜欢打篮球的13人,喜欢打排球的12人,喜欢踢足球的9人,既喜欢篮球又喜欢足球的有2人,既喜欢足球又喜欢排球的有3人,但没有一个男同学同时喜欢三种球类,也没有不喜欢任何一种球的。
有多少男同学既喜欢篮球,又喜欢排球?
18. 五一班30人有14人参加径赛,9人参加田赛,两项都没有参加的有12人,既参加径赛又参加田赛的有多少人?。