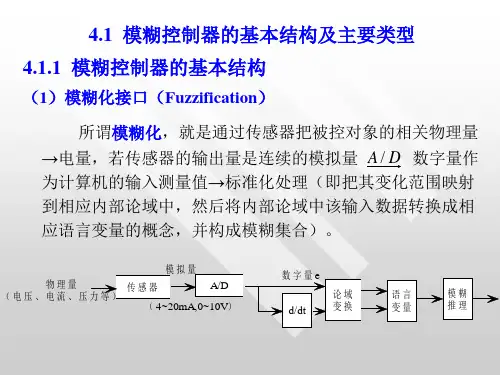
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
We can find from the above example that how does fuzzy mathematics describe the fuzzy conception in real world in the form of math. Using this method, we can handle the fuzzy conception in computer.
2.6.2 Operation of fuzzy relation
Characteristics of fuzzy relation:
1 自反性
x X
Every element in diagonal
R ( x, x) 1
of fuzzy matrix is 1.
RT R
2 对称性
Example 2.6.1 Two people have the fuzzy relations:
“similitude” 自反性(Y)对称性(Y)传递性(N) “enemy” “love”
自反性(N)对称性(Y)传递性(N)
自反性(Y)对称性(?)传递性(?)
“younger” 自反性(N)对称性(N)传递性(Y)
Example 2.5.1:
0.7 0.5 R 0.9 0.2
0.4 0.3 S 0.6 0.8
R S, R S, R ?
C
Notes: A fuzzy matrix and its complement are not complementary events similar with fuzzy sets.
3 Contain: R S R ( x, y) S ( x, y),( x, y) X Y 4 Equal:
R S R ( x, y) S ( x, y),( x, y) X Y
c
T
5 Complement: R Rc ( x, y) 1 R ( x, y),( x, y) X Y 6 Transpose: R R ( y, x) R ( x, y),( x, y) X Y
Y y1 , y2 ,, ym ~ An element rij in fuzzy matrix R means the relation between the ith element x i in X and the jth element y j
in Y .
~ R ( xi , y j ) rij
RU ( S T ) ?
0.4 0.3 S 0.6 0.8
(R S ) (R T ) ?
0.7 0.6 T 0.5 0.7
2.5.efinition:
R nm [0,1]
R (rij )
Example 2.5.5:
0.2 0.5 1 Q 0.7 0.1 0.8
0 .6 0.5 R 0 .4 1 0 .1 0 .9
Q R?
Notes: (popularly)
Q R RQ
(Q R) S (Q S ) ( R S )
2.5.4 Transpose of fuzzy matrix
2.5.1 Basic definitions of fuzzy matrix
If ( i n , j m ), there exist rij [0,1], then means R (rij ) nm is a fuzzy matrix. Usually, nm m all the fuzzy matrixes ( rows, lines). n
1 rij rij 0 rij
R
is called the support matrix of
R
.
Notes: The support matrix R is a Boolean matrix.
2.5.2 Support of fuzzy matrix
Example 2.5.4:
2.6.2 Operation of fuzzy relation
Example 2.6.2
1 0.2 0 R 0.2 1 0.1 0 0.1 1
1 0.2 0 1 0.2 0 1 0.2 0.1 R R 0.2 1 0.1 0.2 1 0.1 0.2 1 0.1 R 0 0.1 1 0 0.1 1 0.1 0.1 1
2.6.1 Definition of fuzzy relation
Fuzzy relation can described by fuzzy matrix when X and Y are finite set. When X Y , it is called the fuzzy relation in X .
CHAPTER 2 Fuzzy Mathematics
2.5 Fuzzy Matrix
2.6 Fuzzy Relation
2.5 Fuzzy Matrix
2.5.1 Basic definitions of fuzzy matrix
2.5.2 Support of fuzzy matrix 2.5.3 Composition of fuzzy matrix
sik (qij r jk ),1 i n,1 k l
j 1
m
The composition of fuzzy matrix is also called as multiplication of fuzzy matrix.
2.5.3 Composition of fuzzy matrix
2.6.2 Operation of fuzzy relation
R and S are two fuzzy relations in X Y .
1 Union:
R S [ R ( x, y), S ( x, y)],( x, y) X Y
2 Intersection: R S [ R ( x, y), S ( x, y)],( x, y) X Y
1
0.8 0.2
0.8
1 0.8
0.2
0.8 1
0.1
0.2 0.8
X
160 170
180
0
0.1
0.2
0.8
1
2.6.1 Definition of fuzzy relation
1 0 .8 R 0 .2 0 .1 0 0 1 0.8 0.2 0.1 0 .8 1 0 .8 0 . 2 0 .2 0 .8 1 0 .8 0 .1 0 .2 0 .8 1 0 .8 0 .2 0.1
( x, y) X X
R ( x, y) R ( y, x)
3 传递性
RR R
R ( x, z ) [ R ( x, y ) R ( y, z )]
y
( x, y), ( y, z ), ( x, z ) X X
2.6.2 Operation of fuzzy relation
Example 2.5.2:
O, E, R M nm
0.7 0.5 R 0.9 0.2
R R c , R RC ?
2.5.1 Basic definitions of fuzzy matrix
Example 2.5.3:
R, S , T nm
0.7 0.5 R 0.9 0.2
3 Complement:
R (1 rij ) nm
c
4 Contain: rij sij (i 1,2,, n; j 1,2,, m) RS 5 Equal:
rij sij (i 1,2,, n; j 1,2,, m)
RS
2.5.1 Basic definitions of fuzzy matrix
height and weight is in table.
2.6.1 Definition of fuzzy relation
Fuzzy relation between height and weight
~ R
140
Y
40 1 50 0.8 60 0.2 70 0.1 80 0
150
0.8
0.2 0.1
2.6.1 Definition of fuzzy relation
2.6.2 Operation of fuzzy relation 2.6.3 Composition of fuzzy relation
2.6.1 Definition of fuzzy relation
Relation: A subset R of a Cartesian product of X and Y , is called a dualistic relation from X to Y (or relation for short).
X x1 , x2 ,, xn
2.6.1 Definition of fuzzy relation
Example 2.5.6
X is the space of height in an area and Y is the space
of weight.
X ,150,160,170,180 ,(cm), 140 Y 40,50,60,70,80 ,(kg), the relation between
2.5.4 Transpose of fuzzy matrix