画组合图形(一)
- 格式:ppt
- 大小:547.50 KB
- 文档页数:18

第12课画组合图形(第一二课时)[教学目标与要求]1、知识与技能:确定画组合图形各部件的起始位置。
2、过程与方法:学生通过自我实践,进行总结提升。
3、情感态度价值观:让学生通过操作,明白图形的构成,需要合乎逻辑,形成一定的构图空间概念。
[教学重点和难点]确定画组合图形各部件的起始位置和角度的选择计算。
[教学准备] 网络机房[课时安排] 2课时[教学过程]第一课时五分钟打字练习一、激趣导入:T:出示房子图形!有哪些基本图形组成?S:正三角形——房子的屋顶正方形——房体长方形——门圆形——窗户T:这些基本的图形我们能不能画出来呢?可以T:复习正多边形,圆形的公式S:REPEAT N[FD L RT 360/N]REPEAT 36[FD L RT 10]设计意图:激发学生学习兴趣,复习旧的知识点。
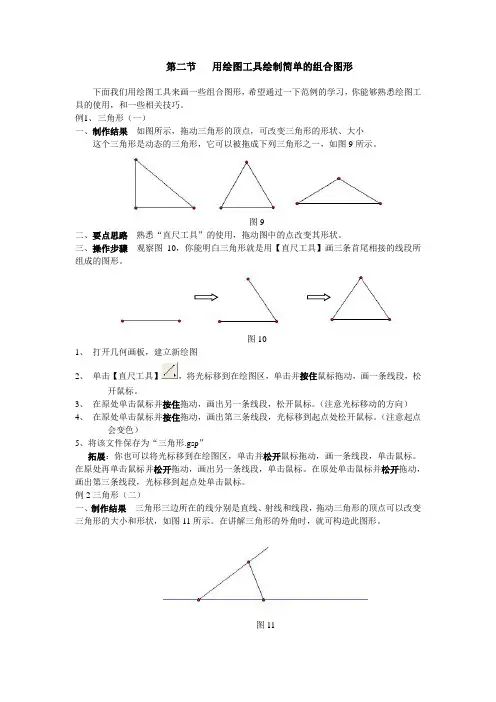
二、探究新知:T:那么如果把他们组合在一起,该如何画呢?下面我们来探讨一些。
S:好!T:确定画房顶的起始角度?S:RT 30T:画正三角形的屋顶S:REPEAT 3[FD 100 RT 120]T:将小海龟移动到画房体的位置和角度上S:RT 60 FD 10T:画正方形的房体S:REPEAT 4[FD 80 RT 90]T:将小海龟移动到画门的起始位置和角度上S:FD 80 RT 90 FD 80 RT 90 FD 10 RT 90T:画出长方形的门S:REPEAT 2[FD 55 LT 90 FD 25 LT 90]T:将小海龟移动到画窗户的位置上S:PU FD 50 LT 90 FD 60 RT 90 PDT:画窗户S:REPEAT 36[FD 2 RT 10]T:影藏海龟S:HT教学意图:通过师生一起操作,完成课本上的例题,引导学生如何画组合图形,重点解决起始位置和起始角度的选择和计算。
课堂练习一:尝试画出立方体。
教学意图:通过学生自主尝试,在实践中操作如何选择画组合图形的起始位置,解决角度的计算问题。

一年级6种图形拼一幅画《一年级 6 种图形拼一幅画》对于一年级的小朋友来说,用图形来拼画是一件既有趣又充满创造力的活动。
当我们给定六种图形,比如圆形、三角形、正方形、长方形、梯形和半圆形,小朋友们的小脑袋里就会开始涌现出无数奇妙的想法。
让我们先来看看圆形。
它圆润可爱,就像一个大大的笑脸。
小朋友们可以把它当作太阳,散发着温暖的光芒,照亮整个世界;也可以把它想象成一个大大的气球,带着小朋友们的梦想飘向远方。
三角形呢,尖尖的角,直直的边,充满了力量。
它可以是一座陡峭的山峰,勇敢的登山者在努力攀登;还可以是一顶漂亮的小帽子,戴在小朋友的头上,可爱极了。
正方形方方正正,规规矩矩。
它可以是一扇窗户,透过它能看到美丽的风景;也能变成一个小盒子,装满了宝贝和秘密。
长方形长长的,扁扁的。
它像是一张舒适的小床,让我们在上面做着甜甜的梦;又或者是一块大大的黑板,老师在上面写下知识的宝藏。
梯形就像一个滑梯,小朋友们快乐地从上面滑下来,笑声回荡在空中;它还可以是一艘小船,在波涛中勇敢前行。
半圆形,就像被切开的大西瓜,甜甜的汁水让人垂涎欲滴;也像弯弯的月亮,在夜空中陪伴着我们进入梦乡。
当把这六种图形组合在一起的时候,一幅充满想象力的画就诞生啦。
比如说,我们可以用一个圆形当作小朋友的脸蛋,两个三角形当作耳朵,一个正方形当作身体,两个长方形当作手臂,一个梯形当作裙子,一个半圆形当作帽子。
这样,一个可爱的小朋友就出现在我们的画里啦,她正欢快地在花园里玩耍,周围是五颜六色的花朵和飞舞的蝴蝶。
又或者,我们用一个大大的圆形当作地球,三角形当作山峰,长方形当作河流,梯形当作田地,半圆形当作彩虹,正方形当作房子。
这样就构成了一个美丽的地球家园,人们在这里快乐地生活着,与大自然和谐共处。
再比如,我们把圆形当作车轮,三角形当作车篷,长方形当作车身,梯形当作道路,半圆形当作路灯,正方形当作交通指示牌。
一幅热闹的街道景象就展现在眼前,车辆来来往往,行人匆匆忙忙。

第5章组合和对齐1、组合对象:修改-组合(Ctrl+G),取消组合(ctrl+shift+G).组合的对象不会放在库里。
先组合的对象放在下层,后组合的对象放在上一层。
直接画组合图形:选择绘图工具,再选择工具箱里的最下面的“紧贴至对象”,即可直接绘制组合对象。
2、对齐面板(ctrl+k):使用对齐命令,至少要有2个对象。
对齐、分布、匹配大小、间隔和相对于舞台。
5-1实例(电影胶片)操作步骤:1)舞台白色背景,黑色边框,红色镂空小方块。
2)整体打散,删除红色小方块。
制作胶片边框。
3)在胶片边框里画矩形。
4)将图片导入到库里。
每个矩形里插入图片。
5)第120帧处插入关键帧,移动胶片位置,设置传统补间。
5-2实例(球体滚动)操作步骤:1)舞台中间画矩形,设置渐变色。
调整到与舞台合适大小,锁定图层。
2)新建图层,绘制网格线,调整角度,旋转45度(ctrl+t)打散。
3)选中物体,选择“任意变形工具”,按”shift+ctrl”拖动光标,调整透视效果。
(超出舞台的部分不会显示)。
4)新建球体图层,绘制球体,调整颜色和高光点。
转换成图形元件。
5)阴影:复制球体,垂直翻转(因为高光点位置正好相反),调整不透明度。
6)复制球体调整大小。
7)新建图层,做动态球体。
15帧插入关键帧,移动球体,调整大小。
第29帧与第1帧相同大小。
插入传统补间。
8)运动球体的倒影:新建图层,复制1帧15帧和19帧内容调整位置和高光点。
插入传统补间。
注意:静止的画面的图层可以合并成一个图层。
Ctrl+x,ctrl+shift+v。




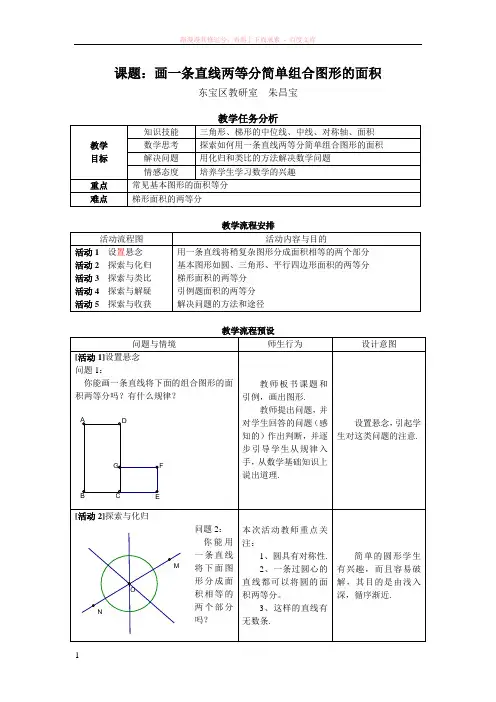
课题:画一条直线两等分简单组合图形的面积东宝区教研室 朱昌宝教学 目标 知识技能三角形、梯形的中位线、中线、对称轴、面积 数学思考 探索如何用一条直线两等分简单组合图形的面积 解决问题 用化归和类比的方法解决数学问题 情感态度培养学生学习数学的兴趣重点 常见基本图形的面积等分 难点 梯形面积的两等分教学流程安排活动流程图 活动内容与目的活动1 设置悬念 活动2 探索与化归 活动3 探索与类比 活动4 探索与解疑 活动5 探索与收获 用一条直线将稍复杂图形分成面积相等的两个部分 基本图形如圆、三角形、平行四边形面积的两等分 梯形面积的两等分 引例题面积的两等分 解决问题的方法和途径问题与情境师生行为 设计意图[活动1]设置悬念 问题1:你能画一条直线将下面的组合图形的面积两等分吗?有什么规律?教师板书课题和引例,画出图形.教师提出问题,并对学生回答的问题(感知的)作出判断,并逐步引导学生从规律入手,从数学基础知识上说出道理.设置悬念,引起学生对这类问题的注意.[活动2]探索与化归问题2: 你能用一条直线将下面图形分成面积相等的两个部分吗?本次活动教师重点关注:1、圆具有对称性.2、一条过圆心的直线都可以将圆的面积两等分。
3、这样的直线有无数条.简单的圆形学生有兴趣,而且容易破解,其目的是由浅入深,循序渐近.EDAB CG FOMN问题与情境师生行为 设计意图问题3:你能用一条直线将下列图形的面积两等分吗?说明理由.[活动3]探索与类比用一条直线两等分矩形、正方形的面积.本次活动教师重点关注:1、两等分三角形的面积至少有三条,目前学生易接受理论支撑是“等底等高的两个三角形面积等积”..2、平行四边形两等分面积只要找到中心对称点,任意过对称中心点的直线都可以将其面积两等分,这样的直线有无数条.3、引导学生关注两等分平行四边形的数学基础知识(分析思路和说理是重点).4、用类比的思想讨论矩形和正方形两等分面积.三角形和平行四边形(含短形和正方形)也是最简单的图形,其目的在于找规律,说理由,用类此的思想同时解决矩形和正方形的等分问题,有一般包涵特殊的思想.问题4:讨论,是否过梯形的O 点作任意一条直线就可以将梯形的面积两等分 教师关注要点: 1、梯形中位线不能将梯形面积两等分(直观法或等高不等底的两个梯形面积不相等).2、过梯形两底的中点的连线可以将梯形面积两等分,为什么? 突出转化的思想,把梯形转化为三角形和平行四边形来考虑,一方面培养学生解决问题的途径(化难为易,应用旧知),另一方面又加强了知识简单的相互联系,灵活运用,达到开发思维的目的.编制这一个活动,给出了两种方法,再对梯形的一般性进行研究,特别是“过上、下底且经过梯形中位线的中点”这三个要素进行讨论,有利于培养学生思维的缜密和严谨,方法一:作梯形的中位线能等分两个相等的面积吗?为什么?3、取AB 中点E ,连接BE 交CB 的延长线于F ,由于S △ADE =S △FBE ,再作FC 中点G ,直线DG 将梯形面积两等分(学生说明理由).方法二:把梯形转化为三角形来等分GFEA C BDDBACODACBF E A CB D方法三:作AD 、BC 中点的连线A CBD4、学生说明理由有利于培养学生在特殊圆形中求一般规律,在一般图形中求特殊解法.举反例是一种反证思想,培养学生发散思维,求异思维,对于问题的理解将更加深入.方法四:把梯形转化为平行四边形来等分5、同转化为三角形道理一样(学生说明理由).方法五:取中位线的中点,在什么条件下作一直线将梯形面积两等分?6、条件:过上下底边并且经过中点的直线可以将梯形面积两等分(要求学生从多个角度说明理由).7、讨论:两等分平行四边形和梯形有什么不同?在条件上有哪些限制,举反例.问题先简单后复杂,解题先易后难,加强思维培养,提高解题能力.[活动4]探索与解疑 解答引例O 2O 1EDABCGF方法一:作两矩形的对角线,两交点O 1O 2连接的直线即为所作.学生实践、教师关注要点:把这个组合图形分成两个基本图形,再利用以上所学的结论(分开看). 基于以上活动、支手实践和规律探索,学生基本上可以从方法一、方法二中解决问题,对于方法三和利用梯形存在困难,因此观察图形特点,从“分”和“补”两个方面通盘考虑问题,使问题的解决更加灵活,手段更加多样,道理更加充分,思路更加清晰. 通过交流,让学生用自FGE A CBDE FA CBD方法二:作两矩形的对角线,两交点O 1O 2连接的直线即为所作.己的语言清楚表达解决问题的过程,提高语言表达能力.方法三:作矩形ABEH 和矩形GFHD 的对角线,O 1O 2所在的直线平分这个组合图形补全图形,从整体入手。
《图形的拼组》教学设计龙玉娥教学目标:1、知识与技能:通过拼、摆、画等活动,让学生进一步感受三角形的特征及三角形与四边形的联系与区别。
2、过程与方法:通过学生的观察、操作,发展学生的动手操作能力、空间想象力和创造力,培养学生动手实践的能力。
3、情感、态度与价值观:学生通过拼摆图形,感受数学之美,激发学生学习数学的积极性。
教学重点:通过欣赏和动手操作,感受三角形与其他图形的关系。
教学难点:发展动手操作能力,空间想象力和创造力。
教学用具:锐角三角形、直角三角形、钝角三角形。
教学过程:一、创设情境1、老师:这几天,我们认识了一位图形王国里的新朋友,它是谁?谁来给大家介绍介绍这位朋友?2、我带来了三角形的双胞胎兄弟,它们是完全一样的三角形。
二、活动一:用同样大小的三角形可以拼出什么图形?1、自主尝试拼摆。
先把同样的三角形分类,再尝试拼一拼,看谁拼出的图形多。
2、汇报展示,师生评议。
师:从你们拼出的图形中发现什么?说明什么?任何两个相同的三角形都可以拼成一个四边形。
3、提问:三角形和四边形有什么不同?4、课件出示四边形,提问:这些图形是由什么样的三角形拼成的?三、活动二:设计图案1、激趣导入:我们认识了三角形、长方形、正方形、圆这些平面图形,你们知道吗,利用这些图形的组合,可以创造出许多有趣、美丽的图案,下面我们来欣赏一幅图。
2、师出示图案:问:看一看它们像什么?它们都是由哪些图形组成的?给这幅图取个什么名字呢?学生回答后,教师说一说这个“守株待兔”的故事,并把寓意讲明。
师:你们瞧,有趣吧。
你们想不想自己也来动手拼一些有趣,漂亮的图案呢?3、各小组拿出学具袋。
(袋内装有各种三角形纸片)师:请各小组把袋子里的图形拿出来,根据老师所给的材料来拼图。
请各小组的同学一起动手来拼一拼。
学生拼图时,教师巡视,加以指点。
4、展示作品,师生评议。
(1)各小组的作品粘贴在黑板上,并给各组的作品起一个好听的名字。
(2)请学生根据图意来组合一下图形,把各组的作品放到你认为的最佳的位置。
第11课组合图形[教学目的与要求](1)学习“直线”、“曲线”等工具的利用方式。
(2)能在图形需要的地址画出一些线条。
(3)通过画,让学生感受图形整体完成的步骤。
(4)让学生在画的进程中,感受图形的整体性,从而培育学生的整体感、大局观。
[课时安排]建议安排2课时。
[教学重点与难点]“直线”、“曲线”等工具的利用方式。
[教材分析与教法建议]一、教材的地位与作用本课要紧介绍“直线”和“曲线”工具的利用方式,但教材并无孤立的讲这两种工具,而是把它们有机的和前面学习过的圆形、方形等结合起来。
如此使教材前后章节彼此联系,使前面学过的知识能学为所用。
教材共分三个部份,第一部份,画洗衣机的机身,先选择“矩形”、“椭圆”等工具画洗衣机的机身,这两种工具都是学生已经熟练把握的,学生应该比较快速的就能够完成了。
然后选择“直线”工具去画机身的其它部份,尽管“直线”是新学习的工具,可是由于学生有前面几节课的学习体会,因此应该不难把握。
“讨论坊”中若是精准画出水平或垂直直线的问题,学生应该能够速度的取得答案。
而“探讨园”中如何画出粗一些的圆形或方形的问题,关于学生来讲可能有一些困难,教师应该加以引导。
第二部份,用“曲线”工具画洗衣机的波浪线和排水管,对学生来讲有必然的难度,教材专门安排了一个画曲线的练习,教师在讲解演示操作后,应该给学生充分的练习时候,并要求学生练习多种曲线。
若是曲线练习得比较到位,那么画波浪线和排水管就会迎刃而解了。
第三部份,用“矩形”、“椭圆”等工具画开关和把手,是对旧知识的应用,学生应该很容易就能够完成。
二、教学方式指导本课介绍了两种工具,其中直线工具,关于已经有了“椭圆”、“矩形”等工具学习体会的学生来讲,应该是比较容易把握的,教师只需略加引导,学生便能完成。
而“曲线”工具,对学生来讲,应该是有必然的困难的。
教师要讲清讲透,并做好演示操作,同时应该给学生充分的练习时刻。
本课是讲课的进程中,还应该注意培育学生对一个图形整体概念的把握。
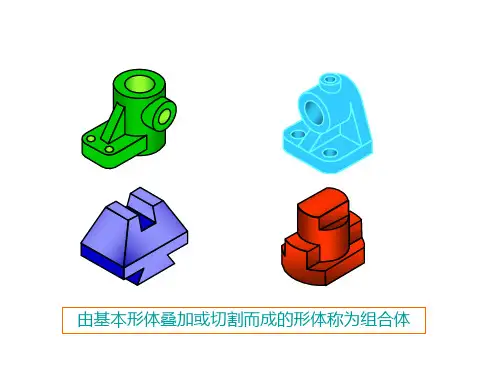
教学内容:组合图形的面积(第九册第五单元)教学目标:1、学生能了解组合图形面积的计算方法,会计算一些比较简单的组合图形的面积。
2、加深对平面图形的认识,培养学生的空间观念。
3、培养学生交流合作及创新意识。
教学重点:掌握计算组合图形的方法教学难点:如何把组合图形变成自己已学过的平面图形即如何合理分解来计算面积.。
(一)情境导入。
师:同学们玩过七巧板吗?(学生举手示意,几乎所有的学生都玩过。
)(评析:学生从幼儿园时代就开始接触七巧板,教师从七巧板入手,容易激发学生的学习兴趣。
)师:(电脑出示以下图形)这些就是用七巧板拼出的图形,你觉得分别像什么?它分别是由什么图形组成的?(二)认识组合图形。
1、拼画组合图形师:我们已经学习了五种平面图形,请同学们从这些简单的平面图形中挑几个,拼画成一个较复杂的图形,并想想你拼画的图形像什么?给大家两分钟时间看谁画得多(学生独立画拼)师:谁愿意把你拼的图形展示给大家?(学生用实物投影展示拼出的图形,并说说像什么。
)师:同学们展示的这些图形有什么共同特点呀?生:我发现这些图形都是几个图形拼出来的。
生:这些复杂的图形都是用几个简单图形拼成的。
师:我们把这样的图形叫做组合图形。
(板书:组合图形)在日常生活中,还见过哪些物体表面是组合图形呢?老师也带来一些资料(三)探索简单组合图形面积计算方法。
1、师:你能算出自己拼出的组合图形的面积吗?生:用三角形的面积加上长方形的面积就行了。
……师:同学们用的方法有什么相同之处?生:都是把几个简单图形的面积加起来。
师:今天这节课我们就一起来研究组合图形的面积(出示课题)2、教师出示下列图形(单位:米):同学们在生活中有没很多这样由几个简单图形拼成的物体平面师:这是小华家客厅地面的平面图,现在准备在客厅铺上木地板。
小华的爸爸说:“你已经上五年级了,算算至少要买多少平方米的地板吧。
”小华接受任务就开始思考,可他发现客厅的形状不是学过的平面图形。