偏振光干涉的相位

偏振光干涉实验报告偏振光实验报告实验1. 验证马吕斯定律实验原理：某些双折射晶体对于光振动垂直于光轴的线偏振光有强烈吸收，而对于光振动平行于光轴的线偏振光吸收很少(吸收o光，通过e光)，这种对线偏振光的强烈的选择吸收性质，叫做二向色性。

具有二向色性的晶体叫做偏振片。

偏振片可作为起偏器。

自然光通过偏振片后，变为振动面平行于偏振片光轴(透振方向)，强度为自然光一半的线偏振光。

如图 P1、图2所示：P1 P2 图1 图2 θA 0 图1中靠近光源的偏振片P1为起偏器，设经过P1后线偏振光振幅为A0（图2所示），光强为I0。

P2与P1夹角为?,因此经P2后的线偏振光振幅为A?A0cos?，2光强为I?A0cos2??I0cos2?,此式为马吕斯定律。

实验数据及图形：从图形中可以看出符合余弦定理，数据正确。

实验2.半波片，1/4波片作用实验原理：偏振光垂直通过波片以后，按其振动方向（或振动面）分解为寻常光（o光）和非常光（e光）。

它们具有相同的振动频率和固定的相位差（同波晶片的厚度成正比），若将它们投影到同一方向，就能满足相干条件，实现偏振光的干涉。

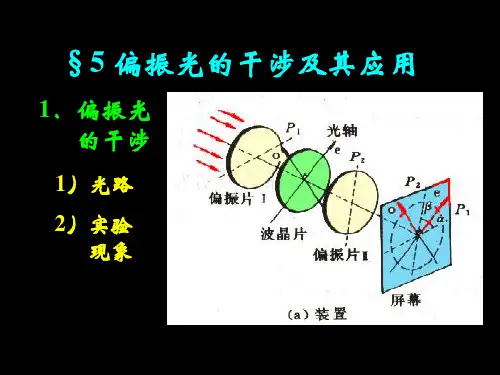
分振动面的干涉装置如图3所示，M和N是两个偏振片，C是波片，单色自然光通过M变成线偏振光，线偏振光在波片C中分解为o光和e光，最后投影在N上，形成干涉。

偏振片波片偏振片图3 分振动面干涉装置考虑特殊情况，当M⊥N时，即两个偏振片的透振方向垂直时，出射光强为：I0(sin22?)(1?cos?)；当M∥N时，即两个偏振片的透振方向平行时，出射4I0(1?2sin2?cos2??2sin2?cos2?cos?)。

其中θ为波片光轴与M2I??光强为：I//?透振方向的夹角，δ为o光和e光的总相位差（同波晶片的厚度成正比）。

改变θ、δ中的任何一个都可以改变屏幕上的光强。

当δ=（2k+1）π（1/2波片）时，cosδ=-1，I??强最大，I//?02sin22?，出射光I0(1?sin2?)2，出射光强最小；当δ=[（2k+1）π]/2（1/4波片）时，cosδ=0，I??I0I(sin22?),I//?0(2?sin22?)。

偏振光干涉演示实验原理嘿，你有没有想过光是一种超级神奇的东西？就像一个神秘的小精灵，有时候它的行为真的很让人捉摸不透呢。

今天我就来给你讲讲偏振光干涉演示实验原理，这可太有趣啦。

我记得我第一次接触这个实验的时候，我和我的小伙伴们都惊掉了下巴。

我们就像一群在宝藏面前的小探险家，充满了好奇和兴奋。

老师站在前面，拿着那些实验仪器，就像是一个魔法师拿着他的魔法道具。

那我们先来了解一下什么是偏振光吧。

你可以把光想象成一群小蚂蚁在行军，普通的光呢，这些小蚂蚁是朝着各个方向乱走的。

但是偏振光就不一样啦，偏振光里的这些小蚂蚁啊，都朝着同一个方向整齐地前进，就像训练有素的士兵方阵。

这是怎么做到的呢？其实啊，有一些特殊的材料或者装置，就像是一个指挥棒，把那些乱走的小蚂蚁梳理得整整齐齐。

好啦，现在我们知道了偏振光，那偏振光干涉又是怎么回事呢？这时候啊，我们就得再引入一些新的角色啦。

比如说有两块偏振片，我们可以把它们想象成两个严格的守门人。

第一块偏振片呢，它只允许某一个方向偏振的光通过，就像是一个只让特定着装的士兵通过的门。

经过第一块偏振片的光，已经变成了方向整齐的偏振光啦。

然后这束偏振光就会遇到下一个情况。

假如中间还有一个双折射晶体，这个双折射晶体可就像一个神奇的迷宫。

偏振光进入这个迷宫后，会被分成两束光，这两束光就像两个双胞胎，但是它们之间又有一点点小差别。

这两束光沿着不同的路径在晶体里走，就像两个小伙伴在迷宫里选择了不同的路线。

当这两束光从晶体里出来后，它们又会遇到第二块偏振片。

这个第二块偏振片就像又一个考验。

这时候啊，这两束双胞胎光又要经历一些变化。

它们会叠加在一起，就像两个小伙伴又走到了一起，手拉手。

那为什么会发生干涉呢？你看啊，这两束光在经过双折射晶体的时候，它们走的路程不一样，就像两个人跑步，一个跑了直道，一个跑了弯道。

这样它们就有了一个路程差。

这个路程差会导致它们的相位发生变化，就像两个人跑步的节奏不一样了。

偏振光干涉的相位差2001年9月第20卷第3期抚州师专JournalofFuzhouTeachersc姆Sept,2001V01.20N0.3偏振光干涉的相位差黄仁忠,王爱星(抚州师范专科学校物理系,江西抚州344o00)摘要:关于偏振光干涉的相住差有两类车同的算法,文章对此进行了对比讨论,指出正璃掌握两类算法中对各项取值的不同规定,避免发生错谥.关键词:偏振光;干涉;相住差中图分类号:0436文献标识码:A文章编号:1(3Ol一635X(20O1)o3一O023一位在两块偏振片P,B之间插入一块光轴平行于晶面的晶片,平行的自然光从P.垂直射人,出射光为线偏撮光,设其光矢量为EI,进入晶片后分解为.光和e光,设其光矢量为和E.再经得到两个光波场,设其光矢量为和,它们相干叠加.关于这两个光波场的相位差△的计算.主要有以下两类表述:=△朔+性(1)/"9=.△+朔+懒(2)式中△是刚进入晶片时.光和e光的相位差,△僻=竿(nu一)d,是.光和e光穿过晶片后产生的附加相位差,△是对投影时引起的相位差.(2)式比(1)式多出一项△,但两式对△伽取值的规定不同,最后结果仍然是一致的.如果不注意区别两式对伽取值的规定,必然导致错误的结果.采用(1)式时,相当于取△=O.关于△的取值,有的教材这样规定:当B,B处于不同象限时(如图1).取△性=;当P-,处于同一象限时(如图2),取△=0….有的教材则采用另一种表述:当晶片光轴位于P_,Pz之问时(即,分居e轴两侧),取△=;当晶片光轴位于,之外时(即P_,B同居e 轴一侧),取△恤=.从以上两图中不难看出.这两种表述是完全一致的其实还可以更直观地表述为:当卫和方向相反时,取△性=,当骂和方向相同时,取△=o】.若采用(2)式计算,当在一,三象限时.取△=o,当EI在二,四象限时,取△^=_|】当e轴和0轴的正方向对轴的两个投影分量方向一致时,取△性=0,当这两个投影分量方向相反时,取△=.】.图1q~Ag/.=0,△性=;图2中△=0,△=O.在这两种情况下,(2)式所得结果都与(1)式相同.然而,e轴和0轴本身并投有正负方向之分,其正负方向完全是建立坐标系时人为约定的.分析发现.这个方向的约定会同时影响在哪个象限及e轴和0轴正方向对P2轴两个投影分量的方向,也就是说.会同时影响△和△啦的取值.因而,△+△伽的值就与e轴和0轴正方向的设定无关,也就使(2)式和(1)式所得结果能始终保持一致.对于如图1所示的情况,P】,B分居e轴两侧,我们将e轴,0轴的正方向作各种不同的设定,从图3,图4,收撬日期:~0Ol一03—29作者简介:黄仁忠(1944一),男,江西临川人,抚州师范专科学校物理系副教授王爱星(1975一),男,江西东乡人,抚州师范专科学校物理系助教图5中可以看到,△和△必有一个为零,另一十为,总有△+△性=,都与(1)式的结果相同.田3中B在第二象限.图4中E在第四象限,两图中e轴,0轴正方向对的投影分量方向都相同,所以柞得到△甲^=,△靴=O;图5中B在第三象限,而t轴,o轴正方向对的投影分量方向相反,于是有△郸=0,图1图2P图3图4△蚋t.对于如图2所示的情况,PI,同居e轴一侧,可以看到,不管e轴,o轴正方向如何设定.△和△恤必同时为(如图6,图7)或同时为零(如图8),总有△+△午=0或h,也都与(1)式的结果相同.值得注意的是,(1)式和(2)式中对△慨取值的规定.是不能混淆的.有的教材采用(2)式计算,△的规定正确,但对于△的取值却是这样规定:若卫和.同方向.则△=0,反方向则△倾=,㈨这显然又采用了(1)式的规定,对于△=0的情况尚不致于出错,但对于△=的情况(如图3,4,6,7),结果却是错图5圉6固,圈B误舯.练上所述.若采用(1)式,△是指和对投影引起的相位差,由这两个投影的方向是否相同来决定取值;若采用(2)式,△是指e轴和.轴的正方向(特别要强调是正方向)对投影引起的相位差.由这两个投影的方向是否相同来决定取值,这是不容混淆的.[参考文就】[1】昊强,郭光灿.光学【M].夸肥:中国科学技术七学出版社,1996.321—322.[2]邦永康,鲍培谛.光学教程[M].成都:四川太学出版社,I992.315.[3]榘绍蒙,刘昌年.盛正华.普通拍理学(第4分册)[M].北京:高等教育出腹社,1994242.[4]赵凯华,钟蠕华.竞学(下册)[M].北京:北京戈学出版社,|984.203—2O4.[5】陈为彰,胡学瑷,刘惠国.光学[M].北京:北京师范大学出版社,1989.307—398. PhaseDifferenceofPolarizedLightInterferenceHUANGRen.z.hong,WANGAi.xing(,Fm/mu如,Fud~ou3㈣,‰)Abstract:There'retwokindsofdifferentcountingmethodsconcerningthep}1asedifference ofp0laltinterferenceinvariousopticalteachingmaterials.1l1earticlehasraisedacomoarabledisct mianaboutit,Ilgolltthe,ightgraspofallkindsofdifferentquotasofsamplingintwokindsofe0.删E llllIods.Soas10avoidthemistakes.脚1^一.s:p0lazedlight;interference;pl1asedifference24。

偏振光干涉中o 光和e 光的相位以课件上的问题为例：设单色平面光波沿z 方向传播，即k //z ：1. 在偏振片P 1之后，晶片C 之前的光场是： )2cos(11z t e A E P λπω−=r r现在事先把它分解为o 光和e 光：)2cos()()2cos()(11e e 1o o 1z t e e e Az t e e e A E P P λπωλπω−⋅+−⋅=r r r r r r r （1）这里1P e r 是沿偏振片P 1的偏振方向的单位矢量，o e r 和e e r是o 光和e 光偏振方向的单位矢量，。

上图表示出了所有的单位矢量，它们都在x －y 平面内。

原则上讲，这些单位矢量的方向是可任意规定的，影响的只是它们之间点积的正负，但为了保证现在的o 光和e 光没有相位差，即cos 函数内不出现π（如果o e r 沿图中的反方向定义，就会引起这个π），则o e r 、e e r 与1P e r应保持上图所示关系。

在上图的规定中，αcos )(1e =⋅P e e r r ，αsin )(1o =⋅P e e rr 。

2. 在晶片C 之后，偏振片P 2之前的光场是：)2cos()()2cos()(11e e 1o o 1z t e e e A z t e e e A E P P λπωδλπω−⋅++−⋅=r r r r r r r （2）与（1）式不同的是，（2）式中的o 光和e 光有了相位差δ，这是由晶片引起的。

这时一般yzkx合成为椭圆偏振光。

3. 在偏振片P 2之后的光场是（对o 光和e 光，只有沿P 2方向的分量可通过）：)2cos())(()2cos())((212212e e 1o o 1z t e e e e e A z t e e e e e A E P P P P P P λπωδλπω−⋅⋅++−⋅⋅=r r r r r r r r r r r 这时的情况是：振动都沿同方向－2P e r方向的、相差恒定的两个波叠加，故可产生干涉。

偏振光相位差和偏振光形态偏振光是指在特定方向上振动的光线，它在某一方向上的电场振动分量远大于其他方向上的分量。

而偏振光的相位差和形态则是与其振动方向和传播路径密切相关的。

让我们来了解一下偏振光的相位差。

相位差是指两束光线之间的光程差，也就是两束光线的振动波峰与波谷之间的间隔。

当两束光线的相位差为0时，它们的振动方向完全一致，我们称之为相干光。

而当相位差为π时，它们的振动方向完全相反，我们称之为相消光。

在介质中，偏振光的相位差可以通过材料的特性来调节，例如液晶材料可以通过电场的作用来改变其相位差。

接下来，我们来探讨一下偏振光的形态。

偏振光的形态可以分为线偏振光、圆偏振光和椭圆偏振光三种。

线偏振光是指振动方向固定的偏振光，它的电场振动方向可以是水平的、垂直的或者在两者之间的任意方向。

圆偏振光是指振动方向随时间变化的偏振光，它的电场振动方向在二维平面上沿着一个圆形轨迹旋转。

椭圆偏振光是指振动方向随时间变化的偏振光，它的电场振动方向在二维平面上沿着一个椭圆形轨迹旋转。

这些不同形态的偏振光可以通过适当的装置来产生和调节，例如偏振片和波片等。

偏振光的相位差和形态对于光学应用具有重要意义。

在光学显微镜中，通过调节偏振片的相对方向，我们可以观察到不同形态的偏振光对样品的影响，从而获得更多关于样品的信息。

在光通信中，通过调节偏振器的相位差和形态，我们可以实现光信号的调制和解调，以实现高速、高容量的光传输。

除了应用领域，偏振光的相位差和形态也对于光的本质研究具有重要意义。

在量子力学中，偏振光的相位差和形态可以用来研究光的量子特性，例如光的自旋和角动量等。

在光学实验中，通过调节偏振光的相位差和形态，我们可以探索光在不同介质中的传播规律和相互作用机制，从而深入理解光与物质的相互关系。

偏振光的相位差和形态在光学领域中起着重要作用。

通过调节偏振光的相位差和形态，我们可以实现光的调制和解调，观察样品的细节，研究光的量子特性，探索光与物质的相互关系。

偏振光干涉演示仪实验现象及原理
偏振光干涉演示仪是一种实验装置，用来观察和研究光的干涉现象，通过控制偏振光的传播方向和振动方向，可以展示出不同的干涉图案。

实验现象：
当一个偏振光束通过一块光学材料（例如长方形玻璃片）时，光束会被分解为两个平行振动方向的偏振光束。

当这两个偏振光束再次叠加在一起时，它们会发生干涉，形成一系列明暗相间的干涉条纹。

这些干涉条纹的形状和分布规律取决于入射光的偏振方向、材料的性质以及材料的厚度。

通过调节偏振光的传播方向和振动方向，可以观察到不同形态的干涉条纹，例如等厚干涉条纹、牛顿环等。

实验原理：
偏振光具有特定的振动方向，其中只有与振动方向垂直的分量能够通过垂直入射的偏振片。

当入射光束通过一块光学材料时，材料会引起光的相位差和干涉效应。

在材料中，光的振动方向可能会发生改变，导致两束偏振光发生相位差。

当这两束光再次叠加时，相位差会导致干涉，形成明暗相间的干涉条纹。

通过改变偏振片的方向和材料的厚度，可以调节相位差，从而
改变干涉条纹的形状和分布。

这样可以用来研究光的干涉现象、材料的光学性质以及光学材料的厚度测量等。

光的干涉、衍射和偏振
1．光的干涉
(1)定义：在两列光波叠加的区域，某些区域相互加强，出现亮条纹，某些区域相互减弱，出现暗条纹，且加强区域和减弱区域相互间隔的现象．
(2)条件：两束光的频率相同、相位差恒定．
(3)双缝干涉图样特点：单色光照射时形成明暗相间的等间距的干涉条纹；白光照射时，中央为白色亮条纹，其余为彩色条纹．
2．光的衍射
发生明显衍射的条件：只有当障碍物的尺寸与光的波长相差不多，甚至比光的波长还小的时候，衍射现象才会明显．
3．光的偏振
(1)自然光：包含着在垂直于传播方向上沿一切方向振动的光，而且沿着各个方向振动的光波的强度都相同．
(2)偏振光：在垂直于光的传播方向的平面上，只沿着某个特定的方向振动的光．
(3)偏振光的形成
①让自然光通过偏振片形成偏振光．
②让自然光在两种介质的界面发生反射和折射，反射光和折射光可以成为部分偏振光或完全偏振光．
(4)光的偏振现象说明光是一种横波．
第1页共1页。

偏振光相位差和偏振光形态偏振光是指在传播过程中，电场振动方向固定的光。

相位差则是指两个光波的相位差异，而偏振光的形态则是指其电场振动方向的特点。

在本文中，我们将探讨偏振光相位差和偏振光形态对光学现象的影响。

在自然界中，光的传播方向是无规律的，因此光是非偏振光。

而当光通过某些介质或经过特定的装置时，光的电场振动方向会被限制在某个特定的方向上，这就形成了偏振光。

偏振光的电场振动方向可以是任意方向，我们通常将其分为水平偏振光和垂直偏振光。

当两束具有不同偏振方向的光波相遇时，它们之间就会存在相位差。

相位差可以通过两个光波的振幅和频率之差来计算。

相位差的大小和符号决定了光波相互叠加后的结果。

当两束相位差为0的偏振光相遇时，它们会叠加形成一个更强的光波，这种现象称为相长干涉。

相长干涉可以在干涉仪中观察到，例如杨氏双缝干涉实验中的干涉条纹。

相位差为π的偏振光相遇时，它们会互相抵消，形成一个几乎没有光的区域，这种现象称为相消干涉。

相消干涉可以在干涉仪的暗条纹中观察到，例如杨氏双缝干涉实验中的暗条纹。

除了相位差的大小，偏振光的形态也会对光学现象产生影响。

在偏振片中，只有与偏振方向一致的偏振光才能通过，其他方向的偏振光则被吸收或折射。

这种特性使得偏振片可以用于光的偏振分析和光的消光实验中。

偏振光的形态还可以通过偏振光的强度和相位来描述。

例如，当偏振光的电场振动方向呈正弦函数变化时，我们称之为线性偏振光。

线性偏振光可以通过偏振片实现，其中振动方向与偏振片的主轴方向一致。

除了线性偏振光，还有圆偏振光和椭圆偏振光。

圆偏振光的电场振动方向呈圆周运动，可以通过光学元件如四分之一波片来实现。

椭圆偏振光的电场振动方向呈椭圆形，可以通过光学元件如椭偏振片来实现。

偏振光相位差和偏振光形态的研究在实际应用中具有重要意义。

例如，在光学通信中，对偏振光的分析和处理可以提高光信号的传输质量和容量。

在显微镜和光谱学中，对偏振光的形态和相位差的研究可以帮助我们获取更多关于样品的信息。

光的偏振和光的相干性光是一种电磁波，它在空间中传播时具有许多特性，其中包括偏振性和相干性。

光的偏振是指光波中电场矢量振动方向的特性，而光的相干性则是描述光波的波动性质。

在本文中，我们将探讨光的偏振和光的相干性的基本原理和应用。

一、光的偏振偏振是指光波传播方向上电场矢量振动的方向。

普通光是由各种方向的振动电场组成的，它们沿着传播方向均匀地振动，具有各向同性。

然而，当光波经过某些介质或通过特定的装置时，电场矢量的振动方向可能被限制在特定平面内，这种光就称为偏振光。

偏振光可以通过偏振片生成，偏振片可以选择性地通过特定方向的振动电场分量，而阻止其他方向的分量通过。

偏振片可以是线偏振片或圆偏振片。

线偏振片只允许特定方向上的电场分量通过，而将其他方向上的分量阻止。

圆偏振片则将电场分量限制在特定方向上的圆轨迹上。

这种偏振光的产生使得光的传播和使用更加灵活和便捷。

偏振光的应用广泛，例如在摄影和电子显示领域。

在摄影中，通过使用偏振片可以减少反射和增强颜色的饱和度，从而获得更加清晰和真实的图像。

在电子显示中，液晶显示器使用偏振片来控制光的传播方向，从而实现图像的显示和调节。

二、光的相干性光的相干性描述了光波的波动性质和波动传输过程中不同分量之间的关系。

相干光是指具有一定关系的振幅和相位的光波。

相干性可以分为时域相干性和空域相干性。

时域相干性是指光波的振幅在时间上保持稳定和一致的特性。

对于完全相干的光，它的振幅在时间上保持恒定，没有出现剧烈的变化。

相反，非相干光的振幅在时间上变化频繁，无法保持稳定。

空域相干性是指光波的传播方向上不同位置处的振幅和相位之间的关系。

具有高空域相干性的光波表现出明显的干涉和衍射现象，反映了光的波动性质。

而空域上相干性较差的光波，则表现出模糊和不清晰的特征。

光的相干性在光学干涉、光学显微镜和激光等领域有广泛的应用。

例如，在干涉仪中，通过将两束相干光叠加，可以产生干涉条纹，从而实现测量和分析。

相位和偏振相位和偏振是物理学中重要的概念，它们在电磁波、光学和信号处理等领域中有着广泛的应用。

本文将对相位和偏振进行详细的介绍和解释。

一、相位在物理学中，相位是描述波动现象的一个重要参数。

它表示波动中的不同状态或位置。

简单来说，相位描述了波动中的“相”，即波动的起伏和变化。

相位通常用角度或弧度来表示，常见的符号是ϕ。

相位的变化可以通过两个波峰或波谷之间的距离来衡量，也可以通过波动在单位时间内传播的距离来衡量。

相位的计算可以遵循一定的规则，如波动传播方向的选择、起始点的选择等。

在光学中，相位的概念非常重要。

光波的相位决定了光的性质和行为。

例如，两个光波的相位差决定了它们的干涉现象，相位的变化也与光的偏振有关。

二、偏振偏振是指光波中电场振动方向的特性。

正常的自然光是无偏振光，即电场振动方向在各个方向上都是随机的。

而当光波在传播过程中受到某些限制或过滤时，光的偏振性质就会发生变化。

光波的偏振可以分为线偏振、圆偏振和椭圆偏振。

线偏振是指电场振动方向沿一条直线，圆偏振是指电场振动方向沿一个圆形轨迹，椭圆偏振是指电场振动方向沿一个椭圆形轨迹。

光的偏振性质对于光的传播和应用有着重要的影响。

例如，在偏光片中，只有与偏振方向一致的光才能透过，其他方向的光则被过滤或吸收。

这种特性广泛应用于光学仪器、光通信和光电子设备中。

相位和偏振是密切相关的。

光波的相位差决定了光的干涉现象，而光的偏振性质也会影响光的相位差。

在干涉现象中，两个光波的相位差决定了干涉条纹的形状和强度。

当两个光波的相位差为整数倍的2π时，它们会互相增强，形成明亮的干涉条纹；而当相位差为奇数倍的π时，它们会互相抵消，形成暗淡的干涉条纹。

而光的偏振性质也会对干涉现象产生影响。

当两个偏振方向不一致的光波相互干涉时，会发生偏振干涉现象。

这种干涉现象可以应用于光学仪器中的干涉仪、薄膜的表面检测等领域。

在光的传播过程中，光波的偏振方向也可能发生变化。

例如，当自然光通过偏光片时，偏振片会选择性地吸收或透过与其偏振方向一致的光波，从而改变光的偏振性质。