半导体物理第二章
- 格式:ppt
- 大小:2.13 MB
- 文档页数:60


1第二章半导体中的杂质和缺陷能级要求:●掌握半导体中杂质的作用与杂质能级;●掌握半导体中的缺陷及其影响重点:浅能级和深能级杂质及其作用,杂质的补偿作用2原子并非固定不动,格点原子在平衡位置附近振动;半导体并非纯净,含有若干杂质(基质以外的任何元素);半导体晶格并非完美(完整),存在各种缺陷:点缺陷线缺陷面缺陷⎩⎨⎧实际半导体材料:⎪⎩⎪⎨⎧杂质来源:⎪⎩⎪⎨⎧§2.1 Si 、Ge 晶体中的杂质能级1、替(代)位式杂质间隙式杂质①原材料纯度不够;②工艺过程中引入玷污;③人为掺入杂质—为改善半导体材料性能;(1)Si 、Ge 都具有金刚石结构,一个晶胞内含有8个原子。
3(2)若视晶体中的原子为球体,且最近原子相切:a r ⋅=⋅3412%34)381(34834883333=×=×=a a a r ππ晶胞体积个原子体积则66%是空的相邻两球的半径之和(直径)为立方体体对角线的1/4。
4(3)杂质原子进入半导体中的存在方式:①位于格点原子间的间隙位置——间隙式杂质(一般杂质原子较小)②取代格点原子而位于格点上——替代式杂质(一般杂质原子大小与被取代的晶格原子大小近似,且价电子壳层结构也较相似){Si 、Ge 是Ⅳ族元素,Ⅲ、Ⅴ族元素在Si 、Ge 中是替位式杂质。
杂质浓度:单位体积中的杂质原子数,表示半导体晶体中杂质含量的多少,杂质浓度的单位为cm -3或/cm 3。
替位式杂质和间隙式杂质52、施主杂质施主能级Si中掺P效果上形成正电中心P + +一个价电子被正电中心P +束缚,位于P +周围,此束缚远小于共价键束缚,很小的能量△E 就可以使其挣脱束缚,形成“自由”电子,在晶格中运动(在导带)。
杂质电离:电子脱离杂质原子的束缚成为导电电子的过程。
杂质电离能:电子脱离杂质原子的束缚,成为导电电子所需的能量。
记作△E D 。
△E D 的值Si 中约0.04~0.05eV Ge 中约0.01eV {}<< E g以Si中掺入Ⅴ族替位式杂质P 为例6施主杂质或N 型杂质:Ⅴ族元素施放电子的过程——施主电离;Ⅴ族元素未电离时呈中性——束缚态或中性态;Ⅴ族元素电离后形成正电中心——施主离化态;⎩⎨⎧E cE vE D+++E g△E D一般情况下,杂质浓度较低杂质原子间的相互作用可以忽略所以施主能级是一些相同能量的孤立能级,即不形成能带。




第2章 半导体中杂质和缺陷能级“水至清则无鱼,人至察则无徒”(班固《汉书·东方朔传》),半导体至纯则难用。
半导体的实用价值,在于其物理性质对杂质和缺陷的灵敏依赖性,因而要通过杂质和缺陷的可控调节来实现。
由于痕量杂质和缺陷的存在也会改变结晶半导体中的周期势场,在禁带中引入电子的允许状态(能级),从而改变材料的电子特性,因而用高科技手段实现对半导体材料杂质和缺陷的精确控制,是半导体材料实用化的基础。
精确控制的含义,首先是高纯度、低缺陷密度材料的制备,然后是可控掺杂和必要时的微缺陷再生。
为此,需要了解杂质和缺陷在半导体的禁带中引入电子能级的微观机理。
§2.1 半导体中杂质和缺陷的施、受主作用一、真实晶体及其禁带中的允许能级1、杂质存在的可能性(1)占空比 已知金刚石和闪锌矿结构的一个晶胞中都包含有八个原子,若近似地把原子看成是等半径r 的圆球,则可以计算出这八个原子占据晶胞空间的百分数如下:按最密排列,两最近邻原子之中心距应等于两球的半径之和2r ,由是知晶胞之体对角线长8r ,晶格常数3/8r a =,八个圆球与一个晶胞之体积比,即金刚石和闪锌矿晶格的原子占空比为34.0163338348333≈=⨯ππr r 这一结果说明,在金刚石型的晶体还有近2/3的空隙。
(2)金刚石结构中的两种间隙 如图2—l 所示,金刚石结构中有两种最大的间隙。
一种是以4条体对角线的无点阵原子端1/4处以及晶胞中心为中心的间隙,称为四面体间隙,用T (tetrahedral )表示,其间可最大容纳半径相同的一个原子。
一个晶胞有5个这样的间隙。
另一种是由三个体对角线原子和三个面心原子围成的六角八面锥形体中的间隙,称为六角锥间隙,用H(Hexangular)表示。
(a) 四面体空隙 (b)六角锥空隙图2—1 金刚石型晶体结构中的两类间隙位置(3) 晶格中的空位(Vacancy ) 在一定温度下,点阵原子有一定几率获得足够能量脱离近邻原子的共价束缚,从格点位置进入间隙位置,产生空位。




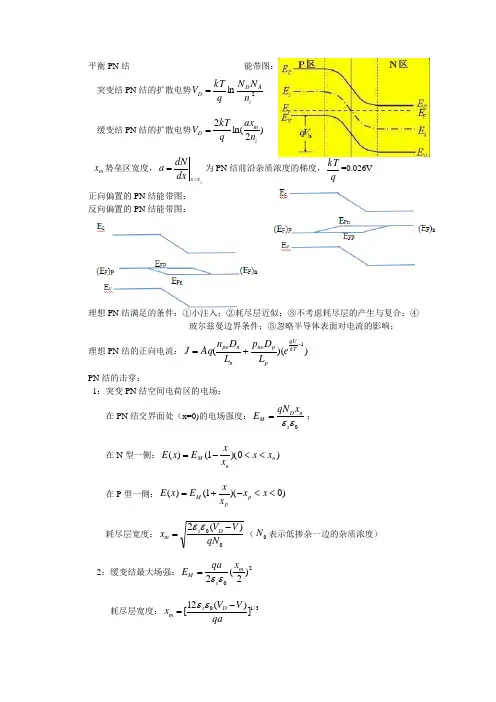
平衡PN 结 能带图:
突变结PN 结的扩散电势2ln i
A D D n N N q kT V = 缓变结PN 结的扩散电势)2ln(2i
m D n ax q kT V = m x 势垒区宽度,j
x x dx dN
a ==为PN 结前沿杂质浓度的梯度,
q kT =0.026V
正向偏置的PN 结能带图:
反向偏置的PN 结能带图:
理想PN 结满足的条件:①小注入;②耗尽层近似;③不考虑耗尽层的产生与复合;④ 玻尔兹曼边界条件;⑤忽略半导体表面对电流的影响; 理想PN 结的正向电流:))((1-+=kT qU p p no n n
po e L D p L D n Aq J
PN 结的击穿:
1:突变PN 结空间电荷区的电场:
在PN 结交界面处(x=0)的电场强度:0εεs n
D M x qN
E =;
在N 型一侧:)0)(1()(n n
M x x x x E x E <<-= 在P 型一侧:)0)(1()(<<-+=x x x x E x E p p
M 耗尽层宽度:0
0)(2qN V V x D s m -=εε(0N 表示低掺杂一边的杂质浓度) 2:缓变结最大场强:20)2(2m s M x qa
E εε=
耗尽层宽度:3/10])(12[qa
V V x D s m -=εε
3:突变结势垒电容m S T x A C 0εε=。