下载文档原格式
《大学物理》刚体力学练习题及答案解析一、选择题1.刚体对轴的转动惯量，与哪个因素无关 [ C ]（A）刚体的质量（B）刚体质量的空间分布（C）刚体的转动速度（D）刚体转轴的位置2.有两个力作用在一个有固定轴的刚体上. [ B ](1)这两个力都平行于轴作用时,它们对轴的合力矩一定是零;(2)这两个力都垂直于轴作用时,它们对轴的合力矩可能是零;(3)这两个力的合力为零时,它们对轴的合力矩也一定是零;(4)当这两个力对轴的合力矩为零时,它们的合力也一定是零.在上述说法中,(A)只有(1)是正确的；(B) (1)、(2) 正确, (3)、(4)错误；(C) (1)、(2)、(3)都正确, (4)错误；(D) (1)、(2)、(3)、(4)都正确.3.均匀细棒OA可绕通过其一端O而与棒垂直的水平固定光滑轴转动，今使棒从水平位置由静止开始自由下落，在棒摆动到竖立位置的过程中，下述说法哪一种是正确的[ A ](A) 角速度从小到大，角加速度从大到小；(B) 角速度从小到大，角加速度从小到大；(C) 角速度从大到小，角加速度从大到小；(D) 角速度从大到小，角加速度从小到大.4．如图所示，圆锥摆的小球在水平面内作匀速率圆周运动，小球和地球所组成的系统，下列哪些物理量守恒（ C ）（A）动量守恒，角动量守恒（B）动量和机械能守恒（C）角动量和机械能守恒（D）动量，角动量，机械能守恒5.一圆盘绕通过盘心且垂直于盘面的水平轴转动，轴间摩擦不计，如图射来两个质量相同，速度大小相同、方向相反并在一条直线上的子弹，它们同时射入圆盘并且留在盘内，在子弹射入后的瞬间，对于圆盘和子弹系统的角动量L以及圆盘的角速度ω则有（ B ）（A）L不变，ω增大（B）L不变，ω减小（C）L变大，ω不变（D）两者均不变6.一花样滑冰者，开始自转时，其动能为20021ωJ E =。
然后他将手臂收回，转动惯量减少为原来的1/3，此时他的角速度变为ω，动能变为E ，则下列关系正确的是（ D ） （A ）00,3E E ==ωω （B ）003,31E E ==ωω （C ）00,3E E ==ωω （D ）003,3E E ==ωω1C 2.B ，3.A ，4.C ，5.B ，6.D二、填空1.当刚体受到的合外力的力矩为零时，刚体具有将保持静止的状态或_____________状态，把刚体的这一性质叫刚体___________。
衡水学院 理工科专业 《大学物理B 》 刚体力学基础 习题命题教师：郑永春 试题审核人：张郡亮一、填空题（每空1分）1、三个质量均为m 的质点，位于边长为a 的等边三角形的三个顶点上。
此系统对通过三角形中心并垂直于三角形平面的轴的转动惯量J 0＝__ ma 2 _，对通过三角形中心且平行于其一边的轴的转动惯量为J A ＝__12ma 2_，对通过三角形中心和一个顶点的轴的转动惯量为J B ＝__21ma 2 。
2、两个质量分布均匀的圆盘A 和B 的密度分别为ρA 和ρ B (ρA >ρB )，且两圆盘的总质量和厚度均相同。
设两圆盘对通过盘心且垂直于盘面的轴的转动惯量分别为J A 和J B ，则有J A < J B 。
3、 一作定轴转动的物体，对转轴的转动惯量J ＝3.0 kg ·m 2，角速度ω0＝6.0 rad/s ．现对物体加一恒定的制动力矩M ＝－12 N ·m ，当物体的角速度减慢到ω＝2.0 rad/s 时，物体已转过了角度∆θ ＝__4.0rad4、两个滑冰运动员的质量各为70 kg ，均以6.5 m/s 的速率沿相反的方向滑行，滑行路线间的垂直距离为10 m ，当彼此交错时，各抓住一10 m 长的绳索的一端，然后相对旋转，则抓住绳索之后各自对绳中心的角动量L ＝__2275 kg·m 2·s 1 _；它们各自收拢绳索，到绳长为5 m 时，各自的速率υ ＝__13 m·s 1_。
5、有一质量均匀的细棒，可绕垂直于棒的一端的水平轴转动。
如将此棒放在水平位置，然后任其下落，则在下落过程中的角速度大小将 变大 ，角加速度大小将 变小 。
二、单项选择题（每小题2分）（ A ）1、有两个力作用在一个有固定转轴的刚体上，下列说法正确的是：A.这两个力都平行于轴作用时，它们对轴的合力矩一定是零；B.这两个力都垂直于轴作用时，它们对轴的合力矩一定是零；C.当这两个力的合力为零时，它们对轴的合力矩也一定是零；D.当这两个力对轴的合力矩为零时，它们的合力也一定是零。
一、选择题［ C ］1、如图所示，A 、B 为两个相同的绕着轻绳的定滑轮．A 滑轮挂一质量为M 的物体，B 滑轮受拉力F ，而 且F ＝Mg ．设A 、B 两滑轮的角加速度分别为βA 和βB ，不计滑轮轴的摩擦，则有(A) βA ＝βB ． (B) βA ＞βB ．(C) βA ＜βB ． (D) 开始时βA ＝βB ，以后βA ＜βB ．图5-18参考答案：设定滑轮半径为Ｒ，转动惯量为J ，如图所示，据刚体定轴转动定律Ｍ=Ｊβ有： 对B ：FR=MgR= J βB ．对A ：Mg-T=Ma TR=J βA, a=R βA, 可推出：βA ＜βB[ D ]2、如图5-8所示，一质量为m 的匀质细杆AB ，A 端靠在粗糙的竖直墙壁上，B 端置于粗糙水平地面上而静止．杆身与竖直方向成θ角，则A 端对墙壁的压力大小(A) 为 41mg cos θ． (B)为21mg tg θ． (C) 为 mg sin θ． (D) 不能唯一确定．[ C ]3、一圆盘正绕垂直于盘面的水平光滑固定轴O 转动，如图5-11射来两个质量相同，速度大小相同，方向相反并在一条直线上的子弹，子弹射入圆盘并且留在盘内，则子弹射入后的瞬间，圆盘的角速度ω(A) 增大． (B) 不变． (C) 减小． (D) 不能确定．图5-8m图5-11参考答案:把三者看作同一系统时,系统所受合外力矩为零, 系统角动量守恒。
设L 为每一子弹相对固定轴O 的角动量大小.故由角动量守恒定律得: J ω0+L-L=(J+J 子弹) ω ω <ω0[ A ]4、质量为m 的小孩站在半径为R 的水平平台边缘上．平台可以绕通过其中心的竖直光滑固定轴自由转动，转动惯量为J ．平台和小孩开始时均静止．当小孩突然以相对于地面为v 的速率在台边缘沿逆时针转向走动时，则此平台相对地面旋转的角速度和旋转方向分别为(A) ⎪⎭⎫ ⎝⎛=R J mR v 2ω，顺时针． (B) ⎪⎭⎫⎝⎛=R J mR v 2ω，逆时针．(C) ⎪⎭⎫ ⎝⎛+=R mR J mR v 22ω，顺时针． (D) ⎪⎭⎫⎝⎛+=R mR J mR v 22ω，逆时针．参考答案：视小孩与平台为一个系统，该系统所受的外力矩为零，系统角动量守恒：0=Rmv-J ω 可得结论。
第三章 刚体的转动习题答案1、对于定轴转动刚体上不同的点来说：线速度、法向加速度、切向加速度具有不同的值，角位移、角速度、角加速度具有相同的值。
2、由sin M r F Fr θ=⨯=可知，（1）0,0F M ≠=，当0r =或者sin 0θ=，即力通过转轴或者力与转轴平行； （2）0,0F M =≠，这种情况不存在； （3）0,0F M ==，这种情况任何时候都存在。
3、根据均匀圆盘对中心轴的转动惯量：221122I mr vr ρ==可知，对于相同几何形状的铁盘和铝盘，密度大的转动惯量大。
通常我们取铁的密度为37.9/g cm ，铝的密度32.7/g cm ，因此铁盘对中心轴的转动惯量大；根据刚体动能定理：21222111d 22A M I I θθθωω==-⎰，可知对铁盘的外力矩要做更多的功。
4、轮A 的转动惯量212I mr =，轮B 的转动惯量2I mr =，根据刚体的转动定律M I β=，因为两者所受的阻力矩相等，可知轮A 的转动角加速度大于轮B 的转动角加速度，故轮A 先停止。
5、舞蹈演员在旋转过程中，可以近似地认为角动量守恒，当其把双手靠近身体时，转动惯量减小，故角速度增大；当其把双手伸开，转动惯量增大，故角速度减小。
6、解：2334d a bt ct dtθω==+-， 2612d b t c t dtωβ==-。
7、解：11200240/60rad s πωπ⨯==，22700290/60rad s πωπ⨯==， 2215025/126rad s t ωωππβ-===∆， 2117803902t t n θωβπ=+==。
8、解：根据均匀球体对直径轴的转动惯量225I mr =，得到地球对自转轴的转动惯量3729.810I kg m =⨯⋅，地球自转角速度2/246060rad s πω=⨯⨯，转动动能22813102k E I J ω==⨯。
9、解：已知030/rad s ωπ=，切断电源后的角位移752150θππ=⨯=，根据匀减速运动规律2220023/2rad s ωωβθβπθ=⇒==，由于电扇是匀减速，可知阻力矩为常量，因此根据刚体转动动能定理22101144.422M I I J θωω=-=-， 可得到转动惯量2244.420.01I kg m ω⨯==⋅，以及阻力矩44.40.1150M N m π=≈⋅。
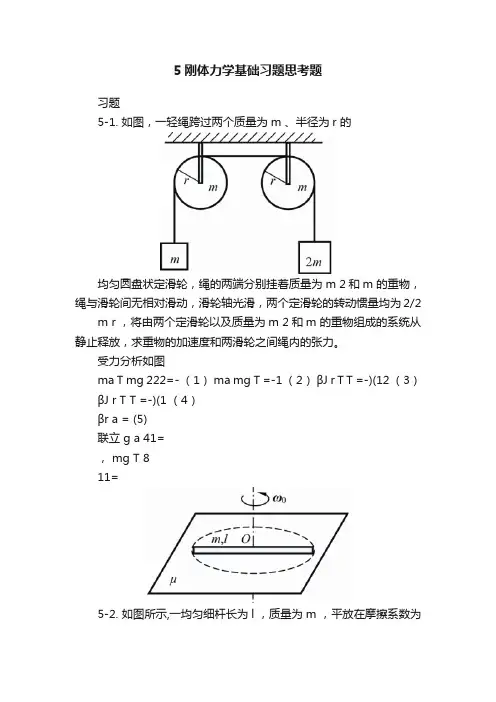
5刚体力学基础习题思考题习题5-1. 如图，一轻绳跨过两个质量为m 、半径为r 的均匀圆盘状定滑轮，绳的两端分别挂着质量为m 2和m 的重物，绳与滑轮间无相对滑动，滑轮轴光滑，两个定滑轮的转动惯量均为2/2 m r ，将由两个定滑轮以及质量为m 2和m 的重物组成的系统从静止释放，求重物的加速度和两滑轮之间绳内的张力。
受力分析如图ma T mg 222=- （1） ma mg T =-1 （2）βJ r T T =-)(12 （3）βJ r T T =-)(1 （4）βr a = (5)联立 g a 41=， mg T 811=5-2. 如图所示,一均匀细杆长为l ，质量为m ，平放在摩擦系数为μ的水平桌面上,设开始时杆以角速度0ω绕过中心O 且垂直与桌面的轴转动，试求:（1）作用于杆的摩擦力矩；（2）经过多长时间杆才会停止转动。
（1）设杆的线lm=λ，在杆上取一小质元dx dm λ= gdx dmg df μλμ==gxdx dM μλ= 考虑对称mgl gxdx M l μμλ?==20412（2）根据转动定律dtd J JB M ω===-tw Jd Mdt 0ω0212141ωμml mglt -=-所以 glt μω30=5-3. 如图所示，一个质量为m 的物体与绕在定滑轮上的绳子相联，绳子的质量可以忽略，它与定滑轮之间无滑动。
假设定滑轮质量为M 、半径为R ,其转动惯量为2/2MR ，试求该物体由静止开始下落的过程中，下落速度与时间的关系。
dtdvmma T mg ==- βJ TR = βR dtdv= 整理 mg dt dv M m =+)21( gdt M m m dv t v ??+=0021 2 Mm mgtv +=5-4. 轻绳绕过一定滑轮，滑轮轴光滑，滑轮的质量为4/M ，均匀分布在其边缘上，绳子A 端有一质量为M 的人抓住了绳端，而在绳的另一端B 系了一质量为4/M 的重物，如图。
第三章思考题3.1刚体一般是由n （n 是一个很大得数目）个质点组成。
为什么刚体的独立变量却不是3n 而是6或者更少？3.2何谓物体的重心？他和重心是不是 总是重合在一起的？ 3.3试讨论图形的几何中心，质心和重心重合在一起的条件。
3.4简化中心改变时，主矢和主矩是不是也随着改变？如果要改变，会不会影响刚体的运动？ 3.5已知一匀质棒，当它绕过其一端并垂直于棒的轴转动时，转动惯量为231ml ，m 为棒的质量，l 为棒长。
问此棒绕通过离棒端为l 41且与上述轴线平行的另一轴线转动时，转动惯量是不是等于224131⎪⎭⎫ ⎝⎛+l m ml ？为什么？3.6如果两条平行线中没有一条是通过质心的，那么平行轴定理式（3.5.12）能否应用？如不能，可否加以修改后再用？3.7在平面平行运动中，基点既然可以任意选择，你觉得选择那些特殊点作为基点比较好？好处在哪里？又在（3.7.1）及（3.7.4）两式中，哪些量与基点有关？哪些量与基点无关？ 3.8转动瞬心在无穷远处，意味着什么？3.9刚体做平面平行运动时，能否对转动瞬心应用动量矩定理写出它的动力学方程？为什么？3.10当圆柱体以匀加速度自斜面滚下时，为什么用机械能守恒定律不能求出圆柱体和斜面之间的反作用力？此时摩擦阻力所做的功为什么不列入？是不是我们必须假定没有摩擦力？没有摩擦力，圆柱体能不能滚？3.11圆柱体沿斜面无滑动滚下时，它的线加速度与圆柱体的转动惯量有关，这是为什么？但圆柱体沿斜面既滚且滑向下运动时，它的线加速度则与转动惯量无关？这又是为什么？ 3.12刚体做怎样的运动时，刚体内任一点的线速度才可以写为r ω⨯？这时r 是不是等于该质点到转动轴的垂直距离？为什么？ 3.13刚体绕固定点转动时，r ω⨯dtd 为什么叫转动加速度而不叫切向加速度？又()r ωω⨯⨯为什么叫向轴加速度而不叫向心加速度？3.14在欧勒动力学方程中，既然坐标轴是固定在刚体上，随着刚体一起转动，为什么我们还可以用这种坐标系来研究刚体的运动？3.15欧勒动力学方程中的第二项()21I I -y x ωω等是怎样产生的？它的物理意义又是什么？第三章思考题解答3.1 答：确定一质点在空间中得位置需要3个独立变量，只要确定了不共线三点的位置刚体的位置也就确定了，故须九个独立变量，但刚体不变形，此三点中人二点的连线长度不变，即有三个约束方程，所以确定刚体的一般运动不需3n 个独立变量，有6个独立变量就够了.若刚体作定点转动，只要定出任一点相对定点的运动刚体的运动就确定了，只需3个独立变量；确定作平面平行运动刚体的代表平面在空间中的方位需一个独立变量，确定任一点在平面上的位置需二个独立变量，共需三个独立变量；知道了定轴转动刚体绕转动轴的转角，刚体的位置也就定了，只需一个独立变量；刚体的平动可用一个点的运动代表其运动，故需三个独立变量。
习题5-1. 如图，一轻绳跨过两个质量为m 、半径为r 的均匀圆盘状定滑轮，绳的两端分别挂着质量为m 2和m 的重物，绳与滑轮间无相对滑动，滑轮轴光滑，两个定滑轮的转动惯量均为2/2m r ，将由两个定滑轮以及质量为m 2和m 的重物组成的系统从静止释放，求重物的加速度和两滑轮之间绳内的张力。
解：受力分析如图ma T mg 222=- （1）ma mg T =-1（2） βJ r T T =-)(12（3） βJ r T T =-)(1（4）βr a =(5)联立g a 41=， mg T 811=5-2. 如图所示,一均匀细杆长为l ，质量为m ，平放在摩擦系数为μ的水平桌面上,设开始时杆以角速度0ω绕过中心O 且垂直与桌面的轴转动，试求:（1）作用于杆的摩擦力矩；（2）经过多长时间杆才会停止转动。
（1） 设杆的线lm=λ，在杆上取一小质元dx dm λ=gdx dmg df μλμ== gxdx dM μλ=考虑对称mgl gxdx M l μμλ⎰==20412（2） 根据转动定律d M J J dtωβ==⎰⎰=-t w Jd Mdt 0ω0212141ωμml mglt -=-所以glt μω30=5-3. 如图所示，一个质量为m 的物体与绕在定滑轮上的绳子相联，绳子的质量可以忽略，它与定滑轮之间无滑动。
假设定滑轮质量为M 、半径为R ,其转动惯量为2/2MR ，试求该物体由静止开始下落的过程中，下落速度与时间的关系。
dtdv mma T mg ==-βJ TR = βR dtdv= 整理 mg dt dv M m =+)21(gdt Mm m dv t v ⎰⎰+=00212M m mgt v +=5-4. 轻绳绕过一定滑轮，滑轮轴光滑，滑轮的质量为4/M ，均匀分布在其边缘上，绳子A 端有一质量为M 的人抓住了绳端，而在绳的另一端B 系了一质量为4/M 的重物，如图。
已知滑轮对O 轴的转动惯量4/2MR J =，设人从静止开始以相对绳匀速向上爬时，绳与滑轮间无相对滑动，求B 端重物上升的加速度？解：选人、滑轮与重物为系统，设u 为人相对绳的速度，v 为重物上升的速度，系统对轴的角动量MuR MvR R MR v u M vR M L -=+--=23)4()(42ω根据角动量定理dtdL M =)23(43MuR MvR dt d MgR -= 0=dt du MRa dt dv MR MgR 232343==所以2g a =5-5. 计算质量为m 半径为R 的均质球体绕其轴线的转动惯量。
证明：设球的半径为R ，总重量为m ，体密度343R m πρ=，将球体划分为许多厚度为dZ 的圆盘， 则盘的体积为 dZ Z R 222)(-π22252182()2155R R J R Z dZ R mR ππρρ-=-==⎰5-6. 一轻弹簧与一均匀细棒连接，装置如图所示，已知弹簧的劲度系数N/m 40=k ，当0θ= 时弹簧无形变，细棒的质量kg 0.5=m ，求在0θ= 的位置上细棒至少应具有多大的角速度ω，才能转动到水平位置？解：机械能守恒22212121kx J mg=+ω 根据几何关系22215.1)5.0(+=+x128.3-⋅=s rad ω5-7. 如图所示，一质量为m 、半径为R 的圆盘，可绕O 轴在铅直面内转动。
若盘自静止下落，略去轴承的摩擦，求：（1）盘到虚线所示的铅直位置时，质心C 和盘缘A 点的速率；（2）在虚线位置轴对圆盘的作用力。
解：在虚线位置的C 点设为重力势能的零点，下降过程机械能守恒221ωJ mgR =2221mR mR J +=Rg 34=ω 34RgR v c ==ω2A v R ω==273y F mg mR mg ω=+= 方向向上 5-8. 如图所示，长为l 的轻杆，两端各固定质量分别为m 和m 2的小球，杆可绕水平光滑固定轴O 在竖直面内转动，转轴O 距两端分别为l 31和l 32．轻杆原来静止在竖直位置。
今有一质量为m 的小球，以水平速度0v 与杆下端小球m 作对心碰撞，碰后以021v 的速度返回，试求碰撞后轻杆所获得的角速度。
解：根据角动量守衡 有022021322)3()32(32v ml m l m l l mv ⋅-⋅+=ωω lv 230=ω5-9. 一质量均匀分布的圆盘，质量为M ，半径为R ，放在一粗糙水平面上(圆盘与水平面之间的摩擦系数为μ)，圆盘可绕通过其中心O 的竖直固定光滑轴转动。
开始时，圆盘静止，一质量为m 的子弹以水平速度v 垂直于圆盘半径打入圆盘边缘并嵌在盘边上，求：(1)子弹击中圆盘后，盘所获得的角速度；(2)经过多少时间后，圆盘停止转动。
(圆盘绕通过O 的竖直轴的转动惯量为221MR ，忽略子弹重力造成的摩擦阻力矩。
)解（1）角动量守恒ωω2221mR MR mvR +=2(2)mvm M Rω=+ （2）2022π3R M M dM dmgr gr rdr MgR R μμμπ====⎰⎰⎰2221()032MgR t MR mR μω⋅∆=+-，()224M m t R Mgωμ+∴∆= 由（1）已得：()22m M m R ω=+v ，代入即得32m t Mg μ∆=v5-10. 有一质量为1m 、长为l 的均匀细棒，静止平放在滑动摩擦系数为μ的水平桌面上，它可绕通过其端点O 且与桌面垂直的固定光滑轴转动。
另有一水平运动的质量为2m 的小滑块，从侧面垂直于棒与棒的另一端A 相碰撞，设碰撞时间极短。
已知小滑块在碰撞前后的速度分别为1v 和2v ，如图所示。
求碰撞后从细棒开始转动到停止转动的过程所需的时间。
(已知棒绕O 点的转动惯量2131l m J=) 碰撞时角动量守恒2211221m v l m l m v l ω=-lm v v m 1212)(3+=ω细棒运动起来所受到的摩擦力矩gl m gxdx l m M l10121μμ==⎰ dt d JM ω=- ⎰-=tgl m d l m dt 01212131μω gm v v m g l t 1212)(232μμω+==5-11. 如图所示，滑轮转动惯量为2m kg 01.0⋅，半径为cm7；物体的质量为kg 5，用一细绳与劲度系数N/m 200=k 的弹簧相连，若绳与滑轮间无相对滑动，滑轮轴上的摩擦忽略不计。
求：（1）当绳拉直、弹簧无伸长时使物体由静止而下落的最大距离。
(2)物体的速度达最大值时的位置及最大速率。
（1）机械能守恒。
设下落最大距离为hmgh kh =221m kmgh 49.02== （2）mgx J mv kx =++222212121ω12222mgx kx v J m ⎡⎤-⎢⎥=⎢⎥+⎢⎥⎣⎦若速度达最大值，0=dxdv)(245.0m kmgx ==1122222222259.80.2452000.245 1.31/0.015(710)mgx kx v m s J m r -⎡⎤⎡⎤⎢⎥-⨯⨯⨯-⨯⎢⎥===⎢⎥⎢⎥++⎢⎥⎢⎥⎣⎦⨯⎣⎦5-12. 设电风扇的功率恒定不变为P ，叶片受到的空气阻力矩与叶片旋转的角速度ω成正比，比例系数的k ，并已知叶片转子的总转动惯量为J 。
（1）原来静止的电扇通电后t 秒时刻的角速度；（2）电扇稳定转动时的转速为多大？（3）电扇以稳定转速旋转时，断开电源后风叶还能继续转多少角度？解：（1）通电时根据转动定律有dt d J M M r ω=- ωP M = ωk M r =代入两边积分 ωωωωd k P J dt t ⎰⎰-=020 )1(2t J ke k P --=ω （2）电扇稳定转动时的转速 k P m =ω （3） θωωωd d J k =- ⎰⎰=-00m d d J kωθωθ kP k J=θ 5-13. 如图所示，物体A 放在粗糙的水平面上，与水平桌面之间的摩擦系数为μ，细绳的一端系住物体A ，另一端缠绕在半径为R的圆柱形转轮B 上，物体与转轮的质量相同。
开始时，物体与转轮皆静止，细绳松弛，若转轮以0ω绕其转轴转动。
试问：细绳刚绷紧的瞬时，物体A 的速度多大？物体A 运动后，细绳的张力多大？解：细绳刚绷紧时系统机械能守恒2220212121mv J J +=ωω ωR v =013v R ω= ma mg T =-μβJ TR =-3mgT μ= βR a =5-14. 质量为m 的小孩站在半径为R 、转动惯量为J 的可以自由转动的水平平台边缘上(平台可以无摩擦地绕通过中心的竖直轴转动)。
平台和小孩开始时均静止。
当小孩突然一相对地面为v 的速率沿台边缘逆时针走动时，此平台相对地面旋转的角速度ω为多少？解：此过程角动量守恒ωJ m r v -=0JmRv =ω5-15. 以速度0v 作匀速运动的汽车上，有一质量为m （m 较小），边长为l 的立方形货物箱，如图所示。
当汽车遇到前方障碍物急刹车停止时，货物箱绕其底面A 边翻转。
试求：（1）汽车刹车停止瞬时，货物箱翻转的角速度及角加速度；（2）此时，货物箱A 边所受的支反力。
解：（1）角动量守恒ω20322ml l mv = l v 430=ω 根据转动定律 β2322ml l mg = l g43=β（2）0ct 0cn cx x 45cos ma 45cos ma ma N -==思考题5-1. 一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮，绳的两端分别悬有质量1m 和2m 的物体 (1m <2m )，如图所示.绳与轮之间无相对滑动，某时刻滑轮沿逆时针方向转动，则绳的张力多大？a m T g m 111=-（1） a m g m T 222=-（2） 插入图5-29 βJ r T T =-)(21（3） βr a = (4)联立方程可得 1T 、2T 。
12T T5-2. 一圆盘绕过盘心且与盘面垂直的轴O 以角速度ω按图示方向转动，若如图所示的情况那样，将两个大小相等方向相反但不在同一条直线的力F 沿盘面方向同时作用到盘上，则盘的角速度 怎样变化？答：增大5-3. 个人站在有光滑固定转轴的转动平台上,双臂伸直水平地举起二哑铃,在该人把此二哑铃水平收缩到胸前的过程中,人、哑铃与转动平台组成的系统的：（A）机械能守恒,角动量守恒;（B）机械能守恒,角动量不守恒,（C）机械能不守恒,角动量守恒;（D）机械能不守恒,角动量不守恒.答：（C）5-4. 在边长为a的六边形顶点上，分别固定有质量都是m的6个质点，如图所示。
试求此系统绕下列转轴的转动惯量：（1）设转轴Ⅰ、Ⅱ在质点所在的平面内，如图a所示；（2）设转轴Ⅲ垂直于质点所在的平面，如图b所示。
以Ⅰ为轴转动惯量29ma J = 以Ⅱ为轴转动惯量 23ma J =以Ⅲ为轴转动惯量25.7ma J =5-5. 如图a 所示，半径分别是1R 和2R 、转动惯量分别是1J 和2J 的两个圆柱体，可绕垂直于图面的轴转动，最初大圆柱体的角速度为0ω，现在将小圆柱体向左靠近，直到它碰到大圆柱体为止。
