集合推理

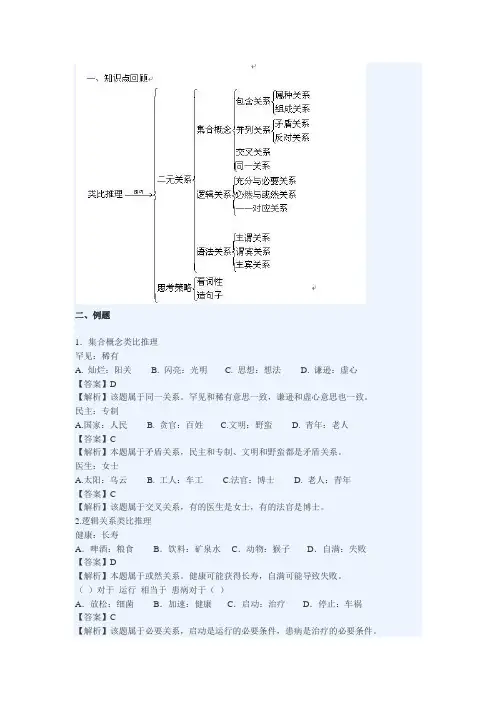
二、例题1．集合概念类比推理罕见：稀有A. 灿烂：阳关B. 闪亮：光明C. 思想：想法D. 谦逊：虚心【答案】D【解析】该题属于同一关系。

罕见和稀有意思一致，谦逊和虚心意思也一致。

民主：专制A.国家：人民B. 贪官：百姓C.文明：野蛮D. 青年：老人【答案】C【解析】本题属于矛盾关系，民主和专制、文明和野蛮都是矛盾关系。

医生：女士A.太阳：乌云B. 工人：车工C.法官：博士D. 老人：青年【答案】C【解析】该题属于交叉关系，有的医生是女士，有的法官是博士。

2.逻辑关系类比推理健康：长寿A．啤酒：粮食B．饮料：矿泉水C．动物：猴子D．自满：失败【答案】D【解析】本题属于或然关系。

健康可能获得长寿，自满可能导致失败。

（）对于运行相当于患病对于（）A．放松：细菌B．加速：健康C．启动：治疗D．停止：车祸【答案】C【解析】该题属于必要关系，启动是运行的必要条件，患病是治疗的必要条件。

身份证∶身份A．执业证∶资格B．结婚证∶配偶C．房产证∶房屋D．毕业证∶学位【答案】C【解析】一一对应关系。

身份证是对个人身份的认证，而房产证是对房屋（所有权）的认证。

3.语法分析类比推理商场：顾客A．发布会：记者B．书店：书C．火车：列车员D．考试：大纲【答案】A【解析】本题属于主宾关系，商场是为顾客开的，发布会是为记者开的，火车是为乘客开的，而不是为列车员开的。

扫描仪：复制A．蜜蜂：酿蜜B．梳子：头发C．MP3:播放D．高尔夫：高雅【答案】C【解析】该题属于主谓关系，扫描仪被用于复制，MP3被用于播放，梳子和头发属于主宾关系，梳子梳头发，蜜蜂酿蜜属于主谓关系，但是主动状态。

所以选择C。

坚定：信念A．统一：思想B．持续：发展C．金融:工具D．平原：草丛【答案】A【解析】本题属于谓宾关系，坚定信念，统一思想都是动宾搭配。

( ) 对于建筑相当于计划对于( )A．设计成果B．图纸工作C．材料战略D．施工目标【答案】B【解析】采用造句法。

回扣1集合、常用逻辑用语、不等式与推理证明1.集合(1)集合的运算性质①交换律：A∪B＝B∪A；A∩B＝B∩A；②结合律：(A∪B)∪C＝A∪(B∪C)；(A∩B)∩C＝A∩(B∩C)；③分配律：(A∩B)∪C＝(A∪C)∩(B∪C)；(A∪B)∩C＝(A∩C)∪(B∩C)；④∁U(A∪B)＝(∁U A)∩(∁U B)；∁U(A∩B)＝(∁U A)∪(∁U B)；⑤A∪B＝A⇔B⊆A；A∩B＝B⇔B⊆A.(2)子集、真子集个数计算公式对于含有n个元素的有限集合M，其子集、真子集、非空子集、非空真子集的个数依次为2n,2n－1,2n－1,2n－2.(3)集合运算中的常用方法若已知的集合是不等式的解集，用数轴求解；若已知的集合是点集，用数形结合法求解；若已知的集合是抽象集合，用Venn图求解.2.四种命题及其相互关系(1)(2)互为逆否命题的两个命题同真同假.3.含有逻辑联结词的命题的真假(1)命题p∨q：若p，q中至少有一个为真，则命题p∨q为真命题，p，q同时为假命题时，命题p∨q为假命题，简记为：一真则真，同假则假.(2)命题p∧q：若p，q中至少有一个为假，则命题p∧q为假命题，p，q同为真时，命题才为真命题，简记为：一假则假，同真则真.(3)命题綈p：与命题p真假相反.4.全称命题、特称(存在性)命题及其否定(1)全称命题p：∀x∈M，p(x)，其否定为特称(存在性)命题：綈p：∃x0∈M，綈p(x0).(2)特称(存在性)命题p：∃x0∈M，p(x0)，其否定为全称命题：綈p：∀x∈M，綈p(x).5.充分条件与必要条件的三种判定方法(1)定义法：正、反方向推理，若p⇒q，则p是q的充分条件(或q是p的必要条件)；若p⇒q，且q⇏p，则p是q的充分不必要条件(或q是p的必要不充分条件).(2)集合法：利用集合间的包含关系.例如，命题p：x∈A，命题q：x∈B，若A⊆B，则p是q 的充分条件(q是p的必要条件)；若A B，则p是q的充分不必要条件(q是p的必要不充分条件)；若p＝q，则p是q的充要条件.(3)等价法：将命题等价转化为另一个便于判断真假的命题.6.一元二次不等式的解法解一元二次不等式的步骤：一化(将二次项系数化为正数)；二判(判断对应方程Δ的符号)；三解(解对应的一元二次方程)；四写(大于取两边，小于取中间).解含有参数的一元二次不等式一般要分类讨论，往往从以下几个方面来考虑：①二次项系数，它决定二次函数的开口方向；②判别式Δ，它决定根的情形，一般分Δ>0，Δ＝0，Δ<0三种情况；③在有根的条件下，要比较两根的大小.7.一元二次不等式的恒成立问题(1)ax 2＋bx ＋c >0(a ≠0)恒成立的条件是⎩⎪⎨⎪⎧ a >0，Δ<0. (2)ax 2＋bx ＋c <0(a ≠0)恒成立的条件是⎩⎪⎨⎪⎧ a <0，Δ<0. 8.分式不等式f (x )g (x )>0(<0)⇔f (x )g (x )>0(<0)； f (x )g (x )≥0(≤0)⇔⎩⎪⎨⎪⎧f (x )g (x )≥0(≤0)，g (x )≠0. 9.基本不等式(1)基本不等式：a ＋b 2≥ab (a ，b ∈(0，＋∞))，当且仅当a ＝b 时取等号. 基本不等式的变形：①a 2＋b 2≥2ab (a ，b ∈R )，当且仅当a ＝b 时取等号；②⎝⎛⎭⎫a ＋b 22≥ab (a ，b ∈R )，当且仅当a ＝b 时取等号.(2)在利用基本不等式求最值时，要特别注意“拆、拼、凑”等技巧，满足基本不等式中“正”、“定”、“等”的条件.10.线性规划(1)可行域的确定，“线定界，点定域”.(2)线性目标函数的最大值、最小值一般在可行域的顶点处取得.(3)线性目标函数的最值也可在可行域的边界上取得，这时满足条件的最优解有无数多个.11.推理推理分为合情推理与演绎推理，合情推理包括归纳推理和类比推理；演绎推理的一般模式是三段论.12.证明方法(1)综合法.(2)分析法.(3)反证法.(4)数学归纳法.1.描述法表示集合时，一定要理解好集合的含义——抓住集合的代表元素.如{x|y＝lg x}——函数的定义域；{y|y＝lg x}——函数的值域；{(x，y)|y＝lg x}——函数图象上的点集.2.易混淆0，∅，{0}：0是一个实数；∅是一个集合，它含有0个元素；{0}是以0为元素的单元素集合，但是0∉∅，而∅⊆{0}.3.集合的元素具有确定性、无序性和互异性，在解决有关集合的问题时，尤其要注意元素的互异性.4.空集是任何集合的子集.由条件A⊆B，A∩B＝A，A∪B＝B求解集合A时，务必分析研究A ＝∅的情况.5.区分命题的否定与否命题，已知命题为“若p，则q”，则该命题的否定为“若p，则綈q”，其否命题为“若綈p，则綈q”.6.在对全称命题和特称(存在性)命题进行否定时，不要忽视对量词的改变.7.对于充分、必要条件问题，首先要弄清谁是条件，谁是结论.8.判断命题的真假要先明确命题的构成.由命题的真假求某个参数的取值范围，还可以从集合的角度来思考，将问题转化为集合间的运算.9.不等式两端同时乘一个数或同时除以一个数时，如果不讨论这个数的正负，容易出错.10.解形如ax2＋bx＋c>0(a≠0)的一元二次不等式时，易忽视系数a的讨论导致漏解或错解，要注意分a>0，a<0进行讨论.11.求解分式不等式时应正确进行同解变形，不能把f(x)g(x)≤0直接转化为f(x)·g(x)≤0，而忽视g(x)≠0.12.容易忽视使用基本不等式求最值的条件，即“一正、二定、三相等”导致错解，如求函数f (x )＝x 2＋2＋1x 2＋2的最值，就不能利用基本不等式求最值；求解函数y ＝x ＋3x (x <0)时应先转化为正数再求解.13.解线性规划问题，要注意边界的虚实；注意目标函数中y 的系数的正负；注意最优整数解. 14.求解线性规划问题时，不能准确把握目标函数的几何意义导致错解，如y －2x ＋2是指已知区域内的点(x ，y )与点(－2，2)连线的斜率，而(x －1)2＋(y －1)2是指已知区域内的点(x ，y )到点(1,1)的距离的平方等.15.类比推理易盲目机械类比，不要被表面的假象(某一点表面相似)迷惑，应从本质上类比.用数学归纳法证明时，易盲目以为n 0的起始值为1，另外注意证明传递性时，必须用n ＝k 成立的归纳假设.。

集合解题方法与技巧集合解题方法与技巧1. 引言在数学和逻辑推理中，集合是一种非常重要的概念。

集合可以理解为由一些确定的、互不相同的元素组成的整体。

集合论是一门研究集合和它们之间关系的数学分支，广泛应用于各个领域，包括数学、计算机科学、统计学等。

在解题过程中，运用集合的常用方法和技巧有助于我们更全面、深刻和灵活地理解问题，找到准确的解决方案。

2. 集合的基本概念与运算在介绍集合解题方法和技巧之前，我们先来复习一下集合的基本概念与运算。

集合可以用大括号{}表示，元素之间用逗号分隔。

集合A={1,2,3,4}表示由元素1、2、3和4组成的集合A。

常用的集合运算有并集、交集、差集和补集。

并集表示两个或多个集合中所有的元素的集合，用符号∪表示；交集表示两个或多个集合中共有的元素的集合，用符号∩表示；差集表示一个集合中除去与另一个集合相同的元素后所剩下的元素的集合，用符号-表示；补集表示一个集合相对于于某个全集的剩余部分的集合，用符号'表示。

3. 集合解题方法3.1 确定问题的关键元素和条件在解题过程中，首先要明确问题给出的条件和需要求解的关键元素。

通过分析问题并提取关键信息，我们可以更好地理解问题的本质和要求。

3.2 利用集合间关系进行推理集合间的运算和关系是我们解题的基础。

通过应用集合的基本运算，我们可以得到更多的信息和结论。

通过求两个集合的交集，我们可以找到两个集合共有的元素；通过求两个集合的差集，我们可以找到一个集合相对于另一个集合的独有的元素。

3.3 使用 Venn 图进行可视化分析Venn 图是一种常用的图形工具，用于可视化分析集合的关系。

通过绘制Venn 图，我们可以清楚地看到集合之间的交集、并集和差集等。

借助Venn 图，我们可以更直观地理解和解决问题。

3.4 利用集合的性质和特点进行推导集合具有多种性质和特点，如互斥性、交换律、结合律等。

通过运用这些性质和特点，我们可以简化问题，从而更容易找到解决方案。

【判断】逻辑判断-集合推理（讲义）例1（2014北京）某公司有些新入职职工拥有博士学位。

该公司所有拥有博士学位的职工都被董事长单独接见过，而该公司所有甲省的职工都没有被董事长单独接见过。

如果以上陈述为真，则以下哪项也一定为真？A.有些新入职职工不是甲省的B.所有新入职职工都是甲省的C.有些新入职职工没有被董事长单独接见过D.有些拥有博士学位的职工是甲省的例2（2017江西）所有刑事侦查专业的大四学生毕业后都当警察了，有的警察是党员，刑事侦查专业的大四学生都不是警察。

由此可以推出的是（ ）。

A.有的党员是刑事侦查专业的大学毕业生B.有的党员不是刑事侦查专业的大四学生C.有的刑事侦查专业的大四学生是党员D.有的刑事侦查专业的大四学生不是党员例3（2018北京）有些参加语言学暑期高级讲习班的学生获得过青年语言学奖。

所有中文专业的三年级硕士生都参加了语言学暑期高级讲习班。

所有中文专业的一年级硕士生都没有参加语言学暑期高级讲习班。

如果以上陈述为真，可以推出A.有些获得过青年语言学奖的学生是中文专业的三年级硕士生B.有些中文专业的三年级硕士生获得过青年语言学奖C.有些获得过青年语言学奖的学生不是中文专业的一年级硕士生D.有些中文专业的一年级硕士生获得过青年语言学奖例4（2018国考）某公司30岁以下的年轻员工中有一部分报名参加了公司在周末举办的外语培训班。

该公司的部门经理一致同意在本周末开展野外拓展训练。

所有报名参加外语培训班的员工都反对在本周末开展拓展训练。

由此可以推出：A.所有部门经理年龄都在30岁以上B.该公司部门经理中有人报名参加了周末的外语培训班C.报名参加周末外语培训班的员工都是30岁以下的年轻人D.有些30岁以下的年轻员工不是部门经理例5（2015山东）所有来自中国的留学生，都住在校园内；所有住在校园内的学生，都必须参加运动会；有些中国留学生加入了学生会；有些心理学专业的学生也加入了学生会；所有心理学专业的学生都没有参加运动会。

逻辑推理三段论解集合推理全文共四篇示例，供读者参考第一篇示例：逻辑推理是一种重要的思维方式，它通过一定的规则和方法来进行推理和分析。

逻辑推理中的“三段论”是一种常用的思维模式，常常被应用于解集合推理问题。

本文将详细介绍逻辑推理中的三段论以及其在解集合推理中的应用。

让我们来了解一下什么是三段论。

三段论是逻辑学中的一种推理形式，由前提、肯定结论和否定结论三个部分组成。

三段论的形式通常是“A是B，B是C，因此A是C”，其中A、B、C分别代表不同的概念或命题。

通过这种形式的推理，我们可以通过已知的前提得出肯定或否定的结论。

在集合推理中，我们常常使用三段论来推理集合之间的关系。

举个简单的例子来说，假设A表示所有人，B表示男性，C表示父亲。

根据已知条件“A是B”（所有人都是男性）和“B是C”（男性都是父亲），我们可以得出结论“A是C”（所有人都是父亲）。

通过这样的三段论推理，我们可以推断出不同集合之间的关系。

除了上面的简单例子外，三段论在解集合推理问题时还可以有更加复杂的应用。

当给出一组复杂的集合关系图形时，我们可以通过运用三段论的思维方式，逐步分析不同集合之间的联系，进而得出正确的结论。

这种方法可以帮助我们清晰地理解集合之间的联系，从而更好地解决问题。

逻辑推理中的三段论是一种非常有效的推理方法，特别适用于解集合推理问题。

通过灵活运用三段论的思维方式，我们可以在解决问题时更加清晰地思考，较好地分析和推断集合之间的关系。

希望本文能帮助读者更好地理解逻辑推理中的三段论，并在实际应用中取得更好的效果。

【2000字】如果需要进一步了解逻辑推理和三段论的相关知识，推荐阅读《逻辑思维与三段论》等相关书籍。

逻辑推理的能力是一种非常重要的思维能力，它可以帮助我们更好地分析问题、推理结论，提高我们的逻辑思维能力。

希望大家都能够在日常生活和学习中灵活运用逻辑思维和三段论，提高自己的思维水平和解决问题的能力。

【2037字】第二篇示例：逻辑推理是一种重要的推理方式，通过逻辑推理可以从已知的前提推断出结论。

逻辑推理题型归纳及例题解析集合或范围重合型解这种题型的重点放在集合的“部分与全体”上，最直观的办法是根据题干提供的条件画个小图，题目即可迎刃而解。

45-46基于以下题干:在某住宅小区的居民中，大多数中老年教员都办了人寿保险，所有买了四居室以上住房的居民都办了财产保险。

而所有办了人寿保险的都没办理财产保险。

45.如果上述断定是真的，以下哪项关于该小区居民的断定必定是真的：I. 有中老年教员买了四居室以上的新房。

II. 有中老年教员没办理财产保险。

III.买了四居室以上住房的居民都没办理人寿保险。

A.I、II和III。

B.仅I和II。

C.仅II和III。

D.仅I和III。

E.仅II。

[解题分析] 正确答案：C。

大多数中老年教员办了人寿保险，而所有办了人寿保险的居民都没办理财产保险，所以大多数中老年教员没办财产保险，这是Ⅱ。

买了四居室以上住房的居民都办了财产保险，而所有办了人寿保险的居民都没办理财产保险，所以，买了四居室以上住房的居民都没办理人寿保险(否则矛盾了)，这是Ⅲ。

中老年教员和四居室以上住房之间没有建立因果联系，推不出Ⅰ来。

46.如果在题干的断定中再增加以下断定：“所有的中老年教员都办理了人寿保险”，并假设这些断定都是真的，那么，以下哪项必定是假的？A.在买了四居室以上住房的居民中有中老年教员。

B.并非所有办理人寿保险的都是中老年教员。

C.某些中老年教员没买四居室以上的住房。

D.所有的中老年教员都没办理财产保险。

E.某些办理了人寿保险的没买四居室以上的住房。

[解题分析] 正确答案：A。

题干发生了一个变化，从“大多数中老年教员都办理了人寿保险”加强为“所有的中老年教员都办理了人寿保险”，这就意味着所有的中老年教员都没办理财产保险。

而买了四居室以上住房的居民都办了财产保险，这就是说“所有的中老年教员”和“买了四居室以上住房的居民”这两个集合没有任何交集。

所以这选项A“在买了四居室以上住房的居民中有中老年教员”就为假了。

逻辑推理三段论解集合推理全文共四篇示例，供读者参考第一篇示例：逻辑推理是一种通过思维和推理来解决问题的方法。

其中的三段论是一种基本的推理模式，由三个命题组成：一个前提，一个结论以及一个中介命题。

通过逻辑推理，我们可以从已知的真实前提中得出正确的结论。

本文将聚焦于三段论解集合推理，探讨其基本原理和应用。

让我们先来了解三段论的基本结构。

三段论由三个命题构成，包括一个首位命题（major premise）、一个中介命题（minor premise）以及一个结论。

首位命题是一个一般性的命题，通常是一个普遍真实的陈述。

中介命题则是一个特殊情况的命题，基于首位命题中的一部分内容。

最终，结论是通过前两个命题进行推理得出的结论性命题。

在三段论中，通过首位命题和中介命题的结合，我们可以得出一个符合逻辑规则的结论。

这种推理方法可以帮助我们理清问题的逻辑关系，从而得出正确的结论。

举例来说，如果首位命题是“所有人类都是哺乳动物”，中介命题是“苏菲是人类”，那么结论就会是“苏菲是哺乳动物”。

而在集合推理中，我们可以利用三段论来推导出集合之间的关系。

集合是数学中一个非常基本的概念，它通过一组元素的集合来定义一个集合。

在集合推理中，我们可以根据已知的集合关系来推导出新的集合关系。

这种推理方法可以帮助我们更好地理解集合之间的关系，解决各种集合问题。

举个例子，如果我们已知集合A包含了所有奇数，集合B包含了所有小于10的数，那么我们可以通过三段论来得出结论：集合A∩B包含了所有小于10的奇数。

这个结论是通过首位命题“所有奇数都在集合A中”和中介命题“所有小于10的数都在集合B中”得出的。

在集合推理中，我们经常会使用几种常见的逻辑操作，比如并集、交集、差集等。

通过这些逻辑操作，我们可以更加精确地推导出集合之间的关系。

这种推理方法在数学、计算机科学等领域有着广泛的应用。

第二篇示例：逻辑推理是一种通过对前提和命题进行推理和论证来得出结论的思维方式。

行测题型类比推理之集合关系问题一、集合关系问题（星级：★★★）1、考试要点：概念的内涵是指所反映的对象的特有属性或本质属性，即对于对象的存在具有决定性意义的属性；也就是说，缺少了这些属性，对象便不存在了。

（如：有关“人”的概念。

文化人类学上，人被定义为能够使用语言、具有复杂的社会组织与科技发展的生物，尤其是能够建立团体与机构来达到互相支持与协助目的。

）概念的外延是指：具有概念所反映的本质属性的对象的范围。

（“人”概念在外延既可以包括婴儿、青年、壮年、老年人，也可以分为非洲人、亚洲人、美洲人，还可以分为古代人、现代人、当代人。

）集合关系（本质上指有关概念对象的范围）是概念在外延上的关系。

它包括全异关系、交叉关系、全同关系和包含关系四种。

全异关系：两个概念在外延上完全不相同。

（比如李白和土豆，诗仙和马铃薯等）并列关系：两个概念是同属的（两个不同的人，但上头的人是同一个，重点是彼此完全不同，但上级相同），包括矛盾关系和反对关系。

如果一个属概念下只有两个子概念，这两个子概念是矛盾关系，比如男人和女人，左手和右手；而如果有两个以上种概念，则任意其中两个是反对关系，比如苹果和桔子。

交叉关系：两个概念在外延上有交叉，它们是交叉关系（重点是在同一个维度），比如妇女和教授，妇女中有教授，教授中有妇女。

全同关系：两个概念在外延上完全相同。

比如等角三角形和等边三角形，中国和世界上人口最多的国家，全同关系的两个概念其实是同一意思的不同表达。

包含关系：一个概念在外延上大于并完全涵盖另外一个，比如水果和苹果。

2、真题：左手：右手与（）在内在逻辑关系上最为相似A.黑色：白色B.幸存者：遇难者C.晴天：阴天D.老人：孩子【解析】正常人只有两只手，除了左手就是右手，两词是矛盾关系。

A选项，除了黑色和白色外还有其他颜色，属于反对关系；C选项，除了阴天和晴天还有其他天气，属于反对关系；D选项，除了老人和孩子还有青年，也是反对关系。

B选项，事故中只有幸存者和遇难者，为矛盾关系，故答案为B.3、【答题秘笈】集合关系是类比推理最基础的考点，比较简单，注意区分矛盾关系和反对关系即可。

行测备考集合推理的四个基本命题国家公务员考试的《行测职业能力测验》包括五大部分内容：言语理解与表达、数量关系、判断推理、常识判断和资料分析，主要考察考生是否具有从事公务员职业必须具备的基本素质和潜在能力。

集合推理又称直言命题，考察参考人员对于集合关系的理解，以及简单的集合关系的转化。

集合推理是公务员考试中的一个难点，也是大多数考生经常放弃的部分。

本文主要一集合推理中的四个基本命题入手，帮助学习者解决集合推理问题。

一、四种基本形式：在集合推理中我们经常用S和P分别表示一个集合，也就是通常我们所说的S集合与P 集合。

两个集合之间的关系主要有4种情况，①所有的S都是P。

②所有S不是P。

③有的S是P。

④有的S不是P。

用欧拉图来表示这四种情况以上就是集合推理的四种基本形式，也是我们常说的四个基本命题，也可以简单翻译成：①所有S都是P翻译成S→P;②所有S不是P翻译成S→-P;③有的S是P翻译成有的S→P;④有的S不是P翻译成有的S→-P。

以上是我们学习集合推理的基础内容。

二、三个换位集合推理主要考察以逻辑学中的换位为主，以递推公式(三段论)为辅。

对于四个基本命题的换位形式共有三种，①所有S是P换位成有的P是S;②所有S不是P换位成所有P不是S;③有的S是P换位成有的P是S“;④有的S不是P是不能换位的。

总结一句口诀肯定形式限量换，否定所有直接换，否定有的不能换。

递推公式主要是A→B B →C 的出的结论为A→ C 但是对于中项的要求是，中项必须在大项和小项中周延一次。

简单的理解就是B→C中B的限定必须是所有。

【例1】某医院所有的医生都是男性，所有的护士都是女性，所有的已婚者都是护士，医务室主任尚未结婚。

A. 医务室主任是男性B. 已婚者中有男性C. 护士中可能有未婚者D. 医生中有的已经结婚【答案】C【解析】本题考察集合推理。

题干中所有已婚是护士，所有护士是女性，可以得出所有已婚是女性，换位的结果是有的女性是已婚的，根据”有的“的范围可知有的女性是已婚，可能存在有的护士可能未婚的情况。