当前位置：文档之家 › 中职机械制图球的截交线PPT课件

中职机械制图球的截交线PPT课件

  • 格式：ppt
  • 大小：1.06 MB
  • 文档页数：23

下载文档原格式

  / 23

合集下载

机械制图——截交线(平面切割平面体)_图文

机械制图——截交线(平面切割平面体)_图文
★ 画出截交线的投影
分别求出截平面与棱面的交线 ，并连接成多边形。
确定截交 线的形状
确定截交线 的投影特性
例1 补全三棱锥斜切后的俯左视图。
s’ Pv 3’
2’
s”3” 2”源自1’ 1”a’b’ c’ c” a” b”
3 1s
2
(3) 连接各点的同面投影即 等截交线的三个投影。 (4) 补全棱线的投影。
具体步骤如下：
(1) 求Pv与s’a’、s’b’、 s’c’的交点1’、2’、3’ 为截平面与各棱线的交点Ⅰ 、Ⅱ、Ⅲ的正面投影。
(2) 根据线上取点的方法，求 出1、2、3和1”、2”、3”
例1 补全三棱锥斜切后的俯左视图。
棱线法！
练一练
习题集P36（1 ）
例3:求六棱柱被截切后的水平投影和侧面投影
机械制图——截交线(平面切割平面体)_图文 .ppt
任务3-2 截交线、相贯线的分析与求作
一、平面与立体相交——截交线
平面与立体表面相交
截断面
产生的交线称为截交线 截交线 。
研究平面切割平面 体零件，其目的就是求 截交线的投影。
截平面
截交线与截断面
截交线的性质：
• 1)截交线是封闭的平面图形。 • 2) 截交线是截平面与立体表
5‫ ׳‬6‫׳‬ 7‫׳‬
1‫ ׳‬2‫׳‬
1‫ ״‬2‫״‬
3‫ ׳‬4‫׳‬
3‫״‬
5‫״‬
7‫״‬
4‫״‬
作图方法:
1 求棱线与截平面 的共有点 6‫ ״‬2 连线
3 根据可见性处理轮廓线
5 7
6
3 1
2 4
练一练
课本P77
面的共有线。
求截交线可归结为求截平面与立 体表面共有点、线的问题。

中职机械制图中职模块五立体表面的交线教学课件 工信版(共52张PPT)

中职机械制图中职模块五立体表面的交线教学课件 工信版(共52张PPT)
平面与立体相交
一、平面与棱柱相交例5-1 求作被截断四棱柱的三面投影，如图5-2（a）所示。
分析：由图5-2(a)正面投影可知，截平面是一个正垂面，因面有上底面和四个棱面，因此截交线是一个五边形（也可以根据截平面与四棱柱的三条棱线及上底面的两条边相交来判断截交线是一个五边形）;五边形的五个顶点分别是截平面与四棱柱的三条棱线及上底面的两条边的交点。
图5-3平面与三棱锥相交
平面与立体相交
作图：（1)作截交线的投影，如图5-3(b)所示。 ①确定截交线的正面投影。 ②求出截交线的水平投影。 ③作出截交线的侧面投影。(2）判别各条截交线投影的可见性，并连线。(3）完成被截切后三棱锥的三面投影图，如图5-3(c)所示。 被截切三棱锥的实体如图5-3(d)所示。
图5-2 平面与四棱柱相交
平面与立体相交
作图：（1）作五个顶点Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ的水平及侧面投影，如图5-2(b)所示。（2）依次连接截交线的五个顶点Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ的同面投影，并区分可见性，即得截交线的各面投影，如图5-2(c)所示。被截断四棱柱的实体如图5-2(d)所示。
图5-2 平面与四棱柱相交
平面与立体相交
平面与平面立体表面相交，其截交线是封闭的多边形。多边形的每一边均是截平面与平面立体的某一表面的交线；多边形的顶点是截平面与平面立体的棱线或底边的交点。因此，求平面与平面立体的截交线就是求平面与直线的交点及平面与平面的交线。平面与曲面立体表面相交，所产生的截交线通常有以下几种情况：（1）由平面曲线围成的封闭图形。（2）由平面曲线和直线段围成的封闭图形。（3）由直线段围成的封闭多边形。求平面与立体的截交线的一般步骤如下：（1）分析立体与截平面的相对位置。（2）分析截交线的形状。（3）投影作图。

机械制图——截交线(平面切割平面体)课件

机械制图——截交线(平面切割平面体)课件

SUMMAR Y
一款专门用于有限元分析的三维 CAD软件，可以进行高质量的三 维建模。
使用三维软件绘制截交线
打开三维建模软件，新建一个 空白文档。
使用软件的绘图工具，根据截 交线的形状和尺寸进行绘制。
根据需要，对截交线进行必要 的修改和调整，确保其符合实 际需求。
保存并导出三维模型，以便后 续应用和展示。
三维模型的应用与展示
REPORT
CATALOG
DATE
ANALYSIS
SUMMARY
机械制图——截交 线(平面切割平面体) 课件
目录
CONTENTS
• 截交线的基本概念 • 平面切割平面体的截交线 • 实际应用中的截交线 • 截交线的三维建模 • 截交线的实际操作练习
REPORT
CATALOG
DATE
ANALYSIS
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
05
截交线的实际操作练习
练习题一：绘制正方体的截交线
总结词
掌握正方体截交线的绘制方法
详细描述
通过平面切割正方体，观察截交线的形状和特点，掌握绘制正方体截交线的基本步骤和 技巧。
练习题二：绘制长方体的截交线
总结词
熟悉长方体截交线的绘制技巧
02
平面切割平面体的截交 线
正方体的切割
正方体在平面切割时，其截交线可能 是一个点、一条直线或一个平面多边 形。根据切割面的位置和角度，截交 线的形状会有所不同。
当切割面与正方体的一个面平行时， 截交线是一条直线；当切割面与正方 体的棱线平行时，截交线是一个平面 多边形；当切割面与正方体的顶点相 交时，截交线是一个点。

机械制图--基本体及截断PPT公开课(58页)

机械制图--基本体及截断PPT公开课(58页)

利用45°线作图
k" k'
k
二、圆锥
由圆锥面和底面组成。
1. 圆圆锥锥的面三是视由图直线SA(母线)
绕与它相交的轴线OO1旋转而 成。
S称为锥顶，圆锥面上过锥 顶的任一直线称为圆锥面的素 线。
SO
A O1
注意：轮廓 素线的投影 与曲面的可 见性的判断
圆锥的三视图画图步骤：
SO
s
s
A O1
a
c d
4 基本体及其截断
4.1 基本体 4.2 平面与立体相交 4.3 几何体的尺寸标注
返回
4 基本体及其截断
教学目标
1．掌握平面立体的投影特征，三视图画 法及表面取点。 2．掌握回转体的投影特征，三视图画法 及表面取点。 3．了解截交线的概念、性质，掌握求作 截交线的基本方法。 4．掌握基本体和截断体的尺寸标注。
O1 A1
平面立体的截交线一定是一个封闭的平面多边形，多边形的各顶点是截平面与被截棱线的交点，即立体被截断几条棱，那么截交线就
是几边形。
平面体一般应注长、宽、高尺寸。
(a) 截平面与上、下底面平行，截面为正五边形
注意：在截交线上不能标注尺寸。
★ 平面体截交线的性质：
如何找椭圆另一根轴的端点（即最前、最后点）
返回
44..11基基本本体体
44..11..11 平平面面体体
•平面体：表面由平面构成的形体 • 棱线：平面上相邻表面的交线
画平面体视图的实质： 画出所有棱线（或表面）的
投影，并根据它们的可见与否， 分别采用粗实线或虚线表示。
一、棱柱
棱柱有直棱柱和斜棱柱。 顶面和底面为正多边形的直棱 柱，称为正棱柱。
返回

机械工程制图截交线(机械)PPT课件

机械工程制图截交线(机械)PPT课件
16
取点的方法
1）轮廓线上取点 2）回转面上取点 3）利用积聚投影设点
积聚投影
17
例5:圆锥被正平面截切，补全正面投影图。
e′
●
●
c′
●
d′
●
a′
● b′
a●
●
c
e
●
●
●
db
E C DB
★判断
•截交线的空间形状？ •截交线的已知投影？
★求交
A
•找特殊点
•补充中间点
•光滑连接各点
★整形
•判断截交线的可见性
● ● ● ●
28
例9：求侧面投影
29
分析、比较
30
例10：求水平投影
●
●
●
●
31
例10：求水平投影
32
例10动画
33
例11：求水平投影
34
例11：求水平投影
35
分析、比较
36
动画演示
37
例12：求半球体截切后的水平投影和侧面投影。
两水个平侧面平与面圆与球圆面球的面 的交交线线，，水侧平面投投影影为为部部分分 圆圆弧弧，，水侧平面投投影影积积聚聚为为直 线直。线。
38
例12：求半球体截切后的水平投影和侧面投影。
水平两面个与侧圆平球面面与的圆交球线 面的的投交影线，，在侧俯面视投图影上为为 部部分分圆圆弧弧，，水在平侧投视影图积上 聚积为聚直为线直。线。
39
例13：求作顶尖的水平投影
●
●
●●
●
●●
●
● ●
● ●
● ●
● ●
首先分析复合回转体由哪些基本回转体组 成的以及它们的连接关系，然后分别求出这些基 本回转体的截交线，并依次将其连接。

机械制图——截交线(平面切割圆锥及球)ppt课件

机械制图——截交线(平面切割圆锥及球)ppt课件
平面与圆球相交，截交线的形状都是 圆，但根据截平面与投影面的相对位置 不同，其截交线的投影可能为圆、椭圆 或积聚成一条直线。
编辑版pppt
9
平面与球相交
例3：求半球体截切后的水平投影和侧面投影。
水两平个面侧截平圆面球截的圆截球交的线 截的交投线影的，投在影俯，视侧图面上投为 影部为分部圆分弧圆，，在水侧平视投图影上 积积聚聚为为直直线线。。
请同学们交作业
习题集P37-38
编辑版pppt
1
想一想
1、什么叫截交线？ 2、截交线有什么性质？ 3、作截交线投影的关键是什么？ 4、如何作回转体截交线的投影？
编辑版pppt
2
任务3-2 截交线、相贯线的分析与求作
截交线
截平面
截平面
截交线
编辑版pppt
3
（2）、平面与圆锥相交（P82）
根据截平面与圆锥轴线的相对位 置不同，截交线有五种形状。
● ●
● ●
●
●
首先分析复合回转体由哪些基本回转体组成 以及它们的连接关系，然后分别求出这些基本回 转体的截交线，并依次将其连接。
编辑版pppt
16
作业 习题集40、41、42
编辑版pppt
17
感谢亲观看此幻灯片，此课件部分内容来源于网络， 如有侵权请及时联系我们删除，谢谢配合！
编辑版pppt
4
编辑版pppt
5
例1: 圆锥被正垂面截切，求截交线，并完成三视图。 （同步练习）
截交线的投影特性？ 截交线的空间形状？
编辑版pppt
6
例1: 圆锥被正垂面截切，求截交线，并完成三视图。 （同步练习）
编辑版pppt
7

例2：习题集P40第2题

机械制图课件-曲面立体的截交线

机械制图课件-曲面立体的截交线

b ca
[例題3] 求圓錐截交線
2' 3'
a'
3"
4'5'
5"
1'
3 5
1
a
解題步驟
1．分析 截平面為正垂
面側平面，截交線為部
分橢圓和梯形的組合；
其水準投影為部分橢圓
2" 和直線的組合，側面投
4"
影為部分橢圓和梯形的
組合；
1"
2．求出截交線上的特殊
點Ⅰ、 Ⅱ、Ⅲ ；
3．出一般點Ⅳ、Ⅴ ；
4．光滑且順次地連接各 點，作出截交線，並且 判別可見性；
5．整理輪廓線。
[例題2] 求圓錐截交線
a' c' b'
a"
c" b"
解題步驟
1．分析 截平面為正平面，截交線 為雙曲線；截交線的水準投影和側 面投影已知，正面投影為雙曲線並 反映實形；
2．求出截交線上的特殊點A、C；
3．求出一般點B ；
4．光滑且順次地連接各點，作出截 交線，並且判別可見性；
5．整理輪廓線。
[例題3] 求圓柱截交線
1'2'
2'
3'4'
4'
24
1' 3'
解題步驟
1．分析 截交線的水準投 影為直線和部分圓，側面 投影為矩形；
2．求出截交線上的特殊點 Ⅰ、Ⅱ、Ⅲ、Ⅳ；
3．順次地連接各點，作出 截交線並判別可見性；
4．整理輪廓線。
13
[例題4 ] 求圓柱截交線
1'2'
2"

机械制图截交[1]

机械制图截交[1]
机械制图截交
PPT文档演模板
2020/11/18
机械制图截交[1]
截交线的性质
①截交线是截平面与立体表面的共 有线，截交线上的点是截平面与立体表 面的共有点。
②截交线一般是封闭的平面图 形。 ③ 截交线形状取决于立体表面的形 状和截平面与立体的相对位置。
一、平面与平面立体相交
• 截交线是一个由直线组成的封闭的平面多边形。 • 截交线的每条边是截平面与棱面的交线。
2） 求一般点 3） 将各点光滑地连接起来，判断截交线的可见性。 4） 整理转向轮廓线
1、平面与圆柱相交
截平面与圆柱面的截交线的形状取决于截平面 与圆柱轴线的相对位置
PV
PV PV
P
垂直 圆
P
P
倾斜 椭圆
平行 两平行直线
例题4：求圆柱体的截交线
1′
1″
2′
2″
Ⅰ Ⅱ
（1 2）
例题5：求圆柱体的截交线
Ⅰ
正垂线
Ⅲ
正平线
a' c'
b'
[例题]
求圆锥截交线
a" c"
b"
解题步骤
1．分析 截平面为正平面，截 交线为双曲线；截交线的水平 投影和侧面投影已知，正面投 影为双曲线并反映实形；
2．求出截交线上的特殊点A、 C；
3．求出一般点B ；
4．光滑且顺次地连接各点，作 出截交线，并且判别可见性；
5．整理轮廓线。
机械制图截交[1]
3rew
演讲完毕，谢谢听讲!
再见，see you again
PPT文档演模板
2020/11/18
机械制图截交[1]
判别可见性。

《机械制图》课件——第3章-2 截交线

《机械制图》课件——第3章-2 截交线
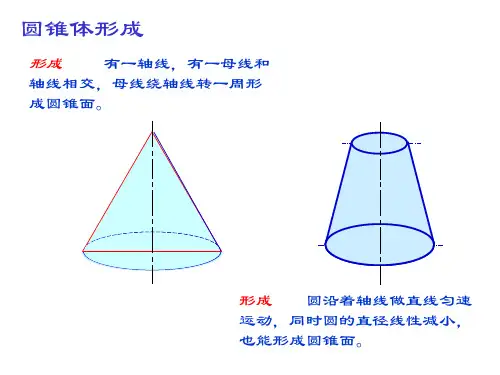
目录
截交线空间形状为椭圆时的水平投影的变化：
设截平面与圆柱轴线的倾角为β，当β的大小变化时 ，其交线的H 投影分别为： 1）β〈 45°时，椭圆长 轴水平；2）β=45°时,水平投影为圆；3）β〉45° 长轴椭垂圆直。
目录
[例3] 求圆柱与正垂面的截交线。
(c’)d’ a’
b’ c”
e”
c
a
b
b”
当截交线的投影为非圆曲线时，其作图步骤为： * 先找特殊点，补充中间点。
* 光滑连接各点，并判断截交线的可见性。 截交线的形状为圆、椭圆或直线段时，可求出特 殊点后直接画出。同时注意判断截交线的可见性。
目录
1. 圆柱的截交线
目录
1. 圆柱的截交线
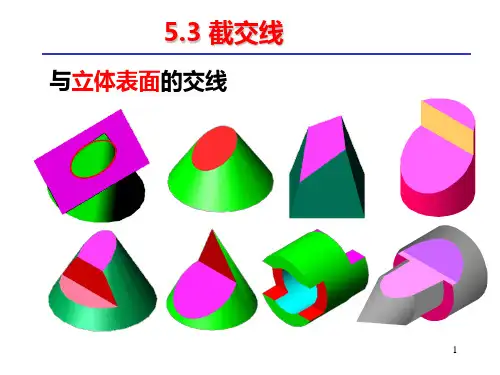
平面与圆柱面相交时，根据平面与圆柱轴线 的相对位置不同，其截交线有三种情况：矩 形、 圆和椭圆。
目录
[例9]求P平面与圆锥截交线的投影。
分析
P平面为正平面 且平行于圆锥的
轴线，与圆锥面
的交线为双曲线
，其H投影积聚
H
在P 上，W投
影
W
积聚在P
出交线的上V，投求影
即可。
目录
[例10]圆锥被正垂面P和侧平面Q作俯视图 和左视图。
目录
3. 圆球的截交线
（1） 圆球截交线的形状
圆球的截交线总是圆。 由于截平面相对于投影面的位置不同，截交线的 投影可能是圆、椭圆或直线。
d” a” e”
解题步骤：
1．分析：截交线的 正面投影积聚在正垂 截面上，水平投影落 在圆柱的投影圆上； 侧面投影为椭圆。只 有侧面投影未知。 2．求侧面投影：先求 出截交线上的四个特 殊点a、b、c、d； 3．求出若干个一般点 e、e1等；

机械制图截交线的画法课件

机械制图截交线的画法课件

标目感情
。合结机有识知性理和识知性感使�来起系 联际实活生的富丰量大与识知课本将�力能的际实系联论 理 d � 力能象想间空高提 c � 力能维 思辑逻的 定一握掌而 从�论结出得理推和识知有已过通生学让�力能理推和移 迁识 知 b �形图件 零察观会学 生学求要 �力能察观炼锻 a
标目力能
。质性 的线 交 截确明� 法画其及析分 的 线交截对握掌�习学的 节 本对 过 通 c 。 念 概 的 线 交 截 立 建 中 脑 头 在 析 分 的 形 图 对 过通 b。 状形 、 构结的线交 截 上件零 单简识认生学使 a
�2
’s
�1
’a
3 。线廓轮理整 4 �性见可别 判且并� 线交截出作 �点各接连地次顺 3 � Ⅳ 、Ⅲ 、Ⅱ、Ⅰ 点 折的上线交截出求 2 �知未影投面侧和影 投平水� 知已影投面 正的线交截 析分 1 骤步题解
2
�3
面 平 截 面 平 截
线 交 截 线 交截
.线有共 的体立切截被和面平截是线交截 。 形图闭封个一是线交截
。 来 出 括 概话 句 一 用 � 么 什 了到看上体何几本基在你�题问出提
料材查调的线交截 和史历械机于关示展体媒多过通生学
。形边多或形图面平的成组线直和 线曲由是者或线曲面平条一是常通�条线的闭封是定一线 交截以所�围范间空的定一有都体立何任于由。上面表体 立在又上面平截在既它�点有共的上面表体立与面平截是 点的上线交截�线有共的面表体立和面平截是线交截 。面平截为称面平 该�线交截为称线交生产面表体立在交相体立与面平
面平截 线交截
念概的线交截
。 置 位 的 线交 截 认 确 生 学 由� 状 形 件 零 的 线 交截有具同不示演幕屏大用�1习练上课

机械制图圆锥和球的截交线(PPT47页)

机械制图圆锥和球的截交线(PPT47页)
平行截切，投影为圆 斜切，投影为椭圆
球体上取点
m’ (s’)
(s) m
m’’
(s’’)
球体上取点
(3’) 1’
(4’) 2’
3” (4”)
1” 2”
(4) 3
(2) 1
球体上取线
球的截交线
球的截交线
应用的例子
补正面和水平投影
补正面和水平投影
选择题1
a
b
c
d
选择题2
a
b
c
d
选择题3
1’ 4’(5’) 2’(3’)
3’’ 5’’ 1’’
4’’ 2’’
3 5 1
4 2
圆锥的截交----椭圆
1’ 3’(4’) 5’(6’)
1”
4”
3”
6”
5”
2’
2”
6 4
1
2
3 5
圆锥的截交----例: 椭圆
例2:圆锥截交（补全俯视图，左视图）(1)
3’(4’)
4’’
3’’
5’(6’) 6’’
人生就像骑单车，想保持平衡就得往前走
•
7、
。202 0年10 月2020/1 0/1520 20/10/ 152020/ 10/151 0/15/2 020
•
8、业余生活要有意义，不要越轨。20 20/10/ 152020 /10/15 October 15, 2020
我们必须在失败中寻找胜利，在绝望中寻求希望
a
b
c
d
选择题4
a
b
c
d
球柱1(改错)
球柱2
球锥1
《机械设计制图》书中章节
P49，第三章第四节 表3-9、常见回转体的投影与投影特性 P51，表3-11 在回转面上取点取线 P58~59，二、平面与立体表面的交线
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
求相贯线的方法： 求相贯线的实质即是求两回转体表面一系列共有
点，然后依次光滑地连接即为相贯线。 方法：辅助平面法 利用积聚性
利用积聚性求相贯线
当两圆柱体的轴线正交时，相贯线的两面投影具有积 聚性，并且已知其投影，由时可求相贯线的第三面投影。
作图方法（1）求特殊点；（2）求一般点；
（3）顺次光滑连接各点，即得相贯线的正面投影。
⑵ 求截交线
当截交线的投影为非圆曲线时，要先 找特殊点，再补充中间点，最后光滑连接 各点。
注意分析平面体的棱线和回转体轮廓 线的投影。⑶ 当单体被多个截平面截切时，要逐个截 平面进行截交线的分析与作图。当只有 局部被截切时，先按整体被截切求出截 交线，然后再取局部。
⑷ 求复合回转体的截交线，应首先分析复 合回转体由哪些基本回转体组成以及它 们的连接关系，然后分别求出这些基本 回转体的截交线，并依次将其连接。
㈡ 圆锥体表面的截交线
表7-2平面与圆锥体相交的各种形式
组合回转体被截切后的投影分析 P 双曲线 直线 直线
圆锥 截面
圆柱1 圆柱2
组合回转体被截切后的投影作图
顶点
小结
重点掌握求立体表面的截交线与相贯线的 作图方法。
立体表面的截交线
⒈ 平面体的截交线一般情况下是由直线组成 的封闭的平面多边形，多边形的边是截平 面与棱面的交线。
求截交线的方法：棱线法 棱面法
⒉ 平面截切回转体，截交线的形状取决于截 平面与被截立体轴线的相对位置。
截交线是截平面与回转体表面的共有线。
⒊ 解题方法与步骤
⑴ 空间及投影分析
☆分析截平面与被截立体的相对位置，以 确定截交线的形状。
☆分析截平面与被截立体对投影面的相对 位置，以确定截交线的投影特性。
⒊ 解题过程
⑴ 空间分析： 分析相交两立体的表面形状， 形体大小及
相对位置，预见交线的形状。 ⑵ 投影分析：
是否有积聚性投影？找出相贯线的已知投影， 预见未知投影，从而选择解题方法。
(2) 求回转体截交线的实质：
• 求截平面与回转体上被截各素线的交点，然后依 次光滑连接。
例：求半球体被截后的俯视图和左视图。
两水个平侧面平截面圆截球圆的球截的交截线 交的线投的影投，影在，俯在视侧图视上图为 上部为分部圆分弧圆，弧在，侧在视俯图视上 图积上聚积为聚直为线直。线。
半球体被截后的视图和立体图。
第四节 相贯线
•相贯线也是机器零件的一种表面交线，与截 交线不同的是，相贯线不是由平面切割几何体 形成的，而是由两个几何体互相贯穿所产生的 表面交线。
零件表面的相贯线大都是圆柱圆锥球面等回转 体表面相交而成。
相贯线的性质：
（1）相贯线是互相贯穿的两个形体 表面的共有线，也是两个相交形体 的表面分界线； （2）由于形体占 有一定的空间，所以，相贯线一般 是闭合的空间曲线，有时则为平面 曲线。
(1)求特殊点及截交线与圆的切点
中点
切点
(2)求一般点
(3)由点连线并整理加深图形
四. 回转体的截交
(1) 回转体截交线的性质：
• 截交线是截平面与回转体表面的共有线。 • 截交线的形状取决于回转体表面的形状及
截平面与回转体轴线的相对位置。 • 截交线都是封闭的平面图形（封闭曲线或由直线 和曲线围成）。
◆两外表
◆一外表面与
面相交
一内表面相交
◆两内表 面相交
⒉ 两圆柱直径的变化对相贯线的影响
曲交 线线 （为 椭两 圆条 ）平
面
交线向大圆柱一侧弯
相贯线的特殊情况 1.两回转体有公共轴线时，相贯为圆
相贯线为直线
小结
立体表面的相贯线
⒈ 相贯线的性质：表面性 共有性 封闭性 ⒉ 求相贯线的基本方法
辅助平面法 积聚性（面上找点）法
例1：补全主视图
圆柱线直投面侧水柱轴；，的面平影面线左其四共投投由分相平右交棱有影影于析交行两线柱线积积相空：，，棱为的，聚聚贯间前其面两四所在在线分后交与段个以 一 矩是析两线圆圆棱相段形两：棱为柱弧面贯圆上立面两轴。分线弧。体与段线别的上表圆直垂与，
例1结果：补全主视图
讨论：
⒈ 相贯线的产生：
三、球的截交线
用一截平面切割球，所形成的截交线都 是圆。当截平面与某一投影面平行时，截 交线在该投影面上的投影为一圆，在其他
两投影面上的投影都积聚为直线。
球被正垂面截切
当截平面与某一投影面垂直时，截 交线在该投影面上的投影积聚为直线，
在其他两投影面上的投影均为椭圆。 如图所示：
球的截交线作图步骤：