巧数图形

巧数图形知识点总结一、巧数图形的定义巧数图形是用数的巧妙组合构成的图形，它们的特点是构造简单、形状美观、规律性强。

巧数图形可以用来培养学生的数学想象力和创造力，同时也可以帮助学生建立几何直观概念，加深对数学知识的理解和应用。

巧数图形的构造方法主要有以下几种：1. 数列构造法：通过数列的递推关系构造图形，例如斐波那契数列、等差数列、等比数列等；2. 几何构造法：通过几何图形的组合构造出新的巧数图形，例如通过三角形、矩形、正多边形等的组合；3. 代数构造法：通过代数式的变换构造出巧数图形，例如平方差公式、配方法、因式分解等。

二、巧数图形的常见类型1. 斐波那契数列构成的图形：斐波那契数列是一个非常有趣的数列，它的每一项都是前两项之和，即f(n)=f(n-1)+f(n-2)，其中f(1)=1，f(2)=1。

将斐波那契数列的相邻两项相连，可以构成一些特殊的图形，如斐波那契螺旋、斐波那契凤凰等。

2. 等差数列构成的图形：等差数列是一个常见的数学概念，它的每一项与前一项的差都相等。

将等差数列的项以一定的规律布局在平面上，就可以构造出一些规律性强、形状美观的图形，如等差数列的排列图形、螺旋图形等。

3. 等比数列构成的图形：等比数列是另一个常见的数学概念，它的每一项与前一项的比都相等。

将等比数列的项以一定的规律布局在平面上，就可以构造出一些具有规律性的图形，如等比数列的排列图形、螺旋图形等。

4. 几何图形的组合：通过组合几何图形，可以构造出一些特殊的图形，如通过三角形的组合构造出五角星、六边形的组合构造出六芒星等。

5. 代数式的变换：通过一些代数式的变换，也可以构造出一些具有规律性和美观性的图形，如通过平方差公式构造出差平方图形、通过因式分解构造出差方形图形等。

三、巧数图形的特性巧数图形具有一些特殊的性质和规律，以下是一些常见的特性：1. 对称性：许多巧数图形都具有对称性，即可以通过某种轴对称变换得到自身。

对称性是一个非常重要的性质，它可以帮助我们更好地理解和分析图形的结构和特点。

巧数图形教案学而思精品文档巧数图形教案学而思:一、规则图形线段角 1. 分类数2. 公式法基本线段数依次加到1.端点,1,基本线段数一数下图中一共有多少条线段,? ? ? ?方法1: 方法2:恰含1条:4条基本线段有4条，所以从4开始加恰含2条:??、??、??条，3，2，1,10恰含3条:???、???条恰含4条:???? 1条注:肩并肩手拉手的规则图形都能用公式总数:4，3，2，1,10 法，关键是找火车头。

二、多层图形1. 多层三角形每层个数×层数,总数数一数图中有多少个三角形,每层个数:3，2，1,层数:2层总数:6×2,1 一共12个。

1 / 11精品文档2. 多层长方形每层个数× 层数 , 总数× , 总数数一数下图中一共有多少个长方形,每层个数:3，2，1,6层数:2，1,3总数:6×3,1一共18个。

三、不规则图形按方向分类分类数按大小分类按方向分类下图中有多少个三角形, ?、?、?、?、?、?6个??、??、??个???、???、???、???、???、???个?????? 1个6，3，6，1,1 一共16个。

:1. 下面图中给出的五个点之间，每两个点之间画一2 / 11精品文档条线段，一共可以画出多少条线段,2. 数一数图中有多少个正方形,3. 数一数下图中一共有多少个三角形,4. 数一数，图中共有个长方形，个三角形，条线段。

:本讲讲的是数图形的方法，根据不同类型的图形有不同的巧妙方法，同学们要仔细辨认图形种类，像是规则图形和多层图形都是有巧妙方法的;如果是不规则图形，那么一定要注意分类，数的时候思路要清楚，这样才不会数错。

二年级数学思维训练数图形教案11、使学生学会解决数线段的问题，掌握有序分类图形的方法。

增强学生应用数学的意识。

2、通过活动，培养学生的口头表达能力、初步的观察推理能力和探究问题的能力。

进一步培养学生的发散思维和创新能力。

第一讲巧数图形【知识要点】：我们已经认识了线段、角、三角形、长方形等基本图形，当这些图形重重叠叠地交错在一起时就构成了复杂的几何图形。

要想准确地计数这类图形中所包含的某一种基本图形的个数，就需要仔细地观察，灵活地运用有关的知识和思考方法，掌握数图形的规律，才能获得正确的结果。

要准确、迅速地计数图形必须注意以下几点：1.弄清被数图形的特征和变化规律。

2.要按一定的顺序数，做到不重复，不遗漏。

【例题精讲】例1：数出下面图中有多少条线段。

试一试：数出下列图中有多少条线段。

（2）（3）例2：数一数下图中有多少个锐角。

试一试：下列各图中各有多少个锐角？例3：数一数下图中共有多少个三角形。

试一试：数一数下面图中各有多少个三角形。

例4：右图中有多少个三角形？例5：数一数下图中有多少个长方形？试一试：数一数，下面各图中分别有几个长方形？例6：数一数，下图中有多少个正方形？（每个小方格是边长为1的正方形）试一试：数一数下列各图中分别有多少个正方形？（每个小方格为边长是1的小正方形）例7：从广州到北京的某次快车中途要停靠8个大站，铁路局要为这次快车准备多少种不同车的车票？这些车票中有多少种不同的票价？试一试：从上海到武汉的航运线上，有9个停靠码头，航运公司要为这段航运线准备多少种不同的船票？这些船票中有多少种不同的票价？【巩固练习】1、数出下列图中有多少条线段。

(3)2、数一数下图中共有多少个三角形。

3、数一数下图中有多少个长方形。

4、下列图形中，不含“*”号的三角形或长方形各有几个？5、数一数下列各图中分别有多少个正方形。

6、从上海至青岛的某次直快列车，中途要停靠6个大站，这次列车有几种不同票价？7、从成都到南京的快车，中途要停靠9个站，有几种不同的票价？。

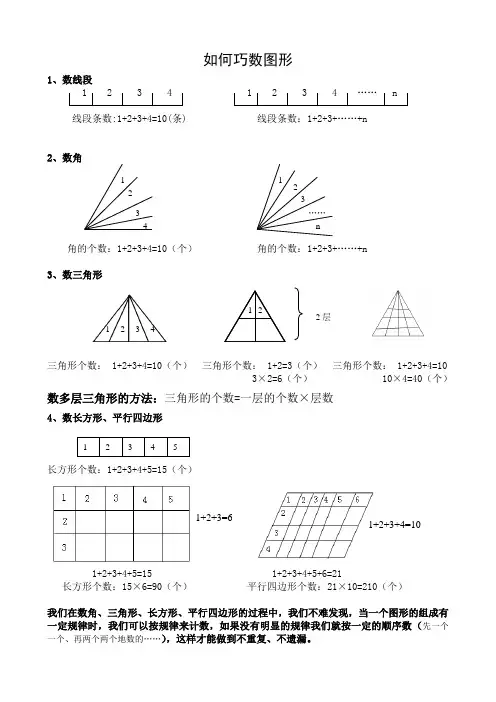
如何巧数图形
1、数线段 1 2 3 4 1 2 3 4 …… n
线段条数:1+2+3+4=10(条) 线段条数：1+2+3+……+n
2、数角
角的个数：1+2+3+4=10（个） 角的个数：1+2+3+……+n
3、数三角形
三角形个数： 1+2+3+4=10（个） 三角形个数： 1+2=3（个） 三角形个数： 1+2+3+4=10 3×2=6（个） 10×4=40（个） 数多层三角形的方法：三角形的个数=一层的个数×层数
4、数长方形、平行四边形
长方形个数：1+2+3+4+5=15（个）
1+2+3+4+5=15 1+2+3+4+5+6=21
长方形个数：15×6=90（个） 平行四边形个数：21×10=210（个）
我们在数角、三角形、长方形、平行四边形的过程中，我们不难发现，当一个图形的组成有一定规律时，我们可以按规律来计数，如果没有明显的规律我们就按一定的顺序数（先一个一个、再两个两个地数的……），这样才能做到不重复、不遗漏。

1 2 3 4 1 2 3 ……
n 1 2 3 4
1 2
2层 1 2 3 4 5 1+2+3=6 1+2+3+4=10
5、数不规则图形。

（1+2+3+4+5+6）×（1+2+3）＋（1+2+3）×（1+2+3+4）－（1+2+3）×（1+2+3）=150。

第一讲巧数图形数出某种图形的个数是一类有趣的图形问题。

数图形虽然很简单，但重复计数和遗漏是经常出现的错误，在细心的同时还要掌握一定的方法和技巧。

几何中的计数问题包括：数线段、数角、数长方形、数正方形、数三角形、数综合图形等。

通过这一讲的学习，可以帮助我们养成按照一定顺序去观察、去思考问题的良好习惯，同时提高我们通过观察、思考去探寻事物规律的能力。

要想有条理、不重复、不遗漏地数出所要图形的个数，最常用的方法就是分类数。

一、数线段我们把直线上两点间的部分称为线段，这两个点称为线段的端点.线段是组成三角形、正方形、长方形、多边形等最基本的元素。

因此，观察图形中的线段，探寻线段与线段之间、线段与其他图形之间的联系，对于了解图形、分析图形是很重要的。

例1、数一数，图中有多少条线段？分析与解：如果我们按照一定的顺序从左往右数，就会发现：以A点为共同端点的线段有：AB AC AD AE AF 5条；以B点为共同端点的线段有：BC BD BE BF 4条；以C点为共同左端点的线段有：CD CE CF 3条；以D点为共同左端点的线段有：DE DF 2条；以E点为共同左端点的线段有：EF 1条；总数为：5+4+3+2+1=15条。

用图示法表示更为直观明了，如右图。

想一想：①由例1可知，一条线段AF上有六个点，就有：总数=5+4+3+2+1条线段。

由此猜想如下规律（见右图）：……………………还可以一直找下去，并且通过实际去按顺序数，经过验证后，能从中得出这样一个结论：当一个图形中包含的所有线段都在同一条直线上时，线段总条数是从1开始的一串连续自然数之和，其中最大的自然数比图形中的总端点数少1.②如果我们把相邻两点间的线段叫做基本线段，那么线段的总条数也是从1开始的一串连续自然数之和，其中最大的自然数等于基本线段的条数（见下图）。

基本线段数线段总条数……………………是不是存在这样的规律，同学们可以自己再举些例子试试看。

巧数图形月 日 姓 名知识要点：1．巧数图形问题包括：数线段、数三角形、数正方形、数长方形等。

2．数图形的个数，不但要有一双好眼睛，还要善于开动脑筋，仔细观察，按顺序分类去做，做到不重复，不遗漏，这样才能数得又快又准。

通过数线段、数三角形、数角等总结出共用的方法：（n －1）＋(n －2)＋(n －3)＋…＋2＋1经典例题：例1．（1）图4-1中有多少条线段？（2）图4-2中共有多少个角？（3）数一数图4-3中共有多少个三角形？例2．图4-4中一共有多少条线段？图4-1图4-2图4-3图4-4例3．数一数图4-5有多少个正方形？例4．图4-6中一共有多少个长方形？就地练兵1．如图4-7所示图中共有条线段。

2．数一数图4-8中有多少个三角形？3．如图4-9所示，图中共有多少条线段？4．数一数图4-10中有多少条线段？图4-5图4-6图4-7图4-8123C图4-10图4-95．图4-11中共有多少锐角？6．如图4-12所示，图中共有 线段，共有 个三角形。

7．图4-13中共有 个三角形。

8．（1）数一数图4-14中有多少个正方形。

（2）数一数图4-15中共有多少个正方形？9．数一数图4-16中有多少个长方形？A OC 1 C 2 C 20B图4-11· · · 图4-12C图4-13 图4-14图4-15图4-16课后大考验姓 名 成 绩1．如图4-17中共有 条线段。

2．数一数，图4-18中有多少条线段？3．图4-19中共有多少个角？4．数一数图4-20有多少个正方形？5．图4-21中共有多少个长方形？AB C D EF G图4-172 3 4 56图4-19图4-20图4-21图4-18。