[高一数学]必修1数学-函数概念

第二章函数1．函数的概念：设A、B是非空的数集，如果按照某个确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f(x)和它对应，那么就称f：A→B为从集合A到集合B的一个函数．记作：y=f(x)，x∈A．其中，x叫做自变量，x的取值范围A叫做函数的定义域；与x的值相对应的y值叫做函数值，函数值的集合{f(x)| x∈A }叫做函数的值域．注意：如果只给出解析式y=f(x)，而没有指明它的定义域，则函数的定义域即是指能使这个式子有意义的实数的集合；函数的定义域、值域要写成集合或区间的形式．2，定义域补充:能使函数式有意义的实数x的集合称为函数的定义域，求函数的定义域时列不等式组的主要依据是：(1)分式的分母不等于零；(2)偶次方根的被开方数不小于零；(3)对数式的真数必须大于零；(4)指数、对数式的底必须大于零且不等于1.(5)如果函数是由一些基本函数通过四则运算结合而成的.那么，它的定义域是使各部分都有意义的x的值组成的集合.(6)指数为零底不可以等于零(7)实际问题中的函数的定义域还要保证实际问题有意义.(又注意：求出不等式组的解集即为函数的定义域。

)构成函数的三要素：定义域、对应关系和值域再注意：（1）构成函数三个要素是定义域、对应关系和值域．由于值域是由定义域和对应关系决定的，所以，如果两个函数的定义域和对应关系完全一致，即称这两个函数相等（或为同一函数）（2）两个函数相等当且仅当它们的定义域和对应关系完全一致，而与表示自变量和函数值的字母无关。

相同函数的判断方法：①表达式相同；②定义域一致(两点必须同时具备)值域补充:（1）、函数的值域取决于定义域和对应法则，不论采取什么方法求函数的值域都应先考虑其定义域.（2）应熟悉掌握一次函数、二次函数、指数、对数函数与各三角函数的值域，它是求解复杂函数值域的基础。

一、 例题变式例1、求下列函数的定义域：（1）43--=x x y (2)()121x f x x =--(3)6522+--=x x x y变式1、求下列函数的定义域： （1）x x y 513-=（2）y （3）0(1)()x f x x x +=-例2、已知等腰三角形的周长为17，写出它的底边长y 与腰长x 之间的函数关系式？并指出函数的定义域。

必修一第一章 集合与函数概念二、函数知识点8：函数的概念以及区间 1》函数概念设A 、B 是非空的数集，如果按某个确定的对应关系f ，使对于集合A 中的任意一个数x ，在集合B 中都有唯一确定的数y 和它对应，那么就称f ：A →B 为从集合A 到集合B 的一个函数，记作y =()f x 注意：①x A ∈．其中，x 叫自变量，x 的取值范围A 叫作定义域②与x 的值对应的y 值叫函数值，函数值的集合{()|}f x x A ∈叫值域.2》区间和无穷大①设a 、b 是两个实数，且a<b ，则：{x|a ≤x ≤b}＝[a,b] 叫闭区间； ②{x|a<x<b}＝(a,b) 叫开区间；③{x|a ≤x<b}＝[,)a b ， {x|a<x ≤b}＝(,]a b ，都叫半开半闭区间.④符号：“∞”读“无穷大”；“－∞”读“负无穷大”；“+∞”读“正无穷大”. 则{|}(,)x x a a >=+∞，{|}[,)x x a a ≥=+∞，{|}(,)x x b b <=-∞，{|}(,]x x b b ≤=-∞，(,)R =-∞+∞.3》决定函数的三个要素是定义域、值域和对应法则. 当且仅当函数定义域、对应法则分别相同时，函数才是同一函数.典例分析题型1：函数定义的考察 例1：集合A=}{40≤≤x x ，B=}{20≤≤y y ，下列不表示从A 到B 的函数是（ ）A 、x y x f 21)(=→ B 、x y x f 31)(=→ C 、x y x f 32)(=→ D 、x y x f =→)(例2：下列对应关系是否是从A 到B 的函数：①}{;:,0,x x f x x B R A →>== ②,:,,B A f N B Z A →==求平方；③B A f Z B Z A →==:,,，求算术平方根； ④B A f Z B N A →==:,,，求平方； ⑤A=[-2,2],B=[-3,3],B A f →:,求立方。

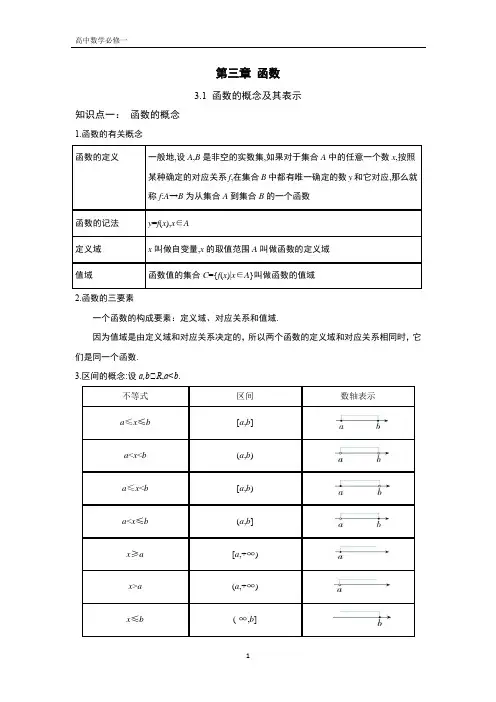
第三章函数3.1 函数的概念及其表示知识点一：函数的概念1.函数的有关概念2.函数的三要素一个函数的构成要素：定义域、对应关系和值域.因为值域是由定义域和对应关系决定的，所以两个函数的定义域和对应关系相同时，它们是同一个函数.3.区间的概念:设a,b∈R,a<b.实数集R可以用区间表示为(-∞,+∞).知识点二：函数的表示法1.函数的三种表示法2.分段函数已知函数y=f(x)，x∈A，如果自变量x在不同的取值范围内，函数有着不同的对应关系，那么我们称这样的函数为分段函数.【思考】1.函数的定义域和值域是否一定是无限集?2.区间是数集的另一种表示方法,是否任何数集都能用区间表示?3.根据函数的定义,任何一个自变量x是否都有唯一的函数值y与之对应?任何一个函数值y 是否都有唯一的自变量x与之对应?4.如何确定分段函数的定义域和值域?【解析】1.不一定.函数的定义域和值域也可能是有限集,如f(x)=1，x∈{1,2,3}.2.不是.如集合{0,1}就不能用区间表示.3.任何一个自变量x都有唯一的函数值y与之对应，但是函数值y不一定有唯一的自变量x 与之对应。

如f(x)=x2中，函数值4有两个自变量2、-2与之对应。

函数中x，y的对应关系是“一对一”或“多对一”,不能“一对多”.4.分段函数的定义域是每一段自变量取值范围的并集,值域也是每一段函数值取值范围的并集.3.1.1 函数的概念基础练一函数的概念1.（多选题）下面选项中,变量y是变量x的函数的是()A.x表示某一天中的时刻,y表示对应的某地区的气温B.x表示年份,y表示对应的某地区的GDP(国内生产总值)C.x表示某地区学生的某次数学考试成绩,y表示该地区学生对应的考试号D.x表示某人的月收入,y表示对应的个税2.下列四组函数中,表示同一个函数的是()3A.y=|x|与y=√x3B.y=√x2与s=(√t)2C.y=2t+1与y=2u+1D.y=1与y=x03.设集合M={x|0≤x≤2},N={y|0≤y≤2},那么下面的4个图形中,能表示以集合M为定义域,集合N为值域的函数关系的有()A.①②③④B.①②③C.②③D.②④二函数的定义域4.函数f(x)=√x−1的定义域为() x−2A.[1,+∞)B.[1,2)C.[1,2)∪(2,+∞)D.(1,2)∪(2,+∞)5.已知某矩形的周长为定值a,若该矩形的面积S是这个矩形的一边长x的函数,则这个函数的定义域是.6.已知函数y=f(x)的定义域为[-2,3],则函数y=f(2x+1)的定义域为.x+1三函数值及函数的值域7.已知集合P={x|y=√x−1},集合Q={y|y=√x−1},则()A.P=QB.P⫋QC.Q⫋PD.P∩Q=⌀8.函数y=√x2−2x+3的值域为.,则f(x)的值域为.9.已知函数f(x)=1x2−2x10.已知函数f(x)的定义域是[0,1],值域是[1,2],则这样的函数可以是f(x)=.11.已知函数f(x)=x2+x-1.);(1)求f(2), f(1x(2)若f(x)=5,求x的值.3.1.2 函数的表示法基础练一 函数的表示法及其应用 1.函数y =x x+1的图象大致是 ( )A B C D2.某同学从家里到学校,为了不迟到,先匀速跑一段时间,跑累了再匀速走余下的路,设在途中花费的时间为t ,离开家的距离为d ,则下面图象中,能正确表示d 与t 的关系的是( )A B C D3.已知函数y =f (x )的对应关系如表,函数y =g (x )的图象为如图所示的曲线ABC ,则g (f (3))的值为 .二 函数解析式的求法5.已知函数f (x +2)=x 2+6x +8,则函数f (x )的解析式为( ) A.f (x )=x 2+2x B.f (x )=x 2+6x +8 C.f (x )=x 2+4x D.f (x )=x 2+8x +66.函数f (x )满足f (1-2x )=-1x ,则f (2)=( )A.2B.-2C.12 D.-12 7.已知函数f (2x -1)=3x -5,若f (x 0)=4,则x 0= .8.已知f (x )是一次函数,2f (2)-3f (1)=5,2f (0)-f (-1)=1,则f (x )= .9.(1)已知函数g (√x +1)=2x +1,求g (x )的解析式;(2)已知f (x )为二次函数,且f (0)=2, f (2)=f (-1)=0,求f (x )的解析式.三 分段函数问题10.已知函数f (x )={√x,x >0,|x +1|,x ≤0,则f (f (-3))=( )A.√3B.1C.2D.√2 11.已知f (x )={x +2,x ≤−1,x 2,−1<x <2,2x,x ≥2,若f (x )=3,则x 的值是( )A.1B.1或32C.1,32或±√3 D.√312.函数f (x )=x +|x |x 的图象是( )A B C D13.(2022山西大同期中)已知函数f (x )={x 2,x ≤0,4−2x,x >0.(1)画出函数f (x )的图象;(2)当f (x )≥2时,求实数x 的取值范围.。

高一数学必修一函数概念的知识点高一数学必修一函数概念的知识点在日常过程学习中，是不是经常追着老师要知识点？知识点在教育实践中，是指对某一个知识的泛称。

哪些知识点能够真正帮助到我们呢？以下是店铺整理的高一数学必修一函数概念的知识点，仅供参考，欢迎大家阅读。

高一数学必修一函数概念的知识点 11、映射的定义2、函数的概念3、函数的三要素：定义域、值域和对应法则。

4、两个函数能成为同一函数的条件当且仅当两个函数的定义域和对应法则完全相同时，这两个函数才是同一函数。

5、区间的概念和记号6、函数的表示方法函数的表示方法有三种。

(1)解析法(2)列表法(3)图像法7、分段函数常见考法本节是段考和高考必不可少的考查部分，多以选择题和填空题的形式出现。

段考中常考查函数的定义域、值域、对应法则、同一函数、函数的解析式和分段函数。

高考中可以和高中数学的大部分章节知识联合考查，但是难度不大，属于容易题。

多考查函数的定义域、函数的表示方法和分段函数。

误区提醒1、映射是一种特殊的函数，映射中的集合A,B可以是数集，也可以是点集或其他集合，这两个集合有先后顺序。

A到B的映射与B到A的映射是不同的。

而函数是数集到数集的映射，所以函数是特殊的映射，但是映射不一定是函数。

2、函数的问题，要遵循“定义域优先”的原则。

无论是简单的函数，还是复杂的函数，无论是具体的函数，还是抽象的函数，必须优先考虑函数的定义域。

之所以要做到这一点，不仅是为了防止出现错误，有时还会为解题带来方便。

3、分段函数是一个函数，而不是几个函数。

分段函数书写时，注意格式规范，一般在左边的区间写在上面，右边的区间写在下面，每一段自变量的取值范围的交集为空集，所有段的自变量的取值范围的并集是函数的定义域。

高一数学必修一函数概念的知识点 2一、函数的概念设A、B是非空的数集，如果按照某个确定的对应关系f，是对于集合A中的任意一个数x，在集合B中都有唯一确定的数f(x)和它对应，那么就称f：A→B为从集合A到集合B的一个函数，记作：y=f(x)，x∈A。

最新人教版高一数学必修1第一章《函数的概念》11.2.1 函数的概念函数是数学中的一个重要概念，它描述了两个非空数集之间的一种确定的对应关系。

具体来说，设 A 和 B 是两个非空数集，如果按照某种确定的对应关系 f，使得对于集合 A 中的任意一个数 x，在集合 B 中都有唯一确定的数 f(x) 与之对应，那么就称 f：A→B 为从集合 A 到集合 B 的一个函数，记作 y = f(x)，其中 x 叫做自变量，x 的取值范围 A 叫做函数的定义域；与 x 的值相对应的 y 值叫做函数值，函数值的集合{f(x)|x∈A} 叫做函数的值域。

显然，值域是集合 B 的子集。

举个例子，如果甲、乙两地相距 30km，某人骑车从甲地去乙地，速度是 12km/h，出发 t 小时后行驶的路程是 s km，则 s 是 t 的函数，记为 s = 12t，定义域是{t|0≤t≤2.5}，值域为{s|0≤s≤30}。

对集合{t|0≤t≤2.5} 中的任意一个实数，在集合{s|0≤s≤30} 中都有唯一的数 s = 12t 与之对应。

对于函数概念的理解，有以下几点：1.“A，B 是非空的数集” 一方面强调了A，B 只能是数集，即 A，B 中的元素只能是实数；另一方面指出了定义域、值域都不能是空集，也就是说定义域为空集的函数是不存在的。

2.函数的三要素是：定义域、对应关系、值域。

定义域就是非空数集 A，而值域不一定是非空数集 B，而是非空数集 B 的子集。

举个例子，设集合A = {x|x≠0.x∈R}，B = R，按照确定的对应关系 f：取倒数，对于集合 A 中的任意一个数 x，在 B中都有唯一确定的数 f(x) 与之对应，于是 y = f(x) 就称为从集合 A 到集合 B 的一个函数。

此时 A 是函数 y 的定义域，而值域D = {y|y≠0.y∈R}，显然D ≠ B，但 D 是 B 的子集。

3.函数定义中强调“三性”：任意性、存在性、唯一性，即对于非空数集 A 中的任意一个元素 x，在非空数集 B 中都有唯一的元素 y 与之对应。

§1·函数的概念（一）函数的有关概念设A ，B 是非空的数集，如果按某个确定的对应关系f ，使对于集合A 中的任意一个x ，在集合B 中都有唯一确定的数)(x f 和它对应，那么就称B A f →:为从集合A 到集合B 的函数，记作)(x f y =， x ∈A其中x 叫自变量，x 的取值范围A 叫做函数)(x f y =的定义域；与x 的值相对应的y 的值叫做函数值，函数值的集合{}A x x f ∈|)(（⊆B ）叫做函数y=f(x)的值域.函数符号)(x f y =表示“y 是x 的函数”，有时简记作函数)(x f . (1)函数实际上就是集合A 到集合B 的一个特殊对应 B A f →:这里 A, B 为非空的数集.（2）A ：定义域，原象的集合；{}A x x f ∈|)(：值域，象的集合,其中{}A x x f ∈|)( ⊆ B ；f ：对应法则 ，x ∈A ， y ∈B（3）函数符号：)(x f y = ↔y 是 x 的函数，简记 )(x f （二）已学函数的定义域和值域1．一次函数b ax x f +=)()0(≠a :定义域R, 值域R; 2．反比例函xkx f =)()0(≠k :定义域{}0|≠x x , 值域{}0|≠x x ; 3．二次函数c bx ax x f ++=2)()0(≠a :定义域R值域：当0>a 时，⎭⎬⎫⎩⎨⎧-≥a b ac y y 44|2；当0<a 时，⎭⎬⎫⎩⎨⎧-≤a b ac y y 44|2（三）函数的值：关于函数值 )(a f例：)(x f =2x +3x+1 则 f(2)=22+3×2+1=11注意：1︒在)(x f y =中f 表示对应法则，不同的函数其含义不一样2︒)(x f 不一定是解析式，有时可能是“列表”“图象”3︒)(x f 与)(a f 是不同的，前者为变数，后者为常数（四）函数的三要素： 对应法则f 、定义域A 、值域{}A x x f ∈|)( 只有当这三要素完全相同时，两个函数才能称为同一函数（五）区间的概念和记号：在研究函数时,常常用到区间的概念，它是数学中常用的述语和符号.设a,b ∈R ,且a<b.我们规定：①满足不等式a ≤x ≤b 的实数x 的集合叫做闭区间，表示为[a,b]； ②满足不等式a<x<b 的实数x 的集合叫做开区间，表示为（a,b ）；③满足不等式a ≤x<b 或a<x ≤b 的实数x 的集合叫做半开半闭区间，分别表示为[a ，b) ,(a ，b]. 这里的实数a 和b 叫做相应区间的端点.这样实数集R 也可用区间表示为(-∞,+∞),“∞”读作“无穷大”，“-∞”读作“负无穷大”，“+∞”读作“正无穷大”.还可把满足x ≥a ，x>a ，x ≤b ，x<b 的实数x 的集合分别表示为[a ，+∞)，（a ，+∞）,(- ∞,b ],(- ∞,b). 【例题解析】例1 判断下列各式，哪个能确定y 是x 的函数？为什么？(1)x 2＋y ＝1 (2)x ＋y 2＝1 (3)1x x 1y --= (4)y=x -1x +-例2 求下列函数的定义域： （1）()f x = (2)xx x x f -+=0)1()(例3 已知函数)(x f =32x -5x+2，求f(3), f(-2), f(a+1).例4 已知⎪⎩⎪⎨⎧+=10)(x x f π )0()0()0(>=<x x x ，求)1(f ，)1(-f ，)0(f ，)]}1([{-f f f讨论：函数y=x 、y=(x )2、y=23xx 、y=44x 、y=2x 有何关系？例5 下列各组中的两个函数是否为相同的函数？ ⑴3)5)(3(1+-+=x x x y 52-=x y ⑵111-+=x x y )1)(1(2-+=x x y练习：下列各组中的两个函数是否为相同的函数？ ① ()f x = 0(1)x -；()g x = 1.② ()f x = x ； ()g x ③ ()f x = x 2；()g x = 2(1)x +.④ ()f x = | x | ；()g x 例6 已知函数)(x f =4x+3，g(x)=x 2,求f[f(x)]，f[g(x)]，g[f(x)]，g[g(x)].复合函数：设 f (x )=2x -3，g (x )=x 2+2，则称 f [g (x )] =2(x 2+2)-3=2x 2+1（或g [f (x )] =(2x -3)2+2=4x 2-12x +11）为复合函数例7求下列函数的值域（用区间表示）：（1）y ＝x 2－3x ＋4； （2）()f x =（3）y ＝53x -+； （4）2()3x f x x -=+.例8 ※ 动手试试1. 若2(1)21f x x +=+，求()f x .2. 一次函数()f x 满足[()]12f f x x =+，求()f x .练习 已知二次函数f (x )=ax 2+bx （a ，b 为常数，且a ≠0）满足条件f (x －1)=f (3－x )且方程f (x )=2x 有等根，求f (x )的解析式.函数的概念习题：1．如下图可作为函数)(x f =的图像的是( )（D ）2.对于函数()y f x =，以下说法正确的有 （ ）①y 是x 的函数；②对于不同的,x y 的值也不同；③()f a 表示当x a =时函数()f x 的值，是一个常量；④()f x 一定可以用一个具体的式子表示出来。

完整版)高一数学必修一函数知识点总结二、函数的概念和相关概念函数是从一个非空数集A到另一个非空数集B的一个确定的对应关系f，使得集合A中的每个数x都有唯一的数f(x)与之对应。

我们把f：A→B称为从集合A到集合B的一个函数，记作y=f(x)，其中x是自变量，A是函数的定义域，而与x对应的y值是函数值，其集合{f(x)| x∈A }是函数的值域。

需要注意的是，在求函数的定义域时，我们需要注意分式的分母不等于零，偶次方根的被开方数不小于零，对数式的真数必须大于零，指数、对数式的底必须大于零且不等于1，以及函数是由一些基本函数通过四则运算结合而成的。

同时，指数为零底不可以等于零，实际问题中的函数的定义域还要保证实际问题有意义。

相同函数的判断方法有两种：表达式相同（与表示自变量和函数值的字母无关）和定义域一致。

在考虑函数的值域时，我们可以使用观察法、配方法或代换法。

函数图象是指在平面直角坐标系中，以函数y=f(x)。

(x∈A)中的x为横坐标，函数值y为纵坐标的点P(x，y)的集合C。

C上每一点的坐标(x，y)均满足函数关系y=f(x)，反过来，以满足y=f(x)的每一组有序实数对x、y为坐标的点(x，y)，均在C上。

我们可以使用描点法或图象变换法来画函数图象，其中常用的变换方法有平移变换、伸缩变换和对称变换。

区间是指数轴上的一段连续的区域，可以分为开区间、闭区间和半开半闭区间。

同时，还有无穷区间。

我们可以使用数轴来表示区间。

映射是指两个非空集合A和B之间的确定对应关系f，使得集合A中的每个元素x都有唯一的元素y与之对应。

我们把对应f：A→B称为从集合A到集合B的一个映射，记作“f （对应关系）：A（原象）→B（象）”。

对于映射f：A→B来说，应该满足集合A中的每一个元素，在集合B中都有象，并且象是唯一的；集合A中不同的元素，在集合B中对应的象可以是同一个。

3.分段函数分段函数是指在定义域的不同部分上有不同的解析表达式的函数。

高一数学必修1函数知识点总结高一数学必修1函数知识点总结函数映射定义：设A，B是两个非空的集合，如果按某一个确定的对应关系，使对于集合A中的任意一个元素x，在集合B中都有唯一确定的元素y与之对应，那么就称对应f：B为从集合A到集合B的一个映射传统定义：如果在某变化中有两个变量x,y,并且对于x在某个范围内的每一个确定的值，定义按照某个对应关系f,y都有唯一确定的值和它对应。

那么y就是x的函数。

记作yf(x).近代定义：函数是从一个数集到另一个数集的映射。

定义域函数及其表示函数的三要素值域对应法则解析法函数的表示方法列表法图象法传统定义：在区间a,b上，若ax1x2b,如f(x1)f(x2)，则f(x)在a,b上递增,a,b是递增区间；如f(x1)f(x2)，则f(x)在a,b上递减,a,b是的递减区间。

单调性导数定义：在区间a,b上，若f(x)0，则f(x)在a,b上递增,a,b是递增区间；如f(x)0a,b是的递减区间。

则f(x)在a,b上递减,最大值：设函数yf(x)的定义域为I，如果存在实数M满足：（1）对于任意的xI，都有f(x)M；函数函数的基本性质最值（2）存在x0I，使得f(x0)M。

则称M是函数yf(x)的最大值最小值：设函数yf(x)的定义域为I，如果存在实数N满足：（1）对于任意的xI，都有f(x)N；（2）存在x0I，使得f(x0)N。

则称N是函数yf(x)的最小值(1)f(x)f(x),x定义域D，则f(x)叫做奇函数，其图象关于原点对称。

奇偶性(2)f(x)f(x),x定义域D，则f(x)叫做偶函数，其图象关于y轴对称。

奇偶函数的定义域关于原点对称周期性：在函数f(x)的定义域上恒有f(xT)f(x)(T0的常数)则f(x)叫做周期函数，T为周期；T的最小正值叫做f(x)的最小正周期，简称周期（1）描点连线法：列表、描点、连线向左平移个单位：y1y,x1axyf(xa)向右平移a个单位：yy,xaxyf(xa)11平移变换向上平移b个单位：xx,y11byybf(x)向下平移b个单位：x1x,y1byybf(x)横坐标变换：把各点的横坐标x1缩短（当w1时）或伸长（当0w1时）到原来的1/w倍（纵坐标不变），即xwxyf(wx)1伸缩变换纵坐标变换：把各点的纵坐标y伸长（A1)或缩短（0A1)到原来的A倍1函数图象的画法（横坐标不变），即y1y/Ayf(x)（xx12x0x12x0x2）变换法关于点(x,y)对称：2y0yf(2x0x)00yy12y0y12y0y关于直线xx0对称：xx12x0x12x0xyf(2x0x)yy1y1y对称变换xx1xx关于直线yy0对称：12y0yf(x)yy2yy12y0y10xx11yf(x)关于直线yx对称：yy1一、函数的定义域的常用求法：1、分式的分母不等于零；2、偶次方根的被开方数大于等于零；3、对数的真数大于零；4、指数函数和对数函数的底数大于零且不等于1；5、三角函数正切函数ytanx 中xk2(kZ)；余切函数ycotx中；6、如果函数是由实际意义确定的解析式，应依据自变量的实际意义确定其取值范围。

高一数学必修一函数的概念与性质知识点总结一、内容描述高一数学必修一函数的概念与性质知识点总结涵盖了高中阶段关于函数基础概念及其性质的核心内容。

文章首先介绍了函数的基本概念，包括函数的定义、表示方法以及函数的性质等。

文章详细阐述了函数的性质，包括单调性、奇偶性、周期性以及复合函数的性质等。

文章还介绍了函数图像的画法及其与性质之间的关系，以及如何利用函数性质解决实际问题。

文章总结了函数在数学学习中的重要性，强调掌握函数概念与性质对于后续数学学习的基础作用。

通过本文的学习，学生可以更好地理解和掌握函数知识，为后续数学学习打下坚实的基础。

1. 简述函数概念的重要性函数是描述自然现象和规律的重要工具。

在物理、化学、生物等自然学科中，许多现象的变化过程都可以通过函数关系进行描述。

物理学中的运动规律、化学中的化学反应速率与浓度的关系等，都需要借助函数概念进行建模和分析。

函数是数学体系中的核心和基础。

函数连接了代数、几何、三角学等多个分支，是数学知识和方法综合运用的基础。

对函数概念的深入理解，有助于我们更好地理解和掌握数学的其它分支和领域。

函数也是解决实际问题的重要工具。

在现实生活中，很多问题的解决都需要建立数学模型，而函数作为构建数学模型的基本元素之一，能够帮助我们准确地描述问题并找到解决方案。

在经济学、统计学、工程学等领域，函数的运用非常广泛。

函数概念的重要性不言而喻。

高一学生在学习数学时，应深入理解函数的概念，掌握其性质和特点，为后续学习和解决实际问题打下坚实的基础。

2. 引出本文目的：总结函数的概念与性质本文旨在系统梳理和归纳高一数学必修一课程中函数的核心概念与基本性质。

函数是数学中的核心概念之一，具有广泛的应用领域。

在高中阶段，学生需要深入理解函数的基础定义、性质和图像特征，为后续学习奠定坚实基础。

本文的目的在于帮助学生全面总结函数的相关知识点，加深对函数概念与性质的理解，以便更好地掌握和应用函数这一重要的数学工具。