霍夫直线检测算法

hough变换直线检测主要原理
霍夫变换是一种在图像空间进行几何形状检测的方法，用于检测平面上的直线。

主要原理如下：
1. 点与直线的表示：霍夫变换使用极坐标系来表示直线，每个点在图像中表示一条通过该点的直线。

直线可以用两个参数表示：r表示离原点的距离，θ表示与x轴的夹角。

2. 累加过程：对每个点，遍历所有可能的直线参数，并在霍夫空间中进行累加。

对于每个点，对应于通过该点的所有直线，累加器中相应位置的值加1。

这个累加过程可以在霍夫空间中的一个二维数组中进行。

3. 阈值检测：当累加器中的某个值超过预设的阈值时，认为该直线存在。

这个阈值可以根据应用需求进行设置。

4. 参数反算：根据累加器中的峰值，反算出对应的直线参数（r和θ），并在图像中绘制出检测到的直线。

霍夫变换的主要优点是对于存在噪声和局部遮挡的图像仍然能够有效地检测直线。

但是其缺点是计算复杂度较高，直线的参数空间较大，需要处理大量的累加器。

同时，霍夫变换对于直线的精确定位和参数估计准确性不高，对于曲线的检测效果较差。

OpenCV---直线检测直线检测相关Hough变换是经典的检测直线的算法。

其最初⽤来检测图像中的直线，同时也可以将其扩展，以⽤来检测图像中简单的结构。

变换图⽰霍夫直线检测的两种⽅法1.获取灰度图像2.canny边缘检测3.获取霍夫直线信息4.算出直线位置，画出每条直线⼀：HoughLines霍夫变换def line_detection(image):gray = cv.cvtColor(image,cv.COLOR_BGR2GRAY)edges = cv.Canny(gray,50,150,apertureSize=3) #apertureSize是sobel算⼦⼤⼩，只能为1,3,5，7lines = cv.HoughLines(edges,1,np.pi/180,200) #函数将通过步长为1的半径和步长为π/180的⾓来搜索所有可能的直线for line in lines:rho,theta = line[0] #获取极值ρ长度和θ⾓度a = np.cos(theta) #获取⾓度cos值b = np.sin(theta) #获取⾓度sin值x0 = a * rho #获取x轴值y0 = b * rho #获取y轴值 x0和y0是直线的中点x1 = int(x0 + 1000*(-b)) #获取这条直线最⼤值点x1y1 = int(y0 + 1000*(a)) #获取这条直线最⼤值点y1x2 = int(x0 - 1000 * (-b)) #获取这条直线最⼩值点x2 y2 = int(y0 - 1000 * (a)) #获取这条直线最⼩值点y2 其中*1000是内部规则cv.line(image,(x1,y1),(x2,y2),(0,0,255),2) #开始划线cv.imshow("image line",image)src = cv.imread("./l.png") #读取图⽚dWindow("input image",cv.WINDOW_AUTOSIZE) #创建GUI窗⼝,形式为⾃适应cv.imshow("input image",src) #通过名字将图像和窗⼝联系line_detect_possible_demo(src)cv.waitKey(0) #等待⽤户操作，⾥⾯等待参数是毫秒，我们填写0，代表是永远，等待⽤户操作cv.destroyAllWindows() #销毁所有窗⼝相关知识补充（⼀）HoughLines⽅法def HoughLines(image, rho, theta, threshold, lines=None, srn=None, stn=None, min_theta=None, max_theta=None): # real signature unknown; restored from __doc__ cv.HoughLines(edges,1,np.pi/180,200)cv2.HoughLines函数输出的是[float, float]形式的ndarray，其中每个值表⽰检测到的线(ρ , θ)中浮点点值的参数。

霍夫变换直线检测原理
霍夫变换（Hough Transform）是一种用来检测图像中的直线的算法，它在图像处理领域非常重要，它可以用来检测图像中的线条，圆和椭圆。

霍夫变换的基本原理是，将输入图像中的每个像素点看作是坐标系中的一个点，然后通过一些函数来确定是否存在直线，圆或椭圆，并将这些函数称为霍夫变换函数。

霍夫变换的直线检测是一个非常重要的过程，它的基本原理是将输入图像中的每个像素点看作是坐标系中的一个点，然后用霍夫变换函数来检测输入图像中是否存在直线。

霍夫变换函数有两种，一种是极坐标函数，另一种是直角坐标函数。

在极坐标函数中，霍夫变换函数的形式是：r=xcosθ+ysinθ，在直角坐标函数中，霍夫变换函数的形式是：y=mx+b。

霍夫变换直线检测的过程大致分为以下几步：首先，将输入图像转换为灰度图像，然后使用适当的滤波算法去除噪声；其次，使用边缘检测算法检测图像的边缘，并获得边缘的像素点坐标；然后，使用霍夫变换函数对边缘的像素点进行拟合，获得直线的参数；最后，使用拟合后的参数对直线进行绘制，完成图像中直线检测的任务。

总而言之，霍夫变换是一种用来检测图像中的直线的算法，它是一种极其重要的算法，它可以有效地检测图像中的线条，圆和椭圆，而其直线检测的原理是，将输入图像中的每个像素点看作是坐标系
中的一个点，然后使用霍夫变换函数拟合像素点，获得直线的参数，最后使用参数对直线进行绘制。

霍夫变换后的直线p值霍夫变换是一种常用的图像处理算法，主要用于检测图像中的直线或其他几何形状。

在霍夫变换中，直线被表示为参数空间中的一个点，而不是在图像中的像素点。

这种表示方式使得直线的检测更加简便和高效。

在霍夫变换中，直线p的值表示直线的参数，通常是两个参数的组合，比如直线的斜率和截距。

通过对图像进行霍夫变换，可以得到参数空间中的一个点，该点对应于图像中的一条直线。

通过遍历整个图像，我们可以得到所有直线的参数点，并通过对这些点的分析和处理，实现对图像中直线的检测和提取。

使用霍夫变换检测直线的过程可以分为以下几个步骤：1. 边缘检测：首先对图像进行边缘检测，将图像中的边缘提取出来。

常用的边缘检测算法有Sobel算子、Canny算子等。

2. 参数空间的建立：根据直线的参数表示方式，建立一个参数空间，通常是一个二维的极坐标空间。

参数空间中的每个点表示一条直线的参数。

3. 点投票：遍历图像中的每个边缘点，将其在参数空间中对应的点进行投票。

每个边缘点的投票数将决定该直线参数点的强度。

4. 参数点的分析和处理：根据参数空间中的投票结果，可以找到投票数最多的几个点，这些点对应的直线参数即为最可能的直线。

可以通过设定一个阈值来确定哪些参数点表示的直线是有效的。

5. 直线的提取：根据最终确定的直线参数，可以将其转换回图像空间，得到图像中的直线。

霍夫变换在图像处理领域有着广泛的应用。

比如在计算机视觉中，可以通过霍夫变换检测图像中的直线，用于目标检测、图像配准等任务。

在自动驾驶领域，可以通过霍夫变换检测图像中的道路线，用于车道线检测和车道保持等功能。

然而，霍夫变换也存在一些限制。

首先，霍夫变换对噪声比较敏感，噪声点容易干扰到参数空间的计算。

其次，霍夫变换的计算复杂度较高，对于大规模图像的处理可能会耗费较多的时间和计算资源。

此外，霍夫变换只能检测直线，对于其他形状的检测需要使用其他的方法。

总结起来，霍夫变换是一种常用的图像处理算法，可以用于检测图像中的直线或其他几何形状。

霍夫直线检测matlab霍夫直线检测（Matlab程序实现）霍夫直线检测算法是一种基于图像的分析方法，它可以检测图像中的直线，适用于任何图像，包括灰度图像和彩色图像。

此方法可用于计算机视觉中检测物体轮廓的任务。

以下是Matlab程序实现霍夫直线检测的步骤：第一步：读取图片使用Matlab的imread函数从文件中读取图像。

im = imread('image.jpg');第二步：把图像转换为灰度图像使用Matlab的rgb2gray函数，把读取的图像转换为灰度图像。

im_gray = rgb2gray(im);第三步：对灰度图像进行边缘检测使用Matlab的edge函数，对图像进行边缘检测，以检测图像中的直线。

im_edges = edge(im_gray,'canny');第四步：使用Hough变换检测直线使用Matlab的hough函数，对图像中的边缘进行Hough变换，以检测图像中的直线。

[H, theta, rho] = hough(im_edges);第五步：绘制Hough变换图形使用Matlab的imshow函数，绘制Hough变换图形，以检测图像中的直线。

imshow(H,[],'XData',theta,'YData',rho);第六步：检测直线使用Matlab的houghpeaks函数，检测图像中的直线。

P = houghpeaks(H,5);第七步：从houghpeaks检测到的顶点中抽取直线使用Matlab的houghlines函数，从houghpeaks检测到的顶点中抽取直线。

lines = houghlines(im_edges,theta,rho,P);第八步：绘制检测到的直线使用Matlab的imshow函数，绘制检测到的直线。

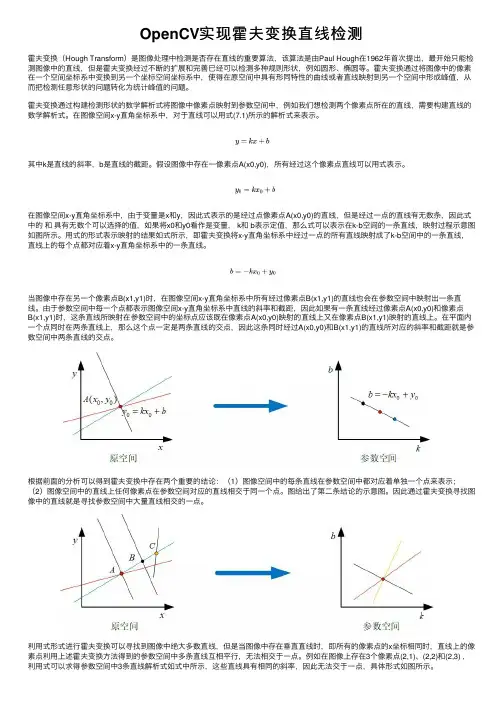
OpenCV实现霍夫变换直线检测霍夫变换（Hough Transform）是图像处理中检测是否存在直线的重要算法，该算法是由Paul Hough在1962年⾸次提出，最开始只能检测图像中的直线，但是霍夫变换经过不断的扩展和完善已经可以检测多种规则形状，例如圆形、椭圆等。

霍夫变换通过将图像中的像素在⼀个空间坐标系中变换到另⼀个坐标空间坐标系中，使得在原空间中具有形同特性的曲线或者直线映射到另⼀个空间中形成峰值，从⽽把检测任意形状的问题转化为统计峰值的问题。

霍夫变换通过构建检测形状的数学解析式将图像中像素点映射到参数空间中，例如我们想检测两个像素点所在的直线，需要构建直线的数学解析式。

在图像空间x-y直⾓坐标系中，对于直线可以⽤式(7.1)所⽰的解析式来表⽰。

其中k是直线的斜率，b是直线的截距。

假设图像中存在⼀像素点A(x0,y0)，所有经过这个像素点直线可以⽤式表⽰。

在图像空间x-y直⾓坐标系中，由于变量是x和y，因此式表⽰的是经过点像素点A(x0,y0)的直线，但是经过⼀点的直线有⽆数条，因此式中的和具有⽆数个可以选择的值，如果将x0和y0看作是变量， k和 b表⽰定值，那么式可以表⽰在k-b空间的⼀条直线，映射过程⽰意图如图所⽰。

⽤式的形式表⽰映射的结果如式所⽰，即霍夫变换将x-y直⾓坐标系中经过⼀点的所有直线映射成了k-b空间中的⼀条直线，直线上的每个点都对应着x-y直⾓坐标系中的⼀条直线。

当图像中存在另⼀个像素点B(x1,y1)时，在图像空间x-y直⾓坐标系中所有经过像素点B(x1,y1)的直线也会在参数空间中映射出⼀条直线。

由于参数空间中每⼀个点都表⽰图像空间x-y直⾓坐标系中直线的斜率和截距，因此如果有⼀条直线经过像素点A(x0,y0)和像素点B(x1,y1)时，这条直线所映射在参数空间中的坐标点应该既在像素点A(x0,y0)映射的直线上⼜在像素点B(x1,y1)映射的直线上。

在平⾯内⼀个点同时在两条直线上，那么这个点⼀定是两条直线的交点，因此这条同时经过A(x0,y0)和B(x1,y1)的直线所对应的斜率和截距就是参数空间中两条直线的交点。

霍夫变换中直线拟合的最小二乘法ichriZ 1.基本概念（1）霍夫变换霍夫变换(Hough Transform) 是图像处理中从图像中识别几何形状的基本方法之一，应用很广泛，也有很多改进算法。

最基本的霍夫变换是从黑白图像中检测直线或线段。

（2）最小二乘法曲线拟合方法的一种，通过最小化误差的平方和寻找数据的最佳函数匹配。

2.适用情况霍夫变换是基于统计的方法，能将图像中的噪声或干扰点的影响消除，但其结果存在精度不够与直线有效区间不易控制的问题；最小二乘法是直线拟合的有效方法，但直接用于拟合时易受干扰点或噪声点影响。

在检测图像中的直线段时，先利用霍夫变换消除无效点的影响，再结合最小二乘法法进行拟合，可以提高检测效果。

3.霍夫变换原理与实现方法(一)霍夫变换原理在平面直角坐标系中一条直线，任取其上一点，有表示参数平面中的一条直线。

再取上另一点则有表示参数平面中的一条直线。

与相交于一点，对应于坐标系中直线即：同一直线上的不同的点在对应的参数平面中对应不同的直线，但都交于同一点，所以可以通过坐标系中的交点来寻找坐标系中的直线。

当坐标系中的直线数量为R时，坐标系中对应R个峰值交点，它们对应于坐标系中的R 条直线。

此种方法不能够表示这类直线，实际中常将原有直线表示为参数方程此直线上的点对应坐标系中的一族三角函数曲线，它们在有效区间内交于一点，对应于坐标系中的。

下图是一个具体例子：交点坐标(二)最小二乘法原理对于给定数据，要求在某个函数类中寻求一个函数，使本文中讨论的是直线的最小二乘法，故均取一次多项式。

设具有如下格式霍夫变换—>其中是待定参数，求具有这种形式的最小二乘法的实质，就是要适当的选择参数，使相应的函数满足条件。

也就是说，点是多元函数的极小点，从而满足方程组因此，可以通过解此方程组（称为法方程组）来求取，以便获得最小二乘解。

当讨论的曲线为代数多项式时，不妨取则有令得方程组即本文中模拟的是直线，使用一次多项式，则约束条件为其中直线表达式为(三)霍夫变换的实现方法图像处理中的二值边缘图，一般是处理离散数据，则根据霍夫变换可按下列步骤实现直线检测：（1）参数空间量化成m*n（m为的等分数，n为的等分数）个单元，并设置累加器矩阵；（2）给参数空间中的每个单元分配一个累加器，并把累加器的初始值置为0；（3）取出直角坐标系中的点带入式，并以量化的值计算出；（4）在参数空间中，找到和所对应的单元，并将该单元的累加器加1，即（5）当直角坐标系中的点都经过（3）（4）两步遍历后，检测参数空间中每个累加器的值，累加器最大的单元所对应的和即为直角坐标系中直线方程式的参数。

霍夫变换检测图像直线算法python实现创作不易，如果对您有帮助，帮忙点赞哦！⼀. 霍夫变换理解：可参考：⼆. 霍夫变换简介：霍夫变换，是将坐标由直⾓坐标系变换到极坐标系，然后再根据数学表达式检测某些形状（如直线和圆）的⽅法。

当 l1直线上的某些点变换到极坐标系下时，表现为某些线（和前⾯点数量⼀致），这些线交于⼀点，通过该点的坐标就能表⽰原先的 l1直线。

三. 霍夫变换⽤于检测图像直线算法实现：①提取图像边缘（可使⽤Canny算法等）[我也实现了它，前⾯Canny算法有问题可以参考我的另⼀篇⽂章：]②实现⼆值图像霍夫变换1. 求出图像对⾓线长：r_max2. 在边缘点 (x,y) 处，t 取[0,180)，步长设为1，根据下式进⾏霍夫变换霍夫变换，(r_ho,t) 表⽰极坐标，(x,y) 表⽰直⾓坐标↑3. 做⼀个⼤⼩为 r_max * 180 的表，变换后⼀个值落在表内某坐标，就将该坐标表内值 + 1，简⾔之，就是在进⾏投票，统计通过哪个点的直线的数量最多（即在原图像上越趋近于⼀条直线）。

③进⾏⾮极⼤值抑制（NMS）操作，使找出的直线落在不同的地点NMS 的算法如下：1. 遍历该表，如果遍历到的像素的投票数⼤于其8近邻的像素投票值，则它不变。

2. 如果遍历到的像素的投票数⼩于其8近邻的像素投票值，则将其设置为0。

④找到20个投票数最多的点（即：直⾓坐标系下20条直线）准备进⾏输出1. np.ravel 将多维数组降为1维2. np.argsort 将数组元素从⼩到⼤排序，返回索引值3. [::-1] 数组反序 -> 得到从⼤到⼩索引值4. [:20] 前20个最⼤投票值的索引5. 根据索引得到坐标（r，t）⑤霍夫反变换后，画出原图中的20条直线，输出图像霍夫逆变换公式↑四. 纯⼿⼯实现 ——> 利⽤霍夫变换检测图像中的直线2import numpy as np3import matplotlib.pyplot as plt45# Canny算法：提取图像边缘6def Canny(img):78# Gray scale9def BGR2GRAY(img):10 b = img[:, :, 0].copy()11 g = img[:, :, 1].copy()12 r = img[:, :, 2].copy()1314# Gray scale15 out = 0.2126 * r + 0.7152 * g + 0.0722 * b16 out = out.astype(np.uint8)1718return out192021# Gaussian filter for grayscale22def gaussian_filter(img, K_size=3, sigma=1.3):2324if len(img.shape) == 3:25 H, W, C = img.shape26 gray = False27else:28 img = np.expand_dims(img, axis=-1)29 H, W, C = img.shape30 gray = True3132## Zero padding33 pad = K_size // 234 out = np.zeros([H + pad * 2, W + pad * 2, C], dtype=np.float)35 out[pad : pad + H, pad : pad + W] = img.copy().astype(np.float)3637## prepare Kernel38 K = np.zeros((K_size, K_size), dtype=np.float)39for x in range(-pad, -pad + K_size):40for y in range(-pad, -pad + K_size):41 K[y + pad, x + pad] = np.exp( - (x ** 2 + y ** 2) / (2 * sigma * sigma))42#K /= (sigma * np.sqrt(2 * np.pi))43 K /= (2 * np.pi * sigma * sigma)44 K /= K.sum()4546 tmp = out.copy()4748# filtering49for y in range(H):50for x in range(W):51for c in range(C):52 out[pad + y, pad + x, c] = np.sum(K * tmp[y : y + K_size, x : x + K_size, c]) 5354 out = np.clip(out, 0, 255)55 out = out[pad : pad + H, pad : pad + W]56 out = out.astype(np.uint8)5758if gray:59 out = out[..., 0]6061return out626364# sobel filter65def sobel_filter(img, K_size=3):66if len(img.shape) == 3:67 H, W, C = img.shape68else:69 H, W = img.shape7071# Zero padding72 pad = K_size // 273 out = np.zeros((H + pad * 2, W + pad * 2), dtype=np.float)74 out[pad : pad + H, pad : pad + W] = img.copy().astype(np.float)75 tmp = out.copy()7677 out_v = out.copy()78 out_h = out.copy()7980## Sobel vertical81 Kv = [[1., 2., 1.],[0., 0., 0.], [-1., -2., -1.]]82## Sobel horizontal83 Kh = [[1., 0., -1.],[2., 0., -2.],[1., 0., -1.]]86for y in range(H):87for x in range(W):88 out_v[pad + y, pad + x] = np.sum(Kv * (tmp[y : y + K_size, x : x + K_size]))89 out_h[pad + y, pad + x] = np.sum(Kh * (tmp[y : y + K_size, x : x + K_size]))9091 out_v = np.clip(out_v, 0, 255)92 out_h = np.clip(out_h, 0, 255)9394 out_v = out_v[pad : pad + H, pad : pad + W]95 out_v = out_v.astype(np.uint8)96 out_h = out_h[pad : pad + H, pad : pad + W]97 out_h = out_h.astype(np.uint8)9899return out_v, out_h100101102def get_edge_angle(fx, fy):103# get edge strength104 edge = np.sqrt(np.power(fx.astype(np.float32), 2) + np.power(fy.astype(np.float32), 2))105 edge = np.clip(edge, 0, 255)106107 fx = np.maximum(fx, 1e-10)108#fx[np.abs(fx) <= 1e-5] = 1e-5109110# get edge angle111 angle = np.arctan(fy / fx)112113return edge, angle114115116def angle_quantization(angle):117 angle = angle / np.pi * 180118 angle[angle < -22.5] = 180 + angle[angle < -22.5]119 _angle = np.zeros_like(angle, dtype=np.uint8)120 _angle[np.where(angle <= 22.5)] = 0121 _angle[np.where((angle > 22.5) & (angle <= 67.5))] = 45122 _angle[np.where((angle > 67.5) & (angle <= 112.5))] = 90123 _angle[np.where((angle > 112.5) & (angle <= 157.5))] = 135124125return _angle126127128def non_maximum_suppression(angle, edge):129 H, W = angle.shape130 _edge = edge.copy()131132for y in range(H):133for x in range(W):134if angle[y, x] == 0:135 dx1, dy1, dx2, dy2 = -1, 0, 1, 0136elif angle[y, x] == 45:137 dx1, dy1, dx2, dy2 = -1, 1, 1, -1138elif angle[y, x] == 90:139 dx1, dy1, dx2, dy2 = 0, -1, 0, 1140elif angle[y, x] == 135:141 dx1, dy1, dx2, dy2 = -1, -1, 1, 1142if x == 0:143 dx1 = max(dx1, 0)144 dx2 = max(dx2, 0)145if x == W-1:146 dx1 = min(dx1, 0)147 dx2 = min(dx2, 0)148if y == 0:149 dy1 = max(dy1, 0)150 dy2 = max(dy2, 0)151if y == H-1:152 dy1 = min(dy1, 0)153 dy2 = min(dy2, 0)154if max(max(edge[y, x], edge[y + dy1, x + dx1]), edge[y + dy2, x + dx2]) != edge[y, x]: 155 _edge[y, x] = 0156157return _edge158159def hysterisis(edge, HT=100, LT=30):160 H, W = edge.shape161162# Histeresis threshold163 edge[edge >= HT] = 255164 edge[edge <= LT] = 0165166 _edge = np.zeros((H + 2, W + 2), dtype=np.float32)167 _edge[1 : H + 1, 1 : W + 1] = edge169## 8 - Nearest neighbor170 nn = np.array(((1., 1., 1.), (1., 0., 1.), (1., 1., 1.)), dtype=np.float32) 171172for y in range(1, H+2):173for x in range(1, W+2):174if _edge[y, x] < LT or _edge[y, x] > HT:175continue176if np.max(_edge[y-1:y+2, x-1:x+2] * nn) >= HT:177 _edge[y, x] = 255178else:179 _edge[y, x] = 0180181 edge = _edge[1:H+1, 1:W+1]182183return edge184185# grayscale186 gray = BGR2GRAY(img)187188# gaussian filtering189 gaussian = gaussian_filter(gray, K_size=5, sigma=1.4)190191# sobel filtering192 fy, fx = sobel_filter(gaussian, K_size=3)193194# get edge strength, angle195 edge, angle = get_edge_angle(fx, fy)196197# angle quantization198 angle = angle_quantization(angle)199200# non maximum suppression201 edge = non_maximum_suppression(angle, edge)202203# hysterisis threshold204 out = hysterisis(edge, 100, 30)205206return out207208# 霍夫变换实现检测图像中的20条直线209def Hough_Line(edge, img):210## Voting211def voting(edge):212 H, W = edge.shape213214 drho = 1215 dtheta = 1216217# get rho max length218 rho_max = np.ceil(np.sqrt(H ** 2 + W ** 2)).astype(np.int)219220# hough table221 hough = np.zeros((rho_max, 180), dtype=np.int)222223# get index of edge224# ind[0] 是符合条件的纵坐标，ind[1]是符合条件的横坐标225 ind = np.where(edge == 255)226227## hough transformation228# zip函数返回元组229for y, x in zip(ind[0], ind[1]):230for theta in range(0, 180, dtheta):231# get polar coordinat4s232 t = np.pi / 180 * theta233 rho = int(x * np.cos(t) + y * np.sin(t))234235# vote236 hough[rho, theta] += 1237238 out = hough.astype(np.uint8)239240return out241242# non maximum suppression243def non_maximum_suppression(hough):244 rho_max, _ = hough.shape245246## non maximum suppression247for y in range(rho_max):248for x in range(180):249# get 8 nearest neighbor250 x1 = max(x-1, 0)251 x2 = min(x+2, 180)253 y2 = min(y+2, rho_max-1)254if np.max(hough[y1:y2, x1:x2]) == hough[y,x] and hough[y, x] != 0: 255pass256#hough[y,x] = 255257else:258 hough[y,x] = 0259260return hough261262def inverse_hough(hough, img):263 H, W, _= img.shape264 rho_max, _ = hough.shape265266 out = img.copy()267268# get x, y index of hough table269# np.ravel 将多维数组降为1维270# argsort 将数组元素从⼩到⼤排序，返回索引271# [::-1] 反序->从⼤到⼩272# [:20] 前20个273 ind_x = np.argsort(hough.ravel())[::-1][:20]274 ind_y = ind_x.copy()275 thetas = ind_x % 180276 rhos = ind_y // 180277278# each theta and rho279for theta, rho in zip(thetas, rhos):280# theta[radian] -> angle[degree]281 t = np.pi / 180. * theta282283# hough -> (x,y)284for x in range(W):285if np.sin(t) != 0:286 y = - (np.cos(t) / np.sin(t)) * x + (rho) / np.sin(t)287 y = int(y)288if y >= H or y < 0:289continue290 out[y, x] = [0,255,255]291for y in range(H):292if np.cos(t) != 0:293 x = - (np.sin(t) / np.cos(t)) * y + (rho) / np.cos(t)294 x = int(x)295if x >= W or x < 0:296continue297 out[y, x] = [0,0,255]298299 out = out.astype(np.uint8)300301return out302303304# voting305 hough = voting(edge)306307# non maximum suppression308 hough = non_maximum_suppression(hough)309310# inverse hough311 out = inverse_hough(hough, img)312313return out314315316# Read image317 img = cv2.imread("../paojie.jpg").astype(np.float32)318319# Canny320 edge = Canny(img)321322# Hough323 out = Hough_Line(edge, img)324325 out = out.astype(np.uint8)326327# Save result328 cv2.imwrite("out.jpg", out)329 cv2.imshow("result", out)330 cv2.waitKey(0)331 cv2.destroyAllWindows()View Code五. 实验结果：原图↑霍夫变换检测到的直线↑六. 参考内容：七. 版权声明：未经作者允许，请勿随意转载抄袭，抄袭情节严重者，作者将考虑追究其法律责任，创作不易，感谢您的理解和配合！。

机器视觉直线检测算法
机器视觉直线检测算法主要包括以下几种：
1. 霍夫变换：这是一种常用的直线检测算法，通过将图像空间中的像素点映射到参数空间中，找到在参数空间中交叉点最多的线段，从而确定直线的位置和方向。

在极坐标下，该算法可以检测直线，但对于接近竖直方向的直线，计算量会增大。

2. RANSAC算法：这是一种鲁棒性较强的参数估计算法，通过随机选择样
本点，拟合模型并计算误差，再根据误差进行模型更新和样本点选择，最终得到符合数据分布的模型参数。

在直线检测中，RANSAC算法可以通过随
机选择两个点，拟合直线模型并计算样本点到直线的距离来检测直线。

3. 边缘检测算法：这是一种常用的图像处理技术，通过寻找图像中灰度值变化较大的像素点，找到图像中的边缘。

由于直线是一种明显的边缘，因此可以通过边缘检测算法来检测直线。

常用的边缘检测算法包括Canny算法、Sobel算法和Laplacian算法等。

这些算法各有特点，可以根据具体的应用场景和需求选择合适的算法。

霍夫直线检测matlab霍夫直线检测——matlab实现一、霍夫直线检测是什么？霍夫直线检测又称“霍夫变换”，是一种运用数学形态学的技术，用于对图像中的线条进行检测的一种算法。

它是一种非常有用的图像处理算法，常被用于机器视觉、机器人导航、边界检测以及机器学习等领域。

二、matlab中的霍夫直线检测1、利用matlab中的函数实现霍夫直线检测matlab中有专用于实现霍夫直线检测的函数，名为houghlines。

其格式为：[H,theta,rho] = houghlines(BW,theta,rho,peaks) 其中BW是要检测的二值图像，theta是取值范围0~pi，rho是取值范围0~Inf，peaks是一个由高累计峰值的行列对组成的矩阵，可以通过houghpeaks函数进行计算得到。

调用houghlines函数时可以将上述几个参数传递给函数，函数会返回一个H矩阵，它是hough 变换投影的累积值的矩阵，用来定位图像中的直线，theta和rho是检测出来的直线的所有参数。

2、用HCircles函数实现霍夫圆检测matlab中还有一个用于实现霍夫圆检测的函数，名为houghcircles。

其格式为：[centers, radii] = houghcircles( BW, mindist,edgesensitivity, suppressradius, suppresscenter, pixelspacing )其中，BW是要检测的二值图像，minDist是圆心之间的最小间距，edgeSensitivity是控制边缘检测强度，suppressRadius是控制圆半径的最小系数，suppressCenter是控制圆心的最小系数，pixelSpacing是控制圆检测的精度。

调用houghcircles函数传递上述参数，函数会返回识别出来的圆心和其半径的参数，从图像中检测出圆的信息。

史上最详细的Hough 直线检测所以这⾥再次回顾⼀下检测直线的算法之——Hough变换。

Hough 直线检测1.直线坐标参数空间在图像x −y坐标空间中，经过点(,)的直线表⽰为：其中，参数a为斜率，b为截矩。

通过点(,)的直线有⽆数条，且对应于不同的a和b值。

如果将和视为常数，⽽将原本的参数a和b看作变量，则式⼦(1)可以表⽰为：这样就变换到了参数平⾯a −b。

这个变换就是直⾓坐标中对于(,)点的Hough变换。

该直线是图像坐标空间中的点(,)在参数空间的唯⼀⽅程。

考虑到图像坐标空间中的另⼀坐标(,)，它在参数空间中也有相应的⼀条直线，表⽰为：这条直线与点(,)在参数空间的直线相交于⼀点(,)，如图所⽰：图像坐标空间中过点(,)和点(,)的直线上的每⼀点在参数空间a −b上各⾃对应⼀条直线，这些直线都相交于点,⽽a0、b0就是图像坐标空间x −y中点(,))和点(,)所确定的直线的参数。

反之，在参数空间相交于同⼀点的所有直线，在图像坐标空间都有共线的点与之对应。

根据这个特性，给定图像坐标空间的⼀些边缘点，就可以通过Hough变换确定连接这些点的直线⽅程。

具体计算时，可以将参数空间视为离散的。

建⽴⼀个⼆维累加数组A(a,b),第⼀维的范围是图像坐标空间中直线斜率的可能范围，第⼆维的范围是图像坐标空间中直线截矩的可能范围。

开始时A(a,b)初始化为0，然后对图像坐标空间的每⼀个前景点(xi,yi),将参数空间中每⼀个a的离散值代⼊式⼦(2)中，从⽽计算出对应的b值。

每计算出⼀对(a,b),都将对应的数组元素A(a,b)加1，即A(a,b)=A(a,b)+1。

所有的计算结束之后，在参数计算表决结果中找到A(a,b)的最⼤峰值，所对应的a0、b0就是原图像中共线点数⽬最多(共A(a,b)个共线点)的直线⽅程的参数；接下来可以继续寻找次峰值和第3峰值和第4峰值等等，它们对应于原图中共线点略少⼀些的直线。

matlab霍夫变换（hough）检测直线 霍夫变换是⼀种特征检测(feature extraction)，被⼴泛应⽤在图像分析（image analysis）、电脑视觉 (computer vision)以及数位影像处理 (digital image processing)。

霍夫变换是⽤来辨别找出物件中的特征，例如：线条。

他的算法流程⼤致如下，给定⼀个物件、要辨别的形状的种类，算法会在参数空间(parameter space)中执⾏投票来决定物体的形状，⽽这是由累加空间(accumulator space)⾥的局部最⼤值(local maximum)来决定。

Hough变换的基本原理在于，利⽤点与线的对偶性，将图像空间的线条变为参数空间的聚集点，从⽽检测给定图像是否存在给定性质的曲线。

clc;clear ; closeset(0,'defaultfigurecolor',[1,1,1])load DATA2.matdata = D1;BW = data;figure(1)imshow(BW)title('原图像');figure(2)subplot 211;%%进⾏霍夫变换[H, theta , rho] = hough (BW);%%绘制霍夫空间imshow(imadjust(mat2gray(H)),[],'XData',theta,'YData',rho,...'InitialMagnification','fit');xlabel('\theta (degrees)'), ylabel('\rho');axis on, axis normal, hold on;colormap(hot);title('霍夫空间')%%峰值P = houghpeaks(H,5,'threshold',0.5*max(H(:)));x = theta(P(:,2));y = rho(P(:,1));plot(x,y,'s','color','black');%lines = houghlines(BW,theta,rho,P,'FillGap',10,'MinLength',10);lines = houghlines(BW,theta,rho,P,'FillGap',10,'MinLength',10);subplot 212imshow(BW) ,hold onmax_len = 0;count = 1;points = zeros(2,2);for k = 1:length(lines)points(count,1) = lines(k).point1(1);points(count,2) = lines(k).point1(2);count =count +1;points(count,1) = lines(k).point2(1);points(count,2) = lines(k).point2(2);count =count +1;xy = [lines(k).point1; lines(k).point2];plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','green');% Plot beginnings and ends of linesplot(xy(1,1),xy(1,2),'x','LineWidth',2,'Color','yellow');plot(xy(2,1),xy(2,2),'x','LineWidth',2,'Color','red');endtitle('直线检测'); 效果如下：。

图像处理之霍夫变换（直线检测算法）_java图像处理之霍夫变换（直线检测算法）霍夫变换是图像变换中的经典手段之一，主要用来从图像中分离出具有某种相同特征的几何形状（如，直线，圆等）。

霍夫变换寻找直线与圆的方法相比与其它方法可以更好的减少噪声干扰。

经典的霍夫变换常用来检测直线，圆，椭圆等。

霍夫变换算法思想：以直线检测为例，每个像素坐标点经过变换都变成都直线特质有贡献的统一度量，一个简单的例子如下：一条直线在图像中是一系列离散点的集合，通过一个直线的离散极坐标公式，可以表达出直线的离散点几何等式如下：X *cos(theta) + y * sin(theta) = r 其中角度theta指r与X轴之间的夹角，r为到直线几何垂直距离。

任何在直线上点，x, y都可以表达，其中 r， theta是常量。

该公式图形表示如下：然而在实现的图像处理领域，图像的像素坐标P(x, y)是已知的，而r, theta则是我们要寻找的变量。

如果我们能绘制每个(r, theta)值根据像素点坐标P(x, y)值的话，那么就从图像笛卡尔坐标系统转换到极坐标霍夫空间系统，这种从点到曲线的变换称为直线的霍夫变换。

变换通过量化霍夫参数空间为有限个值间隔等分或者累加格子。

当霍夫变换算法开始，每个像素坐标点P(x, y)被转换到(r, theta)的曲线点上面，累加到对应的格子数据点，当一个波峰出现时候，说明有直线存在。

同样的原理，我们可以用来检测圆，只是对于圆的参数方程变为如下等式：(x –a ) ^2 + (y-b) ^ 2 = r^2其中(a, b)为圆的中心点坐标，r圆的半径。

这样霍夫的参数空间就变成一个三维参数空间。

给定圆半径转为二维霍夫参数空间，变换相对简单，也比较常用。

编程思路解析：1. 读取一幅带处理二值图像，最好背景为黑色。

2. 取得源像素数据3. 根据直线的霍夫变换公式完成霍夫变换，预览霍夫空间结果4. 寻找最大霍夫值，设置阈值，反变换到图像RGB值空间(程序难点之一)5. 越界处理，显示霍夫变换处理以后的图像关键代码解析：直线的变换角度为[0 ~ PI]之间，设置等份为500为PI/500，同时根据参数直线参数方程的取值范围为[-r, r]有如下霍夫参数定义：[java]view plaincopy1.// prepare for hough transform2.int centerX = width / 2;3.int centerY = height / 2;4.double hough_interval = PI_VALUE/(double)hough_space;5.6.int max = Math.max(width, height);7.int max_length = (int)(Math.sqrt(2.0D) * max);8.hough_1d = new int[2 * hough_space * max_length];实现从像素RGB空间到霍夫空间变换的代码为：[java]view plaincopy1.// start hough transform now....2.int[][] image_2d = convert1Dto2D(inPixels);3.for (int row = 0; row < height; row++) {4.for (int col = 0; col < width; col++) {5.int p = image_2d[row][col] & 0xff;6.if(p == 0) continue; // which means background color7.8.// since we does not know the theta angle and r value,9.// we have to calculate all hough space for each pixel poi nt10.// then we got the max possible theta and r pair.11.// r = x * cos(theta) + y * sin(theta)12.for(int cell=0; cell < hough_space; cell++ ) {13.max = (int)((col - centerX) * Math.cos(cell * hough_int erval) + (row - centerY) * Math.sin(cell * hough_interval));14.max += max_length; // start from zero, not (-max_length)15.if (max < 0 || (max >= 2 * max_length)) {// make sure r did not out of scope[0, 2*max_lenght]16.continue;17.}18.hough_2d[cell][max] +=1;19.}20.}21.}寻找最大霍夫值计算霍夫阈值的代码如下：[java]view plaincopy1.// find the max hough value2.int max_hough = 0;3.for(int i=0; i<hough_space; i++) {4.for(int j=0; j<2*max_length; j++) {5.hough_1d[(i + j * hough_space)] = hough_2d[i][j];6.if(hough_2d[i][j] > max_hough) {7.max_hough = hough_2d[i][j];8.}9.}10.}11.System.out.println("MAX HOUGH VALUE = " + max_h ough);12.13.// transfer back to image pixels space from hough par ameter space14.int hough_threshold = (int)(threshold * max_hough);从霍夫空间反变换回像素数据空间代码如下：[java]view plaincopy1.// transfer back to image pixels space from hough param eter space2.int hough_threshold = (int)(threshold * max_hough);3.for(int row = 0; row < hough_space; row++) {4.for(int col = 0; col < 2*max_length; col++) {5.if(hough_2d[row][col] < hough_threshold) // discard it6.continue;7.int hough_value = hough_2d[row][col];8.boolean isLine = true;9.for(int i=-1; i<2; i++) {10.for(int j=-1; j<2; j++) {11.if(i != 0 || j != 0) {12.int yf = row + i;13.int xf = col + j;14.if(xf < 0) continue;15.if(xf < 2*max_length) {16.if (yf < 0) {17.yf += hough_space;18.}19.if (yf >= hough_space) {20.yf -= hough_space;21.}22.if(hough_2d[yf][xf] <= hough_value) {23.continue;24.}25.isLine = false;26.break;27.}28.}29.}30.}31.if(!isLine) continue;32.33.// transform back to pixel data now...34.double dy = Math.sin(row * hough_interval);35.double dx = Math.cos(row * hough_interval);36.if ((row <= hough_space / 4) || (row >= 3 * hough_spa ce / 4)) {37.for (int subrow = 0; subrow < height; ++subrow) {38.int subcol = (int)((col - max_length - ((subrow - center Y) * dy)) / dx) + centerX;39.if ((subcol < width) && (subcol >= 0)) {40.image_2d[subrow][subcol] = -16776961;41.}42.}43.} else {44.for (int subcol = 0; subcol < width; ++subcol) {45.int subrow = (int)((col - max_length - ((subcol - center X) * dx)) / dy) + centerY;46.if ((subrow < height) && (subrow >= 0)) {47.image_2d[subrow][subcol] = -16776961;48.}49.}50.}51.}52.}霍夫变换源图如下：霍夫变换以后，在霍夫空间显示如下：（白色表示已经找到直线信号）最终反变换回到像素空间效果如下：一个更好的运行监测直线的结果(输入为二值图像)：完整的霍夫变换源代码如下：[java]view plaincopy1.package com.gloomyfish.image.transform;2.3.import java.awt.image.BufferedImage;4.5.import com.process.blur.study.AbstractBufferedImageOp;6.7.public class HoughLineFilter extends AbstractBufferedIma geOp {8.public final static double PI_VALUE = Math.PI;9.private int hough_space = 500;10.private int[] hough_1d;11.private int[][] hough_2d;12.private int width;13.private int height;14.15.private float threshold;16.private float scale;17.private float offset;18.19.public HoughLineFilter() {20.// default hough transform parameters21.// scale = 1.0f;22.// offset = 0.0f;23.threshold = 0.5f;24.scale = 1.0f;25.offset = 0.0f;26.}27.28.public void setHoughSpace(int space) {29.this.hough_space = space;30.}31.32.public float getThreshold() {33.return threshold;34.}35.36.public void setThreshold(float threshold) {37.this.threshold = threshold;38.}39.40.public float getScale() {41.return scale;42.}43.44.public void setScale(float scale) {45.this.scale = scale;46.}47.48.public float getOffset() {49.return offset;50.}51.52.public void setOffset(float offset) {53.this.offset = offset;54.}55.56.@Override57.public BufferedImage filter(BufferedImage src, BufferedImage dest) {58.width = src.getWidth();59.height = src.getHeight();60.61.if ( dest == null )62.dest = createCompatibleDestImage( src, null );63.64.int[] inPixels = new int[width*height];65.int[] outPixels = new int[width*height];66.getRGB( src, 0, 0, width, height, inPixels );67.houghTransform(inPixels, outPixels);68.setRGB( dest, 0, 0, width, height, outPixels );69.return dest;70.}71.72.private void houghTransform(int[] inPixels, int[] outPix els) {73.// prepare for hough transform74.int centerX = width / 2;75.int centerY = height / 2;76.double hough_interval = PI_VALUE/(double)hough_sp ace;77.78.int max = Math.max(width, height);79.int max_length = (int)(Math.sqrt(2.0D) * max);80.hough_1d = new int[2 * hough_space * max_length];81.82.// define temp hough 2D array and initialize the hough 2D83.hough_2d = new int[hough_space][2*max_length];84.for(int i=0; i<hough_space; i++) {85.for(int j=0; j<2*max_length; j++) {86.hough_2d[i][j] = 0;87.}88.}89.90.// start hough transform now....91.int[][] image_2d = convert1Dto2D(inPixels);92.for (int row = 0; row < height; row++) {93.for (int col = 0; col < width; col++) {94.int p = image_2d[row][col] & 0xff;95.if(p == 0) continue; // which means background color96.97.// since we does not know the theta angle and r value,98.// we have to calculate all hough space for each pixel point99.// then we got the max possible theta and r pair.100.// r = x * cos(theta) + y * sin(theta)101.for(int cell=0; cell < hough_space; cell++ ) {102.max = (int)((col - centerX) * Math.cos(cell * hough_int erval) + (row - centerY) * Math.sin(cell * hough_interval));103.max += max_length; // start from zero, not (-max_length)104.if (max < 0 || (max >= 2 * max_length)) {// make sure r did not out of scope[0, 2*max_lenght]105.continue;106.}107.hough_2d[cell][max] +=1;108.}109.}110.}111.112.// find the max hough value113.int max_hough = 0;114.for(int i=0; i<hough_space; i++) {115.for(int j=0; j<2*max_length; j++) {116.hough_1d[(i + j * hough_space)] = hough_2d[i][j];117.if(hough_2d[i][j] > max_hough) {118.max_hough = hough_2d[i][j];119.}120.}121.}122.System.out.println("MAX HOUGH VALUE = " + max_h ough);123.124.// transfer back to image pixels space from hough par ameter space125.int hough_threshold = (int)(threshold * max_hough);126.for(int row = 0; row < hough_space; row++) {127.for(int col = 0; col < 2*max_length; col++) {128.if(hough_2d[row][col] < hough_threshold) // discard it129.continue;130.int hough_value = hough_2d[row][col];131.boolean isLine = true;132.for(int i=-1; i<2; i++) {133.for(int j=-1; j<2; j++) {134.if(i != 0 || j != 0) {135.int yf = row + i;136.int xf = col + j;137.if(xf < 0) continue;138.if(xf < 2*max_length) {139.if (yf < 0) {140.yf += hough_space;141.}142.if (yf >= hough_space) {143.yf -= hough_space;144.}145.if(hough_2d[yf][xf] <= hough_value) {146.continue;147.}148.isLine = false;149.break;150.}151.}152.}153.}154.if(!isLine) continue;155.156.// transform back to pixel data now...157.double dy = Math.sin(row * hough_interval);158.double dx = Math.cos(row * hough_interval);159.if ((row <= hough_space / 4) || (row >= 3 * hough_spa ce / 4)) {160.for (int subrow = 0; subrow < height; ++subrow) { 161.int subcol = (int)((col - max_length - ((subrow - center Y) * dy)) / dx) + centerX;162.if ((subcol < width) && (subcol >= 0)) {163.image_2d[subrow][subcol] = -16776961;164.}165.}166.} else {167.for (int subcol = 0; subcol < width; ++subcol) {168.int subrow = (int)((col - max_length - ((subcol - center X) * dx)) / dy) + centerY;169.if ((subrow < height) && (subrow >= 0)) {170.image_2d[subrow][subcol] = -16776961;171.}172.}173.}174.}175.}176.177.// convert to hough 1D and return result178.for (int i = 0; i < this.hough_1d.length; i++)179.{180.int value = clamp((int)(scale * this.hough_1d[i] + offset )); // scale always equals 1181.this.hough_1d[i] = (0xFF000000 | value + (value << 16 ) + (value << 8));182.}183.184.// convert to image 1D and return185.for (int row = 0; row < height; row++) {186.for (int col = 0; col < width; col++) {187.outPixels[(col + row * width)] = image_2d[row][col];188.}189.}191.192.public BufferedImage getHoughImage() {193.BufferedImage houghImage = new BufferedImage(ho ugh_2d[0].length, hough_space, BufferedImage.TYPE_4BYTE_AB GR);194.setRGB(houghImage, 0, 0, hough_2d[0].length, hough _space, hough_1d);195.return houghImage;196.}197.198.public static int clamp(int value) {199.if (value < 0)200.value = 0;201.else if (value > 255) {202.value = 255;203.}204.return value;205.}206.207.private int[][] convert1Dto2D(int[] pixels) {208.int[][] image_2d = new int[height][width];209.int index = 0;210.for(int row = 0; row < height; row++) {211.for(int col = 0; col < width; col++) {212.index = row * width + col;213.image_2d[row][col] = pixels[index];214.}215.}216.return image_2d;218.219.}转载文章请务必注明出自本博客！！。

霍夫变换直线检测原理 python霍夫变换是一种用于线性特征检测的变换技术，可以在图像中检测出直线、圆、椭圆等曲线形状。

在图像处理领域中被广泛应用，如路线检测、目标追踪、边缘检测等方面。

霍夫变换的基本原理是将直线表示为极坐标形式，即一条直线可以由它在极坐标下的表示方式唯一确定。

在霍夫变换中，将极坐标表示转换成参数表示。

设直线方程为 y = kx + b ，可以将它转换成参数表示方式，即 y = (-x * cosθ + ρ)/sinθ 。

其中，ρ 表示极径，即直线距离原点的距离，θ表示直线与极轴的夹角， k = -cosθ / sinθ , b = ρ / sinθ 。

对于一幅图像中的一条直线来说，通过某个角度θ 和距离ρ 能够由上述公式计算出来。

则图像中所有的直线都可以表达为在霍夫空间（参数空间）上的一条曲线。

霍夫变换最基本的思想是通过在霍夫空间上将曲线的计数器加 1 ，进而找到在原始图像中的直线。

不过，在实际应用中霍夫变换会受到一些误差影响，例如图像中的噪声、光照不均、边缘模糊等因素都会对直线的检测造成影响。

因此，在实际应用中通常需要对图像进行一些预处理，例如滤波、边缘检测等操作来尽量消除噪声和干扰。

在 Python 中，OpenCV 提供了很好的霍夫变换直线检测功能。

下面我们将通过一个例子来介绍如何使用 OpenCV 进行霍夫变换直线检测。

1. 导入相关库import cv2import numpy as npimport matplotlib.pyplot as plt2. 读取图像img = cv2.imread('line_detection.jpg')3. 转换成灰度图像gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)4. 高斯模糊gray_blur = cv2.GaussianBlur(gray,(5,5),0)5. 边缘检测其中，cv2.HoughLines() 函数的参数解释如下：第一个参数 edges 表示边缘检测得到的图像第二个参数 1 表示像素距离的分辨率，即霍夫空间中ρ 的步长第三个参数 np.pi/180 表示角度的分辨率，即霍夫空间中θ 的步长，这里表示以π/180 为步长第四个参数 200 表示阈值，即能够检测到线段的最小长度，可以根据图像实际情况来调节。

一种改进的概率霍夫直线检测算法
李建华;宋刘毅;樊高峰;雷春丽
【期刊名称】《海军工程大学学报》
【年(卷),期】2024(36)1
【摘要】针对概率霍夫直线检测算法检测速率不高、检测精度易受其他特征和连续间断线干扰的缺点,提出了一种改进的概率霍夫直线检测算法。

改进后的算法将注意力集中在直线可能存在的若干个区间,提升了检测速率与精度,在直线检测全过程监控并剔除连续间断线,提升了算法的抗干扰能力。

经过100组铝锭边缘线检测的实验验证,改进后算法相较原算法平均检测速率提升至1.77倍,查准率提升至1.45倍,且改进后算法在其他图片上的检测速率和检测效果相较原算法也有明显提升。

【总页数】7页(P62-68)
【作者】李建华;宋刘毅;樊高峰;雷春丽
【作者单位】兰州理工大学机电工程学院;云南文山铝业有限公司
【正文语种】中文
【中图分类】TP278
【相关文献】
1.基于霍夫直线检测的稀疏盲分离
2.基于改进概率霍夫直线检测的电梯门状态检测方法
3.基于霍夫直线检测与二维透视变换的图像校正恢复算法
4.基于霍夫直线检
测的输电导线过热检测方法研究5.基于霍夫直线检测和区域生长的合成孔径声呐图像线目标提取
因版权原因，仅展示原文概要，查看原文内容请购买。

霍夫变换直线检测 c语言霍夫变换是一种在图像处理中广泛应用的算法，用于检测图像中的直线。

它是由霍夫于1962年提出的，被广泛应用于计算机视觉领域。

霍夫变换的基本原理是将直线表示为参数空间中的点，然后通过统计参数空间中的点的数量来确定直线。

具体而言，对于图像中的每个点，我们可以通过遍历参数空间中的所有可能的直线，来确定该点是否在直线上。

如果该点在直线上，则在参数空间中对应的直线的计数加1。

最后，我们可以根据参数空间中点的数量，来确定图像中的直线。

在C语言中实现霍夫变换的直线检测可以分为以下几个步骤：1. 图像预处理：首先，我们需要对图像进行预处理，以便更好地进行直线检测。

常见的预处理操作包括灰度化、边缘检测等。

通过将彩色图像转换为灰度图像，我们可以简化计算，并且减少噪声的影响。

边缘检测可以帮助我们找到图像中的边缘，从而更好地检测直线。

2. 参数空间的定义：在霍夫变换中，我们需要定义参数空间。

对于直线检测，常用的参数是直线的斜率和截距。

我们可以通过定义一个二维数组来表示参数空间，其中每个元素对应一个直线的斜率和截距。

3. 参数空间的计算：对于图像中的每个边缘点，我们都需要遍历参数空间中的所有可能的直线，并将对应的直线的计数加1。

这可以通过两层循环来实现，外层循环遍历所有可能的斜率，内层循环遍历所有可能的截距。

4. 直线检测：在计算完参数空间后，我们可以根据参数空间中的计数来确定图像中的直线。

通常，我们会设定一个阈值，只有当参数空间中的计数超过该阈值时，才认为该直线存在。

5. 直线绘制：最后，我们可以将检测到的直线绘制在图像上，以便查看结果。

这可以通过在图像上绘制参数空间中计数最大的直线来实现。

需要注意的是，霍夫变换的效果受到参数空间的定义和阈值的选择的影响。

如果参数空间定义得不合理，或者阈值选择不当，可能会导致直线检测的准确性下降。

因此，在实际应用中，需要根据具体情况进行调整和优化。

总结起来，霍夫变换是一种常用的直线检测算法，可以通过对图像进行预处理、定义参数空间、计算参数空间、检测直线和绘制直线等步骤来实现。

Hough 变换直线检测是直接按照hough 变换的定义来进行的, 算法如下:1) 对原始的图像进行二值化, 假设0代表背景, 1代表物体特征点；2) 在参数空间ρ, θ里建立一个累加的数组[],H ρθ , 并且置数组H 中的每一个元素的初值都为零； 对于二值图像中每个以1 表示的点(,)x y , 我们让θ取遍θ轴上所有可能的值, 并根据式(3-3)计算对应的ρ； 再根据ρ与θ的值(假设都已经取整) 对数组进行累加计算([][],,1H H ρθρθ=+) ；3) 然后对数组[],H ρθ 进行局部的峰值检测, 得到被检测直线的参数ρ和θ。

上述的算法受直线中的间隙与噪声的影响较小, 鲁棒性比较强,但其具有运算量太大的缺点, 极端情况下, 它的运算复杂度为3()n ο 。

传统随机hough 变换的具体算法如下：(a)构造一个边缘点集D , 然后初始化参数单元集P NULL = ,循环的次数K = 0 ；(b)从D 中随机的选取3 个点；(c)由这3个点解特征的参数p ；(d)在P 中寻找一个c p ,使它满足p c p δ-≤,如果找到则转(f)；否则就转(e)；(e)将p 插入到P 中,其对应的计数值变为1,转(g)；(f)将c p 所对应的计数的值加1,如果小于指定阈值t N ,转(g)；否则就转(h)；(g)1k k =+；如果 m ax k k > ,则结束；否则，转(b)；(h)c p 是候选圆的特征参数,如果该参数对应圆上的边缘的点数m in pc M M >,转(i)；(i) c p 是真实的圆参数,把落在参数c p 对应的特征上的点从D 中去除,然后判断已经检测到的圆的数目是否已达到规定的数目,若是就结束,否则的话重置P NULL =,0K =,转(b)。

其中m ax k 是规定的检测一个圆的过程中所允许采样的最大的循环次数。

m in M 为圆所必需的最小的点数, 通常设为2r πλ,其中λ是一个固定系数，r 是候选圆的半径。