小升初几何图形面积总汇.

易错知识点1线、角1 .直线没有端点，没有长度，可以无限延伸。

2. 射线只有一个端点，没有长度，射线可以无限延伸，并且射线有方向。

3. 在一条直线上的一个点可以引出两条射线。

4. 线段有两个端点，可以测量长度。

圆的半径、直径都是线段。

5 .角的两边是射线，角的大小与射线的长度没有关系，而是跟角的两边叉开的大小有关，叉得越大角就越大。

6 .几个易错的角边关系：（1）平角的两边是射线，平角不是直线。

（2）三角形、四边形中的角的两边是线段。

（3）圆心角的两边是线段。

7 .两条直线相交成直角时，这两条直线叫做互相垂直。

其中一条直线叫做另一条直线的垂线，这两条直线的交点叫做垂足。

8. 从直线外一点到这条直线所画的垂直线段的长度叫做点到直线的距离。

9. 在同一个平面上不相交的两条直线叫做平行线。

2 三角形1. 任何三角形内角和都是180度。

2 .三角形具有稳定的特性，三角形两边之和大于第三边，三角形两边之差小于第三边。

3. 任何三角形都有三条高。

4. 直角三角形两个锐角的和是90度。

5. 两个三角形等底等高，则它们面积相等。

6 .面积相等的两个三角形，形状不一定相同。

3正方形面积1 .正方形面积：边长×边长2 .正方形面积：两条对角线长度的积÷24三角形、四边形的关系1. 两个完全一样的三角形能组成一个平行四边形。

2. 两个完全一样的直角三角形能组成一个长方形。

3. 两个完全一样的等腰直角三角形能组成一个正方形。

4. 两个完全一样的梯形能组成一个平行四边形。

5 圆把一个圆割成一个近似的长方形，割拼成的长方形的长相当于圆周长的一半，宽相当于圆的半径。

则长方形的面积等于圆的面积，长方形的周长比圆的周长增加r ×2。

半圆的周长等于圆的周长的一半加直径。

半圆的周长公式：Ｃ＝pd¸２＋d或Ｃ＝pr＋２r在同一个圆里，半径扩大或缩小多少倍，直径和周长也扩大或缩小相同的倍数。

而面积扩大或缩小以上倍数的平方倍。

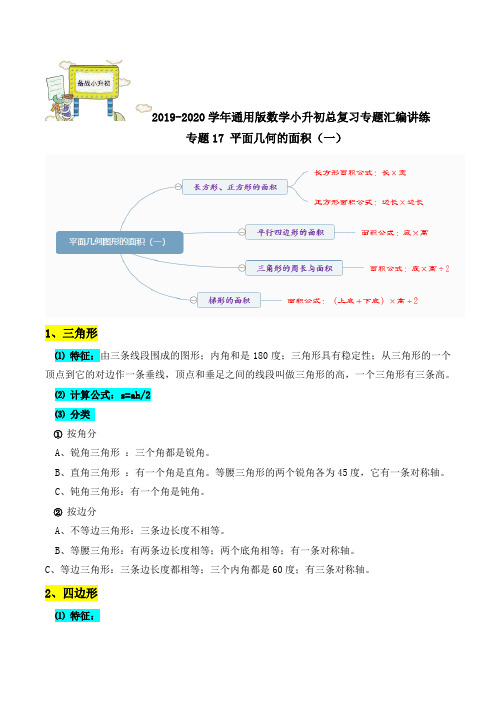
2019-2020学年通用版数学小升初总复习专题汇编讲练专题17 平面几何的面积（一）1、三角形⑴特征：由三条线段围成的图形；内角和是180度；三角形具有稳定性；从三角形的一个顶点到它的对边作一条垂线，顶点和垂足之间的线段叫做三角形的高，一个三角形有三条高。

⑵计算公式：s=ah/2⑶分类①按角分A、锐角三角形：三个角都是锐角。

B、直角三角形：有一个角是直角。

等腰三角形的两个锐角各为45度，它有一条对称轴。

C、钝角三角形：有一个角是钝角。

②按边分A、不等边三角形：三条边长度不相等。

B、等腰三角形：有两条边长度相等；两个底角相等；有一条对称轴。

C、等边三角形：三条边长度都相等；三个内角都是60度；有三条对称轴。

2、四边形⑴特征：①四边形是由四条线段围成的图形。

②任意四边形的内角和是360度。

③只有一组对边平行的四边形叫梯形。

④两组对边分别平行的四边形叫平行四边形，它简洁变形。

长方形、正方形是特殊的平行四边形；正方形是特殊的长方形。

⑵分类①长方形A、特征：对边相等，4个角都是直角的四边形。

有两条对称轴。

B、计算公式：c=2(a+b) s=ab②正方形A、特征：四条边都相等，四个角都是直角的四边形。

有4条对称轴。

B、计算公式：c=4a s=a²③平行四边形A、特征：两组对边分别平行的四边形；相对的边平行且相等；对角相等；相邻的两个角的度数之和为180度；平行四边形简洁变形。

B、计算公式：s=ah④梯形A、特征：只有一组对边平行的四边形；中位线等于上下底和的一半；等腰梯形有一条对称轴。

B、计算公式：s=(a+b)h/2=mh3、圆⑴圆的生疏圆是平面上的一种曲线图形。

圆中心的一点叫做圆心。

一般用字母o表示。

半径：连接圆心和圆上任意一点的线段叫做半径。

一般用r表示。

在同一个圆里，有很多条半径，每条半径的长度都相等。

通过圆心并且两端都在圆上的线段叫做直径。

一般用d表示。

同一个圆里有很多条直径，全部的直径都相等。

三角形等积变形:①: 等底等高旳两个三角形面积相等。

如右图, AB 平行CD,有, 深入可得出②：两个三角形高相等, 面积之比等于底边之比；两个三角形底边相等, 面积之比等于高之比。

两个三角形底边相等，面积之比等于高之比。

③: 共边定理: 如图, △ABC 和△ABD 有公共底边AB,它们另一种顶点旳连线CD 和AB 相交于点E, 则有它们另一种顶点旳连线CD 和AB 相交于点E ，则有 ABC ABD S CE S DE ∆∆=。

（由于ABC AEC ABD AEDS S S S ∆∆∆∆=）鸟头定理:如右图, △AED 和△ABC 有一种公共角, 则有AED ABC S AE AD S AB AC∆∆=⨯蝴蝶定理:如图在任意四边形中, 对角线AC 和BD 相交于O 点, 则有①, 或②ABD DBC S AO S OC∆∆= （由于23ABD DBC S S AO S S OC ∆∆==） 梯形蝴蝶定理:这是蝴蝶定理旳特殊状况, 如图, 在梯形ABCD 中有①221324S S S S ⨯==②221324::::::S S S S a b ab ab =梯形ABCD 面积占旳份数为 DO: OB ＝AO: OC ＝a: b燕尾定理:如图, 在三角形中, AD, BE, CF 相交于点O,则有ABO ACO S BD S DC∆∆= （由于ABO OBD ACO OCD S S S S ∆∆∆∆=） 多种周长面积体积公式1.如图, 已知正方形ABCD 和正方形AEFG 旳边长分别为8和5, 且B, A, E 三点在一条直线上, 求△BDF 旳面积2.如图，圆旳面积和长方形旳面积相等，已知圆旳周长是62.8厘米，求阴影部分旳周长。

（π取3.14）3.已知梯形ABCD 旳下底BC 是上底AD 长度旳1.5倍, 且图中阴影部分和空白部分面积相等, △OBC 面积等于12, 求△OAD 旳面积。

4.如图, 阴影部分面积占正方形面积旳_______％第4题 第5题 5.图中阴影①比阴影②面积小48平方厘米, AB ＝40厘米, 求BC 旳长。

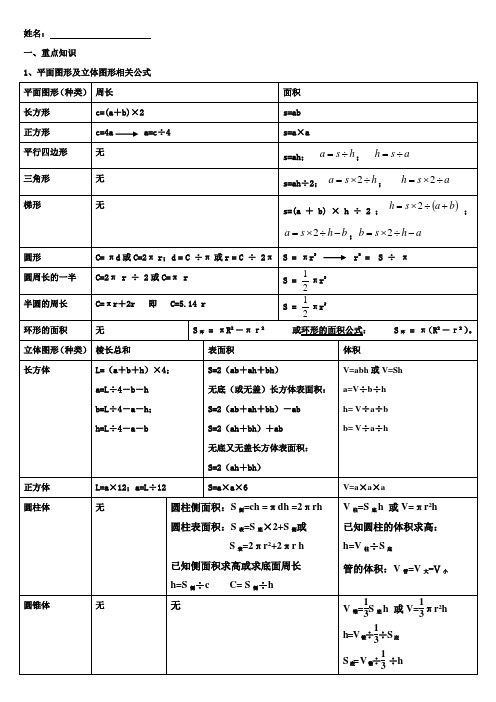
姓名：一、重点知识1、平面图形及立体图形相关公式2、非公式知识点（1）计算圆木、钢管等的根数： (顶层根数+底层根数)×层数÷2（2）在一个正方形里画一个最大的圆，圆的直径等于正方形的边长。

在一个长方形里画一个最大的圆，圆的直径等于长方形的宽。

（3）常用各π值结果：π = 3.14；2π = 6.28；3π = 9.42 ；4π = 12.56 ；5π = 15.7；6π = 18.84； 7π = 21.98 ；8π = 25.12；9π = 28.26；10π = 31.4（4）常用平方数结果：121112= ； 144122= ； 169132= ； 196142= ； 225152= ； 256162= ； 289172= ； 324182= ；361192=（5）锐角：小于90°的角叫做锐角；直角：等于90°的角叫做直角；钝角：大于90°而小于180°的角叫做钝角。

平角：角的两边成一条直线，这时所组成的角叫做平角。

平角180°； 周角：角的一边旋转一周，与另一边重合。

周角是360°。

（6）从一点引出两条射线，所组成的图形叫做角。

这个点叫做角的顶点，这两条射线叫做角的边。

（7）三角形由三条线段围成的图形。

内角和是180度。

三角形具有稳定性。

三角形有三条高。

（8）三角形分类①按角分：锐角三角形 ；直角三角形；钝角三角形；②按边分：不等边三角形；等腰三角形；等边三角形。

（9）平行四边形：两组对边分别平行的四边形。

特征：相对的边平行且相等。

对角相等，相邻的两个角的度数之和为180度。

平行四边形容易变形。

四边形内角和是360度。

二、单位1、长度常用单位 ：* 千米（公里）(km) * 米(m) * 分米(dm) * 厘米(cm) * 毫米(mm) * 微米(um) 单位之间的换算* 1毫米 ＝1000微米 * 1厘米 ＝10 毫米 * 1分米 ＝10 厘米 * 1米 ＝1000 毫米 * 1千米 ＝1000 米 2、面积：就是物体所占平面的大小。

一、体积和表面积三角形的面积=底×高÷2。

公式S= a×h÷2正方形的面积=边长×边长公式S= a2长方形的面积=长×宽公式S= a×b平行四边形的面积=底×高公式S= a×h梯形的面积=(上底+下底)×高÷2 公式S=(a+b)h÷2内角和：三角形的内角和=180度。

长方体的表面积=(长×宽+长×高+宽×高) ×2 公式：S=(a×b+a×c+b×c)×2正方体的表面积=棱长×棱长×6 公式：S=6a2长方体的体积=长×宽×高公式：V = abh长方体(或正方体)的体积=底面积×高公式：V = abh正方体的体积=棱长×棱长×棱长公式：V = a3圆的周长=直径×π 公式：L=πd=2πr圆的面积=半径×半径×π 公式：S=πr2圆柱的表(侧)面积：圆柱的表(侧)面积等于底面的周长乘高。

公式：S=ch=πdh=2πrh 圆柱的表面积：圆柱的表面积等于底面的周长乘高再加上两头的圆的面积。

公式：S=ch+2s=ch+2πr2圆柱的体积：圆柱的体积等于底面积乘高。

公式：V=Sh圆锥的体积=1/3底面×积高。

公式：V=1/3Sh二、算术1、加法交换律：两数相加交换加数的位置，和不变。

2、加法结合律：a + b = b + a3、乘法交换律：a × b = b × a4、乘法结合律：a × b × c = a ×(b × c)5、乘法分配律：a × b + a × c = a × b + c6、除法的性质：a ÷ b ÷ c = a ÷(b × c)7、除法的性质：在除法里，被除数和除数同时扩大(或缩小)相同的倍数，商不变。

阴影部分面积专题小学六年级小学升初中1. 求如图阴影部分的面积.（单位：厘米）2. 如图，求阴影部分的面积.（单位：厘米）3. 计算如图阴影部分的面积.（单位：厘米）4. 求出如图阴影部分的面积：单位：厘米.6.求如图阴影部分面积.（单位：厘米）7.计算如图中阴影部分的面积.单位：厘米.9.如图是三个半圆，求阴影部分的周长和面积.（单位：厘米）11. 求下图阴影部分的面积.（单位：厘米）12. 求阴影部分图形的面积.（单位：厘米）r ------ io ------- 113. 计算阴影部分面积（单位：厘米）14. 求阴影部分的面积.（单位：厘米）15. 求下图阴影部分的面积：（单位：厘米）16. 求阴影部分面积（单位：厘米）17. （2012&泰县）求阴影部分的面积.（单位：厘米）☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆参考答案与试题解析1.求如图阴影部分的面积.（单位：厘米）考点组合图形的面积；梯形的面积；圆、圆环的面积. 1526356分析阴影部分的面积等丁梯形的面积减去直径为4厘米的半圆的面积，利用梯形和半圆的面积公式代入数据即可解答.解答…n 2解：（4+6） X4士2士2-3.14 X士2,2=10— 3.14 X4士2,=10-6.28 ,=3.72 （平方厘米）;答：阴影部分的面积是3.72平方厘米.点评组合图形的面积一般都是转化到已知的规则图形中利用公式计算，这里考查了梯形和圆的面积公式的灵活应用.2.如图，求阴影部分的面积.（单位：厘米）考点组合图形的面积.1526356分析根据图形可以看出：阴影部分的面积等丁正方形的面积减去4个扇形的面积.正方形的面积等丁（10X 10） 100平方厘米，4个扇形的面积等丁半径为（10士2） 5厘米的圆的面积，即：3.14 X 5X 5=78.5 （平■方厘米）. 解答解：扇形的半径是：10 士2,=5 （厘米）；10X 10 -3.14 X 5X 5,100-78.5 ,=21.5 （平方厘米）;答：阴影部分的面积为21.5平方厘米.点评解答此题的关键是求4个扇形的面积，即半径为5厘米的圆的面积.考点组合图形的面积.1526356分析分析图后可知，10厘米不仅是半圆的直径，还是长方形的长，根据半径等丁直径的一半，可以算出半圆的半径，也是长方形的宽，最后算出长方形和半圆的面积，用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解：10 -2=5 （厘米），长方形的面积*X宽=10X 5=50 （平方厘米），半圆的面积=兀r2士2=3.14 X 52-2=39.25 （平■方厘米）,阴影部分的面积=长方形的面积-半圆的面积，=50- 39.25 ,=10.75 （平方厘米）;答：阴影部分的面积是10.75 .点评这道题重点考查学生求组合图形面积的能力，组合图形可以是两个图形拼凑在一起，也可以是从一个大图形中减去一个小图形得到；像这样的题首先要看届丁哪一种类型的组合图形，再根据条件去进一步解答.4.求出如图阴影部分的面积：单位：厘米.考点组合图形的面积.1526356专题平■面图形的认识与计算.分析由题意可知：阴影部分的面积=长方形的面积-以4厘米为半径的半圆的面积，代入数据即可求解.解答解：8X4-3.14 X42-2,=32 - 25.12 ,=6.88 （平方厘米）;答：阴影部分的面积是6.88平方厘米.点评解答此题的关键是：弄活楚阴影部分的面积可以由哪些图形的面积和或差求出.5.求如图阴影部分的面积.（单位：厘米）考点圆、圆环的面积.1526356分析由图可知，正方形的边长也就是半圆的直径，阴影部分由4个直径为4 H 米的半圆组成，也就是两个圆的面积，因此要求阴影部分的面积，首先要算1个圆的面积，然后根据“阴影部分的面积=2X圆的面积”算出答案.解答解：S=^ r2_ ，_ . 2=3.14 X （4士2）=12.56 （平方厘米）;阴影部分的面积=2个圆的面积，=2X 12.56 ,=25.12 （平方厘米）;答：阴影部分的面积是25.12平方厘米.点评解答这道题的关键是重点分析阴影部分是由什么图形组成的，再根据已知条件去计算.考点长方形、正方形的面积；平行四边形的面积；三角形的周长和面积.1526356分析图一中阴影部分的面积=大正方形面积的一半-与阴影部分相邻的小三角形的面积；图二中阴影部分的面积=梯形的面积-平四边形的面积，再将题目中的数据代入相应的公式进行计算.解答解：图一中阴影部分的面积=6X6-2-4X6-2=6 （平方厘米）；图二中阴影部分的面积=（8+15） X （48士8）士 2 - 48=21 （平方厘米）；答：图一中阴影部分的面积是6平方厘米，图二中阴影部分的面积是21平方厘米.点评此题目是组合图形，需要把握好正方形、三角形、梯形及平行四边形的面积公式，再将题目中的数据代入相应的公式进行计算.7.计算如图中阴影部分的面积.单位：厘米.考点组合图形的面积.1526356分析由图意可知：阴影部分的面积皂圆的面积，乂因圆的半径为斜边上的高, 4利用同一个三角形的面积相等即可求出斜边上的高，也就等丁知道了圆的半径，利用圆的面积公式即可求解.解答解：圆的半径：15X 20-2X2-25,=300+ 25,=12 （厘米）；阴影部分的面积：lx 3.14 X 122,4=Lx 3.14 X 144,=0.785 X 144,=113.04 （平■方厘米）;答：阴影部分的面积是113.04平方厘米.点评此题考查了圆的面积公式及其应用，同时考查了学生观察图形的能力.考点组合图形的面积；三角形的周长和面积；圆、圆环的面积. 1526356 分析（1）圆环的面积等丁大圆的面积减小圆的面积，大圆与小圆的直径已知，代入圆的面积公式，从而可以求出阴影部分的面积；（2）阴影部分的面积=圆的面积-三角形的面积，由图可知，此三角形是等腰直角三角形，则斜边上的高就等丁圆的半径，依据圆的面积及三角形的面积公式即可求得三角形和圆的面积，从而求得阴影部分的面积.解答解：（1）阴影部分面积：223.14 X （上）-3.14 X 〔萱），2 2=28.26 - 3.14 ,=25.12 （平方厘米）;（2）阴影部分的面积：3.14 x 32--X （3+3） X3, 2=28.26 - 9,=19.26 （平方厘米）;答：圆环的面积是25.12平方厘米，阴影部分面积是19.26平方厘米.点评此题主要考查圆和三角形的面积公式，解答此题的关键是找准圆的半径. 9. 如图是三个半圆，求阴影部分的周长和面积.（单位：厘米）考点组合图形的面积；圆、圆环的面积.1526356专题平■面图形的认识与计算.分析观察图形可知：图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等，所以图中阴影部分的周长，就是直径为10+3=13厘米的圆的周长，由此利用圆的周长公式即可进行计算；阴影部分的面积=大半圆的面积-以10-2=5厘米为半径的半圆的面积-以3-2=1.5厘米为半径的半圆的面积，利用半圆的面积公式即可求解.解答解：周长：3.14 X （ 10+3）,=3.14 X 13,=40.82 （厘米）;面积：ix 3.14 X [ (10+3) 士2]2—【X 3.14 X (10 士2) 2 2ix 3.14 X (3 士2) 2,=以 3.14 X (42.25 - 25 - 2.25),2=以 3.14 X 15,=23.55 （平方厘米）;答：阴影部分的周长是40.82厘米，面积是23.55平方厘米.点评此题主要考查半圆的周长及面积的计算方法，根据半圆的弧长=兀r,得出图中两个小半圆的弧长之和等丁大半圆的弧长，是解决本题的关键.10. 求阴影部分的面积.（单位：厘米）考点圆、圆环的面积.1526356■刀忻先用“3+3=6'求出大扇形的半径，然后根据“扇形的面积卫*”分别计360算出大扇形的面积和小扇形的面积，进而根据“大扇形的面积-小扇形的面积=阴影部分的面积”解答即可.解：r=3, R=3+3=6 n=120,解答$喙新一点兀=—"■-□OU JuU=37.68 - 9.42 ,=28.26 （平方厘米）;答：阴影部分的面积是28.26平方厘米.点评此题主要考查的是扇形面积计算公式的掌握情况，应主要灵活运用.11. 求下图阴影部分的面积.（单位：厘米）考点组合图形的面积.1526356分析先求出半圆的面积3.14 X （10士2）2-2=39.25平方厘米，再求出空白三角形的面积10X （10士2）士2=25平方厘米，相减即可求解.2解答解：3.14 X （10士2）士2 - 10X （10士2）士 2=39.25 - 25=14.25 （平■方厘米）.答：阴影部分的面积为14.25平方厘米.点评考查了组合图形的面积，本题阴影部分的面积北圆的面积-空白三角形的面积.12. 求阴影部分图形的面积.（单位：厘米）考点组合图形的面积.1526356分析求阴影部分的面积可用梯形面积减去圆面积的1,列式计算即可.42解答解：（4+10） X4士2-3.14 X4 士4,=28 - 12.56 ,=15.44 （平方厘米）;答：阴影部分的面积是15.44平方厘米.点评解答此题的方法是用阴影部分所在的图形（梯形）面积减去空白图形（扇形）的面积，即可列式解答.13. 计算阴影部分面积（单位：厘米）考点组合图形的面积.1526356专题平■面图形的认识与计算.分析如图所示，阴影部分的面积=平行四边形的面积-三角形①的面积，平■行四边形的底和高分另U为10厘米和15厘米，三角形①的底和高分别为10厘米和（15-7）厘米，利用平■行四边形和三角形的面积公式即可求解.解答解：10X 15- 10X （ 15-7）士2,=150- 40,=110（平方厘米）;答：阴影部分的面积是110平方厘米.点评解答此题的关键是明白：阴影部分的面积不能直接求出，可以用平行四边形和三角形的面积差求出.考点梯形的面积.1526356分析如图所示，将扇形①平移到扇形②的位置，求阴影部分的面积就变成了求梯形的面积，梯形的上底和下底已知，高就等丁梯形的上底，代入梯形的面积公式即可求解.=96 士2,=48 （平方厘米）;答：阴影部分的面积是48平方厘米.点评此题主要考查梯形的面积的计算方法，关键是利用平移的办法变成求梯形的面积.15. 求下图阴影部分的面积：（单位：厘米）考点组合图形的面积.1526356分析根据三角形的面积公式：S=ah,找到图中阴影部分的底和高，代入计算即可求解.解答解：2X 3-2=6 士2=3 （平方厘米）.答：阴影部分的面积是3平方厘米.点评考查了组合图形的面积，本题组合图形是一个三角形，关键是得到三角形的底和高.16. 求阴影部分面积（单位：厘米）.考点组合图形的面积.1526356分析由图意可知：阴影部分的面积=梯形的面积-圆的面积，梯形的上底和高[4都等丁圆的半径，上底和下底已知，从而可以求出阴影部分的面积.解答解：（4+9） X4士2-3.14 X42x1,4=13X4士2-3.14 X4,=26 - 12.56 ,=13.44 （平方厘米）;答：阴影部分的面积是13.44平方厘米.点评解答此题的关键是明白：梯形的下底和高都等丁圆的半径，且阴影部分的面积=梯形的面积-[圆的面积.17. （2012&泰县）求阴影部分的面积.（单位：厘米）考点组合图形的面积.1526356分析由图可知，阴影部分的面积=梯形的面积-半圆的面积.梯形的面积（a+b）h,半圆的面积 m兀「2,将数值代入从而求得阴影部分的面积.解答解：*X（6+8） X （6士2）— 3.14 X （6士2）2=以14X3-以 3.14 X 9, 2 '=21 - 14.13,=6.87 （平方厘米）;答：阴影部分的面积为6.87平方厘米.点评考查了组合图形的面积，解题关键是看懂图示，把图示分解成梯形，半圆和阴影部分，再分别求出梯形和半圆的面积.。

小升初图形面积40题一、计算下列图形的面积1、一个正方形边长是4米，面积是()平方米。

2、一个长方形长是6厘米，宽是4厘米，面积是()平方厘米。

3、一个三角形底是8分米，高是5分米，面积是()平方分米。

4、一个梯形上底是3厘米，下底是5厘米，高是4厘米，面积是()平方厘米。

5、一个平行四边形底是10分米，高是4分米，面积是()平方分米。

二、求下列图形的面积6、有一个平行四边形，它的一组邻边分别长5厘米和8厘米，这个平行四边形的面积是多少平方厘米？61、有一个三角形，它的底长是10厘米，高是6厘米，这个三角形的面积是多少平方厘米？611、有一个梯形，它的上底长是3厘米，下底长是5厘米，高是4厘米，这个梯形的面积是多少平方厘米？6111、有一个正方形，它的边长是6厘米，这个正方形的面积是多少平方厘米？三、比较图形的面积大小10、下面的两个图形，哪一个的面积更大一些？101、下面的两个图形，哪一个的面积更大一些？1011、下面的两个图形，哪一个的面积更大一些？下面的两个图形，哪一个的面积更大一些？下面的两个图形，哪一个的面积更大一些？下面的两个图形，哪一个的面积更大一些？小升初组合图形的面积典型试题在数学的学习中，组合图形的面积是一个重要的概念，尤其在小升初阶段，这一概念的重要性更加凸显。

它不仅涉及到基础几何知识，还考察了学生的逻辑思维和问题解决能力。

本文将通过一些典型的试题，探讨如何解决这类问题。

一、理解基本概念我们需要理解什么是组合图形。

组合图形是由两个或两个以上的基本图形组合而成的图形。

例如，一个房子可以由一个矩形和一个三角形组成，一个汽车可以由一个圆形和一个矩形组成。

二、掌握基本方法在计算组合图形的面积时，我们通常使用以下两种方法：1、分解法：将组合图形分解成几个基本图形，然后分别计算每个基本图形的面积，最后将它们相加得到组合图形的总面积。

2、直接计算法：如果组合图形无法分解成基本图形，或者分解起来比较复杂，我们可以直接计算整个组合图形的面积。

【2020】最新⼩升初数学⼏何图形阴影部分⾯积题型⼤全（详细答案解析）六年级阴影部分的⾯积1.求阴影部分的⾯积。

(单位:厘⽶)解：割补后如右图，易知，阴影部分⾯积为⼀个梯形。

梯形上底DE=7-4=3厘⽶，1S =S =DE AB)AD 2?+?阴梯形（=137)42+（=20(平⽅厘⽶)2、求阴影部分的⾯积。

解：S =S 阴梯形，梯形的上底是圆的直径，下底、⾼是圆的半径，S =S 阴梯形=124)22+（=6(2cm )3、如图，平⾏四边形的⾼是6厘⽶，⾯积是54平⽅厘⽶，求阴影三⾓形的⾯积。

解：S =AD AO ?ABCD =54平⽅厘⽶，且AO=6厘⽶，所以AD=9厘⽶。

由图形可知AED ?是等腰直⾓三⾓形，所以AE=AD ，OE=OF=AE-AO=9-6=3cm ，BO=BC-OC=9-3=6cm 。

1S =BO OF 2??阴=1S =632??阴=92cm 。

4、如图是⼀个平⾏四边形，⾯积是50平⽅厘⽶，求阴影积分的⾯积。

解：⽅法⼀：过C 点作CF AD ⊥交AD 于点F ，可知AECF 是长⽅形，⾯积=5×6=302cm ，ABE CFD S =S ??=(50-30)÷2=102cm 。

⽅法⼆：BC=S ABCD ÷AE=50÷5=10cm ，BE=BC-EC=10-6=4cm ，ABE S ?=BE ×AE ÷2 =4×5÷2=102cm5、下图是⼀个半圆形，已知ＡＢ＝10厘⽶，阴影部分的⾯积为24.25平⽅厘⽶，求图形中三⾓形的⾼。

解：S =S -S ?阴半圆=21AB 22π???? ?-24.25=21103.1422???-24.25=152cm ，三⾓形的⾼=2S ?÷AB=2×15÷10=3cm 。

6、如图，⼀个长⽅形长是10cm ，宽是4cm ，以A 点和C 点为圆⼼各画⼀个扇形，求画中阴影部分的⾯积是多少平⽅厘⽶?解：BECD 1S =S -S 4阴⼤圆=ABCD 11S -S S 44??-⼤圆⼩圆=ABCD 11S +S -S 44⼤圆⼩圆=()2213.1410-4-1044 =25.942cm 。