小升初专题知识点归纳汇总——图形与几何

第二部份 空间与图形量的计量一、长度单位是用来测量物体的长度的。

常用的长度单位有：千米、米、分米、 厘米、毫米。

二、长度单位:三、面积单位是用来测量物体的恚面或平面图形的大小的。

常用面积单位：平方 千米、公顷、平方米、平方分米、平方厘米。

四、 测量和计算土地面积，通常用公顷作单位。

边长100米的正方形土地，面积是1公顷。

五、 测量和计算大面积的土地，通常用平方千米作单位。

边长woo 米的正方形 土地，面积是1平方千米。

六、面积单位：（100）七、 体积单位是用来测量物体所占空间的大小的。

常用的体积单位有；立方米、 立方分米（升）、立方厘米（臺升）。

八、 体枳单位；＜1000）九、常用的质量单位有：吨、千克、克。

十、质量单位：十一、常用的时间单位有；世纪、年、季度、月、旬、日、时、分、秒。

十二、时间单位：（60）（一） 形的认识.测量十三、高级单位的名数改写成低级单位的名数应该乘以进率；低级单位的名数改写成高级单位的名数应该除以进率。

十四、常用计最单位用字母表示平面图形【认识.周长、面积】一、用直尺把两点连接起来，就得到一条线段；把线段的一端无限延长，可以得到一条射线；把线段的两端无限延长，可以得到一条直线。

线段、射线都是直线上的一部分。

线段有两个端点，长度是有限的；射线只有一个端点，直线没有端点，射线和直线都是无限长的。

二、从一点引出两条射线，就组成了一个角。

角的大小与两边叉开的大小有关，与边的长短无关。

角的大小的计量单位是O三、角的分类：小于90度的角是锐角；等于90度的角是直角；大于90度小于180度的角是钝角；等于180度的角是平角；等于360度的角是周角。

四、相交成直角的两条直线互相垂直；在同一平面不相交的两条直线互相平行。

五、三角形是由三条线段国成的图形。

围成三角形的每条线段叫做三角形的边，每两条线段的交点叫做三角形的顶点。

六、三角形按角分'可以分为锐角三角形、直角三角形和钝角三角形。

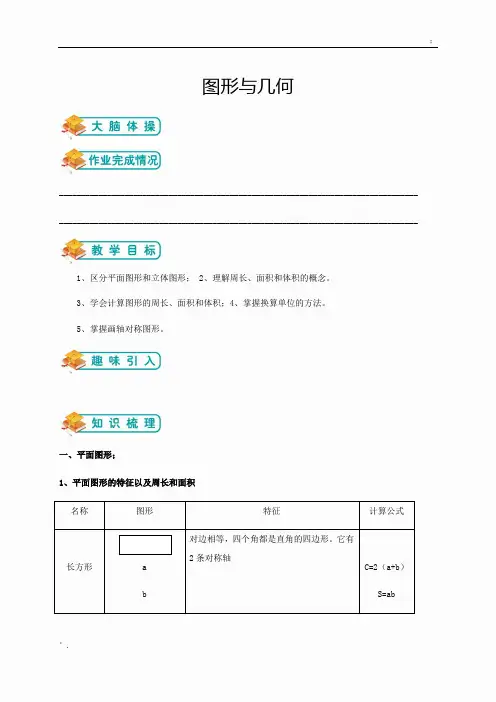
图形与几何__________________________________________________________________________________ __________________________________________________________________________________1、区分平面图形和立体图形；2、理解周长、面积和体积的概念。

3、学会计算图形的周长、面积和体积；4、掌握换算单位的方法。

5、掌握画轴对称图形。

一、平面图形；1、平面图形的特征以及周长和面积名称图形特征计算公式长方形 ab对边相等，四个角都是直角的四边形。

它有2条对称轴C=2（a+b）S=ab正方形a 4条边相等，4个角都是直角的四边形它有4条对称轴C=4aS=a2平行四边形ha 两组对边分别平行（相等）的四边形。

对边平行且相等、对角相等。

内角和为360°平行四边形容易变形。

平行四边形不是轴对称图形；S=ah梯形ahb只有一组对边平行的四边形。

等腰梯形（两条腰相等）直角梯形（有一个角是直角）等腰梯形有一条对称轴。

S=21(a+b)h三角形ha 三条线段围成的封闭图形。

内角和是180°三角形具有稳定性。

等腰三角形有1条对称轴等边三角形有3条对称轴S=21ah圆ro 在同圆或等圆中所有的半径都相等，所有的直径也都相等；直径等于半径的2倍。

圆的周长与它直径的比值为π。

直径所在的直线都是圆的对称轴，C=πd=2πrS=πr2有无数条对称轴。

环形ro R 由两个半径不相等的同心圆组成由无数条对称轴。

S=π(R2-r2)2、三角形的分类（1）按角分：锐角三角形：三个角都是锐角的三角形。

钝角三角形：有一个角是钝角的三角形。

直角三角形：有一个角是直角的三角形。

（2）按边分：等腰三角形：有两条边相等的三角形，两个底角相等，有一条对称轴。

等边三角形：三条边都相等的三角形，三个角都相等，都是60○，有三条对称轴（等边三角形是特殊的等腰三角形）。

小升初专题复习——几何图形一、三视图及展开图例题1：用同样大小的正方体摆成的物体，从正面看到，从上面看到，从右面看到〔 〕A ．B ．C ．D ．变式练习：如图，它是用6个棱长为1分米的正方体拼成的． ①它的外表积是 ． ②它的体积是 ．二、三角形的底边及面积关系例题1：如图．A 、B 是长方形长和宽的中点，阴影局部的面积是长方形面积的 %．例题2：如图，三角形ABC 面积为27平方厘米，AE=CE ，BF=BC ，求三角形BEF 的面积．变式练习1：如图，直角梯形ADCB 中，三角形BEC 、四边形CEAF 和三角形CFD 的面积一样大．BC=16、AD=20、AB=12，求三角形AEF 的面积．教师姓名 学科 数学 上课时间 讲义序号 (同一学生)学生姓名年级六年级组长签字日期课题名称 几何图形变式练习2：如图，梯形ABCD中共有〔〕对面积相等的三角形A． 22 B． 3 C． 4 D． 5变式练习3：在如图中，平行四边形的面积是20平方厘米，图中甲、丙两个三角形的面积比是，阴影局部的面积是平方厘米．三、多边形内角和例题1：把表填完整多边形…边数 3 4 5 6 …内角和180°180°×2 180°×3 180°×5 …变式练习：探索〔1〕完成表格中未填局部．〔2〕根据表中规律，八边形的内角和是度．〔3〕假设图形的边数为a，内角和为s，请你用一个含有字母的关系式表示图形边数及内角和的关系．．图形边数 3 4 5内角和180 180×2 180×3四、长度比拟例题1：面积相等的情况下，长方形、正方形和圆相比，〔〕的周长最短．A．长方形B．正方形C．圆例题2：如图，A是一个圆，B是由三个半圆围成的图形，那么它们周长的大小关系是C A C B．变式练习1：下面三个图形中，哪两个图形的周长相等？〔〕A．图形①和②B．图形②和③C．图形①和③变式练习2：在图形中甲的周长〔〕乙的周长．A．大于B．小于C．等于拓展提升：某高层公寓大火时，小王逃生的时候看了下疏散通道如下图，那么最快逃离到楼梯〔图中阴影〕的通道共有〔〕条．A． 3 B． 9 C． 6 D． 12五、组合图形计数例题1：如图中直角的个数为〔〕个．A． 4 B． 8 C． 10 D． 12例题2：如图，共有〔〕条线段．A． 4 B． 8 C． 10 D． 12例题3：数一数，在右图中共有〔〕个三角形．A．10 B． 11 C． 12 D． 13 E．14A．4 B． 8 C． 10 D． 12变式练习2：如图中直角有〔〕个．A． 1 B． 2 C． 3 D． 4变式练习3：这里共有〔〕条线段．A．三条B．四条C．五条D．六条变式练习4：如下图的7×7的方格内，有许多边长为整数的正方形，其中在有的正方形中黑方格及白方格的个数占一半〔同样多〕．像这样的正方形有〔〕个．A．26 B． 36 C． 46 D． 56E．66变式练习5：图中共有〔〕个长方形．A． 30 B． 28 C． 26 D． 24变式练习6：如图，三角形一共有个．拓展提升1：如图是半个正方形，它被分成一个一个小的等腰三角形，图中，正方形有10 个，三角形有47 个．拓展提升2：如图中，三角形的个数有多少？六、图形的拆拼〔切拼〕例题1：一个圆的周长是15.7分米，把这个圆等分成假设干个小扇形，拼成一个近似的长方形，这个近似的长方形的长是分米，宽是分米．例题2：爸爸给女儿买了一个圆柱形的大生日蛋糕，女儿把蛋糕竖直方向切成22块分给22个小朋友，切成的大小不一定相等．那么至少需切的刀数为？变式练习1：在一块边长为4厘米的正方形的铁皮上，剪出直径为2厘米的小圆片，最多可剪〔〕片．A． 3 B． 4 C． 5 D． 6变式练习2：用一条直线将一个正方形分成两个完全一样的两局部，有几种分法〔〕A． 1种B． 2种C． 3种D． 4种变式练习3：在一块长10分米、宽5分米的长方形铁板上，最多能截取11 个直径是2分米的圆形铁板．拓展提升：请将下面等边三角形按要求分割成假设干个形状和大小都一样的三角形〔1〕分成2个〔2〕分成3个〔3〕分成4个〔4〕分成6个七、立体图形的外表积例题1：把14个棱长为1的正方体，在地面上堆叠成如下图的立体，然后将露出的外表局部染成红色．那么红色局部的面积为〔〕A． 21 B． 24 C． 33 D． 37例题2：如图，在棱长为3的正方体中由上到下，由左到右，由前到后，有三个底面积是1的正方形高为3的长方体的洞，那么所得物体的外表积为．变式练习2：把假设干个边长2厘米的正方体重叠起来堆成如下图的立体图形，这个立体图形的外表积是平方厘米．变式练习3：如图是一个长3厘米、宽及高都是2厘米的长方体．将它挖掉一个棱长1厘米的小正方体，它的外表积〔〕A．比原来大B．比原来小C．不变拓展提升〔难〕：在一个棱长为8的立方体上切去一个三棱柱〔如图〕，那么外表积减少．八、立体图形的体积例题1：如图的体积是．〔单位：厘米〕例题2：一支没有用过的圆柱形铅笔，长18厘米，体积是9立方厘米，使用一段时间后变成了如图的样子，这时铅笔的体积是多少立方厘米？变式练习1：有一棱长为5cm的正方体机器零件，现在它的上下面挖去了一个直径为2cm的圆孔，求剩下机器零件的外表积和体积？九、等积变形例题1：如下图，把底面直径8厘米的圆柱切成假设干等分，拼成一个近似的长方体．这个长方体的外表积比原来增加80平方厘米，那么长方体的体积是立方厘米．例题2：一个酸奶瓶〔如图〕，它的瓶身呈圆柱形〔不包括瓶颈〕，容积是32.4立方厘米．当瓶子正放时，瓶内酸奶高为8厘米，瓶子倒放时，空余局部高为2厘米．请你算一算，瓶内酸奶体积是多少立方厘米？变式练习1：一个圆锥形沙堆，底面积是3.6平方米，高1.2米．把这堆沙装在长2米、宽1.5米的沙坑里，可以装多高？变式练习2：有一种饮料瓶的容积是50立方厘米，瓶身呈圆柱形〔不包括瓶颈〕．现在瓶中装有一些饮料，正放时饮料高度为20厘米，倒放时空余局部的高度为5厘米．瓶内现有饮料立方厘米．变式练习3：水平桌面上放着高度都为10厘米的两个圆柱形容器A和B，在它们高度的一半处有一连通管相连〔连通管的容积忽略不计〕，容器A、B底面直径分别为10厘米和16厘米．关闭连通管，10秒钟可注满容器B，如果翻开连通管，水管向B容器注水6秒钟后，容器A中水的高度是多少呢？〔π取3.14〕变式练习4：A和B都是高度为12厘米的圆柱形容器，底面半径分别是1厘米和2厘米，一水龙头单独向A 注水，一分钟可注满．现将两容器在它们的高度的一半出用一根细管连通〔连通管的容积忽略不计〕，仍用该水龙头向A注水，求〔1〕2分钟容器A中的水有多高？〔2〕3分钟时容器A中的水有多高．十、数阵图中找规律的问题例题1：把自然数依次排成以下数阵：1，2，4，7，11，…3，5，8，12，…6，9，13，…10，14，…15，……现规定横为行，纵为列．求〔1〕第10行第5列排的是哪一个数？〔2〕第5行第10列排的是哪一个数？〔3〕2004排在第几行第几列？变式练习1：淘气用小棒搭房子，他搭3间用了13根小棒，像这样搭15间房子要用〔〕根小棒．A． 60 B． 61 C． 65 D． 75。

图形与几何的知识点图形和几何是数学中重要的分支，涉及了很多基本概念和定理。

在本文中，我们将介绍一些图形和几何的常见知识点，以及它们的应用。

一、点、线、面1. 点是几何中最基本的元素，没有大小和形状，用于定位位置。

2. 线由无数个点连接而成，没有宽度和厚度，可以表示直线、线段和射线。

3. 面是由无数个点和线围成的平面区域，可以是平行四边形、三角形、长方形等。

二、基本图形1. 三角形是由三条边和三个顶点组成，根据边的长度和角的大小可以分为等边三角形、等腰三角形和普通三角形。

2. 四边形是由四条边和四个顶点组成，可以是矩形、正方形、平行四边形、梯形等。

3. 圆是由一个固定点（圆心）和到该点距离相等的一组点组成，半径是圆心到圆上任意点的距离。

三、角和正多边形1. 角是由两条射线共同起点组成的图形，可以通过角的大小来划分为钝角、直角、锐角。

2. 正多边形是具有相等边长和相等内角的多边形，如正三角形、正方形等。

四、几何公式与定理1. 勾股定理：直角三角形两直角边的平方和等于斜边的平方。

2. 正弦定理：在任意三角形中，任意一角的正弦值与它对应的边的比例相等。

3. 余弦定理：在任意三角形中，任意一角的余弦值与其他两边的关系。

4. 面积计算公式：如三角形的面积等于底乘以高的一半，矩形的面积等于长乘以宽。

5. 平行线定理：如果一条直线垂直于另外两条平行直线，那么这两条垂直线也是平行的。

五、应用1. 几何知识在建筑、工程和设计中有广泛的应用，如计算面积、体积和角度。

2. 几何图形的分类和性质有助于解决实际问题，如通过角的大小判断两条线段的相对位置。

3. 几何思维在证明和推理中发挥重要作用，培养了逻辑思维和问题解决能力。

总结：图形与几何的知识点涵盖了点、线、面、基本图形、角和正多边形，以及相关的公式和定理。

这些知识点在实际生活和学习中都有着广泛的应用，对于培养逻辑思维和解决问题能力至关重要。

通过学习和应用这些知识，我们能够更好地理解和运用几何概念，为将来的学习和工作打下良好的基础。

图形与几何的知识点一、基本概念图形与几何是数学中的一个重要分支，研究物体的形状、大小、位置和运动等方面。

在这个领域里，有一些基本的概念和术语我们需要了解。

1. 点：在几何中，点是最基本的概念，没有形状和大小，只有位置。

2. 线段：线段是由两个点确定的一段连续的直线。

3. 直线：直线是由一条连续的线段无限延伸而成的。

4. 射线：射线是由一个端点和一条连续的直线段组成。

5. 角：角是由两条射线共享一个端点而形成的图形。

6. 边：多边形是由线段构成的，每个线段被称为一个边。

二、图形的分类图形可以根据各种属性进行分类，以下是几个常见的分类方式：1. 几何图形：几何图形是平面上的图形，包括点、线、面等。

2. 二维图形：二维图形是在平面上具有宽度和高度的图形，如长方形、正方形、三角形等。

3. 三维图形：三维图形是在空间中具有宽度、高度和深度的图形，如立方体、圆柱体、球体等。

4. 凸多边形和凹多边形：凸多边形是没有内角大于180度的多边形，凹多边形是至少有一个内角大于180度的多边形。

5. 等边图形：等边图形是指具有相等边长的图形，比如等边三角形。

三、图形的性质图形具有一些共同的性质，这些性质有助于我们理解和比较不同的图形。

1. 对称性：图形在某个轴线或点处可以被分成两个相等的部分。

2. 平行性：两条直线在平面上没有点重合，但始终保持相同的间距。

3. 垂直性：两条直线相交，且相交的角为直角（90度）。

4. 相似性：两个图形的形状相似，但大小可能不同。

5. 定理：几何学中有很多定理，如勾股定理、正弦定理、余弦定理等，它们可以用来解决各种几何问题。

四、常见图形的计算公式图形的计算涉及到面积、周长、体积等方面，以下是几个常见图形的计算公式：1. 矩形的面积公式：面积 = 长 ×宽2. 三角形的面积公式：面积 = 底边长 ×高 ÷ 23. 圆的面积公式：面积= π × 半径^24. 圆的周长公式：周长= 2 × π × 半径5. 立方体的体积公式：体积 = 长 ×宽 ×高五、实际应用图形与几何的知识点在实际生活中有许多应用。

易错知识点1线、角1 .直线没有端点，没有长度，可以无限延伸。

2. 射线只有一个端点，没有长度，射线可以无限延伸，并且射线有方向。

3. 在一条直线上的一个点可以引出两条射线。

4. 线段有两个端点，可以测量长度。

圆的半径、直径都是线段。

5 .角的两边是射线，角的大小与射线的长度没有关系，而是跟角的两边叉开的大小有关，叉得越大角就越大。

6 .几个易错的角边关系：（1）平角的两边是射线，平角不是直线。

（2）三角形、四边形中的角的两边是线段。

（3）圆心角的两边是线段。

7 .两条直线相交成直角时，这两条直线叫做互相垂直。

其中一条直线叫做另一条直线的垂线，这两条直线的交点叫做垂足。

8. 从直线外一点到这条直线所画的垂直线段的长度叫做点到直线的距离。

9. 在同一个平面上不相交的两条直线叫做平行线。

2 三角形1. 任何三角形内角和都是180度。

2 .三角形具有稳定的特性，三角形两边之和大于第三边，三角形两边之差小于第三边。

3. 任何三角形都有三条高。

4. 直角三角形两个锐角的和是90度。

5. 两个三角形等底等高，则它们面积相等。

6 .面积相等的两个三角形，形状不一定相同。

3正方形面积1 .正方形面积：边长×边长2 .正方形面积：两条对角线长度的积÷24三角形、四边形的关系1. 两个完全一样的三角形能组成一个平行四边形。

2. 两个完全一样的直角三角形能组成一个长方形。

3. 两个完全一样的等腰直角三角形能组成一个正方形。

4. 两个完全一样的梯形能组成一个平行四边形。

5 圆把一个圆割成一个近似的长方形，割拼成的长方形的长相当于圆周长的一半，宽相当于圆的半径。

则长方形的面积等于圆的面积，长方形的周长比圆的周长增加r ×2。

半圆的周长等于圆的周长的一半加直径。

半圆的周长公式：Ｃ＝pd¸２＋d或Ｃ＝pr＋２r在同一个圆里，半径扩大或缩小多少倍，直径和周长也扩大或缩小相同的倍数。

而面积扩大或缩小以上倍数的平方倍。

小升初图形知识点总结高中一、图形的基本概念图形是几何学的一个重要概念，是数学中的一种几何对象。

图形是由一系列的点和线组成的。

在小学阶段，学生首先学习了点、线、线段、射线、角、多边形等基本概念，这些都是构成图形的基础要素。

1. 点：点是图形的最基本要素，是没有长、宽、厚度的。

点在平面上用圆圈标记表示，用大写字母表示。

2. 线：线是由无数个点连在一起的轨迹，是没有宽度的，用一对箭头表示。

在平面上的线用直线、封闭曲线表示。

3. 线段：线段是由两个不同的端点和这两个端点之间的点组成的部分。

线段没有方向，是定长的。

4. 射线：射线是以一个端点为起点，另一个端点为方向的无穷远的部分。

5. 角：两条射线共享一个端点形成的图形称为角。

角的度量单位为度。

常见的角有直角、锐角、钝角等。

6. 多边形：多边形是由三条以上的线段组成的封闭曲线。

常见的多边形有三角形、四边形、五边形等。

二、图形的基本性质1. 直线性：两点之间唯一确定一条直线。

2. 独一性：通过一点可以作一条唯一的直线。

3. 无限性：通过一点可以作无限个相异的直线。

4. 唯一性：通过一点可以作过直线外的一点的平行线。

5. 一般性：在同一平面上的两条直线要么相交，要么平行。

6. 多边形的内角和公式：n边形的内角和公式为180°×(n-2)。

三、几何图形的分类1. 按几何形状分类：圆形、三角形、四边形、五边形、六边形、多边形。

2. 按图形的相似性分类：全等图形、相似图形。

3. 按图形的性质分类：平行四边形、菱形、长方形、正方形等。

4. 按角度大小分类：直角三角形、钝角三角形、锐角三角形、等腰三角形、等边三角形。

四、几何图形的周长和面积1. 周长：多边形的周长是所有边长的和，圆的周长即为圆的周长为2πr（假定半径为r）。

2. 面积：三角形的面积可以用公式S=1/2×底×高求解，四边形的面积可以用公式S=底×高求解，圆的面积可以用公式S=πr²求解。

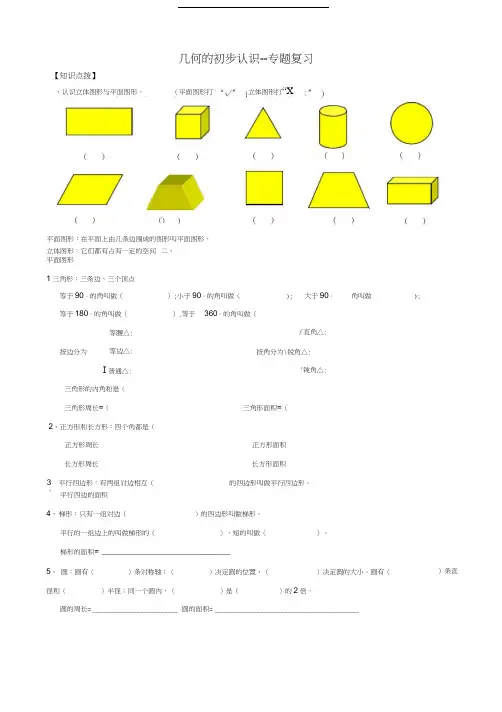
几何的初步认识--专题复习【知识点拨】立体图形：它们都有占有一定的空间二、平面图形1三角形：三条边、三个顶点平行四边的面积4、梯形：只有一组对边（）的四边形叫做梯形。

平行的一组边上的叫做梯形的（），短的叫做（）。

梯形的面积= _____________________________5、圆：圆有（）条对称轴；（）决定圆的位置，（）决定圆的大小。

圆有（径和（）半径；同一个圆内，（）是（）的2倍。

圆的周长= _________________________ 圆的面积= __________________________________________、认识立体图形与平面图形。

;立体图形打“X（平面图形打平面图形：在平面上由几条边围成的图形叫平面图形。

()等于90。

的角叫做（）;小于90。

的角叫做（); 大于90。

角叫做);等于180。

的角叫做（）,等于360。

的角叫做（等腰△:f直角△:按边分为等边△:按角分为\锐角△:I普通△:'钝角△:三角形的内角和是（三角形周长=（三角形面积=（2、正方形和长方形：四个角都是（正方形周长正方形面积长方形周长长方形面积3、平行四边形：有两组对边相互（的四边形叫做平行四边形。

）条直6、由几个独立的几何图形（正方形、长方形、三角形、梯形、平行四边形）组成的图形叫做组合图形，组合图形一半学会运用“分割”与“添补”的方法计算组合图形的面积。

计算组合图形的面积步骤: 1、分图形2 、找条件、算面积三、立体图形1认识长方体和正方体。

(1)面和面相交的边叫做（(2)棱相交的点叫做（）;长方体和正方体都有（）个棱。

(3)长方体和正方体都有（）个面，相对的面完全相同。

(4) 棱可以分为三组。

相对的棱长度相等。

长方体棱长之和长方体表面积长方体体积正方体棱长之和正方体表面积正方体体积2、圆柱和圆锥（1）圆柱的特征：有（）个底面，有（）个侧面, 是曲面，打开是一个（长方形的长是（（2）圆柱的侧面积=（），用字母表示是（圆柱的表面积=圆柱的侧面积+两个底面的面积; 表面积=2 n r X h+2 Xn r2圆柱的体积=底面积X高;V=S圆锥的特征：尖顶，底面是（），侧面是一个曲面，打开是一个扇形, 底面圆周上任一点与顶点之间的距离都相等。

2022年小升初几何图形整理汇编独家原创最新最全命中小升初几何图形整理汇编（知识点与练习题）【知识点一】几何图形的认识1．定义：把从实物中抽象出的各种图形统称为几何图形，几何图形由点、线、面组成. 2．分类：几何图形包括立体图形和平面图形(1)立体图形：图形的各部分不都在同一平面内，这样的图形就是立体图形，如长方体，圆柱，圆锥，球等.(2)平面图形：有些几何图形(如线段、角、三角形、圆等)的各部分都在同一平面内，它们是平面图形．（3）常见的平面图形有如下分类：平面图形{三角形多边形（四边形，五边形……）圆（4）常见的立体图形有两种分类方法：【知识点二】主视图、左视图、俯视图1.定义：一般地，我们把从正面看到的图形，称为主视图；从左面看到的图形，称为左视图；从上面看到的图形，称为俯视图.【知识点三】展开图1、定义：有些立体图形是由一些平面图形围成，将它们的表面适当剪开，可以展开成平面图形，这样的平面图形称为相应立体图形的展开图．要点诠释：(1)不是所有的立体图形都可以展成平面图形．例如，球便不能展成平面图形．(2)不同的立体图形可展成不同的平面图形；同一个立体图形，沿不同的棱剪开，也可得到不同的平面图．【知识点四】点、线、面、体1、定义：长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体,几何体也简称体；包围着体的是面,面有平的面和曲的面两种；面和面相交的地方形成线，线也分为直线和曲线两种；线和线相交的地方形成点．从上面的描述中我们可以看出点、线、面、体之间的关系．此外，从运动的观点看：点动成线，线动成面，面动成体．【知识点五】旋转体例1、下面各组图形都是平面图形的一组是（）A．线段、圆、圆锥、球 B.角、三角形、长方形、圆柱C.长方体、圆柱、棱锥、球D.角、三角形、正方形、圆演练1、下列图形中，与其他三个不同类的是（）例2、将图中的几何体进行分类，并说明理由．演练1、在下列几何体，按其形体分类（填序号），球体有，柱体有，锥体有。

图形与几何知识点整理几何学是研究空间和形状的学科，它探讨了各种图形的性质、特征和关系。

在学习几何学时，有一些关键的知识点需要了解和掌握。

本文将对常见的图形与几何知识点进行整理，并提供相应的解释和例子。

一、点、线、面1. 点：点是几何学中最基本的概念，它没有长度、宽度和厚度，只有位置。

用大写字母表示，如A、B。

2. 线：线由无数个点连在一起形成，它没有宽度，只有长度。

用小写字母表示，如a、b。

3. 面：面由无数个线连在一起形成，它有长度和宽度，但没有厚度。

用大写字母表示，如ABCD。

二、常见图形1. 线段：两个点之间的部分称为线段，用两个点的大写字母表示，如AB。

2. 射线：起始于一个点，沿某个方向无限延伸的部分称为射线，用一个点和一条箭头表示，如→AB。

3. 直线：无限延伸的线称为直线，用两个点的小写字母表示，如ab。

4. 角：由两条射线共享端点的图形称为角，通常用大写字母表示，如∠ABC。

角可以分为锐角（小于90度）、直角（等于90度）和钝角（大于90度）。

5. 三角形：由三条线段组成的图形称为三角形，用三个顶点的大写字母表示，如△ABC。

三角形可以根据边长和角度分为等边三角形、等腰三角形和一般三角形。

6. 四边形：由四条线段组成的图形称为四边形，用四个顶点的大写字母表示，如ABCD。

四边形可以根据边长和角度分为正方形、长方形、菱形和一般四边形。

7. 圆：由一条曲线围成的图形称为圆，用大写字母表示圆心，用小写字母表示圆周上的点，如O、A。

三、图形的性质与关系1. 图形的周长：图形的周长是指图形边缘上的长度总和。

对于矩形和正方形，周长可以通过边长之和乘以2来计算；对于圆，周长可以通过直径乘以π来计算。

2. 图形的面积：图形的面积是指图形内部的空间大小。

对于矩形和正方形，面积可以通过边长之积来计算；对于三角形，面积可以通过底边长度乘以高再除以2来计算；对于圆，面积可以通过半径的平方乘以π来计算。

3. 图形的相似：当两个图形的形状相同但大小不同，我们称它们为相似图形。

本文部分内容来自网络整理，本司不为其真实性负责，如有异议或侵权请及时联系，本司将立即删除！== 本文为word格式，下载后可方便编辑和修改！ ==小升初图形与几何知识点正在读六年级的你们很快就要步入初中了，那么在你们升入初中应该要考一次入学试，下面小编精心为你们准备了一些小升初图形与几何知识点，供大家参考，希望对你们有帮助。

小升初图形与几何知识点一、认识圆1、圆的定义：圆是由曲线围成的一种平面图形。

2、圆心：将一张圆形纸片对折两次，折痕相交于圆中心的一点，这一点叫做圆心。

一般用字母O表示。

它到圆上任意一点的距离都相等。

3、半径：连接圆心到圆上任意一点的线段叫做半径。

一般用字母r表示。

把圆规两脚分开，两脚之间的距离就是圆的半径。

4、直径：通过圆心并且两端都在圆上的线段叫做直径。

一般用字母d表示。

直径是一个圆内最长的线段。

5、圆心确定圆的位置，半径确定圆的大小。

6、在同圆或等圆内，有无数条半径，有无数条直径。

所有的半径都相等，所有的直径都相等。

7.在同圆或等圆内，直径的长度是半径的2倍，半径的长度是直径的。

用字母表示为：d=2r或r=d/28、轴对称图形：如果一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形是轴对称图形。

折痕所在的这条直线叫做对称轴。

(经过圆心的任意一条直线或直径所在的直线)9、长方形、正方形和圆都是对称图形，都有对称轴。

这些图形都是轴对称图形。

10、只有1一条对称轴的图形有：角、等腰三角形、等腰梯形、扇形、半圆。

只有2条对称轴的图形是：长方形只有3条对称轴的图形是：等边三角形只有4条对称轴的图形是：正方形有无数条对称轴的图形是：圆、圆环。

二、圆的周长1、圆的周长：围成圆的曲线的长度叫做圆的周长。

用字母C表示。

2、圆周率实验：在圆形纸片上做个记号，与直尺0刻度对齐，在直尺上滚动一周，求出圆的周长。

发现一般规律，就是圆周长与它直径的比值是一个固定数(π)。

3.圆周率：任意一个圆的周长与它的直径的比值是一个固定的数，我们把它叫做圆周率。

数学小升初关键知识归纳几何形的分类与特征几何形是数学中一个重要的概念，它描述了平面或者空间中的形状和结构。

在小学升初阶段，掌握好几何形的分类与特征对于学生的数学基础打下坚实的基础。

本文将重点介绍几何形的分类与特征，帮助学生更好地理解和掌握这一知识点。

一、点、线和面几何形的最基本的元素包括点、线和面。

点是没有长度、宽度、高度的，只有位置的一个标志，可以用一个小圆点来表示。

直线由无数个点连在一起形成，它没有宽度，只有长度，可以通过两个点确定一条直线。

面是由无数个点和线相互连接形成的，它具有长度和宽度，可以通过三个点确定一个平面。

二、二维几何形的分类在二维几何中，最常见的几何形包括：点、线段、射线、直线、角、三角形、四边形、多边形、圆等。

1. 线段：两个端点确定的线段是一个有限长度的几何形。

2. 射线：一个端点和无限远点连成的线叫做射线，它只有一个方向。

3. 直线：没有端点，无限延伸的线叫做直线，它无方向。

4. 角：由两条不同的射线共享一个端点形成的图形叫做角，根据角度的大小可以分为锐角、直角和钝角。

5. 三角形：由三条线段连接成的封闭图形叫做三角形，根据边长和角度的大小，可以分为等边三角形、等腰三角形和一般三角形。

6. 四边形：由四条线段连接成的封闭图形叫做四边形，例如矩形、正方形、菱形、梯形等。

7. 多边形：由多条线段连接成的封闭图形叫做多边形，例如五边形、六边形等。

8. 圆：由一个中心点和到该中心点距离相等的所有点组成，形成一个封闭曲线。

三、三维几何形的分类在三维几何中，最常见的几何形包括：立方体、正方体、棱柱、棱锥、圆锥、圆柱等。

1. 立方体：具有六个面，六个面都是正方形，每个面的边长相等。

2. 正方体：具有六个面，六个面都是正方形，每个面的边长相等。

3. 棱柱：具有两个相等的平行多边形和若干个连接它们的矩形面。

4. 棱锥：具有一个多边形底面和若干个连接底面顶点的三角形面。

5. 圆锥：具有一个圆形底面和若干个连接底面中心的三角形面。

【小升初】——图形和几何 （基础知识点整理）平面图形
1. 直线、射线和线段
两条直线的位置关系相交平行
重合
两点之间线段最短
2. 角锐角
直角
钝角
平角
周角
3. 三角形
按角的大小划分
锐角三角形
直角三角形钝角三角形按边的关系划分
等腰三角形等边三角形三角形的高4. 四边形
（1）长方形
（2）正方形
（3）平行四边形（4）梯形5. 圆与扇形①在同圆或等圆中，所有的直径都相等，所有的半径都相等
②圆是轴对称图形，它有无数条对称轴，圆的对称轴就是直径所在直线周长和面积公式
立体图形图形与变换轴对称与对称轴
平移
旋转
图形与位置
方向基本方向：上北下南左西右东偏向：如北偏西30°=西偏北60°
确定位置
学会用坐标轴描述简单路线图
观察物体-三视图拓展类三角形与四边形相关的模型问题以及其它的特殊图形可以自行了解。

如：鸟头模型、等积变形、蝴蝶模型、燕尾模型、格点图形等。

图形与几何部分（1）图形的认识知识点：认识平行四边形1．（）的两个梯形一定能拼成一个平行四边形。

[A]形状一样 [B]面积相等 [C]完全相同 [D] 任意2．两个完全一样的锐角三角形，可以拼成一个（）。

[A] 长方形[B] 正方形[C] 平行四边形 [D] 梯形3．先画出这个平行四边形的一条高，再量出它的底和高各是多少厘米（取整厘米数）。

a＝( )厘米 h＝（）厘米4．先观察下图，然后在三角形右边画出一个平行四边形 (用阴影表示）,使平行四边形面积是三角形面积的2倍。

5．用木条钉成一个长方形，沿对角线拉成一个平行四边形。

这个平行四边形与原来的长方形相比：平行四边形的周长（），平行四边形面积（）。

(括号里填“变大”、“变小”或“不变”)6．下面哪些图形是平行四边形?画出每个平行四边形的高。

7．如图,在平行四边形中,已知∠1=40 ,其他各个内角的度数分别是（）、（）、（）。

知识点：认识梯形1. 两个（）梯形可以拼成一个长方形。

[A] 等底等高[B]完全一样[C] 完全一样的直角 [D] 任意2．把一个平行四边形任意分割成两个梯形，这两个梯形的（）总是相等的。

[A]高[B] 面积 [C] 上下两底的和 [D] 周长3．在一个等腰梯形中画一条线段，可以将它分割成两个完全一样的（）。

[A]梯形[B] 平行四边形 [C] 三角形 [D] 长方形4. 右图中有（）个平行四边形，（）个梯形。

5. 按要求在下面图形中画一条线段，分成一个平行四边形和一个梯形知识点：三角形1.用木条给一个长方形窗户加固，若只考虑加固效果的话，采用（）最好。

[B][A]2.在一个平行四边形内画一个最大的三角形，这个三角形的面积是这个平行四边形面积的（）。

3.任意一个三角形都有( )条高。

4.在下面方格中画出一个与已知长方形面积相等的三角形（每个小方格代表1平方厘米）。

5.一个三角形中至少有（）个锐角。

6.已知图中的三角形是原三角形面积的一半，请你把原来的三角形画完整。

立体图形的表面积和体积课标要求1.掌握长方体、正方体、圆柱的表面积和体积的计算公式，并能解决简单的实际问题。

2.理解和掌握等底等高的圆柱和圆锥体积的关系，掌握圆锥体积的计算公式，并能解决简单的实际问题。

3.灵活运用立体图形的表面积和体积的计算公式，解决综合性问题。

考点1 长方体、正方体的表面积和体积计算1.判断（1）棱长是6dm的正方体，它的表面积和体积相等。

（）（2）把一个长方体切成三个长方体，一共增加了9个面。

（）（3）棱长是4cm的正方体，可以加工成4个棱长是1cm的小正方体。

（）2.选择。

（1）如下图，长方体沿虚线切开，表面积比原来增加了（）平方厘米。

A.54B.88C.100（2）一个正方体的棱长总和是48cm，那么这个正方体的表面积是（）cm2。

A.64B.96C.128（3）一个内部长6dm，宽3dm的长方体鱼缸内养了10条金鱼，水面高2.5dm。

强强把金鱼捞出来准备清洗鱼缸，发现水的高度降低到了2.4dm。

10条金鱼的体积约是（）立方厘米。

A.1800B.180C.45 D1.5（4）一个长方体容器，底面是正方形，盛水高1分米，放入6个质量一样的鸡蛋后，水面升高2厘米，要求一个鸡蛋的体积，只需要在知道下面（）这一条信息。

A.6个鸡蛋的表面积是多少 B.长方体容器的表面积是多少C.长方体容器的高是多少的D.长方体的底面周长是多少（5）一个长方体的长宽高分别是a米、b米、h米，如果长宽不变，高增加3米，那么新长方体的体积比原来增加了（）立方米。

A.3abB.3abhC.（3＋h）ab（6）把棱长为2厘米的正方体切成8个完全一样的小正方体，这些小正方体的表面积比原来大正方体的表面积增加了（）平方厘米。

A.8B.16C.24D.323.王芳在一个无盖的长方体玻璃容器内摆了一些棱长为1分米的小正方体（如左下图），做这个玻璃容器至少要用玻璃（）平方米，它的容器是（）立方分米（玻璃的厚度忽略不计）。

平面图形的周长和面积课标要求1.掌握长方形、正方形的周长和面积计算公式，并能解决简单的实际问题，会估计给定的简单图形或不规则图形的面积。

2.掌握三角形、平行四边形、梯形的面积公式，并能解决简单的实际问题。

3.掌握圆、扇形的周长和面积的计算公式，并能解决简单的实际问题。

4.初步运用割、补、平移、旋转等数学方法，综合运用学过的周长、面积公式求组合图形的周长和面积。

考点1 长方形正方形的周长和面积计算1. 用边长是5厘米的两个正方形，拼成一个长方形，拼成的长方形的周长是（ ）厘米，面积是（ ）平方厘米。

2. 用两个完全一样的直角三角形拼成一个面积是20平方分米的长方形，已知直角三角形的一条直角边是8分米，则另一条直角边是（ ）分米。

3. 一张正方形纸先上下对折一次，再左右对折一次，得到的图形是（ ）形，它的面积是原来正方形的（ ），它的周长是原来正方形的多少（ ）。

4. 下图中大圆的半径是5厘米，小圆的半径是3厘米。

长方形的周长是（ ）厘米。

5. 长方形的长和宽分别是a 分米、b 分米（a 、b 是不同的自然数），如果长方形的周长是200分米，那么长方形的面积是（ ）平方分米。

6. 一张正方形纸的边长是12厘米，在它的一个角上剪去一个长4厘米、宽3厘米的长方形后（长方形的边与正方形的边分别平行），剩余图形的周长是（ ）厘米。

7. 一个长方形的周长是72厘米，如果它的宽增加 ，长减少 ，周长仍和原来一样。

那么原来这个长方形的面积是（ ）。

8. 一个等腰三角形底和高的比是8:3，把它沿着底边上的高剪开，拼成一个长方形，这个长方形的面积是192平方厘米，长方形的周长是（ ）厘米。

419.选择（1）如下图，每个小正方形的面积是2cm2，涂色部分的面积是（）cm2。

A.32B.24C.20D.10时（2）如下图，将四张长为16厘米、宽为2厘米的长方形纸条垂直相交平放在桌面上，则桌面被覆盖部分的面积是（）。

A.72cm2B.128cm2C.124cm2D.112cm2（3）一根彩绳和A、B、C三个钉子围成如下图所示的三角形。