山西省晋中市和诚高中高二数学周练试题20文无答案

山西省晋中市和诚高中有限公司2020-2021学年高二数学9月周练试题理考试时间：65分钟 满分：100分一、选择题(共15题，每题3分，共45分)1.下图为某几何体的三视图，则该几何体的表面积是（ ） A.246+ B.244+ C.326+ D.324+2.已知 为球 的球面上的三个点，⊙ 为 的外接圆，若⊙的面积为 ， ，则球 的表面积为（ ）A. B. C. D.3.已知各顶点都在一个球面上的正四棱锥的高3，体积为6，则 球的半径为( )A. 2 B C. D. 34.在正方体ABCD -A 1B 1C 1D 1中，三棱锥D 1-AB 1C 的表面积与正方体的表面积的比为( )A. 1∶1B. 1∶C. 1∶D. 1∶25.如图，将无盖正方体纸盒展开，直线AB 、CD 在原正方体中的位置关系是( )A. 平行B. 相交且垂直C. 异面D. 相交成60°6、在空间四边形ABCD 中，AB 、BC 、CD 的中点分别为P 、Q 、R ，且AC =4，BD =2 ，PR =3，则AC 和BD 所成角的大小为( )A. 90°B. 60°C. 45°D. 30°7.下列命题中①如果一个角的两边与另一个角的两边分别平行，那么这两个角相等；②如果两条相交直线和另两条直线分别平行，那么这两组直线所成的锐角(或直角)相等；③如果一个角的两边和另一个角的两边分别垂直，那么这两个角相等或互补；④如果两条直线同时平行于第三条直线，那么这两条直线平行.正确的结论有( )A. 1个B.2个C. 3个D. 4个8.下列命题中，是假命题的为( )A. 平行于同一直线的两个平面平行B. 平行于同一平面的两个平面平行C.垂直于同一平面的两条直线平行D. 垂直于同一直线的两个平面平行9.如图，已知正方体ABCD-A1B1C1D1，则直线EF是平面ACD1与下列哪个平面的交线?( )A. 平面BDB1B. 平面BDC1C. 平面ACB1D. 平面ACC110.在四面体A-BCD中，E是CD的中点，M、N分别是EA、EB上的点，且则四面体A-BCD的四个表面中所有与MN平行的是()A. 平面ABDB. 平面BCDC. 平面ABCD. 平面ABD与平面ABC11.如图，P为平行四边形ABCD所在平面外一点，Q为PA的中点，O为AC与BD 的交点，下面说法错误的是( ) A. OQ∥平面PCDB. PC∥平面BDQC. AQ∥平面PCDD. CD∥平面PAB12.如图，E，F，G分别是四面体ABCD的棱BC、CD、DA的中点，则此四面体中与过点E、F、G的截面平行的棱的条数是( )A. 0B. 1C. 2D. 3二、填空题（20分）13.如图是正方体的平面展开图，在这个正方体中，①BM∥平面DE；②CN∥平面AF；③平面BDM∥平面AFN；④平面BDE∥平面NCF.以上四个命题中，正确命题的序号是.14.如图，在正方体ABCD-A1B1C1D1中，AB=2，点E为AD的中点，点F在CD上.若EF∥平面AB1C，则线段EF的长度等于.4题图15题图15.如图，四棱锥PABCD的底面是直角梯形，AB∥CD，BA⊥AD，CD＝2AB，PA⊥底面ABCD，E为PC的中点，则BE与平面PAD的位置关系为．16.在长方体中，，，则直线与平面所成角的正弦值为．三、解答题（20分，18题4分）17.如图所示，在△ABC中，∠ABC=90°，SA⊥平面ABC，过点A向SC和SB引垂线，垂足分别是P、Q.求证：(1)AQ⊥平面SBC；(2)PQ⊥SC.18.如图所示，在底面为直角梯形的四棱锥P-ABCD中，AC与BD相交于点E，AD∥BC，∠ABC=90°，PA⊥平面ABCD，AD=2，AB=2 ，BC=6.求证：BD⊥平面PAC.19.如图，在斜三棱柱中，底面是边长为的正三角形，为棱的中点，，，.（Ⅰ）求证：平面；（Ⅱ）求斜三棱柱的体积.试卷答案1、C根据三视图特征，在正方体中截取出符合题意的立体图形，求出每个面的面积，即可求得其表面积.解：根据三视图特征，在正方体中截取出符合题意的立体图形根据立体图形可得：根据勾股定理可得：是边长为的等边三角形根据三角形面积公式可得：该几何体的表面积是： .故选：C.2、A设圆半径为，球的半径为，依题意，得，由正弦定理可得，，根据圆截面性质平面，，球的表面积 .故选：A3、A本题考查四棱锥的外接球问题.设正四棱锥的底面边长为a，由V= a2×3=a2=6，得a= .由题意知球心在正四棱锥的高上，设球的半径为r，则(3-r)2+( )2=r2，解得r=2.4、C本题考查棱锥的表面积.设正方体ABCD-A1B1C1D1的棱长为a，则正方体ABCD-A1B1C1D1的表面积为S2=6a2，且三棱锥D1-AB1C 为各棱长均为a的正四面体，其中一个面的面积为S=a× a=a2，所以三棱锥D1-AB1C的表面积为S1=4S=4× a2=2a2，所以三棱锥D1-AB1C的体积与正方体ABCD-A1B1C1D1的表面积之比为S1∶S2=1∶.5、D本题考查折叠问题与异面直线的关系的判断.将展开图还原为正方体，如图所示，则△ABC是等边三角形，所以直线AB、CD在原正方体中的位置关系是相交成60°.6、A本题考查异面直线的夹角.如图，P、Q、R分别为AB、BC、CD中点，∴PQ∥AC，QR∥BD，∴∠PQR为AC和BD所成角.又∵PQ= AC=2，QR= BD= ，RP=3，∴PR2=PQ2+QR2，∴∠PQR=90°，即AC和BD所成角的大小为90°，故选A项.7、B本题考查空间中直线的关系.对于①，这两个角也可能互补，故①错；对于②，正确；对于③，不正确，举反例：如图所示，BC⊥PB，AC⊥PA，∠ACB的两条边分别垂直于∠APB的两条边，但这两个角既不一定相等，也不一定互补；对于④，由公理4可知正确.故②④正确，所以正确的结论有2个.8、A本题考查两平面间的位置关系.对于A，平行于同一直线的两个平面，其位置关系是相交或平行，故A错误；B，C，D都是真命题.9、B本题考查直线与平面相交.连接BC1.因为E∈DC1，F∈BD，所以EF⊂平面BDC1，故EF=平面ACD1∩平面BDC1.10、D如图，因为，所以MN∥AB.因为AB⊂平面ABD，MN⊄平面ABD，所以MN∥平面ABD，因为AB⊂平面ABC，MN⊄平面ABC，所以MN∥平面ABC.11、C本题考查线面平行的判定.因为O为▱ABCD对角线的交点，所以AO=OC，又Q为PA的中点，所以QO∥PC. 由线面平行的判定定理，可知选项A、B正确，又四边形ABCD为平行四边形，所以AB∥CD，故CD∥平面PAB，D选项正确.12、C本题考查线面平行的判断.只有AC，BD与此平面平行.13、①②③④本题考查线面及面面平行的判定.以ABCD为下底面还原正方体，如图，则易判定四个命题都是正确的.14、本题考查线面平行的性质.∵在正方体ABCD—A1B1C1D1中，AB=2，∴AC=2 .又∵E为AD的中点，EF∥平面AB1C，EF⊂平面ADC，平面ADC∩平面AB1C=AC，∴EF∥AC，∴F为DC的中点，∴EF= AC= .15、平行取PD的中点F，连接EF，AF，在△PCD中，EF綊CD.又因为AB∥CD且CD＝2AB，所以EF綊AB，所以四边形ABEF是平行四边形，所以EB∥AF.又因为EB⊄平面PAD，AF⊂平面PAD，所以BE∥平面PAD.答案：平行16、分析：过作，垂足为，则平面，则即为所求平面角，从而可得结果.详解：依题意，画出图形，如图，过作，垂足为，由平面，可得，所以平面，则即为所求平面角，因为，，所以，故答案为.点睛：本题考查长方体的性质，以及直线与平面所成的角，属于中档题.求直线与平面所成的角由两种方法：一是传统法，证明线面垂直找到直线与平面所成的角，利用平面几何知识解答；二是利用空间向量，求出直线的方向向量以及平面的方向向量，利用空间向量夹角余弦公式求解即可.17、见解析本题考查线面垂直的证明.(1)∵SA⊥平面ABC，BC⊂平面ABC，∴SA⊥BC. 又∵BC⊥AB，SA∩AB=A，∴BC⊥平面SAB.又∵AQ⊂平面SAB，∴BC⊥AQ.又∵AQ⊥SB，BC∩SB=B，∴AQ⊥平面SBC.(2)∵AQ⊥平面SBC，SC⊂平面SBC，∴AQ⊥SC.又∵AP⊥SC，AQ∩AP=A，∴SC⊥平面APQ.∵PQ⊂平面APQ，∴PQ⊥SC.18、见解析本题考查线面垂直的证明.∵PA⊥平面ABCD，BD⊂平面ABCD，∴BD⊥P A.∵∠BAD=∠ABC=90°，∴tan∠ABD= ，tan∠BAC= ，∴∠ABD=30°，∠BAC=60°，∴∠AEB=90°，即BD⊥AC，又PA∩AC=A，∴BD⊥平面PAC.19、(1)见解析;(2)（Ⅰ）根据底面为正三角形，易得；由各边长度，结合余弦定理，可求得的值，再根据勾股定理逆定理可得，可证平面。

山西省晋中市和诚高中2018-2019学年高二数学周练试题（5.4）理（无答案）一、选择题（本题共8小题，每小题7分，共56分．）1.从3，5， 7，11这四个质数中，每次取出两个不同的数分别为a，b，共可得到lg a－lg b的不同值的个数是( )A．6 B．8 C．12 D．162．将2名女教师，4名男教师分成2个小组，分别安排到甲、乙两所学校轮岗支教，每个小组由1名女教师和2名男教师组成，则不同的安排方案共有( ) A．24种B．12种 C．10种 D．9种3．高三(1)班需要安排毕业晚会的4个音乐节目、2个舞蹈节目和1个曲艺节目的演出顺序，要求2个舞蹈节目不连排，则不同排法的种数是( )A．1 800 B．3 600 C．4 320 D．5 0404.某校从8名教师中选派4名同时去4个边远地区支教(每地1名教师)，其中甲和乙不能都去，甲和丙只能都去或都不去，则不同的选派方案有( )A．900种B．600种 C． 300种D．150种5.从1，2，3，4，5这五个数字中任取3个组成无重复数字的三位数，当三个数字中有2和3时，2需排在3的前面(不一定相邻)，这样的三位数有( ) A．51个B．54个 C．12个 D．45个6.将甲，乙等5位同学分别保送到北京大学，上海交通大学，浙江大学三所大学就读，则每所大学至少保送一人的不同保送的方法有( )A．240种B．180种C．150种D．540种7.(x2＋x＋y)5的展开式中，x5y2的系数为( )A．10 B．20 C．30 D．608.(2018·沈阳高二检测)若对于任意实数x，有x3＝a0＋a1(x－2)＋a2(x－2)2＋a3(x －2)3，则a2的值为( )A．3 B．6 C．9 D．12二、填空题（本题共3小题，每小题8分，共24分）9．有5名男生和3名女生，从中选出5人分别担任语文、数学、英语、物理、化学学科的课代表，若某女生必须担任语文课代表，则不同的选法共有________种(用数字作答)．10．四名优等生保送到三所学校去，每所学校至少得一名，则不同的保送方案有________种11.在高三某班进行的演讲比赛中，共有5位选手参加，其中3位女生，2位男生，如果2位男生不能连续出场，且女生甲不能排第一个，那么出场的顺序的排法种数为________．三、解答题（共2小题，每题10，共20分）12.(1)要从5名女生，7名男生中选出5名代表，按下列要求，分别有多少种不同的选法？(1)至少有1名女生入选；(2)男生甲和女生乙入选；(3)男生甲、女生乙至少有一个人入选．(2) 3名男生，4名女生，按照不同的要求排队，求不同的排队方案的方法种数．(1)选其中5人排成一排；(2)排成前后两排，前排3人，后排4人；(3)全体站成一排，男、女各站在一起；(4)全体站成一排，男生不能站在一起．13. 已知在(12x2－1x)n的展开式中，第9项为常数项．求：(1)n的值；(2)展开式中x5的系数；(3)含x的整数次幂的项的个数．。

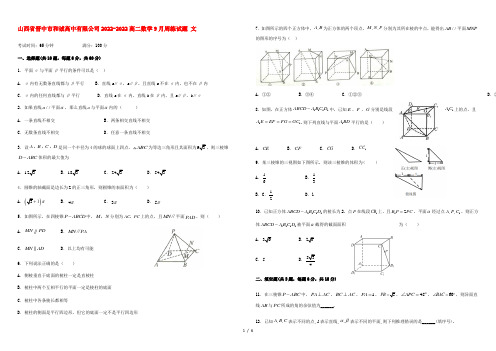
山西省晋中市和诚高中有限公司2022-2022高二数学9月周练试题 文考试时间：65分钟 满分：100分 一、选择题(共10题，每题6分，共60分) 1．平面α与平面β平行的条件可以是（ ）A ．α内有无数条直线都与β平行B ．直线a ∥α，a ∥β，且直线a 不在α内，也不在β内C ．α内的任何直线都与β平行D ．直线a 在α内，直线b 在β内，且a ∥β，b ∥α 2．如果直线//a 平面α，那么直线a 与平面α内的（ ） A ．一条直线不相交 B ．两条相交直线不相交 C ．无数条直线不相交D ．任意一条直线不相交3．设A B C D ，，，是同一个半径为4的球的球面上四点，ABC 为等边三角形且其面积为93，则三棱锥D ABC -体积的最大值为A ．123B ．183C ．243D ．5434．圆锥的轴截面是边长为2的正三角形，则圆锥的表面积为（ ） A ．()3π+１B ．4πC ．3πD ．5π5．如图所示，在四棱锥P ABCD -中，M N ，分别为AC PC ，上的点，且MN ∥平面PAD ，则（ ） A ．MNPD B ．MN PA ∥C ．MN ADD ．以上均有可能6．下列说法正确的是（ ） A ．侧棱垂直于底面的棱柱一定是直棱柱 B ．棱柱中两个互相平行的平面一定是棱柱的底面C ．棱柱中各条棱长都相等D ．棱柱的侧面是平行四边形，但它的底面一定不是平行四边形7．如图所示的四个正方体中，,A B 为正方体的两个顶点，,,M N P 分别为其所在棱的中点，能得出//AB 平面MNP 的图形的序号为（ ）A ．①②B ．③④C ．①②③D ．②8．如图，在正方体1111ABCD A B C D -中，已知E 、F 、G 分别是线段11A C 上的点，且11A E EF FG GC ===.则下列直线与平面1A BD 平行的是（ ）A ．CEB ．CFC ．CGD ．1CC 9．某三棱锥的三视图如下图所示，则该三棱锥的体积为( )A ．16 B ．13B ．C ．12D ．110．已知正方体1111ABCD A B C D -的棱长为2，点P 在线段1CB 上，且12B P PC =，平面α经过点1,,A P C ，则正方体1111ABCD A B C D -被平面α截得的截面面积为（ ）A ．36B ．26C ．5D ．534二、填空题(共3题，每题6分，共18分)11．在三棱锥P ABC -中，PA AC ⊥，BC AC ⊥，1PA =，5PB =，45APC ∠=︒，60BAC ∠=︒，则异面直线AB 与PC 所成的角的余弦值为______.12．已知,,A B C 表示不同的点,l 表示直线,,αβ表示不同的平面,则下列推理错误的是______(填序号).①∈A l ,A α∈,B l ∈,B l αα∈⇒⊂; ②A α∈,A β∈,B α∈,B AB βαβ∈⇒=;③A α∈,A A βαβ∈⇒⋂=. 13．给出下列命题： ①任意三点确定一个平面；②三条平行直线最多可以确定三个个平面；③不同的两条直线均垂直于同一个平面，则这两条直线平行； ④一个平面中的两条直线与另一个平面都平行，则这两个平面平行； 其中说法正确的有_____（填序号）. 三、解答题(共2题，每题11分，共22分)14．如图，长方体1111ABCD A B C D -中，1AB AD ==，12AA =，点P 为1DD 的中点.（1）求证：直线1//BD 平面PAC ；（2）求异面直线1BD 与AP 所成角的正弦值.15．在四面体A BCD -中，点E ，F ，M 分别是AB ，BC ，CD 的中点，且BD ＝AC ＝2，EM ＝1． （1）求证：//EF 平面ACD ； （2）求异面直线AC 与BD 所成的角．和诚中学2022-2021度高二9月周练 文数答案（二）1．C 对A ，若α内的无数条直线都平行，平面α与平面β不一定平行，也可能相交，垂直，A 错 对B ，当直线平行于两平面交线时，符合命题叙述，但平面α与平面β相交，B 错对C ，“α内的任何直线都与β平行”可等价转化为“α内的两条相交直线与β平行”，根据面面平行的判定定理，C 正确 对D ，当两平面相交，直线a ，直线b 都跟交线平行且符合命题叙述时，得不到平面α与平面β平行，D 错 故选C 2．D3．B 详解：如图所示，点M 为三角形ABC 的中心，E 为AC 中点，当DM ⊥平面ABC 时，三棱锥D ABC -体积最大 此时，OD OB R 4===23934ABCSAB == AB 6∴=,点M 为三角形ABC 的中心2BM 233BE ∴== Rt OMB ∴中，有22OM 2OB BM =-=DM OD OM 426∴=+=+=()max 19361833D ABC V -∴=⨯⨯=故选B.4．C圆锥的轴截面是边长为2的正三角形ABC ∆，∴圆锥的底面半径1r =，母线长2l =；表面积212232S r r l πππππ=+⨯⨯=+= 故选C.5．B 解析】∵MN∥平面PAD ，平面PAC∩平面PAD ＝PA ，MN ⊂平面PAC ， ∴MN∥PA. 故选B.考点：直线与平面平行的性质.6．A A 显然正确；棱柱中两个互相平行的平面不一定是棱柱的底面， 例如正六棱柱的相对侧面，故B 错误；棱柱的每条侧棱长相等，而不是各条棱长都相等，故C 错误； 棱柱的底面可以是平行四边形，如长方体，故D 错误.故选：A. 7．C 【解析】由下图可知//AB MO ，故①正确.由下图可知//,//MN BC PN AC ，故平面//MNP 平面ABC ，故//AB 平面PMN ，所以③正确.综上可知①③正确，故选C 选项.8．B 【详解】如图，连接AC ，使AC 交BD 于点O ，连接1A O 、CF ，则O 为AC 的中点，在正方体1111ABCD A B C D -中，11//AA CC 且11AA CC =，则四边形11AAC C 为平行四边形，11//AC AC ∴且11A C AC =，O 、F 分别为AC 、11A C 的中点，1//A F OC ∴且1A F OC =，所以，四边形1A OCF 为平行四边形，则1//CF A O ，CF ⊄平面1A BD ，1AO ⊂平面1A BD ，因此，//CF 平面1A BD . 故选：B.9．A 【方法点晴】本题主要考查三视图和锥体的体积，计算量较大，属于中等题型.应注意把握三个视图的尺寸关系：主视图与俯视图长应对正（简称长对正）,主视图与左视图高度保持平齐（简称高平齐）,左视图与俯视图宽度应相等（简称宽相等）,若不按顺序放置和不全时，则应注意三个视图名称.此外本题应注意掌握锥体的体积公式.10．B先根据平面的基本性质确定平面，然后利用面面平行的性质定理，得到截面的形状再求解. 【详解】1,,A P C 确定一个平面α，因为平面11//AA DD 平面11BB CC ，所以1//AQ EC ，同理1//AE QC ，所以四边形1AEC Q 是平行四边形. 即正方体被平面截的截面. 因为12B P PC =，所以112C B CE =， 即1EC EB ==所以115,23AE EC AC ==由余弦定理得：22211111cos 25AE EC AC AEC AE EC +-∠==⨯所以126sin 5AEC ∠=所以S 四边形1AEQC 1112sin 262AE EC AEC =⨯⨯⨯∠= 11．24在△PAC 中，PA AC ⊥，45APC ∠=︒，则1AC PA ==， 在△ABC 中，BC AC ⊥，60BAC ∠=︒，则60121cos 2AC AB ︒===， 所以222415AB PA PB +=+==，即PA AB ⊥，如图，将三棱锥P ABC -补为长方体MACB NPQO -，连接BN ，AN ， 因为//PN BC ，且=PN BC ，所以四边形BCPN 是平行四边形，则//PC BN ， 所以NBA ∠是异面直线AB 和PC 所成的角，6tan 03PN BC AC ︒==⋅=，则22312AN PN PA =+=+=，22BN PC PA ===，2AB =，在△ANB 中，过点A 作BN 的垂线，垂足为F ，因为2AN AB ==，所以1222BF BN ==，则222cos 24BF NBA AB ∠===.故答案为：24. 12．③解: ①为判断直线在平面内的依据,故正确;②为判断两个平面相交的依据,故正确;③中A α∈,A β∈,则A αβ∈⋂,即αβ⋂为经过点A 的一条直线而不是点A ,故错误. 故答案为：③13．②③ 对①：根据公理可知，只有不在同一条直线上的三点才能确定一个平面，故错误；对②：三条平行线，可以确定平面的个数为1个或者3个，故正确； 对③：垂直于同一个平面的两条直线平行，故正确；对④：一个平面中，只有相交的两条直线平行于另一个平面，两平面才平行，故错误. 综上所述，正确的有②③. 故答案为：②③. 14．（1）证明见解析；（2）12. 【详解】（1）证明：设AC 和BD 交于点O ，则O 为BD 的中点， 连结PO ，又因为P 是1DD 的中点，故1//PO BD又因为PO ⊂平面PAC ，1BD ⊄平面PAC所以直线1//BD 平面PAC（2）由（1）知，1//PO BD ，所以异面直线1BD 与AP 所成的角就等于PO 与AP 所成的角，故APO ∠即为所求； 因为2PA PC ==2122AO AC ==且PO AO ⊥所以1sin2AO APO AP ∠===. 15. 【详解】证明：点E ，F 分别是AB ，BC 的中点，所以EF 是ABC 的中位线，所以//EF AC ，112EF AC ==， EF ⊄平面ACD ，AC ⊆平面ACD ，所以//EF 平面ACD ；（2）解：F ，M 分别是BC ，CD 的中点，所以MF 是DBC △的中位线，所以1//,12MF DB MF DB ==， 所以异面直线AC 与BD 所成的角就是EF 和MF 所成的角，又因为EM ＝1，所以EFM △为正三角形，EF 和MF 所成的角为60︒． 故异面直线AC 与BD 所成的角为60︒.。

和诚中学2019-2020年高二11月周练数学试卷（文）考试时间：60min 分值：100分一、单选题（60分）1．若坐标原点在圆22222240x y mx my m +-++-=的内部，则实数m 的取值范围是（ ）A ．()1,1-B ．,22⎛- ⎝⎭C ．(D ．( 2．一根细金属丝下端挂着一个半径为1cm 的金属球，将它浸没底面半径为2cm 的圆柱形容器内的水中，现将金属丝向上提升，当金属球被拉出水面时，容器内的水面下降（） A ．43cm B ．316cm C ．34cm D ．13cm3．圆22420x y x y c +-++=与直线340x y -=相交于,A B 两点，圆心为P ，若90APB ∠=︒，则c 的值为（ ）A ．8B ．C ．-3D ．3 4．圆心为点()4,7C ，并且截直线3410x y -+=所得的弦长为8的圆的方程为（ ） A ．()()22475x y -+-=B ．()()224725x y -+-= C ．()()22745x y -+-= D ．()()227425x y -+-=5．已知点,A B 分别在圆()2211x y +-=与圆()()22259x y -+-=上，则,A B 两点之间的最短距离为（ ）A ．B ．2-C ．4D ．26．已知圆22:230C x y x ay +++-=（a 为实数）上任意一点关于直线:20l x y -+=的对称点都在圆C 上，则a =（ ）A ．1B ．2C ．1-D ．2-7．直线1y kx =+与圆2210x y kx y ++--=的两个交点恰好关于y 轴对称，则k 等于（ ）A ．0B ．1C ．2D ．38．与圆22:(2)(2)1C x y ++-=关于直线10x y -+=对称的圆的方程为（ ）A.22(1)(1)1x y -++=B.22(1)(1)1x y +++=C.22(1)(1)1x y -+-=D.22(1)(1)1x y ++-= 9．已知圆()()221 221:C x y ++-=，圆 ()()222 2516:C x y -+-= ，则圆1C 与圆2 C 的位置关系是（ ）A.相离B.相交C.外切D.内切10．设m ，n 是两条不同的直线，α，β，γ是三个不同的平面，给出下列命题： ①若//m α，//n β，//αβ，则//m n ；②若//αγ，//βγ，则//αβ；③若m α⊥，n β⊥，//αβ，则//m n ；④若αγ⊥，βγ⊥，则//αβ其中正确命题的序号是（ ）A.①③B.①④C.②③D.②④11．下列四个命题中，其中错误的个数是（）①经过球面上任意两点，可以作且只可以作一个大圆；②经过球直径的三等分点，作垂直于该直径的两个平面，则这两个平面把球面分成三部分的面积相等；③球的面积是它大圆面积的四倍；④球面上两点的球面距离，是这两点所在截面圆上，以这两点为端点的劣弧的长． A ．0 B ．1 C ．2 D ．312．定义1分的地球球心角所对的地球大圆弧长为1海里．在北纬45°圈上有甲、乙两地，甲地位于东经120°，乙位于西经150°，则甲乙两地在球面上的最短距离为（）A ．5400海里B ．2700海里C ．4800海里D ．3600海里二、填空题（20分）13．直线()12230a x y --+=与直线320x y a ++=垂直，则实数a 的值为__________． 14．若()4,2A -，()6,4B -，()12,6C ，()2,12D ．给出下列结论：①//AB CD ；②AB AD ⊥；③AC BD ⊥；④CD CB ⊥．其中正确的结论是________．15．已知点()1,1A ，()1,3B -，()0,0O ，则ABO V 的面积为________．16．若x ，y ，z 满足约束条件4802400x y x y y --≤⎧⎪-+≥⎨⎪≤⎩，则z =__________．三、解答题（20分）17．已知直线1:2(1)40l x m y +++=与2:360l mx y +-=平行.（1）求实数m 的值：（2）设直线l 过点()1,2，它被直线1l ，2l 所截的线段的中点在直线3:20l x y -+=上，求l 的方程.18．已知圆22:2430C x y x y ++-+=.(1)已知不过原点的直线l 与圆C 相切，且在x 轴，y 轴上的截距相等，求直线l 的方程；(2)求经过原点且被圆C 截得的线段长为2的直线方程.参考答案1．D【解析】【分析】将原点坐标代入圆的方程得到不等式，解不等式得到结果.【详解】把原点坐标代入圆的方程得:222002020240m m m +-⨯+⨯+-<解得：m 本题正确选项：D【点睛】本题考查点与圆的位置关系的问题，属于基础题.2．D【解析】【分析】利用等体积法求水面下降高度。

山西省晋中市和诚高中2018-2019学年高二数学周练试题（20）理（无答案）考试时间：60分钟 满分：100分一、选择题（本题共8小题，每小题7分，共56分．）1. 已知函数()π,0,cos ∈+=x x x y ，那么下列说法正确的是（ ） A. 2π=x 是极大值点 B.2π=x 是极小值点 C. 没有极值点 D. 有且只有一个极值点2．已知函数()21ln x x y +-=，则函数的极值情况是( )A ．有极小值B ．有极大值C ．既有极大值又有极小值D ．无极值3. 已知()()x g x f ,是定义在R 是的连续函数（图象连续不断），如果()()x g x f ,当且仅当0=x 时函数值为0，且()()x g x f ≥，则下列情形不可能．．．的是（ ） A ．0是()x f 的极大值，也是()x g 的极大值 B ． 0是()x f 的极大值，不是()x g 的极值C ．0是()x f 的极小值，也是()x g 的极小值D ．0是()x f 的极小值，不是()x g 的极值4．已知函数()qx px x x f --=23的图象与x 轴切于()0,1点，则函数()x f 的极值是( )A ．极大值为427，极小值为0B ．极大值为0，极小值为427C ．极大值为0，极小值为－427D ．极大值为－427，极小值为05. 设函数()x f 定义域为R ，()000≠x x 是()x f 的极大值点，以下结论正确的是（ ）A ．()()0,x f x f R x ≤∈∀B ．0x -是()x f -的极小值点C ．0x -是()x f -的极小值点D ．0x -是()x f --的极小值点6．已知e 为自然对数的底数，设函数()()()()2,111=--=k x e x f kx ，则( ) A ．当1=k 时，()x f 在1=x 处取到极小值 B ．当1=k 时，()x f 在1=x 处取到极大值C ．当2=k 时，()x f 在1=x 处取到极小值D ．当2=k 时，()x f 在1=x 处取到极大值7.函数331x x y -+=有( )A ．极小值－2，极大值2B ．极小值－2，极大值3C ．极小值－1，极大值1D ．极小值－1，极大值38．对于函数()233x x x f -=，给出命题：①()x f 是增函数，无极值； ②()x f 是减函数，无极值；③()x f 的递增区间为()()+∞∞-,2,0,，递减区间为()2,0； ④()00=f 是极大值，()42-=f 是极小值．其中正确的命题有( )A ．1个B ．2个C ．3个D ．4个二、填空题（本题共3小题，每小题8分，共24分）9．函数122+=x x y 当_____=x 时，有极大值______． 10．已知函数()x x x f 33-=的图象与直线a y =有相异三个公共点，则a 的取值范围是________．11．函数a ax x y +-=23在()1,0内有极小值，则实数a 的取值范围是____________.三、解答题（共2小题，每题10，共20分）12. 设函数()()0323>+++=a d cx bx x a x f ，且方程()09=-'x x f 的两个根分别为1和4.若()x f 在()+∞∞-,内无极值点，求a 的取值范围．13.已知函数2ln )(bx x a x f +=图像上点))1(,1(f P 处的切线方程为032=--y x（1）判断方程21)(-=x f 解的个数 （2）若函数4ln )()(-+=m x f x g 在]2,1[e上恰有两个零点，求实数m 的取值范围。

山西省晋中市和诚高中2018-2019学年高二数学周练试题（5.18）文（无答案）一选择题（本题共8小题，每小题7分，共56分．）1．(2018·广东汕头一模)函数f (x )＝11－x＋lg (1＋x )的定义域为 ( ) A ．(－∞，－1) B ．(1，＋∞)C ．(－1，1)∪(1，＋∞) D．(－∞，＋∞)2．(2018·河北保定一模)若f (x )是定义在R 上的函数，则“f (0)＝0”是“函数f (x )为奇函数”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．若f (x )是幂函数，且满足f f ＝3，则f ⎝ ⎛⎭⎪⎫12＝( ) A ．3 B ．－3 C.13 D ．－134．(2018·大连测试)下列函数中，与函数y ＝－3|x |的奇偶性相同，且在(－∞，0)上单调性也相同的是( )A ．y ＝－1xB ．y ＝log 2|x |C ．y ＝1－x 2D ．y ＝x 3－1 5．已知集合M ＝{－1，1，2，4}，N ＝{1，2，4}，给出下列四个对应关系：①y ＝x 2，②y ＝x ＋1，③y ＝x －1，④y ＝|x |，其中能构成从M 到N 的函数的是( )A ．①B ．②C ．③D ．④6．(2018·山东济宁一中月考)某产品的总成本y (万元)与产量x (台)之间的函数关系式是y ＝3000＋20x －0.1x 2(0<x <240，x ∈N *)．若每台产品的售价为25万元，则生产者不亏本(销售收入不少于总成本)时的最低产量是( )A ．100台B ．120台C ．150台D ．180台7．已知定义在区间[0，2]上的函数y ＝f (x )的图象如图所示，则y ＝－f (2－x )的图象为( )8．(2018·安庆二模)定义在R 上的函数f (x )满足f (－x )＝－f (x )，f (x －2)＝f (x ＋2)且x ∈(－1，0)时，f (x )＝2x ＋15，则f (log 220)＝( ) A ．1 B.45 C ．－1 D ．－45二、填空题（本题共3小题，每小题8分，共24分）9．(2018·济南模拟)已知函数y ＝5a x －2＋3恒过点A (m ，n )，则log m n ＝________.10．若函数y ＝f (x )的定义域为[0，2]，则函数g (x )＝f (x ＋1)－f (x －1)的定义域为________．11．(2018·广东广州测试)已知函数f (x )＝ln x ＋1x 2＋3在(1，4)处的切线与g (x )＝ax 2－2x 的图象相切，则a ＝________.三、解答题（共2小题，每题10分，共20分）12．函数f (x )＝1a －1x(a >0，x >0)． (1)判断函数f (x )在(0，＋∞)上的单调性；(2)若函数f (x )在⎣⎢⎡⎦⎥⎤12，2上的值域是⎣⎢⎡⎦⎥⎤12，m ，求a ，m 的值．18．已知函数f (x )是(－∞，＋∞)上的奇函数，且f (x )的图象关于x ＝1对称，当x ∈[0，1]时，f (x )＝2x －1.(1)当x ∈[1，2]时，求f (x )的解析式；(2)计算f (0)＋f (1)＋f (2)＋…＋f (2018)的值．。

和诚中学2018-2019学年度2月周测高二文科数学试题一、选择题（本题共8小题，每小题7分，共56分．）1：若复数221z ii=++，其中i是虚数单位，则复数z的模为（）2D. 22：已知复数1z i=-，则221z zz-=-（）A. 2iB. 2i- C. 2 D. 2-3：设i是虚数单位，且20141i kiki-=-，则实数k等于（）A. 2B. 0C. 1D. 1-4：复数321iz ii=-+，在复平面上对应的点位于（）A．第一象限 B．第二象限 C．第三象限 D．第四象限5：若1a izi+=-是纯虚数，则实数a的值是（）A. 1- B. 0 C. 1 D. 26：若复数()()2321a a a i-++-是纯虚数，则实数a的值是（）A. 1B. 2C. 1或2D. 1-7：已知复数1z=-，z是z的共轭复数，则z z⋅=（）A.14B.12C. 1D. 28:函数xxy ln=在()5,0上的单调性为( )A．单调增函数 B．单调减函数C．在⎪⎭⎫⎝⎛e10，上单调递减，在⎪⎭⎫⎝⎛5,1e上单调递增 D．在⎪⎭⎫⎝⎛e10，上单调递增，在⎪⎭⎫⎝⎛5,1e上二、填空题（本题共3小题，每小题8分，共24分）9：设117,,12ia b R a bii-∈+=-（i是虚数单位），则a b+的值是____________10：设1z是复数，211z z iz=-（其中1z表示1z的共轭复数），已知2z的实部是1-，则2z的虚部是___________11：已知复数1z 满足()()1211z i i -+=-（i 是虚数单位），复数2z 的虚部为2，且12z z ⋅是实数，则2z =____________三、解答题（共2小题，每题10，共20分）12.已知函数()()x e k x x f -=.（1）求()x f 的单调区间； （2）求()x f 在区间[]1,0上的最小值.13、已知函数x x x f ln )(⋅=（1）求函数)(x f 的最小值;（2）若对所有1≥x 都有1)(-≥ax x f ，求实数a 的取值范围.。

山西省晋中市和诚高中2018-2019学年高二数学周练试题（20）文（无答案）考试时间：60分钟 满分：100分一、选择题（本题共8小题，每小题7分，共56分．） 1、下列四个命题正确的是（ ）①线性相关系数r 越大，两个变量的线性相关性越强；反之，线性相关性越小；②残差平方和越小的模型，拟合的效果越好；③用相关指数2R 来刻画回归效果，2R 越小，说明模型的拟合效果越好； ④随机误差e 是衡量预报精确度的一个量，它的平均值为0． A ． ①②③ B ． ②④ C ．②③④ D ．①②④ 2、在回归分析中，残差图中的纵坐标为（ ）A ．残差B ． 样本编号C ．随机误差D ．i yˆ的估计值 3、在画两个变量的散点图时，下面叙述正确的是（ ） A 预报变量在x 轴上，解释变量在y 轴上 B 解释变量在x 轴上，预报变量在y 轴上 C 可以选择两个变量中的任意一个变量在x 轴上 D 可以选择两个变量中的任意一个变量在y 轴上4.两个变量y 与x 的回归模型中，分别选择了4个不同模型，它们的相关指数R 2如下，其中拟合效果最好的模型是( ) A.模型1的相关指数R 2为0.98 B.模型2的相关指数R 2为0.80 C.模型3的相关指数R 2为0.50 D.模型4的相关指数R 2为0.255、为了考察两个变量y x ,之间的线性相关性，甲乙两位同学各自独立地做了10次和15次试验，并且利用线性回归方法求得回归直线21,l l ，已知两人在试验中发现对变量x 的观测数据的平均值都是s ，对变量y 的观测数据的平均值都是t ，那么下列说法正确的是( ) A ．21,l l 必定平行 B ．21,l l 必定重合C ．21,l l 有交点()t s ,D ．21,l l 相交，但交点不一定是()t s ,6、已知有5组数据()()()()()12,10,10,3,5,4,4,2,3,1E D C B A ，去掉哪一组数据后，剩下4组数据的线性相关系数最大（ ）A ． EB ． DC ． BD ． A 7、通过随机询问110名不同的大学生是否爱好某项运动，得到如下的列联表： 则得到的正确结论是（ ）A ． 有99%以上的把握认为“爱好该项运动与性别有关”B ． 有99%以上的把握认为“爱好该项运动与性别无关”C ． 在犯错误的概率不超过0．1%的前提下，认为“爱好该项运动与性别有关”D ． 在犯错误的概率不超过0．1%的前提下，认为“爱好该项运动与性别无关”8.为了解某社区居民的家庭年收入与年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：根据上表可得回归直线方程y ＝b x ＋a ，其中b ＝0.76，a ＝y －b x ，据此估计，该社区一户年收入为15万元家庭的年支出为( ) A.11.4万元 B.11.8万元 C.12.0万元D.12.2万元二、填空题（本题共3小题，每小题8分，共24分） 9..若8名学生的身高和体重数据如下表：第3名学生的体重漏填，但线性回归方程是y ＝0.849x －85.712，则第3名学生的体重估计为________.10.(2017·广州模拟)为了判断高中三年级学生选修文理科是否与性别有关，现随机抽取50名学生，得到2×2列联表如下：已知P (K 2≥3.841根据表中数据，得到K 2＝50×（13×20－10×7）223×27×20×30≈4.844，则认为选修文理科与性别有关系出错的可能性约为________.11.某单位为了了解用电量y (度)与气温x (℃)之间的关系，随机统计了某4天的用电量与当天气温，并制作了对照表：由表中数据得回归直线方程y ＝b x ＋a 中的b ＝－2，预测当气温为－4 ℃时，用电量约为________度.三、解答题（共2小题，每题10，共20分） 12..( 2016·全国Ⅲ)下图是我国2008年至2014年生活垃圾无害化处理量(单位：亿吨)的折线图.注：年份代码1－7分别对应年份2008－2014.(1)由折线图看出，可用线性回归模型拟合y 与t 的关系，请用相关系数加以说明；(2)建立y 关于t 的回归方程(系数精确到0.01)，预测2016年我国生活垃圾无害化处理量.附注： 参考数据：7719.32,40.17,ii i i yt y ===∑∑i=12.646=≈，()()niit t y y --∑回归方程y ^＝a ^＋b ^t 中斜率和截距的最小二乘估计公式分别为：b ^＝121()(),.()niii ni i t t y y a y bt t t ==--=--∑∑13. 某公司生产部门经调研发现，该公司第二、三季度的用电量与月份相关，数据统计如下：(1)核对电费时发现一组数据统计有误，请指出哪组数据有误，并说明理由；(2)在排除有误数据后，求用电量与月份之间的回归直线方程y ^＝b ^x ＋a ^，并计算出统计有误的月份的正确用电量．。

山西省晋中市和诚高中2021-2022高二数学上学期周测试题（9.21，无答案）考试时间：60min 分值：100分一、单选题(12x5=60分)1．在空间，下列命题错误的是（ ）A ．一条直线与两个平行平面中的一个相交，则必与另一个相交B ．一个平面与两个平行平面相交，交线平行C ．平行于同一平面的两个平面平行D ．平行于同一直线的两个平面平行2．平面α内有不共线的三点到平面β的距离相等且不为零，则α与β的位置关系为( ) A ．平行 B ．相交 C ．平行或相交 D ．可能重合 3．能够判定两个平面α，β平行的条件是 ( )A ．平面α，β都和第三个平面相交，且交线平行B ．夹在两个平面间的线段相等C ．平面α内的无数条直线与平面β无公共点D ．平面α内的所有的点到平面β的距离都相等4．正方体ABCD －1111A B C D 中，与平面AC 平行的是( ) A ．平面11A C B ．平面1ADC ．平面1ABD ．平面1BC5．设α，β表示两个平面，l 表示直线，A ，B ，C 表示三个不同的点，给出下列命题： ①若A ∈l ，A ∈α，B ∈l ，B ∈α，则lα；②α，β不重合，若A ∈α，A ∈β，B ∈α，B ∈β，则α∩β＝AB ；③若lα，A ∈l ，则A α；④若A ，B ，C ∈α，A ，B ，C ∈β，且A ，B ，C 不共线，则α与β重合．则上述说法中，正确的个数是（ ）A ．1B ．2C ．3D ．46．如图，将无盖正方体纸盒展开，线段，所在直线在原正方体中的位置关系是（ ）．A ．平行B ．相交且垂直C ．异面D ．相交成7．如图所示，A 是平面BCD 外一点，E 、F 、G 分别是BD 、DC 、CA 的中点，设过这三点的平面为α，则在图中的6条直线AB 、AC 、AD 、BC 、CD 、DB 中，与平面α平行的直线有( ) A ．0条 B ．1条 C ．2条 D ．3条8．如果把两条异面直线看成“一对”,那么六棱锥的棱所在的12条直线中,异面直线的对数共有 ( )A ．12B ．24C ．36D ．489．如图，在正方体ABCD­A 1B 1C 1D 1中，异面直线A 1D 与D 1C 所成的角为( ) A ．30° B．45° C．60° D．90° 10．下列命题中不正确的是（ ） A ．平面∥平面，一条直线平行于平面，则一定平行于平面B ．平面∥平面，则内的任意一条直线都平行于平面C ．一个三角形有两条边所在的直线分别平行于一个平面，那么该三角形所在的平面与这个平面平行D ．分别在两个平行平面内的两条直线只能是平行直线或异面直线11．已知三个不同的平面,,αβγ，一条直线l ，要得到α∥β，必须满足下列条件中的（ ） A ．l l αβ∥，∥且l ∥γ B ．l γ⊂，且l l αβ∥，∥ C ．α∥γ，且βγ∥ D ．以上都不正确 12．能使平面∥平面的一个条件是 （ ） A ．存在一条直线，∥，∥ B ．存在一条直线，,∥C ．存在两条直线，，，，∥，∥D ．存在两条异面直线，，，，∥，∥二、填空题(4x5=20分)13．直线与平面所成角的范围______．14．如图，在正三棱柱111ABC A B C -中，已知它的底面边长为10，高为20，若P 、Q 分别是BC 、1CC 的中点，则异面直线PQ 与AC 所成角的余弦值为_________15．下列正确的个数是________．①如果a 、b 是两条直线，a ∥b ，那么a 平行于经过b 的任何一个平面； ②如果直线a 和平面α满足a ∥α，那么a 与平面α内的任何一条直线平行； ③如果平面α的同侧有两点A ，B 到平面α的距离相等，则AB ∥α. 16．不交于同一直线的三个平面可以把空间分成_____个部分 三、解答题(共20分)17．如图所示，四棱锥P －ABCD 的底面ABCD 为矩形，E 、F 、H 分别为AB 、CD 、PD 的中点．求证：平面AFH ∥平面PCE .18．在正方体1111D C B A ABCD 中，M 、N 、P 分别是BD AD 、1和C B 1的中点.求证：（1）D D C MN 11C //平面； （2）平面MNP //平面D D CC 11.。

山西省晋中市和诚中学2019-2020学年高二数学上学期第六次周练试题 理（11.2）考试时间：60min 分值：100分一、单选题（60分）1．已知过点(2,)A m -和点(,4)B m 的直线为1l ，2:210l x y +-=，3:10l x ny ++=．若12l l //，23l l ⊥，则m n +的值为（ ）A.10-B.2-C.0D.82．已知直线1:2 10l x y +-=，2: 4 30l a x y +-=，若12l l //，则a =（ ）A.8B.2C.12-D.2-3．已知三角形三个顶点()()()5,0,3,3,0,2A B C --，则BC 边上中线所在直线方程是（）A ．1350x y -+=B ．1350x y --=C ．1350x y ++=D ．130x y +=4．当圆22220x y x ky k ++++＝的面积最大时，圆心坐标是()A ．(0，－1)B ．(－1,0)C ．(1，－1)D ．(－1,1) 5．直线310ax y --=与直线2()103a x y -++=垂直，则a 的值是 A ．－1或13 B ．1或13 C ．－13或－1 D ．－13或1 6．若直线2y x =-的倾斜角为α，则sin 2α的值为（ ）A.45B.45-C.45±D.35- 7．过点()1,2A 且与原点距离最大的直线方程是（ ）A.250x y +-=B.230x y -+=C.30x y ++=D.10x y -+=8．若直线l 1：x ＋3y ＋m ＝0(m ＞0)与直线l 2：2x ＋6y －3＝0，则m ＝( )A ．7B ．172C ．14D ．179．已知00ab bc ＜，＜，则直线0ax by c ++=通过( ) 象限A ．第一、二、三B ．第一、二、四C ．第一、三、四D ．第二、三、四10．古希腊数学家阿波罗尼奧斯（约公元前262～公元前190年）的著作《圆锥曲线论》是古代世界光辉的科学成果，他证明过这样一个命题：平面内与两定点距离的比为常数k （k ＞0，k ≠1）的点的轨迹是圆，后人将这个圆称为阿波罗尼斯圆．在平面直角坐标系中，设A （﹣3，0），B （3，0），动点M 满足MA MB ｜｜｜｜＝2，则动点M 的轨迹方程为（） A ．（x ﹣5）2+y 2＝16 B ．x 2+（y ﹣5）2＝9C ．（x +5）2+y 2＝16D ．x 2+（y +5）2＝911．若椭圆22:1C mx ny +=10y +-=交于,A B 两点,过原点与线段AB 中点,则m n=()A.12B.2 D.212．在平面直角坐标系xOy 中，已知点(1,21)A m m --，点()2,1B -，直线l :0ax by +=.如果对任意的m R ∈点A 到直线l 的距离均为定值，则点B 关于直线l 的对称点1B 的坐标为（ ）A.()0,2B.211,55⎛⎫ ⎪⎝⎭C.()2,3D.2,35⎛⎫ ⎪⎝⎭二、填空题（20分）13．已知θ是直线210y x --=的倾斜角，则3sin cos sin 2cos θθθθ-+的值为__________． 14．直线:10l mx y m +--=过定点_____；过此定点倾斜角为2π的直线方程为_____． 15．已知()()2,11,2A B ，，若直线y ax =与线段AB 相交，则实数a 的取值范围是__．16．若直线:230l kx y k ---=与直线240x y -+=的交点位于第二象限，则直线l 的斜率的取值范围为________．三、解答题（20分）17．已知直线1:2(1)40l x m y +++=与2:360l mx y +-=平行.（1）求实数m 的值：（2）设直线l 过点()1,2，它被直线1l ，2l 所截的线段的中点在直线3:20l x y -+=上，求l 的方程.18．已知直线:230l kx y k --+=.（1）若直线l 不经过第二象限，求k 的取值范围；（2）设直线l 与x 轴的负半轴交于点A ，与y 轴的负半轴交于点B ，若AOB ∆的面积为4（O 为坐标原点），求直线l 的方程.参考答案1．A【解析】【分析】利用直线平行垂直与斜率的关系即可得出．【详解】∵l 1∥l 2，∴k AB ＝42m m -+＝－2，解得m ＝－8． 又∵l 2⊥l 3，∴1n -×(－2)＝－1，解得n ＝－2，∴m ＋n ＝－10．故选:A ． 【点睛】本题考查了直线平行垂直与斜率的关系，考查了推理能力与计算能力，属于基础题．2．A【解析】【分析】因为直线1:2 10l x y +-=斜率存在，所以由12l l //可得两直线斜率相等，即可求出。