陕西省西安市第一中学2013届高三上学期期中考试数学(理)试题 Word版含答案
- 格式:doc
- 大小:753.50 KB
- 文档页数:12

长安一中、高新一中、交大附中、师大附中、西安中学高2013届第一次模拟考试数学(理)试题第Ⅰ卷(选择题 共50分)一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合M={x|一3<x<3,x ∈Z ),N={x|x<1},则M N=A .{|3x x -<<1}B .{|02}x x <<C .{-3,-2,-1,0,1)D .{-2,一1,0}2.已知直线a 和平面α,那么a//α的一个充分条件是A .存在一条直线b ,a//b 且b ⊂αB .存在一条直线b ,a ⊥b 且b ⊥αC .存在一个平面β,a ⊂β∥且α//βD .存在一个平面β,α//β且α//β3.如果数列321121,,,,,nn a a a a a a a - …是首项为1,公比为2-的等比数列,则a 5等于A .32B .64C .—32D .—644.过抛物线22(0)y px p =>的焦点作直线交抛物线于1122(,),(,)P x y Q x y 两点,若122,||4x x PQ +==,则抛物线方程是A .24y x =B .28y x =C .22y x =D .26y x = 5.21()nx x -展开式中,常数项为15,则n 的值可以为A .3B .4C .5D .66.若某空间几何体的三视图如图所示,则该几何体的表面积是A .226++B .2(12)6++C .23 D .32262++7.给出15个数:1,2,4,7,1 l ,…,要计算这15个数的和,现给出解决该问题的程序框图(如右图所示),那么框图中判断框①处和执行框②处应分别填入A .16?;1i p p i ≤=+-B .14?;1i p p i ≤=++C .15?;1i p p i ≤=++D .15?;i p p i ≤=+8.已知实数x ,y 满足1(10)||,(,)()2cos (0)||12x x x x y f x x x y ππ---≤<⎧⎧≤⎪⎪=⎨⎨≤<⎪⎪≤⎩⎩则点在函数的图象与坐标轴所围成的封闭图形的内部的概率为A .32πB .14πC .34πD .12π9.台风中心从A 地以每小时20千米的速度向东北方向移动,离台风中心30千米内的地区为危险区。

高三数学理科试题一、 选择题(每小题5分,共60分)1、已知集合M ={0,1,2,3,4},N ={1,3,5},P =M ∩N ,则P 的子集共有( )A .2个B .4个C .6个D .8个2、P= log 23,Q= log 32,R= log 2(log 32),则( )A. R<Q<PB. P<R<QC. Q<R<PD. R<P<Q3、参数方程为1()2x t t t y ⎧=+⎪⎨⎪=⎩为参数表示的曲线是( ). A .一条直线 B .两条直线 C .一条射线 D .两条射线4、设命题p :函数y =sin 2x 的最小正周期为π2;命题q :函数y =cos x 的图像关于直线x =π2对称.则下列判断正确的是 ( )A .p 为真B .q ⌝为假C .p 且q 为假D .p 或q 为真5、若α∈⎝ ⎛⎭⎪⎫0,π2,且21sin cos 24αα+=,则tan α的值等于( )A.22B.33C. 2D. 36、在下列区间中,函数f (x )=e x+4x -3的零点所在的区间为( )A .(-14,0)B .(0,14)C .(14,12)D .(12,34)7、若函数f (x )=13x 3-12ax 2+(a -1)x +1在区间(1,4)内为减函数,在区间(6,+∞)内为增函数,则实数a 的取值范围是 ( )A .a ≤2B .5≤a ≤7C .4≤a ≤6D .a ≤5或a ≥78、若x 是一个三角形的最小内角,则函数sin cos y x x =-的值域是( )A. [B.(-C.[-D.(- 9、设x ,y ∈R ,a >1,b >1,若3x ya b ==,a +b =23,则1x +1y的最大值为 ( ) A .2 B.32 C .1 D.1210、△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c,2sin sin cos a A B b A +=,则b a等于( ) A .2 3B .2 2 C. 3 D. 211、设函数f (x )=2x1+2x -12,[x ]表示不超过x 的最大整数,则函数y =[f (x )]的值域是( ) A .{0,1}B .{0,-1}C .{-1,1}D .{1,1}12、函数y =11-x的图像与函数2sin y x π=(-2≤x ≤4)的图像所有交点的横坐标之和等于( ) A .2B .4C .6D .8二、填空题(每小题4分,共20分):13、命题”“存在01,:2>+-∈x x R x P 的否定P ⌝为__________14、323(9)x dx --⎰=________.15、若曲线4y x =的一条切线l 与直线x +4y -8=0垂直,则l 的方程为 16、从边长为10 cm×16 cm 的矩形纸板的四角截去四个相同的小正方形,作成一个无盖的盒子,则盒子容积的最大值为________3cm .17、 关于函数()cos2cos f x x x x =-,下列命题:①存在1x ,2x ,当12x x π-=时,()()12f x f x =成立;②()f x 在区间,63ππ⎡⎤-⎢⎥⎣⎦上是单调递增;③函数()f x 的图像关于点,012π⎛⎫⎪⎝⎭成中心对称图像; ④将函数()f x 的图像向左平移512π个单位后将与2sin 2y x =的图像重合. 其中正确的命题序号 (注:把你认为正确的序号都填上)三.解答题(本大题共有6个小题,满分70分) 18、(本小题满分10分)函数()sin()1(0,0)6f x A x A πωω=-+>>的最大值为3,其图像相邻两条对称轴之间的距离为π2.(1)求函数f (x )的解析式; (2)设(0,),()222f παα∈=,求α的值.19、(本小题满分10分)已知函数f (x )=-x 2+2ax +1-a 在x ∈[0,1]时有最大值2, 求a 的值.20、(本小题满分12分)已知函数f (x )是定义在R 上的奇函数,且f (x )的图象关于直线x =1对称.(1)求证:f (x )是周期为4的周期函数; (2)若f (x )=x (0<x ≤1),求x ∈[-5,-4]时,函数f (x )的解析式.21、(本小题满分12分)已知向量()x x cos ,22sin 3+=,()x cos 2,1=,x f ⋅=)(.(Ⅰ)求函数()f x 的最小正周期及对称轴方程;(Ⅱ)在△ABC 中,角A ,B ,C 的对边分别是,,a b c 若()4f A =,b=1,△ABC 的面积为,求a 的值. 22、(本小题满分12分)已知f (x )是二次函数,不等式f (x )<0的解集是(0,5),且f (x )在区间[-1,4]上的最大值是12. (1)求f (x )的解析式;(2)是否存在自然数m ,使得方程f (x )+37x=0在区间(m ,m +1)内有且只有两个不等的实数根?若存在,求出所有m 的值;若不存在,请说明理由.23、(本小题满分14分)设函数()()21xf x x e kx =--(其中k ∈R ).(Ⅰ) 当1k =时,求函数()f x 的单调区间; (Ⅱ) 当1,12k ⎛⎤∈⎥⎝⎦时,求函数()f x 在[]0,k 上的最大值M . 西安市第一中学2013-2014学年度第一学期期中考试高三数学理科参考答案二、填空题(共4小题,满分20分):13.”“任意01,2≤+-∈x x R x 14. 36 15. 4x -y -3=016.144 17. ①③三、解答题(共6小题,满分70分)18、(满分10分)函数f (x )=A sin ⎝ ⎛⎭⎪⎫ωx -π6+1(A >0,ω>0)的最大值为3,其图像相邻两条对称轴之间的距离为π2.(1)求函数f (x )的解析式; (2)设α∈⎝ ⎛⎭⎪⎫0,π2,f ⎝ ⎛⎭⎪⎫α2=2,求α的值.解 (1)∵函数f (x )的最大值为3, ∴A +1=3,即A =2.∵函数图像的相邻两条对称轴之间的距离为π2,∴最小正周期T =π,∴ω=2,∴函数f (x )的解析式为y =2sin ⎝ ⎛⎭⎪⎫2x -π6+1. ……………………5分 (2)∵f ⎝ ⎛⎭⎪⎫α2=2sin ⎝⎛⎭⎪⎫α-π6+1=2,∴sin ⎝⎛⎭⎪⎫α-π6=12. ∵0<α<π2,∴-π6<α-π6<π3,∴α-π6=π6,∴α=π3. ……………………10分19、(满分10分)已知函数f (x )=-x 2+2ax +1-a 在x ∈[0,1]时有最大值2,求a 的值.解 f (x )=-(x -a )2+a 2-a +1, ……………………1分 当a ≥1时,y max =f (1)=a ; ……………………3分 当0<a <1时,y max =f (a )=a 2-a +1; ……………………5分 当a ≤0时,y max =f (0)=1-a . ……………………7分 根据已知条件:⎩⎪⎨⎪⎧a ≥1,a =2或⎩⎪⎨⎪⎧0<a <1,a 2-a +1=2或⎩⎪⎨⎪⎧a ≤01-a =2,解得a =2或a =-1. ……………………10分20、(满分12分)已知函数f (x )是定义在R 上的奇函数,且f (x )的图象关于直线x =1对称.(1)求证:f (x )是周期为4的周期函数;(2)若f (x )=x (0<x ≤1),求x ∈[-5,-4]时,函数f (x )的解析式.解析:(1)证明:由函数f (x )的图象关于直线x =1对称,有f (x +1)=f (1-x ),即有f (-x )=f (x +2). ……………………2分又函数f (x )是定义在R 上的奇函数,故有f (-x )=-f (x ).故f (x +2)=-f (x ),从而f (x +4)=-f (x +2)=f (x ),即f (x )是周期为4的周期函数. ……………………6分(2)由函数f (x )是定义在R 上的奇函数,可知f (0)=0.x ∈[-1,0)时,-x ∈(0,1],f (x )=-f (-x )=--x .故x ∈[-1,0]时,f (x )=--x . …………9分x ∈[-5,-4]时,x +4∈[-1,0],f (x )=f (x +4)=--x -4.从而,x ∈[-5,-4]时,函数f (x )的解析式为f (x )=--x -4. …………12分 21、(满分12分)已知向量()x x cos ,22sin 3+=,()x cos 2,1=,x f ⋅=)(.(Ⅰ)求函数()f x 的最小正周期及对称轴方程;(Ⅱ)在△ABC 中,角A ,B ,C 的对边分别是,,a b c 若()4f A =,b=1,△ABC 的面积为,求a 的值.解析:(Ⅰ)2()222cos 2cos 232sin(2)36f x x x x x x π=++=++=++.…………………4分所以最小正周期T=π,对称轴方程为,()26k x k Z ππ=+∈ …… (6分) (Ⅱ)依题意2sin(2)34,6A π++=即1sin(2)62A π+=,由于0A π<<,所以52,66A ππ+=A=3π ………………(9分)又∵1sin 22bc A =且b=1,∴,42c =得c=2,在ABC ∆中,由余弦定理得2222cos 3a b c bc A =+-=,所以a =…………………(12分)22、(本小题满分12分)已知f (x )是二次函数,不等式f (x )<0的解集是(0,5),且f (x )在区间[-1,4]上的最大值是12. (1)求f (x )的解析式;(2)是否存在自然数m ,使得方程f (x )+37x=0在区间(m ,m +1)内有且只有两个不等的实数根?若存在,求出所有m 的值;若不存在,请说明理由.解析:(1)∵f (x )是二次函数,且f (x )<0的解集是(0,5), ∴可设f (x )=ax (x -5)(a >0).∴f (x )在区间[-1,4]上的最大值是f (-1)=6a . 由已知,得6a =12,∴a =2,∴f (x )=2x (x -5)=2x 2-10x (x ∈R ). …………………5分(2)方程f (x )+37x=0等价于方程2x 3-10x 2+37=0设h (x )=2x 3-10x 2+37,则h ′(x )=6x 2-20x =2x (3x -10). ……………………7分当x ∈⎝ ⎛⎭⎪⎫0,103时,h ′(x )<0,因此h (x )在此区间上是减少的;当x ∈⎝ ⎛⎭⎪⎫103,+∞时,h ′(x )>0,因此h (x )是在此区间上是增加的. ∵h (3)=1>0,h ⎝ ⎛⎭⎪⎫103=-127<0,h (4)=5>0, ……………………10分 ∴方程h (x )=0在区间⎝ ⎛⎭⎪⎫3,103,⎝ ⎛⎭⎪⎫103,4内分别有唯一实数根,而在区间(0,3),(4,+∞)内没有实数根,∴存在唯一的自然数m =3,使得方程f (x )+37x=0在区间(m ,m +1)内有且只有两个不等的实数根. ……………………12分 23、(本小题满分14分)设函数()()21xf x x e kx =--(其中k ∈R ).(Ⅰ) 当1k =时,求函数()f x 的单调区间;(Ⅱ) 当1,12k ⎛⎤∈⎥⎝⎦时,求函数()f x 在[]0,k 上的最大值M . 【解析】(Ⅰ) 当1k =时,()()21x f x x e x =--,()()()1222x x x x f x e x e x xe x x e '=+--=-=-令()0f x '=,得10x =,2ln 2x = ……………2分 当x 变化时,()(),f x f x '的变化如下表:右表可知,函数f x 的递减区间为0,ln 2,递增区间为,0-∞,ln 2,+∞.……………………6分 (Ⅱ)()()()1222x x x x f x e x e kx xe kx x e k '=+--=-=-,令()0f x '=,得10x =,()2ln 2x k =, ……………………7分 令()()ln 2g k k k =-,则()1110k g k k k -'=-=>,所以()g k 在1,12⎛⎤ ⎥⎝⎦上递增, 所以()ln 21ln 2ln 0g k e ≤-=-<,从而()ln 2k k <,所以()[]ln 20,k k ∈ 所以当()()0,ln 2x k ∈时,()0f x '<;当()()ln 2,x k ∈+∞时,()0f x '>; 所以()(){}(){}3max 0,max 1,1k M f f k k e k ==--- ………………10分 令()()311kh k k e k =--+,则()()3k h k k e k '=-,令()3kk e k ϕ=-,则()330kk e e ϕ'=-<-<所以()k ϕ在1,12⎛⎤⎥⎝⎦上递减,而()()1313022e ϕϕ⎛⎫⎫⋅=-< ⎪⎪⎝⎭⎭所以存在01,12x ⎛⎤∈⎥⎝⎦使得()00x ϕ=,且当01,2k x ⎛⎫∈ ⎪⎝⎭时,()0k ϕ>, ………………12分 当()0,1k x ∈时,()0k ϕ<, 所以()k ϕ在01,2x ⎛⎫⎪⎝⎭上单调递增,在()0,1x 上单调递减.因为17028h ⎛⎫=>⎪⎝⎭,()10h =, 所以()0h k ≥在1,12⎛⎤⎥⎝⎦上恒成立,当且仅当1k =时取得“=”.综上,函数()f x 在[]0,k 上的最大值()31kM k e k =--. ………………14分。

西安市第一中学2012-2013学年度第二学期期中高三年级数学(理科)试题 命题人:白恒兴一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集为{}{}06,101,2=-+∈=≤≤∈==x x R x B x N x A R U ,则右图中阴影表示的集合为( )A.{}2 B .{}3 C .{}2,3- D .{}3,2-2.复数满足(1)2z i i +=,则复数Z 的实部与虚部之差为( )A .2-B .2C .1D .0 3 .函数()e 2x f x x =+-的零点所在的一个区间是( )A.()2,1--B.()1,0-C.()0,1D.()1,24. 已知圆O:224x y +=,直线l 过点(1,1)P ,且与直线OP 垂直,则直线l 的方程为( ) A. 340x y +-= B. 10y -= C. 0x y -= D. 20x y +-=5.为了得到函数sin(2)3y x π=-的图像,只需将函数sin(2)6y x π=+的图像( ) A.向左平移4π个长度单位 B. 向右平移4π个长度单位 C.向左平移2π个长度单位 D. 向右平移2π个长度单位 6.若,,a b c 是空间三条不同的直线,,αβ是空间两个不同的平面,则下列命题中,逆命题不正确的是( )A .当c α⊥时,若c β⊥,则//αβB .当b α⊂时,若b β⊥,则αβ⊥C .当,b a αα⊂⊄且c 是a 在α内的射影时,若b c ⊥,则a b ⊥D .当b α⊂且c α⊄时,若//c α,则//b c7.已知,a b ∈R ,下列四个条件中,使“a b >”成立的必要而不充分的条件是( )A .1a b >-B .1a b >+C .||||a b >D .22a b>8.已知,x y 满足0,404,x y x y x -≥⎧⎪+-≥⎨⎪≤⎩,则3z x y =+的最小值为( )A.6B.8C.12D.159. 已知2()2f x x x =-,()2(0)g x ax a =+>,若对任意1[1,2]x ∈-,都存在0[1,2]x ∈-,使10()()g x f x =,则a 的取值范围是( ) A.1(0,]2 B.1[,3)2C.[3,)+∞D.(0,3] 10.已知函数⎪⎩⎪⎨⎧≤<-≤≤-+=)10(,1)01(,1)(2x x x x x f , 则⎰-=11)(dx x f ( ) A.124π-+ B. 421π+ C. 41π+ D.122π-+ 二、填空题(每小题5分,共25分)11.某大学对1000名学生的自主招生水平测试成绩进行统计,得到不合格的成绩的频率为0.4,则合格的人数是 .12. 阅读如图程序框图,如果输出的函数值在区间11[,]42 内,则输入的实数x 的取值范围是___________.13. 一个几何体的三视图如图所示(长度单位:cm ),则此几何体的体积是__________㎝3.14.下列四种说法中,①命题“存在2,0x R x x ∈->”的否定是“对于任意2,0x R x x ∈-<”;②命题“p 且q 为真” 是“p 或q 为真”的必要不充分条件;③已知幂函数()f x x α=的图象经过点,则(4)f 的值等于12④某路公共汽车每7分钟发车一次,某位乘客到乘车点的时刻是随机的,则他候车时间超 过3分钟的概率是47. 说法正确的序号是 . 15.选做题:A.对任意x R ∈,2234x x a a -++≥-恒成立,则a 满足________.B.在极坐标系中,点(2,)6P π-到直线l :sin()16πρθ-=的距离是_______.C.如图,点P 在圆O 直径AB 的延长线上,且PB =OB =2,PC 切圆O 于点C ,CD ⊥AB 于点D ,则CD =________.三、解答题:(本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤)16.(本题满分12分)在ABC ∆中,角,,A B C 的对边分别是,,a b c ,点(,)a b 在直线(sin sin )sin sin x A B y B c C -+=上.(1)求角C 的值;(2)若4ab =,求ABC ∆的面积.17. (本题满分12分)已知数列{}n a 的首项为11=a ,其前n 项和为n S ,且对任意正整数n 有:n 、n a 、n S 成等差数列.(1)求证:数列{}2++n S n 成等比数列;(2)求数列{}n a 的通项公式.18. (本题满分12分)如图,四棱锥P -ABCD 中,底面ABCD 是矩形,PA ⊥底面ABCD ,PA =AB =1,AD =3, 点F 是PB 的中点,点E 在边BC 上移动.(1)点E 为BC 的中点时,试判断EF 与平面PAC 的位置关系,并说明理由;(2)求证:无论点E 在BC 边的何处,都有PE AF ⊥;(3)当BE 为何值时,PA 与平面PDE 所成角的大小为45°.19. (本题满分12分)已知232()816(),()254f x x x k k R g x x x x =+-∈=++.(1)求()g x 的极值;(2)[]12123,3,()().x x f x g x k ∈-≤若对任意、都有成立,求的取值范围20. (本题满分13分)一次考试中共有8道选择题,每道选择题都有4个选项,其中有且只有一个是正确的. 评分标准规定:“每题只选一个选项,答对得5分,不答或着打错得0分”. 某考生已确定 有5道题的答案是正确的,其余题中,有一道题都可判断两个选项是错误的,有一道题可 以判断一个选项是错误的,还有一道题因不理解题意只好乱猜.(1)求出该考生得40分的概率;(2)写出该考生所得分数X 的分布列,并求出X 数学期望.21. (本题满分14分)如图,已知抛物线24x y =的焦点为F ,过焦点F 且不平行于x 轴的动直线l 交抛物线于A ,B 两点,抛物线在A 、B 两点处的切线交于点M .(Ⅰ)求证:A ,M ,B 三点的横坐标成等差数列;(Ⅱ)设直线MF 交该抛物线于C ,D 两点,求四边形ACBD 面积的最小值.高三第二学期期中考试数学(理)参考答案一、选择题(每小题5分,共50分)题号 1 2 3 4 5 6 7 8 9 10 答案 A D C D B B A B A B二、填空题(每小题5分,共25分)11.600 12.[2,1]-- 13.2243 14.③④ 15A.[1,5]-1 C.三、解答题(共75分)16.(本题满分12分)解:⑴因点(,)a b 在直线(sin sin )sin sin x A B y B c C -+=上,所以(sin sin )sin sin a A B b B c C -+=,……………..2分由正弦定理,得22()a a b b c -+=,即222a b c ab +-=,……..4分 由余弦定理,得2221cos 22a b c C ab +-==,……………6分又(0,)C π∈,所以060C =………………8分⑵01sin 602S ab ==………………12分17.(本题满分12分)解:⑴因对任意n N +∈有,,n n n a S 成等差数列,所以2n n a n S =+……2分又当2n ≥时,1n n n a S S -=-,所以12()n n n S S n S --=+,………4分即122(12)n n S n S n -++=+-+,又1124S ++=,所以{}2++n S n 成以4为首项、2为公比的等比数列……………6分 ⑵由⑴得112422n n n S n -+++=⨯=,所以122n n S n +=--当2n ≥时,11(22)(212)21n n n n n n a S S n n +-=-=----+-=- 又11a =满足此式,所以21n n a =-……………………12分(或把122n n S n +=--代入2n n a n S =+得通项n a 也可)18.(本题满分12分)解:⑴当E 是BC 中点时,因F 是PB 的中点,所以EF 为PCB ∆的中位线, 故EF//PC ,又因PC ⊂面PAC ,EF ⊄面PAC ,所以EF//面PAC ……4分⑵证明:因PA ⊥底面ABCD ,所以DA ⊥PA ,又DA ⊥AB ,所以DA ⊥面PAB , 又DA//CB ,所以CB ⊥面PAB ,而AF ⊂面PAB ,所以AF CB ⊥, 又在等腰三角形PAB 中,中线AF ⊥PB ,PB CB=B ,所以AF ⊥面PBC. 而PE ⊂面PBC ,所以无论点E 在BC 上何处,都有PE AF ⊥………8分 ⑶以A 为原点,分别以AD 、AB 、AP 为x\y\z 轴建立坐标系,设BE m =, 则(0,0,1)P,D ,(,1,0)E m ,设面PDE 的法向量为(,,)n x y z =,由00PE n PD n ⎧⋅=⎪⎨⋅=⎪⎩,得00mx y z z +-=⎧⎪⎨-=⎪⎩,取(1,3,n m =-,又(0,0,1)AP =, 则由0cos ,sin 45PA n ==,解得m =故当BE =时,PA 与面PDE 成045角……………12分(前2问也可以用空间向量解答) 19.(本题满分12分)解:(1)32'22()254,()61040,13g x x x x g x x x x =++=++==--或,……2分 由单调性即得()g x 极大值为(1)1,g -=-()g x 极小值为228().327g -=-……………………6分 (2)[]12123,3,()()x x f x g x ∀∈-≤、都有成立,即[]max min 3,3()()f x g x -≤上,(3)111,(3)21,g g =-=-min max ()21,()(3)120,g x f x f k ∴=-==-12021,k ∴-≤-141,[141,)k k ≥∈+∞即…………………12分20.(本题满分13分)解:⑴其余3道题中,各题答对的概率分别为12,13,14. 故得40分的概率为111123424P =⨯⨯=………6分 ⑵X 的取值为25、30、35、40…………………8分 1111(25)(1)(1)2344P X ==⨯-⨯-=, 12311312111(30)23423423424P X ==⨯⨯+⨯⨯+⨯⨯=, 1111211131(35)2342342344P X ==⨯⨯+⨯⨯+⨯⨯=, 1(40)24P X ==. 分布列(略) 111113652530354030.442442412EX =⨯+⨯+⨯+⨯=≈………13分21.(本题满分14分)解:(Ⅰ)由已知,得(0,1)F ,显然直线AB 的斜率存在且不为0,则可设直线AB 的方程为1y kx =+(0k ≠),11(,)A x y ,22(,)B x y , 由24,1x y y kx ⎧=⎨=+⎩消去y ,得2440x kx --=,216160k ∆=+>. 124x x k +=,124x x =-…2分由24x y =,得214y x =,所以'12y x =,直线AM 的斜率为112AM k x =, 所以,直线AM 的方程为1111()2y y x x x -=-,又2114x y =, 所以,直线AM 的方程为 112()x x y y =+ ①………………4分 同理,直线BM 的方程为 222()x x y y =+ ②………………5分②-①并据12x x ≠得点M 的横坐标122x x x +=, 即A ,M ,B 三点的横坐标成等差数列.………………………………7分 (Ⅱ)由①②易得y=-1,所以点M 的坐标为(2k,-1)(0k ≠). 所以212MF k k k ==--,则直线MF 的方程为11y x k=-+………………8分设C(x 3,y 3),D(x 4,y 4), 由24,11x y y x k ⎧=⎪⎨=-+⎪⎩消去y ,得2440x x k +-=, 216160k ∆=+>344x x k+=-,344x x =-. …………………………9分又||AB ==24(1)k ==+.…………………………….10分||CD ==214(1)k==+. …………………12分 因为1MF AB k k ⋅=-,所以AB CD ⊥, 所以,2222111||||8(1)(1)8(2)322ACBD S AB CD k k k k=⋅=++=++≥, 当且仅当1k =±时,四边形ACBD 面积的取到最小值32.…………14分。

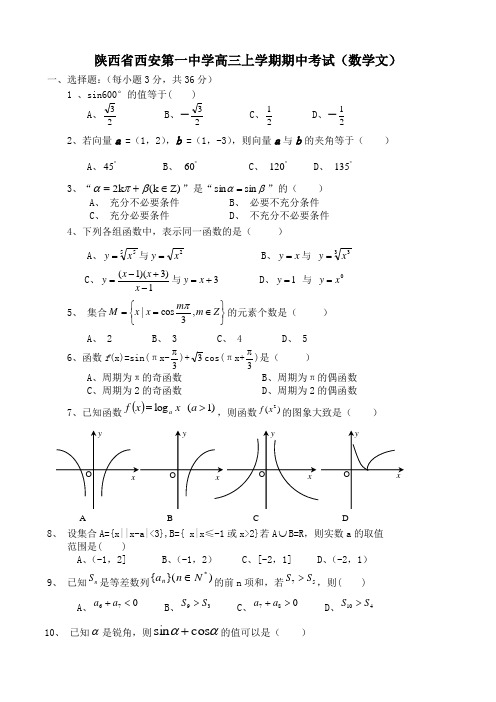
陕西省西安第一中学高三上学期期中考试(数学文)一、选择题:(每小题3分,共36分) 1 、sin600°的值等于( )A 、23B 、-23 C 、21D 、-212、若向量a =(1,2),b =(1,-3),则向量a 与b 的夹角等于( )A 、︒45B 、 ︒60C 、 ︒120D 、 ︒135 3、“)Z k (2k ∈+=βπα”是“βαsin sin =”的( )A 、 充分不必要条件B 、 必要不充分条件C 、 充分必要条件D 、 不充分不必要条件 4、下列各组函数中,表示同一函数的是( )A 、55x y =与2x y =B 、x y =与 33x y =C 、1)3)(1(-+-=x x x y 与3+=x y D 、1=y 与 0x y =5、 集合⎭⎬⎫⎩⎨⎧∈==Z m m x x M ,3cos |π的元素个数是( ) A 、 2 B 、 3 C 、 4 D 、 5 6、函数f (x)=sin(πx-3π)+3cos(πx+3π)是( )A 、周期为π的奇函数B 、周期为π的偶函数C 、周期为2的奇函数D 、周期为2的偶函数7、已知函数())1(log >=a x x f a ,则函数)(2x f 的图象大致是( )8、 设集合A={x||x-a|<3},B={ x|x ≤-1或x>2}若A ⋃B=R ,则实数a 的取值范围是( ) A 、(-1,2] B 、(-1,2) C 、[-2,1] D 、(-2,1) 9、 已知nS 是等差数列)}({*N n a n ∈的前n 项和,若57S S >,则( )A 、76<+a a B 、39S S > C 、87>+a a D 、410S S >10、 已知α是锐角,则ααcos sin +的值可以是( )A B D CA 、 31B 、 32C 、 34D 、 3511、 为了得到函数3lg 10x y +=的图像,只需把函数lg y x =的图像上所有的点( )A 、向左平移3个单位长度,再向上平移1个单位长度B 、向右平移3个单位长度,再向上平移1个单位长度C 、向左平移3个单位长度,再向下平移1个单位长度D 、向右平移3个单位长度,再向下平移1个单位长度12、 设A 、B 、C 是△ABC 的三个内角,且A tan 、B tan 是方程035x x 2=+-的两个实根,那么△ABC 是 ( ) A 、锐角三角形 B 、等腰直角三角形 C 、钝角三角形 D 、以上均有可能二、填空题:(每小题4分,共 13、 命题“若b a ,都是偶数,则b a +是偶数”的否命题...是 。

西安市第一中学2011—2012学年度第一学期期中高三年级数学((理科)试题一、选择题:(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1. 设集合22{||cossin |,}M y y x x x R ==-∈,{|||1xN x i=<,i 为虚数单位,x ∈R },则MN 为()A.(0,1) B 。
(0,1] C 。
[0,1) D 。
[0,1] 【答案】D【KS5U 解析】由22cossin cos2y x x x =-=,所以22{||cos sin |,}M y y x x x R ==-∈{}|01y y =≤≤,由1:11xx x i=<-<<得,所以{|||1x N x i=<,i 为虚数单位,x ∈R }={}|11x x -<<,所以MN ={}|01x x ≤≤,因此选D 。
2。
从甲乙两个城市分别随机抽取16台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲乙两组数据的平均数分别为x 甲,x 乙,中位数分别为m 甲,m 乙,则A.x x <甲乙,m 甲>m 乙B .x x <甲乙,m 甲<m 乙C .xx >甲乙,m 甲>m 乙D .xx >甲乙,m 甲<m 乙【答案】B【KS5U 解析】根据平均数的概念易计算出乙甲x x<,又2022218=+=甲m ,2923127=+=乙m ,故选B.3. 已知函数(3)5(1)()2(1)a x x f x ax x-+≤⎧⎪=⎨>⎪⎩是R 上的减函数,则a 的取值范是( )A .(0,3)B .(0,3]C .(0,2)D . (0,2]【答案】D【KS5U 解析】因为函数(3)5(1)()2(1)a x x f x ax x-+≤⎧⎪=⎨>⎪⎩是R 上的减函数,所以3020(3)52a a a a -<⎧⎪>≤⎨⎪-+≥⎩,解得0<a 2,所以选D 。
陕西省西安市2013届高三第一次质检数学(理)试题本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
全卷满分150分,考试时间120分钟。
第I 卷 (选择题共50分)一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.若向量(23),(47),BA CA ==,,则BC =A .(-2,-4)B .(3.4)C .(6,10)D .(-6.-10) 【答案】A【解析】因为(23),(47),BA CA ==,,所以()2,4BC BA AC =+=--.2.设集合{}|3213A x x =-≤-≤,集合B 为函数1(1)y g x =-的定义域,则AB =A .(1,2)B .[l ,2]C .[1.2)D .(1,2] 【答案】D【解析】集合{}{}|3213|12A x x x x =-≤-≤=-≤≤,集合B 为函数1(1)y g x =-的定义域,所以{}|1B x x =>,所以A B =(1,2]。
3.复数z 满足:(z -i )(1-i )=2.则z=A .一l -2iB .一1十2iC .1—2iD .1+2i【答案】D【解析】设()z a bi a b R =+∈、,因为(z -i )(1-i )=2,所以 ()()(1)1-12a bi i i a b a b i +--=+-++-=,1=21-1=02a b a a b b +-=⎧⎧⎨⎨+-=⎩⎩所以,解得:,所以12z i =+。
4.右图是一个算法的流程图,最后输出的W=A .12B .18C .22D .26【答案】C【解析】开始循环:21,S T S =-=≥不满足S 10,T=T+2=3;再次循环:28,S T S =-=≥不满足S 10,T=T+2=5;再次循环:217,S T S =-=≥满足S 10,此时输出的=17+5=22W S T =+,因此选C 。
西安市第一中学2012-13年度第一学期期中考试 高一数学(必修1)试题一.选择题(本大题共12小题,每小题3分,共36分) 1.下列各项中,能组成集合的是( )(A )高一(1)班的好学生 (B )西安市所有的老人 (C )不等于0的实数 (D )我国著名的数学家2.满足条件{1}{1,2,3}M =的集合M 的个数是( )(A )4 (B )3 (C )2 (D )1 3.已知集合{(,)|2},{(,)|4}M x y x y N x y x y =+==-=,那么集合M N 为( )(A )3,1x y ==-(B )(3,1)- (C ){3,1}- (D ){(3,1)}- 4.各个图形中,不可能是函数y =f (x )的图象的是()5.与函数1+=x y 相同的函数是( )(A )112--=x x y (B)1+=t y (C)122++=x x y (D)2)1(+=x y6.函数211()21x x f x x x⎧+≤⎪=⎨>⎪⎩,则((3))f f =( )(A)15(B )3(C )23(D)1397.函数错误!未找到引用源。
的图像是( )8.函数1()ln(1)f x x =+的定义域为( )(A)[2,0)(0,2]- (B)(1,0)(0,2]- (C)[2,2]- (D)(1,2]- 9.数xx y 26ln +-=的零点一定位于如下哪个区间( )(A)()2,1 (B)()3,2 (C)()4,3 (D)()6,510.列函数的解析式和值域相同,但其定义域不同,则称这些函数为“同族函数”,例如函数2x y =,[]2,1∈x 与函数2x y =,[]1,2--∈x 即为“同族函数”.请你找出下面哪个函数解析式也能够被用来构造“同族函数”的是 ( )(A )x y = (B)x y 2= (C)3-=x y (D)x y 21log =11.设m b a ==52,且211=+ba ,则=m ( ) (A )10 (B )10 (C )20 (D )10012.给定函数①12y x =,②12log (1)y x =+,③|1|y x =-,④12x y +=,期中在区间()1,0上单调递减的函数序号是( )(A )①② (B )②③ (C )③④ (D )①④ 二.填空题(本大题共4小题,每小题3分,共12分)13.幂函数()x f 的图象经过点)41,2(则⎪⎭⎫⎝⎛21f = . 14.函数y =a x -1+1(a >0,且a ≠1)的图象恒过定点________.15.若函数2)1(2)(2+-+=x a x x f 在区间(-∞,4] 上是减函数,那么实数a 的取值范围是______.16.下列各式中正确的...有 .(把你认为正确的序号全部写上) (1)()[]212212-=--;(2)已知,143log <a则43>a ; (3)函数x y 3=的图象与函数x y --=3的图象关于原点对称; (4)函数21x y =是偶函数;三解答题(本大题5小题共计52分)17.(本小题满分10分)已知集合A ={x | 73<≤x }, B={x| 2< x <10}, C={x |x < a }. (1)求 (C )A R ∩B ; (2)若A C ⊆,求a 的取值范围.18.(本小题满分10分)计算:(1)20.52032527()()(0.1)3964π--++-;(2)8log 9log 5.12lg 85lg 21lg 278⋅-+-.19.(本小题满分10分)探究函数4(),(0,)f x x x x=+∈+∝的最小值,并确定相应(1)若124x x =,则1()f x 2()f x (请填写“>, =, <”号);若函数xx x f 4)(+=,(x>0)在区间(0,2)上递减,则在区间 上递增;(2)当x = 时,x x x f 4)(+=,(x>0)的最小值为 ;(3)试用定义证明xx x f 4)(+=,在区间(0,2)上单调递减.20. (本小题满分10分)已知函数()122-+-=ax x x f ,若()x f 在[]1,1-上的最大值为()g a ,求()g a 的解析式.21.(本小题满分12分)已知函数()log (1),()log (1)a a f x x g x x =+=-其中(0>a 且1≠a ),设=)(x h )()(x g x f -(1)求函数()h x 的定义域,判断()h x 的奇偶性,并说明理由; (2)若(3)2f =,求使()0h x <成立的x 的集合;(3)若]21,0[∈x 时,函数()h x 的值域是]1,0[,求实数a 的取值范围.附加题:(本大题10分不计入总分)已知函数()y f x =的定义域为R ,且对任意,a b R ∈,都有()()()f a b f a f b +=+,且当0x >时,()0f x <恒成立,证明:(1)函数()y f x =是R 上的减函数;(2)函数()y f x =是奇函数.二.填空题:(本大题有4小题,每小题3分,共12分)13______________ 14_____________ . 15__________ 16.___________.三解答题(本大题有5小题共52分)17.(本题10分)18. (本题10分)19. (本题10分)20. (本题10分)21. (本题12分)附加题:西安市第一中学2012-13年度第一学期期中考试 高一数学(必修1)参考答案仅供参考一.选择题(本大题有12小题,每小题3分,共36分) .CCDA B D B B B C A B(A )①② (B )②③ (C )③④ (D )①④ 二填空题(本大题有4小题,每小题3分,共12分) 13. 4 .14. (1,2)_ ____15. 3-≤a 16. 3 三解答题17.(本小题满分10分) 解(1) C 3|{<=x x A R 或}7≥x(C )A R ∩B ={ x ∣2<x<3或7≤x<10}........................5分(2) a ≥7........................10分 18.(本小题满分10分)计算:(1)原式=1.3)10(])43[(])35[(213235.02-++--- ………3分=310091635-++ ………4分=94100 ………5分(2)原式=27lg 8lg 8lg 9lg )2255821lg(⋅-⨯⨯ ………8分 =lg10-32………9分 =31………10分19.(本小题满分10分)解:(1) =,(2,+∞) (左端点可以闭) ……………… 2分(2)x=2时,y min =4 ………………… 5分 (3)设0<x 1<x 2<2,则f(x 1)- f(x 2)= )44()()4()4(21212211x x x x x x x x -+-=+-+ =211212121212444()()()x x x x x x x x x x x x ---+=- …………… 8分∵0<x 1<x 2<2 ∴x 1-x 2<0,0<x 1x 2<4 ∴x 1x 2-4<0 ∴f(x 1)-f(x 2)>0 ∴f(x 1)> f(x 2)∴f(x)在区间(0,2)上递减 …………… 10分20. (本小题满分10分)20.解:()()122-+--=a a x x f (3)1当1a ≤-时,()f x 在[]1,1- 上单调减,()()max 122f x f a ∴=-=-- … 5 分 2当11a -<<时,()f x 在[]1,a - 上单调增,在(],1a 上单调()()2max 1f x f a a ∴==-……………………7分3当1a ≥时,()f x 在[]1,1- 上单调增,()()max 122f x f a ∴==- …9分()222,11,1122,1a a g a a a a a --≤-⎧⎪∴=--<<⎨⎪-≥⎩……………………10分21.(本小题满分12分)解(1)定义域()1,1-又()()x h xxx x x h a a-=-+-=+-=-11log 11log ……………4分 (2)2=a()0,1,11011-∈∴<<-<⇒-<+x x x x x 又……………………8分 (3)()()()()()3121,0021,0121,0121121121log 11log ==⎪⎭⎫⎝⎛=⎥⎦⎤⎢⎣⎡>⎥⎦⎤⎢⎣⎡---=---=⎪⎭⎫ ⎝⎛---=-+=a h h x h a x x x x x x x x h a a得上单调递增又在时因此上单调递增在可知令ϕϕ ()()无解上单调递减在时当a h x h a ,1021,010=⎥⎦⎤⎢⎣⎡<<综上3=a ………………………………………………………12分附加题:(本大题10分不计入总分)附加题解答:证明:(1)设12x x >,则120x x ->,而()()()f a b f a f b +=+ ∴11221222()()()()()f x f x x x f x x f x f x =-+=-+< ∴函数()y f x =是R 上的减函数;(2)由()()()f a b f a f b +=+得()()()f x x f x f x -=+- 即()()(0)f x f x f +-=,而(0)0f =∴()()f x f x -=-,即函数()y f x =是奇函数。
西安市第一中学 2011-2012学年度第一学期期中高三年级 数学(理科)试题 一.选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.已知集合P={xx2≤1},M={a}.若P∪M=P,则a的取值范围是A.(-∞, -1] B.[1, +∞) C.[-1,1] D.(-∞,-1] ∪[1,+∞) 的共轭复数记作,若,为虚数单位,则=( ) A. B. C. D. 3.设集合,则为( ) A. B. C. D. 4.已知是上的减函数,那么的取值范围是( ) A. B. C. D. 5.函数的图象是( ) 6.为了得到函数y=的图象,可以将函数y=sin2x的图象( ) A.向右平移个单位长度 B.向右平移个单位长度 C.向左平移个单位长度 D.向左平移个单位长度 7.二项式的展开式中常数项是( ) A.-28 B.-7 C.7 D.-28 8.如图,用K、A1、A2三类不同的元件连成一个系统.当K正常工作且A1、A2至少有一个正常工作时,系统正常工作.已知K、A1、A2正常工作的概率依次为0.9、0.8、0.8,则系统正常工作的概率为( )A.0.960B.0.864C.0.720D.0.576 9.在平面直角坐标系中,由x轴的正半轴、y轴的正半轴、曲线以及该曲线在处的切线所围成图形的面积是( ) A. B. C. D. 10.已知函数,定义如下:当,( ) A有最大值1,无最小值B.有最小值0,无最大值 C.有最小值—1,无最大值D.无最小值,也无最大值 二.填空题(本大题共5小题,每小题5分,共25分) 11.已知 的一个内角为120o,并且三边长构成公差为4的等差数列,则的面积为_______________ 12.已知,且,则的值为 13. 在正三角形中,是上的点,,则 。
14.设函数,观察: 根据以上事实,由归纳推理可得: 当且时, . 15.选做题(请考生在以下三个小题中任选一题做答,如果多做,则按所做的第一题评阅记分) (1).(选修4—4坐标系与参数方程)极坐标方程分别为和的两个圆的圆心距为 ; (2).(选修4—5 不等式选讲)如果关于x的不等式的解集不是空集,则实数的取值范围是 ; (3).(选修4—1 几何证明选讲)如图,AD是⊙O的切线,AC是⊙O的弦,过C作AD的垂线,垂足为B,CB与⊙O相交于点E,AE平分,且AE=2,则AC=; 三.解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤) 16.(12分)在中,角所对的边分别为,且满足. 求角的大小; 求的最大值,并求取得最大值时角的大小. 17.(12分)已知数列满足, . 令,证明:是等比数列;(Ⅱ)求的通项公式。
市一中大学区2017-2018学年度第一学期期中考试高三数学试题(理)一、选择题(本大题共12个小题,每小题5分,共60分.)1.设集合{}|1A x x =>,集合{}2B a =+,若A B φ=,则实数a 的取值范围是( ). A .(,1]-∞-B .(,1)-∞-C .[1,)-+∞D .[1,)+∞【答案】A【解析】本题主要考查集合的运算. 因为{}|1A x x =>且A B 为空集, 所以21a +≤,即1a -≤,所以当1a -≤时,满足A 与B 的交集为空集的条件. 故选A .2.已知为i 虚数单位,若复数1i()1ia z a -=∈+R 的虚部为3-,则||z =( ). A .5B .C .D .【答案】C 【解析】因为1i (1i)(1i)1(1)i 111i 2222ia a a a a a z -----+-+====-+,所以132a+-=-,所以5a =,所以23i z =--,所以z 故选C .3.已知命题:p x ∀∈R ,12(2)0x -<,则命题p ⌝为( ). A .0x ∃∈R ,120(2)0x ->B .x ∀∈R,12(1)0x ->C .x ∀∈R ,12(1)0x -≥D .0x ∃∈R ,120(2)0x -≥【答案】C【解析】解:因为原命题为全称命题,所以原命题的否定是特称命题, 即命题p x ⌝∀∈R ,20x >,的否定是::p x ∃∈R ,20x ≤. 故选C .4.执行如图所示的算法框图,则输出的S 值是( ).A .1-B .23C .32D .4【答案】D【解析】i 1=,1S =-;i 2=,23S =;i 3=,32S =; i 4=,4S =;i 5=, 1S =-;;i 8=,4S =;i 9=,结束循环,输出S 的值是4.故选D .5.设55log 4log 2a =-,2ln ln33b =+,1lg5210c =,则a ,b ,c 的大小关系为( ). A .a b c <<B .b c a <<C .c a b <<D .b a c <<【答案】A【解析】解:∵13log 20a =<,112211log log 132b =>=,0.30110122c ⎛⎫⎛⎫<=<= ⎪ ⎪⎝⎭⎝⎭, ∴a c b <<.故选A .6.若函数()f x 满足1(1)()2f x f x +=,则()f x 的解析式在下列四式中只有可能是( ).A .2x B .12x + C .2x -D .12log x 【答案】C【解析】本题主要考查函数的解析式.由已知该函数具有性质1(1)()2f x f x +=,将此运用到四个选项中:A 项,1(1)2x f x ++=,1()24xf x =,不符合题意,故A 项错误; B 项,3(1)2f x x +=+,11()224x f x =+,不符合题意,故B 项错误;C项,(1)11(1)22()22x x f x f x -+-+==⨯=,符合题意,故C 项正确;D 项,12(1)log (1)f x x +=+,112211()log log 22f x x ==,故D 项错误. 故选C .7.函数e xy x=和图象是( ).A.B.C.D.【答案】C【解析】8.在区间[0,2]上随机取两个数x,y,则[0,2]xy∈的概率是( ).A.1ln22-B.32ln24-C.1ln22+D.12ln22+【答案】C【解析】本题主要考查微积分的基本定理和几何概型.由题意可将所求概率转化为图中阴影部分面积和正方形面积之比,故所求概率212222(ln)2d11ln2442xxS xPS+++====⎰阴影正方形.【注意有文字】故选C.9.设实数x,y满足22010210x yx yx y+-⎧⎪-+⎨⎪--⎩≤≥≤,则11yx--的最小值是().A .5-B .12-C .12D .5【答案】B 【解析】4000x y x y -+⎧⎪⎨⎪⎩≥≤≥所表示的区域如图所示 11y z x -=-表示区域中的点到点(1,1)的斜率, 故原点到点(1,1)的斜率最大. 故选B .10.若将函数π()2sin 23f x x ⎛⎫=+ ⎪⎝⎭的图象向右平移ϕ个单位,所得图象关于y 轴对称,则ϕ的最小正值是( ). A .5π12B .π3C .2π3D .5π6-【答案】A【解析】把该函数的图象右移ϕ个单位,所得图象对应的函数解析式为:π2sin 223y x ϕ⎛⎫=+- ⎪⎝⎭, 又所得图象关于y轴对称,则π3π22πk ϕ-=+,k ∈Z , ∴当1k =-时,ϕ有最小正值是5π12.故选A .11.设函数266,0()34,0x x x f x x x ⎧-+=⎨+<⎩≥,若互不相等的实数1x ,2x ,3x 满足123()()()f x f x f x ==,则123x x x ++的取值范围是( ).A .11,63⎛⎤⎥⎝⎦B .2026,33⎛⎫⎪⎝⎭C .2026,33⎛⎤⎥⎝⎦D .11,63⎛⎫⎪⎝⎭【答案】D 【解析】解:函数266,0()34,0x x x f x x x ⎧-+=⎨+<⎩≥的图象,如图,不妨设123x x x <<,则2x ,3x 关于直线3x =对称,故236x x +=, 且1x 满足1703x -<<; 则123x x x ++的取值范围是:12376063x x x -+<++<+, 即12311,63x x x ⎛⎫++∈ ⎪⎝⎭.故选D .12.已知定义在(0,)+∞上的函数()f x ,满足(1)()0f x >;(2)()()2()f x f x f x '<<(其中()f x '是()f x 是导函数,e 是自然对数的底数),则(1)(2)f f 的范围为( ).A .11,2e e 2⎛⎫⎪⎝⎭B .211,e e ⎛⎫⎪⎝⎭C .(e,2e)D .3(e,e )【答案】B【解析】构造函数()()e x f x g x =,(0,)x ∈+∞,则2()e ()e ()()()(e )e x x x xfx f x f x f x g x ''--'==,由已知()()f x f x '<得()0g x '>在(0,)+∞上恒成立,则函数()g x 在(0,)+∞上递增, 所以(1)(2)g g <,即2(1)(2)e ef f <,又因为()0f x >, 所以根据2(1)(2)e ef f <有2(1)e (2)e f f <,即(1)1(2)e f f <, 再构造函数2()()(e )x f x h x =,(0,)x ∈+∞,2242()(e )()2(e )()2()()(e )(e )x x x x fx f x f x f x g x ''⋅-'==,由已知()2()f x f x '<,所以()0h x '<在(0,)+∞,则函数()h x 在区间(0,)+∞上单调递减, 所以(1)(2)h h >,即24(1)(2)e ef f <,又因为()0f x >, 所以根据24(1)(2)e ef f <有24(1)e (2)e f f <,即2(1)1(2)e f f <,所以21(1)1e (2)e f f <<.故选B .二、填空题(本大题共4小题,每小题5分,共20分) 13.计算11130.7536170.027*********-⎛⎫+--= ⎪⎝⎭__________. 【答案】31【解析】原式1133316412590.33625697295-⎛⎫⨯- ⎪-⎝⎭⎛⎫=-+-+- ⎪⎝⎭3109913643553=-+-+- 31=.14.已知423401234(2x a a x a x a x a x =++++,则2202413()()a a a a a ++-+=__________. 【答案】1【解析】令1x =,得401234(2a a a a a =++++; 令1x =-,得401234(2a a a a a -=-+-+;两式相加得22024130123402413()()()()a a a a a a a a a a a a a a a ++-+=++++⋅++--444(2(2(1)1=⋅-=-=.15.一个类似杨辉三角形的数阵: 则第九行的第二个数为__________.18221891177115653139【答案】见解析【解析】解:观察首尾两数都是1,3,5,7,可以知道第n 行的首尾两数均为21n -, 设第(2)n n ≥行的第2个数构成数列{}n a , 则有323a a -=,435a a -=,547a a -=,,123n n a a n --=-,相加得232335(23)(2)(2)2n n a a n n n n +--=+++-=⨯-=- 23(2)23n a n n n n =+-=-+.因此,本题正确答案是:223n n -+.16.某班班会,准备从包括甲、乙两人的七名同学中选派4名学生发言,要求甲、乙两人中至少有1人参加,则甲、乙都被选中且发言时不相邻的概率为__________. 【答案】见解析【解析】解:22534475A A 1201A A 9401206==--.三、解答题:(共70分)17.(10分)已知函数2π()cos sin 02222f x x x x ϕϕϕϕ⎛⎫⎛⎫⎛⎫⎛⎫++++<< ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭的图像经过点π,13⎛⎫ ⎪⎝⎭.(1)求()f x .(2)在ABC △中,A 、B 、C 的对边为a 、b 、c ,a =,ABC S =△,角C 为锐角且π72126C f ⎛⎫-= ⎪⎝⎭,求C 边长. 【答案】见解析.【解析】解:(1)∵2()cos sin 222f x x x x ϕϕϕ⎛⎫⎛⎫⎛⎫=++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭1cos(2))2x x ϕϕ-+=++11)cos(2)22x x ϕϕ=+-++ π1sin 262x ϕ⎛⎫=+-+⎪⎝⎭,∵图象经过点π,13⎛⎫⎪⎝⎭,∴ππ1sin 21362ϕ⎛⎫⋅+-+= ⎪⎝⎭,即π1sin 22ϕ⎛⎫+= ⎪⎝⎭,即1cos 2ϕ=, ∵π02ϕ<<,∴π3ϕ=, ∴π1()sin 262f x x ⎛⎫=++⎪⎝⎭.(2)∵π17sin 21226Cf C ⎛⎫-=+= ⎪⎝⎭,∴2sin 3C =,∴cos C ==,∵112sin 223ABC S ab C b ==⋅=△, ∴6b =,∴2222cos 5362621c a b ab C =+-=+-=, ∴c =18.(12分)已知ABC △中,D 是BC 上的点,AD 平分BAC ∠,ABD △面积是ADC △面积的2倍. (1)求sin sin BC∠∠.(2)若1AD =,DC =BD 和AC 的长.【答案】见解析.【解析】(1)1sin 2ABD S AB AD BAD =⋅△∠,1sin 2ADC S AC AD CAD =⋅△∠, 因为2ABD ADC S S =△△,BAD CAD =∠∠,所以2AB AC =, 在ABC △中,由正弦定理得:sin sin AC AB B C =∠∠,所以sin 1sin 2B AC C AB ==∠∠. (2)设ADB θ=∠,则πADC θ=-∠. 由(1)知12AC b AB c ==,所以2c b =①,由CD =,所以BD =在ACD △中,由余弦定理,22121π)b θ=+-⨯-⎝⎭,即232b θ=+②,在ABD △中,由余弦定理,2122c θ=+-,即232c θ=-③, 由①②③得1b =,故1AC =.19.(12分)私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:(1)(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取2人进行追踪调查,求恰有2人不赞成的概率.(3)在(2)在条件下,再记选中的4人中不赞成...“车辆限行”的人数为ξ,求随机变量ξ的分布列和数学期望.频率【答案】见解析.【解析】(1)由表知年龄在[15,25)内的有5人,不赞成的有1人,年龄在[25,35) 内的有10人,不赞成的有4人,恰有2人不赞成的概率为:11122464442222510510C C C C C 424666622(2)C C C C 1025104522575P ξ==⋅+⋅=⋅+⋅==.(2) ξ的所有可能取值为:0,1,2,3,226422510C C 4515(0)C C 22575P ξ==⋅==,21112646442222510510C C C C C 41562410234(1)C C C C 1045104522575P ξ⋅==⋅+⋅=⋅+⋅==, 124422510C C 46124(3)C C 104522575P ξ==⋅=⋅==,所以ξ的分布列是:所以ξ的数学期望65E ξ=.20.(12分)已知在直角坐标系xOy 中,圆C参数方程为32cos 42sin x y θθ=+⎧⎨=-+⎩(θ为参数).(1)以原点为极点、x 轴正半轴为极轴建立极坐标系,求圆C 的极坐标方程. (2)已知(2,0)A -,(0,2)B ,圆C 上任意一点(,)M x y ,求ABM △面积的最大值. 【答案】见解析.【解析】(1)圆C 的参数方程为32cos 42sin x y θθ=+⎧⎨=-+⎩(θ为参数),所以普通方程为22(3)(4)4x y -++=,所以圆C 的及坐标方程为26cos 8sin 210ρρθρθ-++=. (2)点(,)M x y 到直线:20AB x y -+=的距离d ,ABM △的面积1π|||2cos 2sin 9|2924S AB d θθθ⎛⎫=⨯⨯=-+=-+ ⎪⎝⎭,所以ABM △的面积的最大值为9+21.(12分)已知函数()|3|f x x =+,()2|11|g x m x =--,若2()(4)f x g x +≥恒成立,实数m 的最大值为t . (1)求实数t .(2)已知实数x 、y 、z 满足22236(0)x y x a a 2++=>,且x y z ++的最大值是20t,求a 的值. 【答案】见解析.【解析】解:(1)根据题意可得(4)2|411|2|7|g x m x m x +=-+-=--,若2()(4)f x g x +≥恒成立, ∴2|3|2|7|x m x +--≥,即2(|3||7|)m x x ++-≤. 而由绝对值三角不等式可得2(|3||7|)2|(3)(7)|20x x x x ++-+--=≥, ∴20m ≤,故m的最大值20t =.(2)∵实数x 、y 、z 满足222236(0)x y z a a ++=>,由柯西不等式可得2222222)))]⎡⎤++⋅++⎢⎥⎢⎥⎣⎦≥,∴21)a x y z ⨯++≥(,∴x y z ++,再根据x y z ++的最大值是120t=,1, ∴1a =.22.(12分)已知二次函数2()1f x x ax m =+++,关于x 的不等式2()(21)1f x m x m <-+-的解集为(,1)m m +,(0)m ≠,设()()1f xg x x =-. (1)求a 的值.(2)()k k ∈R 如何取值时,函数()()ln(1)x g x k x ϕ=--存在极值点,并求出极值点. (3)若1m =,且0x >,求证:[(1)](1)22(*)n n n g x g x x +-+-∈N ≥. 【答案】见解析.【解析】(1)因为关于x 的不等式2()(21)1f x m x m <-+-的解集为(,1)m m +, 即不等式22(12)0x a m x m m ++-++<的解集为(,1)m m +, 所以22(12)()(1)x a m x m m x m x m ++-++=---, 所以222(12)(21)(1)x a m x m m x m x m m ++-++=-+++, 所以12(21)a m m +-=-+,所以2a =-.(2)由(1)得2()21()(1)111f x x x m mg x x x x x -++===-+---,所以()()ln(1)(1)(1)1mx g x k x x k x x ϕ=--=-+---的定义域为(1,)+∞, 所以222(2)1()1(1)1(1)m k x k x k m x x x x ϕ-++-+'=--=---,方程2(2)10x k x k m -++-+=(*)的判别式22(2)4(1)4k k m k m ∆=+---=+.①当0m >时,0∆>,方程(*)的两个实根为11x =<,21x >,则2(1,)x x ∈时,()0x ϕ'<;2(,)x x ∈+∞时,()0x ϕ'>,所以函数()x ϕ在2(1,)x 上单调递减,在2(,)x +∞上单调递增,所以函数()x ϕ有极小值点2x . ②当0m <时,由0∆>,得k <-k >,若k <-,则11x =<,21x =>,故(1,)x ∈+∞时,()0x ϕ'>,所以函数()x ϕ在(1,)+∞上单调递增.所以函数()x ϕ没有极值点,若k >11x =>,21x =>,则1(1,)x x ∈时,()0x ϕ'>;12(,)x x x ∈时,()0x ϕ'<;2(,)x x ∈+∞时,()0x ϕ'>,所以函数()x ϕ在1(1,)x 上单调递增,在12(,)x x 上单调递减,在2(,)x +∞上单调递增, 所以函数()x ϕ有极小值点2x ,有极大值点1x ,综上所述,当0m >时,k 取任意实数,函数()x ϕ有极小值点2x , 当0m <时,k >()x ϕ有极小值点2x ,有极大值点1x ,(其中1x =2x =.(3)因为1m =, 所以1()(1)1g x x x =-+-, 所以1122122412211C C C C C n n n n n n nn n n n n x x xx x xx x------=+⋅+⋅=+++, 令122412C C C n n n nn n n T x x x----=+++,则122412122412C C C C C C n n n nn n nn n n n n n n n T x x x x x x---------=+++=+++, 因为0x >,所以1222441221212C ()C ()C ()2(C C C )n n n n n n n n n n n n n n T x x x x x x --------=++++++=+++012102(C C C +C C C C )2(22)n n n nn n n n n n n -=+++++-=-,所以22n T -≥,即[(1)](1)22n n n g x g x +-+-≥.尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。